Heterogeneity of transcription factor binding specificity models within and across cell lines

Abstract

Complex gene expression patterns are mediated by the binding of transcription factors (TFs) to specific genomic loci. The in vivo occupancy of a TF is, in large part, determined by the TF's DNA binding interaction partners, motivating genomic context-based models of TF occupancy. However, approaches thus far have assumed a uniform TF binding model to explain genome-wide cell-type–specific binding sites. Therefore, the cell type heterogeneity of TF occupancy models, as well as the extent to which binding rules underlying a TF's occupancy are shared across cell types, has not been investigated. Here, we develop an ensemble-based approach (TRISECT) to identify the heterogeneous binding rules for cell-type–specific TF occupancy and analyze the inter-cell-type sharing of such rules. Comprehensive analysis of 23 TFs, each with ChIP-seq data in four to 12 different cell types, shows that by explicitly capturing the heterogeneity of binding rules, TRISECT accurately identifies in vivo TF occupancy. Importantly, many of the binding rules derived from individual cell types are shared across cell types and reveal distinct yet functionally coherent putative target genes in different cell types. Closer inspection of the predicted cell-type–specific interaction partners provides insights into the context-specific functional landscape of a TF. Together, our novel ensemble-based approach reveals, for the first time, a widespread heterogeneity of binding rules, comprising the interaction partners within a cell type, many of which nevertheless transcend cell types. Notably, the putative targets of shared binding rules in different cell types, while distinct, exhibit significant functional coherence.

Transcriptional regulation is mediated by the binding of transcription factors (TFs) to specific DNA elements in the genome (Jacob and Monod 1961; Busby and Ebright 1994). While the in vitro binding specificity of many human TFs has been determined, it is well recognized that the in vitro binding specificity of a TF is not sufficient to explain its condition-specific in vivo binding (Zinzen et al. 2009; Yáñez-Cuna et al. 2012). This realization has spurred investigations of additional determinants of in vivo binding, such as heterogeneity of a TF's binding motif (Hannenhalli and Levy 2002), broader sequence context and interposition dependence (Mathelier and Wasserman 2013), homotypic clusters of binding sites (Dror et al. 2015), cooperative binding of the TF with its partners (Wang et al. 2006; Liu et al. 2016), condition-specific chromatin context (Wang et al. 2006; Heintzman et al. 2009; Gheldof et al. 2010; Kumar and Bucher 2016), and local DNA properties (Dror et al. 2015; Kumar and Bucher 2016). While, overall, both local genomic and epigenomic features are deemed important in determining in vivo occupancy of a TF, recent reports suggest that in vivo binding of a TF can be accurately predicted based solely on the genomic signatures near the binding site without relying on the epigenomic context (Arvey et al. 2012; Dror et al. 2015); this is consistent with additional recent reports, showing that the epigenome itself is encoded by the genomic context (Benveniste et al. 2014; Whitaker et al. 2015).

Prior models of in vivo TF binding have shown that, counter-intuitively, the genomic context of a binding site effectively encodes the condition-specific in vivo binding specificity (Arvey et al. 2012; Mathelier and Wasserman 2013). This can be explained by the substantial plasticity of a TF's interaction with other TFs and the modular nature of TF binding co-operativity (Frietze and Farnham 2011). The availability of specific combinations of interacting TFs can then guide in vivo binding to specific loci where the binding sites of the interacting TFs are present in close proximity to each other, along with the availability of corresponding TFs (Hannenhalli and Levy 2002).

Previous sequence-based modeling of in vivo TF binding was performed in a cell-type–specific fashion (Arvey et al. 2012; Mathelier and Wasserman 2013). These cell-type–specific models exhibit substantial inter-cell-type heterogeneity, which is expected, given the variation in the availability of the potentially interacting TFs. In particular, Arvey et al. (2012) explicitly modeled potential interactions of the primary TFs with multiple additional cofactors, while general sequence properties were used as features by Mathelier and Wasserman (2013). These previous approaches, however, build a single model for a cell type, thus implicitly assuming a homogeneous cell-type–specific TF binding model. As such, previous models have not investigated intra-cell-type model heterogeneity. Intra-cell-type TF binding heterogeneity is expected for the same reasons as inter-cell-type heterogeneity. Moreover, in many instances, a binding specificity model trained in one cell type can predict a subset of in vivo binding in another cell type (Arvey et al. 2012), suggesting that binding models, or parts thereof, are shared across cell types.

The motivation of the current study is to evaluate the heterogeneity of sequence-based, cell-type–specific, in vivo TF binding models and the extent to which binding rules (submodels) are shared across cell types. We have developed an ensemble model-based approach (TRISECT) to reveal both cell-specific and cell-independent rules for the in vivo TF binding. Application of TRISECT to 23 TFs, each with genome-wide in vivo binding data in four to 12 cell types strongly suggests that the cell-type–specific binding rule for a TF consists of multiple submodels, a subset of which are shared across cell types, and points to shared functional underpinnings. This refinement to our understanding of the genomic context of in vivo binding specificity can facilitate future investigations of transcriptional regulation and its genetic determinants.

Results

TRISECT—Ensemble model of TF binding and the clustering of submodels across cell types

An illustration of the TRISECT analysis pipeline is presented by Figure 1A, and a brief description of the pipeline is provided below (for additional details see Methods).

Figure 1.

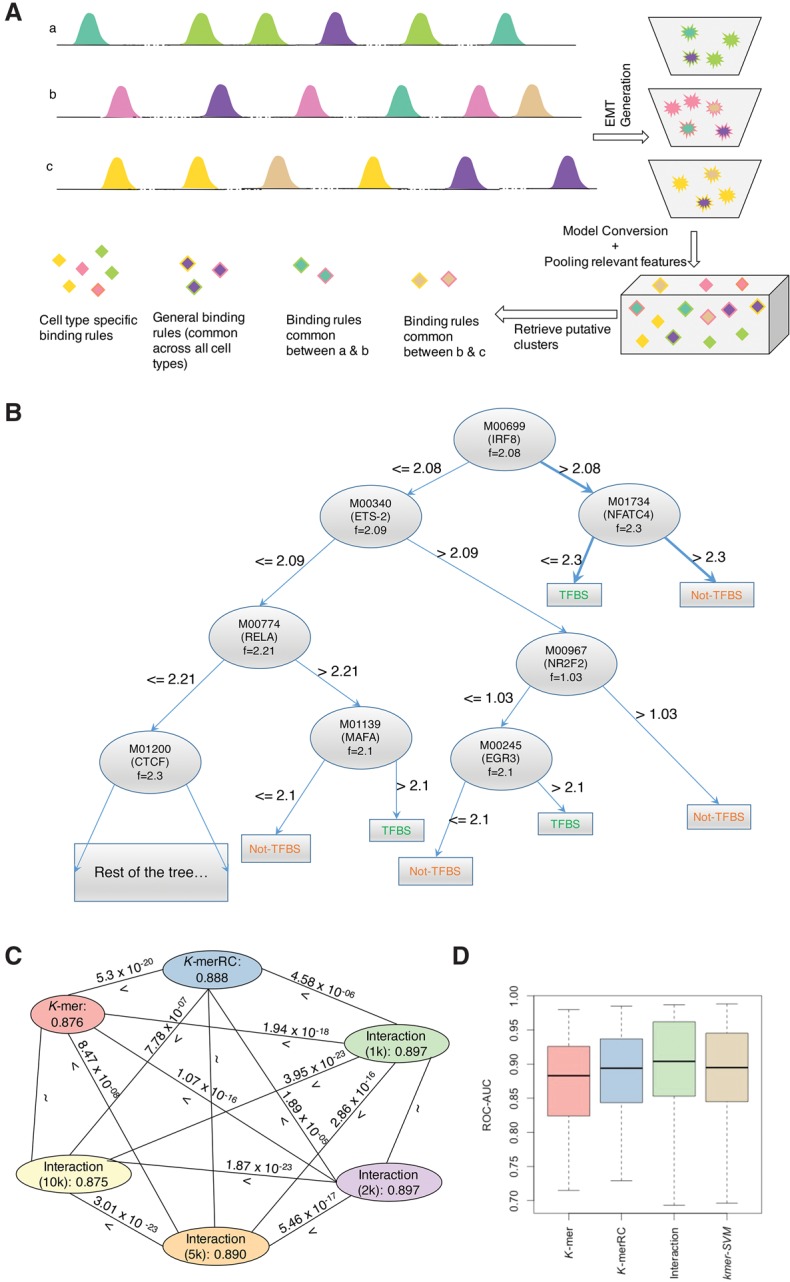
(A) Schematic of TRISECT pipeline. Colors indicate different binding rules or submodels and rows (a–c) represent different cell types. Green, pink, and yellow colors indicate cell-type–specific submodels. Each ensemble model (EMT) is represented by a bucket of submodels (top right). Stars and diamonds with the same color denote corresponding submodels and data points after transformation into reduced feature space, respectively. Each submodel is represented by a decision tree. The submodels across cell types are clustered. Cyan is common between cell types a and b, light brown is common between cell types b and c, and purple is common across all three cell types. (B) An example submodel taken from the Interaction model for CEBPB-GM12878. Each node in the tree is labeled with the TRANSFAC id, corresponding gene name, and the threshold at which the feature is split. Two binding rules are highlighted indicating TF binding and no TF binding. (C,D) Same color is used to denote the models using the same features. (C) Comparison of accuracy between all pairs of feature sets. Nodes are labeled with feature type and mean accuracy. Edges are labeled with “>” (greater) or “<” (less) sign and two-sided Wilcoxon P-value. (D) Accuracy (ROC-AUC) distribution of EMT for K-mer/K-merRC/Interaction (1 k) and those of kmer-SVM models.

Overview

As the first step, we developed an ensemble model (EMT) to discriminate a TF's in vivo bound genomic loci (foreground) from nonbound sites (background), balancing model complexity (number of submodels in the ensemble) against the cross-validation classification accuracy. Given a set of genome-wide loci, bound by a specific TF, we first identified sets of foreground and background (control) sequences. The foreground set consisted of 100-bp sequences centered at the ChIP-seq peak. For stringent background sequences, as done previously (Arvey et al. 2012), we used 100-bp regions ∼200 bp away from the peak location. We considered a variety of feature sets for discrimination (see below). The EMT model was trained using the Adaboost method where each submodel is a decision tree (Fig. 1B) built from a bootstrap sample (Friedman et al. 2000; Friedman 2002, 2008). Next, given a TF's EMT models for all cell types, each cell-type–specific submodel was represented by a point in a d-dimensional space, with d corresponding to the number of relevant features. We constructed clusters of the data points for a TF (representing the submodels across all cell types), using k-nearest neighbors algorithm (k-NN). The submodels within a cluster represent binding rules that are similar within or across the cell types.

EMT feature sets

We considered three feature sets for the 100-bp foreground and background sequences. The first feature set, K-mer, was composed of 6-mer frequencies within each 100-bp sequence (total, 4096 features). The second set, K-merRC, consisted of unified 6-mers and their reverse complement frequencies (total, 2080 features). The third feature set included the binding scores for 981 vertebrate TF motifs from the TRANSFAC 2011 database. We defined the models built from the third feature set as the Interaction model, as the features represent potential TFs that might contribute to the binding of the reference TF (the TF for which EMT was built). For Interaction models, we used four thresholds for motif match in the PWMSCAN tool (Levy and Hannenhalli 2002), where a threshold denotes the background match frequency—one hit in every 1 kb, 2 kb, 5 kb, and 10 kb.

EMT training

We applied TRISECT to 23 TFs, each with ChIP-seq data in four to 12 cell types (a total of 135 TF–cell pair EMTs; Supplemental Table S1). A TF was included in this study if (1) the TF has narrow-peak data for at least four cell lines with at least 4000 bound sites in each cell line, and (2) the TF has an established position weight matrix (PWM) in the TRANSFAC 2011 database. For other information about each TF including family names, see Supplemental Figure S1 for TF web-logos and Supplemental Table S2. EMTs were trained using 75% of the full data set and tested on the remaining 25%. Model details such as the number of submodels, model size, etc., are provided by Supplemental Table S3.

Each EMT includes multiple decision trees, and each path from root to leaf in an estimated decision tree submodel captures one binding rule that asserts how a combination of motifs and their binding affinities contribute to the reference TF's binding. As an illustrative example, Figure 1B shows an arbitrarily selected submodel of CEBPB in the GM12878 cell line. Two of the binding rules are “presence of IRF8 with score >2.08 and presence of NFATC4 with score <2.3”—when these rules are met, the reference TF, CEBPB, is likely to bound. Whereas “presence of IRF8 with score >2.08 and presence of NFATC4 with score >2.3” hinders CEBPB binding. Supplemental Note 1 and Supplemental Figure S2 include further interpretation of a sample submodel (decision tree), a summary of how the reference TF's motifs are distributed among the submodels, and a discussion of model robustness for various parameter choices.

EMT performance

Model accuracy was quantified using area under the receiver operating curve (ROC-AUC) on the 25% test set (Fig. 1C; Supplemental Fig. S2C). We compared the model performances, using a Wilcoxon test across 135 TF–cell type pairs for the six sets of EMTs (K-mer, K-merRC, and Interaction at four thresholds (i.e., Interaction (1 k), Interaction (2 k), Interaction (5 k), Interaction (10 k)) (Fig. 1C). We found that K-merRC significantly outperforms the K-mer model (two-sided Wilcoxon P-value 5.3 × 10⁻²⁰). This is consistent with the fact that TF binding occurs on double-stranded DNA and as such does not have directionality (except in relation with other interacting TFs). Therefore, unifying each k-mer with its reverse complement is more representative of the biological determinants of TF binding. Following this line of reasoning, PWMs can provide an even better abstraction of DNA binding specificity and as expected, the PWM-based models outperform the k-mer–based models (two-sided P-value 4.58 × 10⁻⁶), when comparing K-merRC to Interaction (1 k). Therefore, for submodel clustering and other downstream analyses we selected Interaction (1 k)–based EMT (heretofore referred to as Interaction model).

Comparison with previous model

Next, we compared the EMT model (using K-merRC and Interaction) with a previously published model based on support vector machine (kmer-SVM) (Arvey et al. 2012). In kmer-SVM, the investigators considered both k-mers and their reverse complements of size 8 with minimum matches of size 6. Applying the kmer-SVM pipeline to our data set, the resulting ROC-AUCs for all the TF–cell pairs are listed in Supplemental Table S4. Figure 1D suggests that the Interaction model performs favorably relative to kmer-SVM.

TRISECT reveals intra-cell-type heterogeneity and inter-cell-type sharing of binding rules across cell types

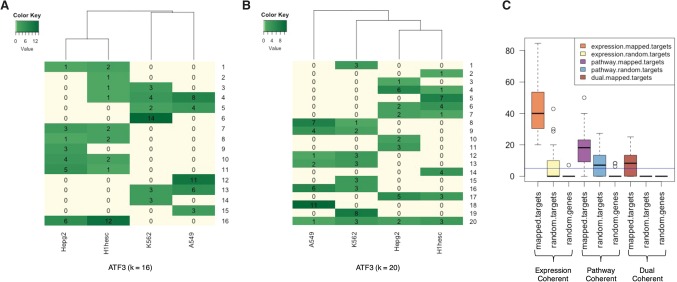
Given the favorable performance of EMT, and its architectural differences to kmer-SVM, we next assessed whether EMT was better able to exploit the heterogeneous binding rules across the genome, as dictated by different combinations of co-occurring and coregulated (i.e., potentially interacting) TFs. Conceptually, a “binding rule” refers to the specific combination of motifs (along with their importance) aiding in the binding of a reference TF. While a general binding rule may be difficult to state concisely, it can be operationally defined in terms of a collective ensemble of cell-type–specific binding rules. Each decision tree (a submodel) operationally defines a binding rule in terms of presence of specific motifs above/below a certain binding score. Furthermore, in general, the relative importance of features decreases with increasing depth of the node in the decision tree, with the first few levels contributing a substantial portion of the decision. Although a decision tree represents a statistical model for TF binding, by applying strict thresholds for motif scores and considering only the top few layers, in principal, a concise “binding rule” can be derived, albeit with some loss of information. For a specific TF and cell type combination, we captured the binding rules by a set of submodels (decision trees). Then to investigate commonality and uniqueness of binding rules for a TF across cell types, we pooled all submodels from all cell-specific EMTs, represented each submodel by feature importance, and clustered all submodels using the k-NN clustering algorithm. Next, we constructed a cluster–membership matrix mapping the number of submodels originating from different cell types within each cluster. As an example, Figure 2, A and B, shows the cluster–membership matrix for the TF ATF3 for cluster sizes 16 and 20. The matrices show both cell-type–specific (Fig. 2A, cluster 6) and ubiquitous (Fig. 2B, cluster 20) clusters. Examining the cluster mapping for all TFs (Supplemental Fig. S3), a wide range of patterns emerge. For certain TFs, many clusters tend to map to a single cell type, suggesting cell-type–specific binding modalities of these TFs (EP300, JUN), while other TFs have ubiquitously applicable binding rules, such as YY1 and TBP, suggesting cell-type–independent binding rules and, presumably, function. Importantly, many clusters consist of submodels from multiple, but not all, cell types. We ensured that inter-cell-type sharing of binding rules is not simply due to the shared binding loci across cell types (Supplemental Note 2; Supplemental Fig. S4). Subsequent analyses are based on k = 16; the reason for this choice is discussed in Supplemental Note 3.

Figure 2.

(A,B) Cluster membership matrix using a k-nearest neighbors algorithm (k-NN), where k = 16 (A) and k = 20 (B). Rows represent clusters and columns represent cell types. Each element in the matrix denotes the number of submodels in the cluster from each cell type. Some clusters consist of submodels from multiple cells (cluster 20 in B), while some others consist of submodels from a single cell type (cluster 6 in A). (C) Functional and expression coherence of submodel clusters: fraction of multi-cell-type clusters found to be coherent using k-NN. y-axis is the coherence percentage. Among the conditions (x-axis), mapped.targets denotes when genes are assigned to cluster based on TRISECT pipeline, random.targets indicates the clusters consisting of random genes among all targets, and random.genes indicates the cluster consisting of random genes. Here, expression coherence was defined using an expression threshold of log₂CPM ≥ 1; i.e., a gene is considered expressed when the log₂CPM ≥ 1. The horizontal line (blue color) denotes the coherence level of 5% of the total multi-cell-types.

Previous research (Worsley Hunt and Wasserman 2014) showed that so-called “zinger” motifs are enriched in ChIP-seq regions of several unrelated TFs. We conducted additional analysis to ensure that our clustering results are not affected by the zinger motifs (Supplemental Note 4; Supplemental Fig. S5). Moreover, it is possible that EMT can falsely yield multiple submodels, even in the absence of heterogeneity, and those submodels can be falsely clustered. By looking at the clustering tendency of the submodels, we examined the heterogeneity across submodels and found that it is possible to separate the submodels into distinct clusters (Supplemental Note 5; Supplemental Fig. S6B,C).

Next, we assessed the functional underpinning of shared binding rules across cell types (for details, see Methods). Specifically, we assessed whether two coclustered loci from different cell types (i.e., those obeying similar binding rules) are functionally associated relative to loci from the same cell type but belonging to different clusters, indicating that they are obeying different binding rules. We measured a cluster-specific score for each binding sequence and assigned each binding site in each cell type to one or more clusters. As per convention, we assigned each binding site to the nearest gene as a potential transcriptional target; 88% of the target genes were within 50 kb from the binding site (median distance, 4.5 kb) (Supplemental Fig. S6G). To assess functional coherence of clusters, we defined two metrics: expression coherence and pathway coherence. Expression and pathway coherence are measured as the fraction of gene-pairs in a cluster (regardless of cell type) that are respectively coexpressed, or belong to the same pathway. We assessed the significance of coherence using a two-sided Fisher's exact test. As shown in Figure 2C, ∼40% (expression coherence) and ∼18% (pathway coherence) multi-cell-type clusters show significantly higher (P-value <0.05) than the background (expectation is 5%), and 5.5% of the clusters show both significant expression and pathway coherence (called dual coherence). Applying a more stringent P-value threshold (<0.001), these coherent percentages are 35% (expression), 10% (pathway), and 4% (dual). Moreover, the expression and pathway coherence are highly correlated across clusters (Spearman correlation = 0.56, P-value = 0.02). As a negative control, we conducted the same set of tests for random clusters with the same size as the real clusters. In both cases, the coherence was no greater than the null expectation (Fig. 2C).

Taken together, these analyses support the existence of heterogeneous sets of TF binding rules governing the in vivo binding and suggest that a subset of rules are shared across cell types with functional implications.

The role of interaction partners in a TF's binding occupancy across cell types

By using 981 PWMs for a comprehensive set of vertebrate TFs as the basis for features, EMT implicitly incorporates the contributions of interaction partners in predicting in vivo binding of the reference TF. To quantify the contribution of putative interacting motifs, we repeated the EMT training and testing using only the PWMs corresponding to the reference TF. Individual TFs are represented by multiple motifs in the literature (ranging from one to eight, with a median of three) (Supplemental Table S2), many of which differ substantially from each other, suggesting potential functional implications (Bulyk et al. 2002; Hannenhalli 2008); e.g., 75% of the intra-TF PWM-pairs have <85% PWM similarity, in contrast to 99% of inter-TF PWM-pairs (Linhart et al. 2008). We refer to these motifs as the reference motifs, and, in contrast to the Interaction model, the EMT model utilizing only the reference motifs is referred to as the NonInteraction model. Supplemental Figure S7 shows the prediction accuracies for the Interaction and the NonInteraction models; the diagonal elements represent the cross-validation accuracies within a cell type, while the off-diagonal elements represent the accuracy when EMT is trained on one cell type (row) and tested on another (column). Comparison of the within-cell-type cross-validation accuracy for the Interaction and NonInteraction models (Fig. 3A; Supplemental Fig. S7) shows that the Interaction models have higher predictive accuracy than NonInteraction models, which is consistent with the expectation that in vivo binding of a TF relies on interactions among several TFs.

Figure 3.

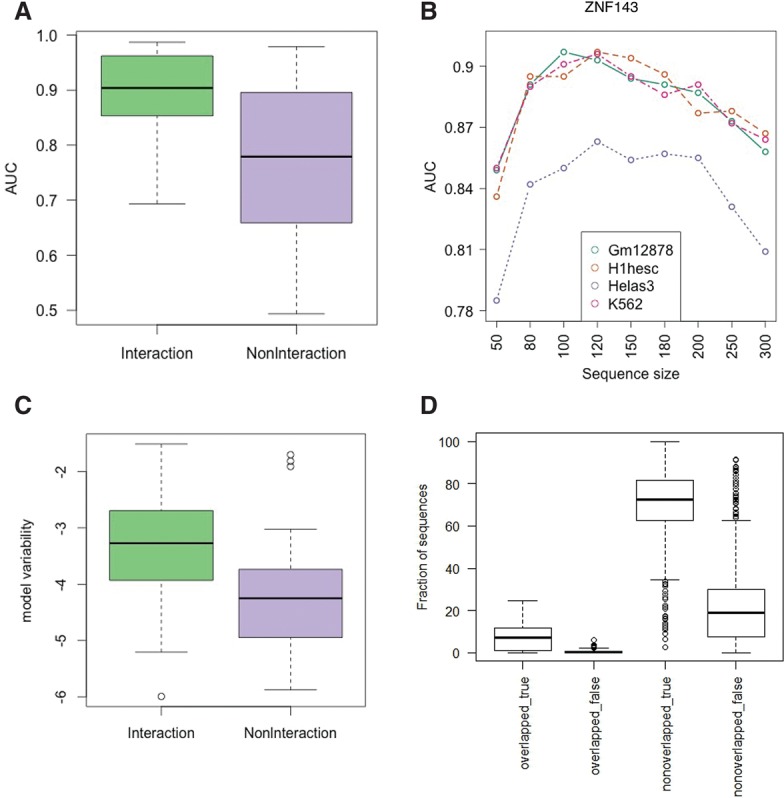
Association between the number of interaction partners and model accuracy. (A,C) Interaction and NonInteraction models are indicated with green and purple, respectively. (A) Comparison of cross-validation prediction accuracy for Interaction and NonInteraction models. (B) The trend of model accuracy with increasing sequence size for TF ZNF143 (selected arbitarily for illustration). Models from each cell line are indicated with different colors. (C) Comparison of model variability in log scale (variability of cross-cell-type performance for each model) for Interaction and NonInteraction models. (D) Distribution of the fraction of test sequences falling into one of the four categories: Overlapped_true denotes correctly and overlapped_false incorrectly classified sequences having at least 50% overlap between training sequences in one cell type and test sequences in another cell type. Nonoverlapped_true denotes correctly classified sequences that do not overlap with any sequence in the training set; nonoverlapped_false, incorrectly.

Next, we conjectured that in the Interaction model allowing for greater numbers of partners enables learning of more complex binding rules, leading to increased binding prediction accuracy. We therefore assessed the effect of the length of the region flanking the binding site on prediction accuracy (see Methods). We note that beyond 100 bp, due to narrowing the gap between the foreground and the background region, the discrimination accuracy is expected to decrease. Despite this, in several cases (Fig. 3B; Supplemental Fig. S8), the increase in ROC-AUC beyond 100 bp suggests that a larger context may be necessary in these cases to capture the binding rules. Nevertheless, we chose a sequence context of 100 bp to make our model comparable to the previously published kmer-SVM (Arvey et al. 2012).

For a given TF, we also quantified the variability of the model accuracy in different cell types (see Methods). We define cross-cell-type prediction accuracy as the performance of a model trained on one cell type and tested on another cell type. For these performance accuracy of models, we expect greater variability for the models relying on cell-type–specific interaction partners than the models only relying on reference motifs. Our analysis supports this expectation (Fig. 3C). However, the small variability in cross-cell-type prediction accuracy when using the NonInteraction model is likely due to the heterogeneity of the TF binding motif. We quantified the inter-motif divergence for each TF as either the number of annotated motifs, or the motif-divergence (defined over all motifs-pairs; see Methods). We found that the performance variability of NonInteraction models is positively correlated with both measures of motif divergence (Spearman correlation = 0.63, 0.67; two-sided P-value = 1.2 × 10⁻³, 6.3 × 10⁻⁴, respectively).

In Supplemental Figure S7, the off-diagonal elements for the Interaction model show higher cross-cell-type performance relative to the same elements for the NonInteraction model. This higher performance suggests that the binding “rules” are shared between cell types. We ensured that the high cross-cell-type performance is not simply due to overlaps in the genomic loci used to train and test the model between cell types; i.e., the genomic loci on which the model was trained in one cell type does not substantially overlap with the loci tested in another cell type. Overall, across TFs and cell type pairs, the fractional overlap in genomic loci ranges from 0% to 10%, with a mean and median of ∼4% (Fig. 3D). This suggests that it is the binding rule, independent of specific sequence instances, that is shared across cell types.

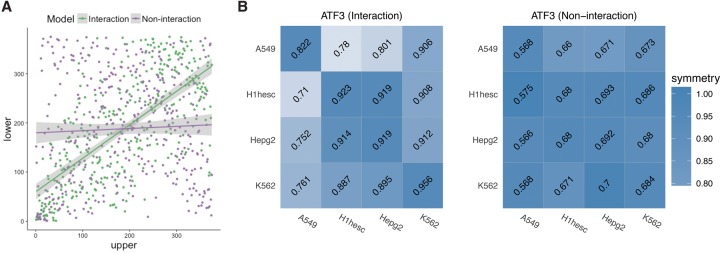
Furthermore, we found that when using the Interaction model, the cross-cell-type accuracy is symmetric. In other words, a high (low) accuracy in cell type Y using EMT trained on cell type X implies a high (low) accuracy in cell type X using the model learned from cell type Y. To demonstrate this symmetry, we normalized the off-diagonal elements of cross-cell performance matrices by the reference AUC by dividing each row by the corresponding diagonal ROC-AUC. As shown in Figure 4A, the lower and upper diagonal ranks are highly correlated (Spearman correlation of upper and lower triangle of resulting matrices is 0.68, two-sided P-value 9.5 × 10⁻⁵³), supporting our claim that the interaction-dependent (therefore genomic-context dependent) binding rules are shared across cell types. In stark contrast, there is a lack of symmetry in cross-cell prediction accuracy when the NonInteraction model is used (Spearman correlation = 0.04, two-sided P-value 0.4) (Fig. 4B; Supplemental Fig. S9).

Figure 4.

Comparing cross-cell-type performance matrix of Interaction and NonInteraction models. (A) Ranks of the normalized symmetry of upper and lower diagonal matrices of cross-cell-type performance. Interaction and NonInteraction models are colored green and purple, respectively. (B) In each matrix, the row represents the cell on which the model is trained, and the column represents the cell from which the test data are used. Diagonal elements are within-cell-type performance, and each matrix is color-coded according to the extent of the nondiagonal element symmetry. The symmetry is calculated by normalizing each row by the reference model (diagonal element).

In summary, our analyses suggest that the cell-type–specific TF interactions play a critical role in determining the cell-type–specific in vivo binding, and EMT reveals some of the interactions underlying the cell-type–specific binding of a reference TF.

TRISECT reveals putative cofactors providing insights into cell-specific biological roles of a TF

Our results so far suggest that cell-type–specific cofactors of a TF are a major driver of cross-cell-type in vivo binding variability. To gain further insights into the functional implications of cell-type–specific cofactors, for each reference TF we identified its cell-type–specific cofactors using the feature importance of the corresponding motif as estimated by the model. To minimize redundancy, we excluded motifs with substantially high co-occurrence frequency with at least one of the reference motifs (see Methods). To further minimize false positives, we assessed the enrichment of motif occurrence within the cell-specific ChIP-seq peaks of the reference TF relative to background and retained only those putative cofactor motifs that were significantly enriched (odds ratio > 1.2 and two-sided P-value <0.05; see Methods). The rationale for choosing 1.2 as the odds ratio threshold is discussed in Supplemental Note 6.

Several lines of evidence support TRISECT-identified cell-type–specific TF cofactors, referred to as putative cofactors. First, we showed that there exists an enrichment of protein–protein interactions (PPIs) among a reference TF and its corresponding cofactors compared with the PPIs among all motifs (Supplemental Table S7a). Additionally, the putative cofactors are enriched for either heterodimerizing TFs or for the TF family that the reference TF belongs to for ∼70% of all TF–cell pair cases (see Methods) (Supplemental Table S7b,c). The enrichment of the same family as that of the reference TF is consistent with the fact that TFs form dimers with other TFs preferably from the same family (Amoutzias et al. 2008; Dror et al. 2015). We also performed protein domain enrichment analysis (Supplemental Table S8) using the DAVID tool (Huang et al. 2009a,b) and found that >80% of enriched domains are involved in homo- or hetero-dimerization consistent with the findings from Supplemental Table S7.

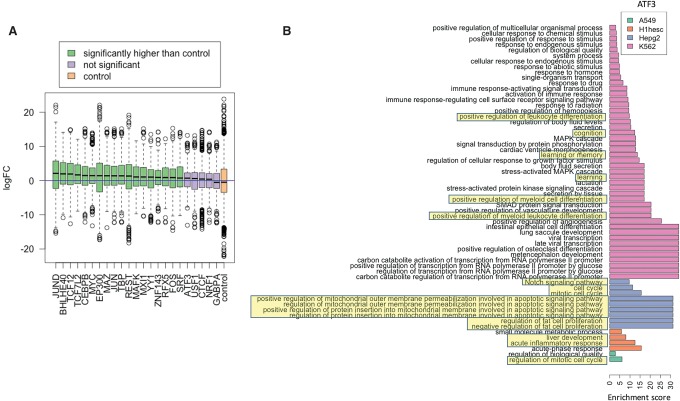
Second, we expect higher expression of putative cofactors in the cell types where they are identified as cofactors by our analysis. For each cofactor (excluding ubiquitous cofactors), we determined the log-fold difference in expression between the cell types where it is identified as a cofactor relative to cell types where it is not (see Methods). The distributions of log fold changes of the cofactors are compared with a control set of fold ratios, as presented in Figure 5A. For most TFs, the cofactors show significantly higher expression in the relevant cell types. This is not true only in five cases: ATF3, USF1, CTCF, NRF1, and GABPA. Among these five cases, CTCF is a known cell-type–independent TF; GABPA and NRF1 exhibit higher cell-type independence than other TFs as shown via an independence test.

Figure 5.

Functional validation of putative cofactors. (A) Each boxplot corresponds to all cofactors of a TF on the x-axis, and the y-axis denotes the log fold change (logFC) of the expression of cofactors in cell types where it is identified as a cofactor (i.e., relevant cells) versus cell types where it is not. The “blue” horizontal line at Y = 0 denotes no fold change. For a TF motif detected as a cofactor in n cell lines, and not in another m cell lines, we calculated log fold change (logFC) in the TF's expression between the two sets of cell lines. Identified cofactors have higher expression in the cell lines they are detected in (relevant cells). (B) Enrichment scores of GO terms obtained from GO analysis of cofactors in four cell types of ATF3 (selected arbitrarily). The known cell-type–specific biological roles are highlighted.

Third, we assessed whether the relationship between a reference TF and its cofactor is symmetric. For this assessment, we limit the analysis to 23 TFs, as for the current study we have models and associated cofactors only for these TFs. Specifically, we assessed whether a reference motif from one TF appears as a cofactor in the TFs whose reference motifs are also reported as cofactors in the first TF. For all X-Y TF pairs where one TF is deemed cofactor of the other and both TFs have available ChIP-seq data in the same cell line, we found that the correlation between the enrichment score of motif X in the binding sequences of TF-Y and vice versa is 0.41 (two-sided P-value = 5.19 × 10⁻¹⁴). This suggests a degree of codependence among TFs for their DNA binding.

Finally, for each TF's cell-type–specific cofactors, we performed biological process (BP) GO term enrichment analysis using the GOrilla tool (Eden et al. 2009) relative to all 981 motifs. We found significant differences in the assigned BP of a TF's cofactors among cell types. Remarkably, the BP can vary across cell types while still being functionally related to the reference TF. As an example, Figure 5B shows the enriched BP (false-discovery rate ≤ 10%) for ATF3 in four cell types. ATF3 is a stress-inducible TF involved in homeostasis regulating cell-cycle, apoptosis, cell adhesion, and signaling (Allen-Jennings et al. 2001; Tanaka et al. 2011). We found that ATF3 cofactors are enriched for cell cycle and proliferation functions in three out of four cell lines. In the stem cell line, the identified cofactors are involved in liver regeneration and inflammatory response, consistent with previous studies showing a direct link between ATF3 induction to liver injury and regeneration in mice (Chen et al. 1996; Su et al. 2002). Furthermore, enrichment of NOTCH and apoptotic signaling among cofactors in the HepG2 cell line is consistent with ATF3's role in glucose homeostasis and other primary liver functions (Allen-Jennings et al. 2001). Surprisingly, we find enrichment of cognition, learning, and memory among the TF cofactors in the leukemia cell line. Since leukemia is a cancerous cell line, nonnative gene expression is not unexpected (Lotem et al. 2004, 2005). While ATF3 is not known to play a direct role in neuronal function, a functionally and structurally related protein CREBBP has a well-documented role in neuronal activity and long-term memory formation in the brain (Mayr and Montminy 2001). This raises the possibility that either ATF3 has an unknown role in cognition or the same set of cofactors are involved in memory formation in conjunction with other TFs.

For other TFs, the enriched GO-terms are listed in Supplemental Table S9 (enrichment scores ranges from 1.22–93.75 with a median of 7.44, false-discovery rate cutoff of 10%). The corresponding discussion based on a review of the literature is provided in Supplemental Note 7; Supplemental Note 8 includes functions of example cofactors in various cells. This can serve as a resource for further investigation into the cell-type–specific binding and function of a broad array of TFs.

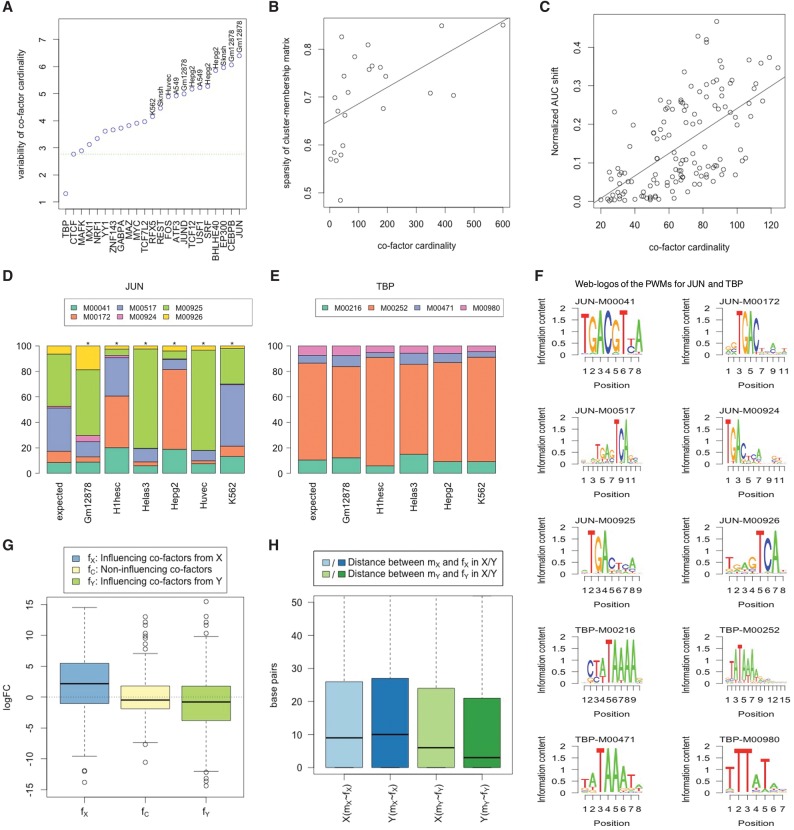
We noted substantial variability in the number of detected cofactors across cell types for a TF. Interestingly, a literature survey suggests that for the cell types for which the reference TF has a specific known function, the number of cofactors in that cell type is comparatively higher. For example, REST has well-known neuronal functions, and its binding sites in neurons exhibit lack of cognate RE1 motifs (Rockowitz et al. 2014), suggesting cofactor dependence. Consistently, SK-N-SH (brain cancer cell line) has the highest cofactor cardinality for REST. Similarly, JUN plays a specific role in hematopoietic differentiation, and we found that GM12878 (normal blood cell line) has the largest number of cofactors (Liebermann et al. 1998). We reasoned that a TF with greater cell-type–specific roles would exhibit greater variability in cofactor cardinality. For each TF, we measured the variability of its cofactor cardinality across cell types. As shown in Figure 6A, interestingly, TFs with ubiquitous and invariant roles such as TBP and CTCF have the least variable cofactor cardinality. Based on the trend shown in Figure 6A, we use the variability of cofactor cardinality as a proxy for the TF's cell type specificity. As an additional support, this proxy also correlates with the sparsity measure of cluster–membership matrix. Specifically, for each TF we computed the sparsity of its cluster–membership matrix (presented in Fig. 2A,B; Supplemental Fig. S3) using the Gini index (Handcock and Morris 1998; Hurley and Rickard 2009). Figure 6B shows that sparsity is positively correlated with the variability of cofactor cardinality (Spearman correlation = 0.66, two-sided P-value = 9.2 × 10⁻⁴ using k-NN).

Figure 6.

EMT model heterogeneity is associated with cell type specificity of cofactors. (A) The plot shows for each TF the variability of cofactor cardinality across cell types. Each point is labeled by cell type where the relevant TF has specific usage, based on the literature, and has the largest number of cofactors. TBP and CTCF are the most ubiquitous TFs. The green dotted horizontal line denotes the variability of cardinality for CTCF cofactors. (B) Sparsity of cell–membership matrix correlates with cofactor cardinality. (C) Normalized ROC-AUC difference of Interaction and NonInteraction models for a specific TF–cell type pair correlates with cofactor cardinality. (D,E) Motif usage for the reference TF in the NonInteraction models of different cells, for JUN and TBP as two extreme examples. y-axis denotes the feature importance of motif usage in the NonInteraction model. The sequence logos for the corresponding reference PWMs are presented in F. (G,H) f_X denotes the influencing cofactors of m_X in cell line X; f_Y, m_Y in Y. (G, left) Log fold change (logFC) between relevant and nonrelevant cell type for influencing cofactors of m_X; (middle) logFC for noninfluencing cofactors; (right) logFC between nonrelevant and relevant cell type for influencing cofactors of m_Y. (H) Genomic proximity of the motif-specific interaction partner with the motif. m_X∼f_X denotes the nearest genomic distances (in base pairs) from m_X motif to any cofactors in the set of f_X and so on.

We also assessed whether differences in prediction accuracy achieved by the Interaction model and the NonInteraction model for a particular TF–cell type pair may reflect the TF's cofactor dependence. We compared cofactor cardinality to the normalized distance between Interaction and NonInteraction model performance (AUC shift). As shown in Figure 6C, the AUC shift is positively correlated with cofactor cardinality (Spearman correlation = 0.65, two-sided P-value = 2.7 × 10⁻¹⁷).

Previous studies have found that the DNA sequence specificity of a TF can be influenced by its interactions with cofactors (Siggers et al. 2011; Slattery et al. 2011). Interestingly, a close inspection of the feature importance estimated by the NonInteraction EMT model shows that for different cell types the composition of utilized reference motifs varies. Figure 6, D and E, presents all cell-type–specific usage of JUN and TBP (see Supplemental Fig. S10 for other TFs); JUN shows significantly different binding specificity from the expected usage in different cell types (marked with asterisks, see Methods), while TBP does not. Notably, such diverse usage is observed using NonInteraction models, suggesting a cell-type–specific motif preference. In Figure 6D, M00925 and M00926 (for JUN) are almost identical (in reverse complement of each other), yet they show very different usage. Even though both PWMs have very similar distributions of scores over the same genomic regions, in most cases M00925 yields a slightly higher score than M00926, and once M00925 is selected by a model, M00926 is deemed as redundant and not considered as important further. Hence, they show dissimilar importance. However, in our downstream analysis for assessing contribution of cell-specific usage, none of them are selected as having cell-specific influence and thus have no impact on the analysis.

We further investigated the potential contribution of cell-type–specific cofactors in modulating the cell-type–specific motif usage for the reference TF. In this regard, we identified pairs of reference motifs (m_X & m_Y) having the most differential usage in cell types X and Y, respectively. For each such pair, we selected a set of candidate cofactors (f_X & f_Y) that could potentially aid the TF for cell-type–specific binding; we call f_X & f_Y “influencing cofactors” of m_X and m_Y, respectively. Next comparing the log fold change (logFC) of f_X & f_Y in cell type X versus Y (Fig. 6G) shows that the influencing cofactors have higher expression in relevant cell types. Moreover, the influencing cofactors are more proximal to the influenced motif in the relevant cell type (for details, see Methods) (Fig. 6H).

Taken together, cell-type–specific cofactors revealed by TRISECT are consistent with their cell-type–specific expression and function, which may be critical in modulating a TF's cell-type–specific biological function.

Discussion

In this study, we have presented a novel ensemble-based framework—TRISECT—to investigate intra-cell-type heterogeneity and inter-cell-type commonality of in vivo TF binding rules. To the best of our knowledge, this is the first study to comprehensively demonstrate that in vivo binding specificity rules are composed of multiple components, or submodels, many of which are shared across multiple cell types. Importantly, nonorthologous targets of binding sites across cell types governed by a shared binding submodel exhibit a greater functional and expression coherence than targets of binding sites in the same cell type that are governed by different binding rules. For each TF, TRISECT identified cell-type–specific cofactors that are supported by gene expression data and literature studies supporting their cell-type–specific function.

We chose Adaboost as our ensemble model due to its architectural advantages with respect to our ultimate goal of analyzing common and distinct binding rules, or submodels, across ensembles learned for each cell type. Boosting ensemble methods, including Adaboost, are designed to learn optimal tree submodels for successive reweighted bootstrap samples. This is in contrast to other ensemble methods, including the popular Random Forest (RF) approach, which seeks to increase variability of submodels by estimating weak submodels from unweighted bootstrap samples. Since our primary goal is to reveal model heterogeneity, we chose to cluster submodels generated by Adaboost rather than Random Forest's weak learners.

In terms of prediction accuracy, EMT compared favorably to the previously reported sequence-based discriminative model (kmer-SVM) (Arvey et al. 2012). Apart from the modeling approach, our study differs from that of Arvey et al. (2012) in several other aspects. The previous study compared the cell-type–specific models for only two cell types (GM12878 and K562), while we have investigated in depth the cell type specificity of TRISECT across four to 12 cell types for each TF. While the previous work primarily discusses cell type specificity and ubiquity of their models, by clustering the cell-type–specific submodels, our work investigates the extent of shared binding rules; cell type specificity and ubiquity are extreme cases thereof. In addition to the cell-type–specific variability in proximal cofactors, we investigated in much greater depth the cross-cell-type variability in the preferred motif for the reference TF. Together, these novel aspects of our study add to the knowledge of sequence information that specify a TF's in vivo binding in various cell types.

Another recent study (Dror et al. 2015) aimed at deciphering the determinants of in vivo occupancy of a TF showed that TF binding specificity is influenced by nearby homotypic sites (for the reference TF), the local nucleotide composition, and certain DNA physical properties. Moreover, the preferred in vivo binding in homotypic clusters was related to a preferred nucleotide composition, e.g., GC-rich for zinc finger TFs and AT-rich for homeodomain reference TFs, in the binding site flanking region. These previous findings are consistent with the fact that the cofactors identified by TRISECT are enriched for the same family of TFs as the reference TF and thus have similar preferences for nucleotide composition to the reference TF. In the previous work (Dror et al. 2015), the accuracy in discriminating bound versus unbound sequences after controlling for the presence of a putative site for the reference TF was modest (ROC-AUC ∼ 0.6). In contrast, we have shown that the motifs for the reference TF alone can discriminate bound sites from unbound control sites with ROC-AUC ∼ 0.78, suggesting that the reference TF is the most informative determinant of in vivo binding, which is indeed expected and was also observed by Pique-Regi et al. (2011). The additional power of discrimination comes either from the presence of cofactor motifs, as suggested before (Hannenhalli and Levy 2002; Arvey et al. 2012), or from nucleotide composition and other DNA physical properties (Dror et al. 2015). Interestingly, DNA flexibility measured by propeller twist (el Hassan and Calladine 1996) is highly dependent on GC content (Hancock et al. 2013), which in turn is related to motif composition, as we have noted. Overall, the three properties of nucleotide composition, DNA physical properties, and motif composition are interrelated. The specific advantage of an ensemble model based on motif composition is that apart from achieving favorable accuracy, it is functionally more interpretable and can provide insight into a TF's cell-type–specific functions.

Context-dependent function of a cis regulatory region requires binding of a specific combination of TFs. This modularity contributes to morphological evolution through changes in cis elements controlling transcription while avoiding the pleiotropic effects of a TF gene's expression change (Prud'homme et al. 2007). Shared submodels of TF binding rules across cell types, as revealed by TRISECT, may suggest shared history of cell types.

The ability of a TF to bind to diverse reference motifs and, in conjunction, interact with diverse combinations of cofactors serves to enhance its functional repertoire across contexts (Meijsing et al. 2009; Arvey et al. 2012). Our analyses reveal a cell-type–specific preference for the reference motif as well as the cell-type–specific interaction partners of a TF. We found the expression of cell-type–specific interaction partners to be higher in the cell types where they are expected to interact with the TF, and their function is consistent with the context based on the literature. Thus, our study provides further support for a TF's cell-type–specific functions and, more importantly, enables further investigation into the mechanisms underlying a TF's diverse cell-specific functions.

Methods

Data processing

We downloaded the ChIP-seq peaks for 23 TFs from ENCODE (Supplemental Table S1; The ENCODE Project Consortium 2013). For each TF we selected only those cell lines for which narrow-peak data were available. We chose the more stringent of the two criteria—top 5000 most significant peaks or FDR q-values <0.2—to select the binding sites. The criteria are reasoned by the availability of enough data to build a model and the backward compatibility of the previous method (Arvey et al. 2012). Notably, not all ENCODE data sets provide q-values, and in that situation, we generated the list of q-values from the given P-values using the qvalue package in R (http://github.com/jdstorey/qvalue). Relative to the center of ChIP-seq peaks, the DNA regions of length 100 bp were identified as the foreground. As negative control, we sampled flanking regions of 100 bp from 200 bp away from the positive sequences. Again, the choice for the size and location of foreground and background can be rationalized by the backward compatibility. In fact, choosing control sequences from near the foreground makes the modeling problem harder than when they are chosen from arbitrary locations in the genome. Moreover, control sequences overlapping with any peak were excluded. Due to the proximity of the negative examples, both foreground and background are expected to have similar GC composition (Arvey et al. 2012) and chromatin accessibility. However, we explicitly controlled for the GC composition using a sequence set balancing technique when comparing the foreground and the background (Whitaker et al. 2015). In the sequence set balancing, the GC percentage is divided into N bins (e.g., we choose N = 100). Then for both the foreground (F) and background (B) sets, the number of sequences falling into each bin are enumerated: F[i] & B[i] where i = 1 to N. Finally, in each bin min(F[i], B[i]) sequences are selected randomly from the foreground and background sets. This way each set of sequences will have similar distribution of GC composition. After sequence set balancing, we discarded any cell line resulting in fewer than 4000 sites. In our list of TFs, EP300 is nonsequence specific. Even so, EP300 is localized to the chromatin by interacting with other motifs. Like Arvey et al. (2012) we include EP300 specifically to reveal those putative interactions.

In addition to the 100-bp foreground and background, we also extracted another six sets of foreground and background of size 120, 150, 180 200, 250, and 300 bp. We keep increasing the size of foreground to check how much additional information was added to the model by the increased sequence size. Note that for all sequence sizes the middle point of the background does not vary; so as the sequence size is increased, the gap between foreground and background decreases.

Learning EMT (Ensemble model of TF binding)

We considered three types of feature set for the sequence specificity model: (1) K-mers, frequencies of 4096 6-mers in the 100-bp sequence; (2) K-merRC, frequencies of 2080 k-mer (k = 6) groups equating a k-mer and its reverse complement; and (3) Interaction (Lk), we obtained all 981 vertebrate positional frequency matrices (PFMs) from TRANSFAC 2011 as features. Each PFM was converted into PWMs, which is a log-likelihood matrix, by (1) adding a pseudocount of 0.2 for “C” and “G”, and 0.3 for “A” and “T” in line with human genome composition, (2) normalizing the frequencies to get probabilities for each base, (3) dividing each base probability by the background probabilities (0.2 for “C” and “G”, and 0.3 for “A” and “T”), and (4) taking the log of the probability ratio. The resulting PWMs were then used to get the motif matches using PWMSCAN (Levy and Hannenhalli 2002). Here, Lk refers to the PWM hit threshold (hit expected every L kb on average in the genome); we used L = 1, 2, 5, or 10. In particular, we use log(1/Lk) as the threshold value to call a PWM “match.” For instance, at L = 1, the expected frequency of matches is once every 1 kb, corresponding to a 20% chance of a match in a 100-bp region or its reverse complement. Previous research showed that clusters of homotypic “weak” binding sites are prevalent in regulatory regions (Gotea et al. 2010), and such a presence of multiple weak binding sites, called a homotypic cluster of binding sites, is preferred to single strong binding site (He et al. 2012). To mimic this binding affinity, from the output of PWMSCAN, we decided to use the sum of PWM-score (−log(match score)) for all matches as the feature value. However, we also collected the “maximum score” and “average score” of binding for each of the training sequences and measured their correlation with our feature value. The high correlations (0.8 and 0.87 respectively) suggest a minimal effect on downstream analysis and overall conclusions. Finally, we used the log sum of PWM-score to compensate for the skewed distribution of the number of binding sites for individual TFs.

We found that the model performance was better for the 1-k than the 2-k thresholds, and at much higher stringency, the model performance significantly deteriorates due to the sparsity of the matches (Supplemental Fig. S2C). Furthermore, we determined the feature importance of the motifs for each model of TF–cell pair at those four thresholds. For each TF–cell pair, we calculated the correlation of the feature importance based on the 1-k threshold with those based on other thresholds, i.e., three correlation values. Thus in total, we calculated 405 correlation measures for 135 TF–cell pairs. We found that 90% of those correlations are significant, ranging from 0.21–0.81 with a median of 0.52 indicating nonsignificant effects of the thresholds on the models. Considering the relative performance of the Interaction (1 k) model, in the subsequent analysis we use them as the representative Interaction model and refer to it as such.

We chose Adaptive boosting (Friedman 2002, 2008) as our composite model where each submodel within the ensemble is a decision tree, and each decision tree is constructed based on a bootstrap sample. We used the Adaboost framework implemented in R gbm package (https://cran.r-project.org/package=gbm). In the framework, Huber loss function is selected to reduce overfitting. We estimated the classification accuracy of the model based on the 25% held-out data set, while 75% of the data were used to build the cell-specific models. In Supplemental Note 1, we summarize the interpretation of a model and parameter choices.

Model conversion, Duda-Hart test, and Hopkins statistics

Each submodel is represented by a point in a d-dimensional space. Each dimension denotes a feature, and the value along the dimension indicates the importance of the feature for the submodel. Therefore, each model (consisting of multiple submodels) can be represented as a set of points in a d-dimensional space, where d ≤ number of features (981). For a model, the feature importance was measured using the prediction performance improvement for out-of-bag sample predictions. We modified the R implementation of gbm package (https://cran.r-project.org/package=gbm) for feature importance to accommodate the calculation for single tree or the submodel in question. In other words, we determined the contribution of a single tree (submodel) in prediction performance improvement using the same out-of-bag samples. We disregarded the features that do not contribute to any submodel. We conducted a Duda-Hart test to show whether the submodels belong to one or multiple clusters. We measured Duda-Hart or dh-ratio (ratio of within-cluster sum of squares and overall sum of squares) for all cluster pairs, based on either cell-type–specific set of submodels or the pooled set of submodels across all cell types for a TF using fpc package in R (https://cran.r-project.org/package=fpc). While calculating dh-ratio, k-NN was used for clustering. Since the final output of k-NN depends on initial random set of centers, the dh-ratio calculation was repeated 1000 times to ascertain robustness. We noted that all test results were significant (P-value <0.001).

Hopkins statistics (H) were measured to check clustering tendency of the submodels. To measure Hopkins statistics (H), the submodels are again represented as a set of points. H is defined by the following:

$$H=\frac{{\sum }_{j=1\dots m}{U}_j^d}{{\sum }_{j=1\dots m}{U}_j^d+{\sum }_{j=1\dots m}{W}_j^d}.$$

W_j is the nearest-neighbor distances of m randomly chosen points (submodels), which demarcate the sampling window. U_j is the minimum distances of the submodels from m random points in the sampling window. To define the sampling window, we either took the 25–75 percentile of the feature values or from δ to max value-δ along each dimension, where δ denotes the standard deviation of the feature value (Zeng and Dubes 1985a,b; Dubes and Zeng 1987). To estimate the P-value, we repeated the above procedure 1000 times and measured the H-value. The P-values range from 0.026 to <0.001.

Clustering submodels

For a TF, we obtained the submodels from all cell types and then clustered all submodels using k-NN, where each submodel is an instance and the features of the instances are individual feature importance obtained in the context of the respective cell-specific model. Before feeding into the k-NN, we remove all the features whose cumulative importance over all submodels is zero. To check robustness, the submodels are also clustered using a XY-fused version of a self-organizing map (Melssen et al. 2006) from the kohonen R package (Wehrens and Buydens 2007). To make it comparable to k-NN, submodels were clustered without preexisting submodel cell labels; i.e., we assumed 100% weight for X map.

Assignment of sequences and target genes to the clusters

A cluster of submodels can be viewed as a new ensemble. Therefore, for each cluster, we built a gbm object by treating the cluster as an ensemble and used it the same way an original Interaction model would score a sequence. Thus, we scored each binding site sequence against each cluster, and a sequence is assigned to a cluster when it is scored above a threshold (of one) by the cluster. The choice of the threshold was based on the rationale that the intercept (bias of the gbm model [https://cran.r-project.org/package=gbm]) of cell-specific models is about one, and for a high-confidence positive sequence, the model score should be greater than the intercept. Each bound sequence (from all cell lines) is mapped to a set of clusters. For each bound sequence, the nearest gene on the genome is considered to be its putative target, as per convention (Zhu et al. 2010). Hence, each cluster corresponds to a set of target genes coming from different cells.

Measuring pathway and expression coherence using Fisher's exact test

To measure the functional coherence, we determined the target gene array of size M-by-N for M clusters and N cell types. The M-by-N array thus includes a set of genes corresponding to each cluster in a particular cell type. We compared gene-pairs from the same row across columns (same cluster, different cells) to a background of gene-pairs along columns from different rows (same cell, different cluster). Then we apply the Fisher's exact test in a cluster-centric fashion by comparing the fraction of coclustered gene-pairs in the foreground compared with the background. The measure is named as expression coherence: whether target gene-pairs from same cluster but different cell lines are more coexpressed than those from different clusters but same cell line. A gene-pair is considered coexpressed if both of the genes are turned on (RNA-seq log₂CPM > 1) in their respective cells; CPM stands for counts per million. CPM, instead of the standard FPKM measure to quantify gene expression, suffices for our purpose as we only compare a gene's expression across samples and not with other genes in the same sample. We showed a similar trend of expression coherence with a different expression threshold (log₂CPM ≥ 5) (Supplemental Fig. S6E,F).

Pathway coherence is also assessed in similar fashion: whether the target genes from different cell lines that are assigned to the same cluster are more functionally related (i.e., in the same pathway) than the target genes coming from the same cell but from different clusters. Pathway data were downloaded from KEGG pathway database (www.genome.jp/kegg).

Robustness of EMT and submodel clustering

While building EMT using the gbm R package, we used the default parameter settings except maximum depth of variable interaction (interaction.depth), minimum number of observations in the trees terminal nodes (n.minobsinnode), and learning rate (shrinkage). Our parameter choices are the following: interaction.depth, 15; n.minobsinnode, 30; and shrinkage, 0.05. To check model and pipeline robustness, we built models with different values of these three parameters and compared the performance and model size (number of learned submodels). We found that performance and model size becomes stable after an interaction depth of 15 (Supplemental Fig. S2D,E), performance and model size do not vary much with the change of n.minobsinnode from 25 to 45 (Supplemental Fig. S2G,H), and performance does not change with shrinkage from 0.1 to 0.5 (Supplemental Fig. S2I). However, model size varies with the shrinkage parameter setting because with a lower learning rate, it takes longer to reach an optimum and it results in an increase in the model size (Supplemental Fig. S2J). Therefore, for different shrinkage parameters, we measured the clustering consistency. To this end, we took the models built with shrinkage = 0.05 as the reference models, and we compared the clustering pattern of reference models with the set of models built using different shrinkage values. More specifically, we determined whether a pair of sequences that falls into the same cluster for the reference model also falls in the same cluster for a different shrinkage value. We found that on average 96% of the sequence pairs fall in the same clusters regardless of shrinkage (Supplemental Fig. S2K).

Model variability and motif divergence

Model variability is defined by its normalized predictability across cell lines. For each model, n ROC-AUC values are obtained using the held-out data set of n cell lines. Cross-ROC-AUC values are normalized by self-ROC-AUC value. Mathematically, $va{r}_{\mathrm{mode}{\mathrm{l}}_i}={\displaystyle \frac{{\sum }_{j\ne i,jϵcells}rocau{c}_j}{rocau{c}_i}}$.

Motif divergence is defined by the following equation: $motif.div{.}_{pwms}={\sum }_{i,j\in pwms}{\displaystyle \frac{dis{t}_{i,j}}{I{C}_i+I{C}_j}}$. Here, dist_i,j = 1/similarity_i,j and IC_i is the information content of the ith motif. Similarity between two PWMs is calculated following the normalized version of the sum of column correlations (Pietrokovski 1996).

Identification of cofactors

EMT provides importance of all features in discriminating the foreground from the background. We retained all features with nonzero importance. From the initial set, we removed any motif that has 60% PWM similarity (consensus overlap) for at least 50% of the binding site locations with any of the reference motifs. Next, we calculated an enrichment score (i.e., odds ratio) of the motif in the foreground binding sites relative to control sites. We retained the motifs with more than 1.2-fold enrichment and two-sided P-value <0.05. The resulting motifs were considered as cofactors. For further analysis, we considered cell-specific cofactors by removing common motifs across cells. In particular, we excluded all cofactors that are common between any two cell lines. The functional cell specificity measure for a TF is determined using the variability of cofactor cardinality of such unique cofactors.

Enrichment of PPI, same family TFs, and heterodimerizing TFs

We obtained PPI data from STRING v10 (Szklarczyk et al. 2011). Using the TRANSFAC 2011 database, we determined the mapping from motifs to Ensembl protein id and the number of motif pairs having PPI. Using hypergeometric test, we calculated the enrichment of PPI between a reference TF and each set of cell-specific cofactors. The test summary indicated that 81% of the TF–cell cases have higher PPI enrichment among the interactions involving reference TFs and their cofactor (Supplemental Table S7a).

We compiled each PWM's family and the list of heterodimerizing PWMs from the TRANSFAC 2011 database. To identify heterodimerizing TFs, we looked for the presence of the keyword “heterodimer” and absence of “no” or “not” in the description of the motif. Supplemental Table S6 shows the heterodimerizing PWMs. Detailed manual inspection of a random subsample suggests that this automated criterion may result in ∼5% false positives. We also noted that occasional use of the term “dimer” instead of “heterodimer” may lead to ∼20% false negatives. For the hypergeometric test of family-enrichment, we compared how many cofactors belong to the family of reference motifs relative to the 981 motifs. Heterodimer enrichment was tested similarly. The enrichment scores (odds ratios) and P-values are reported in the Supplemental Table S7, b and c. The Supplemental Table shows that 70% of the model cofactors are enriched for either heterodimerizing TFs or TFs coming from the same family.

Gene expression and differential gene expression

For gene expression, we used RNA-seq data downloaded from ENCODE (Supplemental Table S5). For each cell line, we obtained between two and four RNA-seq samples depending on the availability and obtained the number of reads aligned to each gene. We corrected for batch effect using the sva R package (Leek et al. 2012). To estimate the differential expression between two sets of cell lines (those in which a TF is deemed a cofactor, and those where it is not), we used the linear model implemented in the limma package in R (Ritchie et al. 2015).

For each cofactor, we determined all possible relevant and nonrelevant cell pairs and took the log fold change (logFC) of the expression in those cells. To determine the control gene expression, we considered the same sets of cell pairs but took the logFC of an arbitrary gene instead of the cofactor. In both cases, we considered only significant differential expressions (logFC values with P-value <0.05) provided by the limma package (Ritchie et al. 2015).

Cell-specific PWM for the reference TF

We obtained relative feature importance of the reference motifs from the NonInteraction models and compared them with random expectation. To calculate the random expectation, 1000 NonInteraction models are learned based on randomly sampled 4000 sites from all binding sites across cell lines. From 1000 models, 1000 relative feature importances were calculated. Each set of relative importance was assumed a point in p-dimensional space where p is the number of reference motifs. We considered the relative importance vectors as data points from multivariate normal distribution and for each vector we calculated the Mahalanobis distances from the centroid, which follows a χ² distribution (Slotani 1964). The degrees of freedom (d) for the χ² distribution were determined using maximum likelihood estimate, and a P-value was generated from a χ² distribution function of d degrees of freedom.

Influencing cofactors, proximity to the influenced motif, and expression in the most used cell type

We identified the influencing cofactor set in the cell type where one motif is used much more frequently than the others. More specifically, for a TF, we identified pairs of motifs and cell types where there is a maximal differential in cell type usage of the two motifs (i.e., one of the motifs has the highest usage in one cell type and the lowest usage in another, and vice versa). For such pairs of cell types X, Y and corresponding reference motifs m_X & m_Y, we determined the candidate motif-specific cofactors f_X & f_Y as follows. We first separated the sequences from cell types X and Y where m_X and m_Y matches are found, respectively. Next, we assessed each putative cofactor's motif enrichment in each sequence set relative to the other sequence set. If the putative cofactor is enriched in X relative to Y, we consider it as a putative influencing cofactor for m_x and likewise for m_y. All other cofactors (f_c) are considered noninfluencing and serve as a negative control.

We measured the fold change (logFC) of all influencing and noninfluencing cofactors in X versus Y using the limma package (Ritchie et al. 2015). To demonstrate the genomic proximity between influenced motif and influencing cofactors, we chose the nearest distance between them among potentially multiple motif matches.

Feature count and gene expression in ubiquitous vs. cell-specific submodels

We designated a cluster as cell-type–specific if all member submodels (at least five) came from the same cell type. We then estimated skewness (https://cran.r-project.org/package=e1071) for each multi-cell-type based on the numbers of submodels contributed to the cluster by various cell types. If the skewness was <25%, we designated the cluster as ubiquitous. For each cluster, we counted the number of relevant features (i.e., with nonzero importance). Among the relevant features, we retained only those which were deemed as putative cofactors for at least one of the cell-specific models in our earlier analysis. The retained cofactors are designated ubiquitous or cell-type–specific based on the label of the cluster they belong to. Any common features from the two sets are removed. For each feature, we collect the expression across cell types in question and measure the skewness of gene expression.

Software availability

Sample data and code are available for download from the Supplemental Material and from the following GitHub repository: https://github.com/mhfzsharmin/trisectr