Controlled mechanical buckling for origami-inspired construction of 3D microstructures in advanced materials

Abstract

Origami is a topic of rapidly growing interest in both the scientific and engineering research communities due to its promising potential in a broad range of applications. Previous assembly approaches of origami structures at the micro/nanoscale are constrained by the applicable classes of materials, topologies and/or capability of control over the transformation. Here, we introduce an approach that exploits controlled mechanical buckling for autonomic origami assembly of 3D structures across material classes from soft polymers to brittle inorganic semiconductors, and length scales from nanometers to centimeters. This approach relies on a spatial variation of thickness in the initial 2D structures as an effective strategy to produce engineered folding creases during the compressive buckling process. The elastic nature of the assembly scheme enables active, deterministic control over intermediate states in the 2D to 3D transformation in a continuous and reversible manner. Demonstrations include a broad set of 3D structures formed through unidirectional, bidirectional, and even hierarchical folding, with examples ranging from half cylindrical columns and fish scales, to cubic boxes, pyramids, starfish, paper fans, skew tooth structures, and to amusing system-level examples of soccer balls, model houses, cars, and multi-floor textured buildings.

Graphical Abstract

Controlled buckling approach for autonomic origami assembly of 3D structures across a wide range of length scales and material types is presented to provide immediate access to 3D microarchitectures with a broad range of topologies. Such assembly allows continuous and reversible control of the configurations. The resulting engineering options have important implications for building future generations of microsystem technologies.

1. Introduction

Origami, the ancient Japanese art of paper folding, involves the transformation of planar paper sheets into macroscopic three-dimensional (3D) sculptures with diverse topologies.^[1] Origami is now a topic of rapidly growing interest in the scientific and engineering research communities due to its potential or use in a broad range of applications, from self-folding microelectronics,^[2–4] deformable batteries,^[5,6] and reconfigurable metamaterials,^[7–9] to artificial DNA constructs.^[10,11] Important recent advances in the fundamental aspects of origami include the identification of mechanisms for bi-stability in deformed configurations,^[7,12,13] and the development of lattice kirigami (a variant of origami that involves both cutting and folding) methods that solve the inverse problem of folding a flat plate into a complex targeted 3D configuration.^[14,15] In parallel, experimental methods are emerging for the assembly of origami structures at the micro/nanoscale. For example, a representative class of approaches relies on self-actuating materials, such as shape memory alloys,^[16,17] shape memory polymers,^[18–20] liquid crystal elastomers,^[4] and hydrogels,^[21–23] for programmable shape changes. These schemes are, however, not directly applicable to many technologically important types of materials, such as semiconductors or metals. Other routes rely on capillary forces (or surface tension forces),^[24–27] or residual stresses in thin films^[28–31] to drive the origami assembly, with the distinct practical advantage of compatibility with established planar device technologies. In most cases, however, such approaches^[24,26–30] are irreversible and offer limited control of parameters such as the folding angle, or folding rate. The results described in the following introduce a set of concepts in which controlled mechanical buckling actuates origami type transformations, in a manner that is fully applicable across material classes from soft polymers to brittle inorganic semiconductors, and length scales from nanometers to centimeters. This assembly scheme also enables active, deterministic control over intermediate states in the 2D to 3D transformation, in a continuous and reversible manner. These ideas complement and extend those that exploit buckling of filamentary ribbons to yield 3D mesostructures with open mesh networks,^[32,33] and of membranes with kirigami patterns of cuts^[34] to form 3D mesostructures with closed curved surfaces, thereby opening the access to a wide range of 3D topologies with levels of geometrical complexity significantly beyond those reported previously. In particular, the previous designs^[33,34] adopt ribbons/membranes with uniform thicknesses as the 2D precursors, thereby leading to deformations mainly in the form of global bending and twisting throughout the entire structures, as a result of the compressive buckling process. These designs do not allow well-controlled folding deformations at desired local regions, as is essential to the notion of origami. The present study introduces a set of concepts that rely on a spatial variation of thickness in the initial 2D structures as an effective strategy to produce engineered folding creases during the compressive buckling process, with capabilities in origami. Demonstrations in the current study include a broad set of 3D structures formed through unidirectional, bidirectional, and even hierarchical folding, with examples ranging from half cylindrical columns and fish scales, to cubic boxes, pyramids, starfish, paper fans, skew tooth structures, in addition to amusing system-level examples of soccer balls, model houses, cars, and multi-floor textured buildings.

2. Results and Discussion

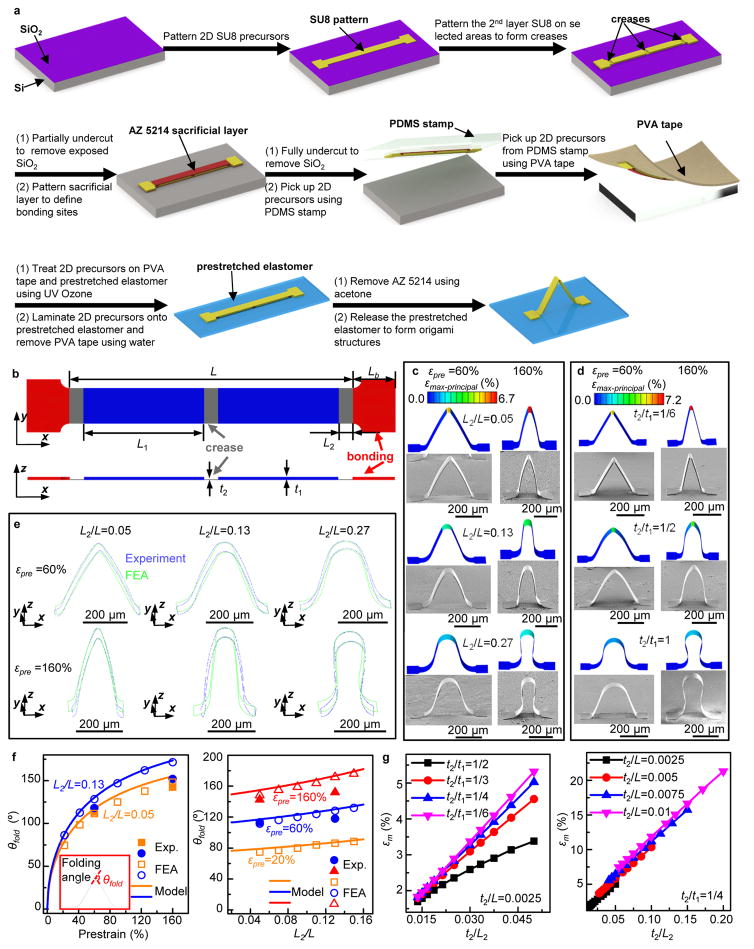
A straight ribbon serves as a simple example to illustrate the overall design concept (Figure 1a). Here, compressive forces associated with relaxation of prestrain in a supporting elastomer substrate exert on a ribbon structure (i.e., the 2D precursor in this case) at selected regions (i.e. bonding region, length L_b; red, Figure 1b), thereby deforming the system into a 3D structure in an overall process similar to that used previously in ribbons/membranes with uniform thickness.^[33,34] The key difference here is that the 2D precursor includes engineered variations in thickness to guide folding deformations at specific, targeted locations. In this example, the ribbon (length L, excluding the bonding locations) consists of five segments (Figure 1b), two (in blue color, each with length L₁ and thickness t₁) of which are thicker than the other three (in gray color, each with length L₂ and thickness t₂). When the thickness ratio (t₂/t₁) is relatively small (e.g., < 1/3), the thick segments undergo negligible deformation while the thin ones accommodate the compression via folding, simply as a consequence of the cubic downscaling of the bending stiffness with thickness. Furthermore, as the length ratio (L₂/L) decreases (e.g., < 0.1) the radius of curvature associated with this folded region decreases. Figure 1c,d illustrates these behaviors through finite element analyses (FEA) and experimental observation for various length and thickness ratios. The FEA used the same dimensions as those in the corresponding experiments. Provided that material properties are independent of length scale, the calculated deformation and strain should remain the same if both the thickness and in-plane dimensions are scaled by the same factor. To provide a quantitative comparison, the borderlines of the SEM images were extracted, and overlaid with corresponding FEA results. Representative results appear in Figure 1e and Figure S1 (Supporting Information) for those configurations shown in Figure 1c,d. The data provide quantitative evidence of the good agreements between FEA and experiments. Some slight differences can appear mainly at regions very close to the bonding areas. Such discrepancies can be attributed to partial delamination. These results indicate that both a small thickness ratio (t₂/t₁ < 1/3) and a small length ratio (L₂/L < 0.1) are required to induce strong folding-type deformations in the thinner segments (referred to as creases in the following). Due to the large stiffnesses, the regions of substrate surface that are bonded with the 2D precursors undergo negligible deformations, such that the compressive strains are accommodated by the other non-bonded regions of substrate. For simplicity, the deformed configurations of creases can be assumed as arcs, while the thicker regions of the ribbons can be assumed to undergo negligible deformations, for relatively large thickness ratios (e.g., t₂/t₁ > 1/4). Then, the following relation can be obtained from geometric analyses,

Figure 1. Conceptual illustration of buckling guided origami.

(a) Schematic illustration of steps for fabricating 3D origami polymer (SU8) structures. (b) Top and cross-sectional views of a straight ribbon with two different thicknesses. FEA results and corresponding SEM images of deformed mesostructures consisting of bilayers of metal (Au) and polymer (SU8) under two different levels (60% and 160%) of prestrain, for the non-uniform ribbons (c) with a fixed thickness ratio (t₂/t₁ = 1/4) and three different length ratios (L₂/L), or (d) with a fixed length ratio (L₂/L = 0.05) and three different thickness ratios (t₂/t₁). (e) Borderlines of the deformed configurations for the mesostructures in (b), where the curves in green and blue correspond to results based on FEA and SEM images, respectively. (f) Folding angle (θ_fold) versus the prestrain (left) for a straight ribbon with a fixed L_b/L = 0.15 and two different length ratios, and versus the length ratio (right) for a straight ribbon with a fixed L_b/L = 0.15 and three different prestrains. (g) Maximum material strain versus the normalized thickness (t₂/L₂) of a straight ribbon (b) under compression with 60% prestrain, for a fixed t₂/L = 0.0025 with a range of t₂/t₁ (left), and a fixed t₂/t₁ = 1/4 with a range of t₂/L (right). In Figure 1c,d, the color in the FEA results corresponds to the magnitude of maximum principal strain. Scale bars, 200 μm.

$$\frac{3L_2}{L}\frac{1}{{\theta }_{\mathit{fold}}}\text{sin}\frac{{\theta }_{\mathit{fold}}}{2}+\left(\frac{1}{2}-\frac{3L_2}{2L}\right)\text{cos}\frac{{\theta }_{\mathit{fold}}}{2}+\frac{L_b}{2L}-\frac{1}{2\left(1+{\epsilon }_{\mathit{pre}}\right)}\left(1+\frac{L_b}{L}\right)=0,$$ (1)

which can be used to determine the folding angle (θ_fold) for a given prestrain. Figure 1f shows that the model predictions agree reasonably well with the FEA and experimental results. These results indicate that an enhanced level of prestrain increases the folding angle evidently.

Since the overall compressive deformation is almost entirely accommodated by these creases, the maximum strains must also occur at these regions. Engineering designs that avoid fracture are important. For a straight ribbon with a small thickness ratio (t₂/t₁ ≤ 1/4), the peak value (ε_m) of the maximum principal strain (ε_{max-principal}) in the buckled 3D structures changes very slowly with further increase of t₂/t₁ (Figure 1g, left), indicating that ε_m becomes almost independent on t₂/t₁ for sharp creases. Due to the nature of bending deformation in the creases, the maximum strain (ε_m) follows a proportional dependence on the normalized thickness (t₂/L₂) for a given prestrain (ε_pre), suggesting a general scaling law, ε_m = F(ε_pre)t₂/L₂, where F(ε_pre) denotes a function that can be determined from FEA. This relation is well supported by FEA results in Figure 1g (right) for a fixed thickness ratio (t₂/t₁ = 1/4) and a wide range of t₂/L. Reductions in the crease thickness (t₂) and increases in the crease width (L₂) act to reduce the maximum strains. Here, the prestrain (ε_pre) of substrate in the case of uniaxial stretching can be defined as the average nominal strain (ε₁₁) of a uniform-strain area identified based on the criterion that the maximum difference of nominal strain ε₁₁ at this area is below ~ 10% of the average value. Figure S2 (Supporting Information) shows this prestrain is approximately equal to the applied strain under uniaxial stretching. The prestrain under biaxial stretching can be defined similarly, as shown in Figure S3 (Supporting Information), where we adopted ε_x-pre and ε_y-pre to denote the two components of normal strain along the two stretching directions. The distribution of maximum principal strain can involve some non-uniformities across the full area of the substrate, especially in the case of biaxial stretching. To simplify the designs based on FEA, the assembly processes were typically performed in the central region of the substrate, where the strain distribution is uniform. Effects of non-uniform strains, to the extent that they are significant, must be incorporated explicitly into the FEA.

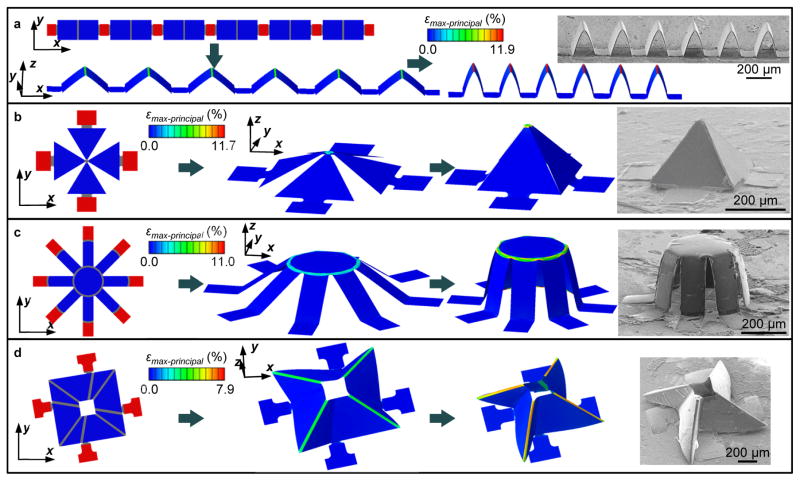
This basic strategy in thickness engineering affords great versatility in the design of mechanical buckling approaches to 3D structures. Figure 2 presents examples achieved with corresponding 2D precursors formed using a photodefinable epoxy (SU8; 2 μm in thickness at the creases, and 6 μm in thickness at the other region; Figure 2a,b), or with thin silicon (200 nm in thickness; Figures 2c,d) on top of the thick region. The left top frame of Figure 2a presents an example that includes six unit cells of large rectangles with creases (gray) located at the center and two ends. The periodically distributed small rectangles (red) adhere strongly to a uniaxially prestrained elastomeric substrate through covalent chemical bonding, while all other regions of the 2D precursors release from the substrate via elimination of a sacrificial interface layer (see Experimental Section for details). Relaxing the prestrain provides compressive forces that trigger out-of-plane buckling to thereby induce folding deformation at the creases. The final configuration corresponds to that of triangular columns, as shown by the results (Figure 2a, the right two frames) of FEA and the scanning electron micrograph (SEM). Effects of fatigue do not appear in the origami structure after they are stretched to ~30% strain repetitively at a frequency of ~1 Hz for ~1000 cycles (Figure S4, Supporting Information). The color of FEA results denotes the magnitudes of maximum principal strains that localize at the creases. The peak values remain below the fracture thresholds of the epoxy. The current analyses assumed that the material properties of the crease region are the same as those in the thicker regions. Therefore, the localized folding deformations result from the structural design with non-uniform thickness, and not from variations in materials properties. Delamination and fracture are the two main forms of failure during assembly. Such failures can be predicted, with reasonable accuracy, based on FEA. Here, our fracture criterion involves a strain threshold; FEA provides guidance on structure geometries that maintain the maximum principal strain below this threshold. Our delamination criterion relies on an energy based comparison of the undelaminated and delaminated states; again, FEA provides guidance. For the design parameters selected based on such calculations, we observe yields of ~ 50 % (i.e. half of the 2D precursors in a given fabrication run yield expected 3D structures) in the experiments. The failures arise from fracture and/or delamination associated with defects introduced in the fabrication process.

Figure 2. Representative examples of origami assembly of 3D mesostructures from correspondng 2D ribbons/membranes.

(a) FEA results (left three panels) that describe the formation of triangular columns made of polymer (SU8), along with corresponding SEM image (rightmost panel) of the final configuration. (b) to (d) Similar results that describe the formation of 3D pyramid (SU8), cylindrical shell (bilayer of silicon and SU8), and a complex ‘windmill’ mesostructure (bilayer of silicon and SU8). The color in the FEA results corresponds to the magnitude of maximum principal strain. Scale bars, 200 μm.

Figure 2b shows an example in which four triangular structures connect at the center with creases. Here, the assembly forms a pyramidal mesostructure, in which a carefully selected level of biaxial prestrain (in the substrate) yields a closed 3D topology. Many other configurations are possible with this scheme, including geometries that resemble a cylindrical shell (Figure 2c) and a windmill (Figure 2d). The latter case has a well-defined chirality, set by the configuration of creases. SEM images and corresponding FEA results of these 3D mesostructures viewed from different angles appear in Figure S5 (Supporting Information). The elastic tensile stiffness of these 3D mesostructures can be analyzed with FEA (Figure S6, Supporting Information), which indicates that the 3D pyramid offers a higher out-of-plane stiffness than the mesostructures that resemble a cylindrical shell and a windmill. The physical nature of the assembly process allows its application across a broad range of material types and length scales. For example, all of the origami inspired mesostructures in Figure 2 can be reproduced using millimeter-scale plastic models, as shown by the optical images in Figure S7 (Supporting Information). The design guidelines associated with crease geometries gleaned from the analyses of straight ribbon geometries (Figure 1) also apply to cases of bidirectional folding, in that narrow regions with small thickness ratios (t₂/t₁ < 1/3) lead to creases (Figure S8, Supporting Information). In all of the geometries examined herein, experimental results are in excellent agreement with FEA predictions, thereby establishing the computational approaches as reliable tools for rapid design optimization. Meanwhile, the thinning design principles applied in origami structures will lead to stress concentration on crease areas. For some 3D structures like structures in Figure 2, the maximum strain on the creases is even beyond 6 %, higher than the fracture strain of a brittle material like silicon (~ 2 %). For device applications, a simple solution is to replace the silicon with stretchable serpentine interconnections in these regions.

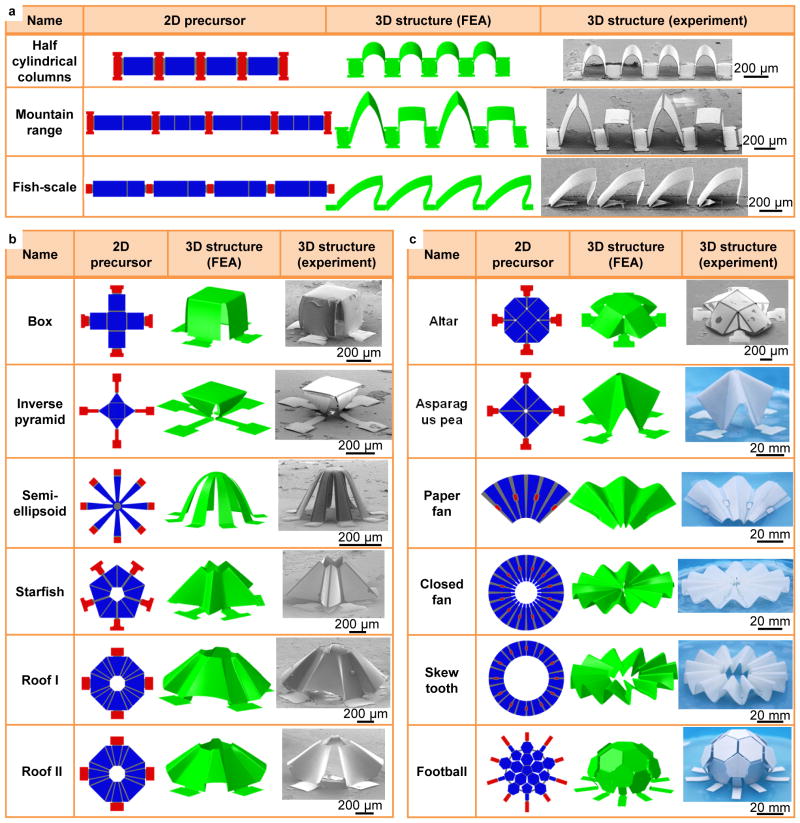
A diverse range of basic origami inspired geometries, each identified with a descriptive name, can be realized with these approaches as summarized in Figure 3. Representative examples formed through uniaxial compression appear in Figure 3a, including geometries that resemble half cylindrical columns, fish scales, and columns with mixed cross-sectional shapes of triangles and rectangles. Origami mesostructures with more complex geometries can be realized using equal biaxial prestrain (ε_pre = ε_x-pre = ε_y-pre) in the substrate as demonstrated in Figure 3b,c, and Figure S9 (Supporting Information). These shapes range from semi-ellipsoids and starfish, to polyhedral topologies (e.g., cube, inverse pyramid, football, etc.), to those (‘closed fan’ and ‘skew tooth’) formed through creases organized circumferentially in an annulus. In addition to the 2D layout of the precursor materials and the locations of the bonding, the patterns of creases provide additional means to control the final 3D geometries. With the same 2D precursor (e.g., an octagonal shape bonded at the centers of four edges), different distributions of creases yield distinct 3D configurations (e.g., ‘Roof I’ and ‘Roof II’ in Figure 3b). During the assembly process, the regions of substrate surface that are bonded with the 2D precursors undergo negligible deformations, such that the compressive strains are accommodated by the other non-bonded regions of substrate. As a result, for some of the origami structures (e.g., inverse pyramid and ‘Asparagus pea’) examined herein, large bonding areas are required to form the desired configurations with levels of biaxial prestrain that can be reproducibly achieved in the silicone materials used for the substrates, e.g., ε_pre < 200%. With the inverse pyramid as an example, a moderate level (~ 134%) of prestrain yields the structure in Figure 3b. With reduced dimensions (1/4 length of the original design) for the bonding areas, a substantially increased strain magnitude (~ 320%) is necessary to yield the same 3D configuration (Figure S10, Supporting Information). All of the origami structures formed at microscale can also be constructed at millimeter (or larger) scales (Figure S11, Supporting Information) with plastic films.

Figure 3. Experimental and computational studies of various origami structures.

(a) 2D precursors, FEA predictions and SEM images for three mesostructures formed with use of uniaxial prestrain in the substrate. (b) and (c) 2D precursors, FEA predictions and experimental (SEM or optical) images for twelve structures formed with use of biaxial prestrain in the substrate. Roof I in (b) is made of polymer (SU8); box and semi-ellipsoid in (b) are made of bilayers of silicon and polymer (SU8); the last five structures in (c) are made of thin plastic films; and all the other origami structures are made of bilayer of metal (Au) and polymer (SU8). The scale bars of SEM and optical images are 200 μm and 20 mm, respectively.

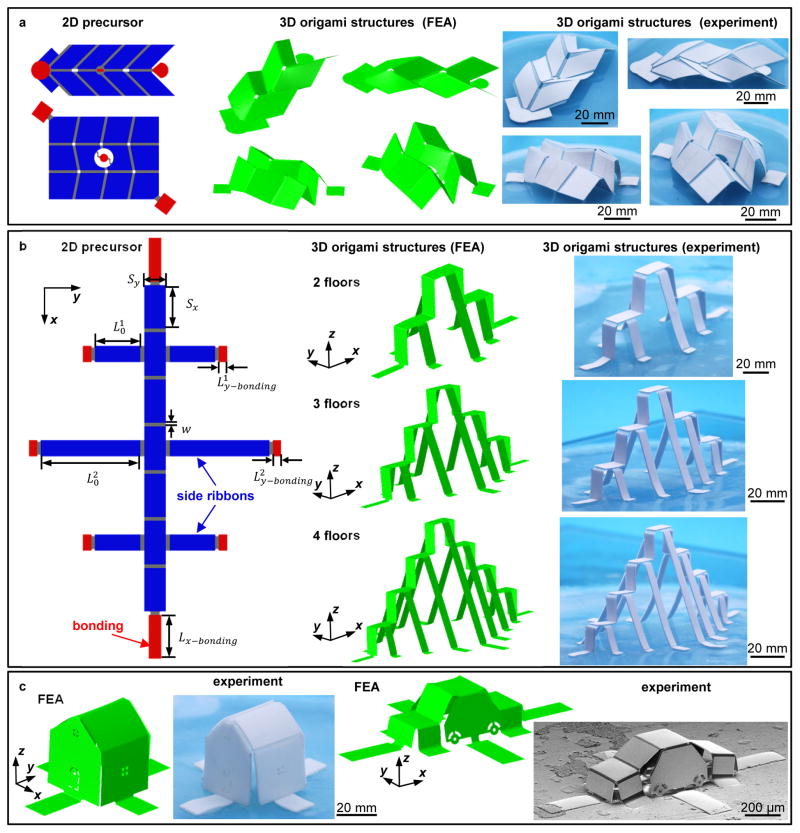
Multiple, hierarchical forms of folding are also possible with appropriate choices in design. Two examples of the well-known Miura-origami construct appear in Figure 4a, each of which use three bonding locations to impart the compressive forces. In the first design (Figure 4a, top), the bonding locations lie at the intersection of differently oriented creases, such that creases originally along horizontal direction (in the 2D state) form a wavy configuration during assembly. In the second design (Figure 4a, bottom), the bonding locations distribute along the diagonal direction of the 2D precursor, such that the assembly tends to shrink the structure into a smaller (and thicker) structure. Examples of origami structures that have multilevel constructions in the out-of-plane direction appear in Figure 4b. Note that the folding of creases can occur in two different directions, based on energetic considerations, for cases of multi-floor designs. This equivalence can be avoided by including supporting beams (e.g., the side ribbons in the left panel of Figure 4b) with optimized lengths to control the folding directions, thereby leading to consistent, desired multi-floor structures. In this study, the strain energies of different possible modes were calculated, to reveal designs in which the strain energy of the targeted configuration is much lower than the other possible modes. Figure S12 (Supporting Information) shows that when a straight ribbon with 8 creases serves as the 2D precursor, the two modes with multiple folds have similar levels of strain energies and that both are larger than the mode that takes the form of a single large arc. Practically, in the absence of defects that coincide with modes that have multiple folds, the single large arc is a unique solution. With the addition of supporting ribbons, a two-floor building in a stepwise configuration can be obtained, because the corresponding strain energy is much lower than the other possible modes, as shown in Figures S12c,d (Supporting Information). Figure 4b (left) shows the illustration of various length parameters in such 2D precursor. Here, the x-directional ribbon consists of seven identical segments (S_x by S_y) connected with creases (w in width). Adhesion to the elastomeric substrate occurs at two rectangular regions (red; L_x-bonding in the x-directional length). Three pairs of side ribbons with lengths of $L_0^1$ or $L_0^2$ connect the vertical ribbon with the bonding locations ( $L_{y-\mathit{bonding}}^1$ or $L_{y-\mathit{bonding}}^2$ in the y-directional length), to assist in the formation of the multi-floor design. To form a stepwise geometry in which each segment of the vertical ribbon orients perpendicular to the neighboring segments in the 3D shape, mechanics models (See Supporting Information for details) that correlate the required prestrain values (ε_x-pre and ε_y-pre) to various geometric parameters (S_x, S_y, w, $L_0^1,L_0^2,L_{y-\mathit{bonding}}^1,L_{y-\mathit{bonding}}^2$ and L_x–bonding) and acute angles (θ₁ and θ₂) between the side ribbons and the y axis in the final geometry are useful. Figure 4b (upper middle and upper right) provides an example of a two-floor building formed with a non-equal biaxial prestrain (ε_x-pre = 96%, ε_y-pre = 110%), which exhibits a clear stepwise configuration along the x axis, with tilt angles of θ₁ = 75° and θ₂ = 68° for the side ribbons. Such designs can be, in principle, extended to origami structures with arbitrary numbers of floors (See Supporting Information for details). Two stepwise structures demonstrated in Figure 4b and Figure S13 (Supporting Information) have three and four floors, respectively, with tilt angles of θ₁ = 75° and θ₂ = θ₃ = θ₄ = 68°, for the side ribbons. For origami structures with multiple (e.g., n > 3) floors, theoretical analyses (Figures S14 and S15, Supporting Information) highlight challenges in realizing upright side ribbons (with θ_i = 90°, i = 1..n) experimentally, due to the practical difficulties in achieving, simultaneously, large bonding sizes ( $L_{y-\mathit{bonding}}^i$, i = 1..n) and large prestrains (ε_y-pre).

Figure 4. 3D structures formed through multiple, hierarchical forms of folding.

(a) 2D precursors, FEA predictions and optical images for two structures involving Miura-origami. (b) Schematic illustration of a representative 2D precursor for a two-floor building, FEA predictions and optical images of stepwise structures with two to four floors. (c) FEA predictions and experimental images for two origami structures (left frame, made of plastic; right frame, made of bilayer of metal (Au) and polymer (SU8)) that resemble a house and a car. The scale bars of SEM and optical images are 200 μm and 20 mm, respectively.

A further extension of these design concepts in multilevel origami allows the assembly of complex recognizable 3D objects under compressive buckling. Figure 4c and Figure S16 (Supporting Information) illustrate two structures that resemble a house and a car, respectively, achieved with tailored values of prestrain (ε_x-pre = 119% and ε_y-pre = 138% for the house; ε_x-pre = 33% and ε_y-pre = 53% for the car). The 2D precursors of these two designs appear in Figure S17 (Supporting Information). For complex origami geometries that involve hierarchical forms of folding, experimental results both in millimeter and micro-scales agree very well with FEA predictions.

Concepts inspired by kirigami involve the addition of patterns of cuts to expand the accessible range of 3D structures. The concepts described previously are readily compatible with such approaches.^[34] Figure 5a,b illustrates that cuts can play similar, but different, roles in the process compared to controlled variations in thickness. For example, patterns of cuts placed at appropriate locations, like those shown in Figure 5a (top), induce folding deformations at the corresponding locations to yield origami structures that are very close to the ‘starfish’ in Figure 3b and ‘Asparagus pea’ in Figure 3c. Such similar roles originate from the same effects of decreased bending stiffness at targeted regions through reduction of their width or thickness. Separately, the removal of material by introduction of cuts additionally reduces the effects of stress concentrations^[34] and allows enhanced levels of flexibility in deformation (e.g., the twisting mode in Figure 5b), which are unobtainable through reductions in thickness (Figure S18, Supporting Information). Figure 5c – f and Figure S19 (Supporting Information) demonstrate that combinations of designs in creases and cuts enlarge substantially the accessible range of 3D topologies. The first structure of Figure 5c (left) corresponds to a closed 3D polyhedron that eliminates the diamond hole through contraction of surrounding surfaces. To its right is an origami structure that resembles a fence, formed mainly through rotation of two main components connected with short creases at the central region. Figure 5d presents two examples of lattice kirigami^[14,15] implemented through the buckling guided approach. Here, bonding locations periodically distributed in a triangular lattice pattern transfer the compressive forces to the 2D precursors, deforming them into a hexagonal array of hexagonal prisms or triangular array of triangular prisms. More complex integration of crease and cut patterns appear in Figure S20 (Supporting Information), which forms a ‘Ziggurat’ architecture (Figure 5e) by means of compressive buckling. Figure 5f corresponds to a variant of three-floor building in Figure 4b, in which well-arranged cuts and creases form textured steps connecting the adjacent planes (parallel with the substrate surface). Such designs can be also extended to the assembly of configurations with a different number of floors, as illustrated in Figure S21 (Supporting Information).

Figure 5. 3D structures inspired by origami and kirigami concepts, through uses of creases and/or cuts.

(a) 2D precursors, FEA predictions and optical images for two folding structures, transformed from kirigami designs with uniform thicknesses. (b) Similar results for two structures that involve not only folding but also twisting, also transformed from kirigami designs with uniform thicknesses. (c) and (d) Similar results for four origami structures, transformed from designs with combined uses of cuts and creases (through non-uniform thicknesses). (e) and (f) Two highly complex 3D structures: a ‘Ziggurat’ architecture, and a three-floor building with textured steps. Scale bars, 20 mm.

The 3D structures formed with the above approach remain tethered to the substrate during the origami assembly, and involve no plastic deformation in designs selected using guidance from FEA modeling. As such, their 3D configurations can be dynamically and reversibly tuned by mechanically loading and unloading the substrate through stretching or bending. Figure 6 and Movies S1 and S2 (Supporting Information), provide two examples for the origami assembly of a soccer ball structure and a multi-floor textured building structure, that illustrate clearly such capabilities. Of particular note is the excellent agreement between the predictions from FEA modeling and the experiments for almost all of the intermediate states. Figure S22 (Supporting Information) illustrate quantitatively the continuous control of the configuration by using different levels of prestrain or applied strain in the substrate.

Figure 6. Tunable and reversible control of 3D configurations based on the origami assembly.

Optical images and FEA predictions that illustrate the reversible process of 2D-3D origami assembly guided by compressive bulking, for (a) a plastic soccer ball and (b) a plastic multi-floor textured building structure.

3. Conclusion

In summary, this paper introduces an approach that exploits controlled mechanical buckling for autonomic assembly of 3D structures across a wide range of length scales and material types, using a combination of origami inspired ideas, theoretical modeling methods and experimental techniques. These design concepts, combined with advanced microfabrication processes provide immediate access to 3D microarchitectures with a broad range of topologies in materials that include those that form the basis of advanced microsystems technologies in electronics, photonics, sensors and microelectromechanical systems. These capabilities allow transformation of virtually any type of existing 2D microsystem technology into a 3D configuration, thereby providing unusual design options in the development of fundamentally new kinds of devices. In addition, the assembly method allows continuous and reversible control of the 3D configurations over intermediate states in the 2D to 3D transformation. Such capabilities can be important in 3D electromagnetic components, such as inductors or antennas, where key properties (e.g., quality factors, resonant frequencies, directionality) can be adjusted in real-time. These structures can also serve as the templates for the guided growth of materials or cells, or even as advanced types of single cell manipulators.

4. Experimental Section

Preparation of origami mesostructures in polymer began with thermal oxidation to form a layer of silicon dioxide (SiO₂, 500 nm in thickness) on a silicon wafer. Next, spin casting and photolithography formed patterns of photodefinable epoxy (SU8, 2 μm in thickness) on the of SiO₂. Spin-casting and photolithography with a second layer of SU8 (4 μm in thickness) yielded 2D precursors with strategically designed variations in thickness (i.e. 2 or 6 μm). Immersion in hydrofluoric acid (HF) removed the buried SiO₂ layer from the exposed regions and also slightly from under the edges of the SU8. Spin casting and photolithography created patterns of photoresist (AZ 5214, 1.6 μm in thickness) on top of the SU8 layers to define the bonding sites. Immersion in HF eliminated the remaining SiO₂ by complete undercut etching. The techniques of transfer printing enabled retrieval of the 2D precursors and their delivery to a piece of water soluble tape (polyvinyl alcohol, PVA). A thin sheet (~ 0.5 mm) of silicone elastomer (Dragon Skin, Smooth-On) served as the assembly platform, stretched to well-defined levels of prestrain (either uniaxial or biaxial) using a customized stage (Figure S23a, Supporting Information). Exposing the prestrained elastomer and the 2D precursors (on PVA) to UV-induced ozone (UVO) yielded hydroxyl termination on their exposed surfaces. Laminating the tape onto the elastomer substrate with the exposed SU8 side down, followed by baking in an oven at 70 °C for 10 min yielded strong covalent bonds via condensation reactions of surface-enriched hydroxyl groups between the elastomer substrate and the exposed regions of 2D precursors. Washing with hot water and then acetone dissolved the PVA tape and the photoresist. Slowly releasing the prestrain completed the origami assembly process. A schematic illustration of steps appears in Figure S24.

Preparation of mesostructures of bilayers of silicon and polymer (SU8) began with photolithographic patterning and reactive ion etching (RIE) of the top silicon layer (200 nm in thickness) to form silicon patterns on a silicon-on-insulator (SOI) wafer. Next, spin casting and photolithography defined the geometries of the first layer of SU8 (2 μm in thickness) on the silicon patterns. Spin casting and photolithography of a second layer of SU8 (4 μm in thickness) in a matching geometry with silicon patterns yielded 2D origami precursors of silicon and SU8 bilayers. The remaining steps of photoresist patterning, HF undercutting, transfer printing and 3D assembly followed procedures described above. A schematic illustration of steps appears in Figure S25.

Preparation of mesostructures of bilayers of metal (gold) and polymer (SU8) began with thermal oxidation to form a layer of SiO₂ (500 nm in thickness) on a silicon wafer. Next, photolithography, electron beam evaporation deposition and liftoff defined patterns of gold (50 nm in thickness) as 2D precursors on the SiO₂. Spin casting and photolithography defined the geometries of the first layer of SU8 (2 μm in thickness) on top of the gold. Spin casting and photolithography of a second layer of SU8 (4 μm in thickness) yielded 2D origami precursors of gold and SU8 bilayers. The remaining steps of photoresist patterning, HF undercutting, transfer printing and 3D assembly followed procedures described above. A schematic illustration of steps appears in Figure S26.

Preparation of structures in plastic films began with mechanical cutting of a base layer (~ 75 μm in thickness) into desired patterns, followed by cutting of patterns to define the thick regions with additional layers of this same material. Most of the plastic structures used a thickness ratio of 1/4, except for the football (Figure 3c), Miura-origami structures (Figure 4a), multi-floor buildings (Figures 4b and 5f), lattice kirigami structures (Figure 5d), and ‘Ziggurat’ architecture (Figure 5e), which used a thickness ratio of 1/8. Adhering additional layers of plastic films onto the base layer through thin, stick double-coated tape (9080A, 3M, Minnesota, USA) yielded 2D precursors for assembly using a prestrained silicone substrate (Figure S23b, Supporting Information). A highly viscous, organic adhesive, i.e., a RTV silicone rubber (706, NAN DA, Jiangsu, China), dispensed at desired locations on the 2D precursors resulted in strong bonding to the silicone substrate, after curing for ~ 2 hours at room temperature. Slowly releasing the prestrain in the substrate completed the assembly process.

All experiments involved a low rate of prestrain release, e.g., > 85 s (for millimeter-scale experiments) and > 120 s (for millimeter-scale experiments) for full release of ~ 100% prestrain, corresponding to a strain rate < 0.012 s⁻¹ (for millimeter-scale experiments) and < 0.0084 s⁻¹ (for micro-scale experiments). Under such circumstances, viscoelastic effects can be neglected, as confirmed by quantitative agreement between experiment and finite element computation that adopts hyperelastic constitutive law for the substrate.