Abstract
The abundant research examining aspects of social-ecological resilience, vulnerability, and hazards and risk assessment has yielded insights into these concepts and suggested the importance of quantifying them. Quantifying resilience is complicated by several factors including the varying definitions of the term applied in the research, difficulties involved in selecting and aggregating indicators of resilience, and the lack of empirical validation for the indices derived. This paper applies a new model, called the resilience inference measurement (RIM) model, to quantify resilience to climate-related hazards for 52 U.S. counties along the northern Gulf of Mexico. The RIM model uses three elements (exposure, damage, and recovery indicators) to denote two relationships (vulnerability and adaptability), and employs both K-means clustering and discriminant analysis to derive the resilience rankings, thus enabling validation and inference. The results yielded a classification accuracy of 94.2% with 28 predictor variables. The approach is theoretically sound and can be applied to derive resilience indices for other study areas at different spatial and temporal scales.
Author keywords: Disaster recovery, Coastal management, Community development, Spatial analysis, Sustainable development, Resilience, Vulnerability, Adaptability, Sustainability, Coastal hazards
Introduction
Coastal communities around the world are facing increasing threats from coastal hazards, due partly to global climate change and partly to the increase in anthropologic activities along the coasts. Coastal hazards include both large-scale, rapid-moving disturbances such as hurricanes and storm surges, and more slow-moving types of disturbances, including coastal land subsidence, sea level rise, and the degradation of ecosystem services over time. Although many coastal hazards are associated with natural processes, the threats are intensified by human action, including rapid population growth, limited planning for land use and infrastructure investment, and lack of comprehensive policy measures to prevent or mitigate hazardous events. The 2005 Hurricane Katrina and the 2010 Gulf of Mexico oil spill disasters are two examples of large-scale disturbances that resulted in significant damages to the Gulf Coast region in the United States (Lam et al. 2009, 2012; LeSage et al. 2011a, b). These coastal hazards affect the health and safety of the communities, as well as their long-term social and economic stability. What makes a coastal community less vulnerable to these hazards and then bounce back after the events, or in other words, become more resilient, is a major question facing environmental researchers and policymakers.
In recent years, many researchers from a wide range of disciplines have examined various aspects of hazards, risk assessment, vulnerability, adaptability, and social-ecological resilience (Cutter et al. 2003; Vogel 2006; Adger and Brown 2010; Tierney 2012). However, most of the literature on resilience tends to be conceptual, with few studies focusing on empirically quantifying the concept. A landmark report produced by the U.S. National Research Council (NRC) emphasized the need to build disaster resilience at both national and local levels, and identified the development of metrics and tools for measuring and monitoring community resilience as one of six key pathways toward building resilience (NRC 2012).
Quantifying resilience, however, is complicated by several factors including the varying definitions of the term applied in the research. In addition, there are difficulties inherent in selecting and aggregating indicators of resilience; and in developing a method for empirical validation for the indices derived. The development of a meaningful and practical resilience index is needed to foster our understanding of what we mean by resilience and how it may be increased. A straightforward resilience assessment model grounded on theoretical principles would support predisaster planning and help guide postdisaster assistance to communities after major disturbances (NRC 2012; Reams et al. 2012).
This paper applies a new approach to measure community resilience to coastal hazards for the 52 counties in the United States along the northern Gulf of Mexico. The resilience inference measurement (RIM) approach considers three elements: exposure, damage, and recovery, and the two relationships linking the three elements: vulnerability and adaptability, in deriving a community resilience index. The RIM approach utilizes statistical methods for empirical validation. In the following sections, the authors first provide a brief background of the issues and related research surrounding resilience measurement. The RIM approach is then introduced. Applying the RIM approach, this paper first conducts a K-means cluster analysis to derive the a priori resilient rankings for the 52 counties. Discriminant analysis is then used to characterize statistically the a priori resilient groups via a number of socioeconomic and environmental indicators. An index of resilience is then constructed using the probability of group membership values derived from the discriminant analysis. The authors argue that the approach is theoretically sound; it is a practical approach to measuring community resilience while enabling empirical validation and providing predictive functions for future inference, thus overcoming several major difficulties in assessing levels of resilience.
Challenges in Measuring Community Resilience
Two main issues in resilience measurement persist, making the development of a practical and generalizable community-resilience index difficult.
Definitional Issues
There are scores of definitions of resilience, and a recent report by the Community and Regional Resilience Institute (CARRI 2013b) provides a useful review of the most commonly used definitions. In brief, the term community resilience has evolved mainly from the literature on social-ecological resilience. The two earliest definitions of resilience seen in this literature are: engineering resilience which refers to how fast a system can return to the original state after a disturbance, and ecological resilience which indicates how far the system could be perturbed without shifting to a different state (Holling 1996; Folke et al. 2002; Walker et al. 2006a, b). Adger and others defined resilience as “the capacity of linked social-ecological systems to absorb recurrent disturbances such as hurricanes or floods so as to retain essential structures, processes, and feedbacks.” They elaborated further that the concept of resilience includes “the degree to which a complex adaptive system is capable of self-organization (emphasis added), and the degree to which the system can build capacity for learning and adaptation (emphasis added)” (Adger et al. 2005). Norris and others considered resilience as a process linking communities’ capacities in response to the disturbance (Norris et al. 2008). The NRC report defined resilience as “the ability to prepare and plan for, absorb, recover from, and more successfully adapt to adverse events” (NRC 2012). Hence, resilience can be regarded as a capacity, a process, an outcome, or a combination of some of the three concepts (Norris et al. 2008; Cutter et al. 2010; Sherrieb et al. 2010; CARRI 2013b).
Many studies link the concepts of vulnerability and resilience, with some broadening the definition of vulnerability to include resilience while others incorporating vulnerability as part of the larger resilience concept. The Intergovernmental Panel on Climate Change (IPCC) (IPCC 2001) considered vulnerability a function of three factors: exposure, sensitivity, and adaptive capacity, and Cutter and others (2003) defined vulnerability as “a measure of both the sensitivity of a population to natural hazards and its ability to respond and recover from the impacts of hazards;” both definitions include aspects of resilience. Recently, the concept of sustainability is included in the dialogue, which adds even more complexity to resilience measurement. In distinguishing the differences and commonalities between vulnerability and resilience and how they are related to sustainability science, Turner proposed the use of the concept of trade-offs (among various sets of environmental services and human outcomes) as a way to merge the three concepts: vulnerability, resilience, and sustainability (Turner et al. 2003; Turner 2010).
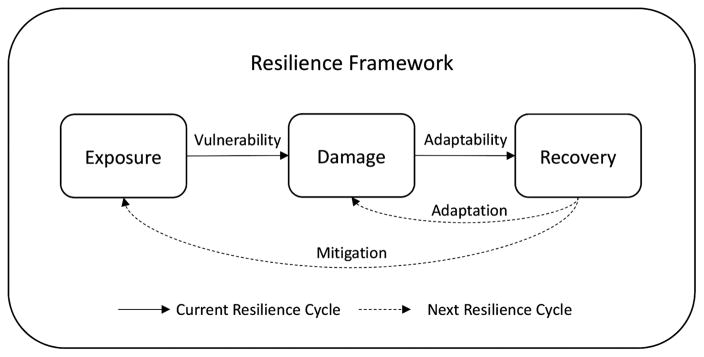
To summarize, researchers in the community acknowledge lingering disagreements over the definition of resilience and its underlying emphasis. Each definition has its own merits and the choice of a definition depends on the application domain (CARRI 2013b). This paper adopts the definition by the NRC report as previously stated (NRC 2012), and considers resilience as comprising both aspects of vulnerability and adaptability (Fig. 1).
Fig. 1.
Resilience inference measurement (RIM) approach (see detailed description in text)
Measurement Issues
There are significant difficulties involved in measuring community resilience. First, the range of definitions of resilience that is evident from a review of related research complicates the task of selecting indicators of the concept. Once appropriate indicators are identified, mathematical and statistical methods will need to be developed to evaluate the indicators iteratively. Second, both social and natural aspects of resilience should be included in a comprehensive assessment, along with a consideration of linkages between natural and social systems, because a system may have high social resilience but low ecological resilience. For example, in some deltaic regions such as the lower Mississippi Delta, levees built to protect highly populated urban areas (e.g., New Orleans) from river flooding may lead to a lack of sediments replenishing surrounding rural lands, which in turn could make the entire region more vulnerable to subsidence and floods (Blum and Roberts 2009). Also, there may be a lag time in observing interaction effects between the two systems, making the measurement of community resilience more difficult. Third, measures of community resilience have seldom been validated. Often, aggregation of indicators of resilience has been performed in the context of one study area, making it difficult to apply the resultant index or model generally to other communities.
There are quite a few composite indices or metrics in the literature that are related to resilience, including, for example, the disaster risk index (Peduzzi et al. 2009), the social vulnerability index (Cutter et al. 2003), the baseline resilience indicator for communities (Cutter et al. 2010), the community assessment of resilience tool (CART), and the community resilience system (CRS) (NRC 2012; CARRI 2013a). These studies have contributed to resilience measurement research in various manners; they also point to the difficulties involved in resilience measurement. To further illustrate the different approaches and the challenges associated with measuring resilience, this paper describes briefly a few studies on measuring vulnerability and resilience, which serve as a background for the rationale of our approach.
The first, as demonstrated in Yusuf and Francisco (2009), represents the most commonly used approach to measuring vulnerability (which includes measurement of adaptive capacity, a core component of resilience). The researchers used an additive-weighting approach to evaluate subnational areas in Southeast Asia in terms of their vulnerability to climate change. They applied the definition developed by the United Nations’ IPCC (2001), which considers vulnerability (V) to be a function of exposure (E), sensitivity (S), and adaptive capacity (C)
The exposure term captures the type of climate-related hazard presented and the degree to which the community is likely to be exposed. Sensitivity refers to the degree to which a system is likely to be affected by climate-related events, and adaptive capacity refers to the ability of residents to adjust to changing threat levels to avoid or mitigate the consequences of climate change. Variables representing each dimension were selected, weighted (somewhat arbitrarily based on related research), and added to become a composite index of the vulnerability of each subnational region in Southeast Asia. Their study identified all the regions of the Philippines, along with some regions in other countries, as the most vulnerable regions to climate change. The study is straightforward and allows for a useful comparison among geographic areas; however, the index is limited by the subjective nature of weight assignments and the index needs empirical verification.
Nelson and colleagues followed a similar but improved approach to assess the vulnerability of Australian rural communities to climate change (Nelson et al. 2010a, b). Recognizing the potential value of measures of community vulnerability in formulating and evaluating the impacts of public policy, they included more measures of adaptive capacity to complement the existing hazard-impact modeling. They created an adaptive-capacity index based on the rural-livelihood analysis framework, which includes indicators from five groups of community resources or capitals: human, social, natural, physical, and financial (Ellis 2000). The selection of variables to represent adaptive capacity was based on a farm survey, and then the weighting of the variables was derived from a principal component analysis of all the indicators. Although the method and the derived index needs further improvement, their studies represent a significant improvement because they emphasize the need to validate the selection of variables and their corresponding weights to represent adaptive capacity.
A third approach is the social vulnerability index, which was developed by Cutter and others to quantify social aspects of vulnerability (Cutter et al. 2003; Cutter and Finch 2008). They constructed the index for all of the counties in the United States. The index is an aggregation of 42 socioeconomic variables available from the U.S. Census and identified in the literature as being related to social vulnerability. The researchers used a principal component analysis to derive 11 factors that accounted for 76.4% of variance of the 42 variables. Then they added the factor scores for each county to create the index scores. The most vulnerable counties were those with the largest positive standard deviations from the mean, and the least vulnerable were those with the largest negative standard deviations. The researchers attempted to verify the accuracy of the index by correlating the scores with the number of presidential disaster declarations that had been issued for each county. They found no correlation (r = −0.099) between the social vulnerability index scores and the disaster declarations. However, the approach pioneered by Cutter and colleagues advanced two important concepts regarding the measurement of resilience or vulnerability: the need to derive the index through statistical modeling and the need to validate the index through empirical comparisons with observable outcome.
Significant effort has been made in identifying the most suitable indicators for disaster resilience. Cutter and others (2010) introduced a new composite indicator called the baseline resilience indicator for communities (BRIC), which is calculated as the arithmetic mean of five subindexes related to social, economic, institutional, infrastructural, and community capacity. However, validation of the composite indicator has not yet been performed. Sherrieb and others (2010) identified an exhaustive list of 88 variables and then used correlation analysis to reduce the set into 17 variables representing two components: social capital and economic development, as indicators of capacities for community resilience. Researchers at the Community and Regional Resilience Institute created a web-based CRS to help planners and leaders assess and improve resilience (CARRI 2013a). The CRS system is a self-guided six-step process that has been found helpful to some communities. However, several of the pilot communities found it difficult to balance a long-term planning project with daily operations on limited resources and did not implement the pilot project prior to the completion of the program. This experience further epitomizes the need to develop practical tools to support planning and decision making.
Materials and Methods
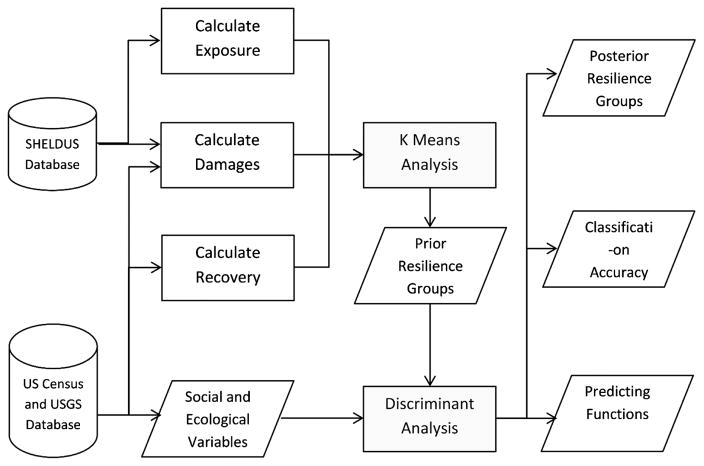
RIM Approach
As previously stated, this paper adopts the definition of resilience used in the NRC report, which is “the ability to prepare and plan for, absorb, recover from, and more successfully adapt to adverse events” (NRC 2012). Thus, the RIM framework proposed in this paper considers resilience a broader concept that includes aspects of both vulnerability and adaptive capacity over time. Specifically, the framework considers three elements: exposure, damage, and recovery, and two relationships: vulnerability and adaptability (Fig. 1). Exposure and damage are observable measures at time t0 when the hazard event happens, whereas recovery is an observable measure reflecting the difference between time t0 and t1 such as population or economic growth. Vulnerability and adaptability are latent relationships between the three elements, whereas resilience capacity, also a latent relationship, is indicated by both vulnerability and adaptability. The time variable t0 can be a point or an interval, referring either to a single-hazard event at a time point or a number of hazard events at a time interval. In this study, the authors used a time interval of 10 years to compute the exposure and damage to coastal hazards and the population growth to allow for sufficient data for comparison across the Gulf Coast counties.
Vulnerability refers to the latent relationship between exposure and damage, whereas adaptability indicates the latent relationship between damage and recovery. If a community (e.g., county) has high exposure to a hazard but sustains low damage, then the community is considered to have low vulnerability. Similarly, if a community sustains high damage but recovers quickly (e.g., return of population), then the community is considered to have high adaptability. Resilience is measured according to the two relationships. A high vulnerability/adaptability ratio is considered low resilience, whereas a low vulnerability/adaptability ratio is considered high resilience. The conceptual framework shown in Fig. 1 is in fact very similar to some broad vulnerability frameworks used by a number of researchers (IPCC 2001; Turner et al. 2003).
Also, Fig. 1 aims to portray the underlying resilience processes—mitigation and adaption—shown in dotted lines in a simplified manner for visualization, where in fact processes leading to resilience are indeed complex. The purpose of showing the underlying resilience processes is to provide a more complete, dynamic view of the resilience processes. In terms of index development, however, only the information on the current resilient cycle is used. The RIM model will evaluate the conditions of the three boxes (exposure, damage, and recovery) and their relations with the underlying capacities (or lack of capacities) as represented by a number of socioeconomic and environmental variables to determine the resiliency of a community. In Fig. 1, mitigation refers to the actions or strategies intended to reduce the likelihood or intensity of exposure, such as CO2 emission reduction designed to decrease global warming, possibly leading to fewer hurricane strikes (IPCC 2007). Adaptation or adaptive measures are the actions or strategies used to adjust the conditions and improve the social, ecological, and built environments to lessen the impacts of disruptive events (Hamin and Gurran 2009). Examples of adaptive measures include elevating housing units and other structures above likely flood levels to avoid or reduce flood damages.
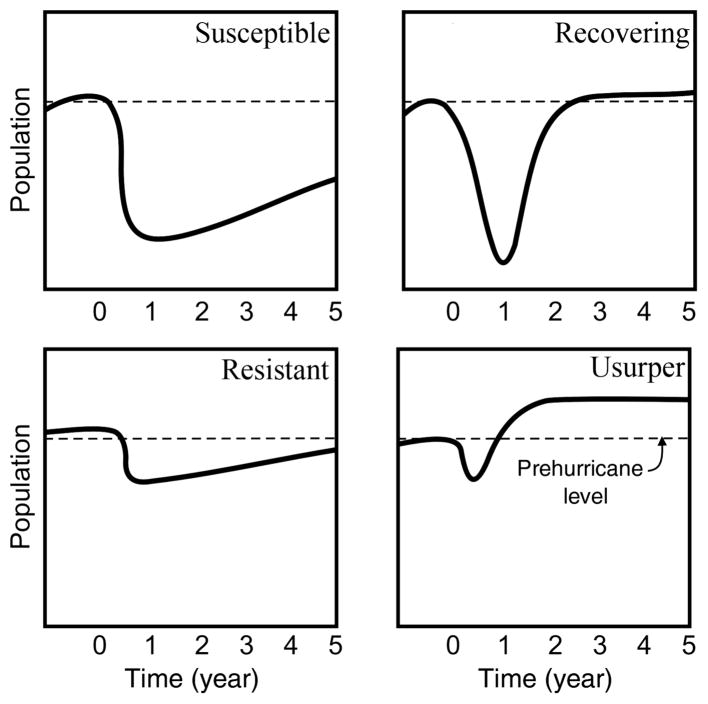
Previous research suggested that the recovery patterns of an ecological system might be described by four states (Bellingham et al. 1995; Batista and Platt 2003; Liu et al, unpublished data, 2006). We modified slightly the names of the four states and adopted them into the RIM framework to represent four resilience rankings. From low-to-high resiliency, they are susceptible, recovering, resistant, and usurper (Fig. 2). We retained the descriptive names used to distinguish the four states observed in the ecological system to maintain consistency, realizing the connotations may be perceived differently in a social system. A susceptible state refers to that community that has been unable to fully recover after a disturbance, such as a hurricane or large-scale flood. A recovering community implies that it is able to fully recover from the episode. A community that felt a much smaller impact (i.e., damage) from the disturbance can be described as resistant. A usurper community is one that is only somewhat influenced by the disruption and exhibits a population increase that exceeds the predisturbance levels.
Fig. 2.
Four states of ecological resilience (Liu et al., unpublished data, 2006)
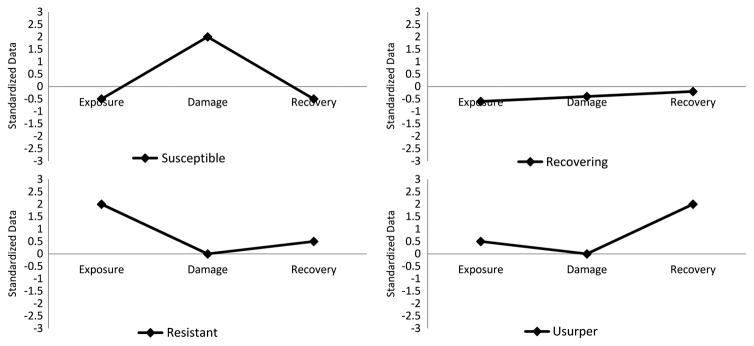
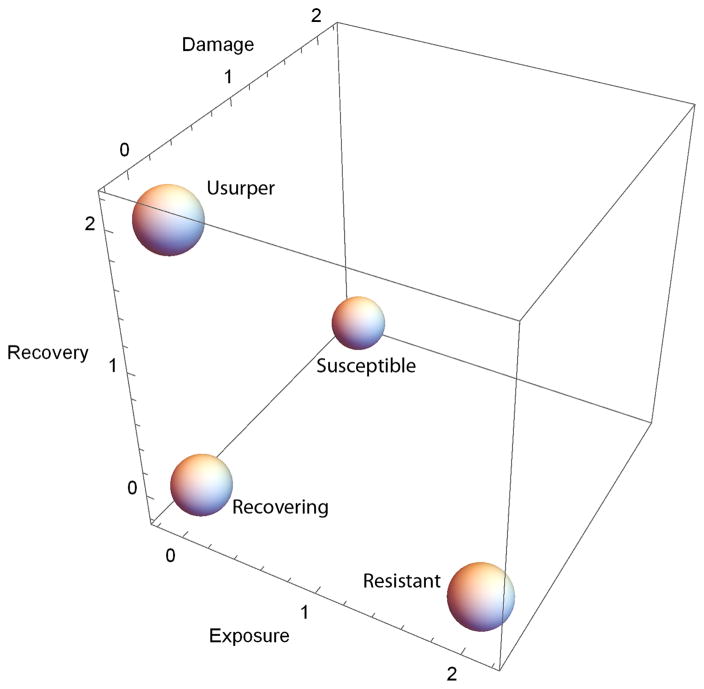
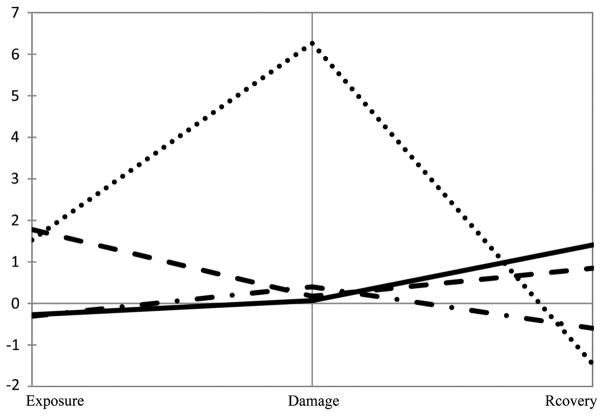
Fig. 3 illustrates the generalized relationships between the four resilience states and the RIM model. The x-axis shows the three elements (exposure, damage, and recovery); and the y-axis shows the deviation of the three variables from their means (i.e., the zero-value lines). The community’s ability (or disability) to minimize the damage at the time of the event can be called vulnerability, as shown by the slope of the hypothetical line between exposure and damage. The higher the slope is when it is in an upward direction, the higher the vulnerability. Similarly, the community’s ability to bounce back over time can be represented by the slope of the hypothetical line between damage and recovery, which can be characterized as adaptive capacity. The higher the slope, indicated by an upward direction, the higher the adaptability. A susceptible system is considered the least resilient system, as it has high vulnerability and low adaptability. A recovering system has about the same vulnerability and adaptability (close to a straight line but can be above, near, or below the mean). A resistant system has low vulnerability and an average adaptability, whereas a usurper system has low vulnerability but very high adaptability. In terms of resilience ranking, we consider adaptability more important, hence the susceptible state is the least resilient, followed by recovering, resistant, and usurper. The same three elements can also be displayed in a three-dimensional plot, as shown in Fig. 4, using the same hypothetical values in Fig. 3.
Fig. 3.
Generalized relationships between the four resilience states and the three elements in the RIM model [the y-axis shows the standardized scores of the three elements from their means (i.e., the zero-value line); the hypothetical lines linking the three elements are used to indicate the general directions of vulnerability and adaptability; see detailed description in text]
Fig. 4.
Generalized relationships between the four resilience states and the three elements in the RIM model, displayed in a three-dimensional form [the axes show the standardized scores of the three elements from their means (i.e., the zeros)]
While these four discrete resilience states observed in ecosystems provide useful insights into recovery patterns and yield additional understanding of resilience, it is unclear if these four types of systems exist in real social systems or communities. One of the goals of this paper is to examine whether the responses of a social system can be characterized by the four states, which could give additional meaning beyond a continuous index score.
The other major challenge of resilience measurement is validation. The proposed RIM model overcomes this issue first by utilizing the K-means clustering method to derive the resilience groups of communities, based on the values of the three elements (exposure, damage, recovery). Once the resilience groups are identified, discriminate analysis is then applied to find out which indicators can be used to characterize or discriminate a county based on its resilience ranking. These indicators can be used to indicate adaptive capacity, and may include socioeconomic, governmental, and/or environmental variables extracted from the literature. Both K-means clustering and discriminant analysis are standard multivariate statistical methods that have been applied widely in many fields (Tabachnick and Fidell 2000).
Once the discriminant analysis yields satisfactory results and the underlying statistical assumptions are met, the same discriminant functions and the same set of indicator variables can be utilized to evaluate the resilience rankings of other counties. Thus, the proposed RIM approach provides a statistical form of validation, as well as an ability to make inferences to other study areas. Furthermore, the probability of group membership values resulting from discriminant analysis can be utilized to derive a resilient score on a continuous scale based on the method derived in Liu and Lam (1985). Fig. 5 is a flowchart showing the procedures used in the RIM approach.
Fig. 5.
Flowchart of the procedures used in the resilience inference measurement (RIM) approach
Given that the discriminant analysis results are satisfactory (e.g., high classification accuracy, statistical assumptions met), the classification score of a case i (e.g., county) for each group j can be computed using the following equation:
| (1) |
where Cij = classification score of case i for group j; V’s = predictor variables; p = number of predictor variables; k = number of groups; and c’s = classification coefficients derived from the discriminant analysis. For example, if there are four resilience groups, then there will be four C scores for each case. Then, the Mahalanobis distances of the classification scores between each individual case to each of the group centroids can be calculated (Nie et al. 1975). Under the assumption of a multivariate normal distribution, the classification scores, hence the Mahalanobis distances, can be converted into probabilities of group membership. A case is assigned to the group that has the highest probability of group membership, which is also called the posterior group membership (Tabachnick and Fidell 2000; Nie et al. 1975).
To convert the resultant group memberships into a continuous resilience index, the authors follow the approach pioneered in Liu and Lam (1985), which can be presented in an equation form here
| (2) |
where I = resilience index; G1 = posterior group membership; G2 = second highest group membership; andP(G1) and P(G2) = probabilities of the respective group membership. For example, if a county has been classified by discriminant analysis as Group 1 and its second highest group is Group 2 with a probability of membership as 0.3, then by applying Eq. (2), the final resilience index would be: (1 × 0.7) ) (2 × 0.3) = 1.3. On the other hand, if a county has been classified as Group 2 and its second highest group is Group 1 with a probability of 0.3, then the resultant index would be (2 × 0.7) ) (1 × 0.3) = 1.7. Theoretically, Eq. (2) can be extended to include calculations using probabilities of more than two groups. However, since the probabilities of group membership of the third and fourth groups were found to be very small, this paper simplifies the calculation by using only the first two groups.
Study Area and Data
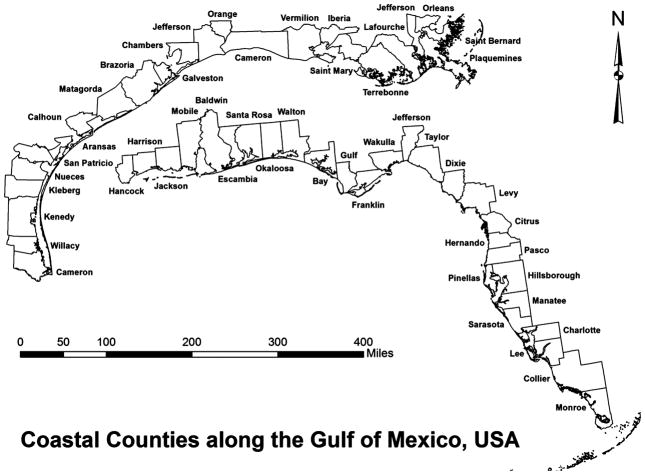
The RIM approach was applied to evaluate the resiliency of the 52 coastal counties along the northern Gulf of Mexico coast in the United States. These counties are considered communities, and they belong to the five states: Texas, Louisiana, Mississippi, Alabama, and Florida (Fig. 6). The time period for all the data was from 1998 to 2008. The three elements for each county were defined as: (1) the exposure to hazards, represented by the number of times a community was hit by hurricanes or climate-related hazards; (2) the damage from exposure to hazards, represented by the property damage; and (3) the recovery, represented by population growth.
Fig. 6.
Fifty-two coastal counties along the Gulf of Mexico, United States
Data for exposure and damage for the coastal counties were obtained from the Spatial Hazard Events and Losses Database for the United States (SHELDUS) maintained by the University of South Carolina (http://www.sheldus.org). The original raw data come from the National Oceanographic and Atmospheric Administration’s (NOAA) National Climate Data Center (NCDC) (http://www.nws.noaa.gov/directives/sym/pd01016005curr.pdf). SHELDUS tabulates the data into a county-level data set and adopts a conservative approach to loss estimation by always using the lowest loss figure where multiple estimates exist. Five major types of coastal hazards were included in this study: coastal (which includes coastal flooding and storm surge), flood, hurricane, thunderstorm, and tornado. SHELDUS Version 10.0 was used during the study. The hazard event types and their definitions are documented in the metadata at the SHELDUS website and can also be found at the NOAA NCDC site. It is noted that the SHELDUS database contains more than the original NCDC data and has been updated substantially since Version 10.0 released in 2012. The last version released was July 2013 and contained approximately 70,000 additional records.
To more accurately represent exposure, this study adjusted the number of hazard events by a weighting method, because some events such as Hurricane Katrina are far more severe than a thunderstorm. The weight of an event type i, wi, was derived as the ratio between the total damage of event type i and the total damage of all events:
| (3) |
The exposure for county x was calculated by Eq. (4)
| (4) |
where Nxi = number of hazards of type i occurred in county x; and BeginDateij and EndDateij = begin and end dates of hazard event j of type i, respectively. Using the ratio between the total damage of an event type and the total damage of all events in the study region to adjust the exposure of a county should not create the multicol-linearity problem. A correlation analysis between the exposure [as defined by Eq. (4)] and the damage variable for the 52 counties shows a low correlation (r = 0.29) (even though some correlation between the two variables should be expected).
The damage variable for each county is the sum of the damage from each event divided by the population of the county at the time of the event. The recovery variable was estimated by the population growth rate between 1998 and 2008. Population and socioeconomic data were obtained from the U.S. Census Bureau at http://www.censtats.census.gov/usa/usa.shtml. Health-related variables were obtained from the area resource file (ARF) produced by the Bureau of Health Professions in the U.S. Department of Health and Human Services.
Using population change as an observable proxy to indicate recovery could be challenging. Indeed, researchers examining sources of recovery following disturbances have not reached consensus on the best way to measure or evaluate recovery (Bevington et al. 2011). Recently, Jordan and Javernick-Will (2013) conducted an extensive review of related studies and categorized the indicators of recovery applied by researchers into four categories or dimensions of recovery: economic, environmental, infrastructural, and social. Indicators of environmental and infrastructure include the condition of the built environment and roads, and the ability to deliver utilities. Economic recovery could be indicated by a range of factors including the number of employees of local business establishments, the number of returning or new businesses, and the average household income levels of residents (Lam et al. 2009, 2012). Returning population to communities affected by disturbances has been used to indicate social recovery (Aldrich 2012; Chang 2010; Finch et al. 2010; Li et al. 2010). The four categories of recovery are related, for example, with repair to infrastructure being necessary to support returning population and businesses (Miles et al. 2012), and the recovery of social systems encouraging the rebuilding of infrastructure components (Tierney and Oliver-Smith 2012). Hence, the recovery indicator could be a combination of variables from different dimensions.
This study uses population change over time as the indicator of recovery. The rationale is that population change over time reflects the wide range of decisions made by individuals and businesses to remain in or move away from an area after disturbances. It is a broad indicator of recovery that takes into account the rational behavior and choices of residents and organizations to locate in communities in the area, even those with higher levels of exposure to natural disturbances. This study assumes that these choices are a cumulative reflection of the judgments and assessments by stakeholders concerning both the current and likely future socioeconomic and physical conditions within their communities. While there may be other logical proxies, the authors note that population change observed on its own may not necessarily indicate recovery or suggest resilience. These aggregated choices are meaningful in the RIM framework in which population change is evaluated in the context of exposure and damages from storms and other natural disturbances over multiple years. Therefore, examining communities along the Gulf Coast that have been subjected to disturbances over time provides an opportunity to observe postdisaster population growth and to identify key factors associated with this indicator of recovery.
In a practical sense, since data on population change is likely to be available across regions and at different spatial scales, using population change over time as a recovery indicator could make future comparison of resilience measurement across space and scales easier.
The exposure and damage data of the 52 coastal counties reveal that the weighted exposure values for 1998–2008 ranged from 0.003 (Kenedy County, Texas) to 28.59 (Escambia County, Florida). The top five counties that had the highest level of exposure were: Escambia, Florida (28.59); Bay, Florida (26.93); Baldwin, Alabama (22.60); Walton, Florida (21.53), and Gulf, Florida (20.89). For the property damage variable, the highest property damage was found in Plaquemine Parish, Louisiana, with a damage of $213,237 per capita, followed by Hancock County, Mississippi ($101,950) and three other parishes in Louisiana: St. Bernard ($93,855), Lafourche ($66,560), and Cameron ($40,478). The least property damage was found in Willacy County, Texas ($3.45 per capita). The high damage figures in Louisiana and Mississippi were undoubtedly affected by Hurricanes Katrina and Rita, which hit the region in August and September 2005.
In terms of population growth rate between 1998 and 2008, the top five counties were all from Florida: Wakulla (39.7%), Pasco (38.8%), Lee (36.3%), Walton (35.3%), and Hernando (32.6%). The lowest population growth rate was found in St. Bernard Parish (−44.3%), Louisiana, followed by three other parishes in Louisiana: Orleans, Plaquemine, and Cameron. The drastic loss of population in these counties was mostly a result of Hurricanes Katrina and Rita.
K-Means Clustering of Resilience Groups
Before conducting the K-means analysis, all three variables (exposure, damage, recovery) were standardized by using the median and the absolute average deviation (AAD). Since the distribution of the values of the damage variable had outliers, standardization by using the median and AAD is more robust than the conventional 0–1 standardization or normalization, because the median method is less sensitive to outlier (Tan et al. 2005).
To test if strong clusters of the data set do exist, 250 random comparison tests were generated. Each random test has the three variables randomized, but holding the same mean and standard deviation of the three variables. If a data set has strong clusters, the sum of squared error of the actual data should decrease more quickly than the random data as the number of clusters k goes up. The R script for K-means analysis was used for this part of the (Peeples 2011). The results did show that a four-cluster solution was the best, and that the four clusters derived did resemble the four states that have been observed in the natural system (Fig. 7). The K-mean analysis resulted in 4, 20, 14, and 14 counties in Groups 1–4 (susceptible, recovering, resistant, and usurper), respectively.
Fig. 7.
Plot of the four K-means clusters on the three elements (solid line = usurper, dashed line = resistant, dash-dot line = recovering, dotted line = susceptible)
Discriminant Analysis of Indicator Variables
The next question is: What are the underlying socioeconomic and environmental characteristics that can predict these resilience rankings? These underlying characteristics could serve as indicators of capacity to make the community less vulnerable and recover quicker and better. Based on previous research on social vulnerability index (Cutter et al. 2003; Cutter and Finch 2008), adaptive-capacity index (Nelson et al. 2010a, b), regional development indices (Nicholas 1998), resilient indicators (Cutter et al. 2010; Sherrieb et al. 2010), and the five capitals from Ellis (2000), as well as consideration of data availability and quality, we selected 28 variables to serve as indicators of a county’s adaptive capacity (Table 1). These variables were grouped into demographic, social, economic, government, and environmental capitals. This study then added the health capital, which is an important component when considering a community’s vulnerability and adaptive capacity. Toxic release inventory data, which could serve as an environmental quality indicator, were considered. However, due to the many missing values, the variable was not used. All variables were normalized by converting them into either densities per square mile, per capita, or percentage (Baker 2009; Li 2011).
Table 1.
Twenty-Eight Indicator Variables Used in the Discriminant Analysis
| Type of variable | Acronym | Variable | Justification |
|---|---|---|---|
| Demographic | PCTBLACK | Percent African American, 2000 | Cutter et al. (2003) |
| PCTHISPANIC | Percent Hispanic, 2000 | Cutter et al. (2003) | |
| PCTKIDS | Percent under 5 years old, 2000 | Cutter et al. (2003) | |
| PCTOLD | Percent over 65 years old, 2000 | Cutter et al. (2003) | |
| AVGPERHH | Average number of people per household, 2000 | Cutter et al. (2003) | |
| Social | PCTNOHS | Percent of the population over 25 with no high school diploma, 2000 | Cutter et al. (2003) |
| PFEMLBR | Percent of the workforce that is female, 2000 | Cutter et al. (2003) | |
| PCTFHH | Percent female-headed households | Cutter et al. (2003) | |
| PCTMOBL | Percent of homes that are mobile homes, 2000 | Cutter et al. (2003) | |
| PCTRENTER | Percent of the population that rents, 2000 | Cutter et al. (2003) | |
| HOUDEN | Number of houses per square mile, 2000 | Cutter et al. (2003) | |
| Economic | PCTPOV | Percent of the population living below poverty, 1999 | Cutter et al. (2003) |
| PCTCVLBF | Percent of the workforce that is employed, 2000 | Cutter et al. (2003) | |
| MVALOO | Median value of owner-occupied housing, 2000 | Cutter et al. (2003) | |
| MEDRENT | Median rent, 2000 | Cutter et al. (2003) | |
| PCTFRMPOP | Percent rural farm population, 2000 | Cutter et al. (2003) | |
| Government | LGFINREVPC | Local government finance, revenue per capita, 2002 | Brooks et al. (2005) |
| GENEXPPC | Local government finance general expenditures per capita, 2002 | Brooks et al. (2005) | |
| PERVOTE | Percent of the population that voted in 2000 presidential election, 2000 | Cutter et al. (2003) | |
| EXPEDPC | Local government finance expenditures for education, 2002 | Brooks et al. (2005) | |
| Environmental | MELE | Mean elevation of the county, 2008 | Baker (2009) |
| Health | INFMTR | 5-year average infant mortality per 10,000 births, 1998–2002 | Nicholas (1998) |
| CHILLD | 3-year average chronic illness deaths per 10,000 individuals, 1998–2000 | Nicholas (1998) | |
| DISNWRK | Disabled and nonworking labor forces per 10,000 individuals, 2000 | Nicholas (1998) | |
| LBWB | 3-year total low-birth-weight babies per 10,000 live births, 1998–2000 | Nicholas (1998) | |
| HUWNF | Households with no fuel used per 10,000 house units, 2000 | Nicholas (1998) | |
| HUWNP | Households with no plumbing per 10,000 house units, 2000 | Nicholas (1998) | |
| MD | Non-federal active medical doctors per 10,000 individuals, 2000 | Nicholas (1998) |
Note: Key references are included as justification.
The mean elevation of a county was derived by the authors through an elaborated geographic information system (GIS) procedure, using the digital elevation data obtained from the U.S. Geological Survey website (http://seamless.usgs.gov). The mean elevation was found to range from 0 m (0 ft) above sea level in Orleans Parish, Louisiana, the county with the lowest elevation in the northern Gulf of Mexico region, to 10.45 m (34.3 ft) above sea level in Mobile County, Alabama.
Data for the 4 a priori groups and 28 predictor variables were input to the SPSS statistical package for discriminant analysis. Discriminant analysis is often used to derive functions that are linear combinations of the predictor variables, using the criterion that the first function will discriminate the groups most (i.e., largest variance), followed by the second function, and so on, until the function derived is no longer statistically significant. Three discriminant functions were derived and found to be statistical significant, which explained 51.37, 36.53, and 12.1% of the total variance, respectively.
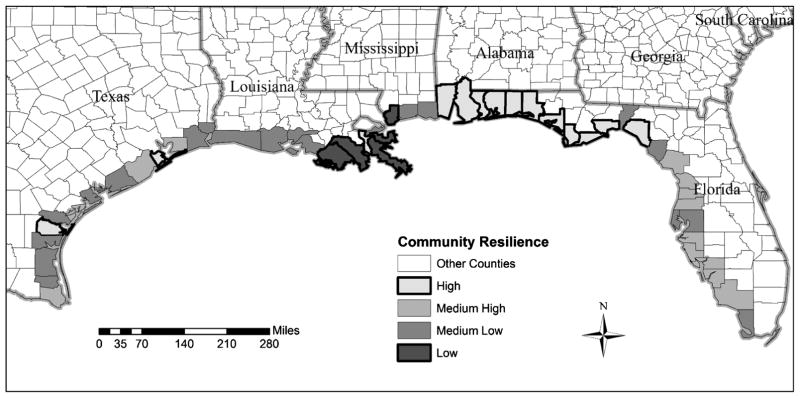
The next step of discriminant analysis is to use the discriminant functions to derive classification functions so that each county can be classified into one of the four groups based on their probabilities of group membership. The groups predicted by discriminant analysis can be compared with the a priori groups, thus providing a means to validate if the a priori groups are accurate. The classification results show that 94.2% of counties were correctly classified, or in other words, only 3 out of the 52 counties were misclassified. The three misclassified counties were: Terrebonne Parish, Louisiana, which was classified by K-means as Group 4, but was found to have a distance closer to Group 1’s centroid, hence it was downgraded from Group 4 (usurper) to Group 1 (susceptible). Nueces County, Texas, was upgraded from Group 2 to Group 4, and Hillsborough County, Florida, was downgraded from Group 3 to 2. Fig. 8 maps the final resilience rankings based on the discriminant analysis result. Applying Eq. (2), we converted the ranks to continuous resilience indices (Table 2). The results show that most of the counties had very low second-highest group probabilities (close to 0.0), therefore, there were only minor changes in the resultant numerical indices. The final results show that of the 52 counties, 5 were classified as Group 1 (susceptible), followed by 20, 13, and 15 in Groups 2–4, respectively.
Fig. 8.
Community resilience rankings derived by the discriminant analysis using 28 predictor variables
Table 2.
Derived RIM Resilience Indices of the 52 Counties
| County | Predicted rank | Second highest | Second-group probability | Resilience index |
|---|---|---|---|---|
| Cameron, TX | 3 | 3 | 0.0 | 3.0 |
| Wallacy, TX | 2 | 3 | 0.0 | 2.0 |
| Kenedy, TX | 2 | 2 | 0.0 | 2.0 |
| Kleberg, TX | 2 | 2 | 0.0 | 2.0 |
| Nueces, TX | 4 | 2 | 0.31 | 3.38 |
| San Patricio, TX | 2 | 3 | 0.03 | 2.03 |
| Aransas, TX | 3 | 3 | 0.0 | 3.0 |
| Calhoun, TX | 3 | 3 | 0.0 | 3.0 |
| Matagorda, TX | 2 | 2 | 0.0 | 2.0 |
| Brazoria, TX | 3 | 2 | 0.11 | 2.89 |
| Galverston, TX | 4 | 4 | 0.0 | 4.0 |
| Chambers, TX | 3 | 3 | 0.0 | 3.0 |
| Jefferson, TX | 2 | 2 | 0.0 | 2.0 |
| Orange, TX | 2 | 2 | 0.0 | 2.0 |
| Cameron, LA | 2 | 2 | 0.0 | 2.0 |
| Vermillion, LA | 2 | 2 | 0.0 | 2.0 |
| Iberia, LA | 2 | 2 | 0.0 | 2.0 |
| St. Mary, LA | 2 | 1 | 0.02 | 1.98 |
| Terrebonne, LA | 1 | 4 | 0.15 | 1.45 |
| Lafourche, LA | 1 | 4 | 0.01 | 1.03 |
| Jefferson, LA | 4 | 1 | 0.01 | 3.97 |
| Orleans, LA | 2 | 2 | 0.0 | 2.0 |
| Plaquemines, LA | 1 | 1 | 0.0 | 1.0 |
| St. Bernard, LA | 1 | 1 | 0.0 | 1.0 |
| Hancock, MS | 1 | 1 | 0.0 | 1.0 |
| Harrison, MS | 2 | 1 | 0.12 | 1.88 |
| Jackson, MS | 2 | 1 | 0.05 | 1.95 |
| Mobile, AL | 4 | 4 | 0.0 | 4.0 |
| Baldwin, AL | 4 | 4 | 0.0 | 4.0 |
| Escambia, FL | 4 | 4 | 0.0 | 4.0 |
| Santa Rosa, FL | 4 | 4 | 0.0 | 4.0 |
| Okaloosa, FL | 4 | 4 | 0.0 | 4.0 |
| Walton, FL | 4 | 4 | 0.0 | 4.0 |
| Bay, FL | 4 | 4 | 0.0 | 4.0 |
| Gulf, FL | 4 | 4 | 0.0 | 4.0 |
| Franklin, FL | 4 | 4 | 0.0 | 4.0 |
| Walkulla, FL | 4 | 1 | 0.03 | 3.91 |
| Jefferson, FL | 2 | 2 | 0.0 | 2.0 |
| Taylor, FL | 4 | 4 | 0.0 | 4.0 |
| Dixie, FL | 2 | 3 | 0.01 | 2.01 |
| Levy, FL | 3 | 3 | 0.0 | 3.0 |
| Citrus, FL | 3 | 3 | 0.0 | 3.0 |
| Hernando, FL | 3 | 3 | 0.0 | 3.0 |
| Pasco, FL | 3 | 3 | 0.0 | 3.0 |
| Hillsborough, FL | 2 | 3 | 0.08 | 2.08 |
| Pinellas, FL | 2 | 3 | 0.01 | 2.01 |
| Manatee, FL | 3 | 3 | 0.0 | 3.0 |
| Sarasota, FL | 3 | 3 | 0.0 | 3.0 |
| Charlotte, FL | 3 | 3 | 0.0 | 3.0 |
| Lee, FL | 3 | 3 | 0.0 | 3.0 |
| Collier, FL | 3 | 3 | 0.0 | 3.0 |
| Monroe, FL | 2 | 2 | 0.0 | 2.0 |
Note: AL = Alabama; FL = Florida; LA = Louisiana; MS = Mississippi; TX = Texas.
Results and Discussion
The resilience index map (Fig. 8) shows a striking, highly spatially contiguous pattern with some minor exceptions. Counties in Florida and Alabama generally had higher resilience to coastal hazards than the other three states. The Florida Panhandle area (such as Escambia, Santa Rosa, Okaloosa, Walton), as well as Alabama’s Mobile and Baldwin Counties, had maintained high population growth, despite having high exposure to coastal hazards such as frequent hurricane strikes. On the other hand, none of the counties in Louisiana and Mississippi had resilience rankings higher than 2, except Jefferson Parish, Louisiana, a suburb of New Orleans, Louisiana, which was classified as Group 4. In Texas, most counties were classified as either Group 2 or 3, with only two counties, Galveston and Nueces, classified as Group 4, the most resilient. As subsequently discussed, these Group 4 counties in Louisiana (Jefferson) and Texas (Galveston and Nueces) were characterized with higher socioeconomic capacity (e.g., higher percent of civilian labor force), which made them more resilient than their neighboring counties.
The five least-resilient counties included four from Louisiana: Lafourche, Plaquemines, St. Bernard, and Terrebonne, and one from Mississippi: Hancock. These counties were severely affected by Hurricanes Katrina and Rita in 2005, which might have skewed the analysis. Since the period of analysis falls in 1998–2008, the present study might not be able to capture the recovery after 2008. However, it is noted that the predictor variables used were recorded in 2000, which serve as indicators of preexisting capacity that would influence a county’s ability to recover (Sherrieb et al. 2010).
To evaluate the discriminating power of the indicator variables, the potency index of each variable was computed (Perreault et al. 1979). The potency index of a discriminating variable is a composite, relative measure of the variable’s total discriminating power across all significant discriminant functions. It is often used when there are more than two significant discriminant functions derived and is computed as follows:
| (5) |
where Potencyi = potency index of variable i; n = number of the significant discriminant functions; lij = discriminant loading of variable i on function j; and ej = eigenvalue of function j. The top 10 variables in descending order were: percent of population over 65 years old (0.19), percent of the workforce that is employed, percent female-headed households, mean elevation, average chronic illness deaths per 10,000 individuals, percent population under 5 years old, percent population without a high school diploma, percent Hispanic population, percent population living below poverty, and median rent (0.07).
An evaluation of the associations between the groups and the indicator variables show that Group 4, the highest resilient group, was highly positively correlated with percent of civilian labor force and mean elevation, and the counties in Group 4 were mostly located in the Florida Panhandle and Alabama area. Higher percentage of civilian labor force might have helped in the rebuilding and recovery process, and higher elevation would make the communities less susceptible to coastal hazards.
Group 3 was highly positively correlated with chronic illness death rates, median rent, and percent of population over 65 years old, and these characteristics were found mostly in counties along the eastern part of the Gulf of Mexico in Florida. Older but wealthier societies characterized by higher proportion of retirees would directly or indirectly increase the resiliency of the communities to coastal hazards.
Group 2 was highly positively correlated with percent of Hispanic, percent of the population living below poverty, percent of population under 5 years old, percent of female-headed households, and percent of the population without a high school diploma; and the counties in Group 2 were mostly from Louisiana, Mississippi, and Texas. Previous research confirmed that household poverty is highest for female-headed households with children that do not have other adult household earners (Snyder et al. 2006). High poverty, high percentage of population under 5 years old, and high percentage of female-headed households interact with each other reciprocally, leading to a community that has lower capacity to bounce back from coastal hazards.
Group 1 had five cases, but a closer look of their socioeconomic characteristics show that they were very similar to those in Group 2. They were the counties that had been severely impacted by Hurricanes Katrina and Rita. They became a distinct group themselves from the K-means analysis only because they had much more property damages than others, and thus they were assigned the lowest ranking of resilience. In other words, counties in Group 1 might be considered special cases, since counties in other groups had not experienced such catastrophes as Hurricanes Katrina and Rita during 1998–2008.
As in any empirical studies that deal with real-world spatial data, there is uncertainty involved when the conclusions are based on analysis of one set of data. Also, there are potential violations of statistical assumptions associated with the use of discriminant analysis for inferential purposes. For the pilot study here, tests of normality were not conducted due to the small number of counties studied. Furthermore, Box-M test of equality of variances among groups could not be computed because there were more numbers of variables than cases in each group. Nevertheless, the use of a small but relatively homogeneous sample in this pilot study has enabled a thorough demonstration of the approach. With further refinements, we expect the same approach can be extended to measure resiliency for many other regions and for different types of hazards.
Future studies to refine the RIM approach could be made in several ways. First, this study focused mostly on social resilience and has not considered ecological resilience. Ecological resilience indicators at the county level are difficult to define and data are not easily available. More research in this area is needed. Second, more resilience indicators, such as those related to social networks and community capital (Norris et al. 2008; Cutter et al. 2010; Aldrich 2012), as well as environmental or infrastructural variables such as development intensity (Brody et al. 2011) and crime rates (Lam et al. 2009; Sherrieb et al. 2010), could be added and tested for a larger study area so that more accurate discriminant functions could be derived and better future inference could be made. Similarly, different growth variables such as business and income growth in addition to population growth could also be tested (Chang 2010; Jordan and Javernick-Will 2013).
Conclusions
This paper aims to contribute to the literature by outlining a methodology to evaluate the resiliency of communities, and by providing an initial assessment of the resiliency of 52 Gulf Coast counties. The ultimate goal is to identify existing capacities that are associated with a community’s ability to reduce damage and bounce back from coastal hazards. The RIM approach, composed of three elements (exposure, damage, and recovery) and two relationships linking the three elements (vulnerability and adaptability), emphasizes statistical validation and enables inference. Four resilience groups were derived by the K-means clustering, and 28 variables that served as indicators of community capacity were tested to characterize the groups via discriminant analysis. The analysis yielded a remarkably high degree of classification accuracy (94.2%), meaning that the 28 variables can be used to explain the resiliency of a county. Generally, coastal counties along the eastern part of the Gulf of Mexico (Florida and Alabama) were found to have higher resilience than the western part of the Gulf (Texas, Louisiana, and Mississippi). High percentage of civilian labor force and high elevation were associated with high resiliency to coastal hazards, whereas high poverty, low education, and high percentage of female-headed households with children were associated with low resiliency.
This pilot study demonstrates that the RIM approach is promising. It also shows that more studies are needed to further refine the approach. The main advantage of the RIM approach is that it can be applied to analyze community resilience of different study regions, at different spatial and temporal scales, or for different types of hazard. We are currently applying the RIM approach to measure resilience in various regions including the Caribbean, China, and the Netherlands, and for different hazards including drought in southwestern United States and earthquake in China. The proxies for the three elements (exposure, damage, and recovery) and the social-ecological capacity indicators would be varied to suit the different study areas. The most important results of applying the RIM approach are a set of metrics that have been empirically validated and their relative weights in contributing to the overall resilience of a community (from the classification functions). These metrics and classification functions can be used to evaluate the effects of increasing (or decreasing) the value of one indicator (such as elevation or employment in this study) on the overall resiliency of a community in the study area. Moreover, the metrics and the classification functions derived from one study area can be applied to other study areas to evaluate the resiliency of their communities, as long as the two study areas have similar characteristics and the statistical assumptions are met. This inferential ability is especially useful to places where real damage data are not available. Therefore, with more testing and refinements in the future, the RIM approach could serve as a useful tool for measuring and identifying indicators that can be promoted to increase resilience for many regions around the world.
Acknowledgments
We appreciate the comments and suggestions from several anonymous reviewers and the guest editor. This material is based upon work supported by the U.S. Bureau of Ocean Energy Management (BOEM) (Grant Nos. M09AC15619, M09AC15620); the U.S. Department of Agriculture (Grant No. USDA 2010-65401-21312); and the U.S. National Science Foundation (Grant No. 1212112). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.
Contributor Information
Nina S. N. Lam, Email: nlam@lsu.edu.
Margaret Reams, Email: mreams@lsu.edu.
Kenan Li, Email: kli4@lsu.edu.
Chi Li, Email: liz0817@gmail.com.
Lillian P. Mata, Email: lillian.p.mata@gmail.com.
References
- Adger WN, Brown K. Editorial: Progress in global environmental change. Global Environ Change. 2010;20(4):547–549. [Google Scholar]
- Adger WN, Hughes TP, Folke C, Carpenter SR, Rockstrom J. Social-ecological resilience to coastal disasters. Science. 2005;309(5737):1036–1039. doi: 10.1126/science.1112122. [DOI] [PubMed] [Google Scholar]
- Aldrich DP. Building resilience: Social capital in post-disaster recovery. University of Chicago Press; Chicago: 2012. [Google Scholar]
- Baker A. MS thesis. Dept. of Environmental Sciences, Louisiana State Univ; Baton Rouge, LA: 2009. Creating an empirically derived community resilience index of the Gulf of Mexico region. [Google Scholar]
- Batista WB, Platt WJ. Tree population response to hurricane disturbance: Syndromes in a southeastern United States old-growth forest. J Ecol. 2003;91:197–212. [Google Scholar]
- Bellingham PJ, Tanner EVJ, Healey JR. Damage and responsiveness of Jamaican montane tree species after disturbance by a hurricane. Ecology. 1995;76(8):2562–2580. [Google Scholar]
- Bevington JS, et al. Measuring, monitoring and evaluating post-disaster recovery: A key element in understanding community resilience. Proc., ASCE Structures Congress; 2011; ASCE, Reston, VA. 2011. [Google Scholar]
- Blum MD, Roberts HH. Drowning of the Mississippi delta due to insufficient sediment supply and global sea-level rise. Nat Geosci Lett. 2009;2(7):488–491. [Google Scholar]
- Brody SD, Gunn J, Peacock W, Highfield WE. Examining the influence of development patterns on flood damages along the Gulf of Mexico. J Plann Educ Res. 2011;31(4):438–448. [Google Scholar]
- Brooks N, Adger WN, Kelly PM. The determinants of vulnerability and adaptive capacity at the national level and the implications for adaptation. Global Environ Change. 2005;15(2):151–163. [Google Scholar]
- CARRI (Community and Regional Resilience Institute) Building resilience in America’s communities: Observations and implications of the CRS pilots. [(Jul 3 2013)];2013a < http://www.resilientus.org/wp-content/uploads/2013/05/CRS-Final-Report.pdf>.
- CARRI (Community and Regional Resilience Institute) Definitions of community resilience: An analysis. [Jan 11 2014];2013b < http://www.resilientus.org/wp-content/uploads/2013/08/definitions-of-community-resilience.pdf>.
- Chang SE. Urban disaster recovery: A measurement framework and its application to the 1995 Kobe earthquake. Disasters. 2010;34(2):303–327. doi: 10.1111/j.1467-7717.2009.01130.x. [DOI] [PubMed] [Google Scholar]
- Cutter SL, Boruff BJ, Shirley WL. Social vulnerability to environmental hazards. Social Sci Q. 2003;84(2):242–261. [Google Scholar]
- Cutter SL, Burton CG, Emrich CT. Disaster resilience indicators for benchmarking baseline conditions. J Homeland Secur Emergency Manage. 2010;7(1) [Google Scholar]
- Cutter SL, Finch C. Temporal and spatial changes in social vulnerability to natural hazards. Proc Natl Acad Sci. 2008;105(7):2301–2306. doi: 10.1073/pnas.0710375105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis F. Rural livelihoods and diversity in developing countries. Oxford University Press; Oxford, U.K: 2000. [Google Scholar]
- Finch C, Emrich C, Cutter SL. Disaster disparities and differential recovery in New Orleans. Popul Environ. 2010;31(4):179–202. [Google Scholar]
- Folke C, Carpenter S, Elmqvist T, Gunderson L, Holling CS, Walker B. Resilience and sustainable development: Building adaptive capacity in a world of transformations. Ambio. 2002;31(5):437–440. doi: 10.1579/0044-7447-31.5.437. [DOI] [PubMed] [Google Scholar]
- Hamin EM, Gurran N. Urban form and climate change: Balancing adaptation and mitigation in the U.S. and Australia. Habitat Int. 2009;33(3):238–245. [Google Scholar]
- Holling CS. Engineering resilience versus ecological resilience. In: Schelze P, editor. Engineering within ecological constraints. National Academy Press; Washington, DC: 1996. pp. 31–44. [Google Scholar]
- MaCarthy J, Canziani O, Leary N, Dokken D, White K, editors. IPCC (Intergovernmental Panel on Climate Change) Climate change 2001: Impacts, adaptation, and vulnerability. Cambridge University Press; Cambridge, U.K: 2001. [Google Scholar]
- IPCC (Intergovernmental Panel on Climate Change) Climate change 2007: Synthesis report. In: Pachauri RK, Reisinger A, editors. Contribution of Working Groups I, II and III to the Fourth Assessment Rep. of the Intergovernmental Panel on Climate Change. Vol. 104 Geneva: 2007. [Google Scholar]
- IPCC (Intergovernmental Panel on Climate Change) Summary for policymakers. In: Field CB, et al., editors. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Rep. of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, U.K: 2014. pp. 1–32. [Google Scholar]
- Jordan E, Javernick-Will A. Indicators of community recovery: Content analysis and Delphi approach. Nat Hazard Rev. 2013:21–28. doi: 10.1061/(ASCE)NH.1527-6996.0000087. [DOI] [Google Scholar]
- Lam NSN, Arenas H, Pace K, LeSage J, Campanella R. Predictors of business return in New Orleans after Hurricane Katrina. PLoS One. 2012;7(10):e47935. doi: 10.1371/journal.pone.0047935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam NSN, Pace K, Campanella R, LeSage JP, Arenas H. Business return in New Orleans: Decision making amid post-Katrina uncertainty. PLoS One. 2009;4(8):e6765. doi: 10.1371/journal.pone.0006765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeSage JP, Pace RK, Lam NSN, Campanella R, Liu X. Do what the neighbors do: Reopening businesses after Hurricane Katrina. Significance. 2011a;8(4):160–163. [Google Scholar]
- LeSage JP, Pace RK, Lam NSN, Campanella R, Liu X. New Orleans business recovery in the aftermath of Hurricane Katrina. J Roy Stat Soc A. 2011b;174(4):1007–1027. [Google Scholar]
- Li K. MS thesis. Dept. of Environmental Sciences, Louisiana State Univ; Baton Rouge, LA: 2011. Temporal changes of coastal community resilience in the Gulf of Mexico region. [Google Scholar]
- Li W, Airriess C, Chia-Chen A, Leong KJ, Keith V. Katrina and migration: Evacuation and return by African Americans and Vietnamese Americans in an eastern New Orleans suburb. Prof Geogr. 2010;62(1):103–118. [Google Scholar]
- Liu KB, Lam NSN. Paleovegetational reconstruction based on modern and fossil pollen data: An application of discriminant analysis. Annu Assoc Am Geogr. 1985;75(1):115–130. [Google Scholar]
- Miles SB, Green RA, Svekla W. Disaster risk reduction capacity assessment for precarious settlements in Guatemala City. Disasters. 2012;36(3):365–381. doi: 10.1111/j.1467-7717.2011.01267.x. [DOI] [PubMed] [Google Scholar]
- Nelson R, Kokic R, Crimp S, Meinke H, Howden SM. The vulnerability of Australian rural communities to climate variability and change. Part I—Conceptualizing and measuring vulnerability. Environ Sci Policy. 2010a;13(1):8–17. [Google Scholar]
- Nelson R, Kokic R, Crimp S, Meinke H, Howden SM. The vulnerability of Australian rural communities to climate variability and change. Part II—Integrating impacts with adaptive capacity. Environ Sci Policy. 2010b;13(1):18–27. [Google Scholar]
- Nicholas DE. MS thesis. Dept. of Geography and Anthropology, Louisiana State Univ; Baton Rouge, LA: 1998. Measuring development in the lower Mississippi delta: An integrated approach. [Google Scholar]
- Nie NH, Hull CH, Jenkins JG, Steinbrenner K, Bent DH. SPSS-statistical packages for the social sciences. 2. McGraw-Hill; New York: 1975. [Google Scholar]
- Norris FH, Stevens SP, Pfefferbaum B, Wyche KF, Pfefferbaum RL. Community resilience as a metaphor, theory, set of capacities, and strategy for disaster readiness. Am J Commun Psychol. 2008;41(1–2):127–150. doi: 10.1007/s10464-007-9156-6. [DOI] [PubMed] [Google Scholar]
- NRC (National Research Council) Disaster resilience: A national imperative. National Academies Press; Washington, DC: 2012. [Google Scholar]
- Peduzzi P, Dao H, Herold C, Mouton F. Assessing global exposure and vulnerability towards natural hazards: The disaster risk index. Nat Hazards Earth Syst Sci. 2009;9:1149–1159. [Google Scholar]
- Peeples MA. R script for k-means cluster analysis. [May 15, 2011];2011 < http://www.mattpeeples.net/kmeans.html>.
- Perreault WD, Behrman DN, Armstrong GM. Alternative approaches for interpretation of multiple discriminant analysis in marketing research. J Bus Res. 1979;7(2):151–173. [Google Scholar]
- Reams MA, Lam NSN, Baker A. Measuring capacity for resilience among coastal counties of the U.S. northern Gulf of Mexico region. Am J Clim Change. 2012;1(4):194–204. doi: 10.4236/ajcc.2012.14016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherrieb K, Norris FH, Galea S. Measuring capacities for community resilience. Social Indic Res. 2010;99(2):227–247. [Google Scholar]
- Snyder AR, McLaughlin DK, Findeis J. Household composition and poverty among female-headed households with children: Differences by race and residence. Rural Sociol. 2006;71(4):597–624. [Google Scholar]
- Tabachnick BG, Fidell LS. Using multivariate statistics. 4. Allyn and Bacon; Boston: 2000. [Google Scholar]
- Tan PN, Steinbach M, Kumar V. Introduction to data mining. 1. Addison-Wesley Longman; Boston: 2005. [Google Scholar]
- Tierney K. Disaster governance: Social, political, and economic dimensions. Ann Rev Environ Resour. 2012;37(1):341–363. [Google Scholar]
- Tierney K, Oliver-Smith A. Social dimensions of disaster recovery. Int J Mass Emergencies Disasters. 2012;30(2):123–146. [Google Scholar]
- Turner BL, et al. Science and technology for sustainable development special feature: A framework for vulnerability analysis in sustainability science. Proc Natl Acad Sci. 2003;100(14):8074–8079. doi: 10.1073/pnas.1231335100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner BL. Vulnerability and resilience: Coalescing or paralleling approaches for sustainability science? Global Environ Change. 2010;20(4):570–576. [Google Scholar]
- Vogel C. Foreword: Resilience, vulnerability and adaptation: A cross-cutting theme of the international human dimensions programme on global environmental change. Global Environ Change. 2006;16(3):235–236. [Google Scholar]
- Walker BH, Anderies JM, Kinzing AP, Ryan P. Exploring resilience in socio-ecological systems through comparative studies and theory development: Introduction to the special issue. Ecol Soc. 2006a;11(1):12. [Google Scholar]
- Walker BH, Gunderson LH, Kinzing AP, Folke C, Carpenter SR, Schultz L. A handful of heuristics and some propositions for understanding resilience in social-ecological systems. Ecol Soc. 2006b;11(1):13. [Google Scholar]
- Yusuf AA, Francisco H. Economy and Environmental Program for Southeast Asia (EEPSEA) Singapore: 2009. Climate change vulnerability mapping for southeast Asia. [Google Scholar]