Guided Formation of 3D Helical Mesostructures by Mechanical Buckling: Analytical Modeling and Experimental Validation

Abstract

Three-dimensional (3D) helical mesostructures are attractive for applications in a broad range of microsystem technologies, due to their mechanical and electromagnetic properties as stretchable interconnects, radio frequency antennas and others. Controlled compressive buckling of 2D serpentine-shaped ribbons provides a strategy to formation of such structures in wide ranging classes of materials (from soft polymers to brittle inorganic semiconductors) and length scales (from nanometer to centimeter), with an ability for automated, parallel assembly over large areas. The underlying relations between the helical configurations and fabrication parameters require a relevant theory as the basis of design for practical applications. Here, we present an analytic model of compressive buckling in serpentine microstructures, based on the minimization of total strain energy that results from various forms of spatially dependent deformations. Experiments at micro- and millimeter-scales, together with finite element analyses (FEA), were exploited to examine the validity of developed model. The theoretical analyses shed light on general scaling laws in terms of three groups of fabrication parameters (related to loading, material and 2D geometry), including a negligible effect of material parameters and a square root dependence of primary displacements on the compressive strain. Furthermore, analytic solutions were obtained for the key physical quantities (e.g., displacement, curvature and maximum strain). A demonstrative example illustrates how to leverage the analytic solutions in choosing the various design parameters, such that brittle fracture or plastic yield can be avoided in the assembly process.

Graphical abstract

Analytic models, finite element analyses and experiments are presented to capture all quantitative aspects of buckling-guided formation of 3D helical mesostructures. The resulting scaling laws include negligible roles of cross-sectional and material parameters on the 3D configurations, enabling predictions of physical quantities with analytic solutions. These findings can serve as design references for assembly of structures optimized for device applications.

1. Introduction

Three-dimensional (3D) helical mesostructures hold great potential for a broad range of applications in microsystem technologies, such as microelectromechanical systems (MEMS),^[1,2] electrodes for lab-on-a-chip systems,^[3,4] and stretchable electronics.^[5,6] To form 3D architectures of helical and other relevant topologies at micro/nanoscale, several classes of fabrication/assembly approaches have been developed by exploiting different working mechanisms.^[2,6–35] Representative approaches include microcontact printing,^[15,16] MEMS lithography/electroplating techniques,^[17–19] manual winding,^[20] residual-stress-induced self-rolling of thin films/belts,^[21–24] controlled mechanical buckling,^[6,32] and 3D additive printing based on direct ink deposition,^[2,25–29] or direct laser writing,^[30,31] (sometimes in combination with liquid metal paste filling^[29] or the electrochemical deposition and plasma etching^[31]). Most of these approaches, such as lithography/electroplating techniques,^[17–19] manual winding,^[20] and 3D additive printing,^[2,25–31] apply directly only to certain classes of materials, e.g., metals and/or polymers, and generally not to high-performance semiconductors (e.g., single-crystal silicon) that are widely adopted in modern high-quality electronics and optoelectronics. Although the methods based on residual-stress-induced self-rolling^[21–24] are naturally compatible with modern planar technologies and offer yields and throughputs necessary for practical applications, they provide access to certain classes of hollow polyhedral or cylindrical geometries, with the upper length scales limited, to certain extent, by the achievable level of residual stresses. In comparison, approaches that rely on buckling in thin 2D ribbons/membranes^[6,14] provide access to a broader range of 3D topologies, while offering a natural compatibility with essentially all modern planar technologies, thereby suggesting many possibilities in building sophisticated classes of 3D electronic, optical, and electromagnetic devices. A powerful feature of this approach^[6,14] is the versatility in the applicable materials, ranging from soft polymers, to brittle inorganic semiconductors, to plastic metals, and length scales, ranging from nanometer, to micrometer, to centimeter length scales. Recent work includes demonstrations of silicon and/or metallic helical mesostructures in various topologies, including straight helices with different chiralities, double helices, nested helices, toroids and conical spirals,^[6] by using variants of filamentary serpentine microstructures as the initial 2D patterns. The underlying relations between the 3D configurations, fracture-induced failure and fabrication related parameters (e.g., prestrain level, the geometric parameters of the serpentine microstructures) require a relevant theory as the basis for the design of structures for specific applications. The mechanics of buckling and postbuckling that govern the 2D-3D transformation are, however, complex, since the deformation of the ribbon-type structures involves not only planar bending deformations, but also twisting and general spatial bending deformations. Previous theories developed either for postbuckling of straight ribbons,^[36–40] or critical buckling of curvy ribbons,^[41,42] cannot be used in the analyses of postbuckling for serpentine microstructures. This paper introduces an analytic model of compressive buckling that is capable of predicting not only the full 3D geometry of helical mesostructures, but also the strain level, of relevance to structural reliability. Systematic finite element analyses (FEA) and experimental measurement on 3D helical mesostructures with different geometries validate the utility of the model. The results provide theoretical insight into the scaling laws of deformation and strain with various parameters, including a negligible effect of material parameters and a square root dependence of curvature on the compressive strain. Furthermore, analytic solutions were obtained for the key physical quantities, including the displacement, twist angle, curvature and strain, which can facilitate design optimization in practical applications.

2. An analytic model for the compressive buckling of serpentine microstructures

Figure 1a presents a schematic illustration of the process for forming three chains of helices with different geometries guided by compressive buckling. The initial 2D precursors correspond to thin serpentine microstructures (as shown in the left, bottom panel of Figure 1b) that are strongly bonded, at certain locations (red circles), with a prestrained elastomeric substrate. Releasing the prestrain imparts compressive forces on the serpentine microstructures, thereby lifting the non-bonded locations out of the plane and into 3D configurations. A theoretical model is introduced below to analyze such postbuckling processes, and to determine the full 3D configuration as well as the strain distribution for different initial geometries and prestrain levels.

Figure 1. Illustration of the buckling-guided formation of 3D helical mesostructures and mechanics model.

(a) Schematic illustration of the compressive buckling process for the 2D serpentine microstructures with three different geometries; (b) Illustration of the mechanics model and coordinate system, showing the undeformed and deformed configurations. The red dots denote the sites of strong bonding with an elastomeric substrate in fabrication. A representative unit cell of the serpentine microstructures consists of two identical arcs, each with the radius of R and top angle of θ₀.

2.1. Geometry, displacement and curvature

Due to the structural periodicity, we focus on the analyses of a representative unit cell in the serpentine microstructure, which consists of two identical arcs, each with a radius of R and top angle of θ₀, as shown in Figure 1b (top). The top angle must be smaller than 5π / 3 to avoid self-overlap of the microstructures, and in practical applications, this parameter is typically in the range of [0, 5π / 4]. To facilitate the buckling, the serpentine microstructure usually adopts an ultra-thin geometry, in which the thickness (t) is much smaller than the width (w), corresponding to a large cross-sectional aspect ratio (e.g., w / t > 20). This class of serpentine microstructures has been widely explored in various stretchable bioelectronic devices as a key design strategy to achieve system-level stretchability.^[43–52]

A Cartesian coordinate system (X,Y,Z) has its origin at the joint of two arcs, where the X and Z axes correspond to the out-of-plane and axial direction of the serpentine microstructure. The unit vectors in such coordinates (X,Y,Z) before deformation are Ẽ_i (i = 1,2,3). A parametric coordinate θ (corresponding to the arc length S=Rθ) denote the location along the central axis of the arcs, such that θ ∈ [0, θ₀] and [θ₀, 2θ₀] represent the first and second arc, respectively. The initial configuration of the central axis, r₀(θ) = X₀(θ)Ẽ₁ + Y₀(θ)Ẽ₂ + Z₀(θ)Ẽ₃, can be represented by the following parametric equation,

$$\{\begin{array}{l}{X}_0=0\hfill \\ Y_0=R\left[cos\left(\frac{{\theta }_0}{2}-\theta \right)-cos\frac{{\theta }_0}{2}\right],\theta \in [0,{\theta }_0],\text{and}\hfill \\ Z_0=-R\left[sin\frac{{\theta }_0}{2}+sin\left(\frac{{\theta }_0}{2}-\theta \right)\right]\hfill \end{array}$$ (1a)

$$\{\begin{array}{l}{X}_0=0\hfill \\ Y_0=-R\left[cos\left(-\frac{3{\theta }_0}{2}+\theta \right)-cos\frac{{\theta }_0}{2}\right],\theta \in [{\theta }_0,2{\theta }_0].\hfill \\ Z_0=R\left[sin\frac{{\theta }_0}{2}+sin\left(-\frac{3{\theta }_0}{2}+\theta \right)\right]\hfill \end{array}$$ (1b)

In the deformation analyses of curvy ribbons, a local coordinate system is usually required to characterize the location of central axis, as illustrated in Figure 1b (top). Before deformation, the corresponding unit vectors are denoted by E_i (i = 1,2,3), where E₃ is the tangential direction; E₁ and E₂ lie in the cross-sectional plane, with E₁ (or equivalently Ẽ₁) along the out-of-plane direction, and E₂ the radial direction of the arcs. During the postbuckling, out-of-plane deformations are induced, thereby transforming the central axis into a spatial curve. A material point of this central axis denoted by r₀ before deformation moves to r = r₀ + U = XẼ₁ + YẼ₂ + ZẼ₃ after deformation, where U is the displacement. The unit vector along the tangential direction of deformed central axis is e₃ = dr/ds, as shown in the right, bottom panel of Figure 1b, where s denotes the arc length after deformation. The other two unit vectors, e₁ and e₂, involve twisting of the cross section along the central axis, and remain in the cross-sectional plane according to Kirchhoff assumptions. Their derivatives are related to the curvature vector κ by Love:^[53]

$$\frac{{\mathit{e}}_i^{\prime }}{\lambda }=\mathit{\kappa }\times {\mathit{e}}_i,(i=1,2,3),$$ (2)

where ( )′ = d( )/dS; λ = ds/dS is the stretch along the central axis; κ₁ and κ₂ denote the curvatures in the (e₂,e₃) and (e₁,e₃) surfaces; and the twisting curvature κ₃ is related to the twist angle ϕ of the cross section by κ₃ = ϕ′/λ. The unit vectors before and after deformation are related by the direction cosine (a_ij, See Supporting Information for details): e_i = a_ij E_j, (i = 1,2,3, summation over j).

$${\mathit{e}}_i=a_{ij}{\mathit{E}}_j,(i=1,2,3,\text{summation}\text{over}j).$$ (3)

According to the finite-deformation beam theory,^[39] the displacement U of the central axis and the twist angle ϕ of the cross section can fully characterize the deformation of a curvy beam. For the serpentine microstructure shown in Figure 1b (top), only the left arc is studied in the following, considering its anti-symmetric geometry in both the un-deformed and deformed configurations. Release of prestrain (ε_pre) in an elastomeric substrate induces a compressive strain, ε_appl = ε_pre / (1+ε_pre), to the serpentine microstructure, leading to its buckling. During the postbuckling, the displacement (Ũ₂) of serpentine microstructures along the Y axis is negligible,^[6] since the compression is applied along the Z axis and the buckling mainly induces out-of-plane displacements (along the X axis). This characteristic indicates the displacement vector can be simplified as U = Ũ₁Ẽ₁ + Ũ₃Ẽ₃ = Ũ₁Ẽ₁ + Ũ₂Ẽ₂ + Ũ₃Ẽ₃, in which Ũ₁= U₁. During postbuckling, the equilibrium requires that the out-of-plane displacement U₁ and twist angle ϕ have the same order, while the in-plane displacements U₂ and U₃ have the same order as the square of U₁ (or ϕ),^[39] i.e., ϕ ~ U₁ and U₂ ~ U₃ ~ (U₁)². Since the axial displacement (Ũ₃) induced by the external compression scales with the applied strain ε_appl, an approximate scaling between the general displacements (U_i and ϕ) and applied strain can be obtained,

$$\varphi \propto \sqrt{{\epsilon }_{\mathit{appl}}},U_1\propto \sqrt{{\epsilon }_{\mathit{appl}}},U_2\propto {\epsilon }_{\mathit{appl}},\text{and}{U}_3\propto {\epsilon }_{\mathit{appl}}.$$ (4)

The above relations show remarkable agreements with FEA results (Figure S1, Supporting Information). Consistent with the intuitive expectations, an approximate proportional relation between the twist angle (ϕ) and parametric coordinate (θ) is observed in FEA (Figure S2a, Supporting Information), indicating that the twist angle can be given by $\varphi =a\theta \sqrt{{\epsilon }_{\mathit{appl}}}$, with the parameter a to be determined. FEA results (Figure S2b, Supporting Information) show that the normalized displacement [U₁(θ)/U₁(θ₀)] is approximately a single-variable function of θ/θ₀, and the distribution of U₁ can be well characterized by (See Supporting Information for details)

$$U_1=bRsin\left(\frac{\pi \theta }{2{\theta }_0}\right){\left(2-\frac{\theta }{{\theta }_0}\right)}^2{\left(\frac{\theta }{{\theta }_0}\right)}^2\sqrt{{\epsilon }_{\mathit{appl}}},$$ (5)

where b is a dimensionless parameter to be determined. It should be noticed that the boundary conditions pose additional considerations on the selection of displacement functions in the energy approach. The axial displacement (Ũ₃) is comprised of two parts, a uniform part [Ũ_3uniform = −ε_applZ₀(θ)] due to the global compression from two ends, and a non-uniform part (Ũ_3nonuniform) due to local bending and twisting. Since the boundary conditions are expressed directly in terms of the displacement components in the local coordinate system (See Supporting Information for details), the constructions of displacement functions for U_2nonuniform and U_3nonuniform are more straightforward. Together with FEA calculations on a wide range of serpentine geometries (Figure S3, Supporting Information), a set of functions that can both satisfy the boundary conditions and fit well the FEA results are adopted, which read

$$U_{2\mathit{nonuniform}}=-R{\epsilon }_{\mathit{appl}}cos\left(\frac{\pi \theta }{{\theta }_0}\right)\left(1-\frac{\theta }{{\theta }_0}\right)\left(\frac{\theta }{{\theta }_0}\right)\left[c_1\frac{\theta }{{\theta }_0}\left(2-\frac{\theta }{{\theta }_0}\right)+\frac{{\theta }_0}{2}sin({\theta }_0)\right],\text{and}$$ (6a)

$$U_{3\mathit{nonuniform}}=R{\epsilon }_{\mathit{appl}}\left[cos{\left(\frac{{\theta }_0}{2}\right)}^{2}cos\left(\frac{\pi \theta }{{\theta }_0}\right)\left(1-\frac{\theta }{{\theta }_0}\right)\theta +c_{2}sin\left(\frac{\pi \theta }{{\theta }_0}\right){\left(1-\frac{\theta }{{\theta }_0}\right)}^3\left(\frac{\theta }{{\theta }_0}\right)\right],$$ (6b)

where c₁ and c₂ are two dimensionless parameters to be determined by the energy minimization detailed in Section 2.2. As shown by Su et al.,^[39] the work conjugate of bending moment and torque is κ̂ =λκ, which can be given in terms of U_i and ϕ by

$${\widehat{\kappa }}_1=-U_2^{″}+\left(\varphi -\frac{U_1}{R}\right)U_1^{″}-\frac{U_1^{\prime 2}}{2R}+\frac{U_3^{\prime }}{R}-\frac{1}{2R}{\left(\varphi -\frac{U_1}{R}\right)}^2+\frac{1}{R},$$ (7a)

$${\widehat{\kappa }}_2=U_1^{″}-\frac{R\varphi -U_1}{R^2},$$ (7b)

$${\widehat{\kappa }}_3={\varphi }^{\prime },$$ (7c)

where the terms higher than the 3^rd power of displacement components are neglected. Insertion of Eqs. (5), (6), and $\varphi =a\theta \sqrt{{\epsilon }_{\mathit{appl}}}$ into Eq. (7) then gives the distribution of curvature components along the 3D helical mesostructures (See Supporting Information for details).

2.2. Energy approach

Due to the ultra-thin geometry of serpentine microstructures, the local strain usually stays at a low level, such that the linear elastic constitutive relations can be adopted. As such, the total strain energy (Π_tot) that mainly consists of in-plane bending energy, out-of-plane bending energy, and twisting energy, can be written as

$$\begin{array}{l}{\mathrm{\Pi }}_{\mathit{tot}}={EI}_1{\int }_0^{{\theta }_{0}R}{\left({\widehat{\kappa }}_1-\frac{1}{R}\right)}^2\mathrm{d}S+{EI}_2{\int }_0^{{\theta }_{0}R}{\widehat{\kappa }}_2^2\mathrm{d}S+{GI}_p{\int }_0^{{\theta }_{0}R}{\widehat{\kappa }}_3^2\mathrm{d}S\\ ={EI}_{2}R\left[{\left(\frac{w}{t}\right)}^2{\int }_0^{{\theta }_0}{\left({\widehat{\kappa }}_1-\frac{1}{R}\right)}^2\mathrm{d}\theta +{\int }_0^{{\theta }_0}{\widehat{\kappa }}_2^2\mathrm{d}\theta +\frac{2}{1+\nu }{\int }_0^{{\theta }_0}{\widehat{\kappa }}_3^2\mathrm{d}\theta \right],\end{array}$$ (8)

for a unit cell of the serpentine microstructure, where EI₁ = (Ew³t)/12 and EI₂ = (Ewt³)/12 are the in-plane and out-of-plane bending stiffness, respectively, GI_p ≈ (Gwt³)/3 is the twisting stiffness for thin ribbons, and ν is the Poisson ratio. Since the serpentine microstructures are highly flexible, the membrane energy is neglected in Eq. (8), which can be introduced as a constraint during the energy minimization. Such constraint can be written in the following form:

$${\int }_0^{{\theta }_0}\left\{{\left[\frac{\mathrm{d}X(\theta )}{\mathrm{d}\theta }\right]}^2+{\left[\frac{\mathrm{d}Y(\theta )}{\mathrm{d}\theta }\right]}^2+{\left[\frac{\mathrm{d}Z(\theta )}{\mathrm{d}\theta }\right]}^2-R^2\right\}d\theta =0.$$ (9)

For any prescribed geometries (w / t, w / R, and θ₀) and external strain (ε_appl), minimization of the total energy by searching over a reasonable range for each dimensionless parameter (a, b, c₁ and c₂) then gives solutions for the four unknowns. The process can be implemented numerically (e.g., using commercial software MAPLE or MATLAB). After the determination of displacement components (ϕ, U₁, U₂ and U₃), the coordinates of every material point in the serpentine microstructure can be obtained, thereby giving the full 3D helical configuration during postbuckling. Equation (8) indicates that the change of in-plane bending curvature should be much smaller than the counterpart of out-of-plane bending and twisting, for ultra-thin (i.e., w / t > 20) geometries of 2D precursors, because of the huge coefficient (w² / t²) in the corresponding energy term.

2.3. Validation of the model by experiments and FEA

Two different sets of experiments (see Experimental Section for details) using both the microscale epoxy (SU8) and millimeter-scale plastic, as well as 3D FEA were carried out to validate the above analytic model. Figure 2a and Figure S4 (Supporting Information) present the model predictions, FEA calculations and experimental results on the deformed configurations under three different levels of applied strain, for a wide range of serpentine geometries (with the arc angle from 30° to 210°). The extent of twisting increases evidently with the arc angle increasing from 30° to 210°. Good agreements can be observed among the results of different approaches, for all of the different geometries and loading levels. Figure 2b–d illustrates the distribution of dimensionless displacement components (ϕ/θ₀), (Ũ₁/L and Ũ₃/L), with L = Rθ₀ denoting the arc length) for a representative 3D helical mesostructure (with θ₀=150°) under different levels of applied strain, which provides quantitative evidence on the accuracy of analytic model. Both the out-of-plane displacement (Ũ₁/L) and twist angle (ϕ/θ₀) reach their maximum magnitudes at the center of 3D helical mesostructures. The distribution of dimensionless in-plane displacements (U₂/L and U₃/L) in the local coordinate system appears in Figure S5 (Supporting Information).

Figure 2. Experimental, numerical and analytical studies of the buckling deformations.

(a) Modeling, FEA, optical images (millimeter-scale experiment), and colorized scanning electron microscope (SEM) (microscale experiment) of 3D helical mesostructures with different arc angles (30°, 90°, 150° and 210°) under different levels of compressive strains (0, 20%, 40% and 60%). The color of FEA results represents the magnitude of maximum principal strain. All of the scale bars in the micro- and millimeter-scale experiments are 500 μm and 5 mm, respectively. (b)~(d) Analytic and FEA results on the distribution of dimensionless pop-up displacement, axial displacement and twist angle for the helical mesostructures (with θ₀ = 150°) under different levels of compressive strains. The geometric parameters include (w / R = θ₀ / 17, t = 75 μm and w = 900 μm) for modeling, FEA and millimeter-scale experiment, and [w / R = θ₀ / 17, t = 7 μm and w ≈ 61 μm for θ₀ = 30°, 90° and 150° (or w ≈ 65 μm for θ₀ = 210°)] for microscale experiment.

3. Results and discussions

After validating the analytic model, this section utilizes the model to analyze the effects of various geometric and material parameters on the 3D helical mesostructures, aiming to establish useful scaling laws that can facilitate the design optimization in practical applications.

In general, the final 3D helical configurations might be affected by three groups of fabrication-related parameters: 1) loading parameter (ε_appl); 2) material parameters (E and ν); 3) geometric parameters (w / t, w / R, and θ₀). The theoretical analyses in Section 2.1 already reveal the dependence [Eq. (4)] of displacement components on the applied strain. Furthermore, the expression [Eq. (8)] of total strain energy indicates that the modulus (E) has essentially no effect on the minimization process, and hence, makes no difference on the 3D configurations. While the Poisson ratio (ν) comes into play in the twisting energy in Eq. (8), both analytic and FEA results show that this material parameter has negligible effects on the primary displacements (ϕ/θ₀ and U₁/L) during postbuckling, as shown in Figure 3a and Figure S6a (Supporting Information), for ν varying in a wide range of [0, 0.5]. This feature is also in accordance with the experiment results in Figure 2a, where two different types of materials (epoxy and plastic) result in nearly the same helical configurations. For thin, slender serpentine microstructures, e.g., with w / t > 20 and w / R < 0.3, the cross-sectional geometric parameters (w / t and w / R) also play negligible roles on the primary displacements (Figures S6b,c and S7), in accordance with our intuitive expectations. The relatively large discrepancy between analytic and FEA results for relatively wide serpentine precursors (e.g., w / R ~ 0.4) is attributed to the neglect of transverse shear effect in the current analytic model. Based on the above analyses, it can be deduced that the dimensionless parameters (a, b, c₁ and c₂) are merely dependent on a single geometric parameter (θ₀) for thin, slender serpentine microstructures. As such, approximate solutions to the parameters (a and b) related to the primary displacements (ϕ and U₁) can be obtained by fitting the analytic results for a wide range of arc angle (θ₀) as

Figure 3. Influence of various geometric and material parameters on the out-of-plane displacement.

Results of precise model calculation, approximate solution and FEA for the dimensionless maximum out-of-plane displacement versus the Poisson ratio (a) and applied strain (b) for helical mesostructures with three different arc angles (θ₀ = 90°, 150° and 210°). (c) Dimensionless maximum out-of-plane displacement versus the arc angle for helical mesostructures with three different applied strains (ε_appl = 10%, 20% and 30%). The parameters adopted in the calculations include w / R = 0.05, w / t = 50 and ε_appl = 20% for (a), and w / R = 0.05, w / t = 50 and ν = 0.27 for (b) and (c).

$$a\left({\theta }_0\right)=1.72-0.29{\theta }_0,b\left({\theta }_0\right)=\left(1.23-0.14{\theta }_0\right){\theta }_0.$$ (10)

Thereby, approximate solutions of ϕ and U₁ are given by

$$\varphi =(1.72-0.29{\theta }_0)\theta \sqrt{{\epsilon }_{\mathit{appl}}},U_1=R{\theta }_0(1.23-0.14{\theta }_0)sin\left(\frac{\pi \theta }{2{\theta }_0}\right){\left(2-\frac{\theta }{{\theta }_0}\right)}^2{\left(\frac{\theta }{{\theta }_0}\right)}^2\sqrt{{\epsilon }_{\mathit{appl}}}.$$ (11)

The predictions of Eq. (11) agree reasonably well with the precise model calculations (according to energy minimization) and FEA results, as shown in Figure 3b,c and Figure S6d,e (Supporting Information). Taking the limit θ₀ → 0 by fixing L = Rθ₀, the 2D serpentine precursor degenerates into a straight ribbon, and the resulting out-of-plane displacement (U₁ / L) and twist angle (ϕ) approaches the counterpart of buckled structure from a straight ribbon [Figure 3c and Figure S6e (Supporting Information)].

Since the 3D helical mesostructures studied above are formed from compressive buckling that relates to both the bending and twisting deformations, a physical quantity, namely, the mode ratio (ρ), is introduced as a metric to classify the resulting 3D mesostructures into two different groups, i.e., the bending dominated and bending-twisting mixed modes.^[6] This quantity is defined by the ratio of the average twisting curvature (|κ̂₃|_avg) to the average out-of-plane bending curvature (|κ̂₂|_avg), noticing the negligible change of in-plane bending curvature for ultra-thin (i.e., w / t > 20) 2D precursors. For the serpentine microstructures used as 2D precursors, the out-of-plane bending and twisting curvatures can be solved by inserting Eq. (11) into Eq. (7), leading to

$${\widehat{\kappa }}_2=\frac{\sqrt{{\epsilon }_{\mathit{appl}}}}{4R{\theta }_0^5}{F}_1\left(\theta ,{\theta }_0\right)=\frac{\sqrt{{\epsilon }_{\mathit{appl}}}}{4R{\theta }_0^5}\left\{\begin{array}{l}\left(1.23-0.14{\theta }_0\right)\left[4{\theta }_0^2\left({\theta }^4-4{\theta }_0{\theta }^3+4{\theta }_0^2{\theta }^2+12{\theta }^2-24{\theta }_0\theta +8{\theta }_0^2\right)-{\pi }^2{\theta }^2{\left(\theta -2{\theta }_0\right)}^2\right]sin\left(\frac{\pi \theta }{2{\theta }_0}\right)\\ +16\pi \left(1.23-0.14{\theta }_0\right){\theta }_0\theta \left({\theta }^2-3{\theta }_0\theta +2{\theta }_0^2\right)cos\left(\frac{\pi \theta }{2{\theta }_0}\right)-4\left(1.72-0.29{\theta }_0\right){\theta }_0^5\theta \end{array}\right\},$$ (12a)

$${\widehat{\kappa }}_3=\frac{\left(1.72-0.29{\theta }_0\right)\sqrt{{\epsilon }_{\mathit{appl}}}}{R}.$$ (12b)

The mode ratio can be obtained accordingly as

$$\rho =\frac{{\int }_0^{{\theta }_{0}R}\left|{\widehat{\kappa }}_2\right|\mathrm{d}S}{{\int }_0^{{\theta }_{0}R}\left|{\widehat{\kappa }}_3\right|\mathrm{d}S}=\frac{{\int }_0^{{\theta }_0}|F_1(\theta ,{\theta }_0)|\mathrm{d}\theta }{4\left(1.72-0.29{\theta }_0\right){\theta }_0^6},$$ (13)

which is a single-variable function independent on the applied strain. Equations (12a) and (12b) show that the twisting curvature keeps almost unchanged in the helical mesostructures, while the bending curvature varies evidently, reaching its peak at the inner region of the mesostructures. This captures well the distribution features of both curvature components (Figure S8, Supporting Information). Figure 4 presents the variations of dimensionless average curvatures (R|κ̂₃|_avg and R|κ̂₃|_avg) and mode ratio with two key parameters (applied strain ε_appl and arc angle θ₀). These results confirmed the square root scaling of average curvatures with the applied strain, as well as the strain-independent feature of mode ratio. With the increase of arc angle (θ₀), the twisting curvature decreases almost in a linear manner, while the bending curvature decreases much faster (Figure 4d,e). Both FEA and theoretical results (Figure 4f) indicate a nearly proportional dependence of mode ratio on the arc angle, i.e., ρ ≈ 0.41θ₀, in which the coefficient of proportionality is determined from the Taylor expansion of Eq. (13). Therefore, the use of a large arc angle for the serpentine precursor can enhance the contribution of twisting deformation evidently. Figure S9 (Supporting Information) presents additional results of FEA and model predictions for the curvatures and mode ratio, which illustrate the negligible effects of Poisson ratio, cross-sectional aspect ratio, and normalized width for the geometries of our current interest.

Figure 4. Influence of geometric parameters on the curvature and mode ratio.

Results of precise model calculation, approximate solution and FEA for dimensionless average curvatures (a,b) and mode ratio (c) versus the applied strain for helical mesostructures with three different arc angles (θ₀ = 90°, 150° and 210°). Dimensionless average curvatures (d,e) and mode ratio (f) versus the arc angle for helical mesostructures with three different applied strains (ε_appl = 10%, 20% and 30%). The parameters adopted in the calculations include w / R = 0.05, w / t = 50 and ν = 0.27.

The curvatures decide not only the mode ratio, but also the maximum strain in the helical mesostructures that is directly related to material failure (e.g., brittle fracture for silicon or plastic yield for metals). In specific, the maximum normal strain ε_bending and shear strain γ_twisting of a certain cross section correlate with the curvature components by ε_bending = t|κ̂₂|/2 and γ_twisting = t|κ̂₃|. According to FEA and model calculations, the maximum strain typically occurs at the center of the helical mesostructures. Hence, the maximum magnitude of principal strain in the helical mesostructure can be obtained as

$${\epsilon }_M=F_2\left({\theta }_0\right)\frac{t}{R}\sqrt{{\epsilon }_{\mathit{appl}}},$$ (14a)

where F₂ is a function given by

$$F_2\left({\theta }_0\right)=\frac{4a\left({\theta }_0\right){\theta }_0^3+b\left({\theta }_0\right)\left(16+{\pi }^2-4{\theta }_0^2\right)+\sqrt{16a{\left({\theta }_0\right)}^2{\theta }_0^4\left(1+{\theta }_0^2\right)+b{\left({\theta }_0\right)}^2{\left(16+{\pi }^2-4{\theta }_0^2\right)}^2+8a\left({\theta }_0\right)b\left({\theta }_0\right){\theta }_0^3\left(16+{\pi }^2-4{\theta }_0^2\right)}}{16{\theta }_0^2}.$$ (14b)

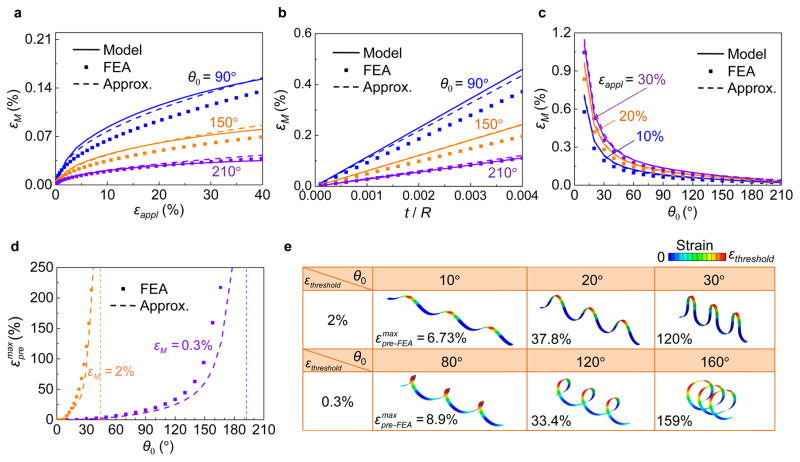
Equation (14) shows the maximum strain (ε_M) is decided by the applied strain (ε_appl), arc angle (θ₀), and normalized thickness (t / R), and is independent on the other parameters (Poisson ratio ν and normalized width w / R), which is in accordance with FEA results (Figure S10, Supporting Information). Figure 5a–c demonstrates that the predictions of analytic solution [Eq. (14)] exhibit reasonable agreement with the FEA and precise model calculations, with both in support of the proportional scaling of maximum strain with the square root of applied strain and the normalized thickness. Here, the discrepancy of theoretical predictions and FEA can be mainly attributed to the overestimate of bending curvature (Figure S8, Supporting Information). The increase of arc angle results in a substantial reduction in the maximum strain, e.g., by ~ 0.6 times from θ₀ = 90° to 180°, suggesting an effective route to enhancing the compressibility of helical mesostructures.

Figure 5. Strain analyses for avoiding failure of helical mesostructures during postbuckling.

Results of precise model calculation, approximate solution and FEA for maximum principal strain of material versus the applied strain (a), normalized thickness (b) and arc angle (c). (d) Maximum prestrain that can be used in the elastomeric substrate, so as to avoid brittle fracture in the silicon helical mesostructures (according to ε_M = 2%), or to avoid plastic yield in the gold helical mesostructures (according to ε_M = 0.3%). (e) Deformed configurations of six different helical mesostructures when the maximum strain reaches the corresponding failure threshold, in which the color of FEA results represents the magnitude of maximum principal strain. The parameters adopted in the calculations include t / R = 0.001 for (a), (c), (d) and (e), and ε_appl = 20% for (b).

As mentioned previously, the buckling guided fabrication of helical mesostructures relies on the release of prestrain in the elastomeric substrate to provide the compressive forces to the serpentine precursors. An excessively large prestrain can, thereby, lead to possible failure in the constituent material. Here, a failure criterion based on the maximum principal strain is adopted for simplicity, in which the threshold (ε_threshold) is assumed to be independent of thickness. Based on Eq. (14a), the applied strain-prestrain relation, ε_appl = ε_pre/(1+ε_pre) and the failure criterion of ε_M = ε_threshold, the maximum prestrain ( ${\epsilon }_{\mathit{pre}}^{max}$) that can be used to avoid material failure is determined as

$${\epsilon }_{\mathit{pre}}^{max}={\left[\frac{R{\epsilon }_{\mathit{threshold}}}{{tF}_2\left({\theta }_0\right)}\right]}^2/\left\{1-{\left[\frac{R{\epsilon }_{\mathit{threshold}}}{{tF}_2\left({\theta }_0\right)}\right]}^2\right\},\text{for}{\epsilon }_{\mathit{threshold}}<\frac{{tF}_2\left({\theta }_0\right)}{R}.$$ (15)

When ε_threshold≥tF₂(θ₀)/R, there is no upper limit for the prestrain, and any level of prestrain would not lead to material failure. In the following analyses, the threshold strain (ε_threshold) is taken as the fracture limit for brittle materials (e.g., 2% for silicon), or the yield strain for metallic materials (e.g., 0.3% for gold). Figure 5d shows the predicted maximum prestrains for silicon and gold helical mesostructures with a representative normalized thickness (t / R = 0.001) and a broad range of arc angles. Both the analytic and FEA results show a higher ${\epsilon }_{\mathit{pre}}^{max}$ at a larger θ₀, and hence, corresponding to a more compact helical mesostructures that can be achieved (Figure 5e). When the arc angle is sufficiently large, e.g., > 192° (corresponding to the vertical dashed line in Figure 5d), such that ε_threshold≥tF₂(θ₀)/R holds true, the silicon helical mesostructures are always safe for any level of prestrain.

Due to the mechanical and electromagnetic properties, the helical mesostructures can be exploited as stretchable interconnects or functional components (e.g., inductors or antennas), which could yield a stretchability higher than the prestrain (ε_pre) used in the assembly, in the condition without any use of solid encapsulation. When a helical mesostructure is under an axial stretching (ε_stretch ≤ ε_pre), the out-of-plane displacement, the curvature components as well as the maximum principal strain still follow a similar square root scaling:

$$U_1,{\widehat{\kappa }}_2,{\widehat{\kappa }}_3,{\epsilon }_M\propto \sqrt{\frac{{\epsilon }_{\mathit{pre}}}{1+{\epsilon }_{\mathit{pre}}}-\frac{{\epsilon }_{\mathit{stretch}}}{1+{\epsilon }_{\mathit{stretch}}}},\text{for}{\epsilon }_{\mathit{stretch}}\le {\epsilon }_{\mathit{pre}}.$$ (16)

This scaling agrees well with the FEA results in Figure S11 (Supporting Information).

4. Conclusion

The work presented here represents systematic studies toward buckling-guided formation of 3D helical mesostructures, through combined analytic modeling, FEA, and experiment. The analytic models, validated by FEA and experiment, suggest negligible roles of material parameters (E and ν) and cross-sectional geometric parameters (w / t and w / R), with dominant roles of applied strain (ε_appl) and arc angle (θ₀), on the final 3D configurations. The resulting scaling laws enable predictions of key physical quantities, including displacement, curvature, mode ratio and strain, using approximate analytic solutions. A demonstrative example based on the analytic solutions illustrates how to select key design parameters (e.g., the prestrain of substrate and geometry of serpentine microstructures), such that brittle fracture or plastic yield can be avoided. Further work could follow by extension of the scaling laws to 2D precursors with membrane configurations. These results can be used as design references for future optimizations in practical applications.

5. Experimental Section

Preparation of 3D helical mesostructures began with thermal oxidation to form a layer of silicon dioxide (SiO₂, 500 nm in thickness) on a silicon wafer. Next, spin casting and photolithography formed patterns of photodefinable epoxy (SU8, 7 μm in thickness) on the SiO₂. Immersion in hydrofluoric acid (HF) removed the buried SiO₂ layer from the exposed regions and also slightly from under the edges of the SU8. Spin casting and photolithography created patterns of photoresist (AZ 5214, 4 μm in thickness) on top of the SU8 layers to define the bonding sites. Immersion in HF eliminated the remaining SiO₂ by complete undercut etching. The techniques of transfer printing enabled retrieval of the 2D precursors and their delivery to a piece of water soluble tape (polyvinyl alcohol, PVA). A thin sheet (~ 0.5 mm) of silicone elastomer (Dragon Skin, Smooth-On) served as the substrate, stretched to well-defined levels of prestrain using a customized stage. Exposing the prestrained elastomer and the 2D precursors (on PVA) to UV-induced ozone (UVO) yielded hydroxyl termination on their exposed surfaces. Laminating the tape onto the elastomer substrate with the exposed SU8 side down, followed by baking in an oven at 70 °C for 10 min yielded strong covalent bonds via condensation reactions of surface-enriched hydroxyl groups between the elastomer substrate and the exposed regions of 2D precursors. Washing with hot water and then acetone dissolved the PVA tape and the photoresist. Slowly releasing the prestrain completed the assembly process of 3D helical mesostructures.

Preparation of helical mesostructures in plastic films began with mechanical cutting of a thin layer (~ 75 μm in thickness) into desired serpentine patterns, followed by cutting of bonding locations in a thin sheet of paper (~ 90 μm in thickness). The pattern of bonding locations corresponds to a certain level of compressive strain applied to the serpentine microstructure. Adhering this paper layer onto a rigid plastic substrate through thin, double-coated tape (9080A, 3M, Minnesota, USA) exposed adhesive bonding locations for purposes of assembly. Sticking the 2D serpentine microstructure at the exposed bonding locations yielded the corresponding 3D helical mesostructures.