Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2016 Jun 10;171(4):2331–2342. doi: 10.1104/pp.15.00972

LobeFinder: A Convex Hull-Based Method for Quantitative Boundary Analyses of Lobed Plant Cells1,[OPEN]

Tzu-Ching Wu 1,2, Samuel A Belteton 1,2, Jessica Pack 1, Daniel B Szymanski 1,*, David M Umulis 1,*
PMCID: PMC4972256  PMID: 27288363

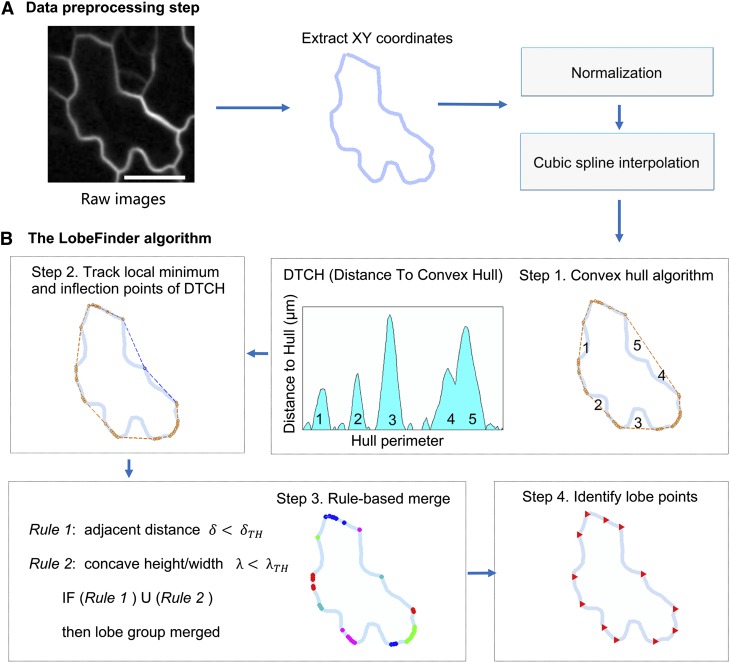
LobeFinder, a new convex hull-based cell phenotyping tool, creates a coordinate system for cell boundary changes and detects lobe positions in epidermal pavement cells.

Abstract

Dicot leaves are composed of a heterogeneous mosaic of jigsaw puzzle piece-shaped pavement cells that vary greatly in size and the complexity of their shape. Given the importance of the epidermis and this particular cell type for leaf expansion, there is a strong need to understand how pavement cells morph from a simple polyhedral shape into highly lobed and interdigitated cells. At present, it is still unclear how and when the patterns of lobing are initiated in pavement cells, and one major technological bottleneck to addressing the problem is the lack of a robust and objective methodology to identify and track lobing events during the transition from simple cell geometry to lobed cells. We developed a convex hull-based algorithm termed LobeFinder to identify lobes, quantify geometric properties, and create a useful graphical output of cell coordinates for further analysis. The algorithm was validated against manually curated images of pavement cells of widely varying sizes and shapes. The ability to objectively count and detect new lobe initiation events provides an improved quantitative framework to analyze mutant phenotypes, detect symmetry-breaking events in time-lapse image data, and quantify the time-dependent correlation between cell shape change and intracellular factors that may play a role in the morphogenesis process.

The size, shape, and angle of leaves are important adaptive traits in natural populations and key determinants of yield in agronomic settings (Zhu et al., 2010). Therefore, it is important to understand the cellular events that collectively, at the levels of the tissues and organs, lead to the formation of durable, lightweight, and appropriately sized leaf blades for efficient light capture (Walter et al., 2009). In Arabidopsis (Arabidopsis thaliana), the growth properties of the epidermis may have particular importance in terms of organ size control (Savaldi-Goldstein et al., 2007), and the growth behaviors of the sectors of the epidermis and individual cells can correlate with organ-level growth behaviors (Zhang et al., 2011; Kuchen et al., 2012). In dicots, the basic cellular unit of the epidermis is the jigsaw puzzle piece-shaped pavement cell, the division and expansion of which drive leaf expansion (Asl et al., 2011).

The biomechanics of pavement cell shape change are complicated (Panteris and Galatis, 2005; Geitmann and Ortega, 2009; Szymanski and Cosgrove, 2009; Szymanski, 2014). Turgor pressure is the driving force for cell expansion. However, the magnitude and directions of cell wall tension forces are difficult to predict because of the presence of adjacent neighboring cells both in the plane of the epidermis and in the underlying mesophyll tissue (Szymanski, 2014). The shape of the cell itself also may influence the stress patterns in the wall, and regions of high cell curvature are predicted to have increased wall stress compared with other domains of the cell (Sampathkumar et al., 2014). The growth trajectory or strain response of the cell also is strongly influenced by heterogeneity in the cell wall, and a current challenge is to understand how differences in cell wall thickness and local cellulose-dependent cell wall anisotropy might contribute to polarized growth in this cell type (Panteris and Galatis, 2005; Szymanski, 2014).

The developmental control of lobe initiation in cotyledons and leaves also is poorly understood. In one early model, lobe initiation was proposed to direct organ shape, with cell elongation and lobe initiation occurring independently in populations of cells to influence organ growth in length and width, respectively (Tsuge et al., 1996; Fu et al., 2002). Other studies, which relied on cell shape measurements from populations of unsynchronized cells, detected correlations between cell size and lobe number, implying a continuous process of cell expansion and lobe initiation (Qiu et al., 2002; Fu et al., 2005). Neither of these models appears to be correct, based on several recent studies that employ either long-term time-lapse imaging of pavement cell morphogenesis (Zhang et al., 2011; Elsner et al., 2012) or cell population analyses that analyzed cells from developmentally staged leaves over time intervals spanning days (Andriankaja et al., 2012) or weeks (Staff et al., 2012). The clear outcome from these studies is that the frequency of lobe initiation clearly depends on the developmental stage and location on the leaf. However, in many instances, lobe initiation is unpredictable. For example, a given cell’s anticlinal (perpendicular to the leaf surface) walls are in contact with several neighboring cells. New lobes can form along either one or several of these cell boundaries, and the factors that define the probability of forming a new lobe at a particular location are not known. Lobe initiation, therefore, is episodic, and morphogenesis appears to include both anisotropic growth during lobe initiation and lobe expansion as well as extended phases of symmetrical cell expansion in which the cell size increases but the overall geometry of the cell remains essentially unchanged (Zhang et al., 2011).

One major limitation in the field is the lack of a robust and objective method to identify new lobes. The discussion above on the cellular and developmental control of lobe formation is based largely on the subjective evaluation of pavement cell segments as being either lobed or unlobed. This has generated confusion and variability in the literature with regard to detecting phenotypes and comparing the severity of phenotypes among different mutants. In some instances, the end points of a midline skeleton of individual pavement cells have been used to estimate lobe number (Le et al., 2006; Staff et al., 2012); however, this method is not very accurate and appears to underestimate lobe number. As an alternative, dimensionless shape descriptors like circularity (4π × cell area/perimeter2), a ratio that approaches 1 for more circular cells and gets smaller as cells become more lobed, are used to test for differences among cells in the complexity of their cell shape (Kieber et al., 1993; Le et al., 2003; Djakovic et al., 2006; Le et al., 2006; Zhang et al., 2008). The major weakness of this approach is that it does not directly reflect lobe number, and there are many equally plausible explanations in which reductions in either lobe initiation or lobe expansion could lead to similar differences in cell shape complexity. In this article, we describe a highly useful convex hull-based MatLab program termed LobeFinder that operates on cell perimeter coordinates extracted from images of pavement cells and returns an array of useful cell shape data, including a value for lobe number and a map of their positions. Based on median scores of manually identified features from a diverse population of pavement cells, LobeFinder predictions outperformed the alternative method of binary image skeletonization and subjective human scoring. The development, validation, limitations, and uses of LobeFinder are described below.

RESULTS

Currently, quantification methods of lobe formation are often focused on the localization of specific factors related to cellular shape change, such as the distribution of actin filaments, the presence of anticlinal microtubule bundles, and qualitative descriptions of cell shape (Fu et al., 2002, 2005). However, because there is no known marker protein for lobe initiation, and because lobe counting results vary greatly between laboratories and among individuals (see below), there is a strong need for a standardized computational approach to measure the number and location of pavement cell lobes.

A number of commercial and open-source software applications are available to quantify the geometry of cell shapes. These methods can be broadly separated into two categories: quantification of descriptive scalar properties such as circularity, roughness, perimeter, area, etc. that describe the shape by descriptive parameters (Russ, 2002; Robert et al., 2008); and image-segmentation approaches that we broadly define here as methods that reduce the pixel information in the raw image into segments or a reduced set of data points that have greater biological meaning (Marcuzzo et al., 2008), such as converting an image of a cell into segmented regions for nucleus, cytoplasm, Golgi, endoplasmic reticulum, etc. automatically. These approaches offer a reduction in the size of the data and a transformation of pixel intensity data into classifications that directly inform the biology of the problem. The Medial Axis Transform (Staff et al., 2012) has been used to quantify pavement cell geometry. The Medial Axis Transform uses the midline points of cells to quantify cell shape differences by tracking the percentage change in angles between linear segments of the branches along the central axes or skeleton. A similar method for tracking the midline of a cell is available as the FIJI plugin AnalyzeSkeleton method (Arganda-Carreras et al., 2010; Schindelin et al., 2012).

In the analysis of pavement cell shape, the most widely used computational method to identify lobes is based on the AnalyzeSkeleton algorithm that detects the midline of irregularly shaped objects, categorizing the pixel properties of the surrounding area and choosing the best path to detect areas of image continuity. Based upon the number of neighboring pixels, some pixel points are ignored or favored over others and a skeletonized representation of the central axes of the cell’s shape and structure is formed. In this method, individual cells are extracted manually from a confocal image of a field of pavement cells (Fig. 1). A midline skeleton is calculated from the binary image, and the skeleton end points are extended to the cell perimeter, depending on the magnitude of the protrusion, to map positions of predicted lobes. As shown in Figure 1, the skeletonize method is not very accurate, and only about half of the lobes that would be identified by a trained scientist are accurately identified with this method. Therefore, this method is useful in determining generalized lobing events, usually well after a new lobe has formed, but is unable to detect slight variations in wall geometry that signify recent lobing events.

Figure 1.

Figure 1.

Open in a new tab

The AnalyzeSkeleton processing technique of lobe identification does not accurately identify pavement cell lobes. Left, Representative confocal images of early stage cotyledon pavement cells. Middle, Calculated midline skeletons of the corresponding pavement cells. Right, Summary of the accuracy of the AnalyzeSkeleton method. Green squares indicate correctly identified lobe points based on the extensions of the skeleton end points, and red arrows indicate missed lobe points compared with voting results. Bar = 20 µm.

Outline of LobeFinder

To overcome the limitations of the previous methods in identifying the position and number of lobes in pavement cells, we developed a new cell geometry analysis approach named LobeFinder. LobeFinder operates on user-supplied cell boundary coordinates that are extracted from high-resolution confocal images of pavement cells of various sizes and shapes. The algorithm is based on a multistep process starting with a convex hull of the cell boundary and a sequence of processing events to robustly identify lobes (Graham, 1972). First, cell boundaries are segmented from the original image. For our analysis of cell boundary variation and lobe detection, existing segmentation methods utilizing gradient vector field SNAKEs or a related approach (Ma and Manjunath, 2000; Roeder et al., 2010) were not sufficiently accurate, frequently merging cells or creating additional cells from an irregularly shaped lobe. The recently published semiautomated method for pavement cell segmentation termed CellECT improves the efficiency of three-dimensional pavement cell segmentation and includes user input to reduce errors (Delibaltov et al., 2016). In the future, CellECT could be modified to output a single set of splined coordinates that accurately depict the boundary of the anticlinal cell wall. We anticipate that as cell segmentation methods improve, LobeFinder will be integrated into an image-processing work flow to enable high-throughput cell phenotyping. However, at present, manual segmentation is the only reliable method to extract cell coordinates, and this can be easily achieved using the polygon selection tool that is available in ImageJ. The ImageJ segmentation tool is advantageous because it allows the user to adjust the position of the cell boundary points and add or delete points as needed.

For this study, confocal images were at a resolution of 3.95 or 2.55 pixels µm−1. After testing a range of sampling densities along the cell perimeter, we found that sampling frequencies of 0.5 to 1.5 points µm−1 were sufficient to yield accurate results for cell shape analyses using LobeFinder because lobe detection was consistent in this range. Sampling frequencies of one point every 2 µm or less led to obvious mismatches between the cell shapes in the raw image and the segmented cells. We recommend sampling cell perimeters at 1 point µm−1 and selecting the spline function within ImageJ to smooth the manual tracing and provide a high density of interpolated points.

Following extraction of the cell perimeter by segmentation, the center of mass of each cell is calculated and moved to the origin. The overall cell size is normalized and scaled by a constant factor to calculate lobe numbers (Fig. 2A). Following analysis, the outputs are rescaled back to micrometers for the outputs reported in the graphical user interface (GUI). This allows the use of the same relative metrics and LobeFinder settings to determine if a lobe is present for cells of different ages and sizes. The normalization step also allows raw images at multiple different resolutions to be processed in LobeFinder. To remove artifacts introduced by the uneven sampling of perimeter points during manual cell segmentation and reorientation, the cell perimeter data are approximated by a cubic spline interpolation.

Figure 2.

Figure 2.

Open in a new tab

Overview of the LobeFinder logic and work flow. A, Cell perimeter positions are manually segmented from raw images, scaled, and resampled. Bar = 20 µm. B, A convex hull, defined as the minimal polygon that encloses the entire given cell perimeter, is computed (step 1), then the perimeter is scanned for missed lobe points (the extrema between segments 4 and 5) using the PeakFinder algorithm within MatLab (step 2). The optimized values for thresholds (δTH and λTH) for rule-based lobe geometry and spacing are used to identify putative lobe points (step 3); then, groups of lobe points are merged, and the final set of predicted lobe positions is extracted (step 4).

The output of the preprocessing steps is a cell perimeter that is scaled, aligned with the center of mass, smoothed and resampled (cubic spline interpolation), and ready for further analysis. To acquire the minimal polygon that surrounds the entire set of coordinates that define the cell boundary (Fig. 2B), we employ the MatLab function convhull, which returns the coordinates of the convex polygon (hull) that contains all the coordinate points of the cell set. The convex hull provides two important features for further analysis: first, it provides information for the minimum convex set that encompasses the entire cell; and second, it provides a convenient coordinate system onto which the cell boundary properties are easily mapped (Fig. 2B, middle). Both of these outputs will serve to subsequently identify key points and structures.

Pavement cells do not typically produce an outline where all of the extrema at the lobe tips are located precisely on the hull. For example, in Figure 2B (upper right), the convex hull produces a line that does not separate regions 4 and 5 by the lobe that is located between the regions, since the lobe does not land on the hull itself. To adjust the hull, the distance between the cell and the hull is calculated and plotted on an axis of position versus distance (Fig. 2B). Using the orthogonal distance to the convex hull to the cell perimeter, the local minima are retrieved, and the convex hull is then refined to capture the interior local minima points. To determine whether there are interior lobe points between adjacent points on the convex hull, we use the program PeakFinder (Yoder, 2011) to determine both local and absolute extrema between hull(i) and hull(j), points on the cell periphery coincident with the hull. PeakFinder identifies the location of the missed lobes, and the hull used to encapsulate the cell is modified to contact the lobe point (Fig. 2B, step 2). These additional processing steps capture the majority of interior lobes that would otherwise be missed, since they do not lie on the hull surrounding each cell. The resulting hull is termed the refined hull because it no longer conforms to the strict definition of a convex hull. The distance to the refined hull (DTRH) plots contain highly useful information on the local patterns of growth. Therefore, the cell and its refined hull are rescaled back to their real dimensions, and the DTRH coordinates are available to be exported within the LobeFinder program. In rare instances, there are relatively large pavement cells in which a cell lobe is bulbous. In these instances, the path of the cell perimeter doubles back on itself on one axis, creating multiple solutions for the DTRH plot. In this subregion of the cell, the PeakFinder routine uses only the smallest distance value, and this can lead to erroneous hull refinements and lobe calls. This morphology is rare in our data set, but a bulbous morphology is the default state in the crenulated boundary of many monocot leaf epidermal cells. For these species, LobeFinder would likely perform well in analyzing early events associated with lobe initiation but likely would fail to accurately count the lobes of fully expanded cells.

Following adjustment of the convex hull, the goal of the algorithm is to identify which of the points on the cell perimeter correspond to the positions of the protrusions. Additionally, not every point on the hull corresponds to a physical lobe on the pavement cell, and to some extent, the identification of a lobe on the cell is subjective in nature, with different individuals identifying different lobe positions and numbers. One design goal of the algorithm is to mimic the expert observer’s approach to identify the geometric features, albeit by an objective computer algorithm. This goal informed the design of the geometric parameters for lobe geometry and spacing that were developed to optimize lobe identification. For each data point in the set of convex hull points (Fig. 2B, step 3), the distance between neighboring points is calculated. This distance between hull points determines if the algorithm should consider adjacent lobe points as part of the same lobe. To cull points on the hull and leave only those that are identified as the center of a lobe, two parameters (δ and λ) for the initial identification of lobes are used: the scaled spacing distance between lobe points (δ) and a ratio of the height (distance between hull and cell boundary) to the width (distance of hull segment) between prospective lobe points (λ). The distance between a lobe point and the convex hull is zero; however, there must be a region between lobes where the distance is nonzero and above some threshold value. This module of the program calibrates LobeFinder to reduce the number of misleading or incorrect lobe points on the convex hull. This calibration is effective in most cases. However, because the parameters are tuned to be sensitive for small deviations in boundary shape, cells with relatively simple shapes with extended domains of the cell boundary that are close to the threshold values for δ and λ are most likely to have false positives.

LobeFinder Optimization and Evaluation

The principal method for the identification of lobes and lobing segments in pavement cells relies on observer-based inspection and identification of lobing events. An important research goal is to standardize pavement cell phenotyping and to create an objective computational method that can accurately quantify cellular geometry and be applied to time-lapse data and large ensembles of images to efficiently calculate population statistics. Therefore, it is necessary to ensure that the algorithm produces consistent and accurate observations.

As an initial test of the sensitivity of the output to variability in an individual’s choice of boundary points for cell segmentation, three pavement cells of varying sizes and shapes were manually segmented three times and analyzed using LobeFinder. For each of these cells, the area, perimeter, and circularity values for the technical replicates were either identical or differed by a fraction of 1%. For the technical replicates, the LobeFinder outputs for lobe number were more variable, with the coefficients of variation for lobe number varying between 0.06 and 0.1. This level of variabilty in the measurement of lobe number was much less than that observed when multiple individuals used subjective criteria to score an identical cell. For example, in our test population of pavement cells (Supplemental Fig. S1), the coefficient of variation for lobe number ranged from 0.03 to 0.21, with 10 of the 15 cells having a coefficient of variation greater than 0.1. In the LobeFinder program, variability in lobe number most often occurred along relatively straight cell perimeter segments with one tracing including a very small feature that was absent in another. The cause for this is discussed further below, but this result makes clear the importance of accurate sampling along the cell perimeter.

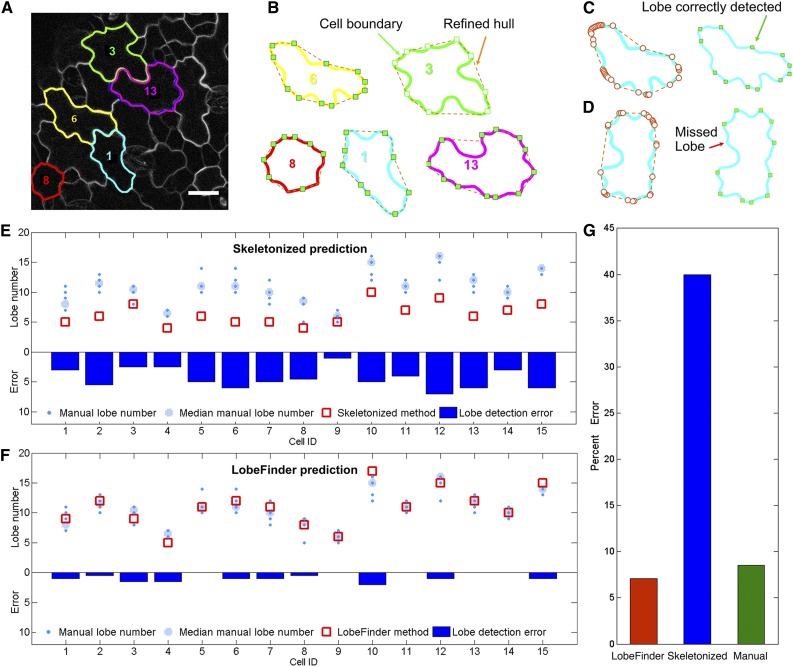
Fifteen randomly selected pavement cells (Supplemental Fig. S1) from a time-lapse data set were used to more thoroughly compare the accuracy of LobeFinder with that of existing methods. The cells had sizes that ranged from 280 to 1,588 µm2 and circularity values that ranged from 0.32 to 0.81. We evaluated how well LobeFinder outputs of lobe number and lobe position would agree with the scores generated by researchers with experience in the analysis of pavement cell shape. For each of the images (examples shown in Fig. 3), six experienced pavement cell scientists visually inspected 8.5- × 11-inch printouts of each cell and identified lobe locations for each raw image. These data were used to determine the accuracy of lobe point position detection and to calculate the number of lobes present for each cell (Fig. 3, C and D). A few of the cells used in the calibration of LobeFinder are shown in Figure 3A. The complete set of images (Supplemental Fig. S1) and a summary of the cell and convex hull properties (Supplemental Table S1) are provided in “Supplemental Data.” A summary of the LobeFinder and voter results is shown in Figure 3, E and F. We next benchmarked LobeFinder and the existing skeletonize method against the images manually curated by members of the two laboratories. The subjective nature of the manual scoring of lobe number is evident in the plots of lobe number (Fig. 3, E and F), with many cells having four or more features that were ambiguous. Therefore, the median lobe number from the manually curated data was used as a standard for comparison.

Figure 3.

Figure 3.

Open in a new tab

Evaluation of LobeFinder accuracy using a calibration data set and parameter optimization. A, Example of a raw image containing five cotyledon pavement cells in the calibration data set. Bar = 20 µm. B, Outlines of extracted cells showing the cell boundary and the unrefined convex hull. C and D, Example output of LobeFinder for two cells in which the correctly identified (green squares) and missed (red arrow) lobes are marked. E, Comparison of the skeletonize method with manually curated results. The light blue circles are the median values from manual lobe identification results for each cell, with individual independent values in small dark blue dots, and red boxes are lobe numbers predicted by the skeletonize method. The dark blue bars plot the absolute value of the differences between the lobe number count from the skeletonize method and the median value from the manual results. F, Comparison of the LobeFinder method with manually curated results. The symbols and bars are as described in E, but here, the red boxes are the lobe numbers predicted by LobeFinder. The dark blue bars are the absolute value differences between the lobe number count from LobeFinder and the median value from manual results. G, Comparison of the percentage errors of the LobeFinder, skeletonize, and manual scoring methods that were calculated using the median lobe number as the correct value for each cell.

Overall, the skeletonize method greatly underestimated lobe numbers (Fig. 3E). Following an initial calibration to optimize the threshold values of δ and λ, the LobeFinder outputs for lobe number closely matched the median lobe numbers from the manually curated images (Fig. 3F). The LobeFinder lobe number error was 5.7 times lower than that of the skeletonize method (Fig. 3G). The accuracy of the manual lobe counts was similar to that of LobeFinder when averaged across all individuals (Fig. 3G); however, for a given cell, there was considerable spread in the lobe counts among the individuals (Fig. 3F). For example, the error rate among the individuals differed by more than 20% for eight of the 15 cells, even though each of the six individuals was similarly trained to score the presence of lobes. This observation reinforces the strong need for objective methods for the quantitative analysis of cells with highly variable shapes and sizes.

Two different types of features were typically identified as a lobe. First, there were instances of an undulation along a cell perimeter segment that was independent of a three-way cell wall junction. This is the classic example of interdigitated growth among two adjacent cells, and we define these features as type I lobes. A second class of cell protrusions, defined here as type II lobes, were instances in which a protrusion was located at a three-way cell wall junction. These tripartite junctions form during cytokinesis, and in some, but not all, cases, the cell can grow asymmetrically at this location, generating a protrusion with a shape that often is indistinguishable from type I lobes. However, the growth mechanism that generates a type II lobe may resemble intrusive growth (Jura et al., 2006), in which one cell expands asymmetrically at the interface of two adjacent cells. This form of asymmetric growth likely differs from that which generates lobes that are independent of tripartite junctions. There is certainly a need to distinguish between these different types when one analyzes phenotypes and gene function. Currently, this is a weakness of LobeFinder, because the program operates on the coordinates of individual cells and information on the cell wall patterns of its neighboring cells is lost. At present, if a user wishes to distinguish type I and type II lobes, one can use the graphical output from LobeFinder to identify the subset of lobes that fall on three-way cell wall junctions. In the future, we hope to use a semiautomated cell segmentation program like CellECT (Delibaltov et al., 2016) to simultaneously extract cell coordinates from fields of cells and track the positions of three-way cell wall boundaries.

To quantitatively evaluate the performance of the algorithm for lobe location, we compared the positions of the predicted lobes against the manually determined lobes within a specified tolerance (0.025 radians). If LobeFinder identified the proper location within the tolerance, it was identified as a true positive (TP; Supplemental Fig. S2). If a predicted LobeFinder point was not within 0.025 radians of a manually identified point, it was considered a false positive (FP). Missed lobe points were defined as false negatives (FN). We did not calculate true negatives, since this would be an ambiguous number to determine and it would not inform the evaluation of the method. Related to these quantities, we also calculated the sensitivity [TP/(TP + FN)] and the false discovery rate (FDR) [FP/(TP + FP)]. Both of these measures are used to determine the effectiveness of the algorithm.

A high sensitivity and a low FDR are the primary objectives for the application of LobeFinder as a tool for the reliable and automated measurement of cell shape properties. Nine different combinations of the parameters δ and λ were tested that covered a wide range of parameter values. The highest parameter values yielded decreased sensitivity and increased false positives; however, there was a fairly broad range of parameter combinations that yielded a sensitivity of approximately 0.8 and an FDR of approximately 0.25 (Supplemental Fig. S2). This indicates a relatively low dependence of the algorithm on the specific parameters. The optimized parameter combinations yielded an average sensitivity of 0.95 or higher and an average FDR of less than 0.2 (Supplemental Fig. S2).

Identification of New Lobes in Time-Lapse Images of Pavement Cells

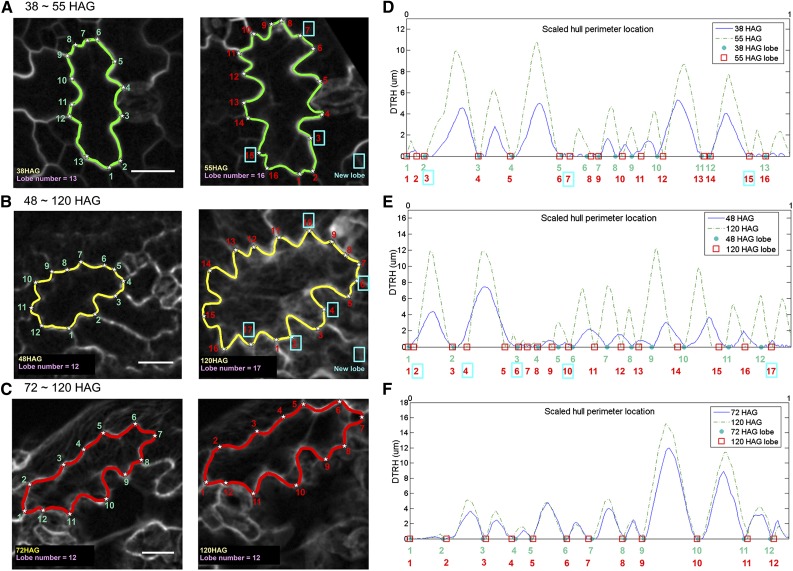
The lobe number, shape, and size properties of pavement cells were analyzed in populations of cells at different intervals of cotyledon development. We applied the LobeFinder program to identify lobes in three time-lapse data sets of pavement cell growth. The first data set represents early growth from 38 h after germination (HAG) to 56 HAG. This slightly overlaps with the second data set from 48 to 120 HAG. The third data set covers 72 to 120 HAG. Data sets 2 and 3 were part of a previous analysis of pavement cell growth (Zhang et al., 2011), and the raw images were reanalyzed here using LobeFinder. Example cells from these three different data sets are shown in Figure 4, A to C. Each showed combinations of symmetrical lateral expansion, with data sets 1 and 2 including more cells that initiated new lobes during the time interval. For example, in the cell that is representative of the 72- to 120-HAG data set, we observed no change in lobe number over the course of time, but it increased in size (Fig. 4C, left to right). In contrast, the cell in the 48- to 120-HAG data set initiated five new lobes (Fig. 4B, left to right), while the cell in the 38- to 55-HAG data set added three new lobes in the time span of 27 h (Fig. 4A, left to right). There is a great deal of variability in pavement cell size and lobe number as a function of cotyledon and leaf development (Elsner et al., 2012; Staff et al., 2012). As a result, in the relatively small windows of time analyzed here, there are examples in which lobe number and cell area are not strictly correlated with developmental time (Table I; Supplemental Table S1). However, differences in lobe initiation rates of individual cells within the time intervals were apparent. Overall, the average number of new lobes per cell was about 2.5 for the 38- to 55-HAG and 48- to 120-HAG populations and 0.5 for the 72- to 20-HAG population (Table I). The percentages of cells in all data sets that grew new lobes were 33% for 72 to 120 HAG, 93% for 48 to 120 HAG, and 80% for 38 to 55 HAG (Table I). These LobeFinder outputs and the average number of lobes per cell at each time point (Table I) indicate that lobing events are prevalent in early stages of growth and that lobing events slow down at some point between 56 and 72 HAG. These results are consistent with the conclusions of a previous study (Zhang et al., 2011).

Figure 4.

Figure 4.

Open in a new tab

LobeFinder can be used to detect new lobes and quantify growth patterns in time-lapse images. A to C, Examples of raw images of pavement cells with manually segmented cell shapes at three different intervals of cotyledon development. A, Pavement cell at 38 (left) and 55 (right) HAG. B, Pavement cell at 48 (left) and 120 (right) HAG. C, Pavement cell at 72 (left) and 120 (right) HAG. The blue boxes indicate the detection of new lobes and their location in the images and on the DTRH plots. D to F, DTRH plots for pavement cells that were rescaled to their original size. The x axes of these plots are the scaled distance along the convex hull perimeter at the two different time points to enable visual comparisons of similar relative positions along the cell boundary at the two time points. The blue line is the DTRH at the initial time point, and the dotted green line is the DTRH at the final time point. The time points in D to F correspond to those of A to C, respectively, and are shown in the legend for each plot. The blue dots and red boxes on the x axis identify lobe locations in the initial and final time points, respectively. Bars = 20 µm.

Table I. Lobe number quantification for cotyledon pavement cells at different developmental stages using LobeFinder.

For 38 to 55 HAG, n = 10 cells; for 48 to 120 HAG, n = 12 cells; and for 72 to 120 HAG, n = 12 cells.

Parameter 38 to 55 HAG
 48 to 120 HAG
 72 to 120 HAG
38 h 55 h 48 h 120 h 72 h 120 h
Averaged lobe number 9.60 ± 2.68 12.10 ± 2.99 8.27 ± 2.89 10.87 ± 2.59 11.17 ± 2.89 11.67 ± 2.46
Percentage with lobe initiation 80 93 33
Average new lobes per cell 2.50 ± 2.46 2.60 ± 1.68 0.50 ± 2.07
Open in a new tab

Additional scalar metric outputs from LobeFinder also correlate with different phases of pavement cell growth; however, they do not directly inform the generation of new lobes. Specifically, for example, the circularity of the individual cells decreases between the two time points (Table II), likely due to the increased expansion of lobes that are initiated primarily in the first 2.5 d after germination. This would also explain the observed decreases in the convexity (ratio of hull perimeter to cell perimeter) and solidity (ratio of hull area to cell area) of pavement cells. Overall, the identification of lobing events and the scalar metrics are consistent with the existence of a permissive developmental window for active lobe formation early in cotyledon development.

Table II. Cell shape descriptors of cells analyzed with LobeFinder.

Feature 38 to 55 HAG
 48 to 120 HAG
 72 to 120 HAG
38 h 55 h 48 h 120 h 72 h 120 h
Circularity 0.60 ± 0.09 0.46 ± 0.11 0.62 ± 0.10 0.49 ± 0.11 0.45 ± 0.13 0.42 ± 0.12
Roundness 0.69 ± 0.06 0.63 ± 0.06 0.70 ± 0.09 0.64 ± 0.09 0.63 ± 0.08 0.61 ± 0.07
Convexity 0.93 ± 0.04 0.85 ± 0.07 0.94 ± 0.03 0.87 ± 0.06 0.84 ± 0.10 0.82 ± 0.10
Solidity 0.86 ± 0.03 0.79 ± 0.05 0.85 ± 0.06 0.80 ± 0.06 0.77 ± 0.06 0.75 ± 0.05
Open in a new tab

Another output from LobeFinder that is useful for cell analyses is a plot of the distance from the refined hull to the cell boundary, which provides a graphical representation of the magnitudes and directions of cell shape change near the cell periphery. This is due to the fact that, as lobes expand, their height and width increase, leading to corresponding changes in the DTRH plots. At the distal tips of cell protrusions, the DTRH is zero and corresponds to a lobe point of the cell of interest in the LobeFinder output. The shape of the cell boundary between lobes is captured by the contour of the DTRH, which is at a local maximum at the most concave position between lobes. Therefore, in a time-lapse experiment, the DTRH plots reflect the local growth behaviors of the adjacent protruding cell and the shape change at the interface between the two cells. In Figure 4, D to F, the DTRH was plotted for each cell at the two different time points. The position along the hull is plotted on the x axis, and this is scaled to the hull length of the initial time point to enable the DTRH values from different time points to be compared at similar relative positions along the hull perimeter. During the 72- to 120-HAG interval (Fig. 4F), growth is highly symmetrical and lobe initiation is rare (Zhang et al., 2011). The corresponding DTRH plots were consistent with this result, because the contours of the plots at the two time points were highly symmetrical with well-aligned peaks. It is important to note that the peak widths for the later time points are compressed because the x axis is scaled. However, as shown previously (Zhang et al., 2011), pavement cell growth during this phase is not perfectly symmetrical, and there were subregions of the DTRH plots that were not symmetrical (Fig. 4F), indicating that some local warping of cell shape occurred during growth. The paired DTRH plots for cells that form new lobes (Fig. 4, E and F) reflected a composite growth behavior. In some regions of the cell-cell interface, growth appeared symmetrical, with proportional increases in peak height and width at similar relative positions. The DTRH plots also revealed an obvious contribution of polarized growth to the shape change, because new peaks were detected. In addition, many of the peaks were shifted in position along the hull perimeter, reflecting symmetry breaking during lobe initiation and the accumulation of local warping during the growth interval.

DISCUSSION

LobeFinder is a novel convex hull-based tool to quantify the local boundary characteristics of a closed geometric shape and identify key features such as pavement cell lobes. The ability of LobeFinder to consistently and accurately identify and position lobes within a pavement cell is an important advance, because currently there is no reliable method to quantify the convoluted shape of pavement cells. Manual definition of lobe number (Fu et al., 2005; Xu et al., 2010) or a feature such as the pavement cell neck width (the shortest distance across the cell between two indentations; Lin et al., 2013) is subjective and variable. Variation in human scoring is a major problem: we document here significant variability in lobe number scoring, even among well-trained individuals (Fig. 3, E and G). The lack of standardized phenotyping methods can contribute to differing conclusions regarding whether a particular mutant has a pavement cell phenotype (Xu et al., 2010; Gao et al., 2015). Manual cell scoring is also time consuming. It requires careful inspection of the cell boundary and the manual annotation of each feature in the image file that is scored as a lobe. Skeletonization of segmented, binary images of cells can identify pavement cell protrusions (Staff et al., 2012), and in some instances, it can be used to detect significant differences between mutant and wild-type plants (Le et al., 2006). However, the skeletonize technique is very inaccurate and tends to miss approximately 40% of all lobes (Fig. 3G). LobeFinder has a much greater accuracy compared with the skeletonize method and performs with an accuracy that is only achieved by averaging the votes of several individuals with extensive experience in pavement cell analysis (Fig. 3G).

The availability of an accurate method to directly identify pavement cell lobes is important because scalar shape descriptors such as circularity are sensitive to multiple features of a cell geometry and do not contain information on the local cell features that are most useful for understanding cell growth behavior. For example, differences between cells in their scalar descriptors could reflect differences in lobe number, reduced lobe expansion, or altered diffuse growth in the midregion of the cells. This point is important because it is often assumed that any mutant with a reduced perimeter-to-area ratio has a lobe initiation defect. LobeFinder directly analyzes the local geometry of the cell and identifies lobes. In this regard, it is a powerful phenotyping tool that can be used to compare populations of cells and cell shape over time. However, the LobeFinder program is not perfect, and because of the local shape and spacing thresholds that are used for lobe detection, there are instances, most often along extended domains of low curvature, in which false positives occasionally are reported. Overall, LobeFinder has great potential for the community, and we anticipate that LobeFinder, provided as a user-friendly program in MatLab (Supplemental Fig. S3), will allow others to use this program to analyze mutants and objectively test for direct effects on lobe initiation.

A major advantage of LobeFinder is that it creates a coordinate system to quantify local growth behaviors at the interface of two cells. Alternative approaches to lobe detection, such as quantification of the local curvature of the cell perimeter using variation in the tangent to the cell boundary as a function of cell perimeter, could operate on splined images to identify regions of local curvature that accurately identify lobes. However, this strategy would not generate a coordinate system to analyze growth. Here, we use LobeFinder and plots of the DTRH in time-series data to illustrate a method to quantify local growth behaviors of an irregularly shaped cell (Fig. 4). For example, the DTRH plots could be analyzed further in time-lapse experiments to generate spatial maps of how the magnitude and direction of growth at the interface of two cells change. These plots clearly indicate the timing, location, and pattern of polarized growth along the interface of interdigitating pavement cells. Importantly, these plots do not reveal the subcellular patterns of growth that explain the shape change. To solve this problem, convex hull-based growth analysis coupled with the use of fiducial marks on the cell wall to track growth patterns (Zhang et al., 2011; Elsner et al., 2012; Staff et al., 2012) could provide improved methods to analyze the subcellular heterogeneity in polarized growth. While this article was being written, a report appeared in which externally applied particles were used to track the growth patterns of the outer wall in fields of developing pavement cells (Armour et al., 2015). The utility of externally applied particles to analyze the growth of the anticlinal wall is uncertain. However, the combined use of DTRH plots, high-density cell wall marking, and time-lapse imaging has the potential to reveal how the polarized growth of individual cells and cell clusters can operate at broader spatial scales to dictate the growth patterns of leaf sectors and even whole organs (Zhang et al., 2011; Kuchen et al., 2012; Remmler and Rolland-Lagan, 2012).

LobeFinder also has immediate applications in terms of more quantitatively dissecting the molecular control of lobe initiation. Hull-based methods and the DTRH plots establish a perimeter coordinate system onto which the temporal and spatial patterns of lobe formation can be graphed (Fig. 4). This is a boon for further analysis, such as the correlation of spatial geometric features with the localization of the cell wall and intracellular signaling and structural factors that are believed to control symmetry breaking. Specifically, LobeFinder can provide the convex hull coordinate system to test for correlations between the local accumulation of proteins such as auxin efflux carriers (Fu et al., 2005; Xu et al., 2010) or microtubules (Panteris et al., 1993; Qiu et al., 2002; Panteris and Galatis, 2005; Ambrose et al., 2007; Kirik et al., 2007; Zhang et al., 2011) and lobe initiation. In this manner, an array of GFP-tagged proteins can be tested to determine those whose localization and activity at the cell cortex specify symmetry-breaking events.

Currently, the greatest limitation for LobeFinder is that it operates on cell coordinates from manually segmented cells. Manual segmentation is a reliable, but time-consuming, process, presenting a major bottleneck for high-throughput phenotyping. As discussed previously, the use of individual, segmented cells also makes it impossible to distinguish between type I and type II lobes, which complicates one’s ability to test for alterative genetic control mechanisms and differing contributions of the lobe types to cell expansion. The obvious solution is an automated cell segmentation program that accurately extracts cell boundary coordinates and marks three-way cell wall junctions in the data set. Currently, there is no existing segmentation method to accurately extract pavement cell coordinates from fields of cells and track three-way junctions. However, the development of watershed-based cell segmentation coupled with user-guided validation in a program like CellECT (Delibaltov et al., 2016) has the potential to be integrated with LobeFinder to create a more robust and efficient cell analysis pipeline.

We show here that LobeFinder is an effective new tool for pavement cell phenotyping and growth analysis. We believe that this algorithm has a broader utility for the quantification of many lobed cell types (Panteris and Galatis, 2005) and the analysis of objects with closed and highly irregular geometric shapes at any spatial scale. For example, there is great interest in the quantitative analysis of leaf shape, and the complex boundary shapes of many types of leaves could be analyzed with LobeFinder. In this context, LobeFinder, could complement other leaf shape analysis programs like LeafProcessor (Backhaus et al., 2010). Similar hull-based methods could operate on projected images of shoots and roots to analyze whole-plant architecture over time. We also believe that LobeFinder could have broad applications in other fields, such as human medicine and environmental science. For example, the progression of irregularly shaped tumors could be quantified over time and correlated with other features such as tumor location or drug treatment regimes. The local spatial dynamics of spreading plumes of contamination, floods, and the retraction of glaciers could be similarly analyzed and tested for cross correlations with any variable of interest. Our efforts will focus on the use and integration of LobeFinder within a completely automated image-analysis platform, with the goal of accelerating discovery in the field of leaf morphogenesis.

MATERIALS AND METHODS

Annotation and Use of the LobeFinder Program

To run LobeFinder, start an instance of MatLab on the workstation (PC, MAC, or Linux) and change the working directory to the install location of LobeFinder. The script and all functions that make up LobeFinder are located in one MatLab m-file: LobeFinder_GUI.m. To run LobeFinder, first create a directory to which all regions of interest (ROIs) of cell perimeter coordinates obtained by manual segmentation are saved. Start the LobeFinder GUI by typing LobeFinder_GUI at the MatLab workspace prompt and < Enter > . This will open an instance of the LobeFinder GUI in a separate window (Supplemental Fig. S3). To import files, click on the Open Folder button to select the folder that contains the ROI files. At this point, one can select the checkboxes for the types of data output files to be generated (CSV, Figures, or MatLab file) as well as the resolution of the images from which the ROIs were extracted. Once the folder and options have been selected, click on the Run button to start the ROI processing. The total number of ROI files being processed will be shown in the image number box on the GUI. To view the results from the LobeFinder processing, select the image number from the image number box. This will populate the GUI with the measured parameters as well as an image of the refined hull, the cell boundary, identified lobe points, and DTRH plot. Moving the cursor over the perimeter of the cell will allow its corresponding position on the DTRH plot to be seen. Depending on the output options selected, a new folder in the directory of LobeFinder will be created ([Output]_NameOfInputFolder) with up to three folders (CSV, FIG_cell, and FIG_dtrh). The CSV folder contains one MatLab mat-file Lobe_result.mat, which contains all results and geometric scalar properties for each ROI in the directory, a CellDescriptors.csv file containing all single-value measurements such as area, perimeter, etc. for all ROIs, and individual DTRH_[nameOfROI] files containing xy values for DTRH plots. FIG_cell and FIG_dtrh folders will contain images of cells and DTRH plots as displayed in the LobeFinder GUI. ROILobeFinder is available for download at the Dryad Digital Repository (http://doi.org/10.5061/dryad.cs78t).

Plant Material and Growth Conditions

Arabidopsis (Arabidopsis thaliana) seeds were grown on one-half-strength Murashige and Skoog medium with 1% Suc and 0.8% Bacto agar under constant illumination at 22°C. Seeds were treated with a 6-h light pulse, cold treated for 3 d, and then placed in the growth chamber. Germination was checked 36 h after plating, and only seedlings with a barely visible radicles were used for further analysis.

Time-Lapse Imaging of Lobe Initiation

For time-point imaging, cell outlines were detected using a tubulin:GFP marker for data sets 2 and 3 as described previously (Zhang et al., 2011). For data set 1, from 38 to 55 HAG, 10 cells were analyzed. For data set 2, from 48 to 120 HAG, 12 cells were analyzed. For data set 3, from 72 to 120 HAG, 12 cell were analyzed. For data set 1, the PIN7:GFP (Blilou et al., 2005) plasma membrane marker was used. The seedlings were mounted in water using a petroleum jelly gasket to form a chambered microscope slide. After initial imaging, the slides were returned to the growth chamber until the next imaging session. Samples were imaged using a Bio-Rad 2100 laser scanning confocal microscope mounted on a Nikon Eclipse E800 stand. Images were obtained with a 60× 1.2 numerical aperture water objective. Samples were excited with a 488-nm laser, and fluorescence signal was collected using a 490-nm long-pass dichroic and a 500- to 550-nm band-pass emission filter. Selected planes from confocal image stacks were converted to maximum intensity projects and were traced with the polygon selection tool in FIJI 4.0 (Schindelin et al., 2012). The coordinates from the ROIs from the manually segmented cells were used as the input for LobeFinder.

Supplemental Data

The following supplemental materials are available.

Supplementary Material

Supplemental Data
supp_171_4_2331__index.html (1.4KB, html)

Glossary

GUI

graphical user interface

DTRH

distance to the refined hull

FDR

false discovery rate

HAG

hours after germination

ROI

region of interest

Footnotes

1

This work was supported by the National Science Foundation (grant nos. IOS/MCB 1249652 and MCB 1121893 to D.B.S.).

[OPEN]

Articles can be viewed without a subscription.

References

  1. Ambrose JC, Shoji T, Kotzer AM, Pighin JA, Wasteneys GO (2007) The Arabidopsis CLASP gene encodes a microtubule-associated protein involved in cell expansion and division. Plant Cell 19: 2763–2775 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Andriankaja M, Dhondt S, De Bodt S, Vanhaeren H, Coppens F, De Milde L, Mühlenbock P, Skirycz A, Gonzalez N, Beemster GT, et al. (2012) Exit from proliferation during leaf development in Arabidopsis thaliana: a not-so-gradual process. Dev Cell 22: 64–78 [DOI] [PubMed] [Google Scholar]
  3. Arganda-Carreras I, Fernández-González R, Muñoz-Barrutia A, Ortiz-De-Solorzano C (2010) 3D reconstruction of histological sections: application to mammary gland tissue. Microsc Res Tech 73: 1019–1029 [DOI] [PubMed] [Google Scholar]
  4. Armour WJ, Barton DA, Law AM, Overall RL (2015) Differential growth in periclinal and anticlinal walls during lobe formation in Arabidopsis cotyledon pavement cells. Plant Cell 27: 2484–2500 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Asl LK, Dhondt S, Boudolf V, Beemster GTS, Beeckman T, Inzé D, Govaerts W, De Veylder L (2011) Model-based analysis of Arabidopsis leaf epidermal cells reveals distinct division and expansion patterns for pavement and guard cells. Plant Physiol 156: 2172–2183 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Backhaus A, Kuwabara A, Bauch M, Monk N, Sanguinetti G, Fleming A (2010) LEAFPROCESSOR: a new leaf phenotyping tool using contour bending energy and shape cluster analysis. New Phytol 187: 251–261 [DOI] [PubMed] [Google Scholar]
  7. Blilou I, Xu J, Wildwater M, Willemsen V, Paponov I, Friml J, Heidstra R, Aida M, Palme K, Scheres B (2005) The PIN auxin efflux facilitator network controls growth and patterning in Arabidopsis roots. Nature 433: 39–44 [DOI] [PubMed] [Google Scholar]
  8. Delibaltov DL, Gaur U, Kim J, Kourakis M, Newman-Smith E, Smith W, Belteton SA, Szymanski DB, Manjunath BS (2016) CellECT: cell evolution capturing tool. BMC Bioinformatics 17: 88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Djakovic S, Dyachok J, Burke M, Frank MJ, Smith LG (2006) BRICK1/HSPC300 functions with SCAR and the ARP2/3 complex to regulate epidermal cell shape in Arabidopsis. Development 133: 1091–1100 [DOI] [PubMed] [Google Scholar]
  10. Elsner J, Michalski M, Kwiatkowska D (2012) Spatiotemporal variation of leaf epidermal cell growth: a quantitative analysis of Arabidopsis thaliana wild-type and triple cyclinD3 mutant plants. Ann Bot (Lond) 109: 897–910 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fu Y, Gu Y, Zheng Z, Wasteneys G, Yang Z (2005) Arabidopsis interdigitating cell growth requires two antagonistic pathways with opposing action on cell morphogenesis. Cell 120: 687–700 [DOI] [PubMed] [Google Scholar]
  12. Fu Y, Li H, Yang Z (2002) The ROP2 GTPase controls the formation of cortical fine F-actin and the early phase of directional cell expansion during Arabidopsis organogenesis. Plant Cell 14: 777–794 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gao Y, Zhang Y, Zhang D, Dai X, Estelle M, Zhao Y (2015) Auxin binding protein 1 (ABP1) is not required for either auxin signaling or Arabidopsis development. Proc Natl Acad Sci USA 112: 2275–2280 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Geitmann A, Ortega JK (2009) Mechanics and modeling of plant cell growth. Trends Plant Sci 14: 467–478 [DOI] [PubMed] [Google Scholar]
  15. Graham RL. (1972) An efficient algorithm for determining the convex hull of a finite planar set. Inf Process Lett 1: 132–133 [Google Scholar]
  16. Jura J, Kojs P, Iqbal M, Szymanowska-Pulka J, Wloch W (2006) Apical intrusive growth of cambial fusiform initials along the tangential walls of adjacent fusiform initials: evidence for a new concept. Aust J Bot 54: 493–504 [Google Scholar]
  17. Kieber JJ, Rothenberg M, Roman G, Feldmann KA, Ecker JR (1993) CTR1, a negative regulator of the ethylene response pathway in Arabidopsis, encodes a member of the raf family of protein kinases. Cell 72: 427–441 [DOI] [PubMed] [Google Scholar]
  18. Kirik V, Herrmann U, Parupalli C, Sedbrook JC, Ehrhardt DW, Hülskamp M (2007) CLASP localizes in two discrete patterns on cortical microtubules and is required for cell morphogenesis and cell division in Arabidopsis. J Cell Sci 120: 4416–4425 [DOI] [PubMed] [Google Scholar]
  19. Kuchen EE, Fox S, de Reuille PB, Kennaway R, Bensmihen S, Avondo J, Calder GM, Southam P, Robinson S, Bangham A, et al. (2012) Generation of leaf shape through early patterns of growth and tissue polarity. Science 335: 1092–1096 [DOI] [PubMed] [Google Scholar]
  20. Le J, El-Assal Sel-D, Basu D, Saad ME, Szymanski DB (2003) Requirements for Arabidopsis ATARP2 and ATARP3 during epidermal development. Curr Biol 13: 1341–1347 [DOI] [PubMed] [Google Scholar]
  21. Le J, Mallery EL, Zhang C, Brankle S, Szymanski DB (2006) Arabidopsis BRICK1/HSPC300 is an essential WAVE-complex subunit that selectively stabilizes the Arp2/3 activator SCAR2. Curr Biol 16: 895–901 [DOI] [PubMed] [Google Scholar]
  22. Lin D, Cao L, Zhou Z, Zhu L, Ehrhardt D, Yang Z, Fu Y (2013) Rho GTPase signaling activates microtubule severing to promote microtubule ordering in Arabidopsis. Curr Biol 23: 290–297 [DOI] [PubMed] [Google Scholar]
  23. Ma WY, Manjunath BS (2000) EdgeFlow: a technique for boundary detection and image segmentation. IEEE Transactions on Image Processing 9: 1375–1388 [DOI] [PubMed] [Google Scholar]
  24. Marcuzzo M, Quelhas P, Campilho A, Mendonça AM (2008) Automatic cell segmentation from confocal microscopy images of the Arabidopsis root. In 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. IEEE, pp 712–715 [Google Scholar]
  25. Panteris E, Apostolakos P, Galatis B (1993) Microtubules and morphogenesis in ordinary epidermal cells of Vigna sinensis leaves. Protoplasma 174: 91–100 [Google Scholar]
  26. Panteris E, Galatis B (2005) The morphogenesis of lobed plant cells in the mesophyll and epidermis: organization and distinct roles of cortical microtubules and actin filaments. New Phytol 167: 721–732 [DOI] [PubMed] [Google Scholar]
  27. Qiu JL, Jilk R, Marks MD, Szymanski DB (2002) The Arabidopsis SPIKE1 gene is required for normal cell shape control and tissue development. Plant Cell 14: 101–118 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Remmler L, Rolland-Lagan AG (2012) Computational method for quantifying growth patterns at the adaxial leaf surface in three dimensions. Plant Physiol 159: 27–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Robert C, Noriega A, Tocino A, Cervantes E (2008) Morphological analysis of seed shape in Arabidopsis thaliana reveals altered polarity in mutants of the ethylene signaling pathway. J Plant Physiol 165: 911–919 [DOI] [PubMed] [Google Scholar]
  30. Roeder AH, Chickarmane V, Cunha A, Obara B, Manjunath BS, Meyerowitz EM (2010) Variability in the control of cell division underlies sepal epidermal patterning in Arabidopsis thaliana. PLoS Biol 8: e1000367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Russ JC. (2002) The Image Processing Handbook, Ed 4 CRC Press, Boca Raton, FL [Google Scholar]
  32. Sampathkumar A, Krupinski P, Wightman R, Milani P, Berquand A, Boudaoud A, Hamant O, Jönsson H, Meyerowitz EM (2014) Subcellular and supracellular mechanical stress prescribes cytoskeleton behavior in Arabidopsis cotyledon pavement cells. eLife 3: e01967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Savaldi-Goldstein S, Peto C, Chory J (2007) The epidermis both drives and restricts plant shoot growth. Nature 446: 199–202 [DOI] [PubMed] [Google Scholar]
  34. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012) Fiji: an open-source platform for biological-image analysis. Nat Methods 9: 676–682 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Staff L, Hurd P, Reale L, Seoighe C, Rockwood A, Gehring C (2012) The hidden geometries of the Arabidopsis thaliana epidermis. PLoS ONE 7: e43546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Szymanski DB. (2014) The kinematics and mechanics of leaf expansion: new pieces to the Arabidopsis puzzle. Curr Opin Plant Biol 22: 141–148 [DOI] [PubMed] [Google Scholar]
  37. Szymanski DB, Cosgrove DJ (2009) Dynamic coordination of cytoskeletal and cell wall systems during plant cell morphogenesis. Curr Biol 19: R800–R811 [DOI] [PubMed] [Google Scholar]
  38. Tsuge T, Tsukaya H, Uchimiya H (1996) Two independent and polarized processes of cell elongation regulate leaf blade expansion in Arabidopsis thaliana (L.) Heynh. Development 122: 1589–1600 [DOI] [PubMed] [Google Scholar]
  39. Walter A, Silk WK, Schurr U (2009) Environmental effects on spatial and temporal patterns of leaf and root growth. Annu Rev Plant Biol 60: 279–304 [DOI] [PubMed] [Google Scholar]
  40. Xu T, Wen M, Nagawa S, Fu Y, Chen JG, Wu MJ, Perrot-Rechenmann C, Friml J, Jones AM, Yang Z (2010) Cell surface- and rho GTPase-based auxin signaling controls cellular interdigitation in Arabidopsis. Cell 143: 99–110 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Yoder N. (2011) PeakFinder. http://www.mathworks.com-/matlabcentral/fileexchange/25500
  42. Zhang C, Halsey LE, Szymanski DB (2011) The development and geometry of shape change in Arabidopsis thaliana cotyledon pavement cells. BMC Plant Biol 11: 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zhang C, Mallery EL, Schlueter J, Huang S, Fan Y, Brankle S, Staiger CJ, Szymanski DB (2008) Arabidopsis SCARs function interchangeably to meet actin-related protein 2/3 activation thresholds during morphogenesis. Plant Cell 20: 995–1011 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhu XG, Long SP, Ort DR (2010) Improving photosynthetic efficiency for greater yield. Annu Rev Plant Biol 61: 235–261 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Data
supp_171_4_2331__index.html (1.4KB, html)
supp_pp.15.00972_PP2015-00972R3_Supplemental_Material_Fig_1.pdf (2MB, pdf)
supp_pp.15.00972_PP2015-00972R3_Supplemental_Material_Fig_2.pdf (309KB, pdf)
supp_pp.15.00972_PP2015-00972R3_Supplemental_Material_Fig_3.pdf (912.1KB, pdf)
supp_pp.15.00972_PP2015-00972Table.docx (23.5KB, docx)

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES