Shock compression response of forsterite above 250 GPa

Shocked forsterite above 250 GPa indicates incongruent crystallization of MgO, its phase transition, and remelting.

Abstract

Forsterite (Mg₂SiO₄) is one of the major planetary materials, and its behavior under extreme conditions is important to understand the interior structure of large planets, such as super-Earths, and large-scale planetary impact events. Previous shock compression measurements of forsterite indicate that it may melt below 200 GPa, but these measurements did not go beyond 200 GPa. We report the shock response of forsterite above ~250 GPa, obtained using the laser shock wave technique. We simultaneously measured the Hugoniot and temperature of shocked forsterite and interpreted the results to suggest the following: (i) incongruent crystallization of MgO at 271 to 285 GPa, (ii) phase transition of MgO at 285 to 344 GPa, and (iii) remelting above ~470 to 500 GPa. These exothermic and endothermic reactions are seen to occur under extreme conditions of pressure and temperature. They indicate complex structural and chemical changes in the system MgO-SiO₂ at extreme pressures and temperatures and will affect the way we understand the interior processes of large rocky planets as well as material transformation by impacts in the formation of planetary systems.

INTRODUCTION

Forsterite (Mg₂SiO₄; Fo) and enstatite (MgSiO₃; En) in the model system MgO-MgSiO₃ are representative of the silicates found in the interiors of terrestrial planets. Their high-pressure phase transitions and phase equilibria are important in understanding the interior structures as well as the impact phenomena during planetary formation and evolution. When heated by high-speed impacts, these silicates will melt when their respective threshold shock pressures are exceeded. For example, Fo melts incongruently to produce a SiO₂-rich liquid (1) above ~13 GPa, whereas En has been known to melt incongruently and produce a liquidus phase of Fo near atmospheric pressures. These melting behaviors are affected by the changes in melt and solid properties as a function of pressure and temperature, and hence change along the shock compression curve referred to as Hugoniot.

Shock compression is a dynamic technique to generate high pressures and high temperatures, and Fo has been investigated up to a shock pressure of ~200 GPa (2–7). These studies led to a proposal that Fo starts to melt at ~150 GPa. The data show a consistent trend below ~100 GPa, but a significant scatter (7) is seen at pressures of 120 to 190 GPa, suggesting a variable degree of melting and/or phase changes. For example, Hugoniot measurements (7) of polycrystalline Fo and its high-pressure polymorph wadsleyite have indicated marked increases in density around 130 to 150 GPa, which were suggested to reflect the appearance of melt. In theory, first-principles molecular dynamics simulations (8) on Mg₂SiO₄ melt and crystalline forsterite show that the Fo Hugoniot above 130 GPa is consistent with the following interpretation: (i) post-perovskite + periclase at pressures below 150 GPa, (ii) periclase + liquid MgSiO₃ at pressures of 150 to 170 GPa, and (iii) liquid Mg₂SiO₄ above 170 GPa. However, there have been no data above 190 GPa to verify these models.

Direct measurements of high-pressure behavior of Fo above 200 GPa are essential to understand the interiors of large planets (super-Earths) as well as large-scale impacts between planetesimals during planetary formations. According to the current status (9–12) of the phase diagram in the system MgO-MgSiO₃, the liquidus of Fo is located at the lowest temperature among crystalline phases of SiO₂, En, Fo, and MgO, suggesting that Fo becomes unstable relative to its melt and that Fo melt is denser than solid at pressures of a few hundred GPa (7). Therefore, verifying and refining these phase relations will have important implications in element partitioning among the phases present during planetary formation processes.

When we consider Fo in the system MgO-SiO₂, it is compositionally between En and MgO. According to the theory (8), Fo Hugoniot above ~200 GPa corresponds to the liquid state, and its structure may change significantly with increasing pressure. In En, a transition from low- to high-density melt at ~300 GPa has been reported with a large volume change (6.3%) (13). However, corresponding first-principles calculations (14, 15) have suggested that liquid En undergoes a phase separation into crystalline MgO and liquid SiO₂ around ~300 GPa at 10,000 K. In contrast, Hugoniot for MgO has been determined up to a pressure of 1.2 TPa, and the phase transitions in MgO were confirmed with the help of theoretical simulations (16, 17).

Thus, a knowledge gap in the model MgO-SiO₂ system exists, and experimental study on Fo is valuable in understanding the properties and dynamic behaviors of silicate melts under extreme conditions. It is essential to know what conditions are required to melt and what melts will appear in the model system MgO-SiO₂. Recent progress in laser shock techniques enables advanced measurements under extreme conditions that cannot be reached by static high-pressure techniques.

RESULTS

We carried out laser shock experiments on single Fo crystals (see Materials and Methods and the Supplementary Materials), as illustrated in Fig. 1. Table 1 summarizes the principal Hugoniot measurements on single Fo crystals through the use of the quartz-reference technique (table S1) (18, 19). Figure 2 shows the experimental relationships between shock velocity (U_s in km s⁻¹) versus particle velocity (u_p in km s⁻¹) and pressure versus density. Two large discontinuities in the Fo Hugoniot were found at u_p of ~7 and ~9 km s⁻¹, indicating that Fo may have characteristic phase transitions and/or reactions. For the melt region above 200 GPa, a linear relationship of U_s to u_p is obtained at u_p of 4.1 to 6.9 km s⁻¹ [U_s = 11.39 (±0.034) + 1.86 (±0.094) (u_p − 4.630)], with σ of 1.6 × 10⁻³, integrating five data sets from Jackson and Ahrens (3) and Mosenfelder et al. (7) and three data sets from the present study (Fig. 2A). These three low-pressure data are on the simple extension of the previous data (Fig. 2, A and B). At higher pressures, our data are represented by U_s = 16.29 (±0.019) + 0.47 (±0.039) (u_p − 8.217), with σ of −1.37 × 10⁻⁴, for u_p of 6.9 to 8.8 km s⁻¹ and U_s = 19.88 (±0.058) + 1.19 (±0.029) (u_p − 11.019), with σ of −3.94 × 10⁻⁷, for u_p >8.8 km s⁻¹. These high-pressure data points are found not to be on a simple extension of the low-pressure data.

Fig. 1. Laser shock experiment of shot 35286.

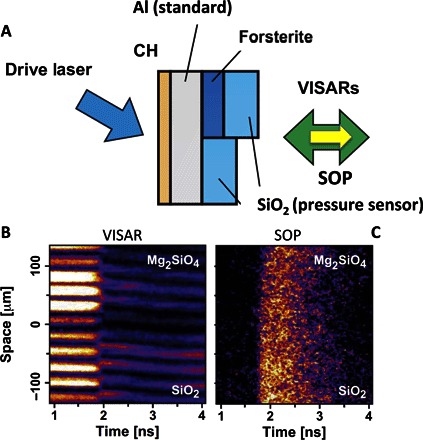
(A to C) Schematic experimental setup and typical measurements by a velocimeter [velocity interferometer system for any reflector (VISAR)] (B) and a pyrometer [streaked optical pyrometer (SOP)] (C). The driving laser was GEKKO XII (Osaka University). VISARs give direct measurements of shock velocities in forsterite and quartz under extreme conditions. The particle velocity in forsterite was calculated using the known shock velocity–particle velocity relation of quartz. This method provides a precise Hugoniot determination of forsterite. A single crystal of forsterite with a thickness of 20 or 50 μm was used as a sample. A typical equation-of-state (EOS) target assembly consisted of polypropylene (CH), aluminum (Al), crystalline α-quartz (SiO₂), and forsterite (Mg₂SiO₄). The CH polymer with a thickness of 15 or 30 μm was used as an ablator to generate a shock wave and to minimize hard x-ray radiations in the laser-plasma interaction region. The aluminum (40 μm thick) and quartz (50 μm thick) were used as the reference materials for the impedance mismatching analysis. The brightness temperature was determined using the gray-body Planck spectrum observed by a calibrated pyrometer (SOP). For details, see the Supplementary Materials.

Table 1. Shock compression data of single-crystal forsterite (initial density of 3.226 ± 0.004 g cm⁻³).

Shot number	Shock velocity (km s−1)	Particle velocity (km s−1)	Pressure (GPa)	Density (g cm−3)	Temperature (103 K)	Reflectivity
33552	14.00 ± 0.42	6.00 ± 0.39	271.0 ± 18.1	5.65 ± 0.40	7.12 ± 0.36	0.0145 ± 0.0023
35283	14.21 ± 0.27	6.22 ± 0.21	285.2 ± 10.3	5.74 ± 0.24	9.43 ± 0.68	0.0174 ± 0.0016
33676	15.70 ± 0.34	6.80 ± 0.23	344.3 ± 12.6	5.69 ± 0.24	8.44 ± 0.49	0.0527 ± 0.0050
37817	16.12 ± 0.17	7.90 ± 0.16	410.9 ± 8.5	6.33 ± 0.18	12.49 ± 0.46	0.0541 ± 0.0103
37779	16.54 ± 0.15	8.74 ± 0.20	466.3 ± 10.8	6.84 ± 0.24	13.88 ± 0.89	0.0987 ± 0.0153
37767	17.74 ± 0.20	9.21 ± 0.22	527.3 ± 12.9	6.71 ± 0.25	16.80 ± 0.64	0.1072 ± 0.0161
36755	17.96 ± 0.29	9.49 ± 0.30	549.7 ± 18.0	6.84 ± 0.36	20.63 ± 2.60	0.183 ± 0.0161
35314	19.99 ± 0.50	10.73 ± 0.37	692.0 ± 26.2	6.96 ± 0.48	—	—
35286	22.63 ± 0.19	13.35 ± 0.23	974.4 ± 17.5	7.87 ± 0.29	33.98 ± 5.48	0.213 ± 0.0324

Fig. 2. Hugoniot relationships for forsterite single crystals.

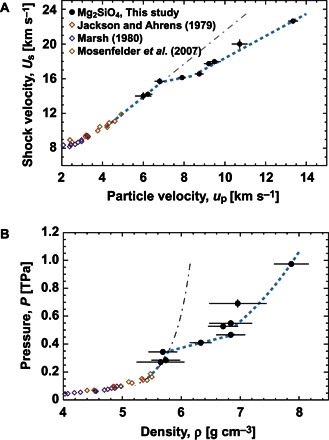
(A) Shock velocity (U_s) and particle velocity (u_p). (B) Pressure and density. Note the remarkable discontinuities around ~350 and ~450 GPa in (B) that correspond to particle velocities at u_p of ~7 and 9 km s⁻¹ in (A), respectively. Experimental setup of target is illustrated in fig. S1, and experimental data are listed in Table 1. Three previous data sets from Jackson and Ahrens (3) (for red diamonds), Marsh (4) (for violet diamonds), and Mosenfelder et al. (7) (for brown diamonds) are compared. The dot dashed lines in (A) and (B) indicate the extended Hugoniot relations given by U_s (km s⁻¹) = 2.93 + 1.82 u_p (km s⁻¹) applicable for a range of u_p of 4.1 to 6.9 km s⁻¹, which is almost the same as the prediction by de Koker et al. (8).

The measured shock temperatures of Fo (Fig. 3) are compared with the melting curves of MgO and phase boundaries in the system MgO-MgSiO₃. Temperature measurements at pressures of 271, 285, and 344 GPa, where their U_s-u_p points are on a simple extension of the gun data (Fig. 2, A and B), displayed an irregular change with increasing shock pressure. In addition, measured reflectivity data (Table 1) indicate significant increases at 344 and 466 GPa in comparison with the lower-pressure data. When the temperature and reflectivity results are combined, they suggest some chemical reactions in the Fo melt, because shock temperature must increase smoothly with shock pressure if no chemical reaction occurs. These results are attributed to exothermic and endothermic reactions.

Fig. 3. Phase diagram for MgO, Mg₂SiO₄ (Fo), and MgSiO₃ (En).

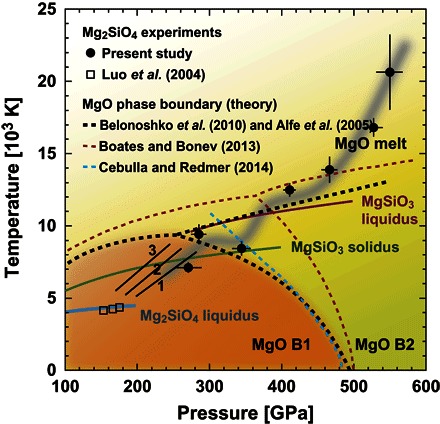
The present data of pressure and temperature on Fo Hugoniot are shown by solid circles with error bars, and the wide gray curve illustrates a possible path along Fo Hugoniot based on the present study. Phase boundaries for the transition of B1 MgO and B2 MgO and for the liquidus and melting curves of compounds Fo, En, and MgO are illustrated together with linearly extended Hugoniots (8) of Fo represented by Fo melt (line 1), liquid MgSiO₃ + B1 MgO (line 2), and postperovskite MgSiO₃ + B1 MgO (line 3). Shock temperatures of Fo measured by Luo et al. (28) are shown in squares. Boundaries for B1-B2 transition (9–11, 14, 29) and melting of MgO, solidus (10, 14) of MgSiO₃, and demixing phase boundary (14) for MgSiO₃ (liq) = MgO (solid) + SiO₂ (liq) as MgSiO₃ liquidus are illustrated for comparison.

DISCUSSION

The first discontinuity of u_p around 7 km s⁻¹ at pressures of 271 to 344 GPa (Fig. 2B) belongs to type C in fig. S1, where the shock wave retains one-wave structure and the transition is accompanied by little volume change. As discussed in the previous studies by Rice et al. (20) and Sekine et al. (21) and in fig. S1, the transition can be thermodynamically interpreted on the basis of the proposed phase diagram in the system MgO-MgSiO₃ (Fig. 3), in conjunction with our temperature measurements on the shocked Fo (Table 1). In summary, the measured temperature at 271 GPa is close to an extrapolation of the calculated results for Fo melt (line 1 in Fig. 3), whereas the temperature at 285 GPa is close to that for liquid En and solid MgO (line 2), but at 344 GPa, the temperature lies considerably below line 1.

When Fo melt is compressed above ~250 GPa, its melt structure will change significantly as predicted theoretically by De Koker and Stixrude (22). It is most likely that only MgO crystals, with very high melting temperature (Fig. 3), crystallize incongruently from Fo melt as predicted for En (14). In theory, crystallization of MgO can occur if a mixture of crystalline MgO and the residual melt becomes more stable than Fo liquid itself on the Hugoniot, especially below 290 GPa and at ~9800 K (14). Both MgSiO₃ and SiO₂ crystals have much lower melting temperatures compared to that of MgO in the system (14, 23).

Because the density changed little at pressures of 271 to 285 GPa (Fig. 2B), it is possible that if MgO crystallized at 271 GPa, it may initially have a B1 structure because the condition is well below the expected phase boundary (10, 14) between B1 and B2. However, because the B1-B2 phase boundary (9–11, 14) is sensitive to temperature and pressure, it is also possible that B2 MgO is formed above 285 GPa, provided that the Hugoniot state reached the phase boundary (9–11, 14). In contrast, the Hugoniot temperature measured at 285 GPa was higher by 1000 to 2000 K than those measured at 271 and 344 GPa (Table 1). These temperature deviations of Fo liquid from a normal temperature increase [~40 K GPa⁻¹ by shock compression in this pressure range (8)] could be explained by the proposed crystallization of MgO and the B1-B2 transition of MgO with a negative slope. If a temperature rise associated with the crystallization of MgO depends on the amount of crystallized MgO, we can estimate its fraction on the basis of the temperature measurements at pressures of 271 and 285 GPa and a normal temperature increase along the Hugoniot (~40 K GPa⁻¹). The resulting estimate, as described in Materials and Methods, yields 0.55 (±0.32) mol of MgO from Mg₂SiO₄, consisting of 2 mol MgO + 1 mol SiO₂, assuming a fusion enthalpy (24) of 77 kJ mol⁻¹ for MgO. This also means that the residual 1.45-mol liquid contains 1 mol liquid En and 0.45 mol liquid MgO (molar fraction of ~0.7 for liquid En).

The enthalpy change associated with the B1-B2 transition of MgO is endothermic (−163 kJ mol⁻¹) (25); thus, if the measured temperature drop at pressures of 285 to 344 GPa happens on the B1-B2 boundary, the average Clausius-Clapeyron slope (dT/dP) can be estimated to be −56 (±48) K GPa⁻¹, which is close to the recent estimate (11). It is also within a range of previous estimates of −26 ± 30 K GPa⁻¹ (26) and −30.4 K GPa⁻¹ (14) at temperatures of 8000 to 10,000 K.

Our net temperature decrease at pressures between 285 and 344 GPa is calculated to be ~3430 K, assuming a normal Hugoniot temperature increase (~40 K GPa⁻¹ for Fo melt) and a thermochemical estimation of temperature decrease from 285 to 344 GPa along the B1-B2 boundary for a constant fraction (0.55 ± 0.32) of incongruently crystallized MgO (3586 ± 2086 K). In conclusion, we suggest that incongruent crystallization and a B1-B2 phase transition of MgO have occurred at pressures from ~270 to 350 GPa. Because a molar fraction of En in the residual liquid is ~0.7, it might have been possible to observe a liquid-liquid transition, as claimed under similar conditions by Spaulding et al. (13). However, we could not confirm this liquid-liquid transition in the present Fo system, and our results are consistent with the theoretical studies by Cebulla and Redmer (11), Boates and Bonev (14), and Militzer (15) that indicate no liquid-liquid transition. Fo is not a simple system and has been found to display various reactions that are not expected from previously proposed phase diagrams in the system MgO-MgSiO₃ under extreme conditions. The present results on Fo also suggest that En may behave incongruently under these extreme conditions to produce SiO₂-rich liquid.

A large and rapid density increase, observed at pressures of 344 to 466 GPa, can be explained by the presence of a compressible residual liquid, because the expected density increase for the B1-B2 phase transition (~4%) (10) is too small to explain a large density change of ~17%. The observed compressibility may correspond to a large density increase associated with a coordination number increase of 6 to 8 for oxygen atoms around Mg atoms in liquid, as of that observed in SiO₂ glass at pressures of 20 to 40 GPa (27). With further increase of shock pressures along the Hugoniot, the amount of MgO (B2) above 466 GPa decreases gradually because of the rise in temperature, and eventually, Fo melt reappears when the Hugoniot temperature reaches the liquidus, as illustrated by the gray curve in Fig. 3 (see also fig. S2). The shock temperature measurements of Fo (28) below 200 GPa and the boundaries for B1-B2 transition of MgO (9–11, 14, 29) are illustrated in Fig. 3.

A second discontinuity of u_p around 9 km s⁻¹ is also observed at pressures of 466 to 550 GPa (Figs. 2 and 3). At pressures around 550 GPa, B2 MgO will melt completely because it is considerably above the melting curve of B2 MgO (Fig. 3). It is noteworthy that the reflectivity has changed significantly at a pressure of ~470 GPa (Table 1 and fig. S3D), suggesting a property change of liquid because MgO has a low reflectivity (16, 17) below 550 GPa. Reflectivity increase above ~470 GPa may support the complete melting of coexisting MgO crystals.

Although nucleation points are required for rapid crystallization, the shock-induced melt may have kept local sites to trigger such rapid crystallization. Fo displays a series of phase transitions upon compression, and because post-perovskite and MgO are solid products just before melting, there could be local nucleation sites for MgO crystallization. Recent experiments on crystallization in shocked SiO₂ have revealed homogeneous nucleation and grain growth in the shock front (30).

Present experimental results have several implications. For large-scale impact models, Fo may play an important role in determining the thermal conditions and melt compositions. If we consider planetary impacts in a head-on impact between Fo-bearing meteorites represented by ordinary chondrite, then pressure and temperature of 300 GPa and 9000 K, respectively, correspond to relative impact velocities of ~13 km s⁻¹. Because these impact velocities are common during planetary formation and Fo is distributed widely in planetary materials, incongruent crystallization of MgO may occur during large-scale impacts. Furthermore, if B2 MgO crystals are denser than the coexisting liquid under these conditions, phase separation could produce a residual liquid composition that is more En-rich. If this condition occurs in a planet’s layer, such as super-Earth’s mantle (31, 32), the compositional variation between an En-rich upper mantle and a MgO-rich lower mantle can be developed by the incongruent crystallization in Fo melt and a separation of dense MgO crystals. MgO in the lower mantle may have a chance to react with the core and be incorporated into the core of massive terrestrial planets. Violent large-scale impacts may thus have affected the chemical stratification of layered mantles in massive terrestrial planets (33). This high MgO content in early Earth’s core compositions could have influenced as the power source for dynamos (34), and also, the present results suggest that head-on impacts between ordinary chondrites at speeds greater than ~17 km/s, corresponding to a shock pressure greater than ~470 GPa, produce complete melts that may cause violent vaporization and play an important role in the planetary formation processes.

MATERIALS AND METHODS

A single crystal of forsterite Mg₂SiO₄ (~22 mm in diameter × 25 mm long) was purchased from Hanamura Optics. The density was measured to be 3.226 ± 0.004 g cm⁻³. Plates were cut and polished to use as targets. Figure 1 schematically illustrates our experimental arrangement and target assemblage for shot 35286. We did not use any high-Z materials in the target assemblage to measure principal Hugoniot and utilized a relatively weak intensity laser (~10¹² to 10¹³ W cm⁻²). The purity of Al was greater than 99.9%, and the initial density was 2.703 g cm⁻³. All of the target components were glued with an ultraviolet cure adhesive. The thickness of the glue layer was typically ~0.7 μm. The refractive indexes of quartz and forsterite at 532 nm (probe wavelength of velocimeter) were 1.547 and 1.660, respectively.

The laser-driven shock experiments were performed using the GEKKO XII laser at the Osaka University. The facility is a neodymium-doped glass laser system. We used three and nine laser beams at the frequency-doubled wavelength of 527 nm and frequency-tripled wavelength of 351 nm, respectively. The temporal shape of the laser pulse was approximately square with a 2.5-ns duration [full width at half maximum (FWHM)] and rise and fall times of ~100 ps each. The focal spot diameter was typically 600 μm or 1 mm with a flat-top distribution resulting in a planar shock front of more than 400 μm in diameter. Kinoform phase plates were used to achieve the uniform super-Gaussian irradiation pattern.

Forsterite Hugoniots were measured using the impedance mismatching technique (35) with Al and α-quartz (16, 17) for the reference. Shock velocities (U_s) of forsterite and quartz were measured with two line-imaging velocity interferometers (line VISARs) (36–38). These VISARs had different velocity sensitivities [velocity per fringe (VPF)] to resolve the 2π-phase shift ambiguities in the interferometry. The sensitivities of the two VISARs were 4.122 and 9.744 km s⁻¹ per fringe by choosing appropriate etalons. The low-VPF VISAR was used for determining the final velocity value because it provides more precise values compared to the high-VPF VISAR. Because our postprocessing of the VISAR images could determine the fringe position to 4 to 5% of an interfringe distance, the multiple fringe shifts allow precise shock velocity measurements to be within a few percent.

The shocked aluminum state was inferred from the measured U_s of quartz (table S1). Then, u_p of forsterite was determined by matching shock impedances of the forsterite and aluminum. Shock pressure P, density ρ, and internal energy E in forsterite were determined from the U_s and u_p of forsterite using the basic conservation relations (35). The use of the α-quartz reference allowed us to precisely infer the aluminum shock state just before the shock crosses the Al-quartz interface because quartz had metallic-like high optical reflectance under shock compression above 150 GPa (39).

The quartz Hugoniot previously established by Hamel et al. (40) has a polynomial U_s-u_p relation given by U_s = (2.40 ± 0.10) + (1.68 ± 0.02) u_p − (0.0155 ± 0.0010) u_p². This formula is valid at a pressure above ~200 GPa. The Al state before shock arrival in the Al-quartz interface was inferred from this quartz Hugoniot point and the knowledge of Al Hugoniot and release curves. The Al Hugoniot we used was U_s = (6.341 ± 0.003) + (1.185 ± 0.002) u_p (41). Release isentropes of Al from the shocked Al state into the quartz state were approximated on the basis of the Mie-Grüneisen EOS. We used a well-known representation of Grüneisen parameter γ that is linear in relative volume: γ = γ₀ (V/V₀), where the subscript 0 denotes the initial value. Impedance matching occurs at the intersection of a forsterite Rayleigh line and the reshock of Al from the inferred Al Hugoniot point. The reshock of Al was also approximated on the basis of the Mie-Grüneisen EOS. The analyzed data are listed in table S1.

Shock temperatures were measured with an SOP (42, 43). Using the VISAR collection optics, thermal radiations from a shock front were collected by the SOP to deduce the brightness temperature of the shocked matter. The SOP system was absolutely calibrated with a NIST (National Institute of Standards and Technology)–traceable standard lamp, and resolved spatially and temporally to image the self-emissions from the shock around a 455-nm wavelength with a narrow bandwidth (38-nm FWHM). The brightness temperature was determined using the gray-body Planck spectrum

$$\mathit{I}(\mathrm{\lambda },\mathit{T})=\mathrm{\epsilon }\frac{2\mathrm{\pi }\mathit{h}{\mathit{c}}^2}{{\mathrm{\lambda }}^5}{({\mathit{e}}^{\frac{\mathit{h}\mathit{c}}{\mathrm{\lambda }{\mathit{k}}_{\mathit{B}}\mathit{T}}}-1)}^{-1}$$ (1)

where ε is the emissivity of the shocked matter. This equation can be reduced to a practical form at the narrow band wavelengths, as described by Miller et al. (42)

$$\mathit{T}=\frac{{\mathit{T}}_0}{\text{ln}(\mathit{A}\mathrm{\epsilon }/\mathit{C}+1)}$$ (2)

where T₀ and A are calibration parameters that depend on the SOP optical system and C is the CCD (charge-coupled device) counts obtained by the streak camera system. The emissivity ε was calculated from the Kirchhoff law, ε = 1 − R, where R was assumed to be independent of wavelength and equal to the shock-front reflectivity measured at 532 nm by the VISAR. The reflectivity of the shocked forsterite was determined relative to both the Al base plate and the shocked quartz used as reflectivity reference (44) in the targets. The uncertainty of the measured temperature increases monotonically from ~5 to ~20% with the temperature increase from 7000 to 30,000 K, respectively. The uncertainties of the reflectivity R and the calibration parameter A (that is, optical system transmission) are the dominant contributors to the uncertainty of the temperature measurements. Typically, the uncertainty of the reflectivity was 9%. The spectra decayed with time were profiled as VISARs (as shock velocities), and the temperatures corresponding to U_s of the Fo sample are listed in Table 1. Figure S3 shows a typical decay profile in shock 37767 and illustrates how we read the shock velocity and emission count for Hugoniot analysis from the obtained profiles, together with the temperature-pressure and reflectivity-pressure relations.

Thermodynamics can be used to inform what phases are present at a specific pressure and temperature. If the Gibbs free energy is known, we can predict what phases are stable. Figure S2 illustrates the energetics in a model system En-MgO with an intermediate compound Fo as a function of pressure P and temperature T. MgO has the highest melting point, and Fo has the lowest in this system. Energetically, Fo is located below the line connecting liquid and solid B1 and represented by point 1, because Fo is a liquid but not a mixture of liquid and B1 MgO. However, with increasing shock pressure, the Fo liquid structure will be greatly altered and the relative energy rises above the energy level for the mixture of liquid and B1 MgO, as illustrated by points 2 and 3. As a result, Fo liquid is unstable relative to the mixture of liquid and B1 MgO. This brings the Fo liquid to a state that favors incongruent crystallization of B1 MgO. Furthermore, when B1 MgO is transformed to the high-pressure B2 structure, incongruently crystallized B1 MgO will follow this transition. Because crystallization is an exothermic process and the high-pressure phase transition is endothermic, the temperature will increase substantially in the exothermic reaction and decrease during the endothermic one. On the other hand, normal shock compression increases both temperature and pressure, and Hugoniot shows a monotonous change as long as no transition occurs.

Figure S1 illustrates a comparison in plots of U_s-u_p, P-ρ, and P-T for phase transitions displaying a one- or two-wave structure. In case of a two-wave structure, phase transitions with volume reduction are likely to show up as a gap in the U_s-u_p and P-ρ plots (fig. S1A). On the other hand, chemical reactions with a volume increase (fig. S1B) will show a discontinuity in the U_s-u_p plot but will retain a one-wave structure. The corresponding P-ρ plot contains a metastable extension of the low-pressure phase. The metastable low-pressure phase is denser than the high-pressure phase and results in volume expansion with increasing pressure (fig. S1B). In the case of the phase transition with a negative P-T slope (fig. S1C), like the B1-B2 transition of MgO, volume and temperature decrease simultaneously. Forsterite is an example that behaves like case B or C in fig. S1, over a range of 200 to 400 GPa, depending on the overall density change.

On the basis of the thermodynamic data for MgO, heat of fusion (24), and the enthalpy change for B1-B2 phase transition (25), we can estimate temperature changes associated with the previously discussed processes, assuming

$$\text{Fo} (\text{liq})=2 \text{MgO} (\text{liq})+{\text{SiO}}_2(\text{liq})\mathrm{\Delta }{\mathrm{H}}_3$$ (3)

$$\text{MgO} (\text{liq})= \text{MgO} (\text{solid})\mathrm{\Delta }{\mathrm{H}}_4$$ (4)

The following reaction (Eq. 5) can be obtained from the reaction Eq. 3 + 2y (Eq. 4), where y represents crystallization of MgO in mole

$$\text{Fo} (\text{liq})=\mathit{y}\text{MgO}(\text{solid})+(2-\mathit{y}) \text{MgO} (\text{liq})+{\text{SiO}}_2(\text{liq})\mathrm{\Delta }{\mathrm{H}}_5$$ (5)

ΔH₅ = ΔH₃ + yΔH₄, where ΔH₄ = 77 kJ mol⁻¹ and ΔH₃ = 8.75 kJ mol⁻¹ (assumed to be 130 meV per atom) (14). ΔH₅ = Cp·ΔT, where heat capacity Cp is 25 J mol⁻¹ K⁻¹ and temperature rise ΔT represents incongruent crystallization of y moles MgO. If Fo liquid and residual liquid are ideally mixed, the term ΔH₃ can be neglected. Our measured temperature difference ΔT at pressures between 271 and 285 GPa was 2300 ± 1000 K, including a normal temperature increase (8) along the Hugoniot (~600 K). The difference (ΔT = 1700 ± 1000 K) gives a value of y = 0.55 ± 0.32, corresponding to the reaction: Fo (liq) = 0.55 MgO (solid) + 1.45 MgO (liq) + SiO₂ (liq). This means that the liquid composition is between Fo and En at pressures of 271 to 285 GPa. If the whole MgO is crystallized incongruently (y = 2), then ΔT = 7110 (= 6510 + 600) K could be expected.

A similar analysis can be made for the B1-B2 where

$$\mathrm{B}1 \text{MgO} =\mathrm{B}2 \text{MgO} \mathrm{\Delta }{\mathrm{H}}_6$$ (6)

When reaction 6 occurs at pressures of 285 to 344 GPa, the Clausius-Clapeyron slope can be estimated as follows: the Hugoniot temperature increase at a constant rate in this pressure range (~40 K GPa⁻¹) is ~2360 K (8), and the measured temperature decrease is 990 (±840) K. The total decrease is ~3350 K. This gives a dT/dP of −56 (±48) K GPa⁻¹. If the fraction of incongruently crystallized MgO is kept as 0.55 ± 0.32, then the expected temperature drop is 3586 (±2086) K, based on the heat capacity Cp of 25 J mol⁻¹ K⁻¹. This is in good agreement with the results on the present temperature measurements.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/8/e1600157/DC1

fig. S1. Hugoniot and phase boundaries.

fig. S2. The phase relations and Gibbs free energies as functions of pressure and temperature.

fig. S3. A typical profile of decay for shot 37767.

table S1. Measured quartz shock velocities and inferred Al states based on the impedance mismatching analysis.