The flagellar motor of Caulobacter crescentus generates more torque when a cell swims backward

Abstract

Caulobacter crescentus, a monotrichous bacterium, swims by rotating a single right-handed helical filament. CW motor rotation thrusts the cell forward ¹, a mode of motility known as the pusher mode; CCW motor rotation pulls the cell backward, a mode of motility referred to as the puller mode ². The situation is opposite in E. coli, a peritrichous bacterium, where CCW rotation of multiple left-handed filaments drives the cell forward. The flagellar motor in E. coli generates more torque in the CCW direction than the CW direction in swimming cells ^3,4. However, monotrichous bacteria including C. crescentus swim forward and backward at similar speeds, prompting the assumption that motor torques in the two modes are the same ^5,6. Here, we present evidence that motors in C. crescentus develop higher torques in the puller mode than in the pusher mode, and suggest that the anisotropy in torque-generation is similar in two species, despite the differences in filament handedness and motor bias (probability of CW rotation).

The differences in the fluid-flows generated in the pusher and puller modes can be approximated by force-dipoles of opposite signs but equal strengths, and the assumption of equal motor-torques is important when comparing the hydrodynamics and rheology of active fluids ^7-12. Given this assumption, that the cells in Vibrio alginolyticus swim twice as fast backward than forward, only when close to solid surfaces, has been attributed to changes in swimming geometries and hydrodynamic interactions with the bounding surfaces ^13,14. However, such mechanisms fail to explain why cells in Pseudomonas putida swim twice as fast backward at large separations from surfaces ¹⁵.

We observed cell bodies that transiently tethered to a glass surface and rotated about an axis normal to the surface. Such cells rotated twice as fast CW than CCW. The filaments remained untethered and rotated freely, as shown by visualization of fluorescently labeled flagella. The cell-body rotation could be understood on the basis of a model that took into account the hydrodynamic interactions between a rolling filament and the underlying surface. The model predicted that CW rotation of a filament drives the tethered cell CCW, and CCW rotation of the filament drives the tethered cell CW. Thus, under moderate viscous loads, the filaments in C. crescentus rotate faster in the CCW direction as in the CW direction. We tested the model by calculating the fraction of the time that motors rotate CW (motor bias or CW_bias) and determined that the CW_bias was 0.8. This was consistent with the observations that C. crescentus swam forward most of the time. The anisotropy in motor speeds disappeared at very high viscous loads, similar to the motor behavior in E. coli ^3,4. Based on these results, we assert that the anisotropy in torque-generation is similar in the two species, although filament handedness and motor bias are opposite.

Cell-body rotation near surfaces

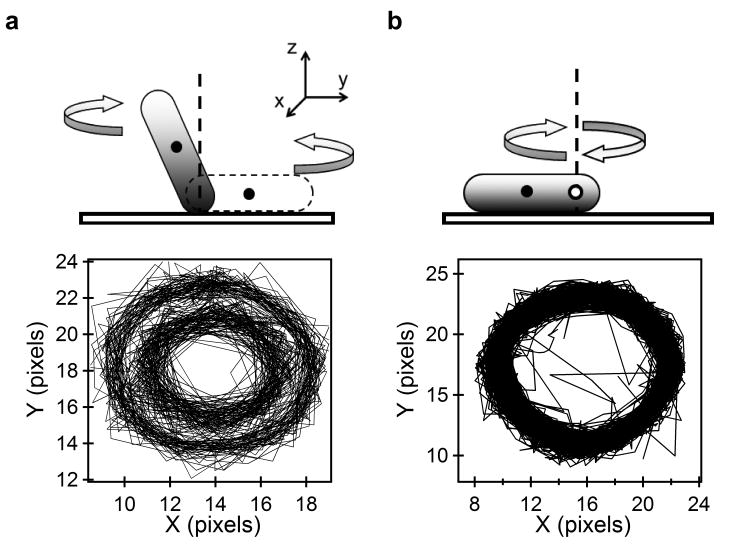
In our experiments, swimming cells of C. crescentus strains lacking pili spontaneously stuck to the microscope coverglass, and rotated in either direction about a single point of attachment. Most cells would detach and swim away after ∼ 1-5 min. Digital video recordings were analyzed as before ¹⁶ to track the lengths/widths of the cells as they appeared in the image plane, their orientations, the center of the cell-body and the point of tether (center of rotation) over time (Materials and Methods). Two types of cell-rotations about the z-axis (the axis normal to the image plane) were observed. In the first case, the cell would remain in-plane when rotating CCW, but would orient vertically when rotating CW, as shown the schematic in Fig. 1a. In this case, the center of the cell-body exhibited concentric circular trajectories (bottom panel), the inner trajectory for CW rotation and the outer trajectory for CCW rotation, as shown in Fig. 1a. Since the hydrodynamic drag on the body was different in these two geometries, we did not include such trajectories for further analysis of motor torques. In the second case, the cell rotated in-plane (Fig. 1b), and the center of the cell-body exhibited a single circular trajectory irrespective of the direction of rotation (bottom panel). Only such cells were selected for further analysis.

Figure 1. Types of cell-tethering.

a) First type of tethering observed in C. crescentus. Rotation geometry (top panel). CCW cell rotation is indicated by the gray cell and CW cell rotation is indicated by the white cell (dashed outline). The black dots show the respective centers of body tracked by the algorithm. The corresponding trajectories traced by the respective black dots are indicated (bottom panel). b) Second type of tethering observed in C. crescentus. Rotation geometry (top panel). The black dot indicates the center of body tracked by the tracking algorithm and the white circle indicates the center of rotation. The corresponding trajectories traced by the center of body are indicated (bottom panel).

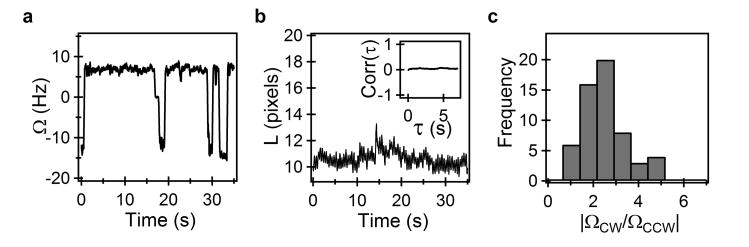
A typical trace of rotation speed, Ω, calculated from the change in cell orientation with time, is shown in Fig. 2a. The magnitudes of the speeds showed a clear difference in the two directions. To quantitatively determine if the variations in speed of rotation were due to changes in tethering geometry, we analyzed the lengths (L) and widths (W) of the cells (projected on the image plane) over time. For the cell shown in Fig. 2a, L vs time is indicated in Fig. 2b over the same time-interval. The length of the tracked cell appeared to remain constant over the duration of our measurement. No significant cross-correlation was observed between either L and Ω (inset in Fig. 2b) or W and Ω (not shown). The point of tether or the center of rotation (see schematic in Fig. 1b and Supplementary Figure S1) also remained unchanged. This indicated that the tethering geometry remained the same in either direction. The distribution of the ratios of the absolute cell-rotation speeds, Ω_CW versus Ω_CCW, is plotted in Fig. 2c (n = 48 motors). The average ratio (Ω_CW/Ω_CCW) was 2.2 ± 0.9 and the average CW cell-rotation speed was ∼ -8 Hz.

Figure 2. Cell-rotation characteristics.

a) Typical cell body rotational speeds over time. Note that the CCW cell rotation speed (positive values) is lower than the absolute CW cell rotation speed (negative values). b) Trace of the length, L, of the cell shown in A) projected on the image plane during the same interval. Inset shows the cross-correlation between Ω and L. c) Distributions of the absolute value of the ratio of cell rotation speeds (n = 48 cells).

The cell body is crescent-shaped. As a result, any significant rotation of the cell about its principal axis (which lies parallel to the surface) would be detectable via changes in the shape of the cell image. Given the asymmetry in the cell shape, changes in the orientation along the principal axis during a switch in the direction of cell-rotation could affect the relative drag coefficients in the two directions. However, no obvious changes in the shape of the cell image were observed regardless of the direction, in the manner expected for a cell rotating about an axis normal to its principal axis (movie 1, 0.75× speed). Furthermore, experiments with straight mutants which are symmetric along the principal axis ¹⁷ revealed a similar anisotropy in relative speeds, as those seen in Fig. 2c. Thus, variations in the relative drag coefficients of the cell-body make insignificant contributions to the anisotropy in rotational speeds.

Visualization of flagella in rotating cells

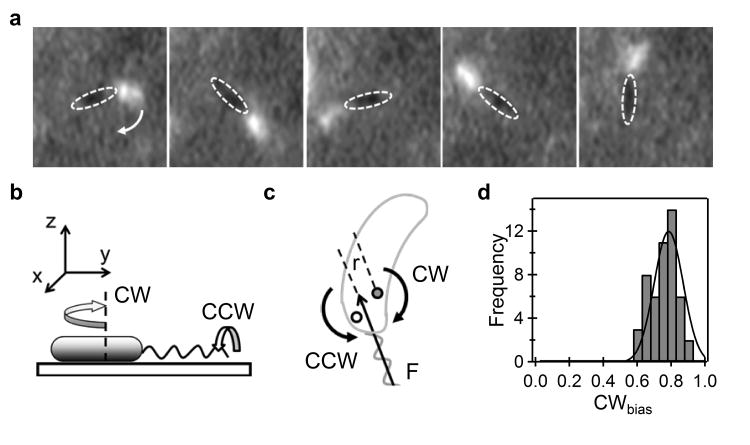
To determine the mechanism of rotation, we fluorescently labeled the flagellar filaments and visualized rotating cells under total internal reflection fluorescence (TIRF) illumination (see Materials and Methods). Fig. 3a and movie 2 show the rotation of a cell with a labeled flagellum. As is evident, the filament goes around with the cell body, rotating about an axis extending from one end of the cell. The cells were not tethered by their flagellar filaments. The tethering point lies on the surface of the cell body, an attachment likely due to non-specific interactions between the cell surface and the surface. We refer to the attachment as a fluid joint, which is likely made up of the polysaccharide that covers the entire cell in Caulobacter Crescentus ¹⁸. Additional discussions on the tether properties have been included in the Supplementary Text (see Supplementary Figures S2 and S3).

Figure 3. Mechanism of cell-rotation.

a) Visualization of fluorescently labeled flagellar filaments. The bright spot indicates the flagellum and the dashed ellipses the cell body. Direction of rotation of the cell body is indicated by the white arrow. b) Model for cell-rotation: CCW rotation of the flagellum causes CW cell rotation through hydrodynamic coupling with the solid substrate. c) Thrust-based mechanisms are unlikely to explain the results in Fig. 2C, since depending on the relative position of the tethering point, the same force F can cause CCW cell rotation (in case of the white tethering point) or CW rotation (in case of the gray tethering point). d) The fraction of time that motors spin CW (the CW_bias calculated on the basis of the model shown in panel b) shows a peak in distribution around 0.8, consistent with previous measurements that show that cells swim forward a majority of the time.

As seen in the movie, the filament is moving sideways. We believe this lateral force is generated by hydrodynamic coupling of the flagellar filament with the underlying surface, as the helix rolls over that surface. To understand this effect, consider a rotating sphere in place of the filament. Since the drag on its bottom surface is higher than the drag on the top surface, the sphere will translate laterally due to its rotation. This mechanism is responsible for the spiraling of E. coli as it swims near a substrate ¹⁹. When C. crescentus rotates over the surface (Fig. 3b) the filament rolls, but the cell body is not able to do so; it is constrained by the fluid joint that tethers it to the surface. It is important to note that when the filament spins CW (when viewed from its distal end), the body turns CCW (when viewed from above). Since the cells rotate about twice as fast CW than CCW (Fig. 2), the filaments must rotate about twice as fast CCW than CW: the CCW motor torque is larger than the CW torque.

Other mechanisms could involve the thrust (F) generated by the rotation of the filament. For a finite distance r between the helix axis and the tethering point, a torque τ (∼ r × F) could cause the cell to rotate as shown in Fig. 3c. However, r is typically small (∼ 100 nm) and hence the thrust would be inadequate to rotate a cell at 4-8 Hz. Furthermore, such a mechanism can cause cell-rotation in either direction at different speeds, depending on the point of tethering (Fig. 3c) and the orientation of the filament (with respect to the cell's principal axis). However, faster CW rotation was predominantly observed in our data. Evidently, such mechanisms do not contribute much to cell rotation (see Supplementary Text).

A fraction of cells (< 1%) were observed to tether and rotate in such a way that they remained perpendicular to the surface in either direction, with the filaments pointing away from the surface. Flagellar interactions with the surface were absent and the cells counter-rotated due to motor-rotation. A similar anisotropy in the speeds of cell-rotation was observed (Ω_CW ∼ 1.5 Ω_CCW), consistent with the hypothesis that motors rotate faster in the CCW direction (Supplementary Figure S3). Next, we irreversibly tethered the filament to the surface which resulted in high loads on the motor. Consistent with previous reports in E. coli, the anisotropy in speeds vanished at these higher loads (Supplementary Figure S4).

Test of the filament roll model

To test our model, we determined the CW_bias. The inversion between cell and filament rotational directions is a direct consequence of the hydrodynamic interactions with the surface, as discussed above. Therefore, the CW_bias is simply the fraction of time that the cell body rotates CCW. The observed CW_bias is shown in Fig. 3d and has an average value of 0.8. Our model thus predicts that the cells swim forward 80% of the time, which is consistent with our observations of swimming cells with fluorescently labeled flagella and those of Liu and co-workers ⁶. This supports the hypothesis of rotational direction-inversion.

Direction-independent swimming speeds

Recent measurements by Liu et al. ⁶ indicated that the body counter-rotation frequency is twice as high in the puller mode in C. crescentus cells that swim in the bulk fluid. This difference was attributed to the differences in the kinematics of swimming in the two directions, since the cells precess along a helical path of higher amplitude in the pusher mode as in the puller mode. Paradoxically, the swimming speeds in the two modes are identical, which indicates that the thrust developed is independent of the direction. Based on our results, we suggest that the torque generated by the motor in the CCW direction and, consequently, the filament rotation frequency, is higher when the cell swims backward (ω_puller ∼ 1.5 to 2 times ω_pusher). Therefore, the counter-rotation frequency in the puller mode is larger as well (Ω_puller ∼ 1.5 to 2 times Ω_pusher). We extended the precession model ⁶ to explain why the overall thrust developed, and hence the swimming speed (V), is independent of the direction of motor rotation. At low Reynolds numbers, the following relations apply for the right-handed helix:

$$\left[\begin{array}{c}{F}_{\mathit{\text{fil}}}\\ {\tau }_{\mathit{\text{fil}}}\end{array}\right]=\left[\begin{array}{cc}{X}_{11}& -X_{12}\\ -X_{21}& X_{22}\end{array}\right]\left[\begin{array}{c}V\\ \omega \end{array}\right]$$ (1)

For the cell, the following relations hold:

$$\left[\begin{array}{c}{F}_{\mathit{\text{cell}}}\\ {\tau }_{\mathit{\text{cell}}}\end{array}\right]=\left[\begin{array}{cc}{Y}_{11}& -Y_{12}\\ Y_{21}& -Y_{22}\end{array}\right]\left[\begin{array}{c}V\\ \mathrm{\Omega }\end{array}\right]$$ (2)

The non-diagonal elements of the resistance tensor Y_ij are non-zero since the cells precess (along a left-handed helical path). The slantwise motion of the cell body during precession develops thrust, adding to that developed by the filament, compensating for the lower motor torque in the pusher mode. The right-hand rule was adopted for determining the sign of ω, and the signs on the elements of Y_ij were adjusted taking into account the opposite directions of body counter-rotation and filament rotation. For force-free and torque-free swimming cells, F_cell + F_fil = 0 and τ_cell + τ_fil = 0. Therefore equations 1 and 2 can be solved to obtain the expression for the ratio of swimming speeds (V_B/V_A) in case A and B, for example when ω_B = 2ω_A and Ω_B = 2Ω_A.

$$\frac{V_B}{V_A}=\frac{{\mathrm{\Omega }}_B({Y^B}_{12}+\frac{X_{12}}{X_{22}}{Y^B}_{22})}{(X_{11}+{Y^B}_{11}+({Y^B}_{12}-X_{12})X_{12}/X_{22})}/\frac{{\mathrm{\Omega }}_A({Y^A}_{12}+\frac{X_{12}}{X_{22}}{Y^A}_{22})}{(X_{11}+{Y^A}_{11}+({Y^A}_{12}-X_{12})X_{12}/X_{22})}$$ (3)

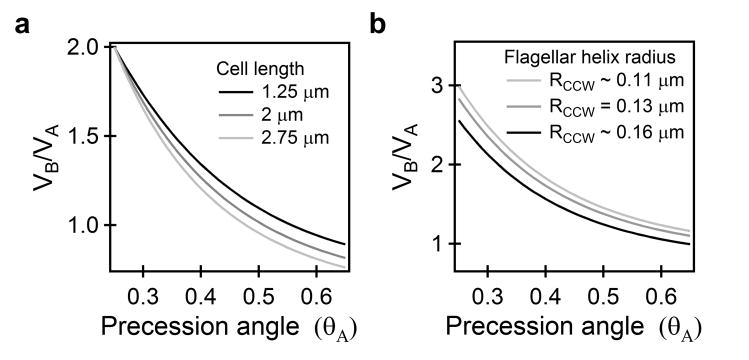
The values of the elements of Y_ij change with the amplitude of precession ⁶. X_ij was calculated using Lighthill's Slender Body Theory ^7,20. First, we assumed that the elements of the resistance tensor X_ij are invariant with respect to the direction of rotation, since we did not observe significant changes in the polymorphic form of the filament (Supplementary Figure S5). During precession, the cell's principal axis makes an angle with the direction of swimming, defined as the angle of precession (θ) ⁶. Assuming an angle of precession θ_B ∼ 0.25 rad, we calculated the ratios from equation 3 for varying θ_A as shown in Fig. 4a. For θ_A ∼ 0.5 rad, swimming speeds for the two cases are equal for all cell lengths analyzed (1.25, 2 and 2.75 μm), even though the filament rotation frequency is twice as large in case B.

Figure 4. Anisotropic motor torques and equal swimming speeds.

a) Predicted ratios of swimming speeds (V_B/V_A) when the filament and cell body rotational frequencies differ in the two cases (ω_B = 2ω_A and Ω_B = 2 Ω_A). Precession angle θ_B = 0.25 rad. b) Effect of change in filament shape with direction of rotation. Precession angle θ_B = 0.35 rad, cell length L = 2.5 μm and R_CW = 0.13 μm. All predictions are from equation 3.

Next, we considered the effect of a change in the shape of the filament with direction of rotation, such that X_ij^CCW ≠ X_ij^CW. Assuming a constant arc length, Λ, we varied the radius of the helix for CCW turns (R_CCW) and determined the pitch (λ_CCW) from the relation Λ = n_c (4 π² R_CCW²+λ_CCW²)^0.5, where n_c is the number of helical turns. The dependence of V_B/V_A on the values of precession angles and the shape of the filament are shown in Fig. 4b (for R_CW = 0.13 μm and θ_B = 0.35 rad). As evident, even a ∼ 20% change in filament helical radius does not significantly alter the ratios. Thus, the lateral force generated by cell-precession is indeed sufficient to overcome the lower motor torque in case A. Note that the values of precession angles in our analysis (θ_B ∼ 0.35 rad and θ_A ∼ 0.5 rad) are in close agreement with the values experimentally measured (θ_puller ∼ 0.35 rad and θ_pusher ∼ 0.49 rad) by Liu et al.

The similarities in motor behavior in C. crescentus and E. coli reported here appear consistent with the structural similarities in the flagellar motors in the two species ²¹, despite the differences in filament handedness. In C. crescentus, flexibility in the polymorphic form of the filament will result in unidirectional motion, since a CW rotating right handed helix and a CCW rotating left handed helix generate thrust in the same direction. One way to prevent such changes in form is to increase the structural integrity by adding multiple flagellins as reinforcements. This could be the underlying reason for the redundancy in flagellin genes in C. crescentus ²². Finally, C. crescentus has an asymmetric developmental cycle ²³, in which a cell irreversibly tethers to a substrate and releases a new swimmer cell after cell-division. It is likely that the higher torque in the puller mode helps the swimmer cell detach quickly from its mother.

Materials and Methods

Strains and plasmids

We used a ΔpilA strain (NA1000) lacking the holdfast for all experiments. For TIRF visualization, site-directed mutagenesis was conducted on the fljK gene to change the codon encoding alanine¹²⁵ to a codon encoding cysteine¹²⁵. The construct was then cloned in pBXMCS-2 ²⁴ using the restriction sites NdeI and XbaI. The plasmid was transformed into strain TPA12 - ΔfljJ-K-L-M-N-O ²² and expression was induced by adding Xylose (∼ 0.08 M) at the start of the growth culture. All strains were grown in peptone-yeast extract (PYE) at 30°C, and kanamycin (20 μg/ml) was added wherever necessary at the start of the growth culture. To label the filaments fluorescently, we used an Alexa Fluor dye (532 nm, maleimide derivative, Life Technologies).

Rotational speed measurements and TIRF imaging

Cells were introduced in tunnel slides and cell rotation was recorded using a digital camera (Thorlabs DCC1240M) at 67 fps with a 40× phase objective and a 1.6× optovar setting, when cells happened to approach and tether transiently to the coverglass. We did experiments with both kinds of coverglass, out of the box and those cleaned with alcoholic KOH. The instances of cell-adhesion were higher in the former and lower in the latter case. However, in either case, CW rotation of the cell was predominantly faster. Cells that were selected for analysis rotated smoothly without pausing for a minimum of ∼ 1 min. To track the center of rotation (point of tether or pivot) in either direction, we constructed single images by averaging several frames together, in which the cells rotated in only one direction. This resulted in a bright spot with a Gaussian intensity profile, the center of which was the point of tether. We applied standard particle tracking algorithms ²⁵ to determine the center of such Gaussian profiles. This gave us the center of rotation for CW and CCW. To track the center of body, which is distinct from the point of tether, we used a segmentation algorithm (MATLAB, Mathworks Inc.) and fitted ellipses to the cell profile. We then determined the cell orientation, the length/width of the cells and the center of the cell-body by fitting ellipses to such binary images. The orientation changed with respect to time, which enabled us to calculate the rotational speeds. The center of the cell-body traced out a circular trajectory which enabled us to discriminate between the geometries discussed in Fig. 1a and b. The cross-correlation between cell lengths (L)/widths (W) and motor speeds was calculated as $\mathit{\text{Corr}}(\tau )=\frac{\sum ({\mathrm{\Omega }}^{\prime }(t+\tau )L^{\prime }(t)-\overline{{\mathrm{\Omega }}^{\prime }}.\overline{L^{\prime }})}{\sum {({\mathrm{\Omega }}^{\prime }(t)-\overline{{\mathrm{\Omega }}^{\prime }})}^2\sum {(L^{\prime }(t)-\overline{L^{\prime }})}^2}$. Ω′ was obtained by normalizing positive Ω values with the mean absolute CCW speed, and negative Ω values were normalized with the absolute mean CW speed. L′ was obtained by centering and scaling L. The setup for simultaneous fluorescence and phase contrast imaging for visualization of the fluorescently-labeled filaments is described elsewhere ²⁶.