Raman analysis of bond conformations in the rotator state and premelting of normal alkanes

Abstract

We perform Raman spectroscopic measurements on normal alkanes (C_nH_2n+2) to quantify the n dependence of the conformational disorder that occurs below the melt temperature. We employ a three-state spectral analysis method originally developed for semi-crystalline polyethylene that posits crystalline, amorphous, and non-crystalline consecutive trans (NCCT) conformations to extract their respective mass fractions. For the alkanes studied that melt via a rotator phase (21 ≤ n ≤ 37), we find that conformational disorder can be quantified by the loss of NCCT mass fraction, which systematically decreases with increasing chain length. For those that melt directly via the crystal phase (n ≥ 40), we observe NCCT conformational mass fractions that are independent of chain length but whose disordered mass fraction increases with length. These complement prior IR measurements which measure disorder via gauche conformations, but have not been able to measure the mass fraction of this disorder as a function of n. An interesting feature of the three-state analysis when applied to alkanes is that the measured fraction of disordered chain conformations in the rotator phase of (10 to 30) % greatly exceeds the mass fraction of gauche bonds (1 to 7) % as measured from IR; we reconcile this difference through DFT calculations.

Introduction

Normal alkanes C_nH_2n+2 comprise a variety of materials ranging from paraffin wax to polyethylenes. In addition, alkane chain segments are an important constituent of biological molecules including fatty acids, long-chain alcohols, and phospholipids. Chain configuration and packing of these molecules directly impacts the physical properties that are critical to industrial processing. Therefore, identifying and quantifying the different structural changes in alkanes is a crucial step towards the efficient handling of these systems at the industrial scale.^{1, 2}

Despite having a simple repeat unit, normal alkanes exhibit a wide variety of structural changes with temperature. Alkanes longer than C₉H₂₀ (abbreviated as C₉) with an odd number of carbon atoms have an orthorhombic packing as the lowest energy structure. This crystal phase consists of alkane molecules in the trans configuration forming stacked lamellae with the long axes of molecules parallel. A cross section of the lamellae cut perpendicular to the chain axis would reveal molecular orientation resembling a herringbone pattern.

The transition between the orthorhombic crystal to the high temperature melt phase is known to depend strongly on n and is mediated by disorder. For 9 ≤ n ≤ 39 alkanes undergo a transition to a rotator phase a few degrees below the melting point.^3–6 Within this phase the molecules lose their herringbone order, but remain in the trans configuration in lamellar stacks, which we refer to as non-crystalline consecutive trans (NCCT). Disorder in the rotator phase takes the form of single gauche (G) and gauche-trans-gauche “kink” (GTG′) conformations as well as twist solitons.⁷ For n > 39 there is no stable rotator phase; instead the formation of nonplanar conformers at just below the melting point.⁸ Premelting is a thermodynamically-favored surface melting of the alkane crystal characterized by the appearance of gauche bonds and possibly chain segments that are NCCT near the chain ends. In the crystal phase, a decrease from 100% crystalline fraction and appearance of NCCT conformers is a signature of conformational disorder; likewise, in the rotator phase, a decrease from 100% NCCT fraction and appearance of amorphous conformers is a signature of conformational disorder.

In the present work, we are concerned with the nature and n dependence of disorder that occur in the rotator phase and during premelting. A thorough understanding of these states provides important information on the nature of the melting transition and underlying thermodynamics. Vibrational spectroscopy is the primary tool to measure conformational states in the crystal and rotator phases of alkanes but there are critical gaps in our ability to measure the n dependence of disorder.^{9, 10} Infrared (IR) spectra have been used to identify and quantify specific gauche-trans sequences along the chain in both the crystal and rotator phases.^{5, 11, 12} Phase transitions between different crystal structures, as well as the crystal-rotator and rotator-melt transitions, have been correlated with changes in the intensities of CH₂ rocking modes in the IR spectra of alkanes.¹³ The IR spectra of selectively deuterium-labeled alkanes have been used to show that gauche bonds tend to appear at the ends of the alkane chain in the rotator phase and become more probable with increasing temperature.¹⁴ While it has been shown that the number of gauche bonds per chain increases with chain length in the rotator phase, the experimental uncertainty prevents a conclusion as to whether there is an increase in the fraction of gauche bonds. The ability to measure this would yield critical information regarding the disappearance of the rotator phase for n > 39. Likewise, measurement of disordered chain conformers during premelting could directly quantify the “melted” chain segments theorized by Flory and Vrij¹⁵ which can only be inferred from specific gauche bonds using IR.⁸

Raman spectroscopy in the fingerprint region provides complementary information to IR and may be able to fill gaps regarding disorder in the rotator phase and premelting phenomenon. The transition from an orthorhombic crystal phase to a rotator phase has been shown to correlate with the loss of a CH₂ bend peak near 1416 cm⁻¹.^{16, 17} Ab initio calculations have shown that intensity changes in the C-C stretch and CH₂ twist regions can be correlated with the number of consecutive trans bonds along a single alkane chain.^{18, 19} In polyethylene, Raman spectroscopy in the CH₂ twist and bend regions have been used to provide quantitative information on the mass fraction of three conformational states: amorphous gauche-rich conformers, orthorhombic crystalline conformers, and non-crystalline consecutive trans (NCCT) sequences.^{20, 21} Through measurement of these three states in the alkanes as a function of n, we hope to shed light on the melting transitions.

While the three-state measurement analysis is well documented in polyethylenes there are questions on how to apply it to alkanes. An important question is the relationship between the mass fraction of (NCCT and amorphous) chain conformers measured via Raman with the total mass fractions of gauche and trans conformers present on the alkane chain. Our initial Raman spectroscopic measurements of a C₂₁ alkane in the rotator phase indicate (10 to 30) % amorphous conformers.²¹ This disordered fraction significantly exceeds the mass fraction of gauche bonds estimated from IR measurements of the C₂₁ alkane, which are on the order of (1 to 7) %.^{14, 22} These differences must be addressed to relate Raman measurements to trans and gauche conformers directly.

In this work, we quantify the chain conformers in the various phases obtained during heating over a range of n. Alkanes from C₂₁ to C₆₀ are used to measure amorphous, crystalline, and NCCT chain conformers. We first consider the Raman spectra of C₂₃ and C₄₁ as representative examples of alkanes that exhibit either a rotator phase or premelting, respectively. We show that the mass fraction of NCCT conformers decreases with chain length, and further varies depending on whether the alkane exhibits a rotator phase. A simple conversion allows us to calculate the maximum number of NCCT bonds per chain generated during the melting process. These measurements are supported by density functional theory (DFT) calculations of Raman spectra which relate the disordered mass fraction to the type of gauche sequence and also provide information on the effect of gauche conformations as a function of position along the chain.

These measurements are important because an increase in the number of gauche bonds is expected to reduce the lamellar spacing in the rotator phase of alkanes,²³ and the fraction of gauche conformers per chain has been implicated as a driving force for rotator-rotator and rotator-melt transitions.^23–25 Both the temperature and type of rotator-rotator phase transition is expected to depend on gauche bonds.²⁵ The gauche concentration increases through the crystal-crystal transitions,^{13, 24, 26} and chain tilt within alkane layers has been attributed to more efficient chain packing due to increased gauche bonds near chain ends.^{25, 27} Molecular dynamics simulations of alkane chains^{28, 29} which directly calculate gauche and trans bond distributions and mean field calculations of alkane packing disorder³⁰ could benefit from an experimental determination of gauche and trans conformer mass fractions. Raman spectroscopic measurements on a wide range of alkanes would provide both quantitative information on the distribution of conformers in different phases as well as provide guidance for potential structures of NCCT precursors in crystallizing polyethylenes.

Materials and Methods

Table I shows the alkanes used in this work. The minimum purity of the alkanes were in the range of (95 to 99.5) %, with the C₃₇ alkane having a purity of 95 % and the remaining alkanes all having a minimum purity of at least 98 %. Large alkane flakes present in the purchased alkanes are broken into smaller pieces prior to sample loading to generate a homogeneous scattering volume for measurement.

Table I.

Normal alkanes used in this work

Name	Molecular Formula	Brand	Nc
Heneicosane	C21H44	Fluka	0.48 ± 0.02
Tricosane	C23H48	Aldrich	0.46 ± 0.03
Pentacosane	C25H52	Aldrich	0.45 ± 0.03
Heptacosane	C27H56	Sigma-Aldrich	0.58 ± 0.03
Heptatriacontane	C37H76	Aldrich	0.58 ± 0.03
Tetracontane	C40H82	Fluka	0.54 ± 0.03
Hentetracontane	C41H84	Fluka	0.47 ± 0.03
Pentacontane	C50H102	Aldrich	0.46 ± 0.03
Hexacontane	C60H122	Aldrich	0.50 ± 0.04

Alkanes are loaded into a Linkam shear cell (CSS 450, Linkam Scientific Instruments Ltd.) by filling a 3/8-inch inner diameter Nitrile standard O-ring placed on the bottom quartz plate, then compressing the sample to a gap thickness of 1 mm. The shear cell is not used in a shearing mode for these experiments, but it provides optical access to the sample at a controlled temperature. Raman measurements are performed in a 180° backscattering mode using a triple grating spectrometer (Horiba T64000) with a spectral resolution of 0.8 cm⁻¹. The sample is excited using linearly polarized light from a 632.8 nm HeNe laser focused to a spot size of approximately 60 μm. The laser is kept at a power level of 30 mW. The longer alkanes (C₅₀ and C₆₀) exhibit strong background fluorescence that is bleached from the sample over a period of 30 minutes using the laser at the maximum intensity. The spectra for these alkanes is collected using a 30 s acquisition time. Spectra of the alkanes in the range of C₂₁ to C₄₁ exhibit minimal background fluorescence and are collected using a 15 s acquisition time. Two accumulations of spectra are averaged together within the LabSpec software (LabSpec 5, Horiba) to improve spectrum quality and remove cosmic rays using a spike filter.

The assignment of fundamental vibrations to various Raman bands have been well-documented in the literature.⁹ Raman spectra are analyzed using a nonlinear least-squares algorithm to determine the best-fit Lorentzian peaks to the experimental profile. An initial guess for the peak widths are estimated from fits of the spectra at room temperature and a temperature at least 10 °C greater than the melt transition. A linear baseline was simultaneously fit to the spectra. A maximum of 4 peaks in the range of (1430 to 1500) cm⁻¹ are included to improve the fit of the crystalline CH₂ bend peak but are not used in the analysis. The 95 % confidence interval on the curve fit is used to calculate the standard error in the peak height, width, and position. The error bars shown in Figures 2 through 4 are the estimated standard error in the calculated value based on the standard error in the peak height and width using propagation of error techniques.

The alkanes are heated in a stepwise fashion from room temperature in increments ranging from (0.5 to 10) °C at a rate of 30 °C/min, then held at the measurement temperature for approximately 2 min before collecting spectra. The temperature of the Linkam shear cell is calibrated using the melting point standards benzoic acid and 4-methoxybenzoic acid purchased from Sigma-Aldrich. Melting of these standards is determined optically, and the reported temperatures are accurate to within ± 0.5 °C. Multiple output spectra are generated over a time period of approximately 5 min; post processing is used to determine if there are any changes in integrated peak intensities in the (1000 to 1500) cm⁻¹ range at a constant temperature. The spectra presented and analyzed at a given temperature have constant peak intensities to within measurement error.

The Raman spectra can be used to calculate mass fractions of conformers using a method described in our previous work²¹ based on a prior analysis of polyethylene spectra by Strobl and Hagedorn.²⁰ The analysis assumes that the chain segments will have one of three conformations: an orthorhombic crystalline conformation (cr), and amorphous gauche-rich conformation (am), or a trans-rich conformation that is not in an orthorhombic crystalline configuration, denoted as noncrystalline consecutive trans (NCCT). A mass balance dictates that the mass fractions of these components must sum to 1:

$${\alpha }_{\text{am}}+{\alpha }_{\text{cr}}+{\alpha }_{\text{ncct}}=1.$$ (1)

The individual mass fractions are calculated based on the following procedure: first, Lorentzian profiles are fit to the Raman spectra in the (1000 to 1500) cm⁻¹ region. Next, the integrated intensities I of each peak are normalized by an invariant I_tw, which is the sum of the trans- and gauche-rich CH₂ twist peak intensities:

$$I_{\text{tw}}=I\left(1296{\text{cm}}^{-1}\right)+I\left(1304{\text{cm}}^{-1}\right).$$ (2)

Normalized peak intensities are denoted by I′. The disordered mass fraction in an amorphous conformation is directly calculated from the normalized CH₂ twist peak intensity of gauche-rich conformers ${\alpha }_{\text{am}}=I\prime (1304{\text{cm}}^{-1})$. The mass fraction of material that is not in the amorphous conformation is ${\alpha }_{\text{ct}}=I\prime (1296{\text{cm}}^{-1})$, the mass fraction of consecutive trans conformers. Based on ab initio calculations,¹⁹ alkane chains with sequences of fewer than 5 trans bonds will not generate a sharp peak in the CH₂ twist (trans) position and instead contribute to the broad amorphous peak located experimentally at 1304 cm⁻¹. This means that the disordered mass fraction can contain smaller sequences of trans bonds distributed among gauche bonds. The consecutive trans mass fraction is equal to the sum of chains in the crystalline and NCCT conformations: α_ct = α_cr + α_ncct. The mass fraction of crystalline chains is obtained from the intensity of the CH₂ bend peak ${\alpha }_{\text{cr}}=I\prime (1416{\text{cm}}^{-1})/N_{\mathrm{c}}$, where N_c is a scale factor. The mass fraction of chains in the NCCT conformation is then calculated via Eq. 1.

The scale factor N_c is chosen for each alkane such that, at room temperature, the alkanes are 100 % crystalline. Values of the scale factor for each alkane are shown in Table I. The uncertainty in N_c is based on propagation of the standard error in the curve fit to the spectra. For all alkanes, the scale factor is in the range 0.45 < N_c < 0.58. There is no systematic change in the scale factor with increasing chain length over the range of alkanes measured, but the scale factors for the C₂₇ and C₃₇ alkanes are greater than one standard deviation away from the mean. The range of scale factors are attributed to orientation in the alkane samples and the strong polarization dependence of the CH₂ twist and bend modes for the alkanes.³¹ This scale factor is assumed to be constant with temperature.

Results

We start by presenting data for two representative alkanes during heating. Raman spectra of the C₂₃ alkane at three temperatures is shown in Figure 1a. At 25 °C the spectra contain sharp peaks in the (1000 to 1500) cm⁻¹ region that are attributed to alkane chains in an all trans conformation along the chain length and an orthorhombic crystalline packing.⁹ When the temperature is increased to 41 °C the crystalline peak at 1416 cm⁻¹ is no longer observed, but the strong C–C stretch peaks at 1060 cm⁻¹ and 1129 cm⁻¹ as well as the sharp CH₂ twist peak at 1296 cm⁻¹ are still present. This indicates that the alkane has transitioned from an orthorhombic crystal packing into a more disordered rotator structure.¹⁷ This loss of order is attributed to increasing rotational disorder in the R_V phase, in which chain segments randomly rotate about the chain axis by ± 90°.³² Increasing the temperature of the alkane above the melt temperature (47.7 °C)⁴ results in the loss of sharp peaks due to trans conformers in favor of broad spectral features in Figure 1a attributed to chain segments comprised of both trans and gauche conformers.³³ Three spectra for the C₄₁ alkane are shown in Figure 1b. The Raman spectra in the orthorhombic crystal phase at 25 °C resemble the C₂₃ spectra at the same temperature. The spectra retains sharp spectral features at temperatures just below the melt transition at 84.3 °C,³⁴ including the orthorhombic crystalline peak. From a qualitative standpoint, there is no characteristic change in spectral features that would indicate a transition prior to melting. Increasing the temperature above the melt transition generates Raman spectra characteristic of the melt state, and at no point during the melting process is there a rotator phase spectrum similar to the one shown for the C₂₃ alkane.

Figure 1.

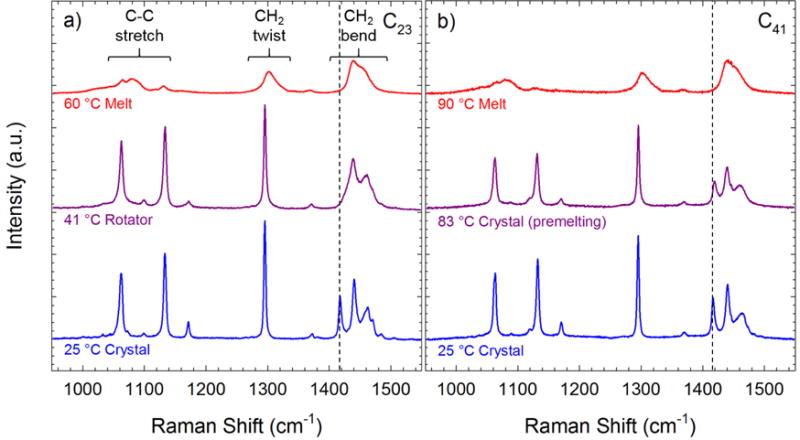
Raman spectra of a) the C₂₃ alkane and b) the C₄₁ alkane at three different temperatures. The spectra are scaled by the integrated intensity of the CH₂ twist region. The dashed line indicates the crystalline peak.

Figure 2 shows the mass fraction analysis as a function of temperature T for the C₂₃ and C₄₁ alkanes. In Figure 2, we define ${\alpha }_{\text{ncct}}^{\ast }$ (horizontal dashed lines) as the maximum value of α_ncct that occurs for a given n over the full temperature range from crystal to melt. For the C₂₃ alkane (Figure 2a), at temperatures less than 41 °C, the mass fractions of the amorphous, crystalline, and NCCT conformers remain constant with increasing temperature. The alkane is completely crystalline in this temperature range, with negligible mass fractions of disordered and NCCT material. When the temperature is increased to 41 °C, the sample enters the rotator state and the mass fraction of chains in the NCCT conformation increases to its maximum, ${\alpha }_{\text{ncct}}^{\ast }(n=23)=0.89$, while the crystalline mass fraction is reduced nearly to zero. This is determined from the disappearance of the crystalline peak at 1416 cm⁻¹ in the Raman spectra at 41 °C, as shown in Figure 1a. Increasing the temperature to 42 °C leads to a loss of the crystalline peak to within measurement sensitivity. The mass fraction in the NCCT conformation decreases monotonically with increasing temperature in the range of (42 ≤ T ≤ 47) °C, while the disordered mass fraction increases. When the temperature exceeds 47 °C an abrupt transition again occurs in the mass fraction distribution corresponding to the abrupt loss of the sharp CH₂ twist peak at 1296 cm⁻¹, with the disordered mass fraction dominating the composition. At this temperature the NCCT mass fraction is approximately 0.03 which is still above the measurement threshold. This low mass fraction is in agreement with rotational isomeric state models for consecutive trans sequences in the melt: a trans-gauche energy of approximately 2 kJ/mol yields trans probabilities near 50% at 50 °C. The probability of 5 consecutive trans sequences is then 0.07, near the measured NCCT mass fraction in the melt state. The disordered mass fraction increases slightly as the temperature increases to 60 °C with a simultaneous decrease in the NCCT mass fraction. The corresponding crystal-rotator and rotator-melt transitions based on DSC measurements¹³ of the C₂₃ alkane agree well with the sharp mass fraction transitions that occur during heating. We emphasize that each thermodynamic phase is identified by a characteristic distribution of chain conformers: the low-temperature crystal phase contains only orthorhombic crystalline conformers, the rotator phase is comprised mostly of NCCT conformers with no crystallinity, and the melt phase is comprised of a majority amorphous chain conformers.

Figure 2.

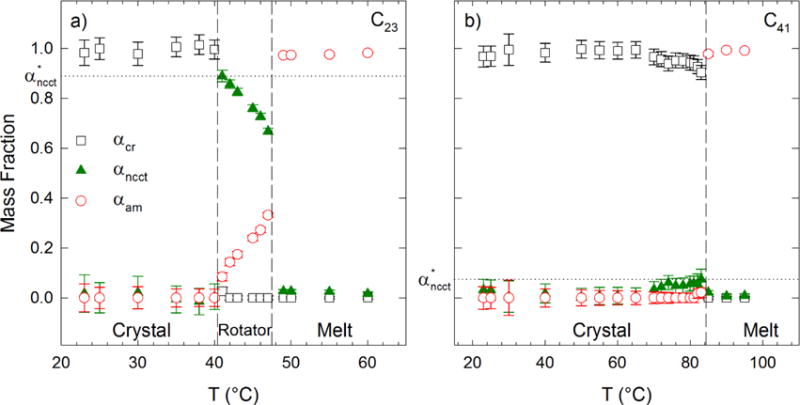
Mass fraction of crystalline, NCCT, and amorphous material in a) the C₂₃ alkane and b) the C₄₁ alkane versus temperature. The dashed lines indicate transitions between phases reported by Maroncelli et al.¹³ and Paunovic and Mehrota.³⁴ The dotted horizontal lines indicate ${\alpha }_{\text{ncct}}^{\ast }$ for each alkane, defined as the maximum value of α_ncct that occurs for a given n over the temperature range.

The mass fraction analysis of the C₄₁ alkane versus temperature shown in Figure 2b indicate a dramatically different melting profile compared to the C₂₃ alkane. At this n, no crystal-rotator phase transition is measured in DSC experiments³⁴ or reported in wide-angle x-ray scattering.³⁵ We observe that the C₄₁ alkane is primarily crystalline from room temperature to the melting point, above which the alkane is primarily in the melt state – the chain conformer distribution allows a clear identification of the thermodynamic phases. At temperatures exceeding 70 °C the crystalline mass fraction decreases with a corresponding increase in NCCT mass fraction. The maximum NCCT mass fraction, ${\alpha }_{\text{ncct}}^{\ast }$, occurs at 83 °C, just prior to melting. The C₂₃ and C₄₁ alkanes are representative of the two characteristic classes of alkanes, and they show dramatically different values of ${\alpha }_{\text{ncct}}^{\ast }$. (The mass fraction of NCCT for all alkanes studied in this work as a function of temperature are provided in the Supplementary Material.)

The chain length dependence of ${\alpha }_{\text{ncct}}^{\ast }$ for both classes of alkane are shown in Figure 3, along with ${\alpha }_{\text{cr}}^{\ast }$ and ${\alpha }_{\text{am}}^{\ast }$, which for a given n are the values of α_cr and α_am that are measured at the corresponding ${\alpha }_{\text{ncct}}^{\ast }$. For alkanes exhibiting a rotator phase, ${\alpha }_{\text{ncct}}^{\ast }$ decreases with chain length. Although modest, the systematic decrease in ${\alpha }_{\text{ncct}}^{\ast }$ indicates that longer alkanes undergoing the crystal-rotator phase transition at higher temperatures show increasing disorder. In contrast, alkanes that only exhibit premelting have no significant chain length dependence on ${\alpha }_{\text{ncct}}^{\ast }$. Within both classes of alkane, ${\alpha }_{\text{am}}^{\ast }$ increases as a function of n.

Figure 3.

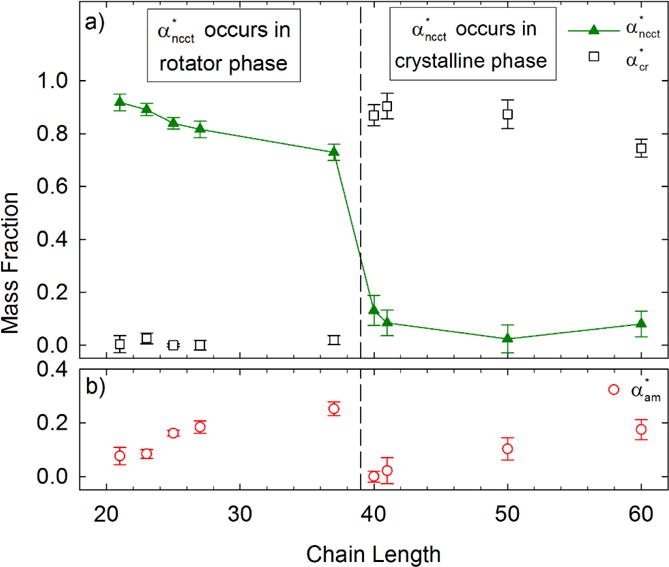
Maximum mass fraction of NCCT conformers, ${\alpha }_{\text{ncct}}^{\ast }$, versus chain length n. The corresponding mass fractions of crystalline ${\alpha }_{\text{cr}}^{\ast }$ and amorphous material ${\alpha }_{\text{am}}^{\ast }$ at the maximum ${\alpha }_{\text{ncct}}^{\ast }$ are also shown. The vertical dashed line separates the lower n alkanes that exhibit a rotator phase from the higher ones that do not.⁶

The mass fraction information shown in Figure 3 can be used to estimate the maximum average number of NCCT bonds per chain to develop a more physical picture of the number of bonds in a consecutive trans conformation without crystalline order. For a chain of length n there are n – 3 dihedral angles of C–C bonds. Since each alkane has a monodisperse chain length, the maximum average number of NCCT bonds per chain $n_{\text{ncct}}^{\ast }$ is estimated by

$$n_{\text{ncct}}^{\ast }={\alpha }_{\text{ncct}}^{\ast }(n-3).$$ (3)

Eq. 3 is used to convert the maximum NCCT mass fraction produced during melting shown in Figure 3 to the maximum average number of NCCT bonds per chain. This value is plotted versus chain length in Figure 4.

Figure 4.

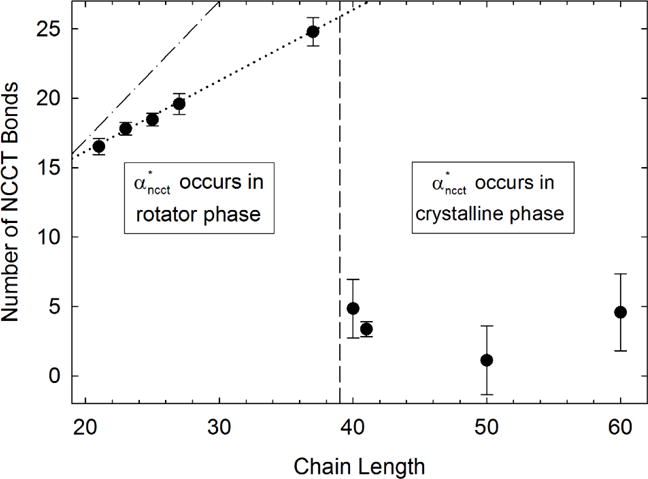
The maximum average number of NCCT bonds $n_{\text{ncct}}^{\ast }$ versus chain length n. The dotted line is a linear regression of the $n_{\text{ncct}}^{\ast }$ values from C₂₁ to C₃₇. The vertical dashed line indicates the longest alkane chain that still exhibits a rotator phase.⁶ The number of NCCT bonds for an all trans alkane is indicated by the dash-dotted line.

Although ${\alpha }_{\text{ncct}}^{\ast }$ decreases with increasing chain length, the number of NCCT bonds per chain increases for chains exhibiting a rotator phase. The dependence of $n_{\text{ncct}}^{\ast }$ on chain length is linear in this region as indicated by the dotted line in Figure 4, with a slope of 0.51±0.07 and intercept of 6.0±1.7. When ${\alpha }_{\text{ncct}}^{\ast }$ occurs during premelting, the number of NCCT bonds per chain is independent of chain length within experimental uncertainty.

Note that the Raman based measurements of conformers do not show abrupt changes at the crystal-crystal or rotator-rotator transitions that have been observed by calorimetry^{27, 36} and x-ray.²³ The smoothly varying NCCT mass fraction for C₂₃ (Figure 2) is qualitatively consistent with the continuous change in the lattice distortion reported from x-ray scattering through rotator-rotator transitions up to 45 °C;²³ however, the constant hexagonal lattice between 45 °C and the melting temperature contrasts with the continued decrease in α_ncct. This indicates that these crystal-crystal and rotator-rotator transitions (and the lattice distortion) are not associated with sharp changes in the distribution of chain conformers; IR measurements show smoothly varying changes in peak intensities,¹³ but are not particularly sensitive to these transitions. The largest latent heat associated with rotator-rotator transitions is nearly two orders of magnitude smaller than the enthalpy of melting for alkanes,²⁷ which indicates that there is little change in chain conformation.

In comparing our results to prior vibrational spectra measurements, we find that the numerical value of the disordered mass fraction α_am calculated using our Raman spectroscopic analysis greatly exceeds the concentration of gauche conformers calculated for normal alkanes using IR techniques.^{8, 13, 14} Both single gauche bonds that occur near chain ends and gauche-trans-gauche (GTG′) sequences are of interest due to the formation of nonplanar alkane conformers, as shown in the examples in Figure 5. The sum of gauche bonds and GTG′ sequences for alkanes in the rotator phase are in the range of (1 to 7) % via IR measurements,¹³ which contrasts with the (10 to 30) % of amorphous conformers that are present in alkanes in the range 21 ≤ n ≤ 37 shown in Figure 3b. The IR measurements of premelting for C₅₀ and C₆₀ alkanes indicate approximately 0.4 and 0.6 GTG′ sequences per chain respectively,⁸ which is equivalent to gauche mass fractions on the order of 1 %. This is roughly an order of magnitude smaller than the mass fraction of amorphous conformers of the C₅₀ and C₆₀ alkanes present during melting in Figure 3b.

Figure 5.

Structures of a C₂₁ alkane in an all trans conformation and with either a single gauche bond or GTG′ sequence.

In resolving this difference between gauche mass fractions and disordered mass fractions, an analysis of the specific vibrational modes used to calculate these conformers is necessary. The IR analysis of gauche conformers relies on the intensity of CH₂ wag peaks in the (1300 to 1350) cm⁻¹ range to calculate the fraction of chains containing a specific non-trans sequence, with gauche bonds at chain ends evaluated from the 1341 cm⁻¹ peak and a GTG′ sequences indicated by the 1306 cm⁻¹ peak.¹³ The wagging modes of alkanes have been analyzed using a simple coupled oscillator theory to show that these modes are not affected by methyl end groups.³⁷ The measurement of amorphous and NCCT conformers via Raman spectroscopy is based on CH₂ twist peaks in the (1290 to 1310) cm⁻¹ region of the spectrum. Peaks in this region do not appear to follow simple coupled oscillator theory,^{37, 38} but the Raman scattering intensities of alkane chains with different amounts of gauche bonds have been calculated by Meier et al.^{18, 39} using ab initio methods. These calculations indicate that approximately five consecutive trans bonds are necessary for the appearance of the sharp 1296 cm⁻¹ peak in the vibrational spectra, whereas consecutive trans sequences of two or fewer contribute to the broad CH₂ twist peak located at 1303 cm⁻¹. A sequence of four trans bonds followed by a gauche bond would only slightly contribute to the NCCT peak based on ab initio calculations,¹⁹ therefore our (10 to 30) % amorphous conformers measured from Raman spectra would indicate as few as (2 to 6) % gauche bonds, similar to values reported via IR. We verify this in more detail through single-chain DFT modeling.

For DFT calculations we generate typical chain configurations for a C₂₁ alkane with either single gauche bonds or GTG′ sequences (see Figure 5) and compute the chain normal modes in the CH₂ twist region. The normal modes are phenomenologically broadened to generate peaks that are then analyzed as Raman spectra to calculate a disordered mass fraction; calculation details and spectra (Figure 7) are included in the Appendix. These fractions are shown in Figure 6 for either a single gauche bond or GTG′ sequence at various positions along the chain. For a single gauche bond, the disordered mass fraction increases with position from the chain end until the seventh bond position and a maximum disordered mass fraction. Similar behavior is observed for the GTG′ sequence. The dashed and dotted lines indicate the mass fraction of gauche bonds input into the DFT calculation for a C₂₁ with either a single gauche bond (one gauche per 18 total dihedral angles) or a GTG′ sequence (two gauche per 18 dihedral angles), respectively.

Figure 7.

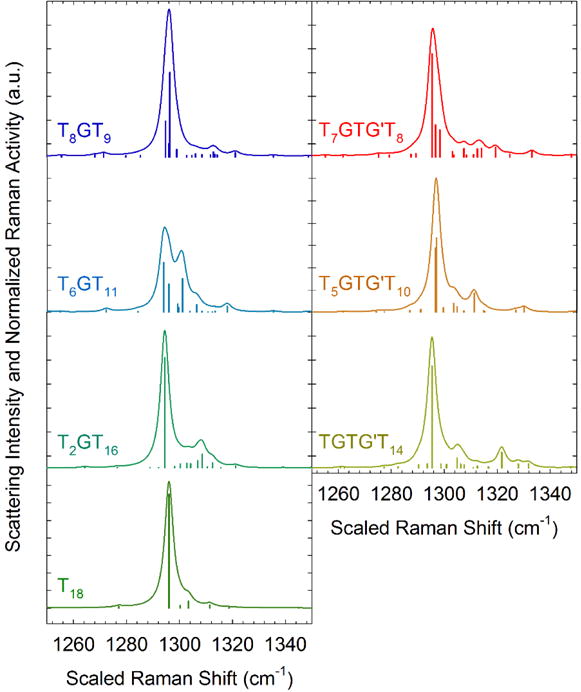
Calculated Raman scattering intensity (smooth lines) and Raman activity (vertical bars) of a C₂₁ alkane in the CH₂ twist region with either gauche bonds or GTG′ sequences. For each plot, the scattering intensity is normalized by the area under the curve in the CH₂ twist region. The Raman activity is normalized by the maximum Raman activity value and scaled to fit under the scattering intensity curve for clarity.

Figure 6.

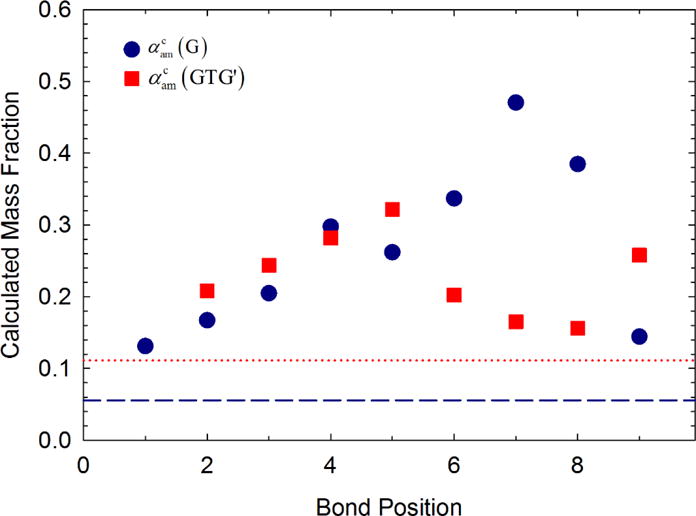
Calculated mass fractions of amorphous conformers ${\alpha }_{\text{am}}^{\mathrm{c}}$ of C₂₁ chains with disorder plotted versus bond position. Both single gauche bonds (G) and GTG′ sequences are shown. The intensity ratio is placed at the trans bond position for alkanes with a GTG′ sequence.

Figure 6 indicates that the numerical value of α_am that would result from a Raman measurement must exceed the numerical value of the mass fraction of gauche bonds that would result from IR measurement. Over the range of positions, the ratio of ${\alpha }_{\text{am}}^{\mathrm{c}}$ to the gauche mass fraction ranges from 2.4 to 8.5 for a single gauche bond and 1.4 to 2.9 for the GTG′ sequence. Although single gauche bonds will increase the calculated disordered mass fraction near the middle of the chain, the occurrence of single gauche bonds become less probable. Prior IR measurements of the C₂₁ alkane indicate that the largest concentration of gauche bonds occurs at chain ends in the rotator phase and decreases exponentially with bond position.¹⁴

We can now compare the ratio between the disordered mass fraction via Raman and the gauche mass fraction via IR. Since the concentration of gauche bonds is expected to decrease an order of magnitude by the fifth bond position,¹⁴ we assume that single gauche bonds only appear in appreciable concentration between the chain end and the fourth bond position. Based on this assumption, the disordered mass fraction via Raman should be in the range of 2.4 to 5.4 times the mass fraction of single gauche bonds for alkanes in the rotator phase. Our measurements of α_am which range from (10 to 30) % would indicate gauche concentrations in the range of (1.9 to 12.5) %. This is similar to the (2 to 7) % reported from IR measurements of alkanes of similar chain length.

In addition, we can use our methodology in combination with prior IR measurements to comment on the existence of single gauche bonds for the cases of the C₅₀ and C₆₀ alkanes, where IR was found to be insensitive.⁸ The scaling factor in the range of 1.4 to 2.9 for GTG′ bonds does not account for the order of magnitude difference between the Raman disordered mass fraction measurement for the C₅₀ and C₆₀ alkanes and the gauche mass fraction based on IR measurements of GTG′ bonds. Since the disordered mass fraction is sensitive to both single gauche bonds and GTG′ sequences, we expect that single gauche bonds are also present in significant quantities during the melting of these alkanes. The existence of single gauche bonds near the melting temperature agrees with the qualitative Raman measurements of Kim et al. performed on the C₅₀ alkane.⁸ IR measurements indicate that the C₆₀ alkane generates a mass fraction of approximately 0.02 gauche bonds due solely to GTG′ sequences prior to melting.⁸ Combining this information with the maximum disordered mass fraction of 0.08 measured via Raman spectroscopy indicates that single gauche bonds are present in a mass fractions of less than 0.02, which indicates that gauche bonds and GTG′ sequences are present in concentrations of comparable magnitude when the C₆₀ alkane exhibits premelting.

Discussion

Although we have assumed that dihedral angles can only exist in a trans or gauche conformation, localized 180° twists (called “twist solitons”) could also be present along the alkane backbone owing to small systematic perturbations in consecutive dihedral angles.⁴⁰ These structures have been proposed to interpret NMR measurements of motion in polyethylene lamellae,⁴¹ and more recent investigations of the C₂₃ alkane have sought to characterize twist solitons in the crystal and rotator phases both computationally and analytically.⁷ IR peak intensities appear sensitive to solitons in the C-C stretch region for a C₁₉ alkane in the rotator phase near the melting temperature.⁴² We cannot rule out the presence of twist solitons or effect of these structures on Raman intensities. However, we note that the mass fraction analysis does not include Raman-active C-C stretch modes. Since the total integrated intensity of the CH₂ twist region is constant, we expect that spectral features due to twist solitons will be overshadowed by either the sharp trans peak or broad amorphous region.

Prior molecular dynamics simulations of finite chains show qualitative similarities to our results. Simulations of C₁₉ alkane⁴³ and C₂₃ alkane⁴⁴ systems show increasing gauche bonds at the chain ends during the crystal-rotator phase transition, which agrees with the increase in the mass fraction of amorphous conformers observed in our experiments.

Our mass fraction measurements over the range of alkane chain lengths provide insight into the effect of chain motion on disorder for the longer alkanes. As chain length increases, alkanes preferentially exhibit segmental motion along the chain axis, which causes premelting of chain ends in lieu of a rotator phase.⁴⁵ The sharp decrease in the disordered mass fraction when increasing chain length between the C₃₇ and C₄₀ alkanes in Figure 3b indicates that the shortest alkanes that do not exhibit a rotator phase also have the least segmental motion of the premelting alkanes. Chains longer than the C₄₀ alkane have a higher melting temperature and therefore more thermal energy for segmental motion prior to melting. The effect of this increased motion is a larger fraction of conformationally disordered chain segments, which is evident in our measurements of the disordered mass fraction with increasing chain length.

A significant benefit of the mass fraction analysis comes from the direct relationship between the chain conformer distribution and the thermodynamic phase of the alkane. Similarly, sharp transitions in the mass fraction distribution occur at phase transition temperatures as shown for the C₂₃ and C₄₁ alkanes. Sharp transitions in peak intensities are also reported in IR spectra at transitions between the crystal, rotator, and melt phases;¹³ however, the IR analysis does not yield quantitative information on the conformer distribution in each phase.

Both the mass fraction of gauche conformers and the mass fraction of amorphous conformers are crucial aspects of theoretical models of phase transitions in linear alkanes. Theoretical models of partial melting in alkanes¹⁵ depend on some amount of terminal methyl groups being “melted.” This “melted” amount is not calculated directly, but must be inferred through thermal measurements. Prior measurements note that the amount of “melted” methyl groups is significantly greater than the amount of gauche bonds per chain by a factor of 3.0 to 4.5 due to the disruption of the crystalline lattice by the gauche bond,⁸ which is well within the range of ratios between disordered and gauche mass fractions estimated via our calculations. Therefore, the mass fraction analysis of Raman spectra provides a direct estimation of the “melted” methyl groups through the disordered mass fraction. This result further highlights the complementary nature of IR and Raman spectroscopy: while IR measurements are sensitive to the type and concentration of specific gauche bond sequences (end gauche versus GTG′) in alkanes, Raman measurements provide a direct measurement of “melted” chain segments through the disordered mass fraction.

Conclusions

Analysis of the Raman spectra over a range of alkane lengths emphasizes the appearance of non-crystalline trans chain segments prior to the melt transition. These NCCT conformers comprise a majority mass fraction when the alkane is in a rotator phase, which decreases with increasing temperature and chain length. Longer alkane chains with no rotator transition produce smaller amounts of NCCT on predominantly crystalline chains prior to the crystal-melt transition. This quantification of NCCT and gauche-rich fractions compliments the observation of specific gauche-trans sequences that can be observed in IR measurements. DFT calculations of the Raman spectra of a C₂₁ alkane with gauche bonds placed sequentially along the chain reveal that the disordered mass fraction can contain a small fraction of conformationally disordered bonds along primarily trans segments. In contrast, the NCCT conformers are comprised of trans sequences devoid of any gauche conformers. We expect that our interpretation and analysis of the Raman spectra of alkanes can be generalized to provide structural information on crystalline molecules with long alkane segments: saturated long-chain alcohols, fatty acids, etc. The Raman measurement also allows for time-dependent characterization of chain conformers during phase transitions between the melt, rotator, and crystalline phases. More directly, the analysis of melting alkanes better characterize the NCCT mass fraction observed during polyethylene crystallization, which is critical to understanding the role of NCCT conformers in polyethylene processing.

Appendix: DFT spectra calculations

Calculations of the Raman spectra are performed using the Gaussian 09 (Gaussian, Inc.) suite of programs.⁴⁶ Geometry optimization to local minima and frequency calculations are performed at the DFT level using the B3LYP functional and the 6-31G(d,p) basis set. The convergence criteria for geometry optimization are a maximum force of 4.5 × 10⁻⁴ Hartree and a maximum root mean squared force of 3 × 10⁻⁴ Hartree/Bohr. The initial dihedral angles of the alkane for trans and gauche bonds are 180° and ± 60°, and no constraints are used to fix the alkane geometry. The Raman scattering intensity is calculated based on the calculated Raman scattering activity and an assumed Lorentzian peak shape with 2 cm⁻¹ peak width for each vibrational mode. To directly relate the calculated spectra to experimental results, we have scaled the calculated Raman shift in the CH₂ twist region by 0.975 for all cases.

Calculations of the Raman spectra are performed for the C₂₁ alkane with either a single gauche bond or GTG′ sequence on the chain, and characteristic Raman scattering activities and intensities in the CH₂ twist region are shown in Figure 7. The type and position of a sequence is indicated by the abbreviation T_a(G or GTG′)T_b, where the subscripts a and b indicate the number of consecutive trans bonds (T). The alkane consisting of all trans bonds T₁₈ shows a vibration at the consecutive trans CH₂ twist position with a strong Raman scattering activity surrounded by vibrational modes of lesser Raman activity, which leads to a single large peak in the scattering intensity with a small shoulder near 1303 cm⁻¹. When a single gauche bond is present on the chain, a greater number of vibrational modes appear in the spectra, especially for Raman shift values in the region corresponding to the amorphous CH₂ twist mode. A gauche bond near the center of the molecule as in T₈GT₉ generates a number of Raman active modes near the consecutive trans peak that are indistinguishable from a single peak. A qualitatively similar effect is seen for GTG′ sequences at various positions in Figure 7.

The calculated spectra in Figure 7 indicate that the presence of gauche bonds increase the scattering intensity in the amorphous region, which we expect to decrease the integrated intensity of the trans CH₂ twist peak relative to the integrated intensity of the same peak in the spectra of the all trans C₂₁ alkane. To relate the calculated spectra to our measurements in the Results section, we must estimate the mass fractions of amorphous and consecutive trans conformers from the calculated scattering intensities shown in Figure 7. Since the calculated spectra contain multiple peaks in the CH₂ twist region instead of the two smooth peaks observed in the experimental spectra, we estimate the calculated consecutive trans mass fraction ${\alpha }_{\text{ct}}^{\mathrm{c}}$ by the ratio of the scattering intensity of the trans CH₂ twist vibration h(1296 cm⁻¹) of the alkane with a single gauche bond to the scattering intensity h_T (1296 cm⁻¹) of the T₁₈ chain: ${\alpha }_{\text{ct}}^{\mathrm{c}}=h(1296{\text{cm}}^{-1})/h_{\mathrm{T}}(1296{\text{cm}}^{-1})$. The calculated disordered mass fraction from conservation of mass arguments is ${\alpha }_{\text{am}}^{\mathrm{c}}=1-{\alpha }_{\text{ct}}^{\mathrm{c}}.$