Constrained Score Statistics Identify Genetic Variants Interacting with Multiple Risk Factors in Barrett’s Esophagus

Abstract

Few gene-environment interactions (G × E) have been discovered in cancer epidemiology thus far, in part due to the large number of possible G × E to be investigated and inherent low statistical power of traditional analytic methods for discovering G × E. We consider simultaneously testing for interactions between several related exposures and a genetic variant in a genome-wide study. To improve power, constrained testing strategies are proposed for multivariate gene-environment interactions at two levels: interactions that have the same direction (one-sided or bidirectional hypotheses) or are proportional to respective exposure main effects (a variant of Tukey’s one-degree test). Score statistics were developed to expedite the genome-wide computation. We conducted extensive simulations to evaluate validity and power performance of the proposed statistics, applied them to the genetic and environmental exposure data for esophageal adenocarcinoma and Barrett’s esophagus from the Barretts Esophagus and Esophageal Adenocarcinoma Consortium (BEACON), and discovered three loci simultaneously interacting with gastresophageal reflux, obesity, and tobacco smoking with genome-wide significance. These findings deepen understanding of the genetic and environmental architecture of Barrett’s esophagus and esophageal adenocarcinoma.

Introduction

With the exception of rare familial cancers, cancer risk is usually determined by a complex interplay between multiple genetic and environmental factors.¹ Alterations in somatic genome can result from exposure to external agents (e.g., tobacco smoking) and infectious agents (e.g., Helicobacter pylori) and from the multifaceted effects of certain host characteristics (e.g., obesity), all generally defined to be “environmental exposures” in this report. Individuals differ in their inherited efficiency to neutralize environmental insults and repair genomic damages. Efforts have long been focused on discovering susceptibility genes involved in carcinogenesis and on characterizing how these genes interact with environmental factors.² Agnostic searches for gene-environment interactions (G × E) have been routinely conducted in genome-wide studies,³ but with very limited success.^{4, 5} Much discussion has been devoted to methodological issues,^{6, 7} such as design and estimation,^{8, 9, 10, 11} power and sample size,¹² and mathematical formulation of interactions.¹³

When multiple environmental factors have been established for a cancer and are available for G × E testing, the standard analytical approach is to interrogate one pair of genotype and exposure at a time and subsequently correct for multiple testing.^{14, 15} This strategy is well interpretable, but not optimal when environmental risk factors are related in cancer etiology, so that genotypes involved in the same etiological pathway may interact with all related exposures. This article develops constrained inferential methods for testing multiple G × E simultaneously, leveraging known biological knowledge on cancer etiology. The methods are motivated by a genome-wide G × E study examining esophageal adenocarcinoma and Barrett’s esophagus (BE/EA [MIM: 614266]) from the Barretts Esophagus and Esophageal Adenocarcinoma Consortium (BEACON), an international consortium composed of studies in Australia, Europe, and North America, where the incidence of esophageal adenocarcinoma has been rising sharply in the past four decades.^{16, 17, 18, 19} Esophageal adenocarcinoma cases are believed to arise from Barrett’s esophagus, a precursor lesion,²⁰ and both conditions share risk factors including gastresophageal reflux symptoms (GERD [MIM: 109350]), obesity, and tobacco smoking.^{21, 22} The results of genome-wide genetic association and a limited search for G × E among known susceptibility loci in BEACON have been reported elsewhere.^{23, 24}

For esophageal adenocarcinoma and its precursor lesion (Barrett’s esophagus), all three well-established risk factors—obesity, gastresophageal reflux, and tobacco smoking—have been linked to local and systemic inflammation and the downstream consequence of oxidative stress that promotes DNA damage and chromosomal instability.²⁰ It is plausible that SNPs in inflammation pathways may modulate induced defense mechanisms against damage caused by these exposures, thereby interacting with all three exposures in a similar fashion. Furthermore, obesity is associated with gastresophageal reflux in the white population.²⁵ Adjustments of p values from testing one exposure-genotype interaction at a time via Bonferroni correction can be overly conservative. In contrast, simultaneously testing for G × E among multiple environmental factors potentially pools small associations and increases power.

To improve power, we consider multivariate G × E testing strategies in which the directions of multiple G × E interactions under the alternative hypothesis are constrained. Suppose θ_{1, …,} θ_p are interaction parameters between a genetic variant and p established environmental factors in a logistic regression model for a cancer case-control study. The null hypothesis that there is no G × E for any of environmental factors is represented by

$${\text{H}}_0:{\theta }_j=0\text{for}j=1,\dots ,p.$$ (Equation 1)

Classical multivariate tests such as Hotelling’s T² test statistics are designed to test any departure from the null hypothesis; they therefore lack power to detect specific types of departure that may be considered plausible based on a priori scientific knowledge, e.g., the inflammation pathway in the etiology of esophageal adenocarcinoma. Restricting alternative hypothesis to be one-sided, θ_j < 0 for some j, for example SNPs in inflammatory pathways may be associated with a lower odds ratio for any of abdominal obesity, gastresophageal reflux, and cigarette smoking, will presumably boost the power. The constraint can also be motivated for the other direction: θ_j > 0. In the form of likelihood ratio tests, this kind of constraint has been investigated for clinical trials with multiple study endpoints.^{26, 27} However, the critical values for computing p values under the asymptotic null distribution of these one-sided statistics are generally difficult to obtain, and maximizing the likelihood under the one-sided constraint can be cumbersome for genome-wide testing.

In the same vein, a more restrictive, but parsimonious, model for interactions was proposed based on Tukey’s 1-df test:^{28, 29, 30} gene-gene or gene-environment interactions are proportional to main effects by a fixed constant. In essence, risk associations of genetic variants or environmental exposures are first summed together by a genetic risk score or an environmental risk score, assuming that each group of risk variables share common underlying etiological pathways. More specifically, this test can be motivated by a latent-variable model, where each group of measured markers serves as a surrogate of an underlying biological phenotype.³⁰ A single interaction parameter then summarizes the deviation from the additive contributions of two risk predispositions, possibly in a transformed risk scale.³⁰ Built on this parsimonious model, it has been proposed to jointly test for both genetic associations and gene-gene or gene-environment interactions.³⁰ A complication of this model is that, when there is no genetic association, as is true for the great majority of variants being examined in genome-wide studies, the interaction parameter vanishes and is not identifiable. The usual hypothesis testing statistics are no longer applicable and specialized procedures have to be developed with simulated null distributions.

In this article, we develop score statistics with aforementioned constraints for multiple G × E in a genome-wide study, because score statistics are computationally attractive as regression parameters are estimated only under the null and, further, they have the same local power as Wald and likelihood ratio statistics. We extend the classical one-sided test to a bidirectional test, in which multiple G × E can be either negative or positive, so that one does not have to specify the direction one at a time. For both one-sided test and bidirectional test, we propose score statistics that are easy to compute and have an exact or easily obtainable asymptotic distribution. For the proportional G×E testing, we modify Tukey’s 1-df model to allow for the interaction not dependent on the genetic main association, and we derive finite-sample correction for the mean and the variance of the score statistic. Such correction, though often ignorable at the usual significance level for one test (type I error rate 0.05), is critical to control genome-wide type I errors, as we show in simulations and the BEACON study. We evaluate the performance of the proposed methods in extensive simulations and apply them in the genome-wide G × E study from BEACON.

Material and Methods

Consider a genetic association study with n participants. Let Y denote the disease status, for example cancer patients versus control subjects. Let X denote the vector of p known risk-associated exposures, and let G denote one of many SNPs under investigation, possibly in a genome-wide study. Typically, the study also assembles covariates including age, gender, and top principal components of genetic variation for controlling population stratification, collectively denoted by W. The interest hereafter is to discover whether G modifies risk associations of some exposures in X. The data therefore consist of n independent and identically distributed random vectors (Y_i, X_i, G_i, W_i), for i = 1, …, n.

Consider a regression model investigating p statistical interactions simultaneously,

$$g\left\{\mathbb{E}\left(Y|G,\mathbf{X},\mathbf{W}\right)\right\}={\beta }_0+{\beta }_{1}G+\stackrel{p}{\sum _{j=1}}{\beta }_{2j}{X}_j+{\beta }_3\mathbf{W}+\stackrel{p}{\sum _{j=1}}{\theta }_j{X}_{j}G,$$ (Equation 2)

where β₁ is the genetic association when all exposures are 0, β_2j is the association of the j^th exposure when the genotype score is 0, θ_j is the interaction between G and X_j, and g is the logit function if Y is a dichotomous outcome or the identical function if Y is a quantitative trait modeled by linear regression.

The null hypothesis for multiple G × E in Equation 2 is expressed in Equation 1, stating that none of p exposure-risk associations changes with the genotype G. Classical multivariate tests are designed to be unrestricted in the alternative hypothesis

$${\text{H}}_{1a}:{\theta }_j\ne 0\text{for}\text{at}\text{least}\text{one}j.$$

Denote the parameters of interest $\mathit{\theta }=\left({\theta }_1,\dots ,{\theta }_p\right)$ and the nuisance parameters $\mathit{\beta }=\left({\beta }_0,{\beta }_1,{\beta }_{21},\dots ,{\beta }_{2p},{\beta }_3\right)$. Let $\mathit{\alpha }=\left(\mathit{\beta },\mathit{\theta }\right)$, $f\left(y;\mathit{\alpha }\right)$ denote the density of Y given covariates, and let

$$\begin{array}{c}\ell \left(\mathit{\alpha }\right)=\stackrel{n}{\sum _{i=1}}\text{log}f\left(Y_i;\mathit{\alpha }\right),\\ S\left(\mathit{\alpha }\right)=\left(\partial /\partial \mathit{\alpha }\right)\ell \left(\mathit{\alpha }\right),\\ \text{and}\mathcal{I}\left(\mathit{\alpha }\right)={\mathbb{E}}_{\mathit{\alpha }}\left\{\left(\partial /\partial \mathit{\alpha }\right)\ell \left(\mathit{\alpha }\right)\left(\partial /\partial {\mathit{\alpha }}^T\right)\ell \left(\mathit{\alpha }\right)\right\}\end{array}$$

denote the log-likelihood, the score function, and the information matrix, respectively. S(α) is partitioned into $\left(S_{\mathit{\beta }},S_{\mathit{\theta }}\right)$ to conform with the partition $\left(\mathit{\beta },\mathit{\theta }\right)$ of α. Similarly, $\mathcal{I}\left(\mathit{\alpha }\right)$ is partitioned into block matrices ${\mathcal{I}}_{\mathit{\beta }\mathit{\beta }},{\mathcal{I}}_{\mathit{\beta }\mathit{\theta }},{\mathcal{I}}_{\mathit{\theta }\mathit{\beta }},{\mathcal{I}}_{\mathit{\theta }\mathit{\theta }}$. Let $\tilde{\mathit{\alpha }}$ denote the maximum likelihood estimator under the null hypothesis H₀. Classical Rao’s score statistic for testing H_1a is

$${\text{T}}_a={\tilde{S}}_{\mathit{\theta }}^T{\left({\tilde{\mathcal{I}}}_{\mathit{\theta \theta }}-{\tilde{\mathcal{I}}}_{\mathit{\theta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{I}}}_{\mathit{\beta \theta }}\right)}^{-1}{\tilde{S}}_{\mathit{\theta }},$$

where $\tilde{S}$ and $\tilde{\mathcal{I}}$ are evaluated at $\tilde{\mathit{\alpha }}$, respectively. When the likelihood is correctly specified, T_a has a ${\chi }_p^2$ distribution in large samples under the null hypothesis.

Testing for One-Sided or Bidirectional Hypothesis

As we elaborated in the Introduction, it is sometimes plausible in cancer epidemiology to test for one-sided multiple G × E simultaneously, for example

$${\text{H}}_{1b}:{\theta }_j\le 0\text{for}j=1,\dots ,p$$

with strict inequality for at least one j. The interest here is specifically in discovering genetic alleles that simultaneously link to a lower association for each of p exposures. The one-sided test can be motivated similarly for θ_j ≥ 0, aiming to discover genetic alleles that link to a higher association for exposures. In a complete agnostic search such as genome-wide testing for G × E, it is perhaps more sensible to formulate the following bidirectional hypothesis

$${\text{H}}_{1c}:{\theta }_j\le 0\text{for}j=1,\dots ,p\text{or}{\theta }_j\ge 0\text{for}j=1,\dots ,p$$

with strict inequality for at least one j. The multiple G × E are constrained to be directional, either all positive or all negative. This bidirectional test has not been seen in the statistical literature. In what follows, we derive score tests for H_1b and H_1c based on an approximated likelihood ratio test.²⁷

Let $\tilde{\mathit{\beta }}$ denote the maximum likelihood estimator of β under H₀, and let $\tilde{\mathit{\alpha }}=\left(\tilde{\mathit{\beta }},\mathbf{0}\right)$, where 0 is a length-p zero vector for $\mathit{\theta }$. Let a sequence of local alternative hypotheses be defined by

$${\text{H}}_{1n}:\mathit{\theta }=n^{-1/2}\mathit{\delta },$$

where δ is a fixed point in ${\mathbb{R}}^p$. By employing Taylor series expansions, we have

$$n^{-1/2}{S}_{\mathit{\theta }}\left(\tilde{\mathit{\alpha }}\right){\to }_d\mathcal{N}\left({\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}\left({\mathit{\alpha }}_0\right)\mathit{\delta },{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}\left({\mathit{\alpha }}_0\right)\right)$$

and

$$n^{-1/2}{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}^{-1}\left(\tilde{\mathit{\alpha }}\right)S_{\mathit{\theta }}\left(\tilde{\mathit{\alpha }}\right){\to }_d\mathcal{N}\left(\mathit{\delta },{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}^{-1}\left({\mathit{\alpha }}_0\right)\right),$$

under H_1n, where ${\mathit{\alpha }}_0=\left(\mathit{\beta },0\right)$, ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}={\mathcal{I}}_{\mathit{\theta \theta }}-{\mathcal{I}}_{\mathit{\theta \beta }}{\mathcal{I}}_{\mathit{\beta \beta }}^{-1}{\mathcal{I}}_{\mathit{\beta \theta }}$. Let $U=n^{-1/2}{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}^{-1}\left(\tilde{\mathit{\alpha }}\right)S_{\mathit{\theta }}\left(\tilde{\mathit{\alpha }}\right)$. Since θ ≤ 0 is equivalent to δ ≤ 0, one may define a score test as follows:

$${\text{T}}_s=n\left[U^T{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}U-\text{inf}\left\{{\left(U-\mathit{\delta }\right)}^T{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}\left(U-\mathit{\delta }\right):\mathit{\delta }\le 0\right\}\right].$$

This is essentially the likelihood ratio statistic for δ ≤ 0 based on a single realization of U:³¹ the first term is the log-likelihood of U under the null hypothesis δ = 0, and the second term is the maximum log-likelihood of U under the alternative hypothesis δ ≤ 0. If the information matrix ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$ is known, the asymptotic null distribution of T_s is a chi-bar-squared distribution that is equivalent to a weighted sum of a sequence of chi-square distributions, where the weights can be computed by algebra in closed forms when p ≤ 4^{31, 32} and by simulations when p > 4. Alternatively, if ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$ is diagonal, close-form expressions of the weights are readily available for any p. In our case, however, ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$ is unknown, depending on β that has to be estimated. Furthermore, it is unlikely to be a diagonal matrix in the context of testing G × E. Consequently the asymptotic null distribution of T_s is difficult to obtain.

We therefore develop an approximate score statistic for one-sided hypotheses, in the same spirit as the approximate likelihood ratio statistic for a normal mean vector with nonnegative components.²⁷ The main advantage is that, after transformation and approximation, the asymptotic null distribution of the score statistic does not rely on the nuisance parameters involved in ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$, and therefore the significance level is much easier to compute, an appealing feature for genome-wide testing.

Let A be a p × p matrix such that

$$A^{T}A={\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }},$$ (Equation 3)

and so z = AU is asymptotically a normal vector with the identity covariance matrix. Such A is not unique, as we discuss the choice of A in the next paragraph. For a chosen A, the score statistic T_s becomes

$$n\left[z^{T}z-\text{inf}\left\{{\left(z-A\mathit{\delta }\right)}^T\left(z-A\mathit{\delta }\right):\mathit{\delta }\le 0\right\}\right].$$

Let b = Aδ. Geometrically, the parameter space under the alternative is the negative orthant. To compute T_s, one has to minimize ${\left(z-b\right)}^T\left(z-b\right)$ for all vectors in the image space $A\left(\mathit{\delta }\right)=\left\{A\mathit{\delta }|\mathit{\delta }\le 0\right\}$, which can be cumbersome. Instead, the proposed test approximates the polyhedral space A(δ) by the negative orthant $\left\{b|b\le 0\right\}$, with A chosen to make the center directions of the two spaces coincide. For the j^th element in z, denoted by z_j, if z_j ≥ 0, $\text{inf}\left\{{\left(z_j-b_j\right)}^2:b_j\le 0\right\}=z_j^2$; if z_j < 0, $\text{inf}\left\{{\left(z_j-b_j\right)}^2:b_j\le 0\right\}=0$. Because z_j and $z_{j\prime }$ are independent, it follows that the approximate score statistic for one-sided hypothesis H_1b is

$${\text{T}}_b=\sum _{j=1}^p{\left(z_j\wedge 0\right)}^2,$$

where $z_j\wedge 0$ denote the minimum of z_j and 0. Because of the independence among z_j values, the asymptotic null distribution is a special case of the chi-bar-squared distribution,²⁷ expressed as ${\sum }_{j=0}^p\left[\left\{p!/j!\left(p-j\right)!\right\}/2^p\right]{\chi }_j^2$, where ${\chi }_j^2$ is the chi-square distribution with j degrees of freedom and ${\chi }_0^2$ is defined as the constant zero.

The degree of approximation depends on the information matrix ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$. If it is diagonal, A can be chosen such that A(δ) is exactly the negative orthant. For an arbitrary information matrix, we can enhance the approximation by choosing the transformation A so that the center direction of A(δ), which is defined to be the direction that forms the same acute angle with any of the edge directions, coincides with the center direction of the negative orthant. For the negative orthant in the two-dimensional space, for instance, the center direction is (−1,−1). For a given A, the p edges of the polyhedral cone are given by

$$f_j=A{e}_j/{\left(e_j^T{\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}{e}_j\right)}^{1/2},$$

with j = 1,2, …, p and e_j is the unit vector for the j^th coordinate. The center direction is then given by

$$d_A={\left\{{\left(f_1,\dots ,f_p\right)}^T\right\}}^{-1}J,$$

where $J={\left(-1,\dots ,-1\right)}^T$, the center direction of the negative orthant. Therefore the center direction of A is required to be

$$d_A=cJ,$$ (Equation 4)

for some c > 0. In Appendix A, we give the details of how to construct A to ensure A(δ) has the same center direction as the negative orthant.

Following the same derivation, the score statistic for the other one-sided test, θ_j ≥ 0 for j = 1, …, p can be constructed as ${\sum }_{j=1}^p{\left(z_j\vee 0\right)}^2$, where $z_j\vee 0$ denote the maximum of z_j and 0. The score statistic for the bidirectional hypothesis H_1c is therefore the maximum of the two test statistics,

$${\text{T}}_c=\text{max}\left(\sum _{j=1}^p{\left(z_j\wedge 0\right)}^2,\sum _{j=1}^p{\left(z_j\vee 0\right)}^2\right).$$

The test statistic now depends on the angle of z_j in orthants other than positive and negative ones, and so the asymptotic null distribution is no longer a chi-bar-squared distribution. Since under the null hypothesis z_j is a vector of independent and standard normal distributions, the null distribution of T_c can be generated by simulation. For genome-wide testing, however, an enormous number of simulations need to be generated to achieve the accuracy needed for genome-wide significance (5 × 10⁻⁸). Though this requires the generation of a large number of simulated statistics (in the order of ∼10⁹–10¹⁰) only once, it is rather cumbersome for genome-wide testing. We propose a simple hybrid procedure that computes p values with adequate accuracy: first, a p value is computed by simulations to the accuracy of the third decimal place; if the simulation-based p value is less than 0.01, then we further compute an approximate, conservative p value by algebraic calculation. The detail of the algebraic approximation is shown in Appendix A. In Figures S1 and S2, we show some numerical analyses comparing simulation-based p values and algebraic approximations. This algebraic approximation works remarkably well: the smaller p value, the better approximation.

Testing for Proportional Interactions

Relative to the one-sided test, a more restrictive alternative hypothesis for multiple G × E in Equation 2 entails

$${\text{H}}_{1d}:{\theta }_j=\gamma {\beta }_{2j}\text{for}\text{some}\gamma \ne 0\text{and}j=1,\dots ,p,$$

so that in the log-odds scale, the interactions are proportional to the exposure main associations. One way to interpret this hypothesis is as follows: because of the shared etiology, the combinatory effect of environmental risk factors can be formulated as an environmental risk score, similar to genetic risk scores commonly used.³³ The genetic variant modifies the disease association of this environmental risk score as a whole. This test is slightly different from Tukey’s 1-df test because the genetic main association, ${\beta }_1$, does not factor in the interactions.²⁸ For genome-wide association studies, ${\beta }_1$ and γ will be 0 for the majority of loci. Given that the exposures are all established risk factors, i.e., ${\beta }_{2j}\ne 0$, the interaction parameter γ is identifiable even if there is no genetic main effect under the null hypothesis ${\beta }_1=0$, avoiding the troublesome identifiability issue.³⁰

The parameters are reduced to the vector $\mathit{\alpha }=\left(\mathit{\beta },\gamma \right)$. The standard Rao score statistic for testing $\gamma =0$, however, shows severe inflated type I errors in the BEACON genome-wide association study (see Figure S3, the quantile-quantile plot). The problem originates in the unique score function derived from the proportional interaction model. The usual expressions for the mean and variance of ${\tilde{S}}_{\gamma }$ need to be corrected for the finite-sample bias, as we derive below.

Let ${\mathcal{X}}_i=\left(1,G_i,{\mathbf{X}}_i,W_i\right)$ be the vector of covariates, and let $\tilde{\mathit{\beta }}$ denote the maximum likelihood estimator for $\mathit{\beta }$ under the null hypothesis. The score function for $\mathit{\beta }$ and γ under the null hypothesis can be written as

$$\begin{array}{c}{\tilde{S}}_{\mathit{\beta }}=\sum _i{\mathcal{X}}_i\left(Y_i-\frac{\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)}{1+\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)}\right),\\ {\tilde{S}}_{\gamma }=\sum _i\sum _j{\tilde{\beta }}_{2j}{G}_i{X}_{ij}\left(Y_i-\frac{\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)}{1+\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)}\right).\end{array}$$

Let ${\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}=\partial {\tilde{S}}_{\gamma }/\partial \mathit{\beta }$. Asymptotic distribution theories for maximum likelihood estimator $\tilde{\mathit{\beta }}$ lead to $\sqrt{n}\left(\tilde{\mathit{\beta }}-\mathit{\beta }\right)=\sqrt{n}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}+o_p\left(1\right)$, and so the usual first-order Taylor expansion of $\left(1/\sqrt{n}\right){\tilde{S}}_{\gamma }$ at $\mathit{\beta }$ yields

$$\begin{array}{c}\frac{1}{\sqrt{n}}{\tilde{S}}_{\gamma }=\frac{1}{\sqrt{n}}{S}_{\gamma }+\frac{1}{\sqrt{n}}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}\left(\tilde{\mathit{\beta }}-\mathit{\beta }\right)+o_p\left(1\right)\\ =\frac{1}{\sqrt{n}}{S}_{\gamma }+\frac{1}{\sqrt{n}}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}+o_p\left(1\right)\end{array}$$

The classical derivation for the large-sample distribution of a score statistic for a composite null hypothesis usually suffice. In this case, however, the first-order Taylor expansion turns out to be inadequate for a genome-wide significance level at 5 × 10⁻⁸. More importantly, ${\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}$ for this proportional interaction model is a function of the outcome variable Y,

$${\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}=\sum _i\left\{-{\mathcal{X}}_i\left(\sum _j{\tilde{\beta }}_{2j}{G}_i{X}_{ij}\right){\mu }_i\left(1-{\mu }_i\right)+{\mathcal{V}}_i\left(Y_i-{\mu }_i\right)\right\},$$

where ${\mu }_i=\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)/\left\{1+\text{exp}\left({\mathcal{X}}_i\tilde{\mathit{\beta }}\right)\right\}$ and ${\mathcal{V}}_i=\left(\mathrm{0,0},G_i{\mathbf{X}}_i,0\right)$. This induces correlation between ${\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}$ and ${\tilde{S}}_{\mathit{\beta }}$ which, if ignored, will result in bias when calculating the mean and the variance of score statistics in finite samples, and consequently inflated type I errors. For example, the expectation of ${\tilde{S}}_{\gamma }$ is no longer 0 in finite samples. We show in Figure S1 a heavily inflated quantile-quantile plot for the standard score test for the proportional interactions. In Appendix A, we show the algebraic development of the finite-sample correction for the mean (denoted by ${\tau }_d$) and the variance (denoted by ${\text{Σ}}_d$) of ${\tilde{S}}_{\gamma }$ after a second-order Taylor expansion,

$$\frac{1}{\sqrt{n}}{\tilde{S}}_{\gamma }=\frac{1}{\sqrt{n}}{S}_{\gamma }+\frac{1}{\sqrt{n}}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}\left(\tilde{\mathit{\beta }}-\mathit{\beta }\right)+\frac{1}{2\sqrt{n}}{\left(\tilde{\mathit{\beta }}-\mathit{\beta }\right)}^T{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}\left(\tilde{\mathit{\beta }}-\mathit{\beta }\right)+o_p\left(\frac{1}{\sqrt{n}}\right),$$

where ${\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}$ is the second derivative of ${\tilde{S}}_{\gamma }$ with respect to β. The corrected score statistic for testing γ = 0 is therefore expressed as

$${\text{T}}_d=\left({\tilde{S}}_{\gamma }-{\tau }_d\right){\text{Σ}}_d^{-1}\left({\tilde{S}}_{\gamma }-{\tau }_d\right).$$

The first-order correction is simpler but turns out to be inadequate to correct for the inflated type I error (Figure S4). In our simulation study and application to the BEACON data shown next, the second-order correction expressed as T_d shows proper control of the type I error in genome-wide significance.

Results

Simulation

We conducted numerous simulations to evaluate the performance of the proposed score statistics. Specifically, a genotype (coded as 0, 1, 2) was generated with minor allele frequency 0.1. Three exposure variables were generated by a multivariate normal distribution with zero means and a covariance matrix (either a diagonal matrix with diagonal elements 1 or a compound symmetric matrix with diagonal elements 1 and off-diagonal elements 0.6). The second and third exposure variables were dichotomized at zero. A logistic model was used to generate a dichotomous disease outcome conditional on the genotype and the exposures. The logarithm of the odds ratio was set to −0.5 for the genotype and (0.7, 0.7, 0.7) for the three exposures. The intercept was set to −4 to generate a disease probability of approximately 5%, under the null hypothesis that none of the exposures interacts with the genotype.

The two correlation structures between exposures generate different levels of correlation in the score functions for the three interaction parameters: a moderate level of correlations for each pair of score functions (<0.5) or a high correlation for each pair of score functions (>0.5). The correlation would affect the performance of the one-side score test and bidirectional test, because it is based on an approximation of the correlation-transformed orthant.²⁷

To evaluate the type I error rate, a cohort was first generated by these probabilistic distributions with a ladder of sample sizes (10⁴, 5 × 10⁴, 10⁵). All case subjects were sampled for simulated genotyping, together with the same number of randomly sampled control subjects. Table 1 shows empirical type I error rates evaluated in 5 × 10⁵ datasets simulated under the null hypothesis, when the nominal p value cut-off was set to be 0.05, 0.001, or 0.0001. The number of case subjects varies from 500 to 5,000, with the same number of control subjects. The upper part shows the scenario where the three environmental exposures are independent and the lower part shows the scenario where they are correlated. In all scenarios, the Bonferroni correction for three separate tests and the classical score test for the unconstrained alternative H_1a shows adequate performance in controlling type I errors. The one-sided test for H_1b shows proper control of type I error rates except slight inflation for significance level 0.001 and 0.0001 under 500 case subjects. The increased correlation hurts the performance of the one-sided score statistic. The bidirectional score statistic for H_1c shows superior control of the type I error rate, because it uses a conservative approximation in the tail of the p value distribution. Under a relative smaller sample size, the naive score statistic for H_1d displays grossly inflated type I error rates when nominal significance is 0.001 or 0.0001, 4 times or 14 times more than the correct level when the exposures are independent. This inflation dissipates when sample size increases, suggesting that the problem is largely driven by erroneous small-sample properties, not the large-sample behavior. In comparison, the corrected score statistic for H_1d shows adequate control of type I error rates for all settings. In genome-wide testing for gene-environment interactions, the power is typically small for the genome-wide significance level (5 × 10⁻⁸), and so the inflation of the type I error rate for the score statistic for H_1d can be concerning. See, for example, the quantile-quantile plot for the BEACON data in Figure S3. As we show in the data analysis later, the correction we proposed for H_1d is necessary to preserve adequate control of type I error.

Table 1.

The Ratio of the Observed Type I Error Rate versus the Nominal Value for the Bonferroni Test, the Unconstrained Score Test, and the Constrained Score Tests

Proportional
n Cases/n Controls	p Value Level	Bonferroni	Unconstrained	One-Sided	Bidirectional	Standard	Corrected
Independent Exposures
500/500	0.05	0.99	1.01	1.1	1.02	1.17	0.88
	0.001	0.97	1.01	1.57	1.07	4.4	1.05
	0.0001	0.88	1.14	1.98	1.32	14.24	1.5
2,500/2,500	0.05	0.98	1.00	1.03	1	1.04	0.98
	0.001	0.94	1.05	1.25	1.07	1.5	1.04
	0.0001	0.98	1.04	1.34	1.10	2.68	1.40
5,000/5,000	0.05	0.98	0.99	1.02	0.99	1.01	0.99
	0.001	0.96	1	1.14	0.97	1.25	1
	0.0001	0.76	1.02	1.18	1.02	1.56	1
Correlated Exposures
500/500	0.05	0.94	0.99	1.09	0.99	1.10	0.91
	0.001	1.03	1.01	1.65	1.1	3.08	1.18
	0.0001	1.34	1.06	2.12	1.34	9.62	2.06
2,500/2,500	0.05	0.98	1.01	1.04	1.01	1.03	0.99
	0.001	1.04	0.99	1.38	1.06	1.48	1.1
	0.0001	0.92	0.80	1.54	0.90	1.92	0.98
5,000/5,000	0.05	0.97	0.99	1.01	0.99	1.01	0.99
	0.001	0.99	1.02	1.21	0.94	1.17	0.99
	0.0001	1.12	0.94	1.34	1.16	1.38	1.04

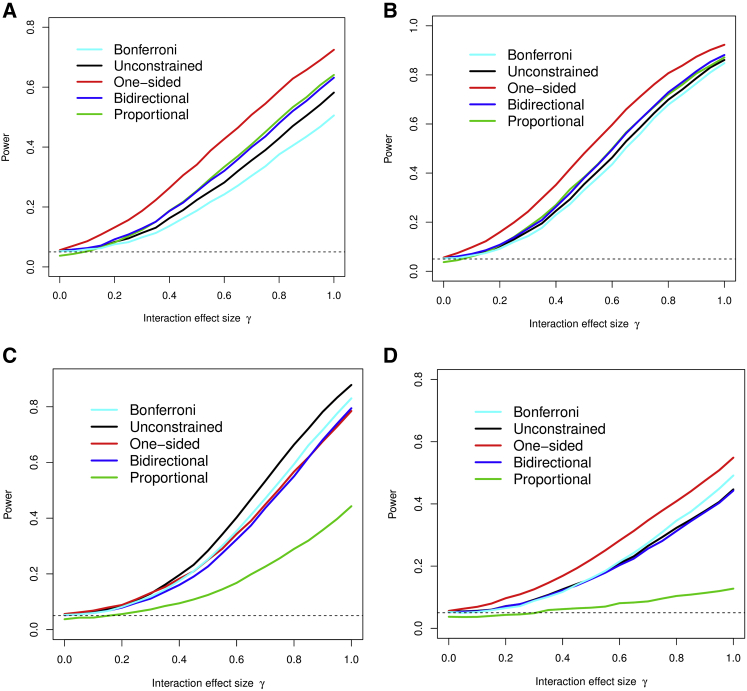
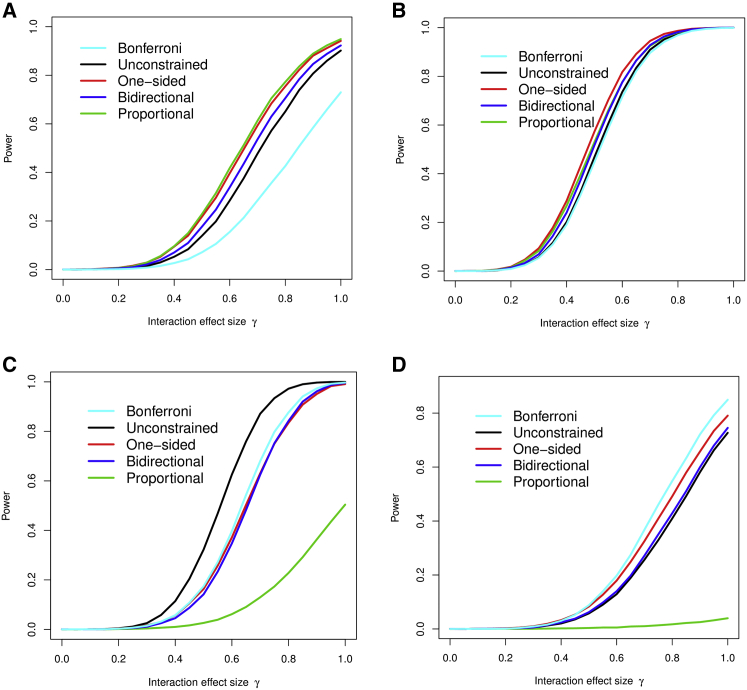
In Figures 1 and 2 we show the power performance for the five methods, in which the Bonferroni correction and the 3-df score test are the benchmarks of the comparison. We consider two scenarios: 500 case and 500 control subjects, significance level 0.05 (Figure 1), and 2,500 case and 2,500 control subjects, significance level 0.0001 (Figure 2). In each scenario, we generate four different sets of interaction parameters: proportional, one-sided (negative), two-sided, and only one non-zero interaction. The latter two sets are designed to test the robustness of the constrained methods when respective modeling assumptions are violated. We show the settings where the exposures are independent and omit the settings with correlated exposures, since the relative comparison between methods did not differ substantially from Figures 1 and 2.

Figure 1.

Statistical Power of the Four Methods Being Evaluated in Four Scenarios with a Small Sample Size

500 case subjects and 500 control subjects; there is no correlation between environmental exposures.

(A) The three interactions are proportional to respective main effects.

(B) The three interactions are not proportional, but one-sided.

(C) The three interactions have different directions.

(D) Two of the three interactions are zero.

Figure 2.

Statistical Power of the Four Methods Being Evaluated in Four Scenarios with a Large Sample Size

2,500 case subjects and 2,500 control subject; there is no correlation between environmental exposures.

(A) The three interactions are proportional to respective main effects.

(B) The three interactions are not proportional, but one-sided.

(C) The three interactions have different directions.

(D) Two of the three interactions are zero.

Figure 1 shows power performance of various methods for 500 case subjects and 500 control subjects with the significance level 0.05. In Figure 1A, the interaction parameters were set to be truly proportional to the respective main effects, namely $\gamma {\beta }_{2j}$ with γ increasing from 0 to 1. Clearly, the Bonferroni method performs the worst among the five methods evaluated, losing 5%–10% power when compared to the unconstrained 3-df score test. The one-sided (negative) score statistic for H_1b shows the best performance in power, consistently higher over the unconstrained score test, with the maximal power gain reaching 15%–20%. The proportional score statistic with finite-sample correction shows the second best performance, slightly better than the bidirectional test. The advantage of the one-sided test over the proportional and the bidirectional test is expected, because the latter two examine differences in both positive and negative directions.

Figure 1B shows the setting in which the interactions are truly one-sided but not proportional to the main exposure effects, specifically, θ_j = γ(−0.75, −0.5, −0.25) with γ increasing from 0 to 1 and the main effects are (0.7, 0.7, 0.7). The order of the performance remains the same as that in Figure 1A, though the difference is smaller. The one-sided score test performs the best in this scenario, whereas the proportional interaction test and the bidirectional test appear to be next in power performance. The Bonferroni method yields nearly identical power as the unconstrained score test.

Figure 1C shows a scenario where the interactions do not have the same sign, nor are proportional to the main exposure effects. Specifically, θ_j = γ(−0.5, −0.75, −0.25) with δ increasing from 0 to 1. This is the setting where the modeling assumptions for the three constrained score tests are violated. Consequently, the unconstrained test and the Bonferroni correction perform better than the constrained tests. The one-side (negative) test and the bidirectional test show some degree of robustness, with similarly lower power performance. The proportional test delivers a substantially inferior power performance relative to the other four tests.

In Figure 1D, we simulate a scenario where two out of the three interactions are 0, θ_j = γ(0, −1.0, 0) with δ increasing from 0 to 1. In this scenario, the Bonferroni method outperforms the unconstrained score test; the bidirectional test is similar to the constrained test; the proportional interaction test performs very poorly because this alternative hypothesis is not at all in the direction for which it is designated. Interestingly, the one-sided test still delivers the best power performance, because these interaction parameter values still conform to the alternative hypothesis H_1b that the interactions lie in the negative orthant.

Figure 2 shows the settings with 2,500 case and 2,500 control subjects, p value cut-off 0.0001. We want to examine the performance of the proposed methods in a large-scale case-control study, like the one in BEACON, and there are a large number of genotypes. The similar pattern as Figure 1 was observed in power comparison: when the alternative hypothesis is directional or proportional, the three constrained score statistics performs better than the standard 3-df test and the Bonferroni correction; notably, the proportional interaction outperforms the one-sided test, suggesting that pooling three exposures into a risk score for interaction really boosts the power when the significance level is far out in the tail; the one-sided test and the bidirectional test can be quite robust against model violation, whereas the performance of the proportional test drops substantially when the alternative hypothesis are not in the same direction. We also note that another feature affecting the performance of the proportional test is the effect size of the main exposure effects (Figure S5). Strong exposure effects and the large sample size, such as the three exposures in the BEACON study, works best for the proportional test, because its performance depends on the variability of the main effect estimates. Based on these simulations, it is compelling to apply the three constrained score tests and the unconstrained score test in the BEACON study.

Data Application

All 1,516 esophageal adenocarcinoma case individuals and 2,416 Barrett’s esophagus individuals in the discovery phase of the BEACON GWAS were included in this investigation, together with 2,187 control participants. A description of the genome-wide study has been published previously.²³ All recruited participants gave informed consent, and this study was approved by the ethics boards of each participating institution. Genetic data for which the authors have IRB permission to make public are available from the dbGaP database (accession numbers phs000869.v1.p1 and phs000187.v1.p1). Three established risk factors were investigated for potential interaction with 922,031 SNPs that were genotyped by the Illumina HumanOmni1-Quad platform and passed quality control: cigarette smoking, body-mass index (BMI), and gastresophageal reflux symptoms. These variables were coded as ever smoking (yes or no), BMI (<25, ≥25 to <30, ≥30 kg/m²), and at least weekly heartburn or weekly reflux (yes or no). A logistic model was fitted for every SNP and the three exposures, separately for EA and BE. Each model included age, sex, the first four principal components derived from genome-wide SNP data to account for population stratification, the SNP main effect (coded as two indicator variables), the three exposure main effects (all coded categorically), and the product of the SNP value (0, 1, or 2, treated quantitatively) and each of the three exposures. The multivariate SNP-exposure interactions were tested by the unconstrained score test, the one-sided test, and the proportional test.

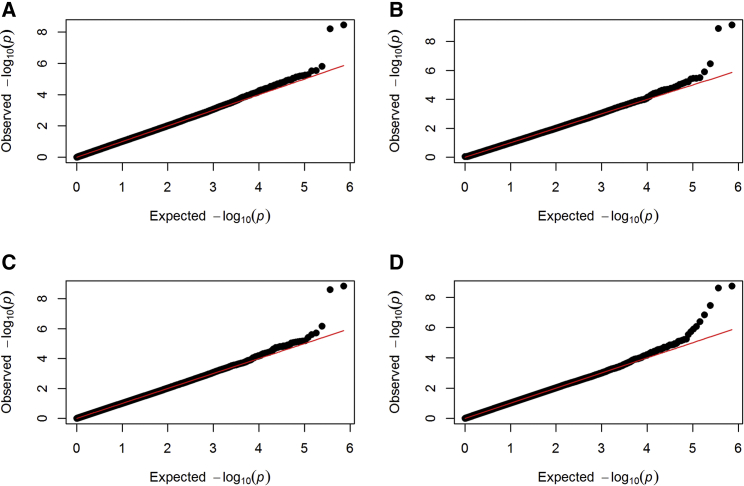
Figure 3 shows the q-q plots for the four genome-wide G × E testing methods for Barrett’s esophagus. The one-sided results for the positive interaction for Barrett’s esophagus, as well as all G × E tests for esophageal adenocarcinoma, did not yield any significant results and therefore were not presented. Figure 3A shows that the unconstrained 3-df score statistics yield two genome-wide significant SNPs on chromosome 7 that are highly correlated (r² = 1; rs11765529, p value 3.48 × 10⁻⁹; rs7798662, p value 6.06 × 10⁻⁹). The same two SNPs remain genome-wide significant when tested by one-sided (negative) score statistics, the bidirectional test, and the proportional interaction test shown in Figures 3B–3D. The proportional interaction test resulted in one additional genome-wide significant SNP, rs4930068 in chromosome 11 (p value 3.51 × 10⁻⁸, Figure 3D). In Figure S3, we show the q-q plot with seriously inflated type I error rates when the finite-sample correction is not applied to score statistics for proportional interactions.

Figure 3.

The q-q Plots for Genome-wide Testing for G × E on Barrett’s Esophagus by the Three Score Statistics

(A) Unconstrained score test.

(B) One-sided score test for negative G × E.

(C) Bidirectional test.

(D) Score test for proportional G × E.

Table 2 shows the estimated odds ratios of the three environmental factors stratified by the number of alleles for the two genome-wide significant SNPs. Barrett’s esophagus and esophageal adenocarcinoma were investigated as cases separately in logistic regression models with three SNP-environment interactions. The interpretation of these ORs is conditional on genotype, age, gender, and the other two exposures being fixed at certain levels. The right half of Table 2 shows the p values from various score tests for G × E testing. For almost every combination of SNP, exposure, and disease combination, the OR decreases with the number of increasing-risk alleles. This decreasing OR with the number of alleles is most strongly seen in GERD, the strongest risk factor, and the trend we found for Barrett’s esophagus is similar to that for esophageal adenocarcinoma, though the latter does not have a genome-wide significance level. Since both the cases of Barrett’s esophagus and the cases of esophageal adenocarcinoma were compared to the same control group, the findings for esophageal adenocarcinoma are not independent replications. Nonetheless, the consistency between Barrett’s esophagus and esophageal adenocarcinoma adds to the evidence for true G × E in the etiological pathway.

Table 2.

The Odds Ratio of the Three Environmental Factors Associated with SNP Genotypes for Barrett’s Esophagus and Esophageal Adenocarcinoma, and the Three Score Tests for Multiple G × E Simultaneously

OR Stratified by the Number of Minor Alleles					G × E p Value
Disease	Risk Factor	0	1	2	Unconstrained	One-Sided	Bidirectional	Proportional
rs11765529
BE	BMI	1.94 (1.74, 2.17)	1.64 (1.24, 2.16)	1.28 (0.08, 19.7)	–	–	–	–
	smoking	1.67 (1.41, 1.98)	0.79 (0.51, 1.21)	0.94 (0.80, 11.1)	–	–	–	–
	GERD	6.39 (5.35, 7.64)	2.09 (1.36, 3.21)	0.69 (0.06, 8.09)	3.48 × 10−9	7.10 × 10−10	1.42 × 10−9	1.81 × 10−9
EA	BMI	1.51 (1.31, 1.74)	1.17 (0.81, 1.69)	–	–	–	–	–
	smoking	1.87 (1.50, 2.35)	1.20 (0.64, 2.27)	–	–	–	–	–
	GERD	3.83 (3.07, 4.77)	2.34 (1.33, 4.11)	–	0.013	0.004	0.0072	0.003
rs4930068
BE	BMI	2.11 (1.80, 2.49)	1.91 (1.64, 2.22)	1.32 (1.01, 1.72)	–	–	–	–
	smoking	1.56 (1.22, 1.99)	1.73 (1.38, 2.18)	0.85 (0.56, 1.28)	–	–	–	–
	GERD	7.91 (6.08, 10.30)	4.75 (3.76, 6.02)	2.86 (1.88, 4.35)	1.53 × 10−6	3.38 × 10−7	6.76 × 10−7	3.51 × 10−8
EA	BMI	1.46 (1.19, 1.79)	1.43 (1.17, 1.74)	1.41 (0.99, 1.99)	–	–	–	–
	smoking	2.14 (1.54, 2.99)	1.67 (1.23, 2.27)	1.08 (0.60, 1.95)	–	–	–	–
	GERD	4.80 (3.48, 6.60)	3.04 (2.26, 4.08)	2.21 (1.24, 3.92)	0.007	0.002	0.004	0.004

Abbreviations are as follows: BE, Barrett’s esophagus; EA, esophageal adenocarcinoma.

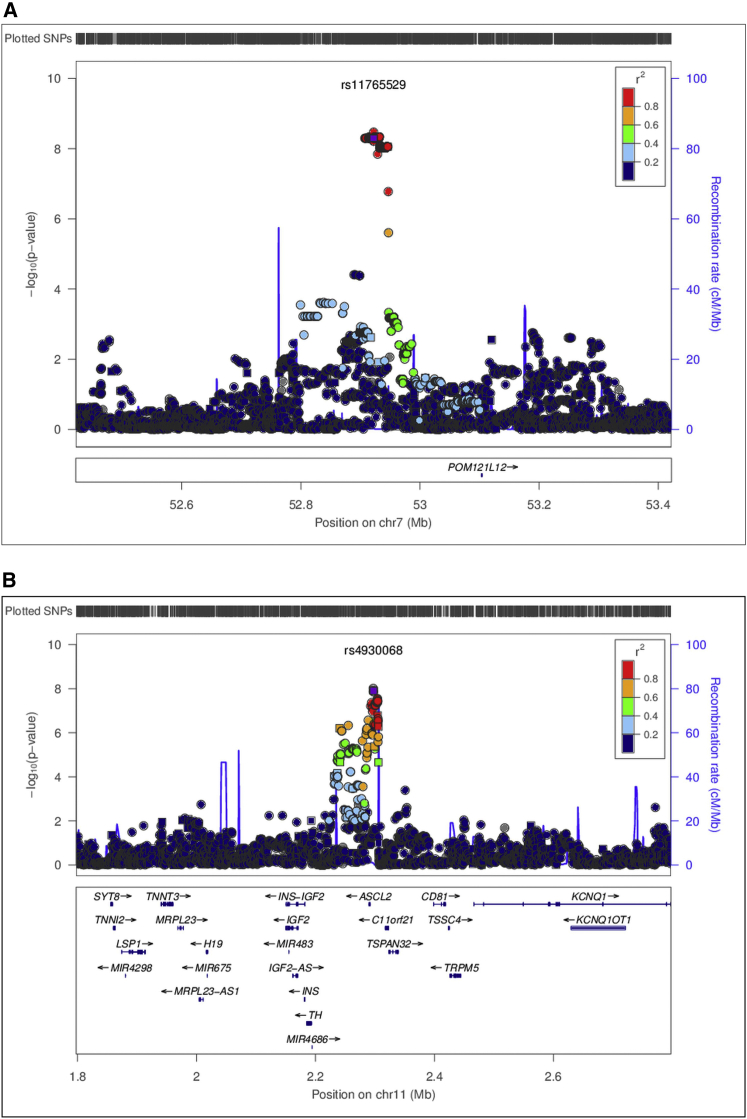
Association analyses were further conducted for imputed SNPs based on the 1000 Genomes Project around genotyped SNPs that showed significant interactions with one of the three risk factors. The details of the imputation procedure have been presented previously.²³ Figure 4 shows the regional interaction associations around rs11765529 and rs4930068, including both genotyped and imputed SNPs within a 1 Mb interval centering around the index SNPs. The index SNPs are marked as purple squares, other genotyped SNPs are marked with squares, and imputed SNPs are marked by circles. The rs11765529 variant is located in a gene-poor intergenic region, ∼160–180 kb from the nearest protein-coding gene, POM121L12 (transmembrane nucleoporin-like 12 [MIM: 615753]). The rs4930068 variant at 11p15.5 is located 5.4 kb upstream (5′) of the transcriptional start site for ASCL2 (MIM: 601886). None of adjacent SNPs showed more significant p values than the index SNPs.

Figure 4.

Regional Association Plot of Genotyped and Imputed SNPs in Proximity to Two Newly Discovered SNPs with Genome-wide Significance

The top portion of the figure has physical position along the x axis, and −log10(p value) for the interaction term on the y axis. The index SNP is marked as a purple square, other genotyped SNPs are marked with squares, and imputed SNPs are marked by circles. The color scheme represents the pairwise correlation (r²) between a given SNP and the index SNP. The bottom portion of the figure shows the position of genes across the region.

(A) Genotyped and imputed SNPs around rs11765529, the p values are from the unconstrained score test.

(B) Genotyped and imputed SNPs around rs4930068, the p values are from the score test for proportional interactions.

We conducted in silico functional characterization of these SNPs in several bioinformatics databases. The two variants at 7p12.1 (rs7798662 and rs11765529) are situated in a gene-poor intergenic region, ∼160–180 kb from the nearest protein-coding gene, POM121L12 (Figure S6A). These two SNPs are separated by ∼24 kb, are in strong linkage disequilibrium (LD) (r² = 1), and are highly correlated (r² = 1) with >100 additional variants in a 40-kb region, based on data from the 1000 Genomes Project³⁴ (Table S1A). rs7798662 modifies a predicted binding motif for the transcription factor Smad3 (MIM: 603109), whereas rs11765529 alters motifs for HDAC2 (MIM: 605164).³⁵ Several correlated SNPs lie in regions marked by enhancer histone modifications or DNase hypersensitivity in multiple tissues or cell lines, based on data from the NIH Roadmap Epigenome Project and ENCODE.^{36, 37} Recruitment of the transcription factor JUND (MIM: 165162) has been reported ∼6.5 kb away from rs11765529. Of potential interest, rs7798662 and rs11765529 lie within a 3.3 Mb region designated as a long-range epigenetic activation (LREA) domain in prostate cancer cells; this region, which encompasses a total of ten genes (including POM121L12) was identified as transcriptionally active in prostate cancer cell lines relative to normal primary prostate cells.³⁸ The POM121L12 protein is largely uncharacterized with respect to biological function, but is related to the POM121 transmembrane nucleoporin, a key component of the nuclear pore complex, which enables transport into and out of the nucleus.^{39, 40}

The rs4930068 variant at 11p15.5 is located 5.4 kb upstream (5′) of the transcriptional start site for ASCL2, which encodes the Achaete-Scute Family bHLH Transcription Factor 2 (Figure S6B). rs4930068 is in strong LD (r² > 0.8) with 41 additional variants located within 20 kb, including 30 SNPs within 8 kb (r² > 0.90).³⁴ rs4930068 lies in a 7,400-bp region characterized as heterochromatin in esophageal tissue, according to chromatin state segmentation data derived from the Roadmap Epigenome Project.³⁷ Multiple SNPs strongly correlated with rs4930068, rs11021967, rs7396048, rs2285567, rs11022026, and rs6578259 are located within segments marked by enhancer histone marks in the esophagus and/or distal gastrointestinal (GI) mucosa and appear to hold high regulatory potential (Table S1). Several of these variants lie within regions characterized by DNase hypersensitivity and transcription factor recruitment (TAL1 [MIM: 187040], USF1 [MIM: 191523], E2F6 [MIM: 602944], ELF1 [MIM: 189973], MAX [MIM: 154950]) in various cells/tissues and modify predicted regulatory binding motifs.³⁶ Some of these SNPs (rs7396048, rs2285567, rs11022026) are potential expression quantitative trait loci (eQTLs) in whole blood or other tissues.³⁶

The ASCL2 protein is a member of the basic helix-loop-helix (HLH) family of transcription factors, which dimerize and bind to DNA via their HLH and basic domains, respectively.⁴⁰ bHLH proteins play important general roles in cell fate specification and lineage-specific transcriptional control. ASCL1 (MIM: 100790) and ASCL2 are essential factors in the development of the neuroectoderm and trophectoderm, respectively,^{41, 42} and both proteins are frequently expressed in human cancers. ASCL2, an apparent target gene of the Wnt signaling pathway, was shown to be upregulated in colorectal neoplasia⁴³ and has been linked to an intestinal stem cell expression signature that defines a majority of colorectal cancers (MIM: 114500)⁴⁴ and may be present in precancerous adenomas.⁴⁵ Low-level expression of ASCL2 mRNA has also recently been reported in BE⁴⁶ while studies in human esophageal cell lines have described induction of ASCL2 mRNA and protein in a sub-population of stem-like spheroid cells derived in culture.⁴⁷ Of particular interest, ASCL2 was shown to suppress expression of the homeobox transcription factor CDX2 (MIM: 600297),⁴⁸ a known early marker of BE,⁴⁹ subsequently downregulated during EA pathogenesis.⁵⁰

Based on our in silico functional characterization of rs4930068 and correlated variants, a potential regulatory role for these SNPs in influencing ASCL2 expression levels appears plausible. However, future laboratory-based studies are clearly required to assess possible functional effects. Recent evidence has suggested that Barrett’s esophagus may represent the outgrowth of a residual embryonic epithelial cell population, rather than squamous-to-columnar trans-differentiation of resident stratified epithelium.^{51, 52} In this context, it is intriguing to consider the possibility that the observed interaction between rs4930068 and GERD in relation to risk of BE might in part reflect alterations in the expression level of ASCL2, a transcription factor with known roles in both development and cancer.

Discussion

In summary, we have proposed constrained testing strategies for identifying interactions between a genotype and multiple related environmental exposures: the one-sided interactions, the bidirectional interactions, and the proportional interactions (on the log OR scale relative to respective main environmental associations). Several statistical contributions were made in this work. First, an approximate score statistic was developed for the one-sided test, which circumvents the difficulty of obtaining an exact asymptotic distribution, and further extended to the bidirectional test. Second, for the proportional interaction test, we proposed a second-order correction to the mean and the variance of the score statistic, which resolved the issue of the inflated type I error rate in genome-wide testing. Our proposed methods were applied to the BEACON study and identified several loci that interact with three environmental exposures in Barrett’s esophagus with genome-wide significance.

Our work is exploratory in nature, as other methodological developments in genome-wide association testing. There is a paucity of established G × E, much due to lower power of such exploration. The goal of our work is to enrich G × E findings that may lead to further validation and functional studies. These G × E could help in risk prediction and stratification, or possibly individualized prevention for modifiable exposures.

Our simulation study suggests that the one-side test nearly always outperforms, if only slightly, the proportional interaction test, even in the scenario where interactions are generated to be proportional. This is primarily due to the proportional test being a two-sided test, and its increased variability because of its dependence on the main associations of environmental exposures. When the latter were estimated with quite some uncertainty, for example, when the sample size is small, the proportional test is not very appealing in power performance. However, in consortium studies where investigators can assemble a large sample size, the proportional test can be advantageous when the interactions are truly directional (Figures 2A and 2B). When such constraint is violated, the proportional test can be powerless as shown in Figures 1C, 1D, 2C, and 2D. The directional test strikes the balance between power and robustness, performing competitively under true model constraints and displaying robustness against model violations.

In cancer epidemiology, if several exposures share some etiological pathways, our simulation shows that testing one exposure at a time is inferior in power to simultaneously testing multiple G × E altogether. We show an example of applying such testing strategies in the BEACON study and we found several interesting genome-wide significant hits. We note that the suitability of the proposed constrained inference depends heavily on study context and a priori scientific knowledge. Other plausible settings include multiple measures of the same underlying exposure profile, such as measures of smoking and diet intake. Investigators should exercise caution when applying the constrained inference since, as we show in the simulation, violations of model constraints can result in deteriorated power.

Beyond the multivariate G × E testing we consider, constrained inference strategies for a single G × E test have been explored. For example, it is often reasonable to constrain the interaction to be quantitative, because epidemiologists believe such interaction is generally unnatural and rare, if it exists at all.⁵³ Some works have been developed along this line, possibly incorporating the powerful but controversial gene-environment independence assumption.^{54, 55} From a methodological point of view, the latter assumption could be incorporated into the constrained score statistics we developed in this article, with some additional work. For the BEACON study, however, this assumption does not hold because BMI and GERD are both phenotypes with substantial genetic susceptibility.^{56, 57}

We close with a brief discussion on generalizing the proposed methods. The Tukey’s test has been formulated to study interactions between multiple genes and multiple environmental exposures. In principle, the one-sided and bidirectional testing strategies can be applied equally to one exposure of interest and a set of SNPs in the gene, or a set of known risk loci. The proportional interaction test naturally applies to this setting. One complexity for the one-sided test is that, in contrast to the BEACON study where all three exposures are known to be hazardous, it may be entirely unknown which alleles of the SNPs in a gene may modify the exposure association in the same direction. Therefore it requires a bit more understanding of the function of the alleles prior to motivating the directional hypotheses for one exposure of interest and a set of SNPs in the gene. The other potential issue for one exposure and a set of SNPs is that the number of SNPs has to be limited, because the dimensionality would affect the degree of freedom in the chi-bar-squared distribution, which will in turn influence power performance.

Consortia

The following BEACON consortium members contributed to this paper: Wong-Ho Chow, Nicholas J. Shaheen, Lesley Anderson, Douglas A. Corley, Marilie D. Gammon, Laura J. Hardie, Jesper Lagergren, and David C. Whiteman. Full addresses are listed in Supplemental Data.

Published: August 4, 2016

Appendix A

Construction of the Transformation Matrix A

As stipulated in Material and Methods, $A^{T}A={\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$ and its center direction should coincide with the center direction of the negative orthant. In addition, it would be appealing that A(δ) is invariant to the order of the elements in U, since the order of the interaction terms tested in the alternative hypothesis should not change the test statistic. We adopt a linear ordering method previously developed to re-arrange U and ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$.⁵⁸ Next we find A that satisfies Equations 3 and 4. Let H = (h₁,…, h_p) be the orthogonal matrix obtained by applying the Gram-Schmidt orthonormalization to the independent set of vectors (J, e₁,…, e_p). Let $C^{T}C={\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$ be the Choleski decomposition of ${\mathcal{I}}_{\mathit{\theta \theta },\mathit{\beta }}$. Let d_c denote the center direction of the image space $C\left(\mathit{\delta }\right)=\left\{C\mathit{\delta }|\mathit{\delta }\le 0\right\}$, and let V = (v₁,…, v_p) be the orthogonal matrix obtained by applying Gram-Schmidt orthonormalization to the independent set of vectors (d_c, e₂,…, e_k). Then A = HV^TC satisfies the conditions of Equations 3 and 4.

Computation of Tail p Values for the Bidirectional Hypothesis by Algebraic Approximation

It is instructive to show the approximation when p = 2. The calculation in a higher dimension follows without difficulty. Specifically, let (z₁, z₂) denote the standard bivariate normal variables. The four quadrants are denoted by ${\mathcal{Q}}_1$, ${\mathcal{Q}}_2$, ${\mathcal{Q}}_3$, and ${\mathcal{Q}}_4$, respectively. The p value for the observed T_c = t is the sum of components from each quadrant. The components of p value in ${\mathcal{Q}}_1$ and ${\mathcal{Q}}_3$ follow a standard ${\chi }_2^2$ distribution. For components in ${\mathcal{Q}}_2$ and ${\mathcal{Q}}_4$,

$$\begin{array}{c}\text{Pr}\left({\text{T}}_c>t|\left(z_1,z_2\right)\in {\mathcal{Q}}_2\cup {\mathcal{Q}}_4\right)=\text{Pr}\left(z_2^2>t,\left|z_2\right|\ge \left|z_1\right||\left(z_1,z_2\right)\in {\mathcal{Q}}_2\cup {\mathcal{Q}}_4\right)+\text{Pr}\left(z_1^2>t,\left|z_1\right|>\left|z_2\right||\left(z_1,z_2\right)\in {\mathcal{Q}}_2\cup {\mathcal{Q}}_4\right)\\ <\text{Pr}\left(z_2^2>t|\left(z_1,z_2\right)\in {\mathcal{Q}}_2\cup {\mathcal{Q}}_4\right)+\text{Pr}\left(z_1^2>t|\left(z_1,z_2\right)\in {\mathcal{Q}}_2\cup {\mathcal{Q}}_4\right)\\ =\text{Pr}\left({\chi }_1^2>t\right)+\text{Pr}\left({\chi }_1^2>t\right)\end{array}$$

It is clear that the bigger t, the better approximation. In Figures S1 and S2, we show a comparison of simulation- based p values and approximation-based p values. For p values < 0.01, the difference is essentially negligible.

Correcting the Mean and the Variance of the Score Statistic for the Proportional Interaction

For dichotomous outcomes, the exact computation of the mean of the second-order Taylor expansion of ${\tilde{S}}_{\gamma }$, namely

$$S_{\gamma }+{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }},$$

can be derived algebraically, since

$$\begin{array}{c}{\tau }_d=\mathbb{E}\left(S_{\gamma }+{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)\\ =\mathbb{E}\left[\left(\sum _i{\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}\right){\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}\left(\sum _i{\tilde{S}}_{\mathit{\beta },i}\right)+\frac{1}{2}{\left(\sum _i{\tilde{S}}_{\mathit{\beta },i}\right)}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}\left(\sum _i{\tilde{S}}_{\mathit{\beta },i}\right)\right]\\ =\sum _i\mathbb{E}\left({\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)\\ =\sum _i{\mu }_i\left({\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i1}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}{\tilde{S}}_{\mathit{\beta },i1}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta },i1}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i1}\right)+\left(1-{\mu }_i\right)\left({\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i0}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}{\tilde{S}}_{\mathit{\beta },i0}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta },i0}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i0}\right),\end{array}$$

where ${\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}={\mathcal{V}}_i\left(Y_i-{\mu }_i\right)$ and ${\tilde{S}}_{\mathit{\beta },i}$ are respective individual contribution from the i^th subject, ${\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i1}$ and ${\tilde{S}}_{\mathit{\beta },i1}$ are contributions from the i^th subject, evaluated at Y_i = 1, and ${\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i0}$ and ${\tilde{S}}_{\mathit{\beta },i0}$ are contributions from the i^th subject, evaluated at Y_i = 0. The second-to-last equality uses the independence between the i^th subject and the j^th subject, if $i\ne j$. The last equality uses the unique feature that Y_i takes two values (1,0) with probability ${\mu }_i$ and $\left(1-{\mu }_i\right)$, respectively. Similar, but more tedious, calculation applies to

$${\text{Σ}}_d=\text{Var}\left(S_{\gamma }+{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}+\frac{1}{2}{\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right).$$

Let $\text{Δ}={\sum }_i-{\mathcal{X}}_i\left({\sum }_j{\tilde{\beta }}_{2j}{G}_i{X}_{ij}\right){\mu }_i\left(1-{\mu }_i\right)$. The key terms involved in the calculation are expressed below:

$$\mathbb{E}{\left(S_{\gamma }+{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)}^2=\sum _i\mathbb{E}{\left(S_{\gamma ,i}+\left(\text{Δ}+{\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}\right){\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)}^2+\sum _{i\ne j}\mathbb{E}{\left({\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },j}\right)}^2$$

$$\mathbb{E}{\left({\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)}^2=\sum _i\sum _j\mathbb{E}{\left({\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)}^2$$

$$\mathbb{E}\left(S_{\gamma }{\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)=\sum _i\left(S_{\gamma ,i}{\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)$$

$$\mathbb{E}\left(S_{\gamma }{\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)=\sum _i\left(S_{\gamma ,i}{\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)$$

$$\mathbb{E}\left(\left({\tilde{\mathcal{H}}}_{\gamma \mathit{\beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)\left({\tilde{S}}_{\mathit{\beta }}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta }}\right)\right)=\sum _i\mathbb{E}\left(\left(\text{Δ}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)\left({\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },i}\right)\right)+\sum _i\sum _j\mathbb{E}\left(\left({\tilde{\mathcal{K}}}_{\gamma \mathit{\beta },i}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },j}\right)\left({\tilde{S}}_{\mathit{\beta },i}^T{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{\mathcal{H}}}_{\gamma \mathit{\beta \beta }}{\tilde{\mathcal{I}}}_{\mathit{\beta \beta }}^{-1}{\tilde{S}}_{\mathit{\beta },j}\right)\right).$$

Web Resources

• dbGaP, http://www.ncbi.nlm.nih.gov/gap

• OMIM, http://www.omim.org/