CONSTANd : A Normalization Method for Isobaric Labeled Spectra by Constrained Optimization

Abstract

In quantitative proteomics applications, the use of isobaric labels is a very popular concept as they allow for multiplexing, such that peptides from multiple biological samples are quantified simultaneously in one mass spectrometry experiment. Although this multiplexing allows that peptide intensities are affected by the same amount of instrument variability, systematic effects during sample preparation can also introduce a bias in the quantitation measurements. Therefore, normalization methods are required to remove this systematic error. At present, a few dedicated normalization methods for isobaric labeled data are at hand. Most of these normalization methods include a framework for statistical data analysis and rely on ANOVA or linear mixed models. However, for swift quality control of the samples or data visualization a simple normalization technique is sufficient. To this aim, we present a new and easy-to-use data-driven normalization method, named CONSTANd. The CONSTANd method employs constrained optimization and prior information about the labeling strategy to normalize the peptide intensities. Further, it allows maintaining the connection to any biological effect while reducing the systematic and technical errors. As a result, peptides can not only be compared directly within a multiplexed experiment, but are also comparable between other isobaric labeled datasets from multiple experimental designs that are normalized by the CONSTANd method, without the need to include a reference sample in every experimental setup. The latter property is especially useful when more than six, eight or ten (TMT/iTRAQ) biological samples are required to detect differential peptides with sufficient statistical power and to optimally make use of the multiplexing capacity of isobaric labels.

The last decades, several new approaches are developed to study differential protein expression in biological systems. In this emerging field of proteomics, liquid chromatography (LC)¹ and mass spectrometry (MS) are the preferred technologies for the separation, identification and quantification of proteins because of its high-throughput capabilities. A typical LC-MS proteomics workflow includes several different steps from the extraction of proteins, their reduction and alkylation to improve unfolding, the enzymatic digestion of proteins into peptides and finally their LC-MS/MS analysis (1). In this LC-MS based setup, the use of mass labels for the relative quantification of proteins gained popularity because labels allow for multiplexing, as multiple biological samples are simultaneously processed in one LC-MS experiment. This simultaneous identification and quantification of samples furthermore benefits a direct statistical assessment of differential peptides and proteins that are measured by the mass spectrometer, as the measurements are affected by the same amount of instrument variability. For this purpose, several labeling methodologies exist, which can be subdivided in metabolic, enzymatic and chemical labeling strategies (2). Metabolic strategies, such as stable isotope labeling by amino acids (SILAC), are promising but still limited to cell cultures or small animals (3). As an alternative, both O¹⁶/O¹⁸ enzymatic exchanges as well as chemical isotope labeling approaches such as isotope coded affinity tags (ICAT) (4) and isotope coded protein labels (5) were developed. With these isotopic labeling approaches, a light variant and heavier variant of each peptide exist in the sample. As a result, the acquired mass spectrum (MS1) is more complicated as a peptide will appear in different mass regions in the spectrum because of the various mass labels. For complex samples it is often cumbersome to disentangle and assemble the quantitative information, and different approaches are recommended. The isobaric labeling strategy, for example, belongs to the chemical labeling subclass and is special because the different, yet intact labels have an equal mass, hence the term “isobaric.” Isobaric labels are popular in proteomic research as these tags allow multiplexing of up to ten samples in one LC-MS run, which reduces measurement time and makes direct intra-experiment comparison possible. The two commercially available labels are called tandem mass tags (TMT) (6-plex or 10-plex) and isobaric tags for relative and absolute quantification (iTRAQ) (4-plex or 8-plex). Both TMT and iTRAQ isobaric tags contain a reporter group and an amino-reactive group, spaced by a balancer group which generates an isobaric mass shift for all tags (6, 7). The reactive group of the tag targets N-termini and free amino groups of lysine, so that all digested peptides are labeled at least once. Relative quantification of the labeled and multiplexed peptides is achieved by the generation of reporter ions with unique masses upon fragmentation of the peptide precursor. Because of this demultiplexing, the signal intensities of these reporter ions in tandem mass spectra (MS2) can be used for the determination of the relative expression difference of peptides in the multiplexed samples (8–11).

An approach that allows for multiplexing various samples not only reduces the LC-MS measurement time considerably, it also substantially reduces the variation in the quantification results (11). However, multiplexing includes additional steps which make this isobaric labeling strategy prone to systematic effects at the level of the wet-lab. This systematic bias is defined as a persistent error that influences the peptide abundances in a sample equally up or down. For example, one of the most common handling errors are pipetting errors that occur when samples are multiplexed or errors in the determination of the protein concentration prior digestion (12). This type of inaccuracies can be remediated by data normalization. Luckily, a plethora of data normalization methods exist that can be borrowed from micro-array, LC-MS or NMR data analysis (12–15). Some of these normalization techniques are already implemented in software packages dedicated for mass spectral data, as the case for the DAPAR implemented in R Bioconductor. This package harbors methods for global rescaling, median or mean centering and a combination of scaling and mean centering (16). Algorithms like quantile normalization (17, 18) are often applied in isobaric labeled proteomic studies and several software packages suited for isobaric labeled data, including Quant (19), IsobariQ (20), Isobar (21) use global normalization methods. Here, the intensity distributions of the measured reporter ions within a quantification channel are realigned such that the mean or median of the distribution is equal across the quantification channels in the multiplexed pool. Another software package, i-tracker, was developed to establish an easy integration of quantitative information and peptide identification and to provide iTRAQ 4-plex reporter ion ratios (22). The authors performed normalization on the estimated peak areas, and in their model, used a percentage contribution of the reporter channels. A few landmark publications combine data normalization in a statistical framework based on ANOVA models or linear mixed models which allows simultaneous normalization and statistical analysis of multiple isobaric experiments (23–27). On the other hand, for a quality control of the samples, data visualization or downstream analysis with machine learning techniques, a simple and correct data normalization, is sufficient.

To this aim, we present a new data-driven and easy-to-use normalization method, named CONSTANd (Constrained Standardization), which is able to remove the systematic effect induced by the labeling protocol in an efficient way. The method can be considered as a data preprocessing step and is tailored for isobaric labeled spectra that entails a constrained optimization problem to estimate a set of scale and normalization parameters. The method is simple to implement and is not demanding on computational resources. Further, CONSTANd scales well with large data sets. Here, we employ the CONSTANd method to a quantitative TMT experiment and illustrate its superiority over quantile normalization and median sweep normalization (24).

EXPERIMENTAL PROCEDURES

Sample Preparation

In this study, three different physiological conditions of the same cell type, each comprising six biological independent samples were used. From the three different experimental conditions, termed A, B, and C, the cell pellets were efficiently lysed using 200 μl RIPA buffer (1x) (Thermo Scientific, Rockford, IL) containing also 1× HALT phosphatase inhibitor (Thermo Scientific) and 1× HALT protease inhibitor (Thermo Scientific), combined with a 30 s during sonication (Branson Sonifier SLPe ultrasonic homogenizer, Labequip, Ontario, Canada) of the sample on ice. After centrifugation of the samples for 15 min at 14,000 × g on 4 °C, the cell pellet was discarded. Next, the protein concentration was determined using the Pierce BCA protein Assay kit (Thermo Scientific).

Before labeling the samples, 15 μg proteins of each sample were reduced using 2 μl of 50 mm tris(2-carboxyethyl) phosphine, supplied with the TMT labeling kit (Thermo Scientific), in a volume of 20 μl 100 mm triethylammonium bicarbonate (TEAB), and incubated for 1 h at 55 °C. After alkylation of the proteins for 30 min in the dark, 6 volumes of ice-cold acetone were added and the samples were incubated overnight at −20 °C. The next day, samples were centrifuged for 10 min at 6000 × g and 4 °C and the acetone was removed. After resolving the pellet with 15 μl 200 mm TEAB, 0.1% Rapigest SF surfactant (Waters, Milford, MA) was added to improve further solubilization of the proteins and the sample was incubated for 5 min at 100 °C. After this, proteins are digested with trypsin (enzyme/protein ratio = 1:20) overnight at 37 °C. The next day, the samples are desalted with Pierce C18 spin columns according to the manufacturer's instructions (Thermo Scientific) before labeling was performed.

TMT Labeling

For the reconstitution of the tags, the TMT labels were dissolved in 41 μl acetonitrile according to the manufacturer's protocol. Subsequently, digested peptides were labeled with the TMT reagents. From every sample, 10 μg was labeled with 4.1 μl of a TMT tag dissolved in acetonitrile and every sample was incubated for 1 h at ambient temperature. The labeling reaction was stopped by adding 2 μl 5% hydroxylamine. After 15 min, a pooled sample was prepared based on the labeled samples with a protein concentration ratio of 1:1:1:1:1:1. An overview of the experimental setup can be found in Table I. It should be noted that the 18 samples that belong to three experimental conditions (A, B, and C) were block randomized over the available TMT labels in such a way that two biological replicates of each condition are present in a multiplexed sample.

Table I. An overview of the experimental setup. Three different experimental conditions (A,B and C) from 6 subjects are block randomized in three sixplex TMT 2D-LC-MS experiments. Each sixplex has 2 biological replicates of each experimental group.

ID/label	TMT6-126	TMT6-127	TMT6-128	TMT6-129	TMT6-130	TMT6-131
tmt1	C1	A1	B1	B2	A2	C2
tmt2	A3	B3	C4	A4	C3	B4
tmt3	B5	C6	A5	C5	B6	A6

Nano Reverse Phase Liquid Chromatography and Mass Spectrometry

To reduce the overall complexity of the TMT labeled samples, a 2D-LC fractionation was performed. In a first dimension, performed offline, samples were separated on an Acquity UPLC system (Waters) with an X-bridge BEH C18 LC column (130 Å, 5 μm particles, 4.6 mm × 150 mm). The column was operated at 40 °C and the following mobile phases were used: mobile phase A: 2% acetonitrile and 0.25% formic acid at pH 9 with H₅NO and mobile phase B: 98% acetonitrile, 0.25% formic acid at pH 9 with H₅NO. A linear gradient from 2% B to 60% B in 9.5 min followed by a steep increase to 90% B in 0.5 min at a flow rate of 1.5 ml/min was used to fractionate the samples in 10 fractions. Next, the peptide fractions were vacuum dried.

The peptide mixture was further separated by reversed phase chromatography on an Eksigent nano-UPLC system using a C18 trap column (Acclaim, PepMap100, 200 μm x 2 cm) coupled to an acclaim C18 analytical column (75 μm x 15 cm, 3 μm particle size) (Thermo Scientific). Before loading, the sample was dissolved in mobile phase A, containing 2% acetonitrile and 0.1% formic acid and spiked with 20 fmol Glu-1-fibrinopeptide B (Glu-fib, Protea Biosciences, Morgantown, WV). A linear gradient of mobile phase B (0.1% formic acid in 98% acetonitrile) in mobile phase A (0.1% formic acid in 2% acetonitrile) from 2% B to 35% B in 110 min followed by a steep increase to 95% mobile phase B in 2 min was used at a flow rate of 350 nl/min. The nano-LC was coupled online with the mass spectrometer using an PicoTip Emitter (New objective, Woburn, MA) coupled to a nanospray ion source (Thermo Scientific). The LTQ Orbitrap Velos (Thermo Scientific) was set up in a MS/MS mode where a full scan spectrum (350–5000 m/z, resolution 60,000) was followed by a maximum of five dual CID/HCD tandem mass spectra (100–2000 m/z) (8, 28). Peptide ions were selected for further interrogation by tandem MS as the five most intense peaks of a full scan mass spectrum. Collision induced dissociation (CID) scans were acquired in the linear ion trap of the mass spectrometer, High Energy collision activated dissociation (HCD) scans in the orbitrap, at a resolution of 7500. The normalized collision energy used was 35% in CID and 55% in HCD. We applied a dynamic exclusion list of 90 s for data dependent acquisition. The entire wet lab and LC-MS procedures were controlled for confounding factors, i.e. any experimental variable that can disturb the relation between the reporter ion intensities and the biological condition of the sample. Consider the hypothetical example, where the TMT-126 and TMT-127 labels are used for a particular condition in the three TMT LC-MS runs. If these labels would have a different fragmentation behavior opposed to the other TMT labels, then this would influence the reporter ion intensities. In this case there is a confounding factor and it would not be possible to relate the intensity effect to the biological condition or the label fragmentation.

Data Analysis

Proteome discoverer (1.3) software (Thermo Scientific) was used to perform database searching against the IPI Mouse 3.87 database using both SEQUEST and MASCOT algorithms, and following settings: precursor mass tolerance of 10 ppm, fragment mass tolerance of 0.5 Da. Trypsin was specified as digesting enzyme and 2 missed cleavages were allowed. Cysteine carbamidomethylation and TMT modifications (N terminus and lysine residues) were defined as fixed modifications and methionine oxidation and phosphorylation (SerThrTyr) were variable modifications. The results were filtered for confident peptide-to-spectrum matches (PSMs) based on a non-concatenated target-decoy approach. The decoy database is a reversed version of the target database. Only first ranked peptides with a global FDR smaller than 5% were included in the results. In the TMT quantification workflow, the most confident centroid method was used with an integration window of 20 ppm. The reporter ion intensities were corrected for isotope contamination by solving a system of linear equations and the known label purity values from the vendor's data sheet. The 10 raw data sets from the offline fractions were analyzed simultaneously in Proteome Discoverer. All sequences and reporter ion intensities of the PSMs that match the confidence requirements were exported to a comma-separated-values spreadsheet for further data-analysis. In-house software was used to normalize, match and merge the three TMT 2D-LC-MS experiments into one condensed data matrix that contains the reporter ion intensities of only the most confident PSM of a non-redundant peptide. A priority was given to the largest ion scores in MASCOT. The matrix was further augmented by peptides with confident and high scoring XCORR scores for SEQUEST. This processing step has led to a 4357 by 18 matrix composed of 18 quantification channels for the 4357 non-redundant and modified peptides. At the intersect, 971 non-redundant modified peptides were observed for all 18 quantification channels.

Statistical Rationale

The data originating from an n-plex isobaric labeling experiment can be represented in a rectangular data format. This format is an m by n data matrix A as presented in equation (1) that stores the information of the reporter ion intensities from a tandem mass spectrum. The columns of this matrix denote the n reporter ion quantification channels that correspond to the multiplexed samples, whereas the rows represent the m peptide identifications that are identified in the LC-MS experiment. More formally, each element a_ij in matrix A represents the intensity of the reporter ion of peptide i in quantification channel j.

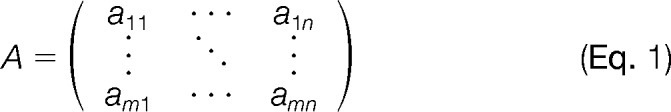with row indices, i = 1,2, … ,m and column indices j = 1,2, … ,n. In order to normalize the data such that the systematic effects are removed, a “new” matrix K needs to be sought for that deviates least from the original data in A while subjected to a set of two equality constraints that are imposed by the isobaric labeling experiment. This problem is known as an optimization problem and can be formally represented by the formula in equation (2).

In this notation the function f(x|A) is the loss function to be minimized over the parameters in x given matrix A. This loss function is composed of a distance metric that measures the similarity between the new matrix K and matrix A. In this optimization problem, the parameters x are row and column multipliers and the new matrix K is a linear transformation of matrix A with the parameters x. The two constrains to which the new matrix K is subjected are denoted by the function g(x|A) and can be inferred from insights about mass spectrometry and the wet-lab procedure. First, the information presented by the reporter ion intensities for a particular peptide is of a relative nature. Therefore, it is intuitive to rescale the reporter ion intensities of a peptide to a percentage contribution that reflects the relative proportion of the peptide quantities in the multiplexed sample. So the first constraint ensures that the normalized reporter ion can be interpreted as a percentage. Second, during the multiplexing of the samples into a pool, a lot of effort is spend to balance the samples such that the multiplexed sample is composed out of equimolar protein concentrations from the individual samples. Therefore, the second constraint ensures that the reporter ion intensities reflect equal protein concentrations and actually removes the systematic bias from the data because of pipetting errors, etc. Because the normalization method is framed as a constrained optimization problem, we term the method CONstrained STANDardization or CONSTANd. In case of a complete data matrix (positive values larger than zero), the constrains can be formulized as follows. The rows, i=1,2,…,m of the new matrix K are restricted to sum to one,

whereas the columns j=1,2,…,n of the new matrix K are required to sum to m × $\frac{1}{n}$,

where k_ij is an element of matrix K. We denote equations (3) and (4) as a scaling constraint and a normalization constraint, respectively. Recall that the restriction in equation (3) ensures that the normalized intensities for a particular peptide i from sample j can be interpreted as a percentage of abundance in the multiplexed sample. The restriction in equation (4) normalizes the distribution of the rescaled intensities such that each sample reflects an equal contribution in the multiplexed sample. Hence, equations (3) and (4) are proposed based on assumptions related to the physical conditions of the experiments. However, we can rewrite them in refined forms to reflect an elegant mathematical symmetry:

These are the final forms of our constraints. The notation K_ι. and K_.j denote the mean of row i and column j of the matrix K.

Several methods are available to solve the constrained optimization problem in equation (2), (5), and (6), like, e.g. linear programming, nonlinear interior point algorithms or via likelihood maximization. However, the symmetry in the constraints allows us to use a straightforward methodology that originates from the field of econometrics. More specifically, the RAS-method (29–33) or more general, the Iterative Proportional Fitting procedure (IPFP) (34, 35) is proposed to solve this type of constrained problem. This procedure is special in the context of the optimization problem described in equation (2), because we do not need to explicitly define a loss function, distance metric or data transformation. Ireland and Kullback (36), Bregman (37) and Bishop et al. (38) illustrate monotonic convergence of entropy, L1 and likelihood for the RAS procedure and we can already mention that our method is compatible with the IPFP theory.

The RAS procedure, also known as matrix raking in computer science, estimates two diagonal matrices R and S that represent the row multipliers and column multipliers. The diagonal matrix R has a size of m by m and the diagonal matrix S has size n by n. These diagonal matrices can be used to transform the original data matrix A by matrix multiplication into the new data matrix K that complies with the proposed constraints. Doing so, m + n degrees of freedom are at our dispose to optimally transform the original data. In matrix notation this becomes:

The algorithmic procedure is explained in more detail in Fig. 1. We follow the procedure as explained by Bacharach, Lahr and Mesnard, Robinson et al. (33, 39, 40). Note that after initialization the RAS procedure advances in pairs of an odd step 2t + 1 and an even step 2t + 2, for iterations t = 0, 1, …., until convergence is obtained at iteration T. The odd steps in the procedure rescale the data such that the matrix complies with the row constraints, i.e. a percentage. The even steps normalize the data matrix to satisfy the column constrains, i.e. the equibalanced sample content. Note that the upper right index in the notation is not a power but an indicator that tracks the steps in the RAS procedure.

Fig. 1.

A detailed outline of the RAS procedure as implemented in the CONSTANd algorithm. After initialization the algorithm iterates in two steps (an odd and even step) until convergence is reached.

Although the RAS procedure explained in Fig. 1 returns the constrained standardized data, the diagonals of the scale and normalization matrix to conduct the data transformation in equation (7) can be easily calculated as:

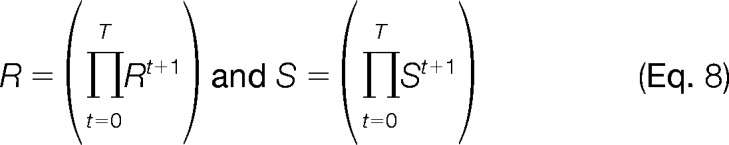Deming and Stephan recommend terminating iterations when the matrix reproduces itself (34). Closeness to row and column marginal or equivalently, goodness-of-fit can be measured by the L1-error as suggested by Friedrich Pukelsheim (41). Pukelsheim illustrates that among many other goodness-of-fit measures the L1-error is the most appropriate for the iterative proportional fitting procedure. To this end, the absolute deviation of the row and column means from the pre-specified marginal are computed in each step of the iteration. Because for odd steps, the rows are matched to their marginal, the row error sum vanishes from the L1-errors. Similarly, for even steps, the column error sum is zero and omitted from the calculation. Equation 9 represents the mathematical formulation of the L1-error for odd and even steps in the iteration.

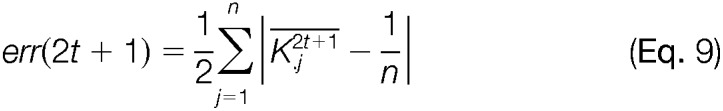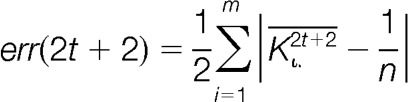We propose to halt the iterations when the L1-error is below the value of 1e-5 or when a maximum of 50 iterations is exceeded. The RAS alogrithm converges asymptotically toward the unique maximum likelihood estimator (MLE) (35, 36) in case of a strictly positive data matrix.

Recall that for a complete data matrix, the reporter intensities in a row are forced to sum to one. In the case of missing observations in the quantification channels, i.e. absence of a reporter ion intensity, the row marginal should account for this missingness as the sample content cannot be longer presented as 100%. Luckily, by presenting the row marginal as a row constraint that restricts the mean of the rows to 1/n, CONSTANd automatically anticipates for missing observations in one TMT LC-MS experiment. However, because of incomplete data we need to accommodate the interpretation of our mathematical operators used in the RAS procedure. In computer science, missing observations are very often denoted by not-a-number (nan) definition, zero values or just empty data cells in a spreadsheet. Therefore, we need to generalize our mathematical operators such that they can handle missing observations in the correct way. The most prominent change can be found in the interpretation of the mean operator in equation 5 and 6. To handle missing data, the mean is redefined as the mean of only the observed data, ignoring nan, zeros or empty data cells in the calculation. The implementation is straightforward and has clear interpretation in terms of the row and column marginals. For example, consider the row constraint in equation (10), when x reporter ions are missing from the data, then the constraint at the right-hand side of the equation remains 1/n. However, we only compute the mean value of the observed data as indicated in the left-hand side (n – x). Translating this new mean operator in terms of the row marginal results no longer in the reporter intensities to sum to one or 100%, instead they will sum to (n-x/n) as displayed in equation (10):

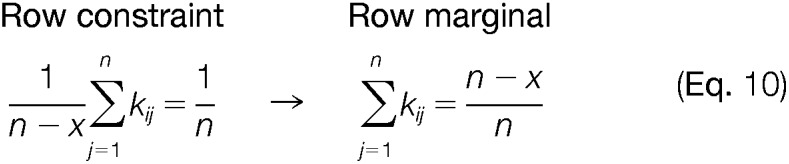In simpler wording, the above situation indicates that the row marginal in case of missing values should not be equal to one, but has to be proportional to the missingness. For example, when two reporter ion intensities are missing in a TMT-6plex then the row marginal should equal to the proportion 4/6th instead of 6/6th. By representing the row marginal as a mean constraint and the notion that the mean is computed from the observed values alone immediately takes care of incomplete data. A fortiori, we conject that the RAS estimates are unbiased under the missing at random (MAR) mechanism. Recall, that the iterative fitting procedure converges asymptotically to the maximum likelihood estimates and that our mean operator ignores missing observations. It is also known that maximum likelihood estimates are unbiased for the MAR mechanism (42), however in the context of the RAS algorithm such a proof is not trivial because we need to construct the observed-data likelihood and compare it with the overall likelihood function which requires integration over the missing values.

Study Set-up

In this study, 18 samples were subdivided in 3 sixplex experiments following a randomized block design controlled for confounding factors. These 18 samples are related to three experimental groups (A,B,C) of the same cell type but under three different physiological conditions. We did not include technical replicates of the samples, because based on previous analysis, we have learned that the technical variability in TMT experimentation is small [44]. This data set will be used to illustrate the capacity of the different, normalization algorithms to remove systematic effects from the data. In our analysis we will not perform a statistical analysis at the protein level, but rather focus on the peptide reporter ion intensities to avoid additional uncertainty from protein inference. The data comes from scientific experimentation in our laboratory and the ground-truth on protein abundance levels is unknown. No benchmark proteins were spiked-in with known ratio's. Therefore, we will quantify the normalization performance based on a correlation analysis at the peptide level as peptide intensities should correspond to the known physiological conditions. For this purpose, we will employ hierarchical clustering and a principal component analysis. When normalization is able to sufficiently remove the systematic effects because of the TMT cassette effect, this will be reflected in the correlation analysis as we expect that three groups corresponding to their biological conditions are found by the analysis. Because the focus of this manuscript is on bioinformatics methodology for data normalization, we make abstraction of the biological conditions in the samples. The biological interpretation of the results of the differential analysis is currently investigated and will be published elsewhere.

RESULTS

Performing differential proteomics experiments using isobaric labeling requires profound data-analysis. In this analysis work flow, data normalization forms a crucial step as it removes the systematic errors in the data prior to a statistical analysis. A normalization method can be deemed successful when the systemic biases from wet-lab procedures and other experimental artifacts are correctly removed from the data, while conserving the information that is related to the biological effects. The CONSTANd method employs constrained optimization to achieve this task in a most optimal manner. As a result, peptides from isobaric labeled data can be efficiently compared within and between a multiplexed experiment that are normalized by the CONSTANd method without the requirement of a reference sample similar in nature as Herbrich et al. (24). Latter property is especially useful when more than six or eight (TMT/iTRAQ) biological samples are required in a quantitative proteomics experiment to detect differential peptides with sufficient statistical power (44).

In order to illustrate the operational characteristics of the CONSTANd algorithm, we have applied this normalization method to a standard TMT sixplex quantitative experiment, where, 3 × 6 samples (representing 18 biologically independent samples from 3 experimental groups) are block randomized and measured in three sixplex TMT 2D-LC-MS experiments as explained in the section about experimental procedures. Fig. 2A graphically displays the intensity distribution of the 18 quantification channels before normalization by means of Tukey boxplots. The boxes in Fig. 2A should be aligned for the 18 quantification channels because the sample is multiplexed in equimolar protein concentrations, which ideally should lead to equal peptide intensity distributions. The deviations between the boxplots seem ignorable, but it is noticeable that the intensities are present on a logarithmic scale with decimal basis. Indeed, the small deviation does indicate a substantial bias in the experiment. This bias becomes more apparent when presenting the data in term of a percentage (i.e. sum to one), as can be seen from supplemental Fig. S1 in the supplementary material. Here the systematic error can be detected clearly as shifts (up or down) in the distribution of intensities in a reporter channel. CONSTANd normalization is applied on each TMT 6-plex experiment individually to remove the systematic shifts from the intensity distribution. Fig. 2B displays the outcome of the normalization procedure and here we observe that the intensity distributions are all aligned around a mean value of 1/6, or equivalently 16.67%.

Fig. 2.

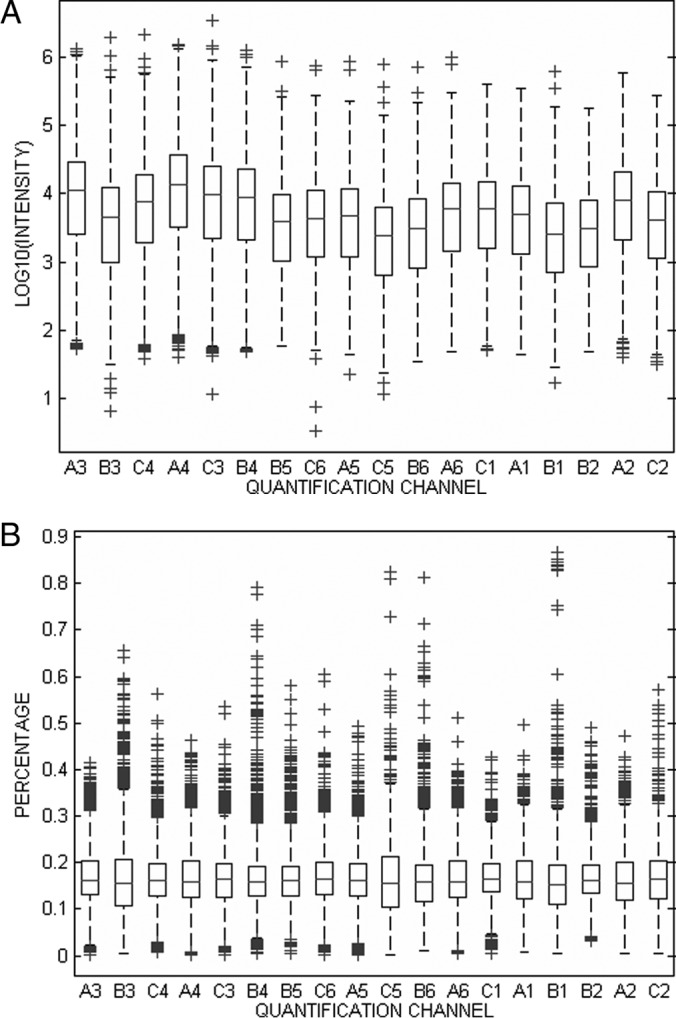
Tukey boxplot of the transformed reporter ion intensities in the 18 quantification channels. The six first boxplots come from experiment TMT2, the next six from TMT3, and the last six from TMT1. A, logarithmically transformed intensities before normalization. B, reporter ion intensities after CONSTANd normalization.

The convergence of the CONSTANd algorithm is fast and takes less than 10 micro-seconds on a Dell Latitude E6530 laptop using MATLAB version R2013a. supplemental Fig. S2A and S2B illustrate the convergence rate for the three TMT 2DLC-MS experiments in function of the consecutive steps in the iterations on the absolute and logarithmic scale of the L1-error. Note that convergence is exponential (log-linear) and that the stopping criteria (L1-error < 1e-5) is reached after 18 to 20 steps, or equivalently 9 to 10 iterations. As can be observed from the figures, convergence is monotone and unique in case of a strictly positive data matrix (35).

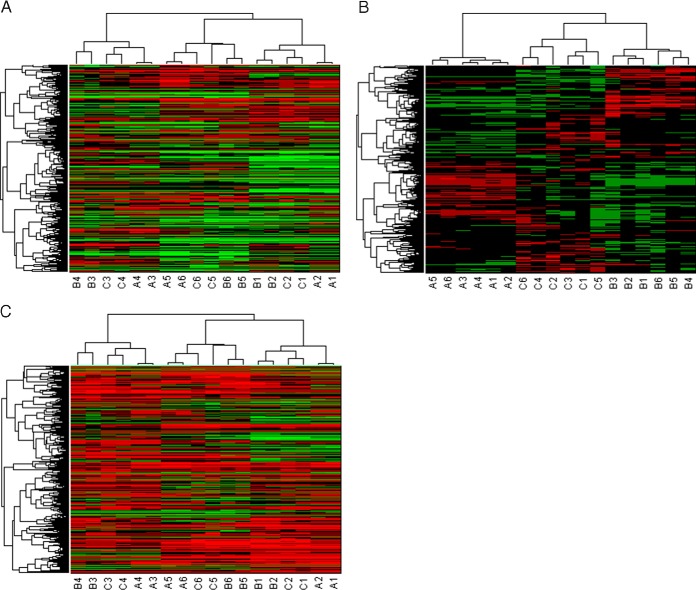
Many classical normalization techniques, already proposed for microarray data, are in use and available to align boxplots. However, these normalization methods, that aim to remediate the systematic biases, are often insufficient for data that is isobaric labeled, as they do not permit to fully correct for the systematic effects induced by sample handling and measurement protocols. To illustrate this favorable property, the CONSTANd algorithm is compared with the popular quantile normalization. Quantile normalization is a non-linear method based on rank statistics that makes the intensity distribution identical in terms of statistical properties (14, 45). Quantile normalization was applied to log₁₀-transformed reporter ion intensities of all three TMT experiments together resulting in 18 identical intensity distributions. The validity of our claims are assessed by a blind hierarchical clustering analysis with Spearman rank correlation as a distance measure and unweighted average distance linkage (46, 47) that should assemble the measured peptide intensities from three TMT sixplex experiments in the study according to their biological subclass. It should be noted that clustering is done on the subset of peptides that were identified and quantified together in the three six-plex experiments, i.e. on the 971 × 18 data matrix of non-redundant and modified peptides. In case of quantile normalized intensities, the clustering fails to group the subjects from the same physiological condition as can be observed from Fig. 3A. Instead, the clustering algorithm groups the subjects that were multiplexed in the same TMT 2D-LC-MS experiments. The grouping of subjects according to the same six-plex experiment illustrates that clustering is driven by the experimental artifacts still present in the data which obscures the biological information. As a consequence, a downstream statistical analysis will be less efficient because of the presence of these experimental artifacts; However, when studying the result of clustering in more detail, it can be noticed that the clustering does group subjects that are related to each other to some extent. For example, in Fig. 3A we observe that the samples of experimental group A, B, and C do form subtrees within the TMT 2D-LC-MS experiment. Hence, for comparing samples within one isobaric labeling experiment, quantile normalization seems sufficient.

Fig. 3.

Hierarchical clustering of the reporter ion intensities. The color code in the heatmap reflect the intensities where green represent the lower intensities and red the higher intensities. The columns of the heatmap are the 18 quantification channels and the rows indicate the 971 non-redundant and modified peptides. The rows and columns are permuted to correspond the clusters form the hierarchical clustering. The dendrogram visually represent the clusters that are found for the peptides (left) and the quantification channels (top). The clustering starts from a single root node and branches in subtrees up toward the leafs (18 leafs for the quantification channels and 971 leafs for the peptides). The distance in the dendrogram illustrates the Spearman correlation. Note that the in vitro (A) condition are stronger correlated than the in vivo conditions (B, C). A, Quantile normalization, the color code in on the log10-scale. B, CONSTANd normalization: the color code is a percentage. C, “Median sweep” normalization, the color code in on the log10-scale. Each quantification channel as a median value of zero.

Hierarchical clustering of the CONSTANd normalized intensities, on the other hand, assembles the data such that they respond to the biological subclasses (Fig. 3B). This correct grouping illustrates that systematic nuisances from the LC-MS measurements are correctly removed, while biological relevant information is maintained and, as a result, further statistical analysis can be performed on the peptide intensities.

Similar observations can be made when looking at the scoring plots from a principal component analysis in supplemental Fig. S3 in the Appendix for quantile supplemental Fig. S3A and CONSTANd supplemental Fig. S3B normalized reporter ion intensities. When the reporter intensities are not subjected to any normalization supplemental Fig. S4, much variability is observed in the scores of principal components. Quantile normalization reduces the variability severely, indicating the importance of normalization. However, the normalization only succeeds partly in its objective, as it only removes the intra-experimental variability, but fails to remove the variability between the TMT 2D-LC-MS experiments. In supplemental Fig. S3A, within an experimental cluster, the quantification channels that are related to each other (A, B, C) are grouped together in sub-clusters, again indicating that quantile normalization is a suitable technique for removing bias in a single multiplexed experiment (intra-experimental). On the other hand, CONSTANd normalization is able to reduce both intra- and inter-experimental variability such that the discriminatory power of the PCA analysis is driven by biology (discrimination of different physiological conditions).

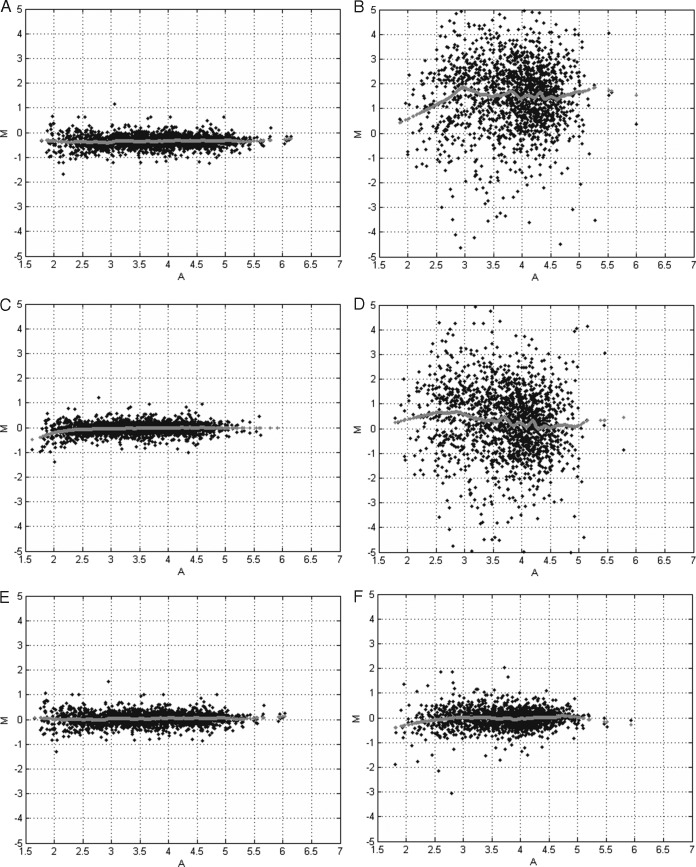
Because of the preferential properties of CONSTANd normalization, reporter ion intensities across different LC-MS experiments can be compared directly without the need of a reference sample. For example, Fig. 4A contains the MA-plot (48) of the unnormalized reporter ion intensities for quantification channel A3 and A4 that originate from the same TMT 2D-LC-MS experiment, i.e. intra-experimental comparison. The MA-plots illustrate the difference of the logarithmic-transformed intensity (y axis) versus the average logarithmic-transformed intensity for each peptide in the two quantification channels. The plot in Fig. 4A shows a clear bias as the data points are slightly off set from the horizontal zero line as indicated by the gray dots that are the result of a lowess smoother (49). Ideally, the data should show a symmetric scatter of points around the horizontal line at zero, which would suggest a simple additive measurement error with a constant variability and without a systematic bias. Both quantile and CONSTANd normalization are able to remove this bias correctly within a TMT LC-MS run, as can be observed from Fig. 4C and Fig. 4E, respectively. When comparing the A3 and A5 quantification channel before normalization between two TMT 2D-LC-MS experiments, i.e. inter-experimental comparison, we see a bias and an inflated variability that is present in Fig. 4B. Quantile normalization is able to remove this bias as it shifts the data cloud to the horizontal zero line as displayed in Fig. 4D by the gray dots. However, the variability in the data remains the same. The real advantage of CONSTANd normalization is its variance reducing properties, such that a statistical comparison of intensities between different LC-MS experiments becomes more efficient. The effect of the variance reduction is observable in the MA-plot in Fig. 4F.

Fig. 4.

Minus-Additive (MA) plots. The x axis displays the average value of the log-intensities between two quantification channels. The y axis depicts the log2-ratio of the intensities between two quantification channels. The gray dots represent the result of a lowess smoother and indicates the center of the data cloud in function of the average log10-transformed reporter ion intensities. A, intra-experimental without normalization (A3 versus A4). Note the bias and low amount of variability that is attributed to the multiplexing. B, inter-experimental without normalization (A3 versus A5). Note the bias and large variability because of experiment-to-experiment variation typical for LC-MS. C, intra-experimental with quantile normalization. The bias is correctly removed by the normalization. D, inter-experimental with quantile normalization. The bias removed, however, the variability is large and obscures further statistical analysis. E, intra-experimental with CONSTANd normalization. The bias is correctly removed by the normalization. F, inter-experimental with CONSTANd normalization. The bias and the experiment-to-experiment variability is correctly removed from the data such that a statistical comparison becomes meaningful.

A similar conclusion can be drawn when comparing the CONSTANd method with the 'median sweep' proposed by Herbrich et al. Latter method normalizes the data by shifting protein median based log10-transformed reporter intensities toward zero. To avoid additional uncertainty because of protein inference, the “median sweep” was applied directly at the peptide level on the three TMT LC-MS runs together. The results of the hierarchical clustering and principal component analysis are depicted in Fig. 3C and supplemental Fig. S3C, respectively. From the figures it is clear that the 'median sweep' normalization is not able to sufficiently remove the systematic effects present in the data as it groups the samples that were multiplexed in the same TMT LC-MS run rather that grouping the samples that belong to the same biological conditions as is the case for CONSTANd normalization.

DISCUSSION

Obtaining relative quantitative information in proteomics experiments can be done in different ways. Labeling numerous samples with different isobaric tags before multiplexing is a powerful technique to reduce the LC-MS time considerably. The strengths of isobaric labeling however, becomes apparent after a profound data-analysis. The boxplots of Fig. 2A, for example, demonstrate that, even when samples are very carefully processed, global biases are present. Usually, the source of the systematic shifts errors observed in the reporter intensities is technical and does not reflect any biological effect. Because of these inconsistencies, a normalization method is required to remove the systematic bias such that the biological information present in the data is not obscured by instrument artifacts. Applying a normalization procedure can eradicate systematic wet-lab errors like pipetting errors, etc., so that a meaningful comparison can be made. On the other hand, it should not be too crude such that biological effects are distorted. Several methods are available to normalize data, such as cyclic LOESS, quantile, and median normalization, etc (43, 50). However, when comparing isobaric labeled data from multiple experimental designs, these methods have their shortcomings or require reference samples in each experimental setup to allow for cross-set comparison (51). Two other publications from Hill et al. and Oberg et al., employ an ANOVA model for the analysis of multiple iTRAQ-based experiments (25, 26). The ANOVA model allows for almost unlimited complex designs where factors can be nested and samples can originate from longitudinal experiments. However, straightforward block randomized case-control experiments that do not include technical replicates do not require such sophisticated methods. In another manuscript, Herbrich et al. describes a framework to compare samples from multiple TMT LC-MS runs and perform a 'medium sweep' normalization prior to statistical analysis. A comparison with CONSTANd normalization illustrates that the 'medium sweep' normalization is not able to remove all the systematic error present in the data.

Therefore, we propose a new and easy to use normalization method, called CONSTANd, which allows accurate normalization of multiplexed, isobaric labeled samples in a data-driven and global manner. Latter terms indicate that all the observed data is used for the normalization procedure. Thus, CONSTANd does not require reference samples, which is a major advantage as reference samples suffer from two major disadvantages. First, reference samples are not of scientific interest and are only included to control technical flaws. Second, by dividing the intensity of reporter ions by a stochastic variable, i.e. the reference sample, you will inflate the variability (52). Also, reference protein sets, spiked-in standards or intermediate control runs are not required to infer the CONSTANd normalization factors.

Many data-driven normalization algorithms employ a measure of central tendency to correct for the global biases and to assure that the quantification channels all have the same central values after normalization by a global shift. The CONSTANd algorithm is also a data-driven normalization method and adopts the expected value (mean) as measure of the central tendency. This global normalization scheme is justified when three key assumptions are fulfilled (53). First, all normalization methods require a reference set of observations that do not vary between the samples. Because CONSTANd is a data-driven normalization algorithm, it will use the complete set of observed peptide quantifications as a reference. This choice is justified when the majority of proteins/peptides do not vary between samples as is the case in typical shotgun proteomics workflows. Because of data-dependent acquisition (DDA), there is a bias toward identifying and quantifying a large percentage of the more abundant house-keeping proteins. In most experimental settings, the expression levels of these house-keeping proteins remain unchanged and therefore the large set of “house-keeping” peptides ensures a robust estimation of the central tendency used in the CONSTANd method (54). Keep in mind that this assumption is crucial, therefore the global normalization does not work for pull-downs or other co-purification steps. When very different enrichment techniques or different PTM pathways are induced, variability is deliberately added to the experiments, i.e. different protocols. For this type of experimentation normalization is best performed by algorithms that are not data-driven but employ spiked-in standards and controls [42] Second because CONSTANd is based on a central tendency, the number of up-regulated proteins/peptides should roughly equal the number of down-regulated proteins/peptides to avoid a bias in the estimate of the mean value. Third, the systematic bias should be proportional with the intensity or equivalently, constant on the logarithmic scale which suggest that the measurement error is additive and can be remediated by one normalization factor per quantification channel to reposition the intensity distribution. Under these three assumptions the constrained mean normalization as applied in CONSTANd is justified. Moreover, CONSTANd uses the mean as a measure for the central tendency. An intensive simulation study has indicated that CONSTANd is able to operate on median and mode as well (data not shown), however these metrics should be used cautiously as no proofs are available that the RAS procedure is compatible with these non-linear statistics.

With CONSTANd, quantified peptides can be interpreted as proportions or equivalently, percentages (i.e. 1/6^th of the multiplexed sample in case of a TMT six-plex) because of the applied constraints. By presenting the reporter ion intensities as a percentage, the heterogeneity caused by peptide-specific ionization efficiencies is taken out of the measurements, i.e. the analysis is performed conditional on the peptide level. This effect can be easily observed when comparing Fig. 2A with supplemental Fig. S1 from the appendix. Fig. 2A displays the intensity distribution on the logarithmic scale, whereas supplemental Fig. S1 presents the data as a percentage before normalization. The systematic shifts (all intensities up or down in the same directions) are more pronounced in the percentage presentation of the intensities. This effect is because of the large variability on the log-intensity distributions extending almost one order of magnitude. When presenting the reporting intensities as a percentage, the variance in the reporter ion channels is reduced so that the shifts become more visible. A convenient artifact of this percentage representation is that a downstream statistical analysis can directly compare/quantify a protein by their relative peptide contributions. At least, after the bias is removed by the CONSTANd algorithm (Fig. 2B). In this sense, the CONSTANd method can be perceived as a simple preprocessing step prior to data visualization or analysis with machine learning techniques that do not have built-in normalization capabilities based on likelihood procedures (25, 26). Furthermore, as a data preprocessing step, CONSTANd is compatible with ANOVA models and linear mixed models in the case more complexity is needed.

Another practical advantage of the CONSTANd method is that when comparing multiple isobaric labeling experiments, the normalization is performed for each experiment independently, in contrast to other normalization methods that require to operate at the complete data structure after collecting all the data. Because CONSTANd does not require reference samples to allow for cross-set comparison, the full multiplexing capacity of the isobaric labels can be used. Furthermore, the diagonal elements of matrix R and S that are returned by CONSTANd have a clear interpretation. The elements of matrix S can be regarded as the normalization parameters that can be used as a measure to indicate the bias present in the quantification channel. In an ideal experiment, for equally balanced protein concentrations, this value should be equal to one. The elements in matrix R can be interpreted as the overall peptide intensity and therefore should correlate well with the precursor ion intensities. This row multiplier can be used to transform the CONSTANd normalized percentages into intensities, for example, to present the data in MA-plots.

The variance-reducing capabilities truly make CONSTANd a favorable tool when data from multiple experiments needs to be combined. This characteristic is noticeable when comparing Fig. 4B with 4F. The inflated variability in the data in Fig. 4B finds its origin in the experiment-to-experiment variability that is typical for LC-MS measurements, and immediately please for multiplexing samples such that this variability does not influence the data as indicated by the low variability in Fig. 4A. By implementing CONSTANd in the data analysis workflow, not only the bias within a multiplexed experiment is removed, but also the bias and variance between the quantification channels of multiple isobaric experiments is removed from the data without affecting the biological information facilitating an optimal comparison. This characteristic makes it different from other normalization approaches, because now multiple multiplexed experiments can be safely combined to increase the statistical power of the experiment. Furthermore, CONSTANd is compatible with data that originates from the multiNotch MS3 approach to avoid ratio compression described by McAlister (55).