Abstract
Inspired by RecA-protein-based homology recognition, we consider the pairing of two long linear arrays of binding sites. We propose a fully reversible, physically realizable biased random walk model for rapid and accurate self-assembly due to the spontaneous pairing of matching binding sites, where the statistics of the searched sample are included. In the model, there are two bound conformations, and the free energy for each conformation is a weakly nonlinear function of the number of contiguous matched bound sites.
I. INTRODUCTION
A. Background and significance of self-assembly
Much study has been devoted to understanding RecA-based homology recognition [1–3], which plays an important role in DNA recombination and repair [4,5]. Homology recognition is an important example of self-assembly due to the spontaneous free energy decrease that occurs when binding sites correctly pair. RecA-based homology recognition and strand exchange provide a good model for the theoretical study of self-assembly for several reasons: (1) The binding sites can be categorized by their position along a linear array; (2) the ssDNA sequence is not known in advance, so steric features in the dsDNA must not play a crucial role in the search; (3) the binding energies are not time dependent; (4) homology recognition distinguishes mismatches using the Watson-Crick pairing energy of an individual base pair (bp) which is of the order of the thermal energy, so such binding energies are readily available in both natural and artificial self-assembly systems; (5) the search is known to be rapid and accurate even in the absence of an irreversible process [6,7], so such a self-assembly strategy should be possible in artificial systems that cannot exploit hydrolysis [9].
In this work, we study an idealized reversible self-assembly system inspired by RecA-mediated homology recognition and demonstrate that the system can offer rapid and accurate self-assembly of long linear arrays of binding sites without requiring time dependent binding energies by combining a weak nonlinearity in the free energy as a function of the number of bound sites with the statistics of a finite sample characteristic of a bacterial genome. In contrast, if only one of the effects is present, self-assembly can be either rapid or accurate, but not both.
B. The speed stability problem for the case of long linear arrays
In effective self-assembly, a searching molecule must find a homologous molecule (homolog) and correctly and stably bind to it as rapidly as possible, where the timing constraint is set by the requirements of the function of the binding. The total search time must include time spent unbound as well as time spent bound in incorrect pairings. Incorrect pairings include binding to mismatched molecules as well as binding to homologous molecules when the binding sites are out of register. For simplicity, we refer to any incorrect binding as binding to a heterolog and assume that a given particular single molecule is searching for the single homolog in a search pool with N distinct possible pairings. If rH is the probability of remaining bound to a homolog once initial binding has occurred, then on average each site must be revisited ~1/rH times during a search. Thus, the mean total time required to bind stably to the homolog is given by
| (1) |
Here N ⟨tunbound⟩ is the average total time per search cycle that the ssDNA-RecA filament is not bound to any dsDNA and N ⟨thet⟩ and ⟨thom⟩ are the total mean times per search cycle spent bound to heterologs and the homolog, respectively.
In what follows we neglect the contribution due to thom. For the perfect homolog, the bias in the random walk causes the average number bound to increase linearly with time, whereas the standard deviation from the average increases as the square root of time. Thus—as we have confirmed computationally—when homologs do unbind, they unbind when very few triplets are bound, so the unbinding times are rapid. In addition, the time penalty associated with searching the whole genome again due to the unbinding from the true homolog results in a much larger time penalty than the penalty associated with thom. Finally, the mean time required for a homolog to complete strand exchange is very brief compared to the unbinding time of the nearest heterolog, so the total time required to complete the homology recognition/strand exchange process is completely dominated by the search time.
The search may be parallelized and is parallelized for RecA [10]; however, sparse parallel searching simply decreases the total time by a linear factor, so it will not change the overall scaling of the result. Thus, in this work we consider searching where only one single contact region between searchers is allowed.
A well known problem with self-assembly is described by the speed stability paradox (SSP). The paradox suggests that self-assembly cannot be both rapid and accurate if the sample being searched contains targets with nearly the same binding energy as the perfectly matched target [11–14]. The protein transcription factor search for targets on DNA is one example of such a self-assembly problem [11,12]. In this work, we present a particularly simple version of the SSP that arises in the self-assembly of two linear arrays of nlength binding sites with a binding energy of −ϵ per matched bound site. Stable and reliable binding of homologs requires a large Boltzmann factor for the bound system, i.e.,
or equivalently
| (2) |
where k is Boltzmann’s constant and T is the temperature. A heterolog with a single mismatched site will have a binding energy of ≈ −(nlength − 1)ϵ. Accurate recognition requires that this nonhomolog must be much less deeply bound than the homolog. Expressed as a Boltzmann ratio, this condition requires
and therefore
| (3) |
However, reliable and rapid unbinding from this near homolog will require that
and thus
| (4) |
It becomes clear that a binding energy linear in the number of bound sites cannot satisfy all these requirements if nlength ≳ 2; however, if nlength = 1, the condition is easily met.
The discussion above only compared the unbinding time for a homolog and a particular near homolog. The total average search time must include all of the heterologs present in the sample, so
| (5) |
where i is an index that labels each class of heterologs, thet,i is the average unbinding time from one such heterolog, and prob(i) is the probability of initially binding to that heterolog. This probability is simply proportional to the fraction of the total sample occupied by that class of heterolog if the initial binding rate is sequence independent, as we assume here.
Consistent with results of previous work [11,12], Eq. (5) shows that thet depends not only on the unbinding time for each particular category of heterolog, it also depends on how prevalent each category is in the sample. In this work, we consider self-assembly modeled on the homology recognition/strand exchange process in bacteria. Bacterial genomes contain <107 bp. We have examined some sequences and determined that with a high degree of accuracy they behave like random sequences with respect to autocorrelation in the sequences [15]. These two properties of bacterial genomes play an important role in resolving the SSP, as we discuss in detail below.
C. Energy nonlinearities provide SSP solutions for the pairing of long linear arrays
From the above analysis, if the binding energy, U(i), is a linear function of i, the number of matched binding sites, then self-assembly of two long linear arrays of length nlength cannot be both rapid and accurate if the sample contains a heterolog with nlength − 1 matching sites. In contrast, if U(i) is a nonlinear function of i, such that −U(nlength)/(kT) ⪢ 1, while U(i)/(kT) = 0 ∀ i < nlenghth then rapid perfect recognition is possible; however, such a nonlinear energy is not physically realizable unless the system exhibits extremely strong collectivity [16].
RecA exploits a nonlinearity in the energy as a function of the number of bound sites; however, in contrast with the nonlinearity mentioned in the previous paragraph, the nonlinearity in the RecA system makes binding increasingly unfavorable as more triplets are bound. The nonlinearity arises from the mechanical tension in the dsDNA bound to ssDNA-RecA filaments, as we discuss in the Supplemental Material [17].
D. Limited samples provide SSP solutions for the pairing of long linear arrays
Earlier work has shown that rapid and accurate searching can be achieved for a linear U(i) if there is a large energy difference between the perfect match and the nearest mismatch present in the sample [11,12]. Consistent with that result, even if U(i) is a linear function of i, rapid and accurate searching is possible in a sample where nlengthϵ/(kT) ⪢ 1, but the number of accidentally matching binding sites with any heterolog in the sample is m ⪡ nlength, such that mϵ ⪡ kT. Unfortunately, this strategy is not available to RecA because it must make homology decisions over 15 bp lengths in a sample containing heterologs with accidental matches that can extend beyond 12 bp.
II. RecA AND THE BIASED RANDOM WALK
The simple biased random walk model of homology recognition presented in this work was inspired by properties of the RecA-based homology recognition/strand exchange process. The structure of the dsDNA [18] combined with recent experimental results [19] suggests that strand exchange is carried out in units of base triplets. In the Supplemental Material [17], we present a detailed discussion of how the dsDNA tension resulting from dsDNA binding to ssDNARecA filaments creates free energy nonlinearities.
Experiments have shown that in the RecA system, the initial sequence independent binding is limited to approximately 9 contiguous bp [20]. The binding of the dsDNA to the ssDNA-RecA filament is highly unstable unless ~9 contiguous homologous bp make the transition to the sequence dependent intermediate strand exchanged conformation [20,21]. Transitions from the sequence independent initial state to the sequence dependent intermediate state are made by base flipping that transfers the Watson-Crick pairing of the bases in the complementary strand from the outgoing strand to the incoming strand, as discussed in detail in the Supplemental Material [17]. Once ~9 contiguous homologous bp make the transition to the the intermediate conformation the binding may become sufficiently stable to allow strand exchange to progress to contiguous triplets [20]. In RecA, the vast majority of initial pairings are rejected before this stage because they do not contain ~9 contiguous homologous bp, but accurate and efficient homology recognition requires rapid and accurate resolution of the rare cases as well. Simulations using other models suggested kinetic trapping in such regions may be problematic [22].
A. Incorporating the nonlinearity in the free energy of dsDNA bound to RecA filaments into the BRW model
The nonlinearity in the free energy of dsDNA bound to ssDNA-RecA filaments has several important functional consequences, but for the purposes of this paper the two major consequences are the following. (1) The minimum initial number of triplets in the strand exchanged intermediate conformation is three, approximately. (2) Triplets can only make transitions between the sequence independent initial conformation and the sequence dependent intermediate conformation if one neighboring triplet is in the sequence dependent intermediate state and the other neighboring triplet is in the initial sequence independent bound state. We also assume that for those triplets that can base flip, the base flipping rate is sufficiently rapid that the population distribution between the initial and intermediate states is at equilibrium. These three conditions allow the kinetics of strand exchange to be modeled as a biased random walk with an initial offset, where the forward progression of strand exchange is more probable for homologous triplets than nonhomologous triplets. Such a system can overcome the SSP if the search is done on a sample with the characteristics of a bacterial genome, as we demonstrate below.
In true RecA-based homology recognition, the energy nonlinearity plays several additional important roles. We consider some of these additional features after we have considered the basic random walk model; however, the goal of this paper is to present a simple minimal system that can overcome the SSP, rather than to model the actual RecA recognition system in detail.
B. Random walk model inspired by RecA
Features of RecA-based homology recognition motivated us to consider a simplified model of process that adds contiguous triplets to the ssDNA-RecA filament after ~3 contiguous homologous triplets all occupy the sequence dependent intermediate state. The model is based on a biased random walk (BRW), as illustrated in Fig. 1. In the random walk model, we simplify the RecA system to an effective two conformation system where each binding site consists of base triplets which make transitions as a unit. In the simplified two conformation system, all of the sequence independent conformations will be considered as one single sequence independent conformation and all of the sequence dependent conformations will be included in the other conformation. In the model, we parametrize the number of binding sites that are initially in the sequence dependent conformation as ninitial,BRW. We assume that they occupy positions i = 1 to i = ninitial,BRW in the array. Similarly, nstep,BRW corresponds to the number of triplets in the sequence dependent conformation at any given time. As a consequence of the energy nonlinearity those triplets occupy positions 1 to i = nstep,BRW in the array.
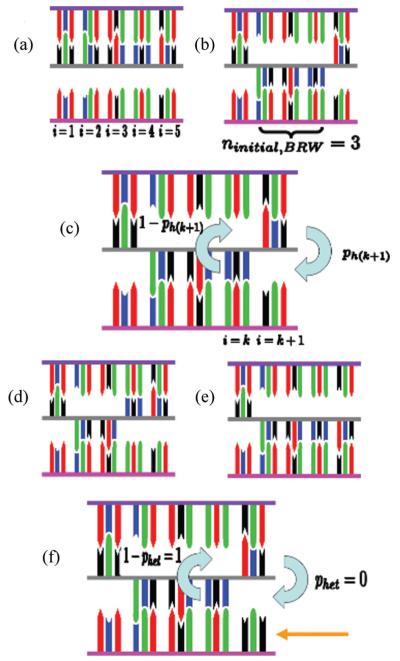
FIG. 1.
(Color) Schematic of the random walk. (a) Initial searching filament and dsDNA bound to the ssDNA-RecA filament in the initial sequence independent state. Outgoing, complementary, and incoming strand backbones are shown in purple, gray, and pink, respectively. Individual bp are shown as green, red, black, and blue rectangles. All of the bp in the dsDNA composed of the outgoing and complementary strands are correctly paired. The bases in the incoming ssDNA are completely unpaired. (b) Initial distribution in the metastable poststrand exchange state after the first checkpoint is passed. (c) Transition probabilities for a homolog for increasing (p) or decreasing (1 − p) the number of triplets in the metastable poststrand exchanged state. The subscript function h(i + 1) is used to emphasize that p is a function of the sequence matching of the (i + 1)th triplet. If the (i + 1)th triplet is homologous, ph(i + 1) = phom; otherwise ph(i + 1) = phet. (d) State distribution after reverse strand exchange of one triplet which changes nbound from 3 to 2. (e) State distribution after an additional triplet is strand exchanged which changes nbound from 3 to 4. (f) Transition probabilities when the neighboring unbound triplet is a nonhomolog, where the orange arrow indicates the nonhomolog.
In the model, the probability p of “moving forward” in the BRW is given by the probability of strand exchanging an additional contiguous triplet since strand exchange transfers bp from the sequence independent conformation to the sequence dependent conformation. Due to the energy nonlinearity, when nstep,BRW triplets are in the strand exchanged state, only the (nstep,BRW + 1)th triplet can undergo strand exchange. As illustrated in Fig. 1, if that triplet undergoes strand exchange, nstep,BRW increases by 1, which corresponds to a step forward in the BRW. Similarly, as a result of the energy nonlinearity, only the triplet with i = nstep,BRW can undergo reverse strand exchange. Reversing strand exchange decreases nstep,BRW by 1, which corresponds to “moving backward” one step in the BRW, as illustrated in Fig. 1. In the model, reverse strand exchange occurs with a probability 1 − p. In sum, when i triplets are bound, either the (i + 1)th triplet must undergo strand exchange or the ith triplet must undergo reverse strand exchange. No other triplet is allowed to change state.
We assume that ph(i + 1), the probability of strand exchanging the (i + 1)th triplet, is dependent on whether the (i + 1)th triplet is homologous. We describe that dependence using the function h(i + 1) such that h(i + 1) = hom if the (i + 1)th triplet is homologous and and h(i + 1) = het if the (i + 1)th triplet is not homologous. Thus, once i triplets have been strand exchanged, if the (i + 1)th triplet is homologous, then the probability that the (i + 1)th triplet will undergo strand exchange is given by ph(i + 1) = phom. Similarly, if the (i + 1)th triplet is not homologous, ph(i + 1) = phet.
In ssDNA-ssDNA pairing, both strands are initially unpaired, so the binding of correct matches is always favorable by >kT [23] and the binding of incorrect matches is approximately neutral. In contrast, in the RecA system the dsDNA begins perfectly correctly paired. Strand exchange transfers the pairing of the complementary strand base triplets from the outgoing strand to the incoming strand, as illustrated in Fig. 1. This poststrand exchange pairing will either be sequence matched, like the initial pairing, or sequence mismatched. If the DNA was not attached to a RecA filament, then strand exchange would be free energetically neutral for sequence matched triplets and free energetically unfavorable for mismatched triplets. For mismatched triplets, the free energy penalty would be approximately equal to the loss of correct Watson-Crick pairing, which is ~2kT [23]. When dsDNA is attached to a RecA filament, the dsDNA is highly extended. As a result, the strand exchange of a correctly matched triplet is actually slightly free energetically favorable if at least one neighboring triplet is already strand exchanged, because strand exchange changes the rise between the neighboring triplets closer to the equilibrium spacing [24].
Given that in the BRW we consider only the evolution after ninitial,BRW triplets have undergone strand exchange, the strand exchange of an additional contiguous homologous triplet is just barely free energetically favorable (~0.2kT ), and the strand exchange of an additional triplet containing a mismatched base is free energetically unfavorable by between ~1kT and ~4kT per mismatched base [23]. These free energy changes associated with strand exchange are qualitatively and quantitatively very different from those for ssDNA-ssDNA pairing, and they play an important role in allowing RecA-based self-assembly to be both rapid and accurate.
Unless noted otherwise, we in this work measure time in terms of the BRW time step. Given that we are considering a time scale for the BRW step for which the base flipping of the bound triplets is in equilibrium, if ΔE is the free energy difference associated with the strand exchange of a given triplet, then the probability of strand exchange is p ∝ exp[~ ΔE/(kT)]. Similarly, reverse strand exchange will occur with probability (1 ~ p) ∝ exp[ΔE/(kT )]. Assuming that only these two events can occur, we can write
| (6) |
Thus, if the free energy decrease due to strand exchange is approximately 0.2kT, then p ≈ 0.6. We note that reverse strand exchange does not immediately result in the unbinding of the dsDNA triplet from the ssDNA-RecA filament since reverse strand exchange leaves the dsDNA in the initial sequence independent bound state.
In summary, in the simplest model, we assume the following. (1) After the initial strand exchange of ninitial,BRW triplets occupies sites i = 1 to i = ninitial,BRW, additional triplets can only strand exchange if one of their neighbors is in the strand exchanged conformation. (2) Reverse strand exchange can only occur for triplets with exactly one strand exchanged neighbor. (3) The values of phet and phom are independent of the number of bound triplets, but when nstep,BRW triplets are bound, the probability of strand exchange is given by ph(nstep,BRW + 1), which is equal to phom if the (nstep,BRW + 1)th triplet is homologous and phet if the (nstep,BRW + 1)th triplet is not homologous. (4) phet = 0 and phom > 1/2. However, we later loosen the constraints on phet.
Thus, in the simplest form the model has five parameters that determine nstep,BRW as a function of time: ninitial,BRW, phom, phet, m, and N. The first three parameters are determined by the properties of the interactions between binding site arrays, whereas m and N are properties of the sample. When we consider self-assembly based on homology recognition, we focus on the case where m and N have the properties determined by bacterial genomes. We seek to minimize the total search time, which Eq. (1) shows is dependent on tunbound, thet, and rH. tunbound is an independent parameter, but thet and rH are determined by ninitial,BRW, phom, phet, m, and N. The value of tunbound will determine the values of ninitial,BRW and phom that optimize recognition for a particular sample.
C. Statistical properties of the sample
Given the assumption that the sequences are random, and knowing that the search proceeds in units of bp triplets, we may extract some basic scalings due to the statistics of the search pool characteristic of homology searching in a bacterial genome. The ssDNA in the ssDNA-RecA filament has a length that is shorter than nlength, the total length of the genome, but it is also longer than the ≈30 triplets required to establish the strand exchange window [8]. As discussed above, we assume that the searching ssDNA-RecA binds to a single position in dsDNA of the bacterial genome being searched and that homology recognition proceeds by adding or subtracting contiguous triplets. The time required to unbind a mismatched pairing depends on m, the number of contiguous accidentally homologous triplets that bind to the ssDNA-RecA filament before a nonhomologous triplets is encountered. Thus, in order to evaluate the total time spent bound unstably to heterologs, we need to determine how many contiguous regions of accidental homology extend to exactly m, where the (m + 1)th triplet is nonhomologous.
For a sequence of length nlength triplets paired with a random second sequence of length m triplets, there are two possibilities, either the m triplets are at the end or they are separated from the end by at least one triplet. For m > nlength there are two possible bindings in which the m triplets are located at the end. The probability that the m triplets match is 1/64m and the probability that the next triplet is nonhomologous is 63/64. Since there are two such possible binding positions, the total probability of encountering m contiguous triplets by binding to an end of the ssDNA-RecA filament is 2(1/64m)(63/64). All other possible bindings that contain m contiguous homologous triplets require that those triplets be flanked on both sides by nonhomologous triplets. For any particular group of m + 2 contiguous triplets, the probability that the “inner” m triplets (i.e., all triplets except for those at the ends of the group) of that group are sequence matched to the inner m triplets of a given m + 2 triplet sequence in the searching ssDNA is (1/64m)(63/64)2. The total number of possible initial bindings that can compare sequence regions of length m + 2 is nlength − m − 1. Thus, the average number of accidental matches with exactly m contiguous triplets is given by
| (7) |
Since commitment to strand exchange is made over sequence regions with length of less than 10 triplets and bacterial genomes have lengths of ~107 triplets, m ⪡ nlength. Thus, the central feature of this equation is the scaling of ⟨naccidental⟩ with m: ⟨naccidental(nlength,m)⟩ ~ . This scaling limits the length of regions of accidental homology. For bacterial genomes nlength ≈ 107. If a particular sequence of three contiguous triplets is randomly paired with another sequence of three contiguous triplets in a bacterial genome, <50 pairings will accidentally match. Similarly, the average number of accidental mismatches containing five contiguous triplets is 0.01 ⪡ 1. Thus, for most bacterial genomes if a five contiguous triplet match is found, the entire sequence is correctly matched. There is no benefit in comparing any more bases; they will all be homologous. Therefore, in vivo RecA must distinguish single bp mismatches that occur within contiguous groups of 15 bp, but it need not distinguish a single mismatch in a group of 30, 60, or 100 bp since such a sequence does not exist within the genome. In contrast, in vitro tests of RecA-mediated homology recognition have included sequences that have much greater sequence matching than in vivo samples [25]. Unsurprisingly, RecA-based recognition in such samples was poor [25]. Furthermore, the rarity of sequences with accidental matches extending over four triplets allows total rapid search times even if the binding energy for such accidental mismatches is sufficiently deep that the binding to such rare mismatches is fairly stable, as we discuss in detail below.
III. RESULTS
A. Basic properties of the biased random walk with phet = 0
We now present some basic features of the BRW to develop further intuition and understanding of the searching system, before we proceed to a detailed discussion of the results. The strand exchange of homologous triplets becomes increasingly favorable as phom approaches 1, while the reverse strand exchange of regions of accidental homology proceeds more rapidly as phom approaches 0. As discussed in detail after Eq. (1), we neglect the time spent unstably bound to the homolog.
Thus, Eq. (1) shows that optimizing the total search time ttot will require optimizing phom to balance the rapid unbinding of heterologs against the number of searches required in order for the homolog to achieve stable binding. In the following, we sometimes write just p instead of phom, for brevity.
By using recurrence relations of the RW in the limit of very long arrays, one can derive the following exact expression for rH,BRW as a function of ninitial,BRW. The strategy uses Pbound(k), the probability that a homolog will remain bound to the the filament if k triplets are initially strand exchanged. If the random walk starts with k strand exchanged triplets, then from the rules of the BRW after the next step the number of strand exchanged triplets will be either k + 1 or k − 1, corresponding to a forward step and a backward step, respectively. Furthermore, the steps occur with probabilities p and 1 − p, respectively. Thus, if the first step is backward, then the probability of remaining bound after the first step is just Pbound(k − 1). Similarly, if the first step is forward the probability of remaining bound is Pbound(k + 1). These are the only two possible steps from the initial condition where k triplets were bound. The probability that the system will take a step forward and remain bound is just the product of p, the probability of taking a forward step, and Pbound(k + 1), the probability of remaining bound if k + 1 triplets are initially bound. Similarly, the probability that the system will take a step backward and remain bound is just the product of (1 − p), the probability of taking a backward step, and Pbound(k + 1), the probability of remaining bound if k + 1 triplets are initially bound. Thus, Pbound(k) must be equal to the sum of the probability of remaining bound if the first step is forward and the probability of remaining bound if the first step is backward, or
| (8) |
It is convenient to reexpress this equation in the form
| (9) |
which yields the characteristic equation
| (10) |
The roots of the characteristic equation are
| (11) |
| (12) |
Thus,
| (13) |
| (14) |
The values of the coefficients can be determined from the boundary conditions Pbound(0) = 0 and Pbound(m) → 1 as m → ∞, which give
| (15) |
In terms of the random walk variables this equation becomes
| (16) |
This suggests that ninitial,BRW > 1 can play a vital role in stabilizing homologs, as is shown in Fig. 2. In the figure, the predictions of Eq. (16) are in good agreement with results obtained using a Markov chain transition matrix treatment in the asymptotic limit as time approaches infinity with absorbing boundaries imposed at nstep,BRW = 0 and nstep,BRW = 30, except for values of p very close to 1/2. The differences at those low p arise because the spread in the random walk can reach the absorbing boundary. The figure shows that for all choices of ninitial,BRW there is a rapid decrease in search time with increasing p for 0.5 < p < 0.55; however, for ninitial,BRW > 2, when p ≈ 0.6, 1/rH,BRW is already near its asymptotic value, which is insensitive to ninitial,BRW, so increasing p above 0.6 or nBRWintial above 3 makes no significant improvement to rH,BRW. This feature is important since the low p values promote the rapid unbinding of long regions of accidental homology. For ninitial,BRW = 1, p continues to reduce 1/rH,BRW until p ~ 0.8, which corresponds to a reduction in free energy of 0.7kT per strand exchanged triplet.
FIG. 2.
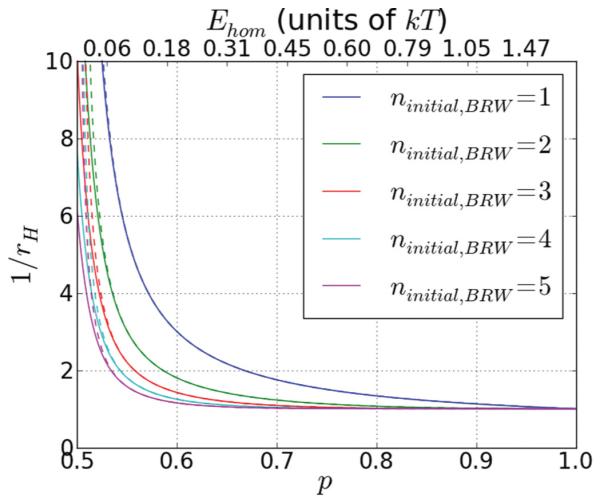
(Color online) The homolog binding rate. We show as a function of p for various values of ninitial,BRW. The lines from top to bottom are for ninitial,BRW = 1 through 5, respectively. The dashed lines show the analytically calculated values in the limit of very long strands, while the solid lines show the values obtained using a Markov chain method with absorbing boundary conditions at nstep,BRW = 0 and nstep,BRW = 30. Note that the bounded case is already in very good agreement with the limiting behavior. For ninitial,BRW > 1, we find a significant significant decrease in (and a significant increase in rH) as p goes from 0.5 to ~0.65, which corresponds to a moderate value of Ehom ~ 0.31kT. After that, only little is gained by further increasing p. For ninitial,BRW = 1 however, the asymptotic value of is only reached as p ≈ 0.8, or Ehom ~ 0.69kT.
B. The biased random walk search time is dominated by the heterologs with the least number of accidental matches
Given that the total search time depends not only on rH, but also on thet, it is important to consider the effects of phom and ninitial,BRW on thet for the rare heterologs that undergo a random walk in the intermediate strand exchanged conformation. The remainder of the initial pairings unbind directly from the initial conformation without undergoing a random walk in the intermediate conformation, and we consider those interactions in a subsequent section.
The average contribution of the BRW to the total heterolog unbinding time is given by
| (17) |
Here, tunbind,BRW(ninitial,BRW,m,p) is the average time spent unbinding from a heterolog after the dsDNA makes a transition to the stable intermediate conformation, where the first mismatch occurs at position m + 1, after m accidental matches. In addition, , as shown in Eq. (7). Crucially, the factor of appears because each contribution to the sum is weighted by the probability of actually encountering m accidental matches. For a bacterial genome with a random sequence of length ~107, Eq. (7) shows that, probabilistically, the maximum number of accidental matches before a mismatch is constrained such that mmax < 7.
For the case of an infinite boundary, if p < 1 the unbinding probability is always 1 since the system will eventually reverse given that it cannot go forward past the reflecting boundary located at the position of the heterolog. Thus, instead of calculating the unbinding probability, it is useful to calculate t(ninitial,BRW,m), the average number of random walk steps required to unbind, as a function of ninitial,BRW and m. Again we generate a recurrence relation, but this time it is a relationship between the unbinding times. In general, if k is the number of triplets in the strand exchanged state, then at the next random walk step the number bound will be either k − 1 or k + 1. Either choice requires one time step, so the number of unbinding steps nunbind(k) must be related to the values for nunbind(k + 1) and nunbind(k − 1) as follows:
| (18) |
With the recurrence relations previously used for Eq. (16), one arrives at a general recurrence relation which can be solved given boundary conditions. The condition nunbind(0) = 0 holds for all values of m. However, the boundary condition for large k changes because of the infinite energy barrier at the position of the heterolog (which in the BRW is represented as p = phet = 0). Thus, for the triplet just before the mismatch,
| (19) |
| (20) |
Applying the two boundary conditions gives
| (21) |
where the result is in units of the random walk time step. Essential in this equation is the scaling with respect to .
Combined with the weighting factor of in Eq. (17), this reveals a key feature of thet,BRW: For , the unbinding times from accidental matches increase faster with increasing m than their frequency of appearance decreases, which causes the heterologs with highest m to dominate the sum in Eq. (17). Conversely, for all , the heterologs with the lowest values of m dominate ⟨thet,BRW⟩.
C. Total search time for the biased random walk
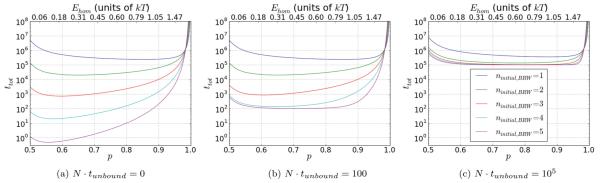
Given the distribution of heterologs in the sample and the average value of the unbinding time for each class of heterolog, one can calculate the total value of ⟨thet,BRW⟩ for all of the heterologs present in the sample. For heterologs that undergo the random walk and face an infinite energy barrier at the position of the heterolog, the total thet as a function of phom for various values of ninitial,BRW is shown in Fig. 3, where the y axis is on a logarithmic scale. The figure illustrates how for p < 64/65, increasing ninitial,BRW dramatically decreases thet. This is because the heterologs with smallest m dominate, but heterologs with m ⩽ ninitial,BRW are excluded from the random walk in the number of strand exchanged triplets. The figure also shows the rapid increase in thet as , when the heterologs with largest m begin to dominate thet. Now, for p > 64/65, we require a free energy difference of ≈2kT between the strand exchanged and reverse strand exchanged state for a single triplet. However, as we note later, such a large free energy decrease due to mechanical stress relief would ruin homology recognition because it would make strand exchange of heterologs favorable. Thus, in all realistic scenarios, p < 64/65 and the heterologs with lowest m dominate ⟨thet⟩.
FIG. 3.
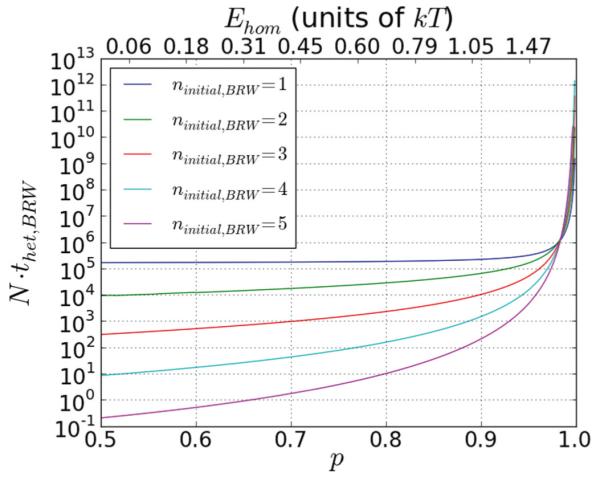
(Color online) Scaling of ⟨thet,BRW⟩. We show the total N⟨thet,BRW⟩ from Eq. (17), for various values of ninitial,BRW. The lines from top to bottom are for ninitial,BRW = 1 through 5, respectively. The times significantly decrease with increasing ninitial,BRW when p has values below 64/65. As p ≳ 64/65 ≈ 0.985, the times increase very rapidly with p and remain finite only because of the finite size search pool.
Though this graph suggests that the total search time would be optimized in the limit where ninitial,BRW approaches infinity, additional factors not included in the graph suggest that though the total search time decreases dramatically when ninitial,BRW is increased from 1 to 3, further increases in ninitial,BRW may not improve the total search time. In vivo, the statistics of the genome limit the maximum length of regions of accidental homology. The limits may vary slightly from genome to genome, but for values above ~6 there will be no decrease in total search time as a function of increasing ninitial,BRW because no sequences of that length are present in the sample. Consideration of the time the filament spends without bound dsDNA as well as the time required to unbind heterologs that do not undergo the BRW will suggest that the total search time may be optimized for values of ninitial,BRW < 6. However, we postpone consideration of those effects until after we have discussed why the results for an infinite barrier (phet = 0) apply under physically realizable conditions, where the barrier for an individual mismatched triplet is only phet ~ kT.
D. Justifying the infinite barrier
By introducing an infinite barrier for advancing past mismatched binding sites, we have essentially enforced nearly perfect specificity in our model. There are two physically realizable systems which provide homology stringency closely approaching the stringency offered by a system with an infinite barrier for a single mismatch: (1) samples with statistics similar to bacterial genomes, where the sparsity of accidental matches provides a statistical barrier and the free energy decrease due to strand exchange of a triplet is considered to be independent of whether previously strand exchanged triplets are sequence matched and (2) a nonlinear free energy penalty that increases as a function of the number of strand exchanged triplets that bind after a mismatched triplet. Such an energy penalty can be justified by considering the mechanical stress on the ssDNA-dsDNA complex when the system attempts to add a triplet subsequent to the binding of a mismatched triplet.
In Fig. 4, we show the results for our analysis of a statistical barrier consistent with the sequence distribution in a bacterial genome. Our results for a barrier created through a nonlinear energy penalty (a nonlinear barrier) are qualitatively the same, which makes sense as from the point of view of the random walk, both simply represent barriers that reduce the probability of advancing past them to zero in a finite width instead of instantly (as in the case of the infinite barrier).
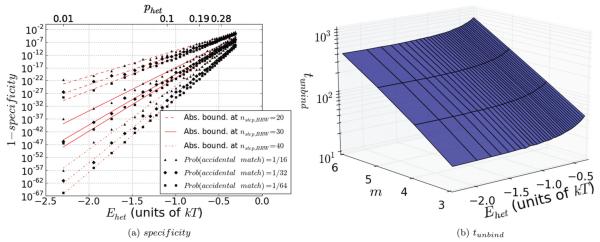
FIG. 4.
(Color online) Results for the statistical well, calculated for phom = 0.7, or equivalently Ehom ≈ 0.42kT, and for ninitial,BRW = 3. In (a), we see a plot of the false positive binding rate, or 1 – specificity, for a given binding event to a heterologous sequence in the sequence dependent state. The specificity has been averaged over all values of m weighted by their relative occurrence frequencies and is given as a function of Ehet, with the corresponding values of phet shown above. The plots were calculated by imposing an absorbing boundary at nstep,BRW = 0 and nstep,BRW = 20,30,40. Although the results change for different positions of the absorbing boundary, the specificity is extremely high in all cases. In order to account for additional possible matches after the first m, results were averaged over many (2000 trials) sequences with random accidental matches after the first m matches. Within each triplet of equally rendered curves, the three lines from bottom to top were calculated with a probability of an accidental match of 1/64, 1/32, and 1/16, respectively. The raw data are shown as squares, diamonds, and triangles, respectively, while the lines represent linear fits. As expected, more matches increase the false positive binding rate. Although the real value is 1/64, the other values where included due to the random nature of the trials in order to provide confident upper bounds, or “worst-case scenarios” for the false positive binding rate. For a mismatch energy penalty of Ehet ~ 1.5kT per triplet, as would be expected purely due to Watson-Crick mismatching, a specificity in excess of 1–10~30 is achieved with a boundary at position 30. In (b), we see the mean unbinding time as a function of m and Ehet. The key feature here is that the exponential dependence of tunbind on m, which was emphasized in Eq. (21) and appears as a linear dependence in this logarithmic plot, is unchanged for different Ehet. The only difference is a constant multiplicative offset to the scaling. This offset is a consequence of the effective width of the statistical well, which is due to the finite value of phet. These two figures indicate that the statistical well behaves essentially like an effective infinite barrier, because it preserves both the specificity and the scaling laws of the infinite barrier.
Figure 4(a) shows on a logarithmic scale the “false positive” binding rate (or 1 − specificity), i.e., the fraction of heterologs that incorrectly fully bind, as a function of the heterolog energy penalty Ehet. The results were calculated using a Markov chain transition matrix model and averaged over all values of m weighted by the respective probabilities. Consistent with experimental results, the solid lines in the graph were made by assuming that an irreversible process occurs when 30 triplets are bound [8], which in the model is represented by an absorbing boundary condition at nstep,BRW = 30. For a heterolog free energy penalty of ~1.5kT, specificities on the order of 1–10−30 can be obtained. The dashed and dash-dotted lines in the figure show the results for absorbing boundaries at nstep,BRW = 20 and nstep,BRW = 40, respectively. Additional accidental matches after the first m matches were introduced randomly with a probability of 1/64, 1/32, and 1/16, corresponding to the three curves, respectively from bottom to top, for each boundary condition. Although the physical value is 1/64, the other curves were included to provide a confident upper bound on the effect of additional accidental matches, which was only statistically quantified as an average of many (2000 trials) random sequences. The figure shows that specificity increases as the position of the absorbing boundary increases. This is reasonable, since each additional heterolog decreases the probability that the spread of the random walk will reach the absorbing boundary. Thus, although in vivo RecA exploits an irreversible process when nstep,BRW ≈ 30, in a system with an infinite number of bases, even better homology recognition can be obtained even without irreversibility. This case is similar to in vitro experiments where the searching filament contained more than 1000 bp and ATP hydrolysis was suppressed [8]. Even though the initial m homologs in the sequence make moving forward favorable, the statistical well can to a high degree of accuracy provide the specificity of an infinite barrier.
Figure 4(b) shows on a logarithmic scale the unbinding time for various values of the free energy penalty Ehet for binding heterologous sites. We consider a system including a region of accidental homology extending up to m and subsequent random sequences of matches and mismatches, with a probability of 1/64 for an accidental match. As in Fig. 4(a), the results were averaged over 2000 such sequences. We found that the effect of additional random matches after the first m was negligible. The results, especially the exponential scaling with m, agree with those for an infinite energy penalty that are given in Eq. (21). The unbinding times are a strong function of m, but they are insensitive to the heterolog energy penalty once it exceeds ~kT. The exponential scaling of the mean unbinding time tunbind as a function of m is independent of the value of phet. The only difference is a constant multiplicative offset to the exponential dependence. This offset is a consequence of the effective width of the barrier which arises when phet ≠ 0.
In sum, the statistical well behaves like an effective infinite barrier with the same scaling laws for unbinding times as an infinite barrier and vanishingly small false positive binding rates. The nonlinear well produces the same qualitative results, except that the parameter characterizing the width of the barrier is not phet, but rather the strength of the nonlinearity. As both effects may play a role in the actual RecA system, the RecA system will give specificity and behavior even closer to an infinite barrier than either of the two effects considered separately.
E. Optimizing total execution time for the biased random walk including diffusion
In the discussion so far, we have only considered time spent bound to dsDNA in the intermediate strand exchanged conformation. For a real biological self-assembling system the search time may not even be dominated by the time during which the dsDNA is bound to and extended by the ssDNA-RecA filament. Rather, it may be dominated by times during which the dsDNA is freely diffusing and not bound to the dsDNA. Equation (1) shows that the total average time spent unbound and diffusing is .
Figure 5 shows the total search time given in Eq. (1) as a function of phom, parametrized by ninitial,BRW. The different panels use different values for ⟨tunbound⟩ from Eq. (1), measured as a fraction of the BRW time step. Minimizing the total search time is a trade-off between minimizing 1/rH (see Fig. 2), which requires higher values of p, and minimizing thet (see Fig. 3), which requires lower values of p. For ninitial,BRW = 1, the minimum search time is achieved for a p > 0.85. In contrast, for ninitial,BRW > 2 and low ⟨tunbound⟩, the search time is minimized for p such that 0.5 < p < 0.6. Furthermore, fairly small values for tunbound already dominate the total time, since the search spends time unbound between all initial binding events, whereas the BRW only happens for a small subset of initial binding events. Thus, optimizing the search parameters simply requires making sure that the parameters are “good enough” such that the RW times do not dominate.
FIG. 5.
(Color online) ttot for various values of tunbound. The legend in (c) applies to all three plots. In each plot, the lines from top to bottom are for ninitial,BRW = 1 through 5, respectively. For negligible diffusion time (a), there are significant differences in the minimal times for varying ninitial,BRW. The minimal values are also shifted: For high ninitial,BRW, the system can afford to use low p and thus minimize thet while retaining high rH, while for low values of ninitial,BRW, higher values of p are required to keep rH from getting too low. As we increase the values for tunbound from (a) through (c), the differences between the curves for different ninitial,BRW become less significant. Furthermore, the minima shift to higher values of p and thus higher values of rH, due to the higher cost for diffusion.
The graphs also show that higher values of tunbound shift the minimum to higher values of p because a higher diffusion time further penalizes low rH,BRW. Similarly, ninitial,BRW becomes less important because the heterolog unbinding time plays less of a role in determining the overall search time. The results make good intuitive sense: Unless the BRW time is very long, the search is simply limited by the time spent off the dsDNA.
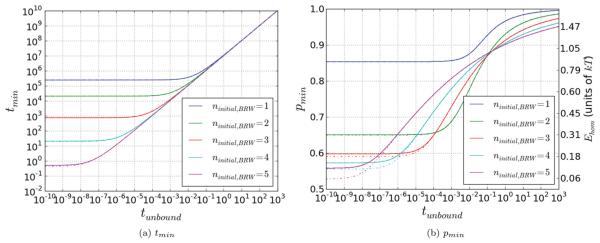
Given the calculated minimal values of ttot as a function of p and ninitial,BRW for a given tunbound, one can plot the optimal values for p, as well as the corresponding minimal values of ttot as a function of tunbound, as shown in Fig. 6. As expected, the graph shows that if ninitial,BRW = 1, values of p ≳ 0.85 are required. Such a large p value corresponds to ≈1kT energy difference between the strand exchanged conformation and the reverse strand exchange conformation for a single triplet. If the decrease in mechanical energy due to strand exchange is too large, it would ruin homology recognition since strand exchange would become favorable for nonhomologs. In contrast with the case where ninitial,BRW = 1, when ninitial,BRW = 3 the required p is only ~0.6, which corresponds to a very reasonable barrier difference of ~0.2kT. Such a small value preserves a significant free energy ~ difference between homologs and heterologs if the free energy cost of a mismatch is the Watson-Crick pairing cost of ~2kT. Thus, having several sites initially bind increases the speed of the search by reducing the number of initial pairings that undergo the random walk and by allowing lower values of p to provide good stability for the homolog; however, increasing ninitial,BRW will no longer decrease the total search time if the search time is dominated by diffusion rather than the random walk unbinding time.
FIG. 6.
(Color) Optimized search. In (a), we obtain the minimal values of ttot as a function of tunbound, by minimizing the curves shown in Fig. 5. The lines from top to bottom are for ninitial,BRW = 1 through 5, respectively. As expected, for low values of tunbound, the difference in time is quite pronounced, with higher ninitial,BRW leading to faster execution. However, as tunbound is increased, the difference between the various curves becomes less and less pronounced. In (b), we plot the corresponding minimizing values of phom, and the respective values for Ehom, as a function of tunbound. In all cases, increasing tunbound forces higher values of p, because of the increased incentive for higher rH. For the same reason, all values for pmin approach 1 as tunbound becomes very large. For low values of tunbound, the curves also approach constant values. In this regime, the optimal p is determined by the trade-off between 1/rH and thet, without any influence by tunbound. The curves were calculated using an absorbing boundary at nstep,BRW = 10,30,40. They are given by the dash-dotted, solid, and dashed lines, respectively. Note that the differences are very small, and especially between nstep,BRW = 30 and 40 are unnoticeable.
F. Optimizing the total search time including bindings that never progress to the biased random walk
Not only does the inclusion of the diffusion time limit the decrease in the total search time that can be obtained by increasing ninitial,BRW, but inclusion of the time spent unbinding from initial pairings that do not progress to the random walk actually suggests that the total search time will begin to increase when ninitial,BRW exceeds ~3. Unfortunately, the progression of structures that lead from B-form dsDNA to dsDNA extended in a conformation that can attempt strand exchange with the ssDNA in the ssDNA-RecA filament is not yet clear, though significant features are beginning to emerge [26]. Furthermore, it is not clear exactly how the initial sequence dependent state unbinds. One can still write a general expression for the total search time that includes a term due to the vast majority of initial pairings that never progress to the metastable intermediate conformation:
| (22) |
Here, ⟨thet,initial⟩ is the average time for a single nonspecific binding to reverse and rH < rH,BRW is now the total probability that a homolog will progress to strand exchange, where unbindings at the initial sequence independent conformation are included. As can be seen from Eq. (17), the term ⟨thet,BRW⟩ carries a linear prefactor of for ninitial,BRW = 3. Thus, the term proportional to ⟨thet,initial⟩ + ⟨tunbound⟩ will be dominant unless the characteristic bound times for the initial conformation are more than 250 000 times shorter than the bound times for the intermediate conformation. However, the stability of near homologs suggests that this might be the case [27]. This difference in linear prefactors can also be seen in a different way. The search comes in contact with on average sites, each of which requires an initial binding, ⟨thet,initial⟩, and a diffusion between sites, ⟨tunbound⟩. In contrast, only <50 of those contacts result in actual sequence dependent binding and require unbinding time, ⟨thet,BRW⟩.
One might first think that the total search time would be minimized by minimizing the binding time for the sequence independent initial conformation. However, rH will decrease if ⟨thet,initial⟩ is decreased, since ⟨thet,initial⟩ will not be long enough to allow ninitial,BRW homologs to progress from the sequence independent conformation to the sequence dependent conformation. In that case, the decrease in rH could dominate over the benefit derived from decreasing ⟨thet,initial⟩ and rH would be much smaller than rH,BRW. Thus, the average time required for ninitial,BRW homologs to make the transition to the intermediate conformation sets a lower bound on ⟨thet,initial⟩. If this transition time to the intermediate state is an increasing function of ninitial,BRW, then, above some limit, raising ninitial,BRW could have adverse effects on the total time, since it would require an increase of ⟨thet,initial⟩. If the triplets flip separately, ⟨thet,initial could increase exponentially with ninitial,BRW.
Search speed and homology stringency will be enhanced if the unbinding rate for ninitial,BRW triplets is much slower for perfect homologs than for groups containing at least one mismatch. This time is affected by both the free energy differences between conformations and the free energy barriers separating the conformations, both of which depend on the conformations of neighboring triplets. Given that strand exchange can only result in a free energy decrease if a contiguous sequence matched triplet is already in the strand exchanged state, then, if ninitial,BRW = 2, strand exchange is unfavorable for both triplets if the initial binding contains a single mismatch, and for the homologous triplet the barrier to reverse strand exchange is the same as the barrier to strand exchange. Similarly, if ninitial,BRW = 3 and there is a single mismatch, then in an initial binding there is at most one contiguous pair of triplets for which strand exchange transition is free energetically favorable and 1/3 of the possible initial bindings contain no such pair. In this case, for contiguous homologous triplets the free energy barrier to strand exchange is slightly lower than the free energy barrier to reverse strand exchange. Larger values of ninitial,BRW will vastly increase the number of possible free energetically favorable combinations with mismatches, which will reduce both the speed and the accuracy of the search. Details of the kinetics would have to be known in order to accurately determine scaling laws.
In conclusion, multiple factors suggest that the total search time is probably optimized when 1 < ninitial,BRW ⩽ 4, consistent with known experimental results for RecA [19,21,28]; however, more experimental and structural information would be required for meaningful optimization of the total search time if factors governing ninitial,BRW are to be accurately included.
IV. DISCUSSION: CONSEQUENCES OF CHOOSING RecA-BASED HOMOLOGY RECOGNITION AS A MODEL
A. Triplets in a bacterial genome
We considered a search through a sample where each binding site represents a bp triplet searching a sample with the statistics of a bacterial genome. Testing in triplets allows the presence of a single bp mismatch to make strand exchange unfavorable for the entire triplet, even if the other two bases are homologous and stacking interactions are not considered. In addition, the stacking interaction between neighboring bases within a triplet may make the free energy difference between a homologous triplet and a triplet containing one mismatch significantly larger than the average Watson-Crick pairing energy for the mismatched base because a single base mismatched within a triplet will make the binding of the neighboring base or bases less free energetically favorable.
Furthermore, having the quantized unit as triplets also greatly lowered the search time for the random walk: The number of random walk steps would be 3 times greater for a search done in single bases. Random walking 5 steps backward is much faster than walking back 15 since the time scales as the square of the number of steps in an unbiased random walk and exponentially in the number of steps in a BRW. Finally, the assumption that the search is done in triplets with four possible choices for each base caused the probability of an accidental binding site match to be 1/64. This sparsity of accidental matches creates a large free energy barrier that prevents mismatches with ~4 contiguous homologous triplets from progressing very far past a mismatch at the fifth triplet, even if the energy barrier for a given mismatched triplet is only a few kT [29].
B. Effect of energy nonlinearities on the model
There are two essential features of the random walk model that are physically realized by energy nonlinearities. (1) There is a weakly bound, sequence independent initial conformation for which the binding of ⩽ninitial,BRW contiguous sites is free energetically favorable, but binding of more sites is highly improbable unless all ninitial,BRW contiguous sites are homologous and make the transition to the sequence dependent conformation, which allows an additional contiguous site to be added to the sequence independent conformation. (2) Strand exchange and reverse strand exchange is allowed for sites only at the “ends” of the filament, i.e., for sites with exactly one strand exchanged neighbor.
Though not mentioned explicitly in the model, the upper bound on the number of dsDNA bp that can bind in the sequence independent initial state plays an important role in search speed. The nonlinearity allows the binding energy for the sequence independent initial state to be favorable for up to three triplets, but increasingly unfavorable for more unless they make a transition to the sequence dependent state. If the energy were linear, either the initial sequence independent state would always be favorable or unfavorable. If it is favorable, either homologs will bind too weakly, or all sequences will bind too deeply because binding more triplets would be favorable regardless of homology, consistent with the SSP. If the energy were unfavorable, the binding of homologs would be much less probable, resulting in increases in the search time due to reductions in rH.
The energy nonlinearity not only places an upper bound on the number in the sequence independent conformation, but it also places a lower bound on the number in the first sequence dependent intermediate conformation. The lower bound of ≈3 on ninitial,BRW occurs because of the decrease in free energy due to strand exchange. The decrease is a consequence of the reduction in the tension on the dsDNA caused by the large free energetically unfavorable extension in the rises between B-form triplets [24]. Thus, strand exchange becomes favorable only through the reduction in tension when a rise is transferred from the highly extended sequence independent conformation to the less extended sequence dependent strand exchanged conformation. This implies that that strand exchange cannot be favorable for one triplet even if it is homologous, though it could be favorable for two contiguous homologous triplets. Experimental results suggest that strand exchange is not significantly favorable until three contiguous homologous triplets occupy the strand exchanged state [21]. Thus, the limit on ninitial,BRW is a consequence of the combined effects of the energy nonlinearities in the initial state and the intermediate state.
The second feature of the energy nonlinearity allows reverse strand exchange only if the triplet has a non-strand exchanged neighbor. This constraint combined with ninitial,BRW ≈ 3 allows homologs to progress to complete strand exchange even though the longest contiguous region of accidental homology completely unbinds fairly rapidly. In the absence of these features due to the energy nonlinearity, the SSP applies.
C. Features of RecA-based self-assembly not in the model
In the RW model we have significantly simplified the physics of RecA-assisted DNA strand exchange to extract important information about the basic trade-offs and requirements for self-assembly. However, there are several features of the RecA-based self-assembly that are not captured in the RW, the most important of which we briefly address here.
1. Features not directly involving the biased random walk model
First, in bacterial chromosomes the ssDNA is attached to dsDNA that forms part of the same chromosome; however, in our discussion, we did not consider pairing of the ssDNA with the dsDNA of which it is a part. We only considered interactions with the other sister chromosome in the cell. With the exception of repeated genes, no such bindings between the ssDNA and the dsDNA of which it is a part will extend beyond five contiguous homologous bp, so such bindings would at most double the total search time without changing the scaling with other variables.
Second, experimental results have shown that RecA-ssDNA filaments conduct parallel searches where several widely separated ~3 triplet bindings are explored simultaneously [10]. Experiments have further shown that this effect significantly improves the searching time, but the effect is only linear in the number of sites considered simultaneously, so such bindings would linearly reduce the total search time without changing the scaling with other variables.
Third, we assumed that the dsDNA completely unbinds from the filament after each attempted pairing with the ssDNA; however, the initial binding of unextended B-form dsDNA to lysines at the outer edge of the filament may allow one initial unextended binding to explore several different extended registrations with respect to the ssDNA. This feature would greatly reduce the total search time since free diffusion in solution would not be required between each possible different registration between the dsDNA and the ssDNA [30,31]. However, the possible registrations for such an initial binding are limited, so complete unbinding of the dsDNA from the ssDNA-RecA filament is probably also required after some moderately exhaustive search of different possible registrations. In this case, the linear prefactor for the diffusion time in Eqs. (1) and (22) would be smaller than for the case where complete unbinding follows each particular registration comparison.
Fourth, bacterial chromosomes are not completely unstructured [32,33] and the sister being searched for homology recognition is probably very close to the searching ssDNA. Thus, the overall linear prefactor would not be proportional to N ~ 10 000 000, but rather some small fraction of N. For instance, if the sister is within 20 10-kb domains of the searcher, then only 200 000 possible pairings would need to be searched [34].
2. Features directly involving the biased random walk model
In the random walk we made the unbinding probability for a triplet contingent on the sequence of its contiguous unbound neighbor in order to force a change in conformation at every time step, where each time step was assumed to have the same size. In reality, the conformation of the system does not have to change at each quantized time step; however, if time is measured in the average units required for a conformation change the average results will be approximately correct.
In addition, in the RecA system phom is actually an increasing function of the number of bound triplets [35]. Also, the free energy penalty due to a single mismatch in a triplet may be greater than the average Watson-Crick pairing penalty due to two effects: (1) a decrease in the stacking of the matched bases due to the presence of a mismatched neighbor and (2) an increase in mechanical stress on correctly paired bases in a triplet because the mismatched base does not share the stress. That increased stress may distort the bonds between the bases, which could reduce the Watson-Crick pairing energy of homologous bases in the triplet. Both features probably offer additional speed and sequence discrimination.
Furthermore, in the RecA system reverse strand exchange is not completely forbidden for strand exchanged triplets for which both nearest neighbors are in the strand exchanged state. The rate is simply lower, and it decreases as a function of the number of triplets in the strand exchanged state. This feature allows nonhomologs to “bail out” of the strand exchanged state in a time that is faster than the time required for a random walk to fully reverse strand exchange. This can increase searching speed as long as the average bailout time is longer than the time required for homologs to progress past ~5 triplets, after which the bailout becomes highly unlikely.
Finally, in the RecA system, there is final poststrand exchange conformation which does not exist in the BRW model. As a result of the nonlinearities in the free energy, the transition to the final conformation may be unfavorable unless ~5 triplets have completed strand exchange, where the final conformation energy may also be sequence dependent. This final transition will provide further stability for homologs and may provide additional stringency beyond that offered by the random walk in the intermediate conformation that was considered here.
V. CONCLUSIONS
In accordance with the SSP, rapid and accurate self-assembly of long linear arrays of individual binding sites is difficult if the binding energy is a linear function of the number of bound sites, even if the target sample does not have any region of contiguous accidental homology that extends beyond ~5 binding sites. In contrast, the simple toy model considered here shows that rapid and accurate pairing of longer arrays is possible for a search where each binding site consists of a DNA triplet if the following additional conditions are met: (1) the sequence distribution of the target is similar to the distribution of a bacterial genome; (2) the system includes several bound conformations; (3) transitions between bound conformations are governed by checkpoints that test the homology of groups of contiguous triplets, where passing each successive checkpoint requires a longer contiguous homologous region; (4) the binding energy for each conformation becomes nonlinearly unfavorable as the number of triplets in that conformation increases. In the BRW model, the effects of the energy nonlinearity are simplified to produce the following constraints: (1) a triplet can only make transitions between the two conformations occupied by its nearest neighbors, so a triplet cannot make a transition if both of its neighbors are in the same conformation; (2) there is an upper bound to the number of triplets that can bind in any conformation, where each successive conformation has a longer upper bound; (3) even for homologs, transitions are unfavorable unless a minimum number of triplets have already made the transition
In such a system, the speed stability paradox can be overcome because the multiple conformations combined with the energy nonlinearity place lower and upper bounds on the number of contiguous homologous triplets for which binding in a given conformation is free energetically favorable. The combination allows the binding to begin with the weakly free energetically favorable sequence independent binding of ~3 triplets to an ssDNA-RecA filament; however, adding more triplets to this initial conformation is increasingly free energetically unfavorable due to the energy nonlinearity. This allows the initial binding of ~3 triplets to be very rapid because it is free energetically favorable without resulting in kinetic trapping due to the sequence independent addition of more triplets [36].
By preventing additional triplets from binding in the initial sequence independent state, the energy nonlinearity forces a decision: Either the three initially bound triplets rapidly unbind, or the three triplets make a transition to the first sequence dependent bound conformation. In addition, the nonlinearity makes the transition between bound conformations unfavorable unless a minimum number of contiguous homologous triplets have already made the transition. If the total free energy decrease due to the transfer of all three contiguous homologous triplets is only ~0.6kT and the penalty for a single mismatch is >kT, then the statistics of the sample combined with the energy nonlinearity may allow all but ~1/250000 of the initial bindings to unbind very rapidly because they include at least one mismatch.
If the three initially bound triplets are all homologous, all the triplets can make the transition to the first sequence dependent bound conformation. That transition slightly stabilizes the binding of the three initial triplets and allows more triplets to be added to the filament. Thus, the minimal binding time for the initial sequence independent conformation is set by the average time required for the transition of three contiguous homologous triplets from the initial conformation to the first sequence dependent conformation. This requirement is much weaker than the requirement that the homolog be stable when the three triplets are bound. Subsequent to the transition of the three homologous triplets to the first sequence dependent state, a BRW governs the transfer of triplets between the sequence dependent and sequence independent conformations. Given that the random walk begins with ~3 triplets in the sequence dependent bound conformation, a very slight bias in the random walk allows homologs to strongly stabilize their binding by adding ⩾30 bound triplets.
In contrast, the statistics of the genome and/or the energy nonlinearity prevent strand exchange from progressing significantly past a nonhomologous triplet [37]. Since such sequences cannot move forward, the random walk will eventually reverse, resulting in complete unbinding. That unbinding can occur fairly quickly since the forward bias is slight and the number of steps that must be reversed is less than the ~5 triplet upper bound on the length of regions of contiguous accidental homology. However, the unbinding time may still be on the order of the total time required to unbind all of the initial pairings that include at least one mismatch. Results of simulations suggest that a free energy decrease of ~0.2kT per triplet optimized the total search time if homologs have infinite lengths or an irreversible transition occurs when ~30 triplets are bound, while providing a sequence stringency in excess of 10−10.
Though RecA-based recognition requires only two levels of checkpoints (bp triplets and triplets of bp triplets), a general system consisting of a series of checkpoints that test homology matching of ~3 groups of contiguous sites could provide good recognition in a system with regions of accidental homology extending beyond five sites. In sum, though our discussion was inspired by the RecA system of strand exchange, the central features of our model are certainly more widely applicable and might provide better insight into the success in generalized self-assembly problems.
ACKNOWLEDGMENTS
We are grateful to Yariv Kafri, Chantal Prevost, Darren Yang, and Efraim Feinstein for useful discussions. Partial support for M.P. was provided by N.I.H. Grant No. RO1 GM025326 to N. Kleckner.
Footnotes
PACS number(s): 87.15.A−, 81.16.Dn, 87.14.gk, 87.15.kj
References
- [1].Roca A, Cox M. Crit. Rev. Biochem. Mol. Biol. 1990;25:415. doi: 10.3109/10409239009090617. [DOI] [PubMed] [Google Scholar]
- [2].Kowalczykowski S, Eggleston A. Annu. Rev. Biochem. 1994;63:991. doi: 10.1146/annurev.bi.63.070194.005015. [DOI] [PubMed] [Google Scholar]
- [3].Rosselli W, Stasiak A. J. Mol. Biol. 1990;216:335. doi: 10.1016/S0022-2836(05)80325-0. [DOI] [PubMed] [Google Scholar]
- [4].Howard-Flanders P, West S, Stasiak A. Nature (London) 1984;309:215. doi: 10.1038/309215a0. [DOI] [PubMed] [Google Scholar]
- [5].West S. Nat Rev Mol Cell Biol. 2003;4:435. doi: 10.1038/nrm1127. [DOI] [PubMed] [Google Scholar]
- [6].Menetski J, Bear D, Kowalczykowski S. Proc. Natl. Acad. Sci. USA. 1990;87:2125. doi: 10.1073/pnas.87.1.21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].In vitro, in the absence of an irreversible process, the maximal number of bound triplets n is unlimited and has been shown to exceed 300 triplets [8]. In vivo, an irreversible process occurs after ~30 triplets are bound to the filament [8].
- [8].van der Heijden T, Modesti M, Hage S, Kanaar R, Wyman C, Dekker C. Mol. Cell. 2008;30:530. doi: 10.1016/j.molcel.2008.03.010. [DOI] [PubMed] [Google Scholar]
- [9].The last property implies that no necessary transition can require a free energy that is greatly in excess of the available thermal energy.
- [10].Forget AL, Kowalczykowski S. Nature (London) 2012;482:423. doi: 10.1038/nature10782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Bénichou O, Kafri Y, Sheinman M, Voituriez R. Phys. Rev. Lett. 2009;103:138102. doi: 10.1103/PhysRevLett.103.138102. [DOI] [PubMed] [Google Scholar]
- [12].Sheinman M, Bénichou O, Kafri Y, Voituriez R. Rep. Prog. Phys. 2012;75:026601. doi: 10.1088/0034-4885/75/2/026601. [DOI] [PubMed] [Google Scholar]
- [13].Slutsky M, Mirny L. Biophys. J. 2004;87:4021. doi: 10.1529/biophysj.104.050765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Gerland U, Moroz J, Hwa T. Proc. Natl. Acad. Sci. USA. 2002;99:12015. doi: 10.1073/pnas.192693599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Except for rare occasions of repeating genes.
- [16].A mismatch penalty of 10kT would also give good recognition; however, obtaining that mismatch is challenging. If the penalty comes from a long range repulsive interaction, the two arrays will never come together. If the penalty comes from mismatched Watson-Crick pairing, then base flipping will never occur. If the penalty comes from a very short range interaction that does not require previous unbinding of a similar interaction, then the good recognition could be obtained, but we have not yet found a physically realizable system that embodies this requirement.
- [17].See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevE.88.012702 for a detailed overview of RecA-mediated homology recognition and strand exchange.
- [18].Chen Z, Yang H, Pavletich N. Nature (London) 2008;453:489. doi: 10.1038/nature06971. [DOI] [PubMed] [Google Scholar]
- [19].Ragunathan K, Joo C, Ha T. Structure. 2011;19:1064. doi: 10.1016/j.str.2011.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Xiao J, Lee A, Singleton S. Chem. Bio. Chem. 2006;7:1265. doi: 10.1002/cbic.200600038. [DOI] [PubMed] [Google Scholar]
- [21].Hsieh P, Camerini-Otero C, Camerini-Otero R. Proc. Natl. Acad. Sci. USA. 1992;89:6492. doi: 10.1073/pnas.89.14.6492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Fulconis R, Dutreix M, Viovy J-L. Biophys. J. 2005;88:3770. doi: 10.1529/biophysj.104.055269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].SantaLucia JJ. Proc. Natl. Acad. Sci. USA. 1998;95:1460. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Peacock-Villada A, Yang D, Danilowicz C, Feinstein E, Pollock N, McShan S, Coljee V, Prentiss M. Nucleic Acids Res. 2012;40:10441. doi: 10.1093/nar/gks769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Bazemore L, Folta-Stogniew E, Takahashi M, Radding C. Proc. Natl. Acad. Sci. USA. 1997;94:11863. doi: 10.1073/pnas.94.22.11863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Saladin A, Amourda C, Poulain P, Férey N, Baaden M, Zacharias M, Delalande O, Prévost C. Nucleic Acids Res. 2010;38:6313. doi: 10.1093/nar/gkq459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Sagi D, Tlusty T, Stavans J. Nucleic Acids Res. 2010;38:2036. doi: 10.1093/nar/gkl586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Lee A, Xiao J, Singleton S. J. Mol. Biol. 2006;360:343. doi: 10.1016/j.jmb.2006.04.065. [DOI] [PubMed] [Google Scholar]
- [29].Of course, if the sample is constrained so that the nearest available nonhomolog has m ⩽ N sequence matches, then the energy gap between the two arrays can allow excellent homology stringency; however, in such a system the total number of distinguishable arrays would be limited by m regardless of the total length N of the arrays. More importantly, if the energy were linear then all of the binding sites would have to interact at once in correct registration in order to overcome the SSP. Those constraints actually represent the simple case where the N individual molecular contacts would be more correctly described as one single binding site that includes many molecular interactions.
- [30].Koslover E, de La Rosa M. Díaz, Spakowitz A. Biophys. J. 2011;101:856. doi: 10.1016/j.bpj.2011.06.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ragunathan K, Liu C, Ha T. eLife Sci. 2012;1:e00067. doi: 10.7554/eLife.00067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Fisher JK, Bourniquel A, Witz G, Weiner B, Prentiss M, Kleckner N. Cell. 2013;153:882. doi: 10.1016/j.cell.2013.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Postow L, Hardy CD, Arsuaga J, Cozzarelli NR. Genes Dev. 2004;18:1766. doi: 10.1101/gad.1207504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Weiner A, Zauberman N, Minsky A. Nat. Rev. Microbiol. 2009;7:748. doi: 10.1038/nrmicro2206. [DOI] [PubMed] [Google Scholar]
- [35].Vlassakis J, Feinstein E, Yang D, Tilloy A, Weiller D, Kates-Harbeck J, Coljee V, Prentiss M. Phys. Rev. E. 2013;87:032702. doi: 10.1103/PhysRevE.87.032702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].In contrast, in a system with a binding energy proportional to the number of bound triplets, adding more triplets would always be either favorable or unfavorable regardless of the number bound; therefore, either initial testing will be unfavorable, or the sequence independent binding would become increasingly deeply bound as more triplets were added, resulting in kinetic trapping.
- [37].In vitro experiments featuring a single mismatched triplet followed by a series of matched triplets do show that skipping over a single triplet is not forbidden if subsequent regions contain substantial accidental homology.