Measures of Diagnostic Accuracy: Basic Definitions

Abstract

Diagnostic accuracy relates to the ability of a test to discriminate between the target condition and health. This discriminative potential can be quantified by the measures of diagnostic accuracy such as sensitivity and specificity, predictive values, likelihood ratios, the area under the ROC curve, Youden's index and diagnostic odds ratio. Different measures of diagnostic accuracy relate to the different aspects of diagnostic procedure: while some measures are used to assess the discriminative property of the test, others are used to assess its predictive ability. Measures of diagnostic accuracy are not fixed indicators of a test performance, some are very sensitive to the disease prevalence, while others to the spectrum and definition of the disease. Furthermore, measures of diagnostic accuracy are extremely sensitive to the design of the study. Studies not meeting strict methodological standards usually over- or under-estimate the indicators of test performance as well as they limit the applicability of the results of the study. STARD initiative was a very important step toward the improvement the quality of reporting of studies of diagnostic accuracy. STARD statement should be included into the Instructions to authors by scientific journals and authors should be encouraged to use the checklist whenever reporting their studies on diagnostic accuracy. Such efforts could make a substantial difference in the quality of reporting of studies of diagnostic accuracy and serve to provide the best possible evidence to the best for the patient care. This brief review outlines some basic definitions and characteristics of the measures of diagnostic accuracy.

Introduction

Diagnostic accuracy of any diagnostic procedure or a test gives us an answer to the following question: "How well this test discriminates between certain two conditions of interest (health and disease; two stages of a disease etc.)?". This discriminative ability can be quantified by the measures of diagnostic accuracy:

• sensitivity and specificity

• positive and negative predicative values (PPV, NPV)

• likelihood ratio

• the area under the ROC curve (AUC)

• Youden's index

• diagnostic odds ratio (DOR)

Different measures of diagnostic accuracy relate to the different aspects of diagnostic procedure. Some measures are used to assess the discriminative property of the test, others are used to assess its predictive ability (1). While discriminative measures are mostly used by health policy decisions, predictive measures are most useful in predicting the probability of a disease in an individual (2). Furthermore, it should be noted that measures of a test performance are not fixed indicators of a test quality and performance. Measures of diagnostic accuracy are very sensitive to the characteristics of the population in which the test accuracy is evaluated. Some measures largely depend on the disease prevalence, while others are highly sensitive to the spectrum of the disease in the studied population. It is therefore of utmost importance to know how to interpret them as well as when and under what conditions to use them.

Sensitivity and specificity

A perfect diagnostic procedure has the potential to completely discriminate subjects with and without disease. Values of a perfect test which are above the cut-off are always indicating the disease, while the values below the cut-off are always excluding the disease. Unfortunately, such perfect test does not exist in real life and therefore diagnostic procedures can make only partial distinction between subjects with and without disease. Values above the cut-off are not always indicative of a disease since subjects without disease can also sometimes have elevated values. Such elevated values of certain parameter of interest are called false positive values (FP). On the other hand, values below the cut-off are mainly found in subjects without disease. However, some subjects with the disease can have them too. Those values are false negative values (FN). Therefore, the cut-off divides the population of examined subjects with and without disease in four subgroups considering parameter values of interest:

• (true positive (TP) –subjects with the disease with the value of a parameter of interest above the cut-off

• (false positive (FP) –subjects without the disease with the value of a parameter of interest above the cut-off

• (true negative (TN) –subjects without the disease with the value of a parameter of interest below the cut-off

• (false negative (FN) –subjects with the disease with the value of a parameter of interest below the cut-off

The first step in the calculation of sensitivity and specificity is to make a 2x2 table with groups of subjects divided according to a gold standard or (reference method) in columns, and categories according to test in rows (Table 1.).

Table 1.

2x2 table

	Subjects with the disease	Subjects without the disease
positive	TP	FP
negative	FN	TN

Sensitivity is expressed in percentage and defines the proportion of true positive subjects with the disease in a total group of subjects with the disease (TP/TP+FN). Actually, sensitivity is defined as the probability of getting a positive test result in subjects with the disease (T+|B+). Hence, it relates to the potential of a test to recognise subjects with the disease.

Specificity is a measure of a diagnostic test accuracy, complementary to sensitivity. It is defined as a proportion of subjects without the disease with negative test result in total of subjects without disease (TN/TN+FP). In other words, specificity represents the probability of a negative test result in a subject without the disease (T-|B-). Therefore, we can postulate that specificity relates to the aspect of diagnostic accuracy that describes the test ability to recognise subjects without the disease, i.e. to exclude the condition of interest.

Neither sensitivity nor specificity are not influenced by the disease prevalence, meaning that results from one study could easily be transferred to some other setting with a different prevalence of the disease in the population. Nonetheless, sensitivity and specificity can vary greatly depending on the spectrum of the disease in the studied group.

Predictive values

Positive predictive value (PPV) defines the probability of having the state/disease of interest in a subject with positive result (B+|T+). Therefore PPV represents a proportion of patients with positive test result in total of subjects with positive result (TP/TP+FP).

Negative predictive value (NPV) describes the probability of not having a disease in a subject with a negative test result (B-|T-). NPV is defined as a proportion of subjects without the disease with a negative test result in total of subjects with negative test results (TN/TN+FN).

Unlike sensitivity and specificity, predictive values are largely dependent on disease prevalence in examined population. Therefore, predictive values from one study should not be transferred to some other setting with a different prevalence of the disease in the population. Prevalence affects PPV and NPV differently. PPV is increasing, while NPV decreases with the increase of the prevalence of the disease in a population. Whereas the change in PPV is more substantial, NPV is somewhat weaker influenced by the disease prevalence.

Likelihood ratio (LR)

Likelihood ratio is a very useful measure of diagnostic accuracy. It is defined as the ratio of expected test result in subjects with a certain state/disease to the subjects without the disease. As such, LR directly links the pre-test and post-test probability of a disease in a specific patient (3). Simplified, LR tells us how many times more likely particular test result is in subjects with the disease than in those without disease. When both probabilities are equal, such test is of no value and its LR = 1.

Likelihood ratio for positive test results (LR+) tells us how much more likely the positive test result is to occur in subjects with the disease compared to those without the disease (LR+=(T+|B+)/(T+|B-)). LR+ is usually higher than 1 because is it more likely that the positive test result will occur in subjects with the disease than in subject without the disease.

LR+ can be simply calculated according to the following formula:

LR+ = sensitivity / (1-specificity)

LR+ is the best indicator for ruling-in diagnosis. The higher the LR+ the test is more indicative of a disease. Good diagnostic tests have LR+ > 10 and their positive result has a significant contribution to the diagnosis.

Likelihood ratio for negative test result (LR-) represents the ratio of the probability that a negative result will occur in subjects with the disease to the probability that the same result will occur in subjects without the disease. Therefore, LR- tells us how much less likely the negative test result is to occur in a patient than in a subject without disease. (LR-=(T-|B+)/(T-|B-)). LR- is usually less than 1 because it is less likely that negative test result occurs in subjects with than in subjects without disease. LR- is calculated according to the following formula:

LR- = (1-sensitivity) / specificity

LR- is a good indicator for ruling-out the diagnosis. Good diagnostic tests have LR- < 0,1. The lower the LR- the more significant contribution of the test is in ruling-out, i.e. in lowering the posterior probability of the subject having the disease.

Since both specificity and sensitivity are used to calculate the likelihood ratio, it is clear that neither LR+ nor LR- depend on the disease prevalence in examined groups. Consequently, the likelihood ratios from one study are applicable to some other clinical setting, as long as the definition of the disease is not changed. If the way of defining the disease varies, none of the calculated measures will apply in some other clinical context.

ROC curve

There is a pair of diagnostic sensitivity and specificity values for every individual cut-off. To construct a ROC graph, we plot these pairs of values on the graph with the 1-specificity on the x-axis and sensitivity on the y-axis (Figure 1.).

Figure 1.

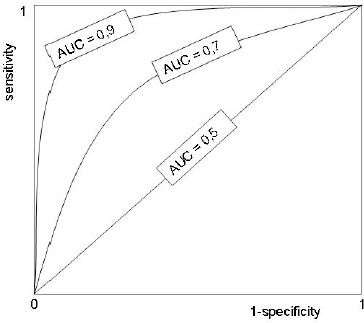
ROC curve

The shape of a ROC curve and the area under the curve (AUC) helps us estimate how high is the discriminative power of a test. The closer the curve is located to upper-left hand corner and the larger the area under the curve, the better the test is at discriminating between diseased and non-diseased. The area under the curve can have any value between 0 and 1 and it is a good indicator of the goodness of the test. A perfect diagnostic test has an AUC 1.0. whereas a nondiscriminating test has an area 0.5. Generally we can say that the relation between AUC and diagnostic accuracy applies as described in Table 2.

Table 2.

Relationship between the area under the ROC curve and diagnostic accuracy

area	diagnostic accuracy
0.9 – 1.0	excellent
0.8-0.9	very good
0.7-0.8	good
0.6-0.7	sufficient
0.5-0.6	bad
< 0.5	test not useful

AUC is a global measure of diagnostic accuracy. It tells us nothing about individual parameters, such as sensitivity and specificity. Out of two tests with identical or similar AUC, one can have significantly higher sensitivity, whereas the other significantly higher specificity. Furthermore, data on AUC state nothing about predicative vales and about the contribution of the test in ruling-in and ruling-out a diagnosis. Global measures are there for general assessment and for comparison of two or more diagnostic tests. By the comparison of areas under the two ROC curves we can estimate which one of two tests is more suitable for distinguishing health from disease or any other two conditions of interest. It should be pointed that this comparison should not be based on visual nor intuitive evaluation (4). For this purpose we use statistic tests which evaluate the statistical significance of estimated difference between two AUC, with previously defined level of statistical significance (P).

Diagnostic odds ratio (DOR)

Diagnostic odds ratio is also one global measure for diagnostic accuracy, used for general estimation of discriminative power of diagnostic procedures and also for the comparison of diagnostic accuracies between two or more diagnostic tests. DOR of a test is the ratio of the odds of positivity in subjects with disease relative to the odds in subjects without disease (5). It is calculated according to the formula: DOR = (TP/FN)/(FP/TN).

DOR depends significantly on the sensitivity and specificity of a test. A test with high specificity and sensitivity with low rate of false positives and false negatives has high DOR. With the same sensitivity of the test, DOR increases with the increase of the test specificity. For example, a test with sensitivity > 90% and specificity of 99% has a DOR greater than 500.

DOR does not depend on disease prevalence; however like sensitivity and specificity it depends on criteria used to define disease and its spectrum of pathological conditions of the examined group (disease severity, phase, stage, comorbidity etc.).

Diagnostic effectiveness (accuracy)

Another global measure of diagnostic accuracy is so called diagnostic accuracy (effectiveness), expressed as a proportion of correctly classified subjects (TP+TN) among all subjects (TP+TN+FP+FN). Diagnostic accuracy is affected by the disease prevalence. With the same sensitivity and specificity, diagnostic accuracy of a particular test increases as the disease prevalence decreases. This data, however, should be handled with care. In fact, this does not mean that the test is better if we apply it in a population with low disease prevalence. It only means that in absolute number the test gives more correctly classified subjects. This percentage of correctly classified subjects should always be weighed considering other measures of diagnostic accuracy, especially predictive values. Only then a complete assessment of the test contribution and validity could be made.

Youden's index

Youden's index is one of the oldest measures for diagnostic accuracy (6). It is also a global measure of a test performance, used for the evaluation of overall discriminative power of a diagnostic procedure and for comparison of this test with other tests. Youden's index is calculated by deducting 1 from the sum of test’s sensitivity and specificity expressed not as percentage but as a part of a whole number: (sensitivity + specificity) – 1. For a test with poor diagnostic accuracy, Youden's index equals 0, and in a perfect test Youden's index equals 1. Youden's index is not sensitive for differences in the sensitivity and specificity of the test, which is its main disadvantage. Namely, a test with sensitivity 0,9 and specificity 0,4 has the same Youden's index (0,3) as a test with sensitivity 0,6 and specificity 0,7. It is absolutely clear that those tests are not of comparable diagnostic accuracy. If one is to assess the discriminative power of a test solely based on Youden's index it could be mistakenly concluded that these two tests are equally effective.

Youden’s index is not affected by the disease prevalence, but it is affected by the spectrum of the disease, as are also sensitivity specificity, likelihood ratios and DOR.

Design of diagnostic accuracy studies

Measures of diagnostic accuracy are extremely sensitive to the design of the study. Studies suffering from some major methodological shortcomings can severely over- or under-estimate the indicators of test performance as well as they can severely limit the possible applicability of the results of the study. The effect of the design of the study to the bias and variation in the estimates of diagnostic accuracy can be quantified (7). STARD initiative published in 2003 was a very important step toward the improvement the quality of reporting of studies of diagnostic accuracy (8, 9). According to some authors, the quality of reporting of diagnostic accuracy studies did not significantly improve after the publication of the STARD statement (10, 11), whereas some others hold that the overall quality of reporting has at least slightly improved (12), but there is still some room for potential improvement (13, 14).

Editors of scientific journals are encouraged to include the STARD statement into the Journal Instructions to authors and to oblige their authors to use the checklist when reporting their studies on diagnostic accuracy. This way the quality of reporting could be significantly improved, providing the best possible evidence for health care providers, clinicians and laboratory professionals; to the best for the patient care.