Estimation of Sparse Directed Acyclic Graphs for Multivariate Counts Data

Summary

The next-generation sequencing data, called high throughput sequencing data, are recorded as count data, which is generally far from normal distribution. Under the assumption that the count data follow the Poisson log-normal distribution, this paper provides an L₁-penalized likelihood framework and an efficient search algorithm to estimate the structure of sparse directed acyclic graphs (DAGs) for multivariate counts data. In searching for the solution, we use iterative optimization procedures to estimate the adjacency matrix and the variance matrix of the latent variables. The simulation result shows that our proposed method outperforms the approach which assumes multivariate normal distributions, and the log-transformation approach. It also shows that the proposed method outperforms the rank-based PC method under sparse network or hub network structures. As a real data example, we demonstrate the efficiency of the proposed method in estimating the gene regulatory networks of the ovarian cancer study.

1. Introduction

Probabilistic graphical models are often used to find conditional dependencies between expression levels of different genes in regulatory networks or pathways (Friedman, Hastie, and Tibshirani, 2008). Gaussian graphical models have been commonly used to infer gene networks since gene expression data from microarray technology can be approximated by normal distribution after log transformation. However, recently, the next-generation sequencing technology, which is also called high throughput sequencing, has been applied for measuring gene expressions and monitoring genome-wide transcription (Marioni et al., 2008). The data for each gene from the next-generation sequencing are counts based on sequencing reads. Such count data have been approximated as Poisson distribution or negative binomial distribution (Srivastava and Chen, 2010; Anders and Huber, 2010). However, the statistical analysis of multivariate counts data has proved difficult due to insufficient parametric class representing correlation structures (Aitchison and Ho, 1989).

Most literature on the graphical model, either an undirected graph or a directed graph, is based on Gaussian distribution. Undirected graph models imply full conditional independence graphs, where an edge between two nodes is absent if and only if the corresponding random variables are conditionally independent (Lauritzen, 1996; Hastie, Tibshirani, and Friedman, 2009). Such dependency is obtained by a nonzero element in the inverse covariance matrix for Gaussian variables. A graphical lasso algorithm is a popular method for the sparse inverse covariance estimation (Friedman, Hastie, and Tibshirani, 2008). If the number of variables is larger than the sample size, several penalized methods have been proposed to estimate the inverse covariance matrix.

Directed acyclic graphs (DAGs) are a special class of directed graphical models, where all the edges are directed edges and contain no directed cycles (Pearl, 2000). A connection in DAGs can be made from a causal inference by applying the directed Markov property under certain assumptions (Pearl, 2000; Friedman, Hastie, and Tibshirani, 2008). Estimation of the structure of DAGs from observed data has been studied by many groups (for review, see Neapolitan (2004); Daly, Shen, and Aitken (2011)). The most common way to estimate the structure of DAGs is a score-and-search approach, in which a network is identified by maximizing a certain objective function (Neapolitan, 2004), and often heuristic search algorithms are developed to find a high score (Daly, Shen, and Aitken, 2011). Other approaches to estimate the structure of DAGs are the constraint-based approach such as the PC-algorithm (Spirtes, Glymour, and Scheines, 2000), which uses statistical tests to find conditional independence of data, or the hybrid approach, which combines the score-and-search approach and the constraint-based approach to make a computationally competitive algorithm in high-dimensional settings. To estimate the DAG under known variable order in high dimensional data, the L₁-penalized likelihood approach was first studied by Shojaie and Michailidis (2010). The likelihood was formulated as a function of the adjacency matrix of the graph, and it is converted to separable lasso problems (Shojaie and Michailidis, 2010), which resulted in an efficient algorithm to estimate the structure of directed graphs. Fu and Zhou (2013) proposed an L₁-penalized likelihood approach to estimate sparse DAG structures with experimental intervention. The proposed objective function has a log term, which causes non-convexity. Han et al. (2014) used an approximated convex objective function based on the L₁-penalized likelihood to estimate DAGs given an unknown order of variables.

Unlike Gaussian distribution, a graphical model under count data is rarely studied even though the next-generation sequencing technology generates more precise data with count values. Allen and Liu (2013) propose a local Poisson graphical model, which is essentially a neighbor selection algorithm to find the undirected graph. Choi et al. (2013) proposed the undirected graphical model based on Poisson distribution. For estimating DAGs of non-normal data, Harris and Drton (2013) proposed the Rank-based PC-algorithm (RPC), which uses nonparametric rank correlation coefficients.

In this paper, we propose an L₁-penalized likelihood approach based on multivariate Poisson log-normal distributions to estimate DAGs for multivariate count data. An efficient solution search algorithm is proposed to estimate the DAG by optimizing a lasso-based objective function within feasible computational time for high dimensional data. To the best of our knowledge, this is the first method that estimates DAGs for multivariate count data based on L1-penalized likelihood without knowing variable orders. Here, the variable orders indicate directional causal relationships between variables. The organization of this paper is as follows. In Section 2, we define the model formulation and derive the objective function by approximation, and discuss iterative optimization algorithms to estimate DAGs under unknown variable order. In Section 3, we investigate the performance of the proposed method by simulation studies. The real data application is studied in Section 4, and we conclude our results in Section 5.

2. Mathematical Formulation

In this section, we explain the multivariate Poisson log-normal model for count data, and the objective function based on the penalized likelihood followed by iterative optimization algorithms.

2.1 Multivariate Poisson log-normal model

Suppose that we have p random variables, Y₁, Y₂, Y₃, …, Y_p. Let Y be a vector with p random variables, say Y = [Y₁, Y₂, …, Y_p]^T. Y_k (k = 1, 2, …, p) follows a Poisson distribution Poisson(ϕ_k), where ϕ_k follows a log-normal distribution for k = 1, 2, …, p, such that

$$\mathit{log}({\varphi }_k)={\sigma }_k{X}_k+{\mu }_k.$$ (1)

X = [X₁, X₂, …, X_p]^T follows a multivariate-normal distribution MN(0, Σ_X). Only Y_k (k = 1, 2, …, p) is observed, while X_k is the underlying hidden variable.

The likelihood can be represented by

$$P(\mathbf{Y}\mid \mu ,\sigma ,{\mathrm{\sum }}_X)=\int P(\mathbf{Y},\mathbf{X}\mid \mu ,\sigma ,{\mathrm{\sum }}_X)d\mathbf{X}=\int P(\mathbf{Y}\mid \mathbf{X},\mu ,\sigma )\times P(\mathbf{X}\mid {\mathrm{\sum }}_X)d\mathbf{X}.$$ (2)

Define y_jk as the j_th realization of Y_k, and define the data matrix y = [y_jk], where j = 1, 2, …, n, and k = 1, 2, …, p. y_j is the column vector of the j_th row of y. The term in (2), P(Y|X, μ, σ), can be extended by independence of Y_k given X. Thus,

$$\sum _{j=1}^n\sum _{k=1}^{p}logP(y_{jk}\mid X_k,\mu ,\sigma )=\sum _{j=1}^n\sum _{k=1}^p\left[C_{jk}{X}_k+F_{jk}-\mathit{exp}\left({\sigma }_k{X}_k+{\mu }_k\right)\right],$$

where C_jk = y_jkσ_k and F_kj = y_jkμ_k − log(y_jk!). y_jk! means y_jk × (y_jk − 1) ×⋯× 2 × 1.

Parameters μ_k and ${\sigma }_k^2$ can be estimated by the marginal expectation and variance of Y_k. After we define the sample mean ${\overline{y}}_k={\sum }_{j=1}^n{y}_{jk}/n$ and the sample variance ${\widehat{\sigma }}_{y_k}^2={\sum }_{j=1}^n{(y_{jk}-{\overline{y}}_k)}^2/n$, μ̂_k and ${\widehat{\sigma }}_k^2$ can be obtained by methods of moments,

$${\widehat{\sigma }}_k^2=log\left[\frac{{\widehat{\sigma }}_{y_k}^2-{\overline{y}}_k}{{\overline{y}}_k^2}+1\right]$$ (3)

and

$${\widehat{\mu }}_k=log{\overline{y}}_k-\frac{1}{2}{\widehat{\sigma }}_k^2.$$ (4)

Note that the multivariate Poisson log-normal model allows an unequal mean and variance of Y_k, which is more flexible than a simple Poisson distribution.

Equation (2) shows that the likelihood of Y is defined by two parts: the likelihood of y_j given the latent variable X, and the likelihood of X with covariance matrix Σ_X. In the next section, we use Linear Structural Equations to model the DAG structures on latent variable X.

2.2 Linear structural equations regarding hidden variable X

To obtain the relationships among Y₁ to Y_K, we define the graphical relationship from the hidden variable X. The variable and underlying causal relation can be represented by graph G = (V, E), where V indicates the node set and E indicates the edge set represented by V × V. We assume that the graph G is a DAG, so (i, j) is not in E if (j, i) belongs to E. In the underlying relationship, j is denoted as a parent if i ← j, and the set of parent nodes for a child node i is represented by pa_i. The structural equation model (Pearl, 2000) explains the underlying causal relationship of random variables in a DAG. Let Γ = [Γ₁, Γ₂, …, Γ_p]^T be a vector of latent variables, which is not observed but assumed to follow a normal distribution as

$$\mathbf{\Gamma }~MN(0,D),$$

where D is a diagonal matrix with the entries ${\sigma }_{{\mathrm{\Gamma }}_1}^2,{\sigma }_{{\mathrm{\Gamma }}_2}^2,\dots ,{\sigma }_{{\mathrm{\Gamma }}_p}^2$. We assume that the variances may be unequal and unknown. The structural equation model for the underlying relation in the graph is

$$X_i=\sum _{j\in p{a}_i}{a}_{ij}{X}_j+{\mathrm{\Gamma }}_i,$$ (5)

where a_ij is a direct underlying causal effect from a parent j to a child i. We can represent Equation (5) by the matrix form X = AX + Γ, where X = [X₁, X₂, …, X_p]^T, and A is the adjacency matrix by

$$A=\left(\begin{array}{ccccc}0& a_{12}& \cdots & a_{1(p-1)}& a_{1p}\\ a_{21}& 0& \cdots & a_{2(p-1)}& a_{2p}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{(p-1)1}& a_{(p-1)2}& \cdots & 0& a_{(p-1)p}\\ a_{p1}& a_{p2}& \cdots & a_{p(p-1)}& 0\end{array}\right).$$

The form in (5) can be a compact form expressed by X = (I − A)⁻¹Γ. Thus, X is a vector of multivariate normal variables with E[X] = 0 and Var[X] = (I − A)⁻¹D((I − A)⁻¹)^T. In other words, X follows the multivariate normal distribution MN(0, Σ_X), where ${\mathrm{\sum }}_{\mathbf{X}}^{-1}={(I-A)}^T{D}^{-1}(I-A)$. The log-likelihood of A and D can therefore be expressed by

$$-\frac{n}{2}logP(\mathbf{X}\mid A,D)\propto \frac{1}{2}log\mid D^{-1}\mid -\frac{1}{2}{\mathbf{X}}^T{(I-A)}^T{D}^{-1}(I-A)\mathbf{X}.$$ (6)

Apparently, we can learn the structure of the graph G by estimating the adjacency matrix A. For directed graphs, A is not symmetric since A_ij and A_ji represent the edge from node X_j to X_i and the edge from node X_i to X_j in G, respectively. In fact, if the underlying graph G is a DAG, A_ij and A_ji cannot both be non-zero. Therefore, there needs to be acyclic restrictions on the structure of the adjacency matrix A of a DAG.

Let T_A denote the structure matrix induced by A, where the (i, j)_th entry of T_A is 1 if A_ij ≠ 0. The following lemma proposed in Han et al. (2014) conveniently establishes the relationship between A and the acyclic restriction.

Lemma 1

The adjacency matrix A is acyclic if and only if

$$\sum _{l=1}^{\mathit{min}(\mathit{Card}(T_A),p)}\sum _{m=1}^p{\left[T_A^l\right]}_{m,m}=0,$$ (7)

where min() means a minimum value function, and Card(T_A) is the number of non-zero entries indicating a cardinality of T_A. $T_A^l$ indicates l times the product of T_A matrix, and ${[T_A^l]}_{m,m}$ indicates the (m, m) entry of the matrix $T_A^l$.

For many applications, it is often the case that the underlying DAG structure is sparse. It is therefore important to find a sparse structure for the adjacency matrix A. Therefore, the estimation of DAGs can be pursued by minimizing the penalized likelihood function in terms of A under the acyclic restriction of the structure matrix, T_A, as follows.

$$\begin{array}{ll}\underset{A}{min}\hfill & -\frac{n}{2}logP(\mathbf{X}\mid A,D)+\lambda (A)\hfill \\ s.t.\hfill & T_A\text{satisfies}\text{the}\text{acyclic}\text{constraint}(7),\hfill \end{array}$$ (8)

where λ(A) is a penalty function.

The recent work of Shojaie and Michailidis (2010) assumed a known ordering of the variables to simplify the optimization, which eliminates the need for the acyclicity constraint. The computation for optimizing function (8) without assuming known variable orders is challenging because it is a mixed integer nonlinear optimization problem with the acyclicity constraint. Fu and Zhou (2013) proposed a heuristic algorithm based on a coordinate descent search approach. Han et al. (2014) proposed a meta-heuristic search algorithm, called the Discrete Improving Search with a TABU (DIST) algorithm, and they presented its effectiveness and computational efficiency.

2.3 Penalized likelihood and iterative optimization

Based on the log-likelihood l(A, D|y_j, μ, σ) for each y_j, we define the objective function as the lasso penalized log-likelihood of A in terms of the observation matrix y, which is

$$S(A,D\mid y,\mu ,\sigma ,\lambda )\equiv -\frac{2}{n}\sum _{j=1}^n\ell (A,D\mid {\mathbf{y}}_j,\mu ,\sigma )+\lambda \mid A\mid$$ (9)

where λ is a penalty parameter, and |A| is the L₁-norm defined as |A| = Σ_i Σ_j |A_ij|. By replacing μ and σ with their marginal estimates μ̂ in (3) and σ̂ in (4), the problem is essentially to minimize Equation (9) with respect to A and the nuisance parameter D under the acyclic constraint (7). The log-likelihood of the observed data can be represented by the log-likelihood of the complete data as

$$-\frac{2}{n}\sum _{j=1}^n\ell (A,D\mid {\mathbf{y}}_j,\widehat{\mu },\widehat{\sigma })=-\frac{2}{n}\sum _{j=1}^{n}log\int \mathit{exp}\left[\ell (A,D\mid {\mathbf{y}}_j,\mathbf{X},\widehat{\mu },\widehat{\sigma })\right]d\mathbf{X}$$ (10)

However, ∫exp[ℓ(A, D|y_j, X, μ̂, σ̂) dX in Equation (10) does not have a closed form, which makes the minimization problem much more challenging. We propose a second order Laplace integral approximation of S(A, D|y, μ̂, σ̂, λ) into a function with a closed form, S(A, D|y, χ̂, μ̂, σ̂, λ), which is defined as

$$\begin{array}{l}S(A,D\mid y,\widehat{\chi },\widehat{\mu },\widehat{\sigma },\lambda )\equiv -\frac{2}{n}\sum _{j=1}^n\left[\frac{1}{2}log\mid D^{-1}\mid -\frac{1}{2}{\widehat{\chi }}_j^T{(I-A)}^T{D}^{-1}(I-A){\widehat{\chi }}_j\right]\\ -\frac{2}{n}\sum _{j=1}^n\left[-\frac{p}{2}log(2\pi )\right]\\ +-\frac{2}{n}\sum _{j=1}^n\sum _{k=1}^p\left[C_{jk}{\widehat{\chi }}_{jk}+F_{jk}-\mathit{exp}\left({\widehat{\sigma }}_k{\widehat{\chi }}_{jk}+{\widehat{\mu }}_k\right)\right]\\ +\frac{1}{n}\sum _{j=1}^{n}log\left|{(I-A)}^T{D}^{-1}(I-A)+{\mathit{diag}}_{k=1}^p({\widehat{\sigma }}_k^2\mathit{exp}({\widehat{\sigma }}_k{\widehat{\chi }}_{jk}+{\widehat{\mu }}_k)\right|\\ +\lambda \mid A\mid ,\end{array}$$ (11)

where χ̂_j = arg max_X log P (X, y_j|A, D, μ̂, σ̂), and χ̂ is the n × p matrix defined as χ̂ = [χ̂₁, χ̂₂, χ̂₃, …, χ̂_n]^T. χ̂_jk is the (j, k) entry of χ̂ matrix. By introducing the intermediate estimated variable χ̂, the objective function S(A, D|y, χ̂, μ, σ, λ) has a closed form. The details are in Web Appendix A of Supplementary Materials.

Based on the Laplace approximation, we propose an iterative optimization procedure to minimize the objective function by iteratively estimating χ̂, A, and D until χ̂ converges. We iterate two steps: estimating χ̂ at fixed A and D; and minimizing the penalized log-likelihood objective function over the two parameters A and D respectively given the estimated χ̂. The details of the algorithm are outlined below.

We first estimate χ̂ by maximizing the log-likelihood of the complete data over X at each iteration t given Â^(t) and D̂^(t), which is

$${\widehat{\chi }}_j^{(t)}=\mathit{arg}\underset{\mathbf{X}}{max}logP(\mathbf{X},{\mathbf{y}}_j\mid {\widehat{A}}^{(t)},{\widehat{D}}^{(t)},\widehat{\mu },\widehat{\sigma }),$$ (12)

As discussed in the previous two sections, log P(X, y_j|Â^(t), D̂^(t), μ̂, σ̂) can be decomposed into log P(y_j|X, μ, σ) + log P (X|A, D), the sum of log-likelihood of y_j given latent variable X, and the log-likelihood of X under the DAG adjacency matrix A and variance matrix D. As further detailed in Web Appendix B of Web-based Supplementary Materials,

$${\widehat{\chi }}_j^{(t)}=\mathit{arg}\underset{\mathbf{X}}{max}\left[-\frac{1}{2}{\mathbf{X}}^T{(I-{\widehat{A}}^{(t)})}^T{({\widehat{D}}^{(t)})}^{-1}(I-{\widehat{A}}^{(t)})\mathbf{X}+{\mathbf{X}}^T{C}_j-\mathit{exp}{(\widehat{\mu })}^T\mathit{exp}(\widehat{\sigma }\ast \mathbf{X})\right],$$ (13)

where * indicates an element-by-element multiplication. Maximizing Equation (13) is a separate optimization problem in terms of j. Maximizing Equation (13) can be achieved by a gradient search algorithm such as a quasi-Newton method with box constraints of a lower and upper bound (Byrd et al., 1995). We use the function optim() in R package.

We then minimize the objective function S(A, D̂^(t)|y, χ̂^(t), μ̂_k, σ̂_k, λ) with respect to the parameter matrix A given χ̂^(t). Note that this minimization is subject to the acyclic restriction of the structure matrix T_A.

$$\begin{array}{lll}{\widehat{A}}^{(t+1)}\hfill & \hfill =\hfill & \mathit{arg}\underset{A}{min}S(A,{\widehat{D}}^{(t)}\mid y,{\widehat{\chi }}^{(t)},{\widehat{\mu }}_k,{\widehat{\sigma }}_k,\lambda )\hfill \\ \hfill \hfill & s.t.\hfill & T_{\widehat{A}}^{(t+1)}\text{satisfies}\text{the}\text{acyclic}\text{constraint}(7).\hfill \end{array}$$ (14)

As detailed in Supplementary Materials (Web Appendix A), S(A, D̂^(t)|y, χ̂^(t), μ̂_k, σ̂_k, λ) can be further approximated by

$$S(A,{\widehat{D}}^{(t)}\mid y,{\widehat{\chi }}^{(t)},{\widehat{\mu }}_k,{\widehat{\sigma }}_k,\lambda )\propto \frac{1}{n}\sum _{k=1}^p{\Vert {\widehat{\chi }}_k^{(t)}-{\widehat{\chi }}^{(t)}{\mathbf{a}}_k\Vert }_2^2+\frac{1}{n{({\widehat{\sigma }}_{{\mathrm{\Gamma }}_k}^2)}^{(t)}}\sum _{k=1}^p{\Vert g_k-g{\mathbf{a}}_k\Vert }_2^2+\lambda \sum _i\sum _j\mid a_{ij}\mid -\frac{2}{n}\sum _{j=1}^n\sum _{k=1}^{p}Q({\widehat{\chi }}_{jk}^{(k)},y_{jk},\widehat{{\mu }_k},\widehat{{\sigma }_k}),$$ (15)

where a_k is a coefficient vector, [a_k1, a_k2, …, a_k(p−1), a_kp]^T, which is a column vector representing a k^th row in A matrix. g is the matrix of [g_jk] with $\frac{1}{g_{jk}}={\sigma }_k\mathit{exp}\{({\sigma }_k{\widehat{\chi }}_{jk}+{\mu }_k)/2\}$, and g_k is the k_th column vector of g. Q(χ̂_jk, y_jk, μ_k, σ_k) is a term independent of A, defined by

$$Q({\widehat{\chi }}_{jk},y_{jk},{\mu }_k,{\sigma }_k)=y_{jk}{\sigma }_k{\widehat{\chi }}_{jk}+y_{jk}{\mu }_k-log(y_{jk}!)-\mathit{exp}\left({\sigma }_k{\widehat{\chi }}_{jk}+{\mu }_k\right)-log({\sigma }_k)-\frac{{\sigma }_k{\widehat{\chi }}_{jk}+{\mu }_k}{2}.$$

Minimizing Equation (15) becomes separable lasso problems in terms of k.

This problem of minimizing function (15) with the acyclic constraint (7) is very similar to the optimization of function (8). We propose to use the DIST algorithm detailed in Han et al. (2014) and in Web Appendix B of Web-based Supplementary Materials. Last, we update D̂^(t+1) by

$${\widehat{D}}^{(t+1)}=\mathit{diag}\left[\sum _{j=1}^n\frac{1}{n}(I-{\widehat{A}}^{(t+1)}){\widehat{\chi }}_j^{(t)}{\left((I-{\widehat{A}}^{(t+1)}){\widehat{\chi }}_j^{(t)}\right)}^T\right].$$

The description of the complete algorithm referred to as Poisson Log-Normal DAG estimation (plnDAG) is shown in Figure 1. For the initial step, we set A⁽⁰⁾ = 0, D⁽⁰⁾ = I, and ${\widehat{\chi }}^{(0)}={\left[{\widehat{\chi }}_1^{(0)},{\widehat{\chi }}_2^{(0)},\dots ,{\widehat{\chi }}_n^{(0)}\right]}^T$ such that ${\widehat{\chi }}_{jk}^{(0)}$, which is the k^th entry of ${\widehat{\chi }}_j^{(0)}$, is a standardized value from $\frac{log{y}_{jk}-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}$. The iterative optimization steps estimate A, D, and χ repeatedly numerically until ||χ̂^(t) − χ̂^(t+1)|| < δ, or we stop the algorithm at a certain step κ. The essence of the proposed algorithm is similar to the Expectation Conditional Maximization (ECM) algorithm, which can be viewed as a joint maximization method for the objective function over the parameters and latent variables by fixing one argument and maximizing over the others (Neal and Hinton, 1999; Hastie, Tibshirani, and Friedman, 2009).

Figure 1.

The description of the plnDAG algorithm.

For some joint distributions, there exist possibly many factorizations of the likelihood function (10). Those DAGs encode the same set of joint distributions, called an equivalence class. Equivalent DAGs cannot be distinguished from observational data. The equivalence class can be described by a completed partially directed acyclic graph (cpDAG) (Chickering, 1995, 2002), which has the following properties: every directed edge exists in all DAGs of the equivalence class, and for every undirected edge X_i − X_j, there exists a DAG with X_i → X_j and a DAG with X_i ← X_j in the equivalence class. Chickering (1995, 2002) discussed an algorithm to extend a DAG to a cpDAG by identifying the reversible edges in the DAG estimate. We can also apply the algorithm on DAG_Â to obtain cpDAG_Â. This step is implemented by essentialGraph() function of R package ggm (Chickering, 1995, 2002).

2.4 Selection of the penalty parameter

For a pre-determined integer K, one can employ a K-fold cross-validation (CV) method to select the best tuning parameter in the proposed plnDAG model by criteria such as minimizing the prediction error or the Bayesian information criterion (BIC) (Rothman et al., 2008; Yuan and Lin, 2007). This is sometimes computationally expensive for high-dimensional count data. Meinshausen and Buhlmann (2006) proposed an α-based λ, ${\lambda }_{\alpha }=\frac{2{\widehat{\sigma }}_{X_k}}{\sqrt{n}}\left[1-{\mathrm{\Phi }}^{-1}\left(\frac{\alpha }{2p^2}\right)\right]$, where Φ⁻¹() is the cumulative distribution function of N(0, 1), to control the error rate α of the neighborhood estimation with computational simplicity. Shojaie and Michailidis (2010) demonstrated the asymptotic consistency for ${\lambda }_k(\alpha )=\frac{2{\widehat{\sigma }}_{X_k}}{\sqrt{n}}\left[1-{\mathrm{\Phi }}^{-1}\left(\frac{\alpha }{2p(k-1)}\right)\right]$. Here, we adopt a similarly defined α-based λ as

$${\lambda }_k(\alpha )=\frac{2}{\sqrt{n}}\left[1-{\mathrm{\Phi }}^{-1}\left(\frac{\alpha }{2p(p-1)}\right)\right].$$ (16)

3. Simulation Study

In this section, we discuss the simulation study for the proposed algorithm, plnDAG, and compare it with other existing methods. We consider various simulation scenarios in terms of dimension-to-sample size ratio, network topological structure, and density. Edges are created according to either a random topological structure or a hub topological structure (Margolin et al., 2006). In a random network, edges are randomly created so that each node is equally likely to be connected to any other node. In a hub network, edges are created from a small number of hub nodes to their child nodes. The hub network structure mimics many real biological networks where only a small number of nodes are regulators and each of them has many targets to regulate (Margolin et al., 2006). To create a hub network, we first pick a certain proportion P_h of nodes to be hub nodes (parents’ nodes), then simulate edges from the selected hub node to multiple child nodes. We explored P_h = 20% and 10%. We use the number of variables, p = 200, and the sample size n = 100 for the scenario of n < p and n = 400 for the scenario of n > p. The density of the graph is defined by d, which indicates the average number of parents per child. We use d = 1 or d = 2, and the edges are distributed randomly. For the connectivity of graphs, we control the minimum number of parents for each child by 1 and the maximum number by 3. For the existing edge (i, j), the value of a_i,j in matrix A is set at 0.8. The latent variables Γ_k’s are generated from independent standard normal distributions. The multivariate normal distributions with variables, X₁, …, X_p, are generated from the linear structural equations of (5). Then, to generate Poisson data based on (1), we set μ_k = μ and σ_k = σ for k = 1, 2, …, p. Based on gene expressions in ovarian cancer discussed later, the scatter plot of μ̂’s and σ̂’s is in Web Appendix H of Web-based Supplementary Materials. The scatter plot, which is fitted by a smoothing spline, shows a decreasing trend of σ as μ increases. We select μ =2, 5, and 8, and we select σ which is on the fitted line or maximum σ given μ. Thus, we can investigate the performance in the case of average variability and large variability given each μ. The combinations of (μ, σ) are (2,1.2), (2,2), (5,0.7), (5,1.5), (8,0.5), and (8,1.5). We use 20 replications for each scenario, and for the stopping rule in the plnDAG method, we use δ = 10⁻⁹ and κ = 15.

We adopt Receiver Operating Characteristic (ROC) curves to examine the true and false positive rates (TPR and FPR) plotted across a range of λ(α) values. TPR is calculated by $\frac{TP}{TE}$, where TP (True Positive) is the number of correctly detected edges regardless of directionality, and TE is the number of true edges simulated in the DAG. FPR is calculated by $\frac{FP}{(p(p-1)/2-TE)}$, where FP (False Positive) is the number of edges detected by mistake. In addition, we calculate the False Discovery Rate (FDR) as 1 − TP/EE, where EE is the number of all estimated edges. In addition, we consider directed TP(dTP) as detected edges with correctly estimated directions; and directed FDR as dFDR = 1 −dTP/EE. Therefore, for a cpDAG estimate, correctly detected directions, undecided directions, or reversely detected directions are counted as TPs if the true edge is estimated, but only correctly detected directions are counted as dTPs. These two sets of metrics can comprehensively assess the performance of each method with respect to edge detections and direction detections.

3.1 Comparison of the plnDAG method with the alternative approaches

We apply the plnDAG method following Section 2.3, and compare its performance with the performance of three alternative methods. The first approach is to directly apply the L₁-penalized likelihood framework assuming multivariate normal distribution, referred to as a like-norm approach. The second comparison method is to first log-transform the count data, then apply the L₁-penalized likelihood model assuming multivariate normal distribution to the transformed data. We refer to it as a like-log approach. Note that log-transformation is a widely applied approach for multivariate count data. For both approaches, to find the solution to minimize the L₁-penalized likelihood objective function under a multivariate normal distribution, we use the DIST search algorithm by Han et al. (2014), which shows improvements in performances over the coordinate descent search algorithm (Fu and Zhou, 2013). The DIST algorithm is also used to estimate Equation (14) in the proposed plnDAG algorithm. As the same optimization algorithm is used to optimize Equation (14), the differences in simulation performances can be attributed to the model difference. The third approach is the RPC-algorithm by Harris and Drton (2013), which incorporates rank-based correlations with the PC-algorithm.

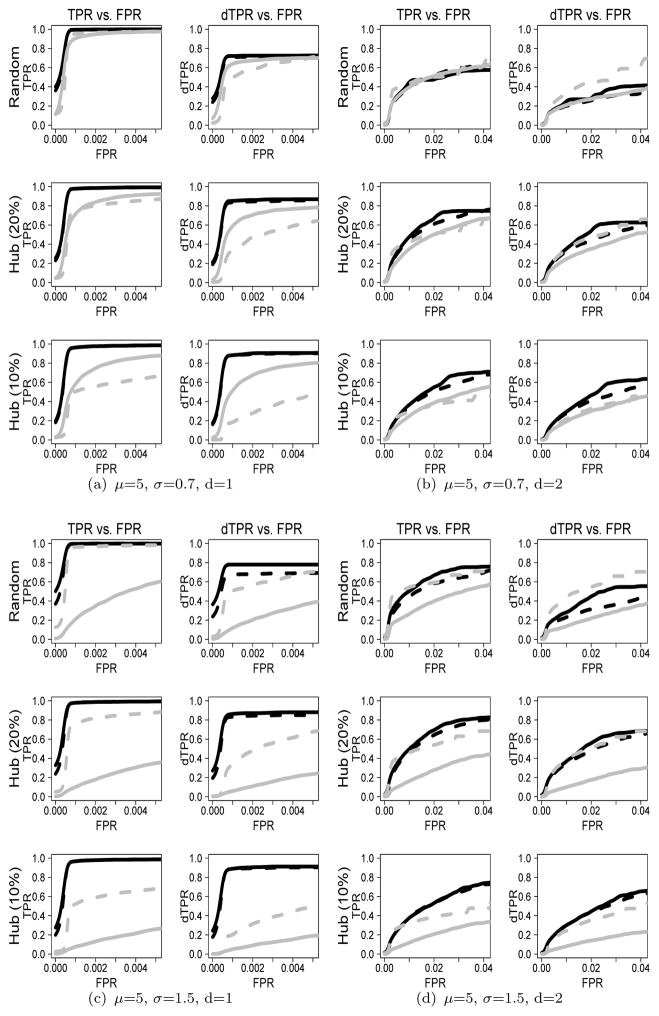
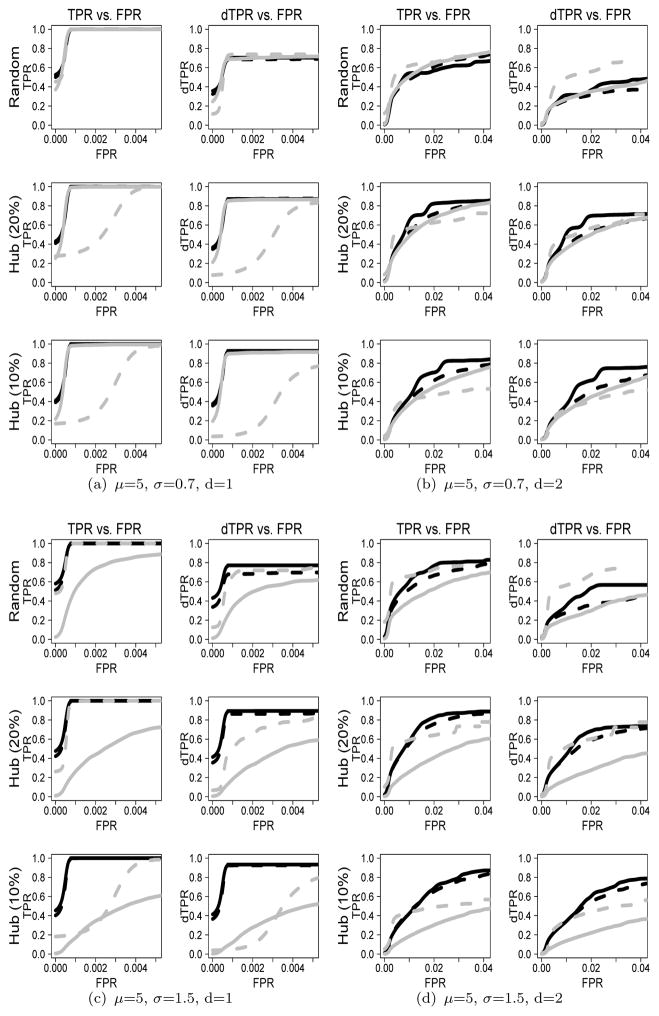
To investigate the performance of the plnDAG method with other methods, we show the ROC curves for μ=5 when p=200 and n=100 (n < p) and p=200 and n=400 (n > p) in Figures 2 and 3, respectively. The ROC curves for μ=2 or μ=8 show similar patterns, which are in web Appendix C of Supplementary Materials.

Figure 2.

ROC curves based on TPR (dTPR) vs. FPR when μ=5 and n=100: The solid black line indicates the plnDAG method, the dashed black line indicates the like-log approach, the solid gray line indicates the like-norm approach, and the dashed gray line indicates the RPC method. The upper panel (Figures (a) and (b)) shows ROC curves for μ = 5 and σ = 0.7, and the lower panel (Figures (c) and (d)) shows ROC curves for μ = 5 and σ = 1.5.

Figure 3.

ROC curves based on TPR (dTPR) vs. FPR when μ=5 and n=400: The solid black line indicates the plnDAG method, the dashed black line indicates the like-log approach, the solid gray line indicates the like-norm approach, and the dashed gray line indicates the RPC method. The upper panel (Figures (a) and (b)) shows ROC curves for μ = 5 and σ = 0.7, and the lower panel (Figures (c) and (d)) shows ROC curves for μ = 5 and σ = 1.5.

We first compare the plnDAG method (solid black line) with the like-norm approach (solid gray line) which assumes multivariate normal distribution. For the count data with small σ/μ ratios such as (μ, σ)=(5,0.7), the ROC curves between the plnDAG and the like-norm approaches are relatively close. However, the performance difference is clearly shown as σ/μ ratios increase, where the count data deviate more from normal distributions. The TPRs and dTPRs of the like-norm approach are much lower than those of the plnDAG method for all scenarios. Similar patterns are also shown in the scenarios of μ=2 and μ=8 in Web Appendix C of Supplementary Materials. Under the scenarios of μ = 5, the like-log approach (dashed black line), which assumes multivariate normal distribution of the log transformed data, showed performances close to those of the plnDAG methods for sparse networks. When the underlying graphs get less sparse, the performance difference between the two methods increases. The plnDAG showed higher TPRs and dTPRs especially for random structures and for directed edge detections. The performance difference between the plnDAG method and the rank-based RPC method (dashed gray line) depends on network structures and sparsity. Under the random network structure, the plnDAG method showed better or close performances for sparse networks, but was out-performed by the RPC method for dense networks. However, the performance of the RPC method is negatively impacted under hub network structures, and the impact is more severe as more edges are concentrated around a smaller number of hub nodes (i.e., from random networks to hub networks (Ph=10%)). The decrease in performance is also more severe in small sample sizes (e.g., n = 100 than n = 400). The PC-like approaches, such as the RPC method, utilize a universal threshold on the conditional independence tests to control sparsity on a whole view. For hub networks with unbalanced edge distributions, this universal sparsity control approach might generate an overly-sparse estimate around the hub nodes. On the other hand, the penalized likelihood based objective function is more flexible, so it generates more robust performance with respect to the underlying random or hub network structure.

To estimate DAGs, the plnDAG method estimates μ̂ and σ̂ first in Equations (3) and (4), then plugs the estimates into the objective function S(A, D|y, μ̂, σ̂, λ). To investigate the effect of the plug-in approach, we compared its performance to that of the plnDAG method with S(A, D|y, μ, σ, λ) where the Poisson parameters μ and σ are from the true values in simulations. The ROC curves of the two approaches are in Web Appendix D of Supplementary Materials. As the curves show, the performances are almost identical. We also compared the values of the objective function S(A, D|y, μ̂, σ̂, λ) estimated by the second order Laplace integral approximation in Equation (11) with its values estimated by numerical calculation in simulations for p = 5 (Web Appendix E of Supplementary Materials). As shown, the ratios between the values obtained from the two approaches from all simulations with various parameters are randomly distributed around 1 and bounded between 95% to 110%. Therefore, we believe the approximation performs reasonably well and enables the algorithm to be computed much faster.

The computational time of the plnDAG is very efficient and feasible. Table 1 shows the computational time of the three methods based on all cases of d, μ, and σ. Note that the computational time of the RPC method is small for sparse networks when d = 1, but significantly increases as the network gets dense when d=2; while the plnDAG is reasonably fast for all scenarios.

Table 1.

Computational time (minutes) under p = 200

Structure	d	μ	σ	n=100	like-log	like-norm	RPC	n=400	like-log	like-norm	RPC
				plnDAG				plnDAG
Random	1	2	1.2	4.1	0.6	0.4	0.9	5.1	0.4	0.4	1
	1	2	2	2.8	0.5	0.3	0.7	3.9	0.4	0.3	0.5
	1	5	0.7	0.8	0.5	0.4	0.7	1.1	0.4	0.4	0.9
	1	5	1.5	1.4	0.5	0.4	1.1	2.6	0.6	0.5	0.8
	1	8	0.5	0.8	0.5	0.5	1.1	1.2	0.5	0.6	0.8
	1	8	1.5	1.1	0.5	0.4	1	2	0.6	0.6	0.8
	2	2	1.2	6.8	0.4	0.6	355.6	10.7	0.6	0.8	7360.5
	2	2	2	6.9	0.5	1	295.8	10.1	0.8	0.9	5418.4
	2	5	0.7	4.2	0.7	0.8	201.2	7.1	0.9	1.2	1770.4
	2	5	1.5	5.8	0.9	1.3	277.1	11.3	1.4	1.8	684.3
	2	8	0.5	4.4	2.2	1.9	328.2	9.4	3.1	3	779.9
	2	8	1.5	4	3.1	1.4	342.4	5.7	3.5	1.8	1043.0
Hub (10%)	1	2	1.2	4.1	0.6	0.3	1	7.6	0.7	0.3	7.1
	1	2	2	4.2	0.6	0.2	1.2	10.9	0.7	0.2	9.8
	1	5	0.7	0.7	0.3	0.3	1.3	0.9	0.3	0.4	18.7
	1	5	1.5	1	0.4	0.3	1.7	1.8	0.3	0.4	22.8
	1	8	0.5	0.6	0.3	0.4	1.7	0.7	0.4	0.5	22.3
	1	8	1.5	0.7	0.3	0.3	1.6	1.4	0.3	0.4	22.1
	2	2	1.2	11.9	0.9	0.5	137.4	24.1	1	0.6	971.1
	2	2	2	6.9	1.1	0.5	104.3	12.3	1.1	0.5	450.3
	2	5	0.7	2.1	0.5	0.4	52.5	3.8	0.6	0.5	126.7
	2	5	1.5	2.1	0.6	0.6	47.5	3.2	0.7	0.6	90.9
	2	8	0.5	1.3	0.6	0.7	46.0	1.6	0.9	1	82.7
	2	8	1.5	1.3	0.6	0.5	44.5	1.9	0.9	0.6	83.9

3.2 Performance of the plnDAG

To investigate the performance of the plnDAG method, we first examine its performance as a function of the λ(α). For this purpose, we showed the Matthew’s correlation coefficient (MCC) of the plnDAG along a range of λ(α) (Web Appendix F of Supplementary Materials). The above simulation results suggest that the performance of the plnDAG method is not very sensitive to the choice of α as long as α is in a reasonable range; however, a value of α = 0.1 seems to deliver more reliable estimates for most simulated scenarios.

Table 2 summarizes the average performance and CPU time of the plnDAG method at λ(α = 0.1) over 20 replicates for each combination of network density, μ, σ, and the number of nodes (p=200 or 500) when d=1 and n=100. The summary table for n=400 is in Web Appendix G of Supplementary Materials. Results in the tables suggest that the plnDAG method can efficiently estimate DAGs with reasonable performance accuracy and running time even for high dimensional sparse networks (p = 500 and n = 100 or 400). Under the sparse network, most FDRs are controlled below 10%, and dFDRs are controlled below 30%.

Table 2.

Summary of the simulation results of the plnDAG method with λ(α = 0.1) under the sparse network (n=100)

Structure	μ	σ	p	λ(α = 0.1)	TPR (dTPR)	FDR (dFDR)	computational time (minutes)
Random	2	1.2	200	0.94142	0.92 (0.66)	0.02 (0.29)	2.6
	2	1.2	500	1.01372	0.90 (0.67)	0.01 (0.27)	13.3
	2	2	200	0.94142	0.97 (0.71)	0.03 (0.29)	2.5
	2	2	500	1.01372	0.97 (0.73)	0.02 (0.26)	15.6
	5	0.7	200	0.94142	0.98 (0.70)	0.01 (0.29)	0.7
	5	0.7	500	1.01372	0.97 (0.74)	0.01 (0.25)	5.1
	5	1.5	200	0.94142	0.99 (0.77)	0.02 (0.24)	1.7
	5	1.5	500	1.01372	0.99 (0.79)	0.01 (0.21)	9.9
	8	0.5	200	0.94142	0.98 (0.71)	0.01 (0.28)	0.8
	8	0.5	500	1.01372	0.98 (0.74)	0.01 (0.25)	5.1
	8	1.5	200	0.94142	0.99 (0.77)	0.02 (0.24)	1.1
	8	1.5	500	1.01372	0.99 (0.79)	0.01 (0.21)	7.2
Hub (20%)	2	1.2	200	0.94142	0.87 (0.74)	0.02 (0.17)	2.5
	2	1.2	500	1.01372	0.90 (0.67)	0.01 (0.26)	13.3
	2	2	200	0.94142	0.95 (0.81)	0.08 (0.21)	2.4
	2	2	500	1.01372	0.97 (0.74)	0.02 (0.26)	15.2
	5	0.7	200	0.94142	0.95 (0.82)	0.02 (0.15)	0.6
	5	0.7	500	1.01372	0.97 (0.74)	0.01 (0.24)	5.2
	5	1.5	200	0.94142	0.97 (0.85)	0.05 (0.17)	1.3
	5	1.5	500	1.01372	0.99 (0.79)	0.01 (0.21)	8.2
	8	0.5	200	0.94142	0.96 (0.83)	0.02 (0.15)	0.5
	8	0.5	500	1.01372	0.98 (0.74)	0.01 (0.25)	5.1
	8	1.5	200	0.94142	0.97 (0.85)	0.05 (0.17)	1.1
	8	1.5	500	1.01372	0.99 (0.79)	0.01 (0.21)	6.6
Hub (10%)	2	1.2	200	0.94142	0.88 (0.80)	0.05 (0.13)	1.6
	2	1.2	500	1.01372	0.90 (0.67)	0.01 (0.26)	13.9
	2	2	200	0.94142	0.94 (0.84)	0.21 (0.29)	2.8
	2	2	500	1.01372	0.97 (0.74)	0.03 (0.26)	15.0
	5	0.7	200	0.94142	0.95 (0.87)	0.04 (0.12)	0.5
	5	0.7	500	1.01372	0.97 (0.74)	0.01 (0.24)	5.9
	5	1.5	200	0.94142	0.97 (0.89)	0.08 (0.16)	1.1
	5	1.5	500	1.01372	0.99 (0.78)	0.01 (0.22)	8.6
	8	0.5	200	0.94142	0.96 (0.88)	0.04 (0.12)	0.6
	8	0.5	500	1.01372	0.98 (0.74)	0.01 (0.25)	5.1
	8	1.5	200	0.94142	0.97 (0.90)	0.09 (0.16)	0.9
	8	1.5	500	1.01372	0.99 (0.78)	0.01 (0.22)	6.9

4. Application

We applied the plnDAG algorithm to derive the gene networks in a dataset of 265 ovarian adenocarcinomas tumor samples (The Cancer Genome Atlas Research Network, 2011), obtained from TCGA (http : //tcga - data.nci.nih.gov/docs/publications/ov₂011). The goal of our application is to find regulatory relationships among genes, that is, to determine which are the regulators (Transcription Factor encoding genes) and which are the regulated target encoding genes, through the analysis of mRNA expression data obtained by the level 3 data with RNASeqV2 platform that contains normalized count data. Several papers in the literature have found a list of genes, which have important roles in ovarian cancer growth or treatment. Bolton et al. (2012) has studied candidate genes related to ovarian cancers for several decades with respect to biological pathways. The list of 38 important candidate genes is shown in Web Appendix H of Supplementary Materials.

The gene-gene interaction networks provided in NetBox (http://cbio.mskcc.org/tools/netbox/index.html), which extracts the information of gene interaction from four curated data sources: Human Protein Reference Database (Keshava Prasad et al., 2009), Reactome (Joshi-Tope et al., 2005; Matthews et al., 2009), NCI-Nature Pathway Interaction Database (Schaefer et al., 2009), and MSKCC Cancer Cell Map (http://www.mskcc.org/) were used as the basis to evaluate the performance of the plnDAG algorithm.

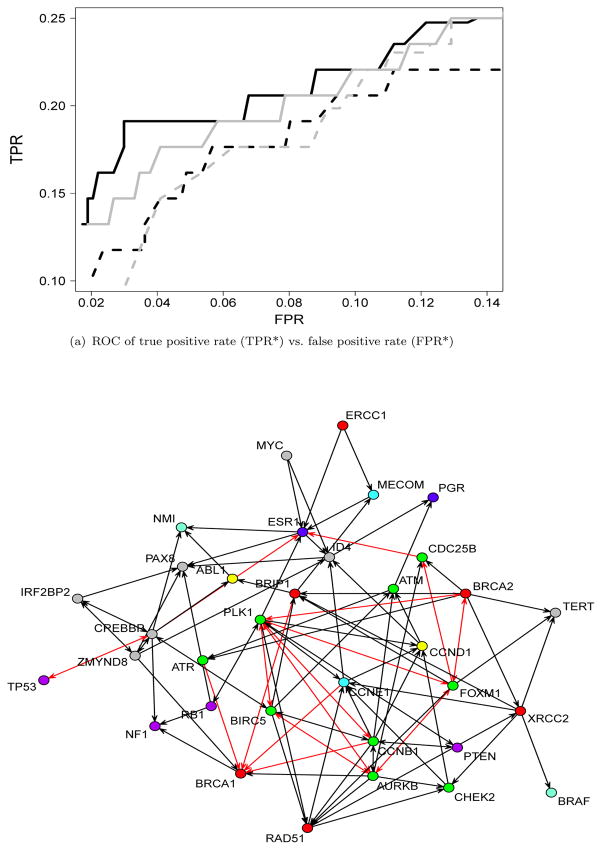
After we estimate the network, we check how many edges are overlapped with the previously found interactions. Since there may be undetected interactions at a current stage in this area, we calculate how many edges among those detected from the plnDAG method, the like-log approach, the like-norm approach, or the RPC method are overlapped with the known interactions. Figure (a) shows true positive rate (TPR*) and false positive rate (FPR*) based on known interactions. TPR* is defined by DE/KE, and FPR* is defined by (EE-DE)/(p(p-1)/2-KE), where DE is the number of detected edges (overlapped with known interactions), KE is the number of known interactions, and EE is the number of total estimated edges. The range of x-axis (FPR*) in the plot is from about a half of the number of genes to the triple of it. As the plot shows, the plnDAG method has more overlapped edges than the other methods given the same number of estimated edges. The estimated network by the plnDAG with the penalty parameter selected by the formula in (16) is shown in Figure (b). The nodes are colored based on their functional roles. The edges that are overlapped with the known interactions are colored in red. The overlapped edges are in the edges among the genes functioning in DNA repair (BRCA1, BRCA2, BRIP1), FOXM1 signaling (PLK1, CCNB1, AURKB, BIRC5, CDC25B, FOXM1, and ATR), steroid hormone (ESR1), and therapeutic target gene (CCNE1). In addition, the tumor suppressor (TP53) and the cell cycle control gene (CREBBP) are also overlapped.

5. Conclusion and Discussion

This paper discusses how to estimate the structure of directed acyclic graphs under the count data. We provide the L₁-penalized likelihood model based on the Poisson log-normal distribution under the assumption that the variances of latent variables are unknown, and variable ordering is unknown. The observed data are assumed to be compounded Poisson data, but the underlying variables follow multivariate normal distributions based on the coefficient matrix. We also propose an efficient solution search algorithm based on iterative optimization steps. The coefficient matrix is estimated by separable lasso problems, and the unobserved data parameters of the normal distribution are estimated by separate optimization problems.

The simulation result shows that our proposed method outperforms the approach based on the assumption of the normal distribution in most cases. It also performs better than or as well as the data transformed approach. The proposed method performs better than the rank-based PC method under the sparse network or hub network. Overall, our proposed method is robust against the network structure, the variability of the data, and dimensionality (dimension-to-sample size ratio) with good performance. We also discuss how to apply it to the gene expression data in ovarian cancer. It is the first method to explore DAGs for multivariate count data, and it is efficient and achieves satisfactory performance.

It is not straightforward to find the asymptotic property in the plnDAG algorithm because A is not identifiable. Shojaie and Michailidis (2010) discussed variable selection consistency of DAGs with the L₁-penalized likelihood under normal distribution in sparse network when the variable order is known. Fu and Zhou (2013) studied the model selection consistency when the variable order is unknown but the data have experimental interventions. Chickering (2002) mentioned that searching for solutions within the same equivalence class requires additional computational time, so searching for solutions among equivalence classes is efficient. If two graphs are under the same equivalence class, the objective function values based on the L₁-penalized likelihood are same. The plnDAG algorithm incorporating the DIST algorithm improves the objective function value at each iteration, so score equivalence does not affect the computational time much.

Figure 4.

ROC curves and an estimated network for ovarian adenocarcinomas tumor data