Electric Dipole Transition Moments and Solvent-Dependent Interactions of Fluorescent Boron–Nitrogen Substituted Indole Derivatives

Abstract

Fluorescent analogues of the indole side chain of tryptophan can be useful spectroscopic probes of protein–protein and protein–DNA interactions. Here we present linear dichroism and solvent-dependent spectroscopic studies of two fluorescent analogues of indole, in which the organic C═C unit is substituted with the isosteric inorganic B–N unit. We studied the so-called “external” BN indole, which has C_2v symmetry, and the “fused” BN indole with C_s symmetry. We performed a combination of absorption and fluorescence spectroscopy, ultraviolet linear dichroism (UV-LD) in stretched poly(ethylene) (PE) films, and quantum chemical calculations on both BN indole compounds. Our measurements allowed us to characterize the degree of alignment for both molecules in stretched PE films. We thus determined the orientations and magnitudes of the two lowest energy electric dipole transition moments (EDTMs) for external BN indole, and the two lowest energy EDTMs for fused BN indole within the 30 000–45 000 cm⁻¹ spectral range. We compared our experimental results to those of quantum chemical calculations using standard density functional theory (DFT). Our theoretical predictions for the low-energy EDTMs are in good agreement with our experimental data. The absorption and fluorescence spectra of the external and the fused BN indoles are sensitive to solvent polarity. Our results indicate that the fused BN indole experiences much greater solvation interactions with polar solvents than does the external BN indole.

Graphical Abstract

INTRODUCTION

A useful strategy to study the local interactions of biological macromolecules is to perform spectroscopic measurements on biomolecular complexes that are site-specifically substituted with a fluorescent chromophore that structurally mimics a naturally occurring chemical group. A likely target for such studies is the indole side chain of the amino acid tryptophan, which can function in the recognition of nucleic acid target sequences by regulatory proteins.¹ For example, when tryptophan is positioned near the surface of a DNA binding protein, its indole side chain may intercalate between exposed purine bases. Such indole–purine associations can contribute to the stability of a protein–DNA complex by as much as ~7 kcal/mol.² Although this interaction is thought to involve π-orbital stacking of flanking heteroaromatic groups,¹ much remains unclear about the local conformations and structural motifs adopted by these complexes and their associated transition states.

Recently, there has been growing interest in fluorescent probes that can be site-specifically positioned within protein-nucleic acid constructs, which can function as reporters of local DNA base conformation.³ For example, fluorescent analogues of nucleic acid bases have been developed that can be substituted for natural bases within DNA. Fluorescent probes, such as the adenine analogue 2-aminopurine (2-AP), the cytosine analogue pyrrolo-cytosine (PC), and the guanine analogue 6-methyl isoxanthopterin (6-MI) absorb light at a much lower energy than do the natural bases or amino acids. Short oligomeric DNA constructs with one or two fluorescent base analogue probes substituted for native bases can thus be optically excited at near-UV wavelengths and detected with minimal perturbation to native biomolecular structure. Recent spectroscopic studies of such systems reveal that the electronic properties of the probe fluorophores are sensitive to the degree of stacking with flanking bases.^3–6

When two fluorescent chromophores are placed at nearby positions, their electric dipole transition moments (EDTMs) can couple so that they form collective electronic excitations called excitons.^7–9 The strengths and energies of the excitons are sensitive to the local conformation of the chromophore dimer, and this effect can be observed using circular dichroism (CD) and two-dimensional fluorescence spectroscopy (2DFS).⁵ Simple models of the electronic coupling between chromophores can be used to predict experimental absorption, CD, and 2DFS data, provided that the strengths and directions of the monomer EDTMs are known.⁶ For example, the local conformation of the 2-AP dinucleotide in aqueous solution was recently elucidated using 2DFS,⁵ where the structural assignment required knowledge of the low-lying EDTMs of the 2-AP chromophore.¹⁰

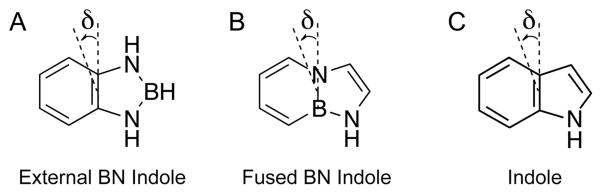
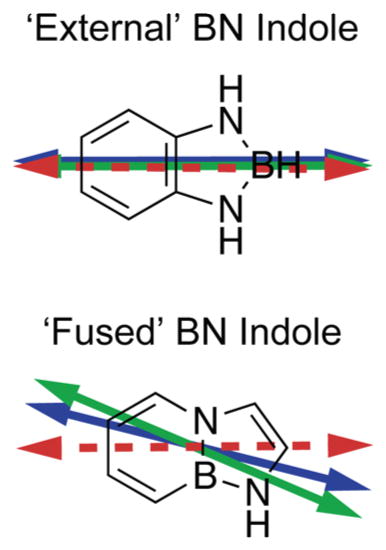
Although fluorescent nucleic acid base analogues are readily available, there exist few amino acid side-chain analogues that offer similar advantages to study local interactions within protein–DNA complexes. In this work, we study two fluorescent analogues of the indole chemical group in which the organic C═C unit is substituted with the isosteric inorganic B–N unit. These derivatives can serve as potential tryptophan analogues because they emit fluorescence at wavelengths that can be readily separated from background signals emanating from nucleic acids and proteins.^11,12 In Figure 1, we show the structures of the two BN indole derivatives that are the focus of our current study: 1,3,2-benzodiazaboroline, referred to as an “external” BN indole (shown in panel A), and the “fused” BN indole, which contains the 1,2-dihydro-1,2-azaborine core (shown in panel B). The peak absorbance of natural indole in acetonitrile occurs at 268 nm (37 313 cm⁻¹),¹¹ the peak absorbance of the external BN indole occurs at 283 nm (35 335 cm⁻¹), and that of the fused BN indole occurs at 297 nm (33 670 cm⁻¹).

Figure 1.

Chemical structures are shown of (A) the “external” BN indole, (B) the “fused” BN indole, and (C) the natural indole. The inplane angle δ is defined relative to the short molecular axis, as shown. The external BN indole (A) is assigned to the C_2v symmetry group.

In this work, we determined the orientations and magnitudes of the lowest energy EDTMs of the external and fused BN indole derivatives. We performed a combination of absorption and fluorescence spectroscopy, UV linear dichroism (UV-LD) in stretched poly(ethylene) (PE) films, and quantum chemical calculations of these compounds. Our results provide the necessary information to assign EDTMs to the two lowest energy electronic transitions for external BN indole, and the two lowest energy transitions for the fused BN indole within the 30 000–45 000 cm⁻¹ spectral range. Our electronic structure calculations were performed using density functional theory (DFT) on the equilibrium geometry ground state, followed by an excited state point energy calculation using the BL3YP and ωB79X basis sets. Our theoretical results for the lowest energy EDTMs are in very good agreement with our experimental measurements.

We further investigated the effects of solvent polarity on the absorption and fluorescence spectra for both the external and fused BN indole compounds. As the polarity of the solvent increased, the peak emission shifted to longer wavelengths. This sensitivity of the excited state reorganization energy to solvent polarity is a measure of the coupling between the electronic transition and the locally relaxing solvent environment and further suggests that these compounds may be useful probes for studies of local interactions within macromolecular complexes.

The results of these studies provide new information to interpret spectroscopic signals from BN indole compounds, which may be incorporated into proteins as fluorescent tryptophan analogues. Our determination of the lowest energy EDTMs can be used to calculate the electronic couplings between a BN indole and a neighboring chromophore, such as a second BN indole, an aromatic amino acid, or a nucleic acid base. Such information can be used to predict spectroscopic signals, such as absorbance, CD, and 2DFS, to aid in the determination of conformations of the BN indole with adjacent chromophores. The results of solvent-dependent studies of absorption and emission spectra can be used to estimate the hydrophobicity of the local environment around a particular tryptophan, and how this environment changes upon conformational rearrangements or ligand binding.

MATERIALS AND METHODS

Experimental Procedures

Chemicals

External (1,3,2-benzodiazaboroline) and fused BN indoles were synthesized as described previously.¹¹ Low-density poly(ethylene) (PE) was purchased from Goodfellow Corporation and used as received. All organic solvents used in the absorption experiments were spectrophotometric grade.

Film Preparation

PE film sheets (0.01 cm thick) were cut into 7.50 × 2.50 cm² rectangles. These were uniaxially stretched to 5 times their original length using a mechanical stretcher, as described previously.^6,7,13 Both the external and fused BN indoles were introduced into the stretched films by submersion of the polymer material into a saturated solution of the compound in chloroform at room temperature. After 3 h, the film was removed from solution and allowed to dry. A blank reference sample was prepared following the aforementioned procedure, but in this case the film was treated with neat chloroform. The above procedures were carried out in a glovebox to minimize the effects of oxidation of the BN indole compounds.

Spectroscopy

Solution absorption spectra were measured using a Cary 3E UV–visible spectrophotometer. Fluorescence emission/excitation spectra were measured using a Horiba Jobin-Yvon FluoroMax-3. LD and absorption spectra of the PE films were simultaneously measured using a JASCO CD spectrophotometer running in LD mode (Horiba Jobin-Yvon, J-720). All LD spectra were corrected by subtracting the background LD spectra obtained from a blank stretched PE film sample. All absorption and emission spectra were obtained using solutions of the same concentration (2 × 10⁻⁵ M).

Quantum Chemical Calculations

Time dependent density functional theory (TDDFT) calculations of the external and fused BN indoles were performed for comparison to our experimental measurements of the electronic transition energies and EDTMs.¹⁴ For small molecules, TDDFT can achieve an average accuracy of 0.2–0.5 eV for the transition energies of singlet excitations. However, EDTMs and oscillator strengths have not been studied as thoroughly as transition energies.⁶ Nevertheless, the shapes of the electronic absorption spectra predicted by these methods tend to match the lowest energy transitions quite well. TDDFT calculations of the lowest energy electronic transitions were carried out using the Becke B3LYP and the ωB97X (long-range corrected functional) basis sets. Ground electronic state equilibrium geometry optimizations were carried out using TDDFT, followed by single-point energy calculations in the first excited state using the two respective methods. B3LYP and ωB97X calculations were carried out using Spartan 10 (Q-Chem program).¹⁵ Minimum moment of inertia calculations were based on the B3LYP-ground state optimized structures.¹⁶

Theoretical Considerations for Linear Dichroism Measurements

We performed linear dichroism studies on PE film samples, which were treated with the two BN indole compounds illustrated in Figure 1. These PE films were uniaxially strained to induce a macroscopic alignment of the BN indole EDTMs.

We define the linear dichroism (or LD) as the difference between the absorption of light polarized parallel and perpendicular to the uniaxial strain direction, where A_||(ν̄) is the absorption of light oriented in the stretching direction of the polymer and A_⊥(ν̄) is the absorption of light oriented perpendicular to the stretching direction.

$$\text{LD}(\overline{\nu })=A_{\Vert }(\overline{\nu })-A_{\perp }(\overline{\nu })$$ (1)

The reduced linear dichroism (LD^r) is given by

$${\text{LD}}^{\mathrm{r}}(\overline{\nu })=\frac{\text{LD}(\overline{\nu })}{A_{\text{iso}}(\overline{\nu })}$$ (2)

where A_iso(ν̄) is the absorption of light in an isotropic sample. A_iso(ν̄) can be calculated from the polarized components of the strained sample, according to¹⁰

$$A_{\text{iso}}(\overline{\nu })=\frac{A_{\Vert }(\overline{\nu })+2A_{\perp }(\overline{\nu })}{3}$$ (3)

LD^r(ν̄) depends only on the orientations of the EDTMs, which absorb at frequency ν̄.⁶ The value of the LD^r is expected to be constant across an isolated absorption band that is characterized by a single EDTM.

For a planar molecule, the value of the LD^r associated with the ith EDTM can be written as^7,10

$${\text{LD}}_i^{\mathrm{r}}=3(S_{yy}{sin}^2{\theta }_i+S_{zz}{cos}^2{\theta }_i)(i\text{th}\text{in-plane}\text{transition})$$ (4)

where S_xx, S_yy, and S_zz are called the Saupe orientation parameters. These parameters specify the orientational distribution of the BN indole molecules within the strained PE film. By convention, we assume a Cartesian coordinate system with z-axis parallel to the strain direction.⁷ Furthermore, for the planar molecules under consideration, we take the y-and z-axes to lie within the molecular plane, and the x-axis to be normal to that plane.⁶ The angle θ_i defines the orientation of the ith EDTM relative to the z-axis.

For each electronic transition, we determined the value of LD^r according to the method of Thurstrup, Eggers, and Michl (the TEM method).¹⁷ We constructed linear combinations of the polarized spectra according to A_||(ν̄) − dA_⊥(ν̄), where the constant d is called the “reduction coefficient”. The value d_i for which the ith spectral feature vanishes yields the corresponding value for ${\text{LD}}_i^{\mathrm{r}}$ according to

$${\text{LD}}_i^{\mathrm{r}}=3\frac{d_i-1}{d_i+2}$$ (5)

Ideally, the Saupe parameters in eq 4 would be determined using an independent set of experimental observations. For example, infrared LD measurements might have been used to identify the directions of a specific N–H vibrational transition moment. In principle, by combining the results of infrared LD with the assumption that the molecule aligns with its long axis parallel to the film strain direction, one could solve eq 4 for the values of the Saupe parameters. Unfortunately, our attempts to obtain the infrared LD spectra for our samples were unsuccessful due to insufficient signal intensity in comparison to background absorption by the PE film. For this reason, we followed an alternative approach to determine the Saupe parameters by taking advantage of the C_2v symmetry of the external BN indole, and the fact that the molecular structures of both BN indole compounds are similar enough that they are expected to orient identically in the stretched films. We calculated the minimum principle moments of inertia using the computed ground state geometry of each molecule, and these were confirmed to lie parallel to the long molecular axes in both cases. On the basis of the C_2v symmetry of the external BN indole, we assumed that the lowest energy (i = 1) EDTM lies parallel to the long molecular axis. We thus determined the values of the Saupe parameters using our experimental LD data of the external BN indole. We first determined the value of S_zz according to

$${\text{LD}}_1^{\mathrm{r}}=3S_{zz}(\text{lowest}\text{energy}\text{in-plane}\text{transition}\text{of}\text{external}\text{BN}\text{indole})$$ (6)

We next estimated the value of S_yy using the minimum LD^r that corresponds to the in-plane short axis transition, and which satisfies the inequality

$$3S_{yy}\le {\text{LD}}_{i\ne 1}^{\mathrm{r}}(\text{in-plane})\le 3S_{zz}$$ (7)

Finally, the value for S_xx was determined using the constraints

$$S_{xx}+S_{yy}+S_{zz}=0$$ (8)

and

$$S_{zz}\ge S_{yy}\ge S_{xx}$$ (9)

To determine the angle θ_i of the ith EDTM for the fused BN indole, we substituted the above values for the Saupe parameters into eq 4. This procedure yielded two possible values of θ_i, one positive and one negative. We selected from these two possibilities by comparison to our computational results. The transformation from the angle θ_i, which describes the EDTM orientation relative to the uniaxial strain direction, to the angle δ_i in the plane of the BN indole molecule, is given by the simple relation δ_i = ±θ_i + 90°. This follows from our assumption that the long molecular axes of both BN indole derivatives lie parallel to the strain direction in the films.

RESULTS AND DISCUSSION

Isotropic Absorption and Reduced Linear Dichroism Spectra

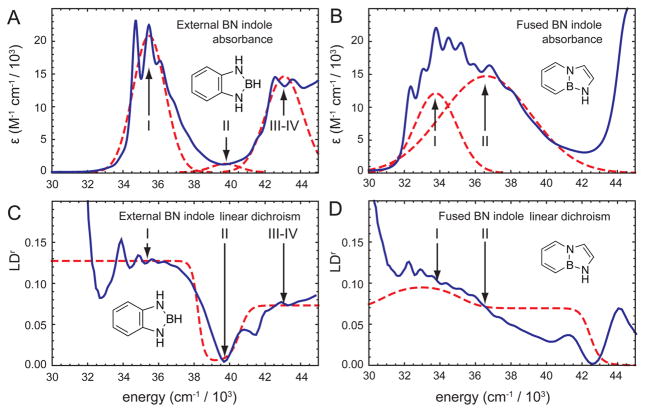
In Figure 2A, we show the absorption spectrum of the external BN indole. The spectrum exhibits two pronounced features, which can each be described as a distinct electronic-vibrational progression. By applying a Gaussian decomposition analysis to the spectrum, we identified peak I centered at 35 473 cm⁻¹ (282 nm) and peaks III–IV centered at 43 086 cm⁻¹ (232 nm). As we explain below, our results suggest that the feature identified as peaks III–IV represents two overlapping transitions, which cannot be spectroscopically resolved. We further identified peak II as a weakly absorbing transition centered at 39 756 cm⁻¹ (252 nm). In Figure 2B, we show the absorption spectrum of the fused BN indole, which displays a strong asymmetric band centered at 35 120 cm⁻¹ (285 nm). Gaussian decomposition of this broad line shape produced two underlying features, which we identified as peak I centered at 33 771 cm⁻¹ (296 nm) and peak II centered at 36 612 cm⁻¹ (273 nm).

Figure 2.

Results of polarized absorption measurements of the BN indole derivatives in stretched PE films. (A, B) The experimental absorption spectra (blue) of the external BN indole (A) and the fused BN indole (B) are shown in comparison to fits of these data to Gaussian functions (dashed red curves). Transitions are numbered according to the same scheme as in Table 1. (C, D) The experimental LD^r spectra (blue) of the external BN indole (C) and the fused BN indole (D) are shown in comparison to the calculated LD^r spectra (dashed red), which are based on the experimental transition moment orientations, intensities, energies, and peak widths obtained from a simultaneous fit to the data shown in (A) and (B), respectively.

We used eq 2 to construct the experimental LD^r spectra for the external and fused BN indole compounds from our polarization-dependent measurements (Figure 2C,D, respectively). For the case of the external BN indole (Figure 2C), the constant value of the LD^r in the neighborhood of peak I suggests that this feature is representative of a single electronic transition. For the case of the fused BN indole (Figure 2D), the sloped form of the LD^r in the vicinity of the strong low-energy band is consistent with our decomposition of this peak into two separate electronic transitions, which we identified as peak I and peak II.

Following the TEM procedure, we calculated the numerical values of the signal ( ${\text{LD}}_i^{\mathrm{r}}$) for the ith electronic transition using eq 5.⁶ Both the experimental absorption spectra and the LD^r spectra were fit to a model that assumed each underlying feature to be Gaussian with adjustable center energy ν̄_i, line width parameter σ_i and intensity I_i.

$$A_{\text{calc}}(\overline{\nu })=\sum _{i=1}^3{I}_i{\mathrm{e}}^{{(\overline{\nu }-{\overline{\nu }}_i)}^2/2{\sigma }_i^2}$$ (10)

$${\text{LD}}_{\text{calc}}^{\mathrm{r}}(\overline{\nu })=\frac{1}{A_{\text{calc}}(\overline{\nu })}\sum _{i=1}^3{\text{LD}}_i^{\mathrm{r}}·I_i{\mathrm{e}}^{{(\overline{\nu }-{\overline{\nu }}_i)}^2/2{\sigma }_i^2}$$ (11)

The results of this fitting procedure are shown in Figure 2, and the optimized values of the line shape parameters are given in Table 1. We note that our attempts to model these data using Lorentzian line shapes did not provide qualitatively better fits.

Table 1.

Results of Gaussian Fits to Absorption and LD Data Shown in Figure 2

	transition	ε (M−1 cm−1)a	ν̄ (cm−1)b	λ (nm)c	σ (cm−1)d
external BN indole	1	20 700	35 473	282	2135
	2	1 300	39 756	252	1898
	3	14 600	43 086	232	2468
fused BN indole	1	12 100	33 771	296	2813
	2	14 600	36 613	273	4491

^aMolar extinction coefficient.

^bCenter transition energy in wavenumbers.

^cCenter transition wavelength in nanometers.

^dAbsorption line width.

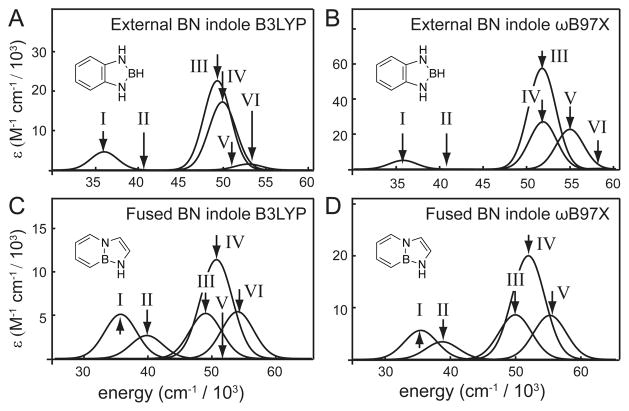
We next compared our experimental results to quantum chemical calculations. In Figure 3, we present our calculations of the absorption spectra for the external and the fused BN indoles using the B3LYP and ωB97X basis sets. These models indicate that both BN indole ring systems are planar in their ground electronic states, and that all of the lowest energy electronic transitions exhibit π → π* character.

Figure 3.

Calculated absorption spectra of the external and fused BN indole derivatives, showing each underlying absorption band with an assumed full width at half-maximum ~5 cm⁻¹. Transitions are numbered according to the same scheme as shown in Table 2.

For the external BN indole, both B3LYP and ωB97X models predict very similar results (Figure 3A,B, Table 2). There is a single low-energy electronic transition, which we have assigned to the lowest energy feature near ~36 000 cm⁻¹ (peak I). The next transition is dark, and we have assigned its presence to the weakly absorbing, experimentally observed feature near ~40 000 cm⁻¹ (peak II). The significant change in LD^r that we observe at this energy supports the assignment of this feature to an electronic transition with a polarization different from that of peak I. Both theoretical models predict the existence of four closely spaced transitions that contribute collectively to a single absorption band, ranging from 45 000–60 000 cm⁻¹, although there is minor disagreement between the two models about the intensities of the higher-energy transitions. We note that both models predict that transitions III and IV have nearly equal energies, so that these would be difficult to excite and detect separately.

Table 2.

Results of Computational and Experimental Electronic Parameters for External and Fused BN Indole

transition	B3LYP			ωB97X			experimental
	ν̄ (cm−1)a	fb	δ (deg)c	ν̄ (cm−1)	f	δ (deg)	ν̄ (cm−1)	f	δ (deg)
External BN Indole
I	35 600	0.0793	90	35 600	0.0846	90	35 473	0.20	90.0
II	40 100	0.0022	179.9	40 900	0.0012	180	39 756	0.01	180.0
III	49 100	0.3902	90	51 600	0.9921	90	43 086	0.16	±48.3d
IV	49 700	0.2973	180	51 700	0.4637	179.9	43 086	0.16	±48.3d
V	50 700	0.0007	91	54 800	0.3920	90
VI	52 900	0.025	145	58 200	0.0063	0
Fused BN Indole
I	35 200	0.1385	90	35 200	0.1513	76	33 771	0.34	66.9
II	39 300	0.0722	168	38 500	0.0935	166	36 613	0.56	133.5
III	48 500	0.142	81	49 700	0.2327	68
IV	50 200	0.3096	138	51 700	0.5452	139
V	51 800	0.0003	90	55 000	0.2316	52
VI	53 500	0.1462	174.5

^aCenter transition energy in wavenumbers.

^bOscillator strength.

^cAngle of in-plane polarized EDTM relative to short axis of the indole derivative molecules.

^dAngle δ_3–4 lies between the long-axis and short-axis polarization directions, which are assigned to calculated transitions III and IV of the external BN indole.

For the fused BN indole, both theoretical models predict the existence of two low-energy transitions near ~35 000 and ~40 000 cm⁻¹, respectively, which we have assigned to peaks I and II. Higher energy transitions were also predicted for the fused BN indole, ranging from 45 000 to 60 000 cm⁻¹ (peaks III–VI). Although the two theoretical models produced qualitatively similar results, our B3LYP calculations predicted an additional weak transition (assigned to transition V) in comparison to the ωB97X calculations.

We determined the Saupe parameters for the external BN indole making use of its C_2v symmetry. We first made the assumption that the lowest energy transition lies parallel to the long molecular axis. We then assigned peak I to an in-plane π → π* transition, and using eq 6, we determined the value of S_zz = 0.0424. Similarly, we assumed that peak II, which exhibits the lowest value of the LD^r, corresponds to an in-plane transition perpendicular to the long molecular axis.⁷ We estimated the value for S_yy = 0.0017 using a similar method as in the determination of S_zz.⁷ We then used the inequality expression given by eq 7 to ensure the parameters of the constraints were satisfied with our estimated Saupe values. Finally, using eq 8, we estimated the value of S_xx = −0.0441.

Determination of the EDTM Orientation Angles

For the external BN indole, both B3LYP and ωB97X calculations indicated that the lowest energy transition is polarized within the molecular plane and lies parallel to the long molecular axis. The second, weak transition has a polarization angle parallel to the short molecular axis. These theoretical predictions are in very good agreement with the results of our experimental absorption and LD measurements of the external BN indole in stretched PE films, for which our theoretical interpretations were aided by the relatively high symmetry of the molecule. We assumed that the external BN indole orients with its long molecular axis parallel to the stretching direction of the PE film.^7,18 It was thus possible to determine the orientational parameters S_xx, S_yy, and S_zz for the external BN indole directly from our analysis of its experimental LD^r spectrum, as we described above.

The value of the experimental LD^r spectrum for the external BN indole is relatively constant across the region spanning ~35 000–37 000 cm⁻¹, indicating that the spectral feature labeled peak I corresponds to a single electronic transition (Figure 2A,C). Furthermore, the value of the LD^r is positive and maximum within this region, suggesting that the polarization of this transition lies within the plane of the molecule and is aligned parallel to its long axis. The minimum value of the LD^r within the region ~39 000–40 500 cm⁻¹ (corresponding to peak II) suggests that this is a short-axis polarized transition.

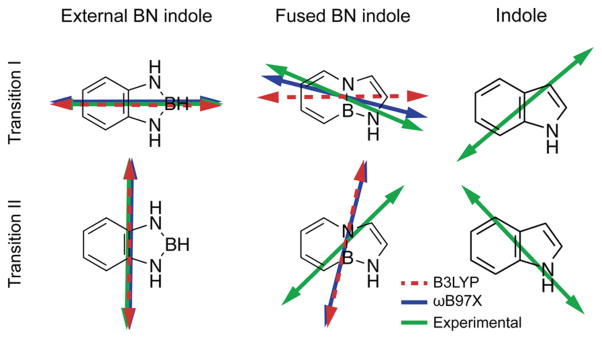
We used the values for the orientational parameters, in combination with eq 4, to calculate the value of the EDTM angle δ_3–4 = ±48.3° for peaks III–IV of the external BN indole. Though no single transition in this molecule can have such an intermediate polarization orientation due to its C_2v symmetry, our theoretical calculations predict that this feature consists of multiple, closely spaced transitions. We note that the value we have determined is in agreement with the predictions of our theoretical calculations, assuming that peaks III–IV represents a weighted sum of overlapping transitions with nearly equal contributions with orientations 90° and 180°. These closely spaced transitions appear in the experimental spectrum as a single feature, with an LD^r value consistent with an intermediate EDTM angle. The values that we estimate for δ_i, which correspond to peaks I, II, and III–IV of the external BN indole, are summarized in Table 3.

Table 3.

Experimentally Derived Orientation Parameters and In-Plane Polarized EDTMs

		Sxx	Syy	Szz	δ1 (deg)a	δ2 (deg)	δ3–4 (deg)
external BN indole	eq 4	−0.0441	0.0017	0.0424	90	180	±48.3
fused BN indole	eq 4	−0.0441	0.0017	0.0424	66.9	133.5

^aAngle of in-plane polarized EDTM relative to short axis of the indole derivative molecules.

To determine the EDTMs of the fused BN indole, we made the assumption that the orientational parameters that we estimated for the external BN indole were the same for the two molecules. Because the shapes and mass distributions of both indole derivatives are nearly equivalent, these molecules are expected to orient similarly within the stretched PE films. This is supported by our calculations of the minimum principle moments of inertia, which are nearly identical for the two molecules, and align parallel to the long molecular axes.

Although the molecular frame of the fused BN indole is expected to orient within the stretched PE film similarly to the external BN indole, the polarization directions of the EDTMs are expected to be different. The lowest-energy absorption band of the fused BN indole extends from ~32 000–40 000 cm⁻¹ (Figure 2B). This broad, asymmetric feature exhibits vibrational fine structure for samples prepared in the PE films. As we discuss further below, this vibrational fine structure was similarly observed in solutions of nonpolar solvents, and systematically decreased in solutions of higher polarity. The value of the LD^r over this region of the spectrum decreases continuously (Figure 2D), suggesting the existence of two overlapping transitions that we have identified as peaks I and II. We note that both the B3LYP and ωB97X computational models predict two separate electronic transitions under this band (Figure 3C,D), both having π → π* character. In addition, because the values of the LD^r are positive throughout this region, both transitions must be polarized primarily along the long molecular axis.

We determined the orientation angles of the EDTMs for peak I and peak II of the fused BN indole by substituting the appropriate experimental values for the LD^r into eq 4 (Figure 4). The lowest-energy transition (peak I) has π → π* character and is centered at ~33 771 cm⁻¹. The B3LYP model predicts this transition to have δ₁ = 90°, whereas the ωB97X model predicts δ₁ = 76°. The experimental value was determined to be δ₁ = 66.9°. Peak II appears as a shoulder on the blue side of the primary absorptive feature, with center energy at ~36 613 cm⁻¹. The calculated values of the EDTM orientation angle for peak II are δ₂ = 168° using the B3LYP model, and δ₂ = 166° using the ωB97X model. The experimentally determined value for peak II is δ₂ = 133.5°.

Figure 4.

Comparison between computational and experimental inplane polarized EDTMs of the external and fused BN indole derivatives. Also shown are the corresponding low-energy transitions of indole. Experimental results are indicated in green, B3LYP in dashed red, and ωB97X in blue. The experimental EDTMs for indole are taken from ref 19.

Solute–Solvent Interactions of BN Indole Derivatives

In the above discussion, we examined the upward electronic transitions of the BN indole derivatives, which are associated with their absorption spectra. We next considered the downward electronic transitions associated with fluorescence, and how this depends on solvent conditions. The electronic charge distribution of an aromatic molecule in the electronic ground state is generally very different from that in the electronic excited state, which can lead to very different solute–solvent interactions.¹⁸ The center energy and width of the absorption line shape depends on the equilibrium distribution of solvent configurations that couple to the electronic ground state.^20,21 When a solution phase fluorescent chromophore absorbs an optical photon, the electronic charge distribution becomes polarized in the direction of the EDTM. Immediately after the chromophore is electronically excited, its energy can be stabilized by rapid structural reorganization of the local solvent shell, which depends on the physical and chemical properties of the solvent. Provided that solvent reorganization is much faster than fluorescence, the center energy and fluorescence line shape is a property of the equilibrium distribution of solvent configurations that couple to the electronic excited state.^20,21 The degree to which the excited state is stabilized by solvent reorganization is characterized by the Stokes’ shift, which is the energy difference between the peak absorption and fluorescence line shapes.²² The Stokes’ shift is the average optical energy that is absorbed by the system and converted into heat before the emission of fluorescence. The solvent reorganization energy λ is defined as one-half of the Stokes’ shift.

To gain insight into the nature of the solute–solvent interactions for the BN indole derivatives, we examined the dependence of the absorption and fluorescence line shapes on solvents of varying chemical structure and polarity.²³ There are two general categories of solute–solvent interactions. A “universal interaction” refers to the influence of the solvent as a dielectric medium that depends on the static dielectric constant ε and the refractive index n. Such universal interactions, which may be modeled using the Onsager theory of dielectrics, can explain the systematic red shift of fluorescence with increasing solvent polarity.¹⁸ A “specific interaction”, on the contrary, depends on the detailed molecular properties of the solute and the solvent, such as the ability to form hydrogen bonds, to electronically couple through dipole–dipole interactions, or to undergo collisions. ^18,23,24 Such specific interactions can lead to the loss of vibrational fine structure in both the absorption and fluorescence spectra.

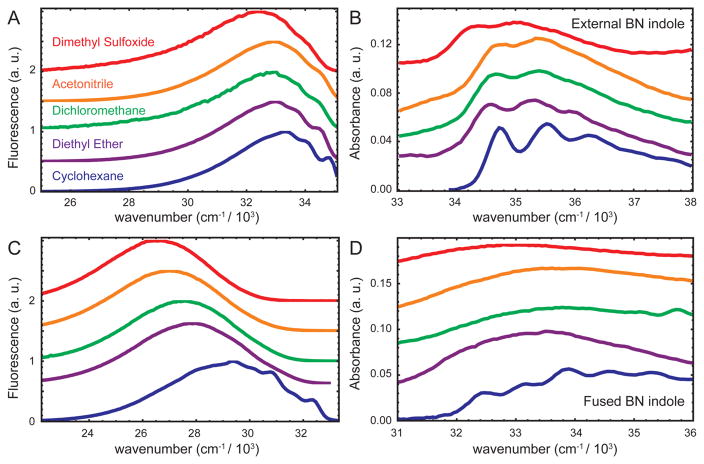
In Figure 5, we show the absorption and fluorescence spectra of the external and fused BN indole derivatives in various solvents. The solvents are arranged in order of increasing polarity and dielectric constant: cyclohexane (ε = 2.0) < dimethyl ether (4.3) < dichloromethane (9.1) < acetonitrile (37.5) < dimethyl sulfoxide (46.7).²⁵ This order of arrangement can also be described as nonpolar < chlorinated < polar. In Table 4, we list the absorption and fluorescence band maxima for these solutions, as well as the associated Stokes’ shifts and relative quantum yields. We define the relative quantum yield as the maximum fluorescence intensity of a given sample divided by the absorption intensity at the excitation wavelength.

Figure 5.

Experimental fluorescence and absorption spectra of the external (A and B) and fused (C and D) BN indole derivatives for five different solvents, as indicated in panel A. In each panel, the spectra have been vertically offset for clarity.

Table 4.

Solvent Dependent Absorption and Fluorescence Spectra

compound	solvent	${\lambda }_{\text{ab}}^{max}(\text{nm})$ a	εmax(M−1 cm−1)b	λex (nm)c	${\lambda }_{\mathrm{F}}^{max}(\text{nm})$ d	RQYe	SS (cm−1)f
external BN indole	cyclohexane	281.5	5 809	285	300	1.000	18.5
	diethyl ether	283.0	7 928	285	303	0.316	20.0
	dichloromethane	282.5	13 656	285	303	0.035	20.5
	chloroform	281.5	8 586	285	299	0.001	17.5
	acetonitrile	283.0	20 348	285	304	0.482	21.0
	dimethyl sulfoxide	286.0	3 698	285	309	0.116	23.0
fused BN indole	cyclohexane	295.0	13 105	295	341	1.000	46.0
	diethyl ether	298.5	58 080	303	358	0.680	59.5
	dichloromethane	296.0	21 810	295	363	0.582	67.0
	chloroform	290.5	50 300	295	367	0.005	76.5
	acetonitrile	297.5	42 008	295	370	0.686	72.5
	dimethyl sulfoxide	305.0	14 807	295	378	0.688	73.0

^aAbsorption maximum wavelength.

^bExtinction coefficient at absorption maximum.

^cExcitation wavelength for detection of fluorescence spectra.

^dFluorescence spectrum maximum wavelength.

^eRelative quantum yield.

^fStokes’ shift.

For the external BN indole, the absorption spectra shown in Figure 5B exhibited the same qualitative features as those previously discussed in stretched PE films (Figures 2A). Although the absorption maximum was relatively insensitive to solvent conditions, the vibrational fine structure we observed in PE films (ε = 2.2) was similarly present in cyclohexane. This vibrational fine structure progressively diminished with increasing solvent polarity, as expected due to the effects of specific solute–solvent interactions. The loss of vibrational fine structure was also observed in the corresponding fluorescence spectra (Figure 5A). Increasing the solvent polarity resulted in an enhancement of the Stokes’ shift and a reduction of the relative fluorescence quantum yield, as expected. For the chlorinated solvents, dichloromethane and chloroform (not shown in Figure 5), the quantum yield was nearly zero. These observations are consistent with the known fluorescence quenching properties of chlorinated solvents.²³

For the fused BN indole, we observed effects similar to those for the external BN indole. We observed vibrational fine structure in both the fluorescence (Figure 5C) and absorption spectra of the fused BN indole in cyclohexane (Figure 5D), similar to that in the stretched PE films (Figure 2B). The vibrational fine structure dampened as the solvent polarity was increased, which is likely due to specific solute–solvent interactions. As for the case of the external BN indole, chlorinated solvents strongly quenched the fluorescence intensity of the fused BN indole. Although the peak absorbance was relatively insensitive to solvent polarity, the magnitude of the Stokes’ shift for the fused BN indole was much greater in polar solvents than for the external BN indole case. This latter result indicates the existence of stronger coupling between the lowest energy EDTMs and solvent reorganization for the fused BN indole than for the external BN indole. The enhanced solute–solvent interaction for the fused BN indole, relative to the external BN indole, may be a consequence of its larger oscillator strength (Table 2) as well as a larger difference between the ground and excited state dipole moment.

CONCLUSIONS

By performing absorption and LD spectroscopic measurements of external and fused BN indole derivatives in stretched PE films, we identified the two lowest energy electronic transitions for the external BN indole, and the two lowest energy electronic transitions for the fused BN indole. Our analysis of these data made use of the known C_2v symmetry of the external BN indole, which allowed us to determine the orientations of the EDTMs for both molecules (summarized in Figure 4). As required by its symmetry, the external BN indole has its first two lowest energy transitions polarized along its long and short molecular axes, respectively (i.e., δ₁ = 90° and δ₂ = 180°). In contrast, the fused BN indole has its two lowest energy electronic transitions polarized at angles that deviate from its long and short molecular axes (i.e., δ₁ = 66.9° and δ₂ = 133.5°). We further supported our experimental determination of the EDTM polarization directions by performing B3LYP and ωB97X TDDFT quantum chemical calculations. Our experimental results for these low-energy transitions are in very good agreement with our theoretical calculations.

We examined the dependence of the absorption and fluorescence line shapes of the external and fused BN indole derivatives on solvents of varying chemical structure and polarity. As the solvent polarity was increased in solutions of the compounds, vibrational fine structure broadened and progressively disappeared, and the fluorescence Stokes’ shift increased. The Stokes’ shift was notably much greater for the fused BN indole than for the external BN indole. Because dielectric relaxation is expected to scale with oscillator strength,¹⁸ our observations are consistent with the larger oscillator strength we observe for the fused BN indole relative to the external BN indole. In future work, these results will be used to interpret in structural terms spectroscopic measurements of the local conformations of site-specifically positioned BN indole derivatives within protein-nucleic acid complexes. Such experiments have the potential to reveal details of the local interactions of amino acid side groups and nucleic acid bases important to enzymatic processes responsible gene regulation.