Abstract
Grid cells in medial entorhinal cortex (MEC) can be modeled using oscillatory interference or attractor dynamic mechanisms that perform path integration, a computation requiring information about running direction and speed. The two classes of computational models often use either an oscillatory frequency or a firing rate that increases as a function of running speed. Yet it is currently not known whether these are two manifestations of the same speed signal or dissociable signals with potentially different anatomical substrates. We examined coding of running speed in MEC and identified these two speed signals to be independent of each other within individual neurons. The medial septum (MS) is strongly linked to locomotor behavior and removal of MS input resulted in strengthening of the firing rate speed signal, while decreasing the strength of the oscillatory speed signal. Thus two speed signals are present in MEC that are differentially affected by disrupted MS input.
Keywords: entorhinal cortex, grid cell, medial septum, path integration, theta rhythm
Introduction
The medial entorhinal cortex (MEC) is a critical component of the brain's spatial navigation system. Grid cells in MEC are spatially modulated neurons with firing fields on the vertices of tessellating triangles covering the entire environment (Fyhn et al., 2004; Hafting et al., 2005). The regular nature of grid cell spatial receptive fields has led to the suggestion that they are path integrators (McNaughton et al., 2006), neurons that track relative location within an environment based on the speed and direction of an animal's movement. Two general classes of computational models have been employed to generate the spatially repeating firing pattern of grid cells using either oscillatory interference or attractor dynamics (McNaughton et al., 2006; Fuhs and Touretzky, 2006; Guanella and Verschure, 2006; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008; Blair et al., 2008; Burak and Fiete, 2009; Navratilova et al., 2011; for review, see Zilli 2012), although recent models have combined elements of both of these approaches (Hasselmo and Brandon, 2012; Schmidt-Heiber and Hausser, 2013; Hasselmo and Shay, 2014; Bush and Burgess, 2014). All of these models require a running speed signal to code for movement through space, although the mechanisms employed to generate grid cell firing differ in a number of key respects across models. The speed signal is generally modeled with oscillatory activity that varies in frequency as a function of running speed or a firing rate that varies linearly as a function of running speed in oscillatory interference and attractor dynamics models respectively. Recent modeling work from our lab has also suggested that MEC interneurons with either speed modulation of intrinsic oscillatory frequency or firing rates may be responsible for speed coding in MEC and thus be critical for the generation of grid cells (Hasselmo and Shay, 2014).
The two signals necessary for path integration computations have been experimentally demonstrated to be present in MEC. Neurons coding for head direction (HD) arise in an ascending circuit beginning in the lateral mammillary nucleus that ultimately reaches MEC (Taube, 2007; Sargolini et al., 2006). The disruption of HD input to MEC disrupts grid cell spatial periodicity as predicted by computational models (Winter et al., 2015). Speed modulated activity is present in a diverse set of brain regions including MEC (Sargolini et al., 2006; Jeewajee et al., 2008; Wills et al., 2012), with a recent report demonstrating a dedicated group of speed cells in MEC cells that code running speed through their firing rates (Kropff et al., 2015). Speed signals have been shown in MEC principal neurons as increases in firing rates as a function of running speed (Sargolini et al., 2006; Wills et al., 2012; Kropff et al., 2015), and similarly in MEC interneurons (Beutfering et al., 2014; Kropff et al., 2015). In addition, the intrinsic theta frequency oscillatory firing of MEC grid cells is positively modulated by running speed (Jeewajee et al., 2008), while similar information is not currently available for MEC interneurons. It is currently not known whether the increases in firing rate and theta oscillatory frequency as a function of running speed are different physiological manifestations of the same speed signal impinging upon MEC circuits or dissociable signals with potentially different anatomical substrates. In fact, to date the anatomical pathways by which running speed information reaches MEC circuits have yet to be elucidated.
The medial septum (MS) is well positioned anatomically to influence the ongoing activity of neurons throughout the entorhinal cortex, since it projects across the entire dorso-ventral axis (Alonso and Kohler, 1984). Theta oscillations in the local field potential (LFP) throughout the hippocampal formation, which are dependent upon the MS (Winson, 1978; Mitchell et al., 1982; Mizumori et al., 1990; Buzsaki, 2002), have long been linked to locomotor behavior (Vanderwolf, 1969). The frequency of theta oscillations throughout the entorhinal cortex and hippocampus are positively modulated by running speed (Rivas et al., 1996; Sławińska and Kasicki, 1998; Jeewajee et al., 2008; Hinman et al., 2011). Several classes of theta phase locked interneurons in the hippocampus have speed modulated firing rates, while several additional classes of hippocampal interneurons that are not theta phase locked lack speed modulated firing rates (Czurko et al., 2011). Within the MS itself, neurons have firing rates that vary as a function of running speed (Zhou et al., 1999) and the theta rhythmic burst frequency of MS neurons is modulated by running speed (King et al., 1998; Zhou et al., 1999; Welday et al., 2011), with a subpopulation of these cells also exhibiting head directional tuning (King et al., 1998; Zhou et al., 1999). Additionally, glutamatergic neurons in MS are strongly linked to locomotor behavior as optogenetic stimulation has been shown to induce running behavior and to be responsible for the running speed modulation of the firing rates of neurons in the hippocampus (Fuhrmann et al., 2015). Thus both anatomical and physiological data point to MS as a potential substrate by which the speed signal necessary for normal grid cell firing reaches MEC.
Results
Linear and saturating increases in firing rate
Running speed information is critical to models of grid cell generation, which generally employ a positive linear running speed signal. Thus we first sought to identify the nature by which the firing rates of MEC neurons respond as a function of running speed. A total of 332 cells were recorded from MEC as rats foraged in an open field environment, which included grid cells (N=45), conjunctive grid-by-head direction cells (N=20), HD cells (N=157), border cells (N=14), spatially uncharacterized cells (N=65) and interneurons (N=31). Many MEC neurons' firing rates increase as a function of running speed (Sargolini et al., 2006; Wills et al., 2012; Kropff et al., 2015) and this increase appeared linear in response to running speed in numerous neurons, although many neurons appeared to have firing rates that plateaued after the animal reached moderate speeds and thus were not fit well with a linear function. Therefore, we employed a maximum likelihood estimation approach to parametrically optimize the fit between running speed and firing rate to both a linear and saturating exponential curve for each cell separately. For both fits we conducted an F-test comparing each fit to a uniform fit with the p-value threshold for the F-tests set based on spike shuffling procedure such that greater than 99% of a shuffled p-value distribution lay above those of the cells we identified as significantly speed modulated. Next, we performed a nested model comparison between the two fits, using an F-test with the null hypothesis being a linear fit. This required the saturating exponential model to reduce the error of the fit enough to justify the additional terms of the saturating exponential function. The result of this approach was the determination for each cell whether 1) its firing rate was statistically significantly modulated by running speed and 2) it was significantly better fit with a saturating exponential function than a linear function (Fig. 1A, B). This approach was applied using a point estimate on spikes temporally binned to individual video frames (∼33 ms) of all behavioral epochs with a running speed greater than 2 cm sec-1 in order to ensure that we did not incorrectly identify firing rate changes due to behavioral state as changes due to running speed.
Figure 1.
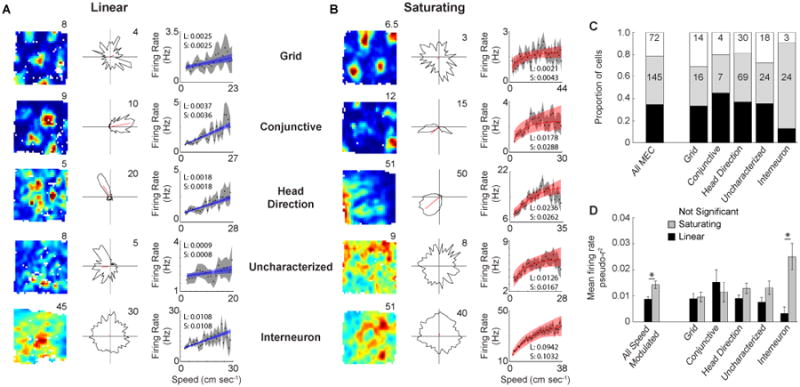
Linear and saturating coding of running speed by the firing rate of MEC neurons. A. Spatial rate map (left), head direction polar plot (middle) and firing rate versus running speed plot (right) for a grid cell, conjunctive cell, head direction cell, uncharacterized cell and interneuron (top to bottom) that linearly code running speed. Each plot shows the best fit function with confidence intervals (blue and red for linear and saturating cells respectively) as obtained using maximum likelihood estimation on temporal bins and also shows the mean value of running speed bins (black dots) and associated confidence intervals (gray). The inset values in each plot are the pseudo-r2 values for the linear (L) and saturating (S) fits. B. Same as in A, but for saturating cells. C. Proportions of each cell type coding running speed linearly and exponentially. The values indicate the number of cells. D. Mean +/- SEM firing rate pseudo-r2 values for linear and saturating cells. * p < 0.005
Overall ∼78% of MEC neurons had firing rates that were significantly modulated by running speed (260 out of 332 total MEC cells), with the majority of each cell type showing statistically significant modulation of firing rate by running speed (Fig. 1C; grid: 31/45; conjunctive: 16/20; HD: 127/157; uncharacterized: 47/65; interneuron: 28/31). We identified similar proportions of speed modulated neurons through the use of multiple different approaches including by binning the data based on running speed (∼70%), as has been previously reported (McNaughton et al., 1998; Wills et al., 2012; Fig. S1A), as well as through the use of only linear regression on temporal bins and a shuffling procedure for the determination of significant speed modulation (∼65% with r-values < 1st percentile or > 99th percentile; Kropff et al., 2015; Fig. S1B, E). The use of speed bins appears to overestimate the strength of the relationship between firing rate and running speed (Fig. S1D-F), likely due to averaging out variability in the firing rate dependent on other factors, but the best fit functions obtained using temporal and speed bins were very similar. Both the slopes and y-intercepts estimated by the two methods were highly correlated (slope: r = 0.87, p < 1 × 10-10, y-intercept: r = 0.98, p < 1 × 10-10; Fig. S1G-H), although the use of temporal bins resulted in slightly lower slopes (Wilcoxon signed rank test: p < 5 × 10-8) and slightly higher y-intercepts (Wilcoxon signed rank test: p < 1 × 10-10) than obtained through the use of speed bins. The correspondence between the two approaches can be seen in each plot of firing rate versus running speed throughout the paper (Fig. 1A, B; 2E; 3A-D; 5B; 7B-C), which show the best fit line and confidence intervals based on temporal binning (light red or light blue) overlaid on the estimated firing rate and confidence intervals based on binning the data using running speed bins (black dots and gray shading).
The path integration mechanisms employed in grid cell models require the running speed signal to be linear in nature, which previous accounts of speed modulation have generally assumed rather than explicitly tested. Of the 260 cells identified as having significant speed modulation of their firing rate, the majority were actually better fit using a saturating exponential (which we refer to as ‘saturating cells’) function rather than a linear function (Fig. 1C; 145 of 260). Similar proportions of saturating and linear cells were identified for each putative principal cell type (Fig. 1C; grid: 36% saturating / 33% linear; conj: 35% sat / 45% lin; HD: 44% sat / 37% lin; uncharacterized: 37% sat / 35% lin). For interneurons, an overwhelming majority were better fit with the saturating exponential function rather than the linear function (Fig. 1C; interneuron: 77% sat / 13% lin). Overall saturating cells had higher firing rate pseudo-r2 values than linear cells (Fig. 1D; Wilcoxon rank sum test: p < 0.005), although this appeared to be primarily mediated by interneurons as they were the only cell type to show a difference between the firing rate pseudo-r2 values for saturating and linear cells (Fig. 1D; Wilcoxon rank sum test: p < 0.01). Thus, the vast majority of neurons in MEC have speed modulated firing rates, but the firing rates of most speed modulated neurons saturate and therefore do not linearly follow running speed across the full range of behaviorally manifested running speeds and this did not result from the animal reaching higher maximum speeds during sessions where saturating cells were identified (Wilcoxon rank sum test: n.s.; Fig. S1I,J).
Having statistically identified speed modulated neurons, whether linear or saturating, we next sought to confirm the positive nature of the relationship between firing rate and running speed as has been previously observed (Sargolini et al., 2006). We calculated the speed modulation of each significantly speed modulated cell as the difference between the firing rate predicted by the best fit line (either linear or saturating) at the maximum and minimum running speed divided by the difference in maximum and minimum running speed. Overall, the speed modulation of firing rates of MEC neurons was positive (Fig. 2A; Wilcoxon signed rank test: p < 1 × 10-10), which was the case for each individual cell type as well (Fig. 2A; Wilcoxon signed rank test: grid: p < 1 × 10-6; conj: p < 0.0005; HD: p < 1 × 10-9; uncharacterized: p < 1 × 10-7; interneuron: p < 1 × 10-5). The median predicted firing rate when the animal's speed goes to zero (y-intercept) was also positive for the speed modulated MEC cells (Fig. 2B; Wilcoxon signed rank test: p < 1 × 10-10), as well as for each individual cell type (Fig. 2B; Wilcoxon signed rank test: grid: p < 1× 10-6; conj: p < 0.0005; HD: p < 1 × 10-10; uncharacterized: p < 0.001; interneuron: p < 1 ×10-5). The interneurons appeared to have greater variability of their slopes and y-intercepts, which may be due to the fact that there is a great deal of heterogeneity in mean firing rate amongst neurochemically distinct interneurons that cannot be differentiated based on extracellular recordings.
Figure 2.
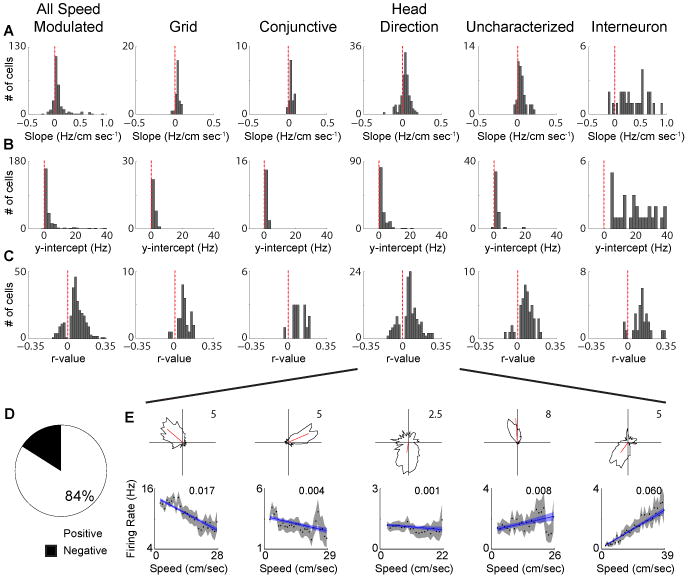
A subset of negatively speed modulated MEC cells. A. Distributions of the slope between firing rate and running speed. B. Distributions of y-intercepts of relationship between firing rate and running speed.C. Distributions of r-values between firing rate and running speed. D. Proportion of positively and negatively speed modulated cells. E. Head direction polar plots (top) and firing rate versus running speed plots (bottom) for five head direction cells with significant firing rate speed modulation, but with varying magnitudes and polarities of speed modulation. The inset value in each plot is the firing rate pseudo-r2 value for the linear fit.
Despite the average positive nature of the speed modulation of MEC cells, a sizable proportion actually show negative speed modulation (Fig. 2C-E; 42/260 = 16%). This facet of speed modulation in MEC is especially apparent when considering the r-values for the relationship between firing rate and running speed, as cells can be seen to fall on either side of zero (Fig. 2C). The majority of cells have a strong, positive relationship between firing rate and running speed, yet the negatively speed modulated cells also appear to have a strong relationship between firing rate and running speed albeit in the opposite direction. The positively speed modulated cells have a slightly stronger relationship between firing rate and running speed than the negatively modulated cells (Positive cells: median pseudo r2 = 0.007; Negative cells: median pseudo-r2 = 0.003; Wilcoxon rank sum test: p <1 × 10-6). The majority of negatively modulated cells were head direction cells (26 out of 42 negatively modulated cells), although negative speed modulation was not restricted to head direction cells and there was no apparent relationship between the strength of head directional tuning and the direction or degree of speed modulation (Fig. 2E). Cells carrying this negative firing rate speed signal were recorded simultaneously on the same tetrode with cells carrying the positive firing rate speed signal, so both speed signals are present in highly localized areas within MEC.
Increased theta oscillatory frequency as a function of running speed
In addition to the firing rate of MEC neurons being modulated by running speed, the amplitude and frequency of theta rhythmicity throughout the hippocampal formation is also positively modulated by running speed both in the LFP (McFarland et al., 1975; Slawinska and Kasieki, 1998; Hinman et al., 2011) and the spiking of individual neurons (Jeewajee et al., 2008; Maurer et al., 2005; Welday et al., 2011; Stensola et al., 2012; Fig 3A-D). Recent simulations of the generation of grid cells either assume or generate interneuron firing properties with speed modulated theta frequency spiking that induces rebound spiking in grid cells (Hasselmo and Shay, 2014; Hasselmo, 2013). Here we employed a recently developed technique utilizing maximum likelihood estimation to determine attributes of theta rhythmic firing (Climer et al., 2015), such as modulation depth and intrinsic frequency, and we conditionalized these features of rhythmicity on running speed. This provides information regarding the manner in which theta rhythmic firing varies as a function of running speed. Overall, the majority of MEC cells exhibited significant theta rhythmic spiking irrespective of speed (All MEC: 235/322; Fig 3E), with 65 out of the 235 theta rhythmic cells displaying theta skipping (Brandon et al., 2013), and this was the case for each individual cell type as well (grid: 40/45; conjunctive: 18/20; HD: 90/157; uncharacterized: 47/65; interneuron: 30/31; Fig 3E). Amongst significantly theta rhythmic cells, the depth of theta modulation varied as a function of running speed in nearly half of the cells (109 out of 235 theta rhythmic cells; Fig S2A) indicating that these cells become more theta rhythmic at higher running speeds. This parallels previous reports that the amplitude of LFP theta oscillations increase in amplitude with running speed at sites within the hippocampal formation (Hinman et al., 2011; Long et al., 2014). A majority of theta rhythmic cells also had oscillatory frequencies that significantly varied as a function of running speed (139 out of 244 theta rhythmic cells; Fig 3F), with a majority of each cell type following the same pattern (grid: 20/40; conjunctive: 13/18; HD: 50/90; uncharacterized: 26/47; interneuron: 26/30; Fig 3F). This is displayed in the plots (Fig 3A-D) as a decrease in the lags in the peaks of the autocorrelation as a function of running speed, which, when converted to frequency, yields a positive slope between running speed and theta frequency (conversion not done for individual examples), as has been previously observed in both the LFP and single cells. Each cell type had mean positive r-values and slopes between oscillatory frequency and running speed (Fig 3G,H), which result in approximately 0.25 – 0.675 Hz changes in oscillatory frequency across a typical behavioral range of running speeds (e.g. 50 cm sec-1). Note that this small magnitude of frequency change matches the scale required in computational models of grid cells.
Figure 3.
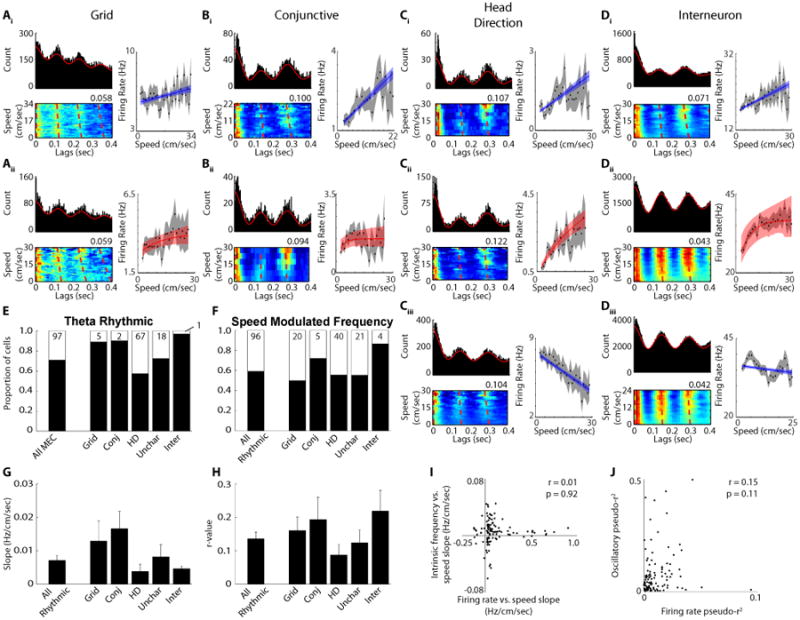
Speed modulation of oscillatory theta frequency. A - D) Three plots are shown for ten different example neurons. Traditional autocorrelations showing theta rhythmicity (top left plot), spike time lags as a function of running speed (the value at the top right corner of each plot indicates the maximum conditional probability of firing (red) shown in the plot with the sum of each running speed row equals a conditional probability of 1) (bottom left plot) and firing rate versus running speed (right). Ai - Di) Cells with positive linear relationships between firing rate and running speed. Aii - Dii) Cells with saturating relationships between firing rate and running speed. Ciii - Diii) Cells with negative linear relationships between firing rate and running speed. E) The proportion of cells with significant theta modulation. F) The proportion of theta rhythmic neurons with significantly speed modulated oscillatory frequencies. G) The mean +/- SEM slope of the relationship between oscillatory frequency and running speed. H) The mean +/- SEM r-value of the relationship between oscillatory frequency and running speed. I) There is no relationship between the firing rate versus running speed slopes and the oscillatory frequency versus running speed slopes. J) There is no relationship between the firing rate pseudo-r2 values and the oscillatory frequency pseudo-r2 values.
As different models of grid cell firing have employed firing rate and oscillatory frequency speed signals and both signals are present in MEC, we next asked whether the two speed signals are related to each other within individual cells. Since both the firing rate and oscillatory speed signals are positive on average, we investigated whether they are just different physiological manifestations of the same speed signal. The slope between oscillatory theta frequency and running speed is independent of each cells slope between firing rate and running speed (Fig 3A-D, I), with the correlation between the two slopes being non-significant for the entire population of speed modulated cells (Fig. 3I; r = 0.01, n.s.), as well as when each cell type was considered on their own (Fig S2H; grid: r = -0.21, n.s.; conjunctive: r = 0.41, n.s.; HD: r = 0.17, n.s.; uncharacterized: 0.01, n.s.; interneuron: r = -0.03, n.s.). Additionally, there was no relationship between the pseudo-r2 values for the firing rate and oscillatory speed signals among all speed modulated cells (Fig 3J; r = 0.15, n.s.) or for any of the cell types on their own (Fig S2I; grid: r = 0.21, n.s.; conjunctive: r = -0.31, n.s.; HD: r = 0.15, n.s.; uncharacterized: -0.08, n.s.; interneuron: r = 0.12, n.s.). The same pattern held when comparing the slopes and pseudo-r2 values for the depth of theta modulation versus running speed and the firing rate versus running speed slopes and pseudo-r2 values (Fig S2D-G), with all comparisons yielding non-significant correlations. Thus the manner in which a cell's firing rate and intrinsic theta frequency vary as a function of running speed are unrelated, suggesting that firing rate and oscillatory frequency are independent cellular properties and their two respective speed signals are dissociable.
Theta Phase of spiking
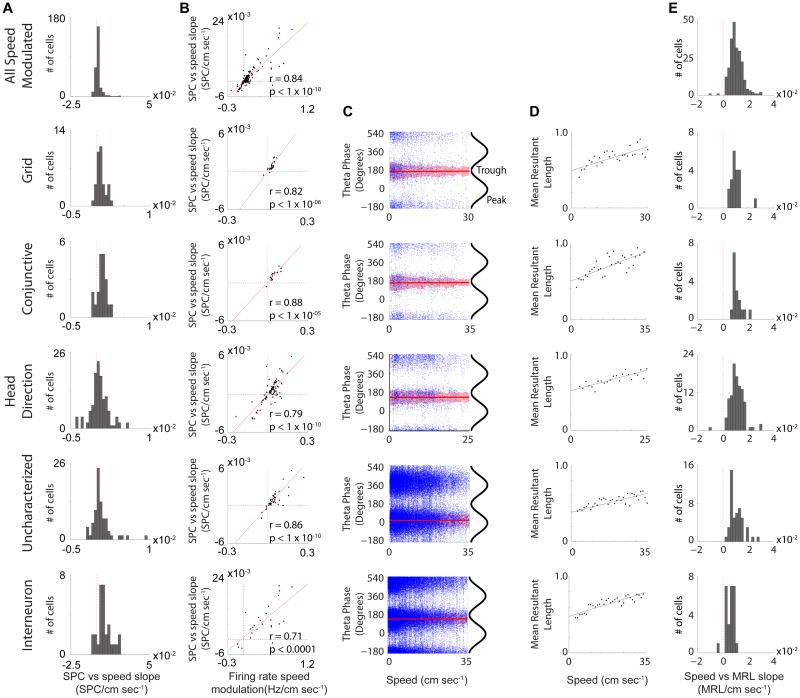
Given that the oscillatory frequency of MEC neurons increases as a function of running speed, the increase in firing rate observed in most neurons could potentially be a result of a greater number of theta cycles occurring per second with the same number of spikes within each cycle. Therefore we investigated whether the number of spikes occurring within each theta cycle varies as a function of running speed for those cells that were identified as having significantly speed modulated firing rates. Just as there was a mean positive relationship between firing rate and running speed, there was a mean positive slope between the number of spikes per theta cycle (SPC) and running speed for the overall set of speed modulated neurons (Fig. 4A; Wilcoxon signed rank test: p < 1 × 10-10), as well as for each individual MEC cell type (Fig. 4A; Wilcoxon signed rank test: grid: p < 1 × 10-5; conj: p < 0.001; HD: p < 0.0005; uncharacterized: p < 0.0005; interneuron: p < 0.0005). Additionally, there was a strong relationship between firing rate versus running speed slopes and the SPC versus running speed slopes (Fig. 4B; All Speed Modulated: r = 0.84, p < 1 × 10-10; grid: r = 0.82, p < 1 × 10-06; conj: r = 0.88, p < 1 × 10-05; HD: r = 0.79, p < 1 × 10-10; uncharacterized: r = 0.86, p < 1 × 10-10; inter: r = 0.71, p < 0.0001) and there was no relationship between the slope of SPC versus running speed and the slope of theta oscillatory frequency versus running speed (All Speed Modulated: r = -0.04, n.s.; grid: r = 0.26, n.s.; conj: r = 0.18, n.s.; HD: r = 0.03, n.s.; uncharacterized: r = -0.27, n.s.; interneuron: r = 0.18, n.s.). This indicates that the change in firing rate as a function of running speed is not a reflection of the greater number of theta cycles per second occurring as an animal moves faster, thus further supporting the dissociation between the firing rate and oscillatory speed signals.
Figure 4.
Increased phase locking as a function of running speed. A. Distributions of the slope between the number of spikes per theta cycle and running speed. B. Scatter plots showing the strong relationship between the SPC versus running speed slopes and the firing rate versus running speed slopes. The red line in each plot is the regression line. C. Theta phase of spiking versus running speed for example cells. The circular-linear best fit line is in red and the shaded region is the circular standard deviation of spiking at each running speed. D. Mean resultant length (phase locking) versus running speed for each of the cells in C. E. Population distributions of slopes between mean resultant length and running speed. Virtually all cells have a positive slope between phase locking and running speed.
Neurons throughout the hippocampal formation and related structures have been shown to spike at selective phases of LFP theta rhythm (i.e. theta phase locking; Fox et al., 1986; Csicsvari et al., 1999; Mizuseki et al., 2009). The overwhelming majority of neurons were theta phase locked (257 out of 282 MEC neurons = 91%; grid: 34/38; conj: 20/20; HD: 111/124; uncharacterized: 51/58; interneuron: 30/30). Since the number of spikes per theta cycle and the depth of theta modulation change as a function of running speed, we asked whether the preferred theta phase of firing and strength of theta phase locking varies as a function of running speed. Linear-circular correlations (Kempter et al., 2012) between the theta phase of spikes and running speed were computed for each theta phase locked neuron (Fig. 4C). No cells were found to have significant correlations, thus indicating that the preferred theta phase of firing does not vary as a function of running speed in MEC neurons. While the preferred theta phase of firing does not vary according to running speed, the strength of theta phase locking (mean resultant length (MRL)) increases as an animal runs faster (Fig 4D). Most theta phase locked cells had significant correlations between MRL and running speed (201 out of 257 = 78%), with all but two cells having a positive slope between MRL and running speed (Fig 4E). So despite variation in firing rate, depth of theta modulation and oscillatory frequency as a function of running speed, MEC neurons do not show changes in preferred theta phase of firing according to running speed, but do become theta phase locked at faster running speeds.
Enhanced firing rate speed signal in the absence of MS input
The MS is well positioned to provide a speed signal to MEC and has been shown to be responsible for speed modulation of CA1 firing rates (Fuhrmann et al., 2015). Therefore we tested whether the MS is responsible for propagating the speed signal present in MEC neuron firing rates by analyzing the data during pharmacological inactivation of MS during the recording of speed modulated MEC neurons. The total proportion of MEC neurons with significantly speed modulated firing rates did not change during MS inactivation or the first recovery session (Fig 5A; MS inactivation: Chi-square = 0.51, n.s.; 3 – 6 hour recovery: Chi-square = 0.98, n.s.) nor did the proportion of linear and saturating cells (MS inactivation: Chi-square = 0.04, n.s.; 3 – 6 hour recovery: Chi-square = 0.82, n.s.), although there was a slight reduction in the proportion of speed modulated cells during the 24 hour recovery session (Chi-square = 5.75, p < 0.05). Given that the same proportion of cells is significantly speed modulated during MS inactivations, we next asked whether the strength of speed modulation changes. Surprisingly, speed modulation of MEC neuron firing rates became stronger during MS inactivation, as indicated by increased pseudo-r2 values during MS inactivation as compared to baseline recordings for all MEC cells with significant speed modulation (Wilcoxon signed rank test: p = 1.57 × 10-05; Fig. 5B,C). Each cell type appeared to display a similar pattern of increased pseudo-r2 values during MS inactivation, although subsequent statistical testing demonstrated that grid cells, uncharacterized cells and interneurons were the only cell types to significantly increase during MS inactivation (Wilcoxon signed rank test: grid: p < 0.05; conj: n.s.; HD: n.s.; uncharacterized: p < 0.005; interneuron: p < 0.05; Fig. 5C). The change in the pseudo-r2 values appeared to result from a strengthening of the relationship between firing rate and running speed as there was no significant change in the slope of the relationship (Fig S3B; Wilcoxon signed rank test: All speed modulated: n.s.; grid: n.s.; conj: n.s.; HD: n.s.; uncharacterized: n.s.; interneuron: n.s.), although considering the saturating and linear separately indicated that there was a significant increase in the slopes of the linear cells and no change in the saturating cells (Wilcoxon signed rank test: linear: p < 0.05; saturating: n.s.; Fig S3B). As has previously been reported (Brandon et al., 2011), the firing rate of grid cells decreased during MS inactivation, while the firing rates of the other putative principal cell types were unaffected (see Fig. 3 in Brandon et al., 2011). Similarly to grid cells, interneuron firing rates also decreased during MS inactivation (Wilcoxon signed rank test: p < 1 × 10-5; Fig. S3A). The decrease in mean firing rate was the likely cause of a decrease observed in the y-intercept of the relationship between firing rate and running speed (Fig S3C; Wilcoxon signed rank test: All speed modulated: p < 8.52 × 10-5), which was restricted to interneurons (grid: n.s.; conj: n.s.; HD: n.s.; uncharacterized: n.s.; interneuron: p < 0.0005). In summary, in the absence of MS input, firing rates of MEC neurons become more strongly modulated by running speed.
Figure 5.
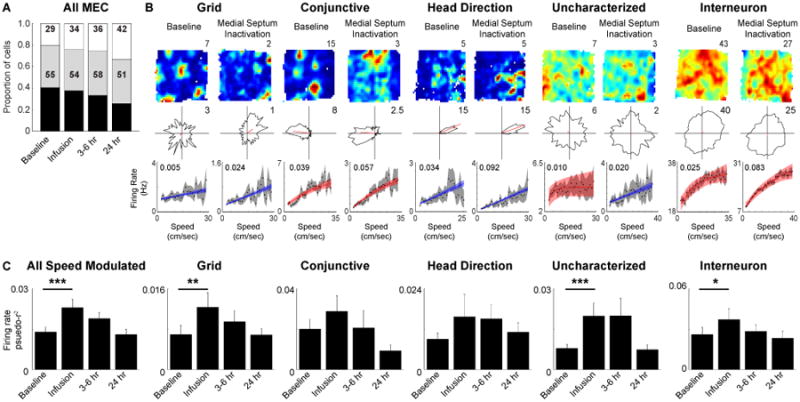
Enhanced firing rate speed signal during MS inactivation. A. Proportion of significantly speed modulated MEC cells does not change during MS inactivation. B. Spatial rate maps (maximum firing rate (Hz) indicated above each map), head direction polar plots (maximum radial axis limit (Hz) indicated in top right corner of each plot) and firing rate versus running speed plots with inset firing rate pseudo-r2 values (top to bottom) during the baseline recording (left) and MS inactivation recording that commenced about 15 min after the end of the infusion (right) for an example cells. C. Mean +/- SEM firing rate pseudo-r2 values across each recording session showing an increase in the strength of firing rate speed modulation during MS inactivation. * p < 0.05, ** p < 0.005, *** p < 0.0005
Disrupted oscillatory speed signal in the absence of MS input
When MS is inactivated there is a substantial decrease in theta rhythmicity in the LFP, yet a surprising number of individual MEC cells retain theta rhythmicity in their spike trains (Brandon et al., 2011, 2013). In the cells examined during MS inactivation there is a clear loss of theta rhythmicity in some cells, resulting in a decrease in the proportion of significantly theta rhythmic neurons during MS inactivation that returns to baseline levels during recovery recordings (Fig 6A, B; MS inactivation: Chi-square = 16.66, p < 0.00005; 3 – 6 hour recovery: Chi-square = 0.17, n.s.; 24 hour recovery: Chi-square = 0.01, n.s.). Despite the decrease in the proportion of theta rhythmic neurons, a majority of MEC cells actually retained theta rhythmicity during MS inactivation (73 out of 141 MEC cells; Fig 6A, C). Given that the firing rate speed signal remains present in MEC neurons during MS inactivation, we asked whether the cells that remain theta rhythmic during MS inactivation continue to have that oscillatory activity positively modulated by running speed. The proportion of theta rhythmic cells with speed modulated frequencies did not significantly change during MS inactivation or either recovery session (Fig 6A; MS inactivation: Chi-square = 2.21, n.s.; 3 – 6 hour recovery: Chi-square = 0.01, n.s.; 24 hour recovery: Chi-square = 0.14, n.s.), yet unlike the firing rate speed signal that showed increased pseudo-r2 values during MS inactivation the pseudo-r2 values for the oscillatory speed signal were reduced during MS inactivation among cells that remained theta rhythmic (Fig 6D; Wilcoxon signed rank test: p < 0.0005) suggesting a decrement in the oscillatory speed signal in the absence of MS input. A similar pattern was observed for each individual cell type, although only the interneurons showed a statistically significant decrease during MS inactivation (Fig 6D; Wilcoxon signed rank test: p < 0.05). The variation of the depth of theta modulation as a function of running speed was also decreased similarly to the modulation of frequency during MS inactivation among all theta rhythmic cells (Fig S5A; Wilcoxon signed rank test: p < 0.005) and again only among the interneurons when each cell type is considered individually (Wilcoxon signed rank test: p < 0.05). Overall, the strength of the coupling between oscillatory frequency and oscillatory amplitude and running speed is decreased in during MS inactivation.
Figure 6.
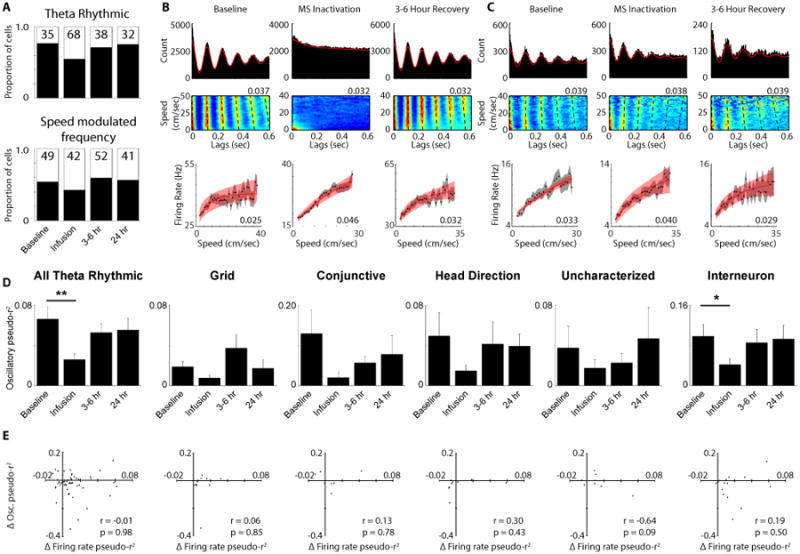
Disruption of oscillatory speed signal during MS inactivation. A. The proportion of significantly theta rhythmic cells (top) and the proportion of theta rhythmic cells with significantly speed modulated oscillatory frequencies (bottom). B. Traditional spike time autocorrelation (top), spike time lags as a function of running speed density plot speed (the value at the top right corner of each plot indicates the maximum conditional probability of firing (red) shown in the plot and the sum of each running speed row equals a conditional probability of 1) (middle) and firing rate versus running speed plot (bottom) for an example interneuron. C. Same plots as in B, but for an interneuron that remains theta rhythmic during MS inactivation. D. Mean +/- SEM pseudo-r2 values between oscillatory frequency and running speed for all theta rhythmic cells and broken down by each individual cell type as well. E. Lack of a relationship between the change in firing rate pseudo-r2 values and the change in oscillatory frequency pseudo-r2 values between baseline and MS inactivation for all cell types. * p < 0.05, ** p < 0.0005
The slopes and r-values for the firing rate and oscillatory speed signals were shown above to not be related to each other and the two speed signals also respond in opposite directions to the removal of MS input, so we further confirmed the independence of the two signals by investigating whether any relationship exists between each cells firing rate speed signal change and oscillatory speed signal change during MS inactivation. It is clear that the two signals are independent simply by the fact that there is a group of cells that lose theta rhythmicity, and the associated oscillatory speed signal, during MS inactivation, but have an enhanced firing rate speed signal (Fig 6B). A majority of cells that lose theta rhythmicity have either increased firing rate versus running speed pseudo-r2 values (52%) or transition from having non-significant firing rate versus running speed relationships to significant relationships (9%) during MS inactivation (Fig S5B). Additionally, the cells that lose theta rhythmicity have significantly increased firing rate versus running speed pseudo-r2 values during MS inactivation similar to the overall population of speed modulated cells (Wilcoxon signed rank test: p < 0.005; Fig S5C). Yet even among cells that retain theta rhythmicity there is no relationship between how their oscillatory speed signal and firing speed signal changes (Fig 6C, E). Correlations between the change in pseudo-r2, r-value or slope for the firing rate and oscillatory frequency speed signals were all non-significant across cell types (Fig 6E, Fig S5F, G) and the same was also true when comparing the changes to depth of theta modulation versus running speed and the firing rate speed signal changes (Fig S5D, E). Thus there is not only a lack of any baseline relationship between the firing rate and oscillatory speed signals, but the two signals do not manifest related changes in response to MS inactivation.
Discussion
Multiple speed signals in MEC
If an animal is navigating on the basis of path integration, the internal representation of its location within an environment needs to be continuously updated based on the combined information of the speed and direction of movements. Models of grid cells generally employ path integration mechanisms in order to generate regularly repeating spatial firing fields and these models traditionally require directional and linear speed information (McNaughton et al., 2006; Fuhs and Touretzky, 2006; Burgess et al., 2007; Hasselmo, 2008; Blair et al., 2008; Burak and Fiete, 2009). Both speed and directional information have been shown to be present in MEC (Sargolini et al., 2006; Wills et al., 2012; Brandon et al. 2013; Kropff et al., 2015). The current work detailed the multiple ways in which MEC neurons respond to running speed. First, the firing rates of the majority of MEC neurons are significantly modulated by the running speed of the animal, yet the majority of those cells had firing rates that saturate rather than linearly tracking running speed and a sizable percentage (16%) are actually negatively modulated by running speed. Second, the majority of theta rhythmic MEC cells have an oscillatory frequency that is modulated by running speed. Third, there is no consistent relationship between the firing rate and oscillatory frequency speed signals suggesting the two running speed signals to be independent. Fourth, inactivation of MS resulted in an increase in the strength of the relationship between firing rate and running speed and, fifth, the strength of the speed modulation of oscillatory frequency by running speed was reduced by the same MS inactivation. The results from the MS inactivation experiments provide further evidence for the independence of the two commonly employed speed signals in grid cell models and additionally helps to build our understanding of the pathways by which running speed information may (or may not) reach MEC circuits.
While all path integration based computational models of grid cell generation require a speed signal, they differ in the physiological expression of that signal. Attractor network models generally include a firing rate based speed signal. This type of speed signal has found support among multiple reports demonstrating the speed modulation of the firing rates of various MEC neurons (Sargolini et al., 2006; Wills et al., 2012; Kropff et al., 2015), most notably the recent report showing the existence of a dedicated group of speed cells in MEC (Kropff et al., 2015). In order to generate equally spaced and stably positioned grid firing fields the speed signal must be linear, which is a critical aspect as non-linearities in the speed signal will result in the accumulation of error in a path integrator. By explicitly fitting the relationship between firing rate and running speed with both a linear and non-linear function, we show that there are cells present in MEC that meet the necessity of coding running speed linearly, despite the majority of cells saturating at moderate running speeds and thus coding running speed non-linearly. This is an important facet of MEC speed coding for future studies to consider as most of the cells identified as having a non-linear relationship between firing rate and running speed could be misidentified as having a linear relationship if only a linear fit is employed. Excluding those cells that code running speed non-linearly, there are clearly still cells that fulfill the requirement of responding linearly and a number of those cells do not have a spatial correlate including both putative uncharacterized principal cells and interneurons. While the current work is unable to assess the context invariance of the speed coding of these cells, as was shown for speed cells (Kropff et al., 2015), it is likely that at least some of the uncharacterized cells and interneurons with linearly responding firing rates are speed cells. In addition to identifying putative positive speed cells, we also found a sizable proportion of negatively speed modulated cells (16%). This is an intriguing property given recent work on the presence of negatively speed modulated cells in CA2 that code for space during immobility (Kay et al., 2016) and thus could be recipients of input from negatively speed modulated MEC cells via entorhinal-hippocampal synapses (Chevaleyre and Siegelbaum, 2010) or alternatively could provide negatively speed modulated output back to MEC via hippocampal-entorhinal projections (Rowland et al., 2013).
Unlike attractor dynamic models of grid cells, oscillatory interference models generally employ a speed signal present in the oscillatory frequency of cell spiking rhythmicity. The oscillatory theta frequency of cells has previously been shown to increase as a function of running speed in MEC (Jeewajee et al., 2008; Brandon et al., 2013), hippocampus (Geisler et al., 2007; Welday et al., 2011), MS (King et al., 1998; Welday et al., 2011) and anterior thalamus (Welday et al., 2011), as well as the frequency of LFP theta oscillations throughout the hippocampal formation (Rivas et al., 1996; Sławińska and Kasicki, 1998; Jeewajee et al., 2008; Hinman et al., 2011). The current findings further support the speed dependent variation of oscillatory theta frequency of single cell spiking through the use of a novel maximum likelihood estimation approach to identifying variation in rhythmic properties as a function of running speed. This technique allows for the examination of continuous behavioral segments and is more robust in detecting significant rhythmicity with lower spike counts than previously employed approaches (Climer et al., 2015). A majority of the theta rhythmic MEC cells had oscillatory frequencies that significantly varied according to running speed, which included cells of every subtype considered (Fig 3), and the slope of the relationship matched that typically employed by oscillatory interference models. Virtually all interneurons had speed modulated oscillatory frequencies, which lends support to recent grid cell modeling work that employed theta rhythmic inhibition from MEC interneurons to grid cells that has a speed modulated frequency as a mechanism for coding running speed (Hasselmo and Shay, 2014).
Given that both the firing rate and oscillatory frequency of MEC generally showed increases as a function of running speed, we addressed the question as to whether perhaps the speed dependent firing rate and oscillatory frequency changes within a single cell were related physiological manifestations of a single running speed signal impinging upon MEC circuits. This was not the case as there was no correlation between the manner in which a cell's firing rate and oscillatory frequency varied as a function of running speed. The independence of the two signals was further supported by the opposite direction of the changes in the strength of each signal during MS inactivation, with the firing rate speed signal becoming stronger and the oscillatory frequency speed signal becoming weaker across the overall population. Two critical questions are raised by the effects of MS inactivation on the two speed signals. First, what is the function of each speed signal given that they are simultaneously present within the same circuit and can we identify whether one or the other is necessary for the generation of grid cells? It is difficult to conceptualize a system in which both speed signals operate simultaneously within the same circuit for the same purpose, whether that is generating grid cells or not. Second, given that neither speed signal was abolished during MS inactivations, by what anatomical pathway does running speed information reach MEC? Below we discuss each of these questions with the latter addressed first followed by the former.
Locomotion modulated firing rates have been observed in an overwhelmingly large number of cortical and subcortical structures (outside of motor generation regions), including primary visual cortex (Niell and Stryker, 2010), primary auditory cortex (Fu et al., 2014), barrel cortex (Fu et al., 2014) retrosplenial cortex (Cho and Sharp, 2001), posterior parietal cortex (Whitlock et al., 2012), postrhinal cortex (Furtak et al., 2012), entorhinal cortex (Sargolini et al., 2006; Wills et al., 2012; Kropff et al., 2015), striatum (Yeshenko et al., 2004), medial and lateral septum (King et al., 1998; Zhou et al., 1999), lateral hypothalamus (Bender et al., 2015) and the hippocampus (McNaughton et al., 1983). It is difficult to identify any single circuitry that could propagate running speed information throughout the hippocampal formation based on these varied structures, but recently glutamatergic neurons in MS were shown to be responsible for speed modulation in CA1 (Fuhrmann et al., 2015). Yet despite the fact that MS projects strongly to MEC (Kondo and Zaborszky, 2016) and our inactivations abolished LFP theta oscillations and grid cells in MEC (Brandon et al., 2011), speed modulation of MEC firing rates was actually enhanced during MS inactivations in opposition to our hypothesis. The possibility exists that running speed signals emanate from a more ventral region in the diagonal band of Broca that our inactivation may not have reached. One possible mechanism for the enhancement of the firing rate speed signal in MEC during MS inactivation is that the speed signal emanating from the hippocampus is lost, as is suggested by recent work demonstrating that MS glutamatergic neurons are responsible for speed modulation in hippocampus. Given that speed cells in MEC and hippocampus show prospective and retrospective relationships with running speed respectively (Kropff et al., 2015), the removal of the slightly temporally misaligned hippocampal speed signal input to MEC may lead to the observed enhanced firing rate speed signal in MEC.
As for the first question raised by the presence of two independent running speed signals in MEC, it seems unlikely that both signals could provide running speed information used to update a path integrator. Modeling work demonstrates the feasibility of either signal providing running speed information, in principle, but there is currently no indication that both signals could be used simultaneously. One possibility is that the different speed signals arise from different sources, with one speed signal coding the self-motion signal from the brainstem whereas another speed signal may arise from computation of speed based on changes in visual stimuli such as optic flow (Raudies and Hasselmo, 2015). Given that most models of grid cells are based on path integration, requiring both head direction and running speed information, manipulation of either component should result in corresponding changes in grid cell firing. Removal of head direction information results in the loss of grid cells (Winter et al., 2015), although it is not known whether the same manipulation also alters the coding of running speed. During MS inactivation head direction cells remain intact (Brandon et al., 2011), yet grid cell spatial periodicity is disrupted (Brandon et al., 2011; Koenig et al., 2011). The current work demonstrated that during MS inactivation when grid cells are disrupted there are alterations of both the firing rate coding of running speed and the rhythmicity code for running speed that could lead to changes in path integration in different grid cell models. A path integrator using a firing rate speed signal, as in attractor dynamic models, that is enhanced during MS inactivation would result in a change in grid cell spatial scale, which is not observed during MS inactivation. Alternatively, a path integrator using a rhythmicity speed signal coded by changes in frequency, as in oscillatory interference models, would accumulate error with the diminished coding of speed by frequency of rhythmicity observed during MS inactivation.
Another possibility is that one of the speed signals maintains an alternative purpose. The running speed of an animal has profound effects on temporal coordination throughout the hippocampal formation. Movement through space is one of the most basic behaviors performed by an animal and, as the rate of movement through space increases, most other behaviors of the animal must be performed with increasing speed. Perceptual judgments, memory based decisions and motor outputs must all take place on shorter timescales with less temporal allowance for correcting erroneous neuronal computations or behavioral actions. Such a situation requires faster and/or more efficient intra- and inter-regional communication, which can be achieved through increased phase locking, faster frequency oscillations and greater coherence between sites.
Activity throughout MEC and much of the hippocampal formation becomes increasingly tuned within the theta frequency range at faster running speeds. Theta coherence between MEC and the hippocampus, as well as across the septotemporal axis of the hippocampus, increases as a function of running speed (Hinman et al., 2011, 2013), thus potentially satisfying the need for more efficient intra-and inter-regional communication. The increase in theta frequency both intrinsically within individual cells and in the LFP translates to shorter cycle durations and thus to information transfer at shorter timescales. The current work demonstrated that, in addition to oscillating at a faster frequency, the magnitude of the intrinsic rhythmicity of MEC neurons is also increased as an animal runs faster. The increased depth of theta rhythmic firing by MEC neurons likely contributes to the increase in LFP theta amplitude observed as an animal runs faster (McFarland et al., 1975; Kemere et al., 2013) and will increasingly bring their postsynaptic targets into the theta rhythmic regime.
Neurons in MEC not only exhibit increased theta rhythmicity as a function of running speed, but we have also shown that they become increasingly theta phase locked at faster running speeds. Theta phase locking of spikes increased, while the theta phase at which they spike does not vary. By maintaining the same theta phase of firing across different running speeds this maintains constant phase relationships between different cell populations, such as the two groups of entorhinal neurons that fire on opposite phases of theta (Misuzeki et al., 2009; Newman and Hasselmo, 2014). Overall, this tuning in the theta frequency range at faster running speeds may allow for more efficient communication on shorter timescales throughout the entorhino-hippocampal memory circuit during behaviors that restrict the time allowed for processing incoming information and executing memory based actions.
Materials and Methods
Subjects
This paper uses data gathered during experiments for which some results have previously been published (Brandon et al., 2011, 2013). Six adult male Long-Evans rats (500-650g) obtained from Charles River Labs (Wilmington, MA) were used. All experimental procedures were approved by the Institutional Animal Care and Use Committee for the Charles River Campus at Boston University. Detailed methods are provided in the supplemental materials.
Statistics
Normality of distributions was not assumed, so comparisons were made using non-parametric statistics. Comparisons of single distributions for a difference from zero were performed using Wilcoxon sign-rank tests. For comparisons of two distributions Wilcoxon sign-rank or Wilcoxon rank-sum tests were used. The general approach taken was to perform the various statistical tests on the full set of relevant cells and then divide the cells into the different functional cell types and perform the same statistical test on each individual cell type.
Supplementary Material
Highlights.
Two dissociable running speed signals are present in medial entorhinal cortex (MEC)
Medial septal (MS) inactivation strengthens the firing rate speed signal in MEC
Speed modulation of intrinsic theta frequency is decreased during MS inactivation
A sizable percentage of MEC neurons are negatively speed modulated
Acknowledgments
Support for this work was provided by ONR MURI grant N00014-10-1-0936, NIMH R01 MH60013 and MH61492.
Footnotes
Author Contributions: M.P.B. and M.E.H. designed the experiments. M.P.B. conducted experiments. J.R.H., J.R.C. and G.W.C. analyzed data. J.R.H., J.R.C., G.W.C. and M.E.H. wrote the paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alonso A, Kohler C. A study of the reciprocal connections between the septum and the entorhinal area using anterograde and retrograde axonal transport methods in the rat brain. J Comp Neurol. 1984;225(3):327–343. doi: 10.1002/cne.902250303. [DOI] [PubMed] [Google Scholar]
- Bender F, Gorbati M, Cadavieco MC, Denisova N, Gao X, Holman C, Korotkova T, Ponomarenko A. Theta oscillations regulate the speed of locomotion via a hippocampus to lateral septum pathway. Nat Commun. 2015;6:8521. doi: 10.1038/ncomms9521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair HT, Gupta K, Zhang K. Conversion of a phase- to a rate-coded position signal by a three stage model of theta cells, grid cells, and place cells. Hippocampus. 2008;18(12):1239–1255. doi: 10.1002/hipo.20509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science. 2011;332(6029):595–599. doi: 10.1126/science.1201652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandon MP, Bogaard AR, Schultheiss NW, Hasselmo ME. Segregation of cortical head direction cell assemblies on alternating theta cycles. Nat Neurosci. 2013;16(6):739–48. doi: 10.1038/nn.3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burak Y, Fiete IR. Accurate path integration in continuous attractor network models of grid cells. PLOS Comp Biol. 2009;5(2):e1000291. doi: 10.1371/journal.pcbi.1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N, Barry C, O'Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17(9):801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess N. Grid cells and theta as oscillatory interference: theory and predictions. Hippocampus. 2008;18(12):1157–1174. doi: 10.1002/hipo.20518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bush D, Burgess N. A hybrid oscillatory interference/continuous attractor network model of grid cell firing. J Neurosci. 2014;34(14):5065–79. doi: 10.1523/JNEUROSCI.4017-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33(3):325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- Chevaleyre V, Siagelbaum SA. Strong CA2 pyramidal neuron synapses define a powerful disynaptic cortico-hippocampal loop. Neuron. 2010;66(4):560–572. doi: 10.1016/j.neuron.2010.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho J, Sharp PE. Head direction, place, and movement correlates for cells in the rat retrosplenial cortex. Behav Neurosci. 2001;115(1):3–25. doi: 10.1037/0735-7044.115.1.3. [DOI] [PubMed] [Google Scholar]
- Climer JR, Ditullio R, Newman EL, Hasselmo ME, Eden UT. Examination of rhythmicity of extracellularly recorded neurons in the entorhinal cortex. Hippocampus. 2015;25(4):460–473. doi: 10.1002/hipo.22383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, Mamiya A, Buzsaki G. Oscillatory coupling of hippocampal pyramidal cells and interneurons in the behaving rat. J Neurosci. 1999;19(1):274–287. doi: 10.1523/JNEUROSCI.19-01-00274.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czurko A, Huxter J, Li Y, Hangya B, Muller RU. Theta phase classification of interneurons in the hippocampal formation of freely moving rats. J Neurosci. 2011;31(8):2938–2947. doi: 10.1523/JNEUROSCI.5037-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox SE, Wolfson S, Ranck JB., Jr Hippocampal theta rhythm and the firing of neurons in walking and urethane anesthetized rats. Exp Brain Res. 1986;62(3):495–508. doi: 10.1007/BF00236028. [DOI] [PubMed] [Google Scholar]
- Fu Y, Tucciarone JM, Espinosa JS, Sheng N, Darcy DP, Nicoll RA, Huang ZJ, Stryker MP. A cortical circuit for gain control by behavioral state. Cell. 2014;156(6):1139–1152. doi: 10.1016/j.cell.2014.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhrmann F, Justus D, Sosulina L, Kaneko H, Beutel T, Friedrichs D, Schoch S, Schwarz MK, Fuhrmann M, Remy S. Locomotion, theta oscillations, and the speed correlated firing of hippocampal neurons are controlled by a medial septal glutamatergic circuit. Neuron. 2015;86(5):1253–1264. doi: 10.1016/j.neuron.2015.05.001. [DOI] [PubMed] [Google Scholar]
- Fuhs MC, Touretzky DS. A spin glass model of path integration in rat medial entorhinal cortex. J Neurosci. 2006;26(16):4266–4276. doi: 10.1523/JNEUROSCI.4353-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furtak SC, Ahmed OJ, Burwell RD. Single neuron activity and theta modulation in postrhinal cortex during visual object discrimination. Neuron. 2012;76(5):976–988. doi: 10.1016/j.neuron.2012.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fyhn M, Molden S, Witter MP, Moser EI, Moser MB. Spatial representation in the entorhinal cortex. Science. 2004;305(5688):1258–1264. doi: 10.1126/science.1099901. [DOI] [PubMed] [Google Scholar]
- Geisler C, Robbe D, Zugaro M, Sirota A, Buzsaki G. Hippocampal place cell assemblies are speed-controlled oscillators. Proc Natl Acad Sci. 2007;104(19):8149–54. doi: 10.1073/pnas.0610121104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guanella A, Verschure PF. A model of grid cells based on path integration mechanism. In: Kollias SD, Stafylopatis A, Duch W, Oja E, editors. Artificial Neural Networks – ICANN 2006, Part 1, LNCS4131. Springer; Berlin: 2006. [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Science. 2005;436(7052):801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME. Grid cell mechanisms and function: contributions of entorhinal persistent spiking and phase resetting. Hippocampus. 2008;18(12):1213–1229. doi: 10.1002/hipo.20512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME. Neuronal rebound spiking, resonance frequency and theta cycle skipping may contribute to grid cell firing in medial entorhinal cortex. Phil Trans R Soc Lond B Biol Sci. 2013;369(1635):20120523. doi: 10.1098/rstb.2012.0523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Brandon MP. A model combining oscillations and attractor dynamics for generation of grid cell firing. Front Neural Circuits. 2012;6:30. doi: 10.3389/fncir.2012.00030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME, Shay CF. Grid cell firing patterns may arise from feedback interaction between intrinsic rebound spiking and transverse traveling waves with multiple heading angles. Front Syst Neurosci. 2014;8:201. doi: 10.3389/fnsys.2014.00201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinman JR, Penley SC, Long LL, Escabí MA, Chrobak JJ. Septotemporal variation in dynamics of theta: speed and habituation. J Neurophysiol. 2011;105(6):2675–2686. doi: 10.1152/jn.00837.2010. [DOI] [PubMed] [Google Scholar]
- Hinman JR, Penley SC, Escabí MA, Chrobak JJ. Ketamine disrupts theta synchrony across the septotemporal axis of the CA1 region of the hippocampus. J Neurophysiol. 2013;109(2):570–579. doi: 10.1152/jn.00561.2012. [DOI] [PubMed] [Google Scholar]
- Jeewajee A, Barry C, O'Keefe J, Burgess N. Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus. 2008;18(12):1175–1185. doi: 10.1002/hipo.20510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay K, Sosa M, Chung JE, Karlsson MP, Larkin MC, Frank LM. A hippocampal network for spatial coding during immobility and sleep. Nature. 2016;531(7593):185–190. doi: 10.1038/nature17144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemere C, Carr MF, Karlsson MP, Frank LM. Rapid and continuous modulation of hippocampal network state during exploration of new places. PLoS ONE. 2013;8(9):e73114. doi: 10.1371/journal.pone.0073114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King C, Recce M, O'Keefe J. The rhythmicity of cells of the medial septum/diagonal band of Broca in the awake freely moving rat: relationships with behavior and hippocampal theta. Eur J Neurosci. 1998;10(2):464–477. doi: 10.1046/j.1460-9568.1998.00026.x. [DOI] [PubMed] [Google Scholar]
- Kondo H, Zaborsky L. Topographic organization of the basal forebrain projections to the perirhinal, postrhinal and entorhinal cortex in rats. J Comp Neurol. 2016 doi: 10.1002/cne.23967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig J, Linder AN, Leutgeb JK, Leutgeb S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science. 2011;332(6029):592–595. doi: 10.1126/science.1201685. [DOI] [PubMed] [Google Scholar]
- Leung LS, Y HW. Theta-freqeuency resonancse in hippocampal CA1 neurons in vitro demonstrated by sinusoidal current injection. J Neurophysiol. 1998;79(3):1592–1596. doi: 10.1152/jn.1998.79.3.1592. [DOI] [PubMed] [Google Scholar]
- Long LL, Hinman JR, Chen CM, Escbai MA, Chrobak JJ. Theta dynamics in rat: speed and acceleration across the septotemporal axis. PLoS One. 2014;9(5):e97987. doi: 10.1371/journal.pone.0097987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer AP, Vanrhoads SR, Sutherland GR, Lipa P, McNaughton BL. Self-motion and the origin of differential spatial scaling along the septo-temporal axis of the hippocampus. Hippocampus. 2005;15(7):841–852. doi: 10.1002/hipo.20114. [DOI] [PubMed] [Google Scholar]
- McFarland WL, Teitelbaum H, Hedges EK. Relationship between hippocampal theta activity and running speed in the rat. J Comp Phyiol Psychol. 1975;88(1):324–328. doi: 10.1037/h0076177. [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Barnes CA, O'Keefe J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp BrainRes. 1983;52(1):41–49. doi: 10.1007/BF00237147. [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the ‘cognitive map’. Nat Rev Neurosci. 2006;7(8):663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
- Mitchell JS, Rawlins JN, Steward O, Olton DS. Medial septal area lesions disrupt theta rhythm and cholinergic staining in medial entorhinal cortex and produce impaired radial arm maze behavior in rats. J Neurosci. 1982;2(3):292–302. doi: 10.1523/JNEUROSCI.02-03-00292.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizumori SJ, Perez GM, Alvarado MC, Barnes CA, McNaughton BL. Reversible inactivation of the medial septum differentially affects two forms of learning in rats. Brain Res. 1990;528(1):12–20. doi: 10.1016/0006-8993(90)90188-h. [DOI] [PubMed] [Google Scholar]
- Mizuseki K, Sirota A, Pastalkova E, Buzsaki G. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron. 2009;64(2):267–280. doi: 10.1016/j.neuron.2009.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navratilova Z, Giocomo LM, Fellous JM, Hasselmo ME, McNaughton BL. Phase precession and variable spatial scaling in a periodic attractor map model of medial entorhinal grid cells with realistic after-spike dynamics. Hippocampus. 2011;22(4):772–789. doi: 10.1002/hipo.20939. [DOI] [PubMed] [Google Scholar]
- Niell CM, Stryker MP. Modulation of visual responses by behavioral state in mouse visual cortex. Neuron. 2010;65(4):472–479. doi: 10.1016/j.neuron.2010.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raudies F, Hasselmo ME. Differences in visual-spatial input may underlie different compression properties of firing fields for grid cell modules in medial entorhinal cortex. PLoS Comput Biol. 2015;11(11):e1004596. doi: 10.1371/journal.pcbi.1004596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas J, Gaztelu JM, Garcia-Austt E. Changes in hippocampal cell discharge patterns and theta rhythm spectral properties as a function of walking velocity in the guinea pig. Exp Brain Res. 1996;108(1):113–118. doi: 10.1007/BF00242908. [DOI] [PubMed] [Google Scholar]
- Rowland DC, Weible AP, Wickersham IR, Wu H, Mayford M, Witter MP, Kentros CG. Transgenically targeted rabies virus demonstrates a major monosynaptic projection from hippocampal area CA2 to medial entorhinal layer II neurons. JNeurosci. 2013;33(37):14889–14898. doi: 10.1523/JNEUROSCI.1046-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312(5774):758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Schmidt-Heiber C, Hausser M. Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nat Neurosci. 2013;16(3):325–331. doi: 10.1038/nn.3340. [DOI] [PubMed] [Google Scholar]
- Sławińska U, Kasicki S. The frequency of rat's hippocampal theta rhythm is related to the speed of locomotion. Brain Research. 1998;796(1-2):327–331. doi: 10.1016/s0006-8993(98)00390-4. [DOI] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI. The entorhinal grid map is discretized. Nature. 2012;492(7427):72–78. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- Taube JS. The head direction signal: Origins and sensory-motor integration. Annu Rev Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
- Vanderwolf CH. Hippocampal electrical activity and voluntary movement in the rat. Electroencephalogr Clin Neurophysiol. 1969;26:407–418. doi: 10.1016/0013-4694(69)90092-3. [DOI] [PubMed] [Google Scholar]
- Welday AC, Shlifer IG, Bloom ML, Zhang K, Blair HT. Cosine directional tuning of theta cell burst frequencies: evidence for spatial coding by oscillatory interference. J Neurosci. 2011;31(45):16157–16176. doi: 10.1523/JNEUROSCI.0712-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock JR, Pruhl G, Dagslott N, Moser MB, Moser EI. Functional split between parietal and entorhinal cortices in the rat. Neuron. 2012;73(4):789–802. doi: 10.1016/j.neuron.2011.12.028. [DOI] [PubMed] [Google Scholar]
- Wills TJ, Barry C, Cacucci F. The abrupt development of adult-like grid cell firing in the medial entorhinal cortex. Front Neural Circuits. 2012;6:21. doi: 10.3389/fncir.2012.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winson J. Loss of hippocampal theta rhythm results in spatial memory deficit in the rat. Science. 1978;201(4351):160–163. doi: 10.1126/science.663646. [DOI] [PubMed] [Google Scholar]
- Winter SS, Clark BJ, Taube JS. Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science. 2015;347(6224):870–874. doi: 10.1126/science.1259591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeshenko O, Guazzelli A, Mizumori SJ. Context-dependent reorganization of spatial and movement representations by simultaneously recorded hippocampal and striatal neurons during performance of allocentric and egocentric tasks. Behav Neurosci. 2004;118(4):751–769. doi: 10.1037/0735-7044.118.4.751. [DOI] [PubMed] [Google Scholar]
- Zhou TL, Tamura R, Kuriwaki J, Ono T. Comparison of medial and lateral septal neuron activity during performance of spatial tasks in rats. Hippocampus. 1999;9(3):220–234. doi: 10.1002/(SICI)1098-1063(1999)9:3<220::AID-HIPO3>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Zilli EA. Models of grid cell spatial firing published 2005-2011. Front Neural Circuits. 6:16. doi: 10.3389/fncir.2012.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.