HCN hyperpolarization-activated cation channels strengthen virtual nicotinic EPSPs and thereby elevate synaptic amplification in rat sympathetic neurons

With the use of dynamic clamp to create virtual synapses, this study shows that hyperpolarization-activated cation current (h-current; I_h) strengthens fast excitatory postsynaptic potentials and synaptic amplification in sympathetic neurons. The manipulation of the voltage dependence of a virtual I_h also shifted gain. These results reveal a new physiological role for hyperpolarization-activated cation channels in the sympathetic motor system.

Abstract

The influence of hyperpolarization-activated cation current (h-current; I_h) upon synaptic integration in paravertebral sympathetic neurons was studied together with expression of hyperpolarization-activated cyclic nucleotide-gated (HCN) subunit isoforms. All four HCN subunits were detected in homogenates of the rat superior cervical ganglion (SCG) using the PCR to amplify reverse-transcribed messenger RNAs (RT-PCR) and using quantitative PCR. Voltage clamp recordings from dissociated SCG neurons at 35°C detected I_h in all cells, with a maximum hyperpolarization-activated cation conductance of 1.2 ± 0.1 nS, half-maximal activation at −87.6 mV, and reversal potential of −31.6 mV. Interaction between I_h and synaptic potentials was tested with virtual fast nicotinic excitatory postsynaptic potentials (EPSPs) created with dynamic clamp. The blocking of I_h with 15 μM ZD7288 hyperpolarized cells by 4.7 mV and increased the virtual synaptic conductance required to stimulate an action potential from 7.0 ± 0.9 nS to 12.1 ± 0.9 nS. In response to stimulation with 40 s long trains of virtual EPSPs, ZD7288 reduced postsynaptic firing from 2.2 to 1.7 Hz and the associated synaptic amplification from 2.2 ± 0.1 to 1.7 ± 0.2. Cyclic nucleotide binding to HCN channels was simulated by blocking native I_h with ZD7288, followed by reconstitution with virtual I_h using a dynamic clamp model of the voltage clamp data. Over a 30-mV range, shifting the half-activation voltage for I_h in 10 mV depolarizing increments always increased synaptic gain. These results indicate that I_h, in sympathetic neurons, can strengthen nicotinic EPSPs and increase synaptic amplification, while also working as a substrate for cyclic nucleotide-dependent modulation.

NEW & NOTEWORTHY

With the use of dynamic clamp to create virtual synapses, this study shows that hyperpolarization-activated cation current (h-current; I_h) strengthens fast excitatory postsynaptic potentials and synaptic amplification in sympathetic neurons. The manipulation of the voltage dependence of a virtual I_h also shifted gain. These results reveal a new physiological role for hyperpolarization-activated cation channels in the sympathetic motor system.

this study examines the interaction in rat sympathetic neurons between the hyperpolarization-activated cation current (h-current; I_h) and virtual fast excitatory postsynaptic potentials (EPSPs). The I_h flows through channels encoded by four genes, designated hyperpolarization-activated cyclic nucleotide-gated (HCN)1–4, which belong to the superfamily of cyclic nucleotide-gated ion channels (Biel 2009; Craven and Zagotta 2006; Kaupp and Seifert 2001; Pape 1996; Robinson and Siegelbaum 2003). Originally named as the “funny” current, or f-current, because of its unusual voltage dependence, I_h was discovered in the sino-atrial node and cardiac Purkinje fibers (Brown et al. 1979; DiFrancesco 2010; DiFrancesco and Ojeda 1980), where it plays an essential role in generating the heart's intrinsic pacemaker activity. Subsequent work detected I_h in a variety of central and peripheral neurons, where it can influence the resting potential (V_rest), membrane excitability, rhythmic firing, and integration of synaptic potentials (George et al. 2009; Pape 1996; Pape and McCormick 1989; Siegelbaum 2000). In the periphery, I_h has been identified in subtypes of autonomic neurons by its voltage dependence, together with sensitivity to Cs⁺, insensitivity to Ba²⁺, and dependence on Na⁺. These neuronal groups include afterhyperpolarization-type myenteric neurons in the gut (Galligan et al. 1990; Rugiero et al. 2002; Xiao et al. 2004), parasympathetic neurons in the cardiac ganglion (Cuevas et al. 1997; Edwards et al. 1995; Hogg et al. 2001; Xi-Moy and Dun 1995), and sympathetic neurons in paravertebral ganglia (Jobling and Gibbins 1999; Lamas 1998; Lamas et al. 1997; Tokimasa and Akasu 1990). In addition, I_h is developmentally regulated in parasympathetic neurons (Hogg et al. 2001), and its modulation mediates some excitatory effects of pituitary adenylate cyclase-activating polypeptide (Merriam et al. 2004; Tompkins et al. 2009). Despite this widespread cellular expression pattern, the implications of I_h for fast synaptic transmission in autonomic neurons remain largely unexplored.

The possible importance of I_h in sympathetic neurons became apparent to us during experiments to assess the repetitive firing elicited by long depolarizing current pulses in neurons dissociated from the rat superior cervical ganglion (SCG) (Springer et al. 2015). When hyperpolarizing current pulses were applied to construct steady-state current-voltage relations, SCG neurons displayed very prominent sag responses, which in some cases, were >40 mV in amplitude at negative potentials [see, for example, Fig. 1 in Springer et al. (2015)]. Although sag depolarizations at negative voltages are a hallmark of I_h activation, rarely have such large responses been reported. Moreover, Springer et al. (2015) observed similar sag responses in whole-cell current clamp recordings from the intact SCG, as well as in cell culture, thus suggesting that I_h expression is a normal feature of rat sympathetic neurons and not a consequence of in vitro growth conditions. In preliminary experiments, application of ZD7288, a selective blocker of HCN channels (BoSmith et al. 1993; Harris and Constanti 1995), antagonized the sag response, thereby providing additional evidence for activation of inward I_h at negative potentials.

Fig. 1.

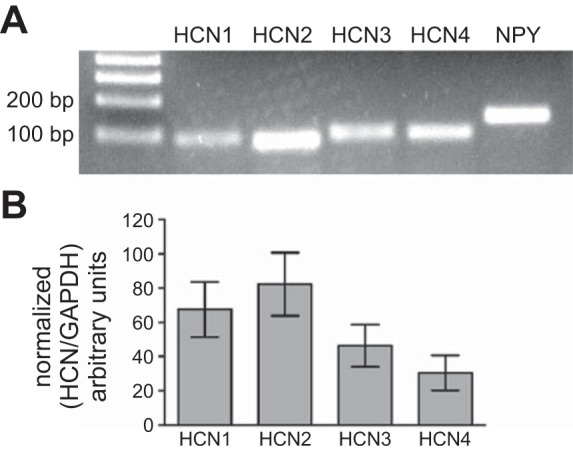
Detection of all 4 HCN isoforms in SCG homogenates. A: standard RT-PCR included NPY as a positive control. Left lane, 100 bp size ladder. B: normalized qPCR data from SCG taken from 4 rats (means ± SE). Samples from different animals were used in A and B.

The present work was undertaken to identify the HCN subunits normally expressed in the SCG and to assess their functional consequences for fast synaptic excitation. To approach this problem, membrane excitability was probed with virtual fast nicotinic EPSPs of defined strength that were created using the dynamic clamp method (Springer et al. 2015). Voltage clamp measurements were then used to construct a mathematical model of the hyperpolarization-activated cation conductance (h-conductance; g_h). The implementation of the model under dynamic clamp permitted experiments to reconstitute a virtual I_h after pharmacological blockade of the native g_h. The results confirm that low levels of g_h expression help to regulate the normal V_rest of sympathetic neurons, and they reveal for the first time that g_h effectively strengthens the impact of subthreshold virtual, fast EPSPs upon postganglionic spike generation. We also found that these effects have the capacity to elevate synaptic amplification in sympathetic ganglia and are modulated by shifts in the voltage dependence of g_h activation, similar to those produced by binding of cyclic nucleotides to HCN channels.

MATERIALS AND METHODS

Animal use.

All experiments used Sprague-Dawley rats (CD strain; Charles River Laboratories, Wilmington, MA). The Institutional Animal Care and Use Committee at the University of Pittsburgh approved all animal protocols for this study.

Standard RT-PCR analysis.

SCGs were dissected from adult female and male rats that had been killed by CO₂ inhalation and then homogenized in 200 μl glass microtissue grinders (#885470-0000; Kimble Chase, Vineland, NJ). Total RNA was extracted using the RNeasy Micro kit (#74004; Qiagen, Valencia, CA) that contained homogenization buffer and genomic DNA elimination buffer. RNA was reverse transcribed to cDNA using the RT² First Strand kit (#330404; Qiagen). PCR primers were designed (Table 1) to span exon boundaries with guanine-cytosine (GC) content close to 50% and melting temperatures in the range of 55–60°C and then synthesized by Integrated DNA Technologies (IDT; Coralville, IA). Amplification reactions (25 μl) contained 1 μl cDNA; 5 μl 1.125 mM dNTP; 2 μl, 20 μM forward primer; 2 μl, 20 μM reverse primer; and 0.25 μl DreamTaq DNA polymerase (#EP0702; Thermo Fisher Scientific Life Sciences, Waltham, MA). The thermocycling protocol consisted of 94°C for 2 min, 36 cycles of 94°C for 30 s, 60°C for 45 s, and 72°C for 90 s, followed by 72°C for 7 min and cool down to 4°C. PCR products for each of the four HCN subunits and neuropeptide Y (NPY) were run on 2% agarose gels with 0.01% ethidium bromide, visualized on a UV transilluminator, and photographed using a Kodak EDAS 290 Electrophoresis Analysis System.

Table 1.

Primer sets used for PCR detection of HCN and control mRNAs

Gene	GenBank Accession	Forward (5′ → 3′)	Reverse (5′ → 3′)	Amplicon Size, bp	Exon Location
RT-PCR Primers
HCN1	NM_053375.1	TTGGAGAAATATGCCTGCTG	GTCCACCGAAAGGGAGTAAA	89	6–7
HCN2	NM_053684.1	ACAACATGGTGAACCACTCG	CCAATACAGAGCATGTGGCT	79	3–4
HCN3	NM_053685.1	CGCTTCGGGAGGAGATTAT	GTACTGCGGTGACGAAACTG	96	5–6
HCN4	NM_021658.1	ATCAACGGCATGGTGAATAA	CGTCCGTACCCAATACACAG	92	3–4
NPY	NM_012614.2	TGGCCAGATACTACTCCGCT	ATGGAAGGGTCTTCAAGCCT	154	2–3
qPCR Primers
HCN1		CTTCGGATCGTGAGGTTTAC	TGCACTGGCGAGATCATA	123	2–3
HCN2		CGTGCGTTTCACCAAGA	ATGCTGATCAGGTTACAGATG	144	2–3
HCN3		CCTGCGCATCGTTAGATT	GGTCGTAGGTCATGTGAAAG	113	2–3
HCN4		AGCAGGAGAGGGTTAAGTCA	CATCAGCAACAGCATCGTCA	92	1–2
GAPDH	NM_017008.4	TCTCTGCTCCTCCCTGTTC	GTAACCAGGCGTCCGATAC	120	1–3

Quantitative PCR.

Total RNA was extracted from SCGs, removed from 4 postnatal day 42 male rats using the same methods as for RT-PCR. RNA from each sample was reverse transcribed into cDNA using iScript Reverse Transcription Supermix (#1708840; Bio-Rad Laboratories, Hercules, CA). The RT reaction contained 4 μl iScript Supermix, 1 μg RNA, and nuclease-free water to a 20-μl final volume. The RT thermal cycling protocol consisted of priming for 5 min at 25°C, reverse transcription for 20 min at 46°C, followed by RT inactivation for 1 min at 95°C. Quantitative PCR (qPCR) primers for each HCN isoform and for GAPDH (Table 1) were designed to span exon boundaries, with GC content near 50% and melting temperatures ranging from 55 to 60°C, and were synthesized by IDT. Amplification reactions (20 μl) were run in triplicate and contained 1 μl undiluted cDNA, 10 μl SsoAdvanced Universal SYBR Green Supermix (#172-5271; Bio-Rad Laboratories), 0.25 μl each of sense and anti-sense primers (final concentrations 250 nM), and 8.5 μl water. The qPCR protocol (CFX96 qPCR system; Bio-Rad Laboratories) included the following: 30 s at 95°C, followed by 40 cycles of 5 s at 95°C and 1 min at 60°C. Melt curves were obtained by increasing the sample temperature from 65 to 95°C in 0.5°C steps.

The efficiency (E) of primer pairs was determined in duplicate qPCR measurements of the threshold cycle (C_t) for increasing volumes of cDNA (0.5, 1, and 2 μl). The slopes of linear fits of log₁₀ (microliters cDNA) vs. C_t were used to calculate the primer efficiency (E = 10^[−1/slope]). E values were 1.855 for GAPDH, 2.022 for HCN1, 2.1136 for HCN2, 2.007 for HCN3, and 1.985 for HCN4. C_t was corrected by multiplying by log₂(E). Relative HCN expression levels were calculated from corrected C_t as R_(HCN/GAPDH) = 2^−ΔCt, where ΔC_t = C_t−GAPDH − C_t−HCN (Pfaffl 2001).

Cell culture.

Primary cultures of dissociated, sympathetic neurons were prepared as described previously (Springer et al. 2015). Pups were anesthetized with isoflurane (Piramal Critical Care, Bethlehem, PA) and killed by thoracotomy and cutting the heart. For each dissociation, SCGs were dissected from a litter of 15-day-old rat pups and placed into chilled L-15 media (#SH30525.01; GE Healthcare HyClone, Logan, UT). Ganglia were de-sheathed, cut into pieces, and enzymatically digested at 37°C for 30 min in 2 mg/ml collagenase type 4 (#LS004186; Worthington Biochemical, Lakewood, NJ) in L-15, followed by 30 min in 0.25% trypsin (#15050-057; Thermo Fisher Scientific Life Sciences) with gentle agitation every 10 min. Trypsin was neutralized by diluting 1:10 with growth media that contained MEM (Richter's modification with l-glutamine; #SH30601.01; GE Healthcare HyClone), 10% FBS (#S11150; Atlanta Biologicals, Norcross, GA), 1% penicillin-streptomycin (Cat. No. #B21210; Atlanta Biologicals), 10 ng/ml nerve growth factor (#BT-5017; Harlan Bioproducts, Indianapolis, IN), and 0.4 μM cytosine arabinoside hydrochloride (C6645; Sigma-Aldrich, St. Louis, MO). Digested tissue was pelleted by centrifugation at 100 g for 1 min, suspended in 1 ml growth medium, and triturated using three flame-polished Pasteur pipettes with graded tips. Cells were plated onto 8–12, 12 mm poly-d-lysine/laminin-coated glass coverslips (#354087; Corning, Corning, NY) in a multi-well plate and incubated at 37°C in 5% CO₂ for 1 h for cell attachment. Then, 0.5 ml growth media was added and changed daily.

Electrophysiology.

Whole-cell perforated patch clamp recordings at 35–36°C were made from SCG neurons after 2–4 days in vitro. External solution contained the following (in mM): 146 NaCl, 4.7 KCl, 20 HEPES, 0.6 MgSO₄, 1.6 NaHCO₃, 0.13 NaH₂PO₄, 2.5 CaCl₂, and 7.8 dextrose, adjusted to pH 7.4 with NaOH, and bubbled with 100% O₂. Internal solution contained the following (in mM): 94 K⁺-gluconate, 30 KCl, 10 phosphocreatine di(tris) salt, 10 HEPES, 0.2 EGTA, 4 Mg₂ATP, and 0.3 Na₂GTP, adjusted to pH 7.3, with KOH. Stock solution of amphotericin B (40 mg/ml DMSO) was added to the internal solution for a final concentration of 200 μg/ml. Measurements were started once patch perforation had reduced access resistance to <15 MΩ. No corrections were made for a calculated tip potential of 14 mV, except when noted. Chemicals were purchased from Sigma-Aldrich.

Measurement of I_h.

Voltage clamp recordings were made using an Axopatch 200 amplifier, Digidata 1440A interface, and pCLAMP 10 software (Molecular Devices, Sunnyvale, CA). Cell size was determined from the whole-cell capacitance compensation of the amplifier. Series resistance was monitored throughout the experiment and compensated 85–90%. Current recordings were low-pass filtered at 1 kHz and digitized at 10 kHz. To isolate I_h, voltage protocols were executed before and after bath application of 10–15 μM ZD7288, an I_h-specific channel blocker (#ab120102; Abcam, Cambridge, MA).

Dynamic clamp implementation of virtual synapses and virtual I_h.

Dynamic current clamp recordings were made using an Axoclamp 2B amplifier (Molecular Devices) and a G-clamp interface and software running at 20 kHz (Kullmann et al. 2004). After establishing a stable recording in current clamp mode, the series resistance was fully compensated using the amplifier bridge circuitry. Voltage recordings were low-pass filtered at 3 kHz. Two types of conductance were implemented with the dynamic clamp: a nicotinic conductance to produce virtual synaptic activity and a g_h to study its role in synaptic integration.

Virtual synaptic current (I_syn) was modeled by Eq. 1

$${\mathrm{I}}_{\mathrm{s}\mathrm{y}\mathrm{n}}\mathrm{(}\mathrm{t}\mathrm{)}\mathrm{=}{\mathrm{g}}_{\mathrm{s}\mathrm{y}\mathrm{n}}\mathrm{(}\mathrm{t}\mathrm{)}\hspace{0.17em}\mathrm{\cdot }\hspace{0.17em}\mathrm{S}\hspace{0.17em}\mathrm{\cdot }\hspace{0.17em}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{-}{\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}}\mathrm{)}$$ (1)

where synaptic conductance [g_syn(t)], as a function of time, was calculated as the sum of two exponentials, with time constants of 1 (τ_rise) and 7 ms (τ_decay) (Springer et al. 2015; Wheeler et al. 2004). V_m is the membrane potential at a given time, reversal potential (E_rev) = 0 mV, and S is a scaling factor used to adjust the strength of individual synapses.

The strengths of virtual synapses were calibrated in each neuron to the threshold synaptic conductance (thresh-g_syn), defined as the minimum g_syn needed to elicit an action potential (Kullmann and Horn 2006; Schobesberger et al. 2000). Thresh-g_syn was found by an automated binary search algorithm that delivered virtual EPSPs of varying strength at 0.5 Hz and settled on a solution within 10 trials (Kullmann et al. 2004). The stability of each cell recording was monitored throughout experiments by repeatedly measuring thresh-g_syn.

To measure synaptic gain, 40 s conductance command templates for the dynamic clamp were designed to mimic the noisy bursts of EPSPs, characteristic of baroreceptor-entrained synaptic activity in rat vasomotor neurons (Springer et al. 2015). Presynaptic convergence was mimicked by implementing one strong suprathreshold synapse set to 300% thresh-g_syn and eight weak subthreshold synapses set to 60% thresh-g_syn. We assumed an average heart rate of 5 Hz and a 20% on/off duty cycle for bursts of synaptic activity during each heartbeat. To achieve an average presynaptic firing rate (f_pre) of 1 Hz/synapse, they each fired randomly at 5 Hz during the active 40-ms period within the 200-ms cardiac cycle. The method for calculating exponentially distributed random intervals between synaptic events was as described previously (Springer et al. 2015; Wheeler et al. 2004). Templates were constructed at 50 μs resolution so that the dynamic clamp could operate at 20 kHz. Synaptic gain was calculated as the frequency of postsynaptic action potentials (f_post) divided by f_pre (Wheeler et al. 2004). The same approach has been shown previously to produce average postsynaptic firing rates in the range of 2.3–2.6 Hz when secondary synapses were set to 90% thresh-g_syn (Springer et al. 2015). This is only slightly lower than the 2.9-Hz average firing rate reported for rat vasomotor sympathetic neurons in vivo (Bratton et al. 2010). Further comparison of the two approaches reveals the limitations of each. Bratton et al. (2010) estimated that individual synapses fired at 1.38 Hz and that two or three synapses were active in most cells. The division of f_post by f_pre indicates that the in vivo synaptic gain was 2.1, which is slightly lower than estimated by Springer et al. (2015). However, the microelectrode damage associated with in vivo recording would lead to an underestimate of gain (Springer et al. 2015). In addition, the counting of active synapses in vivo relied on distinctions in EPSP amplitude, which can be hampered by the fact that they fluctuate from one response to the next and sometimes straddle threshold. By contrast, our model for this study may overestimate the number of active synapses and underestimate their strength by holding them fixed at a value well below threshold. Despite these uncertainties concerning the exact number of active synapses in living animals and their precise strength, our approach successfully approximated in vivo postsynaptic firing rates and estimates of synaptic gain.

Virtual I_h as a function of voltage and time was implemented by Eq. 2

$${\mathrm{I}}_{\mathrm{h}}\mathrm{(}\mathrm{V}\mathrm{,}\mathrm{t}\mathrm{)}\mathrm{=}\stackrel{}{{{\overline{g}}_{}}_h}\hspace{0.17em}\mathrm{\cdot }\hspace{0.17em}{\mathrm{m}}_{\mathrm{t}}\hspace{0.17em}\mathrm{\cdot }\hspace{0.17em}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{-}{\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}}\mathrm{)}$$ (2)

where ḡ_h was the maximum g_h, which could be set to any value through the G-clamp software, and m_t was the level of activation at a given time, which varied between zero and one. The value of m_t was initialized by calculating it over a 10-s period using the V_rest and the steady-state activation (m_∞) relation for g_h and then connecting the output to the current injection circuitry of the recording amplifier. Thereafter, m_t was updated during each 50 μs time step (Δt) of the dynamic clamp feedback loop with the following logic. If m_∞ at time step t was greater than m_∞ at time step t − 1, then m_t was calculated as m_t = m_t−1 + [Δt·(m_∞ − m_t−1)/τ_activation], where τ_activation is the time constant for activation. Alternatively, if m_∞ at time step t was less than m_∞ at time step t − 1, then m_t was calculated as m_t = m_t−1 + [Δt · (m_∞ − m_t−1)/τ_deactivation], where τ_deactivation is the time constant for deactivation. Functions for m_∞, τ_activation, and τ_deactivation are presented along with the underlying data in results.

Analysis.

Curve fitting was done using Igor Pro 6.3 (WaveMetrics, Lake Oswego, OR), and statistical comparisons were made using GraphPad InStat (GraphPad Software, La Jolla, CA). Grouped data are expressed as the means ± SE.

RESULTS

Expression of HCN subunits in the SCG.

Standard RT-PCR detected mRNAs for all four HCN isoforms in the SCG of adult rats (Fig. 1A). NPY was included in the experiment as a positive control. qPCR, using a second set of primers (Table 1), also detected all four HCN isoforms. Melt curves for qPCR reactions confirmed that each amplified a single reproducible peak. The correction of the C_t data for amplification efficiency and normalization of GAPDH expression suggested that HCN1 and HCN2 were present in higher abundance than HCN3 and HCN4 (Fig. 1B). However, none of the differences in HCN levels were statistically significant (ANOVA).

Voltage clamp analysis of I_h.

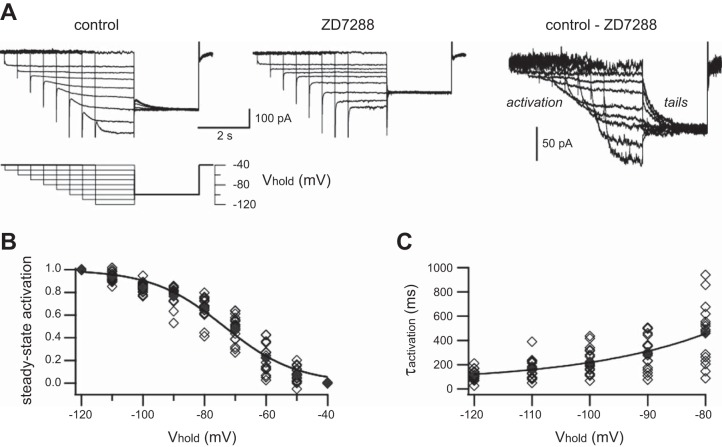
I_h was observed in all neurons where stable perforated patch recordings were obtained. Figure 2A illustrates currents recorded from one cell at 35°C. The jumping of the holding potential (V_hold) from −40 to −120 mV in 10 mV hyperpolarizing steps activated an inward current that became faster and larger with increasing hyperpolarization. The protocol used shorter steps at more negative potentials, because they were sufficient to achieve m_∞ of I_h and avoided the instability of currents sometimes engendered during prolonged, large hyperpolarizations. The inward relaxation currents produced by hyperpolarization were blocked by bath application of 10–15 μM ZD7288. I_h was taken as the difference between currents measured in the absence and presence of ZD7288. During wash-in of ZD7288, the resting membrane potential measured under current clamp hyperpolarized from −55.7 ± 1.4 mV to −60.4 ± 1.6 mV (n = 16; P = 0.0002, paired t-test), thus indicating that I_h is active in resting sympathetic neurons. The action of ZD7288 did not reverse during 1 h of washing. The magnitude of I_h was reduced >50% when measured at room temperature (22°C; not shown).

Fig. 2.

Steady-state activation (m_∞) and activation kinetics of I_h in rat SCG neurons. A: families of membrane currents recorded under voltage clamp from 1 SCG neuron. The same voltage protocol (bottom) was used to measure currents in normal saline (top left) and after addition of 15 μM ZD7288 (top middle). I_h was isolated by subtracting the 2 sets of records (top right). B: the inverse sigmoidal relation that describes m_∞ as a function of voltage was determined by plotting the amplitudes of normalized tail currents measured at −100 mV (see Eq. 3). The data from 18 neurons were fit to a Boltzmann relation (solid line; see Eq. 4) with V_1/2 = −73.6 mV. C: exponential time constants for activation (τ_activation) as a function of voltage from −80 to −120 mV were determined by single exponential fits at the onset of current relaxations. The voltage dependence of τ_activation data was then fit (solid line) to an exponential function (see Eq. 5). Data from individual cells (◇); means (⧫).

After conditioning voltage steps to activate I_h, the membrane potential was jumped to −100 mV to obtain a family of tail currents having the same driving force (Fig. 2A). To determine the voltage dependence of m_∞, the amplitudes of individual tail currents were measured, normalized (Eq. 3), and plotted as a function of voltage (Fig. 2B).

$${\mathrm{m}}_{\mathrm{\infty }}\mathrm{=}\mathrm{(}\mathrm{I}\mathrm{-}{\mathrm{I}}_{\min \mathrm{}}\mathrm{)}\mathrm{/}\mathrm{(}{\mathrm{I}}_{\max \mathrm{}}\mathrm{-}{\mathrm{I}}_{\min \mathrm{}}\mathrm{)}$$ (3)

I_min is the tail current amplitude after stepping from −120 to −100 mV, and I_max is the tail current after stepping from −40 to −100 mV. The voltage dependence of m_∞ was then fit to a Boltzmann relation (Eq. 4 and Fig. 2B).

$${\mathrm{m}}_{\mathrm{\infty }}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{)}\mathrm{=}\mathrm{1}\mathrm{/}\mathrm{[}\mathrm{1}\mathrm{+}\exp \mathrm{}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{-}{\mathrm{V}}_{\mathrm{1}\mathrm{/}\mathrm{2}}\mathrm{)}\mathrm{/}\mathrm{s}\mathrm{]}$$ (4)

where V_1/2, the voltage for half-maximal activation, was found to be −73.6 mV, and s, the slope factor, was found to be 11.7 (n = 18 neurons). By taking the calculated tip potential of 14 mV into account, we estimate that the true V_1/2 was −87.6 mV.

Time constants for I_h activation (τ_activation) were determined by fitting exponential functions to inward current relaxations during initial steps to different voltages (Fig. 2A). Although two components of activation were seen in a few cells at −100 to −120 mV, this was not the case in the majority of cells. We therefore used a single exponential function to fit all of the data and then built an empirical model for I_h activation kinetics as a function of voltage (Eq. 5 and Fig. 2C).

$${{{\tau }_{activation}}_{}}_{}\left({\mathrm{V}}_m\right)\mathrm{=}53.5+67.7\hspace{0.17em}\cdot \hspace{0.17em}\exp \left[(V_m+120)/-22.4\right]$$ (5)

With the extrapolation of this relation to the vicinity of normal V_rest, τ_activation is 1 s at −60 mV and 1.3 s at −55 mV.

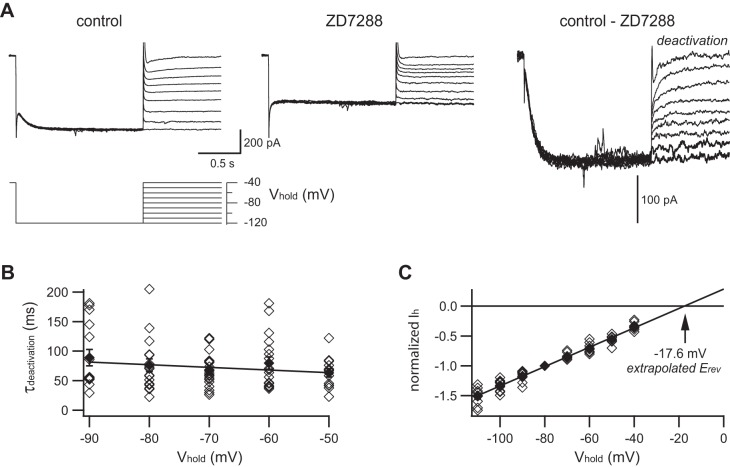
The kinetics of I_h deactivation and its E_rev were assessed with a protocol (Fig. 3A) that first fully activated I_h by stepping to −120 mV for 1.5 s, followed by 10 mV steps to less hyperpolarized potentials (−110 to −40 mV). Unlike the steep voltage dependence of I_h activation kinetics, the voltage dependence of deactivation was very shallow in the range from −90 to −50 mV, with time constants typically between 50 and 100 ms (Fig. 3B). The kinetics of I_h deactivation was therefore fit to a simple linear relationship (Eq. 6).

Fig. 3.

Deactivation kinetics and reversal potential of I_h in rat SCG neurons. A: each family of membrane currents was in response to the voltage protocol (bottom). This is a different neuron than shown in Fig. 1. Currents were measured in normal saline (top left) and after addition of 15 μM ZD7288 (top middle). Difference currents are taken as I_h (top right). B: the time constant for deactivation (τ_deactivation) was determined by fitting a single exponential to the current relaxations after stepping from −120 mV to test voltages ranging from −50 to −90 mV. The voltage dependence of τ_deactivation was fit to a straight line (see Eq. 6). C: the reversal potential (E_rev) of I_h was determined by plotting instantaneous current amplitudes after stepping from −120 mV to test voltages ranging from −40 to −110 mV. Data in each neuron were normalized to the response at −80 mV. A straight line fit to the data predicts an extrapolated reversal potential of −17.6 mV. Data from 18 neurons (◇); means ± SE (⧫).

$${\mathrm{\tau }}_{\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{)}\mathrm{=}\mathrm{40.9}\mathrm{-}\mathrm{0.45}{\hspace{0.17em}\cdot \hspace{0.17em}\mathrm{V}}_{\mathrm{m}}$$ (6)

E_rev was estimated from the peak tail current amplitudes, normalized for each cell to the tail current amplitude at −80 mV. The pooled data were fit to a straight line and extrapolated to the x-intercept at −17.6 mV (Fig. 3C). By taking the calculated tip potential of 14 mV into account, we estimate that the true E_rev of I_h was −31.6 mV.

The fully activated I_h, measured at −120 mV, showed little dependence on cell size, as reflected by whole-cell capacitance (Fig. 4A). These values were then used to calculate the maximum g_h (Eq. 7)

Fig. 4.

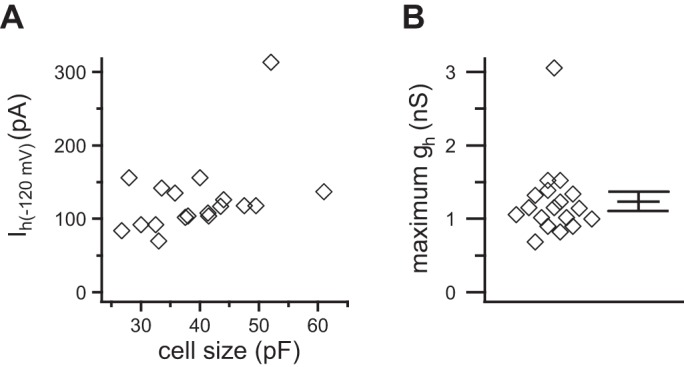
Summary of maximum I_h and ḡ_h in 18 SCG neurons. A: the maximum I_h measured at −120 mV varied little as a function of whole-cell capacitance. B: values for ḡ_h were tightly clustered between 0.7 and 1.7 nS/cell. Individual cells with the mean ± SE plotted to the right (◇).

$$\mathrm{(}\stackrel{}{{{\overline{g}}_{}}_h}\mathrm{)}\mathrm{=}{\mathrm{I}}_{\mathrm{h}\mathrm{(}\mathrm{-}\mathrm{120}\hspace{0.17em}\mathrm{}\mathrm{m}\mathrm{V}\mathrm{)}}\mathrm{/}\mathrm{(}{\mathrm{V}}_{\mathrm{m}}\mathrm{-}{\mathrm{E}}_{\mathrm{r}\mathrm{e}\mathrm{v}}\mathrm{)}$$ (7)

In 18 neurons, ḡ_h was 1.2 ± 0.1 nS (range 0.7–3.1 nS; Fig. 4B).

I_h enhances synaptic strength.

After completing the voltage clamp analysis, additional experiments were done to test whether I_h alters the efficacy of fast EPSPs. With the use of the dynamic clamp method, we measured the effect of ZD7288 upon thresh-g_syn. Figure 5A illustrates an example from a cell, where the blocking of I_h with 15 μM ZD7288 doubled the amount of virtual synaptic conductance required to initiate an action potential. This indicates that hyperpolarization-activated cation channels (h-channels) normally act to enhance the strength of subthreshold EPSPs. In a group of 16 neurons (Fig. 5B), the addition of 10–15 μM ZD7288 increased thresh-g_syn from 7.0 ± 0.9 nS to 12.1 ± 2.0 nS (P < 0.0001, Wilcoxon matched-pairs signed-rank test). As in the initial experiments (previous section), ZD7288 hyperpolarized the V_rest in this group of cells from −54.4 ± 1.0 mV to −59.2 ± 0.9 mV (Fig. 5C; n = 16; P < 0.0001, paired t-test). There was a strong negative correlation (r = −0.829, P < 0.0001) between the relative increase in thresh-g_syn produced by blocking g_h and the associated hyperpolarization of V_rest (Fig. 5D). One might imagine that the increase in total membrane conductance produced by tonic activation of g_h in a resting cell would create a shunt that reduces synaptic efficacy by reducing the size of fast EPSPs, but this is not the case. Because g_h produces a depolarizing shunt that is excitatory due to its E_rev being positive to spike threshold, the resulting inward I_h depolarizes V_rest. By lowering the amount of synaptic conductance needed to fire an action potential, g_h increases the efficacy of fast EPSPs.

Fig. 5.

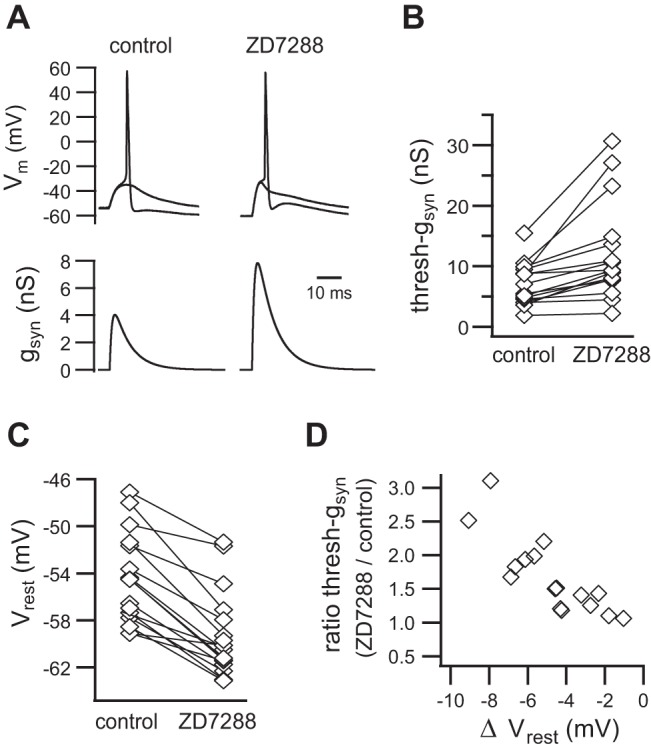
I_h strengthens virtual nicotinic synapses by lowering thresh-g_syn. A: an example of virtual EPSPs that straddle threshold before and after adding ZD7288 to block I_h. Thresh-g_syn doubles in the absence of I_h. B: similar data from 16 neurons. C: the blocking of I_h also hyperpolarizes V_rest. D: the reduction of thresh-g_syn by ZD7288 is proportional to the change in V_rest (ΔV_rest).

I_h enhances synaptic amplification.

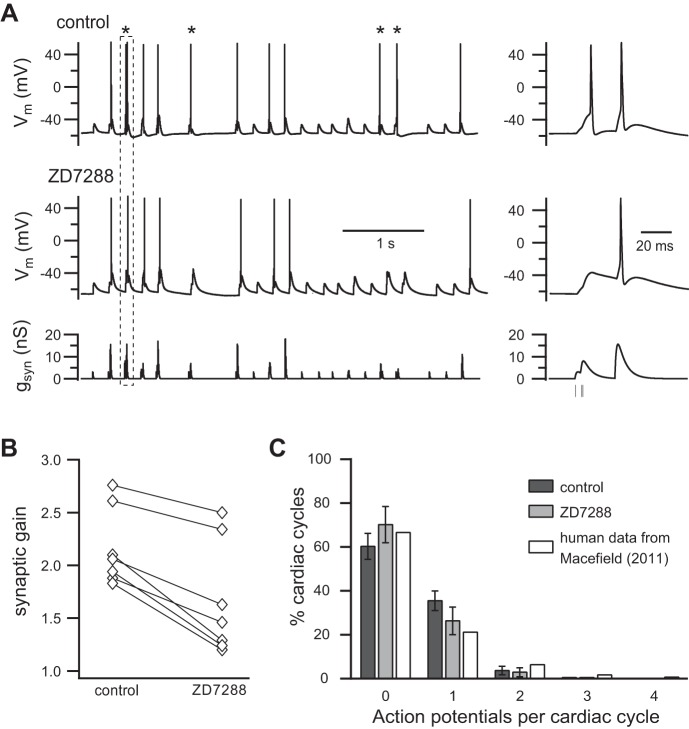
One would expect that the strengthening of subthreshold secondary synapses by I_h should also enhance summation of subthreshold EPSPs, enabling them to drive more spikes and thereby, to increase synaptic gain. To test this hypothesis using dynamic clamp, we stimulated neurons for 40 s with a conductance template that contained a pattern of virtual synaptic events designed to mimic the physiological convergence of strong and weak synapses onto rat SCG neurons (Springer et al. 2015) and to produce a realistic postsynaptic firing rate (Bratton et al. 2010). Thresh-g_syn was measured in each cell and used to calibrate the template so that it contained one primary synapse at 300% thresh-g_syn and eight secondary synapses, each at 60% thresh-g_syn. Every synapse fired at an average rate of 1 Hz in a noisy bursting pattern entrained to the cardiac cycle (see materials and methods). Figure 6A illustrates a 5-s sample from one such experiment. The lower trace shows the bursting synaptic conductance template, and the upper traces show the postsynaptic responses measured before and after blocking I_h with 15 μM ZD7288. An important feature of this approach is that the identical complex conductance template can be applied repeatedly, and changes in the response can be assessed for each synaptic event. In this case, inspection of the records revealed a clear example of a secondary EPSP triplet that generated an action potential under control conditions but failed to do so in ZD7288 (Fig. 6A). This contrasted with an adjacent, primary EPSP that remained suprathreshold in strength when I_h was blocked. The overall reduction in postsynaptic spike output during the entire 40-s trial was quantitated and used to measure synaptic gain (f_post/f_pre). In seven neurons tested this way, the blocking of I_h reduced synaptic gain (Fig. 6B) from 2.2 ± 0.1 to 1.7 ± 0.2 (P = 0.0008, paired t-test). This corresponds to a reduction of the average postsynaptic firing rate from 2.2 to 1.7 Hz, and it indicates that postsynaptic h-channels have the capacity to elevate use-dependent synaptic gain in sympathetic ganglia.

Fig. 6.

I_h increases synaptic gain. A: neurons were stimulated with a pattern of virtual synaptic conductance (g_syn) that reflected the convergence of strong and weak synapses firing in a noisy burst pattern (see Dynamic clamp implementation of virtual synapses and virtual I_h for details). g_syn command template applied to the dynamic clamp (bottom); neuronal response before (top) and after (middle) addition of ZD7288. The traces at left show a 5-s segment from a longer, 40-s stimulation sequence. Asterisks denote 4 action potentials that disappeared when I_h was blocked. Each of these spikes was driven in control saline by summation of weak subthreshold EPSPs (60% thresh-g_syn). By contrast, spikes initiated by individual strong synapses (300% thresh-g_syn) were impervious to I_h blockade. The dashed box highlights a sequence whose time course has been expanded at the right. In it, one can see a triplet of virtual secondary EPSPs that reach threshold and fire an action potential in control saline but fail to do so in ZD7288. B: synaptic gain was calculated by measuring the average rate of postsynaptic firing (f_post) during 40 s of stimulation and dividing it by the average presynaptic firing rate used to construct the presynaptic template (f_pre = 1 Hz). In 7 of 7 neurons tested this way, the inhibition of I_h reduced synaptic gain. C: in each of the 7 cells used to measure synaptic gain, spikes in each cardiac cycle were counted and used to plot the distribution of spikes/cardiac cycle. Comparison human data for vasoconstrictor neurons are replotted from Macefield (2011).

A notable feature of our model used to create dynamic clamp templates was that it generated synaptic activity in a subset of cardiac cycles (Fig. 6A). Since only some virtual EPSPs reached threshold, action potentials were triggered in an even smaller subset of cardiac cycles. Occasionally, two spikes were seen during a single cardiac cycle (Fig. 6A). These observations recapitulate aspects of intracellular recordings from vasoconstrictor neurons in anesthetized rats (Bratton et al. 2010) and extracellular single-unit recordings from awake, healthy human subjects (Macefield 2011). Indeed, changes in vasoconstrictor sympathetic activity are often characterized in the human microneurography literature in terms of the proportion of cardiac cycles where spikes are generated. We therefore analyzed our data to determine the effect of I_h blockade and to compare it with human data from 33 vasoconstrictor neurons [see Fig. 3F in Macefield (2011)]. Each of the 7 cells used to measure synaptic gain had been stimulated with 40 s templates containing 200 cardiac cycles. We found that spikes occurred in just under 40% of the cycles (Fig. 6C) and that double spikes occurred in <5% of the cycles. We only observed one instance of a triple spike and never saw a quadruple spike. Consistent with the reduction of synaptic gain produced by ZD7288 (Fig. 6, A and B), the blocking of I_h caused an increase in the proportion of cardiac cycles with no spikes and decreases in the proportion of cycles with one or two spikes. Perhaps more interesting, the distribution of spikes/cycle that we observed was quite similar to the human data described by Macefield (2011), which are replotted in Fig. 6C.

Shifting the voltage dependence of g_h modulates synaptic gain.

In other systems, cAMP modulates I_h by binding directly to HCN channels and shifting the voltage dependence (V_1/2) of activation (Biel et al. 2009; Craven and Zagotta 2006). The raising of cAMP can shift V_1/2 by up to 20 mV in the depolarizing direction (Chen et al. 2001; DiFrancesco and Tortora 1991; He et al. 2014; Ishii et al. 1999; Ludwig et al. 1998), and the lowering of cAMP can shift V_1/2 by up to 10 mV in the hyperpolarizing direction (DiFrancesco and Tromba 1988). To test whether such a mechanism could possibly alter synaptic gain in sympathetic neurons, we designed an experiment in which native g_h was blocked with ZD7288 and then reconstituted with a virtual g_h using dynamic clamp (materials and methods).

The ability of virtual g_h to mimic native g_h was verified by simulating I_h in real time using the G-clamp system in an open-loop configuration. After setting ḡ_h to 1.5 nS, voltage clamp protocols were applied to the dynamic clamp through the V_m input, and the calculated current outputs were monitored. Figure 7 illustrates the simulated currents obtained using the same protocols that had been used to measure activation and tail currents (Fig. 2A) and deactivation (Fig. 3A). Apart from the noise associated with physiological currents, the simulations reproduced all salient features of I_h in SCG neurons.

Fig. 7.

Families of I_h simulated in real time using the G-clamp dynamic clamp system with ḡ_h set to 1.5 nS and 20 kHz temporal resolution. A: I_h elicited by the same protocol used in Fig. 2 to measure the voltage dependence of steady-state activation (m_∞) from tail currents and the voltage dependence of activation kinetics (τ_activation). B: I_h elicited by the same protocol used in Fig. 3 to measure the voltage dependence of deactivation (τ_deactivation) and the reversal potential (E_rev) for I_h. As expected, the calculated currents replicated the form of physiological currents.

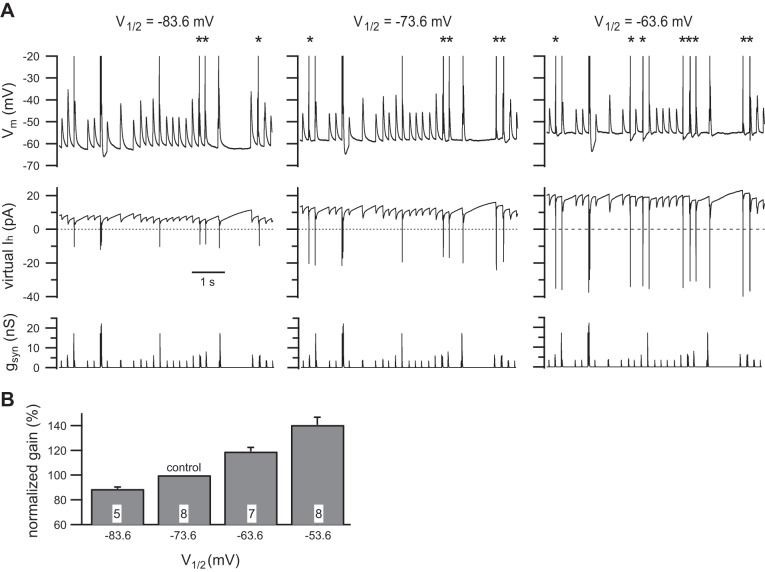
In recordings from eight neurons, it required 1–2.5 nS of virtual g_h (V_1/2 = −73.6 mV) to restore V_rest to its initial value before addition of ZD7288. Importantly, the virtual g_h also restored thresh-g_syn (6.0 ± 0.8 nS with native g_h and 6.0 ± 1.1 nS with virtual g_h; n = 8; P = 0.7422, Wilcoxon matched-pairs signed-rank test), thus providing further validation of the model g_h. The value of thresh-g_syn was then used to scale the same 40-s-long noisy bursting pattern of virtual synaptic activity described in the previous section. With this stimulus template, we first measured synaptic gain with V_1/2 = −73.6 mV and then with V_1/2 shifted in 10 mV steps to −63.6 mV, −53.6 mV, and −83.6 mV. Figure 8A illustrates 6.5 s segments from one cell showing that the shifting of V_1/2 to −63.6 mV increased the spike output, and the shifting of it to −83.6 mV decreased the spike output. Regardless of the starting point, depolarization of 10 mV shifts in V_1/2 always increased synaptic gain in 18 of 18 comparisons made in 8 neurons. Normalization of the synaptic gain data from each cell to the value at V_1/2 = −73.6 mV and the combination of the results showed that depolarization of V_1/2 by 10 and 20 mV increased synaptic gain by 19.2 ± 3.2% (n = 7) and 40.6 ± 6.1% (n = 8), respectively (Fig. 8B). Hyperpolarization of V_1/2 by 10 mV reduced synaptic gain by 11.0 ± 1.5% (n = 5). Together, these results support the possibility that signaling through cyclic nucleotides in sympathetic neurons may fine tune synaptic amplification by modulating the excitatory strength of nicotinic synapses that are normally subthreshold in strength.

Fig. 8.

The shifting of the voltage dependence of steady-state I_h activation modulates synaptic gain. A: example of an experiment where native g_h was blocked with ZD7288 and then reconstituted with virtual g_h at 3 different levels of V_1/2. Each set of records shows the same 6.5-s segment from a longer, 40-s sequence. The dynamic clamp command signal (bottom) was constructed to contain converging strong (300% g_syn) and weak (60% g_syn) synapses, firing in a noisy burst pattern at average frequencies of 1 Hz. The inward virtual I_h generated by the dynamic clamp (middle) became larger as V_1/2 was moved from −83.6 to −63.6 mV. Note that inward currents have a positive sign, because they follow the standard convention for current clamp data. As a consequence of activating more I_h at rest, the shifting of V_1/2 in the depolarizing direction also depolarized V_rest by a few millivolts. This can be seen in the membrane potential records (top). In these data, one can also see changes in the number of action potentials driven by summation of weak EPSPs (asterisks): 3 spikes when V_1/2 = −83.6 mV, 5 spikes when V_1/2 = −73.6 mV, and 8 spikes when V_1/2 = −63.6 mV. This indicates that shifting V_1/2 in the depolarizing direction has the effect of increasing synaptic gain. B: grouped data summarizing the effect of shifting V_1/2 upon synaptic gain. In each cell, the gain values were normalized to the gain observed when V_1/2 = −73.6 mV. The n for each measurement is denoted in the bars.

DISCUSSION

Results from this study show that the rat SCG expresses all four HCN subunit isoforms (Fig. 1A) and that functional expression of I_h enhances postsynaptic excitability in a way that strengthens fast EPSPs (Fig. 5, A and B) and enhances synaptic amplification (Fig. 6). Our results (Figs. 2 and 3) also confirm previous observations of I_h in paravertebral sympathetic neurons (Jobling and Gibbins 1999; Lamas 1998; Lamas et al. 1997; Tokimasa and Akasu 1990) and the conclusion that g_h is partially active in cells at rest and thereby serves to depolarize V_rest (Fig. 5C) by almost 5 mV (Lamas 1998). Unlike the previous studies of sympathetic neurons, the present experiments were performed at physiological temperature and focused on synaptic integration.

Heterogeneity of HCN subunit expression.

All four HCN isoforms were detected by standard RT-PCR and by qPCR (Fig. 1) using two sets of primers directed at different exon-spanning domains (Table 1). This result is similar to an earlier analysis that also detected all four subunits in myenteric neurons of the mouse distal colon (Xiao et al. 2004). The earlier study concluded that HCN3 was barely detectable and that HCN1 and HCN2 were present at higher levels than HCN4. More detailed studies of subunit expression at the single-cell level will be required to identify the subunits that encode I_h in sympathetic SCG neurons, to determine whether the channels are homomeric or heteromeric, and to identify possible differences between h-channels in functional subtypes of sympathetic neurons.

ḡ_h is small but powerful.

We found that ḡ_h ranged from 0.7 to 3.1 nS (Fig. 4), did not vary with cell size, and generated currents that were typically no more than 100 or 200 pA when fully activated (Figs. 2 and 3). The small size of I_h compared with other voltage-gated currents in sympathetic neurons, which can be nanoamperes in magnitude, helps to explain why they have not drawn much attention in the past. Most studies of sympathetic ganglia have used microelectrodes, which introduce shunts on the order of 3–10 nS that can distort excitability and mask the influence of I_h (Springer et al. 2015). Giga-seal patch recordings, such as those used here, result in much higher input resistances than in microelectrode recordings and thereby, allow small currents, such as I_h, to exert powerful effects on excitability. This enabled us to observe the increase in thresh-g_syn when g_h was blocked with ZD7288 (Fig. 5, A and B).

Implications for synaptic amplification, neuromodulation, and blood pressure control.

The ability of g_h to enhance synaptic amplification is a natural consequence of the reduction in thresh-g_syn, as predicted by the synaptic gain theory (Karila and Horn 2000; Kullmann and Horn 2006; Springer et al. 2015; Wheeler et al. 2004). When synaptic amplification is >1 (Fig. 8), it signifies that the number and frequency of action potentials leaving the ganglion are greater than that of spikes entering the ganglion. Under the conditions of our experiments, gain resulted in an approximate doubling of the firing rate. The blocking of I_h reduced gain from 2.2 to 1.7. This amplification may be especially important in baroreceptor-entrained sympathetic neurons, because they are embedded in a negative-feedback loop that uses gain to control blood pressure.

Future examination of synaptic amplification in sympathetic ganglia should recognize that many gaps remain in our understanding of this system. Bratton et al. (2010) have suggested that the synaptic activity they observed in anesthetized rats may be driven by only two or three synapses, not the full complement of eight or nine synapses in our model of synaptic convergence. However, the in vivo analysis was constrained by the need to infer convergence from indirect measures, such as EPSP amplitudes. Such efforts are complicated by the fluctuations that naturally occur in EPSP size. In addition, our model used synapses of fixed strength: how would their efficacy change if they fluctuated in size? Despite the simplifying assumptions built into our model, it was capable of generating realistic postsynaptic firing rates and realistic distributions of spikes/cardiac cycle. Might it be possible in the future to design stronger mechanistic predictions using our experimental approach to synaptic amplification that could then be tested in single-unit studies of human vasoconstrictor neurons?

Finally, the present study suggests that HCN channels may contribute to the regulation of ganglionic synaptic gain through their expression level and through modulation by binding of cyclic nucleotides. When cyclic nucleotide-mediated shifts in g_h activation were incorporated into our dynamic clamp model of virtual g_h, it produced clear shifts in synaptic gain (Fig. 8). Additional experiments will be needed to determine whether catecholamines and neuropeptides that stimulate and inhibit cyclic nucleotide accumulation in sympathetic neurons produce significant modulation of synaptic gain that results from changes in g_h.

GRANTS

Support for this work was provided by the Great Rivers Affiliate of the American Heart Association through Grant-in-Aid 13GRNT1685007.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

P.H.M.K., K.M.S., K.L.C., M.G.S., and J.P.H. conception and design of research; P.H.M.K., K.M.S., K.L.C., I.A., and M.G.S. performed experiments; P.H.M.K., K.M.S., K.L.C., I.A., M.G.S., and J.P.H. analyzed data; P.H.M.K., K.M.S., K.L.C., I.A., M.G.S., and J.P.H. interpreted results of experiments; P.H.M.K., K.L.C., I.A., and J.P.H. prepared figures; K.L.C. drafted manuscript; P.H.M.K., K.M.S., K.L.C., I.A., M.G.S., and J.P.H. edited and revised manuscript; P.H.M.K., K.M.S., K.L.C., I.A., M.G.S., and J.P.H. approved final version of manuscript.