Multiscale modeling of cellular epigenetic states: stochasticity in molecular networks, chromatin folding in cell nuclei, and tissue pattern formation of cells

Abstract

Genome sequences provide the overall genetic blueprint of cells, but cells possessing the same genome can exhibit diverse phenotypes. There is a multitude of mechanisms controlling cellular epigenetic states and that dictate the behavior of cells. Among these, networks of interacting molecules, often under stochastic control, depending on the specific wirings of molecular components and the physiological conditions, can have a different landscape of cellular states. In addition, chromosome folding in three-dimensional space provides another important control mechanism for selective activation and repression of gene expression. Fully differentiated cells with different properties grow, divide, and interact through mechanical forces and communicate through signal transduction, resulting in the formation of complex tissue patterns. Developing quantitative models to study these multi-scale phenomena and to identify opportunities for improving human health requires development of theoretical models, algorithms, and computational tools. Here we review recent progress made in these important directions.

INTRODUCTION

With the completion of the sequencing of human genomes and the advent of individual genomes,^[1–3] we are gaining full access to the genetic blueprints of human cells. However, much of the behavior of cells depends on the control of expression of genes. Cells from different tissues posses the same genome but exhibit different properties and perform different functions. Understanding how genetic information is selectively expressed and how epigenetic control establishes the specific expression patterns of proteins are fundamental problems of biology and problems with important implications in the treatment of disease.

As large scale epigenetic profiling studies have shown, covalent modification such as DNA methylation and post-translational modifications of proteins play important roles in controlling the expression of genes.^[4,5] The epigenetic states of cells can also arise from the network of multiple molecular components itself.^[6–9] Often under stochastic control, different biological phenotypes can result from the same molecular network, as there may exist multiple peaks in the stationary probabilistic landscape of the reaction network.^[6,9] With specific wirings, cells can maintain heritable states depending on the physiological conditions without covalent bond modifications.^[6–9]

Furthermore, recent studies based on fluorescence in-situ hybridization (FISH), chromosome conformation capture and related techniques have demonstrated the importance of the spatial organization of genome in determining cellular phenotypes.^[10–14] The uncovering of massive amount of long range interactions in chromatins in different cells^[11–14] suggests the existence of a complex three-dimensional folding landscape of chromosomes. The discovery of hierarchical structural units such as topologically associated domains (TAD) points to the existence of complex folding machineries that provide cooperative control of gene expression.

Quantitative understanding of both stochastic networks and genome folding requires the development of fundamental theory, models, and algorithms so that effective computational analysis can be efficiently carried out. Once differentiation of cells is complete and different cell types are formed, another important task is to understand and model how populations of different cells interact and form different patterns of tissue, and how insight into complex processes such as wound healing can be gained through computational studies.

In this review article, we examine recent progress in the development of theoretical model, algorithms, and computational methods for computing the probability landscape of stochastic network, for predicting three-dimensional structures of folded chromosomes, and for understanding tissue pattern formation.

Stochastic network and discrete chemical master equation

Networks of interacting molecules are the basis of the regulatory machineries of cells. When the copy numbers of molecules involved are small (μM to nM range, or 1 – 10² copies of molecules in a 10μM³ cell),^[15,16] stochasticity can play significant roles in cellular processes such as gene regulation, protein synthesis, and signal transduction.^[15,17–21] Well-known examples of cellular epigenetic states controlled by a stochastic network include the decision network of switching between the lysogenic and the lytic phases of phage lambda,^[6,15,22,23] and the competence transition network of Bacillus subtilis.^[24]

A stochastic network is characterized by its time-dependent probability landscape, namely, the probability of the network to be at each possible microstate, namely, the vector of copy numbers of molecular species in the network. Knowledge of the full probability landscape of a network will identify all epigenetic states, which correspond to the peaks in the landscape, as well as transitions and transition probabilities between them. The basic theoretical framework for studying a stochastic network is given by the discrete chemical master equation (dCME)^[25,26]

$$\frac{\mathit{dp}\left(\mathit{x},t\right)}{\mathit{dt}}=\sum _{{\mathit{x}}^{\prime }}\left[A\left({\mathit{x}}^{\prime },\mathit{x}\right)p\left({\mathit{x}}^{\prime },t\right)-A\left(\mathit{x},{\mathit{x}}^{\prime }\right)p\left(\mathit{x},t\right)\right],$$ (1)

where p(x, t) is the probability of the network in the microstate x, A(x^′, x) is the matrix of transition rates between microstates x, and x^′.

Computing probabilistic landscape

However, analytically solving the dCME is not possible except for a few simple models with one or two nodes. The stochastic simulation algorithm (SSA) and related techniques have been widely used for studying stochastic networks.^[25,27] By generating Monte Carlo samples of trajectories of reactions of a network using SSA, one can infer properties of the stochastic network through analysis of millions of sampled trajectories.^[25] However, SSA is inefficient in sampling rare events, as most computing time is spent on following high-probability paths. In addition, the assessment of convergence becomes difficult when the network is complex.^[28–31] Overall, it is generally difficult to know if an accurate solution to the dCME of a network has been found. One does not know if all major probabilistic peaks have been identified and different epigenetic states located, or if important ones with significant probability mass in the usually high dimensional space are undetected. It is also difficult to know if the locations of identified probabilistic peaks are correctly mapped. One also does not know if a computed probabilistic landscapes is overall erroneous and how such errors can be quantified. Furthermore, the best possible accuracy one can achieve with a given finite computing resources is generally unknown. One also does not know what computing resource is required so solutions with accuracy within a predefined tolerance can be obtained. These issues can be resolved using recently developed ACME method as described in a later section.

Biased Sampling for Barrier Crossing

To improve the efficiency of sampling rare events, Kuwahara and Mura developed the weighted SSA (wSSA) algorithm by biasing each reaction rate using a pre-determined constant, with the overall summation of reaction rates unchanged.^[28] Further development introduced biases to reaction selection and significantly improved sampling efficiency for rare events.^[29,30] These methods, however, do not address the issue of crossing barriers, which arises in multistable networks with a complex probability landscape. In reference,^[31] a general theoretical framework for obtaining optimized biases in sampling individual reactions for estimating probabilities of rare events was developed. In addition, a practical algorithm called adaptively biased sequential importance sampling (Absis) method for efficient probability estimation was also given.^[31] By using a look-ahead strategy and by enumerating short paths from the current microstate, the reaction-specific and state-specific forward and backward moving probabilities of the system were estimated, which are then used to bias reaction selections. The Absis algorithm can automatically detect barrier-crossing regions, and can adjust bias adaptively, with bias determined by the outcome of exhaustively generated short paths.^[31] Test results on the biochemical networks (see Fig 1 for the example of the Schögle bistable model) showed that the Absis method can accurately and efficiently estimate rare event probabilities, often with smaller variance than other importance sampling algorithms.^[31]

Figure 1.

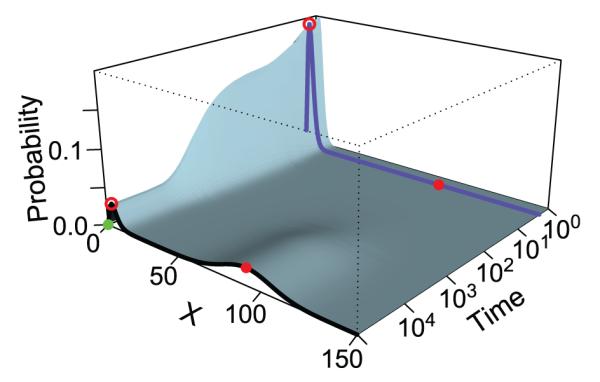
The time-evolving probability and transition probability of rare events of the bistable Schlögl model. The blue and black curves show the landscape at t = 2 and at the steady state, respectively. The two high probability regions at the steady state (black curve) are located at x = 4 (red circle on black curve) and x = 92 (red dot on black curve), respectively. They are separated by a high barrier of low probability. The initial state x = 0 (green dot) is near the first peak, and the target state (red dot) is at the center of the second peak. The probability landscape at time t = 2 (blue curve) shows a much sharper peak centered at x = 3 (red circle on blue curve). The transition from x = 0 to x = 92 within t = 2 is a rare event and the transition paths have a steep barrier to cross. The probability of this rare event can be sampled effectively using the Absis method (adapted from reference^[31]).

Direct solution of dCME models

Several methods have been developed towards the goal of directly computing the full probability landscape of a stochastic network. These include the finite state projection (FSP), the sliding window method, the finite buffer dCME method, as well as several other techniques.^[23,32–36] The FSP method is based on a truncated projection of the state space and uses numerical techniques to compute the time-evolving probability landscapes.^[32,37,38] However, the use of an absorbing boundary leads to the accumulation of errors as time proceeds, therefore making it unsuitable to study long-time and steady state behavior of a network. The sliding window method is also based on truncation of the state space. To ensure small truncation error, a large number of states must be included, as the size of the state space takes the form of a n-dimensional hypercube, with n the number of molecular species. This makes it difficult to achieve the desired level of accuracy.

A bottleneck problem for solving the dCME directly is to have an efficient and adequate account of the discrete state space. As the copy number of each of the n molecular species takes an integer value, conventional methods of state enumeration incorporate all vertices in a n-dimensional hypercube nonnegative integer lattice, which has an overall size of $O\left({\prod }_{i=1}^n{b}_i\right)$, where b_i is the maximally allowed copy number of molecular species i. State enumeration rapidly becomes intractable, both in storage and in computing time. To address this issue, we developed the finite buffer discrete CME (fb-dCME) method for efficient enumeration of the state space.^[33] It uses a buffer queue with a fixed number of molecular tokens to keep track of the remaining number of states that can be enumerated. Instead of including every state in a hypercube, it examines only states that can be reached from a given initial state. This approach has been extended in the Accurate Chemical Master Equation (ACME) method,^[39,40] in which the stochastic network is decomposed into independent components, each equipped with its own finite state space controlled by a separate buffer queue. Molecular species in each component can be transformed into each other through mass-balance reactions.

The ACME method is provably optimal in space and in time required for state enumeration, and exhibits very effective use of the overall finite state space. The size of the overall truncated state space is $O\left({\prod }_j\left(\begin{array}{c}\hfill B+n_j\hfill \\ \hfill n_j\hfill \end{array}\right)\right)$, a product of the volumes of n_j-simplices, with n_j the number of molecular species in the j-th component of the network. While maintaining the same maximum copy number of molecules, the truncated space is dramatically smaller than the n-dimensional hypercube, which has an overall size of $O\left({\prod }_j{B}^{n_j}\right)$. The reduction of state space is roughly ${\prod }_j\left(n_j!\right)$, therefore the size of the state space is much smaller than that generated using the conventional hypercube method.

Furthermore, a broad mathematical framework for analytical estimation of steady state probability solutions has been developed.^[39] Importantly, an overall upper-bound estimation of the truncation errors has been obtained from theoretical analysis using the techniques of aggregation of microstates by buffer usage, factorization of a quotient matrix, and stochastic ordering.^[39,40] This enabled estimation of truncation error a priori without actually carrying out costly trial solutions of the dCME for the purpose of error estimation. It also allows determination if the truncation error for a given computing environment is within a pre-defined tolerance threshold. In addition, it informs on the minimal size of state space required to achieve a given level of accuracy.

The ACME method works for arbitrary networks, including those with strong couplings between species. With this optimal method for state enumeration, numerical methods for solving large linear systems can be applied to directly solve the dCME equation.

Multistability of common motifs

Network motifs consisting of 1–4 nodes are small subunits that occur frequently and often have defined functions.^[41] They are the small building blocks of more complex regulatory networks. It is important to understand their roles in maintaining the multistability of different epigenetic states.

Studies based on deterministic models showed that multistability can arise only when feedback and cooperativity are present.^[42] However, multistability can arise from stochastic network motifs which would go undetected if deterministic network models are used. The smallest network motif exhibiting stochastic multistability is that of the self-regulating gene. It was shown that a probabilistic landscape with multiple peaks can appear when the rates of gene expression in bound and unbound forms of DNA are well separated and switching between the bound and unbound states is slow.^[43]In this case, the multistability, however, cannot be captured using deterministic ordinary differential equation (ODE) models or simple Fokker-Plank approximation of the dCME.^[43] Overall, stochastic multistability in simple network motifs remain poorly characterized.

The ACME method can be applied to study the stochastic behavior of motifs of gene regulatory network. As an illustration, we discuss the motif of a single input module.^[44] There are three genes in this network. GeneA, GeneB, and GeneC express protein A, B, and C, respectively (Fig 2A). Protein A inhibits both GeneB and GeneC, both in turn activate the expression of protein A. Multistability exist in the probabilistic landscape of this simple motif computed using the ACME method, where bistabilities for expression of proteins A, B, and C can be clearly seen (Fig 2B and 2C).

Figure 2.

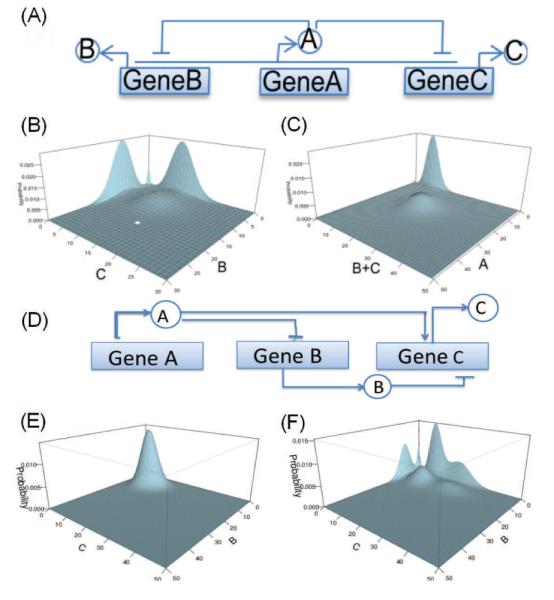
Single input network module. (A) Its network architecture. Steady state probability landscapes for (B) proteins B and C, and (C) proteins A and B+C. (D) The network architecture of the incoherent feed-forward loop. Steady state probability landscapes (E) with one peak and with (F) six peaks.

With the ACME method, we can examine systematically the stochastic behavior of all major network motifs with 3–4 nodes, including negative feed-back loops,^[45] feed-forward loops,^[46] and four-nodes bifan networks.^[47] For example, the results of computation of the probability landscape using ACME for the incoherent feed-forward loop (Fig 2D) showed that the stationary probabilistic landscape of the motif changes from that of one peak (E) to that of six peaks (F) when network parameters are altered. With the ACME method, we can characterize the probability landscapes of these motifs and identify key factors defining their stochastic multistabilities. We can now explore the full parameters space and construct phase diagrams of multistability of many network motifs. These results can be useful for constructing synthetic gene networks for desired stochastic properties.

Epigenetic decision network of cellular fate

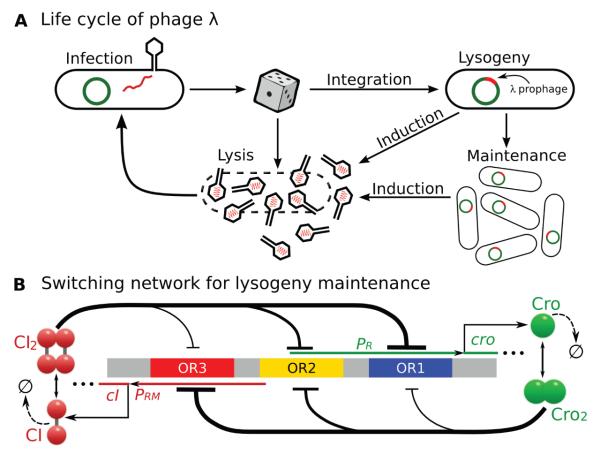
Bacteriophage lambda is a virus that infects E. coli cells (Fig 3). A molecular circuitry controls phage lambda to choose between two productive modes of development, namely, the lysogenic phase and the lytic phase (Fig 3A). In the lysogenic phase, phage lambda represses its developmental function, integrates its DNA into the chromosome of the host E. coli bacterium, and is replicated in cell cycles for potentially many generations. When threatening DNA damage occurs, for example, when UV irradiation increases, phage lambda switches from the epigenetic state of lysogeny to the lytic phase and undergoes massive replications in a single cell cycle, releasing 50–100 progeny phages upon lysis of the E. coli cell.^[22]

Figure 3.

Different selection of cell fate of E. coli infected by phage lambda and a model of the epigenetic circuit for lysogeny maintenance. (a) The lysogenic and lytic phases of phage lambda. (b) A simplified model of the epigenetic switch for lysogeny maintenance. (Modified from reference^[23]).

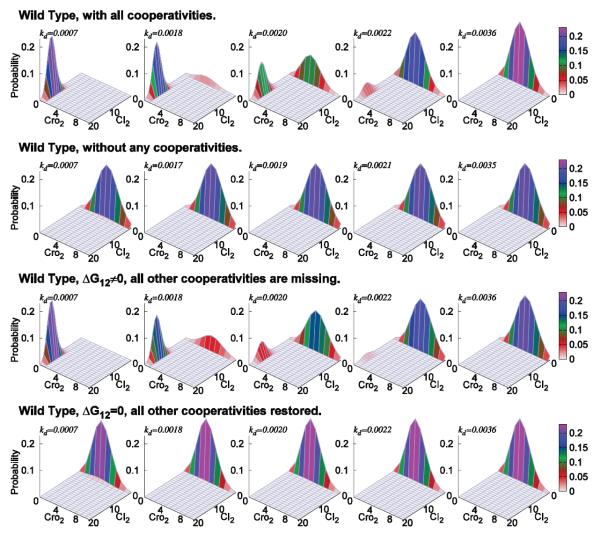
To study how lysogeny is maintained and how it transitions to the lytic state, we used a simplified stochastic model for the molecular regulatory network that controls the epigenetic switch in phage lambda (Fig 3b).^[23] With a total of 54 reactions involving 13 molecular species and around 1.7 million microstates, the effects of UV irradiation can be modeled by increasing the CI degradation rates k_d due to the response of the SOS system. The steady state probability associated with each of these microstates are computed from dCME after state enumeration.^[23] Fig 4 (row 1) shows the probability landscape of phage lambda projected to the subspace of CI and Cro dimers at five different UV irradiation conditions, each modeled with a different CI degradation rate k_d. With a high copy number of the CI₂ repressor, the lysogenic phase of the phage lambda is maintained, whereas a high copy number of Cro₂ protein signifies the lytic phase.^[48] A clear picture of the landscape in lysogeny, at the start of transition, during mid-transition, at the end of transition, and in lysis can be seen.

Figure 4.

The probability landscape of the epigenetic circuits of lysogeny maintenance in phage lambda. (Row 1) For wild type phage lambda, at the CI degradation rate of k_d = 7.0 × 10⁻⁴/s, probability landscape centers at locations with high copy numbers of CI₂ and close to 0 copy of Cro₂. This corresponds to the lysogenic phase of phage lambda. When k_d increases from k_d = 1.8 × 10⁻³/s to 2.2 × 10⁻³/s, the peak located at lysogenic phase gradually diminishes, whereas the peak located at lytic phase gradually increases. At about k_d = 2.0×10⁻³/s, phage lambda has about equal probability to be in either lysogenic or lytic phase. When CI is degraded at a faster rate of k_d = 3.6 × 10⁻³/s, the probability landscape centers at locations where there are higher copy numbers of Cro dimer and close to 0 copy of CI. This corresponds to the lytic phase of phage lambda. (Row 2) When all cooperativities are removed from the model, lysogeny cannot be achieved. (Row 3) When only the cooperativity of ΔG₁₂ is restored, wild-type behavior is largely restored. (Row 4) When all other cooperativities except ΔG₁₂ are restored, lysogeny still cannot be achieved (Modified from reference^[23]).

Calculation results also showed that wild-type phage lambda can maintain a constant level of repressor over a wide range of repressor degradation rates and is stable against UV irradiation, ensuring heritability of the lysogenic state. Furthermore, it can switch efficiently to the lytic state once repressor degradation increases past a high threshold by a small amount. Novel findings including the role of cooperativity, effects of mutations and hair-triggers, and the origin of network robustness, are discussed in reference.^[23]

The example of the decision network of phage lambda demonstrated that realistic systems can now be directly studied using the ACME method. A detailed network of 16-dimensional MAPK network that can be studied using the ACME method is shown in Figure 5, with its probability landscape computed exactly.^[40] This is a significant improvement over current practice in which one introduces simplifications to reduce this network into that of 3-4 nodes, with consequences unknown, so SSA simulation can be carried out.

Figure 5.

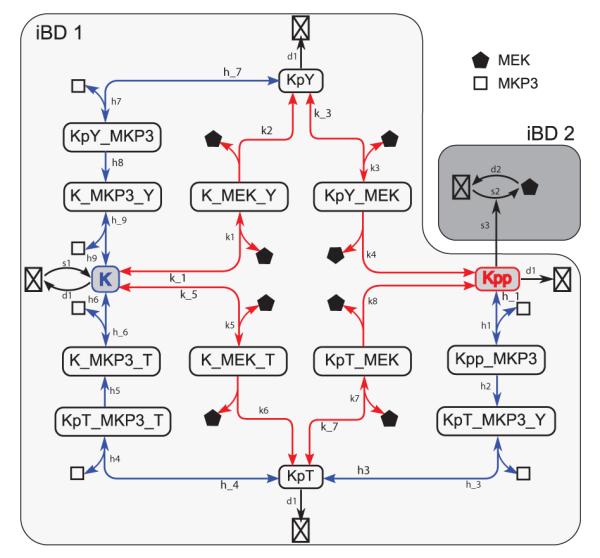
A detailed network model of the MAPK cascade. The ERK(K) phosphorylation is catalyzed by the kinase MEK, whereas MEK synthesis is up-regulated by dual phosphorylated ERK(Kpp). Detailed reactions during the dual phosphorylation process of the ERK(K), the synthesis and degradation of MEK are explicitly modeled. Red and blue arrows represent phosphorylation and dephosphorylation reactions, respectively. Bidirectional arrows represent reversible reactions. The network can be partitioned into two components, as shown in two shaded areas of different color. There are a total of 16 molecular species and 35 individual reactions in the network. (Modified from reference^[40]).

Chromatin folding and Cellular States

Recent development of fluorescence in-situ hybridization (FISH), chromosome conformation capture (3C) and related techniques (4C, 5C, Hi-C) enabled large-scale discovery of long-range chromatin looping interactions among distant chromosomal elements,^[10–14] as well as the identification of Topologically Associated Domains(TAD).^[49–51] Understanding the spatial organization of the genome in a cell nucleus provides an important route towards gaining insight into the mechanisms of gene activities and the maintenance of cellular epigenetic states.^[52]

Global scaling properties of chromosome folding

FISH and chromosome conformation capture studies revealed important global scaling properties of the human genome, including the relationship between contact probability P_c(s) and loop length s,^[13] the spatial distance R²(s) between elements and the loop length s, as well as the leveling-off effects of spatial distances between genomic elements as their genomic distances increases.^[10,11]

The fractal globule (FG) model^[13] was the first model developed to describe the global folding properties of the human genome, as it can explain the scaling relationship between P_c(s) and s. However, it does not account for the leveling-off effects observed in FISH experiments.^[10,11] Subsequently, the Strings and Binders Switch (SBS) model was developed, which pointed to a more heterogeneous structural ensemble, in which the scaling properties of the individual structures depend on the concentration of binder molecules such as architectural proteins.^[53] However, scaling in the SBS model strongly depend on the choice of model parameters, and all observed scaling properties cannot be accounted for using a fixed set of parameters.

Chromosomes reside within the severely confined space of the cell nucleus. However, the direct effects of nuclear confinement on chromatin folding and compaction are not known. A detailed computational model, named Constrained Self-Avoiding Chromatin (C-SAC), was developed for studying the folding properties of chromosomes (Fig 6A).^[54] In C-SAC, nuclear confinement is explicitly modeled and ensemble of chromatin chains are generated inside the severely confined cell nucleus. This was achieved by overcoming the challenging problem of attrition in sampling using the geometrical sequential important sampling technique.^[54–61]

Figure 6.

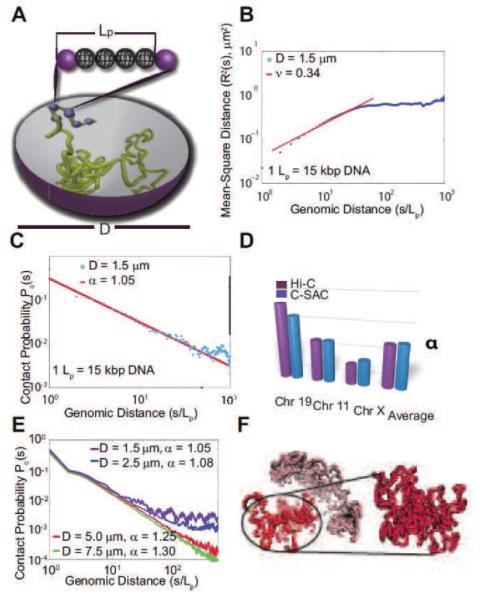
The physical model of C-SAC chains and its scaling properties. (A) Schematic representation of the C-SAC model. A chromatin fiber is represented by a self-avoiding polymer chain with a persistence length L_p. Polymers are grown as chains inside a spherical confined space of a diameter D. (B) The scaling of R²(s) from 10,000 chains of length 1,000L_p in log₁₀ scale. (C) The scaling of contact probability P_c(s). (D) Comparison of exponent α of P_c(s) between C-SAC and Hi-C data.^[13] Values of α for different chromosomes^[13,53] were compared to those calculated separately for different clusters of C-SAC chains. (E) P_c(s) vs. chain length s for different confinement sizes D. (F) A random C-SAC chromatin chain with independent substructures. A singular domain-like conformation is shown in detail (adapted from reference^[54]).

Results using C-SAC showed that spatial confinement of the nucleus is responsible for much of the experimentally observed scaling behavior of chromosome folding (Fig 6B-E).^[10,11,13] The C-SAC model also predicts the formation of highly interactive sub-structures that may give rise to topological domains (Fig 6F).^[50] A recent study further suggested that the segregated organization of chromosome is due to the onset of glassy dynamics when long chromosome chains are confined into small nuclei.^[62] These findings highlight the importance of nuclear confinement and how its size change may regulate epigenetic programming of cells, as in the case of transitioning from stem cells to differentiated cells.^[53,54]

Genome-wide structures of multi-chromosomes in yeast

Understanding different cellular states in mammalian cell differentiation requires knowledge of genome-wide interactions of chromatins. Budding yeast is an excellent model system for constructing genome-wide models of multi-chromosomes, as its transcription machineries have been well studied and the roles of genome organization well understood.^[63]

Nevertheless, there is some controversy on the extent that the genome organization of yeast is dictated by the architectural properties of the cell nucleus. Recent computational studies showed that yeast chromosomes behave as randomly folded flexible self-avoiding polymer chains subject to the constraints derived from nuclear landmarks and nuclear confinement.^[64,65] However, correlations of modeled inter-chromosomal interactions with experimentally captured interactions are modest at best.^[64,65] The question whether the genome organization of budding yeast is fully dictated by physical tethering of the landmarks and the excluded-volume of the self-avoiding chains is unresolved. Another study showed that once observed interactions are corrected using a null model, the genome organization of the budding yeast no longer exhibit the properties of randomly folded polymer chains with constraints.^[66]

To shed light into the nature of the organization of yeast chromosome, we developed a three-dimensional chromosome model incorporating constraints derived from electron/light microscopy experiments to mimic the nuclear environment and its effects on the folding of the yeast genome (Fig 7A). Large ensembles of model genomes (~200,000) were generated using different constraints. Our results showed that the organization of the yeast genome, including interchromosomal interactions is indeed dictated to a large extent by the confinement of the cell nucleus and the physical tethering of the centromeres.^[61]

Figure 7.

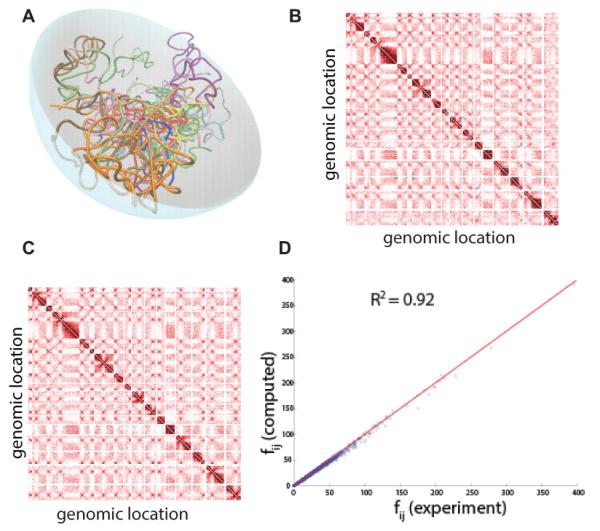
Multi-chromosome model of budding yeast. (A) Schematic representation of yeast genome in the confined nuclear space. Different chromosomes are represented in different colors. (B) Heatmap of interactions that are taken from biochemical experiments.^[14] Each block represents a chromosome and darker color indicates higher frequency interaction. (C) Heatmap of interactions that are averaged from predicted model genomes built without using any biochemical data. The heatmap generated using predicted models is very similar to the measured heatmap in (C). (D). Experimentally measured interaction frequencies correlate well with predicted interaction frequencies from our model (see reference^[61] for more details.

Comparison of computatioanlly generated ensembles of folded chromosomes g with those from 3C-based studies showed that the majority of measured interactions regulating important cellular functions are captured by our model (at an accuracy of 92%, Fig. 4B-D).^[61] Furthermore, preliminary study suggests that these computationally captured interactions can be used to extract biologically specific interactions from experimental data, as they arise from the nuclear architecture of the cell nucleus and can be subtracted. This would allow predictions of novel transcription regulatory mechanism in budding yeast that are experimentally testable.

Spatial structures of functional loci of chromatin in different cell states

Experimental data from chromosome conformation capture studies can capture detailed promoter-enhancer interactions at the locus level. However, the captured information is intrinsically two-dimensional pairwise contact frequencies. Such captures may also be limited by the distribution of restriction enzyme sites and the sequence mappability. Constructing 3D structures of a gene locus can help to obtain detailed structural understanding of promoter-enhancer interactions and how they may affect transcriptional machineries and regulate cellular epigenetic states. Several polymer models of chromatin in genome or locus level have been developed,^{[13,14,53,62,64–73]} and many can generate structures of chromatins from 3C/5C measurements, capturing many known interactions.

There are many difficulties in constructing accurate 3D models of a gene locus. Random interactions from non-specific formaldehyde fixation,^[74] introduce complexity as it is challenging to distinguish biologically relevant interactions from non-specific random spatial interactions. As measurements of 3C/5C are from a mixture of cell populations, full ensembles of 3D chromatin chains need to be generated to collectively best describe the bulk measurements and to reveal specific interactions from experiments.^[75]

We have developed a method that can generate well-sampled ensembles of high-resolution chromatin chains of a specific locus. Our method can remove non-specific physical interactions from 3C measurements and can incorporate data of specific interactions. We have applied our method to study the chromatin structures of the α-globin locus, which is differentially expressed in normal (GM12878) and cancer (K562) cell lines.^[70] (Fig 8A-B) Comparison of differences in their spatial structures will help to understand how spatial organization of the genome affects the expression level of this important gene and will allow identification and interrogation of patterns of spatial interactions. Preliminary results showed that the differential expression of α-globin is strongly influenced by the folding landscape of chromatin, such as the formation of different chromatin globules, in agreement with previous studies.^[70] In addition, our model predicts specific novel interactions that are not captured by 3C experiments because of primer design. A subset of such predicted interactions are found to be biological important as verified by an independent studies (Fig 8C).^[76]

Figure 8.

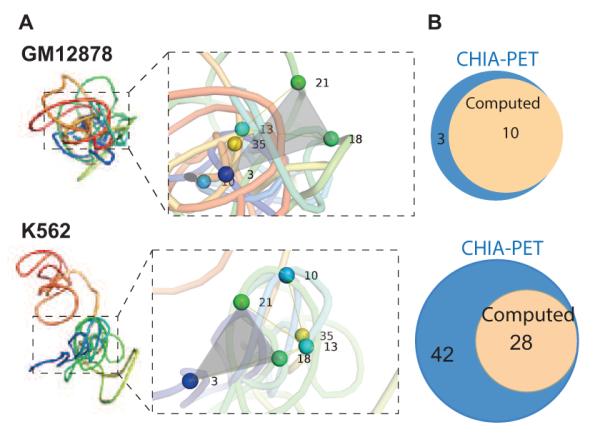
Structural models of the α-globin gene domain. (A) Representative three-dimensional chromatin chains of the α-globin gene domain in the GM12878 and the K562 cell lines. The α-globin gene domain has only one domain and is more compact in the GM12878 cell. In the K562 cell, the α-globin gene domain has two distinct domains that form a more extended structure. Close-up views of selected sites for comparison between cell lines are also shown, with specific nodes noted. (B) Comparison between the number of CTCF- (top) and RNAPol2-mediated (bottom) interactions based on the predicted model (beige) and based on measurements from an independent experimental study using the technique of CHIA-PET (blue, reference^[76]).

Cell model for tissue pattern formation

Fully differentiated cells under epigenetic control grow, divide, and migrate to form tissue. Regulation of cell growth and cell-cell interactions plays fundamental roles in tissue formation, organ development, and cancer progression.^[77–80] The coordinated efforts of a large number of cells to form an organ is a complex process that is not yet fully understood. Tissue formation occurs with precision and persistence, extending beyond individuals and even generations. We do not yet have the full picture of how changes in properties of individual cells such as cell size, shape, geometry, lineage, division, growth rate, and death affect tissue formation and the whole organism. Neither do we have sufficient information on how and when cell-cell interactions become important. It is challenging to design and conduct experimental studies to identify and differentiate specific effects of individual cell attributes and cell-cell interactions on tissue and organ development. Computational studies can generate useful hypothesis that can complement experimental studies in providing important insights.

Mechanical models of cell

Several computational methods have been developed to model tissue formation. These include the cellular Potts model, center-based model, finite element models and vertex models. Below we briefly summarize these methods (see Sëma et al.^[81] for a detailed comparison).

The cellular Potts model is used for studying cell behavior, where each cell is modeled as a collection of about 25–50 lattice sites.^[82] Each lattice site can be modeled as a square, triangle, or a hexagon. Size of the cells is constant and neighboring cells interact with specific binding energy, which models the underlying biology, e.g., cadherin interactions.^[83] Cell shape and topology are not modeled directly in the cellular Potts model and realistic modeling of cell shapes often requires extensive post-processing. Metropolis moves are often used to indirectly model cell proliferation. The state of a randomly picked lattice site is first proposed to change into that of its neighbor. This proposal is then evaluated for acceptance or rejection according to certain probability determined by energy calculation. Cell motions are also implemented as a result of energy minimization after stochastic fluctuations of flips of lattice sites introduced by Metropolis moves.^[83]

The center-based model approximates each cell by an isotropic, elastic, and adhesive sphere.^[84] Cell growth, division, and migration can be modeled by this model. It is specifically designed to study details of pair-wise cell forces where cellular interactions can be treated as interactions between homogeneous elastic sticky spheres.^[84] However, detailed descriptions of cell shapes are not included, and any shape deviation from sphere is ignored.^[84] As a result, center based models are not well-suited to study details of the biological problems that involve dynamic changes in cell shape and topology.

Finite element methods model cell shapes realistically but have inflexible boundary conditions and cannot model dynamic changes in cell shape such as cell growth, cell migration, cell birth, and cell apoptosis.^[85–87]

Vertex models minimizes the energy under forces acting on cell junctions (represented as vertices) to model cell shapes. These models are specifically designed to study packing and remodeling of epithelial cells.^[88,89] They can be used to study cell birth, growth, migration, and apoptosis at varying degrees as they can realistically model cell size, shape, and elasticity.^[90–94] However, there are some limitations in the current vertex models. For example, cells are always polygonal and do not have boundaries with curvature. Cell growth is also not modeled in detail. In addition, initial conditions require a plural number of cells (e.g., ≥16 cells), often with periodic boundary conditions. Cell death can only be modeled for the special case associated with a specific type of topological change.^[89]

Chimeric methods such as the viscoelastic cell model by Jamali et al.^[95] and the immersed boundary framework by Rajniak^[96] can model realistic cell shape, cell growth, cell division, cell motion, and cell-cell interactions. However, they are not suitable for simulating large tissues due to the model choice of representing the shape of a cell by a network of linear Voigt elements or by a collection of boundary points connected through linear springs, which leads to substantial computational overhead.

Dynamic vertex model of cells

We have recently developed a physical model of cell and a simulation algorithm that incorporates cell size, shape, lineage, growth rate, death rate, and different cell-cell interactions (Fig 9^[81]). Our method can model monolayered tissue formation by following the growth process of either a single cell, or a group of cells with arbitrarily pre-arranged spatial relationship, unlike previous studies that must start with a specific pre-existing cellular pattern.^[89,91,94] Our method can model cell proliferation and programmed cell death without the constraints from unrealistic boundary conditions and can incorporate different growth rates due to the effect of specific growth factors. Moreover, our model represents the geometry of cells more accurately, with inner cells treated as polygons and outer cells as disc segments, as seen in in vivo studies.^[97]

Figure 9.

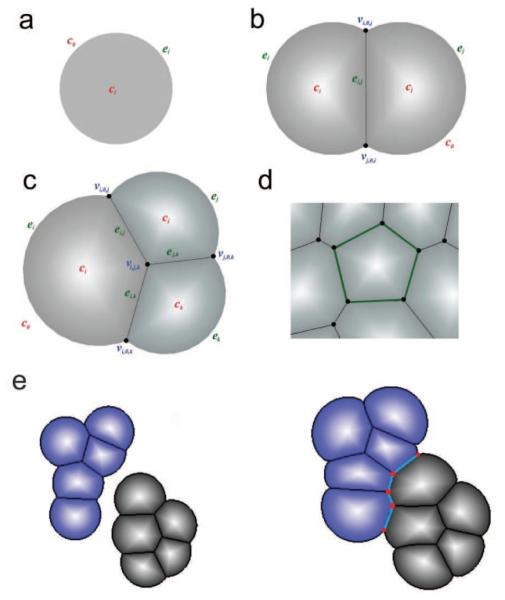
Dynamic vertex model: (a) An isolated cell is modeled as a disk. (b) A cell is modeled as a disk segment when contacting other cell(s). An outer edge e_i is an arc or a circle, representing the boundary between cell c_i and the outside medium (denoted as c₀). An inner edge e_i,j occurs when a cell c_i is in contact with another cell c_j. Their shared boundary is modeled as a straight line segment. When two cells c_i and c_j make contact, their outer edges (arcs) e_i and e_j intersect at two vertices v_i,0,j and v_j,0,i which are also the two end-points of the inner edge e_i,j (c) When three cells c_i, c_j and c_k intersect, they form a vertex v_i,j,k. (d) A cell completely surrounded by other cells is represented as a polygon. (e) Fusion of two growing tissues. New edges and vertices formed are highlighted.

In our method, we assume force equilibrium and adopt small step sizes in cell volume changes. Time-specific, cell-type specific, and location specific parameter values for cell growth or shrinkage and tissue mechanical properties can be introduced. Our implementation of the model using the Half-Edge data structure is very efficient and robust, and provides additional benefit of no overhead with regards to time and storage in maintaining the list of neighboring cells for each cell. We were able to simulate tissues with a large number of cells (~20,000) in a very short amount of time (e.g., <1 hour).^[81,98]

Pattern formation of tissue

We have used our dynamic vertex model^[81,98] to examine the mechanisms regulating topological changes in tissue formation. Specifically, we studied the effects of orientation of division plane, differential proliferation, and mechanical forces on animal epithelial cells.^[99,100] By incorporating cell rearrangements, we succeeded in reproducing the commonly observed topological distributions of cells in natural proliferating animal epithelial, regardless of the orientation of division plane. Different schemes of division plane generated different frequency of hexagonal cells, consistent with experimental observations. Moreover, in our simulations of proliferating cells interfacing quiescent cells, we found that differential proliferation and increased tension on the boundary together reproduced the observed topological changes. Our simulation showed that both division plane orientation and mechanical forces play important roles in cell topology in animal proliferating epithelial.^[99,100]

We have also used our dynamic vertex model to study the mechanisms of regulating tissue elongation in drosophila wing.^[101] Our simulation on the effects of directional cues and reduced cell size on tissue elongation indicated that oriented cell divisions and oriented mechanical forces act as directional cues during tissue elongation. In addition, we found that reduced cell size may significantly promote tissue elongation in conjunction with the directional cues. Our findings suggest that cell divisions without cell growth play essential roles in tissue elongation.^[101]

We have also used our dynamic vertex model to study the effects of mechanical properties on tumor invasion.^[102] Our simulations show increased adhesion to extra-cellular matrix (ECM) and decreased adhesion among tumor cells result in invasive tumor behavior. Moreover, our simulations show increased stiffness and increased degree of degradation of ECM promote tumor invasion, resulting in invasive tumor morphologies.^[102] We have further improved this vertex based model into a stochastic spatial dynamic model by incorporating the inhibition growth rate, proliferation and differentiation probabilities of individual cells through feedback loops controlled by secreted factors from neighboring cells.^[103] Our simulations show that with proper strengths of inhibition to growth and stem cell divisions, the tissue is capable of achieving a homeostatic size control.^[103]

Dynamic finite element model and wound healing

Built upon the dynamic vertex model, we have further developed a novel cell model approach based on dynamic finite element method (dFEMC) that can model explicitly cells with realistic cell elasticity, cell-cell interactions, and can model complex cell shapes and their dynamic changes during cell proliferation, cell migration and cell apoptosis. In addition, it can be used to study a large population of cells in the tissue.^[104]

In dFEMC, we assume cells have linear elasticity.^[105] Both external and internal stresses can deform the cell. Cell deformation in turn can generate internal stresses. Following standard elastic models,^[106] we use strain tensor to measure the local deformation of the cell. Denote the displacement of a point x in cell as u(x) = [u₁(x), u₂(x)]^T, the strain tensor ϵ of x can be defined as ϵ = [ϵ_x1, ϵ_x2, ϵ_x2x1]^T = Bu. Taking into account the properties of cell material, the stress tensor σ of internal stress in a cell in response to cell deformation can be written as σ = Dϵ. With the strain and stress tensors defined, the elastic strain energy of a cell, along with work done by external forces (x) can be written as $E\left(\mathit{u}\right)=\frac{1}{2}{\int }_{\Omega }{\mathit{u}}^T{B}^T\mathit{DB}\mathit{u}d\mathit{x}-{\int }_{\Omega }{f}^T\mathit{u}\mathit{dV}$

In our model, the boundary ∂Ω of a cell Ω with specific shape is represented by a set of discrete points ∂Ω = {x = [x₁, x₂]^T}. Triangular mesh tilling up the body of the cell Ω is then constructed using the farthest point sampling method based on Delaunay triangulations,^[107] which generates internal discrete point set {Int(Ω) : x = [x₁, x₂]^T} and partitions the cell domain into a set of triangular elements {T_Ω : T_e = [x₁, x₂, x₃]^T : x_i ∈ ∂Ω ⋃ Int(Ω))} (Figure 11a and 11b).

Figure 11.

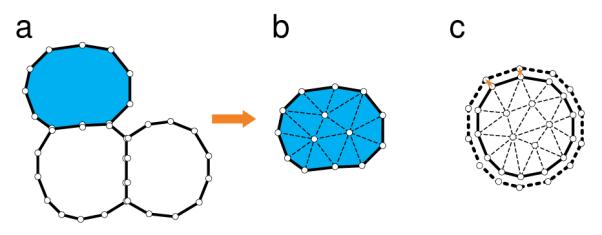
Geometric democratization of cells: (a) An example of a toy model of a tissue consisting of 3 cells. The boundary of each cell is represented by a set of vertices. (b) Each cell is tiled by a triangular mesh generated using the farthest point sampling method based on Delaunay triangulation.^[107] (c) Cell grows incrementally, with volume change attributed to individual boundary element that sum to ΔV (adapted from references^[81,104]).

Each triangular element T_e is defined by three nodes either from ∂Ω or Int(Ω). The strain energy of each T_e under external force and/or internal forces is at its minimum when ∂E(u)/∂u = 0. This can be used to obtain the equilibrium solution of displacement describing cell deformation, which can be written as K^eu^e = f^e, where K^e is the element stiffness matrix of T_e, u^e the displacement vector of nodes in T_e, f^e the discredited force vector exerted on nodes in T^e. Upon assemblage of all elementary stiffness matrix into a global stiffness matrix, we obtain a large sparse linear system Ku = f. The behavior of the whole cell system at a specific time then can be simulated by solving this linear equation.

In many physiological process, cells migrate under chemical and mechanical cues. For example, during the re-epithelialization process in wound healing, cells migrate to the wound bed and repair the tissue. A rapidly moving cell often adapts its shape dynamically and may completely rebuild its cytoskeleton and adhesive structures during the migration process.^[109] To gain understanding of the influence of intercellular adhesions and transmission of mechanical signal on the collective migration of cells, it is important to take into account dynamic changes in cell shape, along with changes in cell behavior associated with mechanical signal transmission.

We have applied our dFEMC method to study cell proliferation, apoptosis and tissue fusion.^[104] We were able to reproduce suppression of tumor tissue growth under the treatment of curcumin and DMSO which influences the growth rate of cancer cells, as observed in clinical experiment.^{[104,110,111]} Differential suppression effects of curcumin and DMSO treatments from our simulation were consistent with experimental observations,^[108] where curcumin exhibited stronger suppression effect on cancer cells than DMSO agent (Figure 12).

Figure 12.

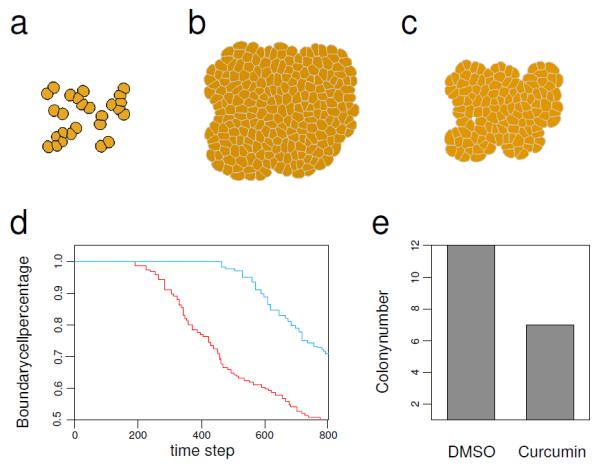
Cancer cell growth under suppression induced by antitumor agents. (a). The initial state of cell growth. (b). Tumor tissue after 800 time steps using growth parameter modeling the effects of suppression from DMSO. (c). Tumor tissue after 800 time steps using growth parameter modeling the effects of suppression from curcumin. (d). The percentage of boundary cells, namely, the number of cell on boundary of the tissue over the total cell number, at each time step for DMSO treatment (red) and for curcumin treatment (blue). The higher boundary cells percentage corresponds to a more scattered cell population. (e). The colony number for DMSO and curcumin treatments. We count every 9 cells as one colony. The colony number ratio between the two treatments, 12 against 7, is consistent with the colony number ratio between the two treatments found in experiment studies^[108] (see reference^[104] for details).

The dFEMC method can be further applied to study skin wound healing, a complex process involving many different cell types, signal transduction networks, as well as mechanical cell-cell interactions (Fig 13). It can help to delineate the differential roles of chemical signal and mechanical force in regulating processes such as re-epithelialization and granulation during wound healing, and can identify the specific effect of cytokines such as TGF-β in reconstruction of granulation tissue during wound healing.

Figure 13.

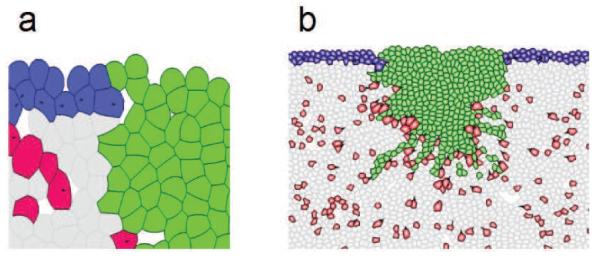
Application of the dFEMC model to study wound healing. (a) Detailed view of the wound tissue including multiple cell types and clot elements. Green: wound element; Blue: keratinocyte cells; Red: fibroblast cells; Gray: elements of extra-cellular matrix. (b) A global view of a snapshot of a simulation of the process of wound healing.

CONCLUSIONS

Multiscale modeling of biological systems can aid in formulating theoretical models and can reveal fundamental insight into biological systems. It also has the promise to uncover new opportunities for disease treatment and health interventions. Previous computational studies at the molecular levels of proteins and RNAs have already generated important insight (not reviewed here, but see^[112,113]). Computational techniques such as master equation treatment of protein folding^[114] and sequential importance sampling of polymers can serve as the basis for developing effective computational techniques for studying stochastic network and for understanding chromosome folding.^[55–60] The intricate geometry and topology of macromolecule with tens of thousands of atoms bears strong resemblance to problems encountered in studying cells and tissue.^[115,116]

The development of computational algorithms such as the ACME method for computing the probability landscape of a stochastic network discussed here is significant. With orders of magnitude reduction in the size of the state space, it enables accurate solution of the dCME for a large class of problems, whose solutions were previously unobtainable. For example, the state space of the MAPK network (Fig 5) can be reduced by 6–9 orders (e.g., from 1.0 × 10¹⁶ to 6.2 × 10⁶), allowing a stochastic problem otherwise unsolvable to be computed on a desktop computer.^[39,40] With explicit formulas for error bounds, the accuracy of the solution of a stochastic network can now be reliably estimated, and we gain the certainty of knowing if there are any probability peaks missing from our computational solution, hence no longer suffer from possible unknown unknowns. We can also assess rapidly the best possible accuracy we can achieve for a given computing environment. Such advancement has important implications, as we will be able to access hidden peaks and valleys of complex probabilistic landscapes, allowing quantitative models of epigenetic states corresponding to disease and healthy states, and the rare stochastic transitions between them to be developed and computed.^[117,118]

There is a large amount of data on chromatin interactions available from studies using chromosome conformation capture and related techniques. We now have access to detailed knowledge of pairwise interactions among genomic elements, many of which are important for nuclear activities. Computational construction of three-dimensional structures of chromatin can overcome significant limitations in these experimental techniques and can covert 2D mappings of genomic interactions into 3D spatial models of gene loci as well as the full genome. With genome-wide epigenetic studies pointing to potential enhancers along the 1D genome, 3D models of chromatins can facilitate interpretation and integration of epigenetic information, enabling mechanistic understanding of the temporal and spatial pattern of genome organization associated with cell differentiation. We expect future development of computational predictions of structural models of gene locus and global folding of genome will aid in the discovery of many novel higher order gene-enhancer interactions. Such knowledge will help to understand the control mechanism of the epigenetic states of stems cells and differentiated cells, with important implications in regenerative medicine.

Fully differentiated cells of different types grow, divide, interact, and migrate to form tissues with complex pattern. A fundamental question is how mechanical properties and chemical signaling specifically affect cell behavior and tissue formation. As mechanical stress exerted at cell-cell junctions and its transmission between cells cannot be easily measured experimentally, computational cell models such as those described here can play important roles in identifying the roles of mechanical cues and chemical cues in regulating the growth, division, and collective migration of different cell types. The dynamic finite element model (dFEMC) of cells discussed here can realistically model cell growth, death, migration, along with accurate description of cell shapes. It can also integrate effects of chemical network and mechanical forces, and can be used to study cellular pattern formation in complex processes such as wound healing, with the promise of generating new treatment strategies.

Figure 10.

Simulation of tissue elongation. (a) Oriented cell divisions drive tissue elongation, but only to a limited extent (black). Reduced cell size, when combined with oriented cell divisions, enhances tissue elongation (red). (b) Morphology of the elongated tissue (see reference^[101]) for details.