Dose expansion cohorts in Phase I trials

Abstract

A rapidly increasing number of Phase I dose-finding studies, and in particular those based on the standard 3+3 design, are being prolonged with the inclusion of dose expansion cohorts (DEC) in order to better characterize the toxicity profiles of experimental agents and to study disease-specific cohorts. These trials consist of two phases: the usual dose escalation phase that aims to establish the maximum tolerated dose (MTD), and the dose expansion phase that accrues additional patients, often with different eligibility criteria, and where additional information is collected. Current protocols do not always specify whether and how the MTD will be updated in light of the new data accumulated from the DEC. In this paper, we propose methods that allow monitoring of safety in the DEC by re-evaluating the MTD in light of additional information. Our working assumption is that, regardless of the design being used for dose escalation, during the DEC we are experimenting in the neighborhood of a target dose with an acceptable rate of toxicity. We refine our initial estimate of the MTD by continuing experimentation in the immediate vicinity of the initial estimate of the MTD. The auxiliary information provided in such an evaluation can include toxicity, pharmacokinetic, efficacy or other endpoints. We consider approaches specifically focused on the aims of DEC that examine efficacy alone or simultaneously with safety and compare the proposed tests via simulations.

1 Introduction

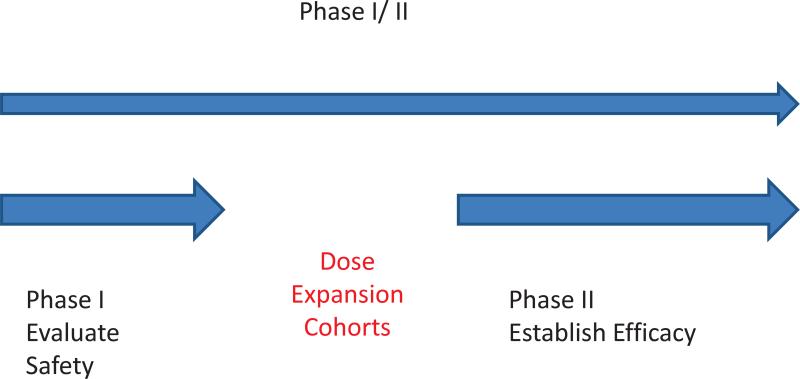
Phase I trials are increasingly using dose expansion cohorts to better characterize the toxicity profiles of experimental agents or to study disease specific cohorts before selecting an appropriate dose and patient population upon which closer attention will be focused for the Phase II study [Iasonos and O'Quigley 2013, Manji et al. 2013]. The experimental setting for the dose expansion cohort (DEC) differs in two important ways from that of the Phase I study. The first difference is the recruitment criteria: DEC patients are likely to belong to a more narrowly and more sharply defined targeted category of patients, for example disease specific or histology specific cohorts. The second difference relates to the information gathered on the DEC patients; efficacy data as well as additional safety data are gathered on DEC patients. Furthermore, Phase I trials with dose expansion cohorts do not have the same objectives as Phase I/II trials such that Phase I trials with DEC raise numerous, new design considerations as they fall somewhere in between Phase I, Phase I/II or Phase II trials (Figure 1). There is currently no design specific to DEC, a shortcoming recently identified by several independent groups [Manji et al. 2013, Iasonos and O'Quigley 2013, Dahlberg et al. 2014].

Figure 1.

Illustrating the use of dose expansion cohorts following a dose escalation study.

In this paper, we propose methodology that takes into account the information provided from the additional patients treated at the maximum tolerated dose (MTD) as part of an expansion cohort, and we re-evaluate the recommended Phase II dose (RP2D) based on the information provided by all the data. The proposed design will provide efficacy estimates on multiple levels, so that investigators can decide which dose to take forward to a phase II testing. Over the last 20 years much work has been done on model based designs for Phase I dose-finding studies [O'Quigley, Pepe and Fisher 1990, Iasonos et al. 2008, Yuan Y 2011], which includes methods that can simultaneously deal with a bivariate outcome of toxicity and efficacy [Yuan Y 2011, O'Quigley, Hughes and Fenton 2001]. Phase I dose-finding studies carried out according to a model-based design are very easily adapted to take on board the additional dose-expansion cohort. Whenever possible we would recommend that any Phase I dose-finding trial use one of the model based approaches, for several reasons that have been reported previously [Iasonos et al. 2008] including the ability to readily extend to situations involving an expansion cohort. However, the algorithmic 3+3 design continues to be used in many Phase I trials [Rogatko et al. 2007] though current usage rates are not available. Despite clinical investigators’ reluctance to move away from the 3+3 design, analysis methods for the DEC are needed since the 3+3 no longer applies. Current practice consists of simply treating patients at the estimated MTD with no planned analysis of the observed outcomes of the patients accrued during DEC. Our purpose is to develop designs for DEC that will be applicable regardless of the type of design used in the dose escalation stage, including Phase I trials based on the 3+3 design, which accounts for the great majority of current trials.

Phase I protocols with dose expansions consist of two phases: the dose escalation phase followed by a dose expansion phase (Figure 1). During the dose escalation phase, the MTD is estimated; during the expansion phase, an additional number of patients (6, 10 or more) are treated at the estimated MTD [Topalian et al. 2012]. While the MTD is estimated by the dose escalation phase, the RP2D is based on the combined safety data (pre and post dose expansion), and this is the dose level selected for future trials. Any toxicities observed among the additional patients being treated at the expansion phase, while reviewed by clinical investigators are not part of the dose escalation algorithm followed to establish the MTD. There are cases where the RP2D is lower or higher than the MTD [Manji et al. 2013, Isambert et al. 2012] in light of the safety evaluation during the expansion phase, pharmacokinetic studies or efficacy assessment. The basis of our paper is that there is still considerable uncertainty in the selection of the MTD after the dose escalation part, and zooming into the vicinity of the MTD while exploring other endpoints beyond safety will help guide the choice of the RP2D.

The aims of Phase I trials with DEC can be twofold depending on whether the objective is to recommend the MTD based on safety alone, or to further investigate for evidence of efficacy in a selected patient population. Unlike Phase I/II trials, where the Phase II part of the protocol aims to target a dose with a specific efficacy threshold, Phase I trials with DEC are considered more exploratory in nature, and often no efficacy is being measured during pre-expansion. As such, Phase I protocols with expansion cohorts often aim to establish a safe dose and at the same time obtain initial evidence about whether to take the investigational drug forward to a larger Phase II study and if so, at which dose level. Thus, DEC do not necessarily need to include all patients at a single dose level, or target a dose with an efficacy threshold as in the Phase II setting, but instead can further explore more than a single dose level. At the end of the study, after accruing a number of additional patients at the expansion phase, there might be an indication that the MTD chosen based on safety alone has low efficacy. The recommendation then might be that investigators either need to add additional patients at the expansion phase (to better estimate the efficacy rate), or that a higher dose should be considered, which is more likely to show activity. Alternatively, investigators could test multiple levels in the expansion phase with the aim of selecting the dose with a higher efficacy rate. Whether the efficacious level is unsafe and abandonment of the investigational drug should be considered altogether is one of the questions the proposed methodology aims to address. In the following sections, we develop these ideas in a more formal setting.

2 Methods

Our main idea is to use a model based design and guide the dose allocation of the expansion cohort based on all available data, i.e. using the data gathered both pre- and post- DEC. Our focus here is the Continual Reassessment Method (CRM) [O'Quigley, Pepe and Fisher 1990], although we could employ any other model based design. CRM assumes that the dose-toxicity curve can be locally approximated through a simple working model and as accumulated data on patients’ responses are obtained, we update this model, and assign the next patient at a level closest to an acceptable toxicity rate, θ, based on some measure of distance.

We assume the trial consists of k ordered dose levels, d₁, d₂, . . . , d_k, and a total of N patients. The assigned dose level for patient j is denoted as X_j, and the binary toxicity outcome is denoted as Y_j, where Y_j= 1 indicates a dose-limiting toxicity (DLT) for patient j, and 0 indicates absence of a DLT. We denote the true probability of toxicity at X_j = x_j by: R(x_j) = Pr (Y_j = 1|X_j = x_j), x_j ∈ {d₁, d₂, . . . , d_k}.

O'Quigley and Shen (1996) used a simple working model for the dose toxicity relationship of the form, $\psi (d_i,a)={\alpha }_i^a$, where a ∈ (0, ∞) is the unknown parameter and α_i are the standardized units representing the discrete dose levels d_i or skeleton. Optimal model skeletons can be selected by following the work from Lee and Cheung (2011). Since drugs are assumed to be more toxic at higher dose levels, ψ(d_i, a) is assumed to be an increasing function of d_i. The derivative of log likelihood as a function of the dose toxicity parameter a, after j patients have been treated, can be expressed as:

$${\mathcal{U}}_j\left(a\right)=\sum _{i=1}^k\left[t_i\left(j\right)\frac{{\psi }^{\prime }}{\psi }(d_i,a)+(n_i\left(j\right)-t_i\left(j\right))\frac{-{\psi }^{\prime }}{1-\psi }(d_i,a)\right]$$ (1)

where n_i(j) and t_i(j) are the number of patients treated and the number of DLTs, respectively, at each dose level i out of a total of j patients. The true MTD is the dose such that arg min_i Δ(R(d_i), θ), where Δ(R(d_i), θ) denotes the distance from the target acceptable rate θ. For example, in the field of dose finding studies, it is common to use the Euclidean distance, Δ(R(d_i), θ) = |R(d_i) – θ|. Once the current estimate of â is obtained by solving ${\mathcal{U}}_j\left(a\right)=0$, and R̂(d_i) = ψ (d_i, â) are calculated, the estimated MTD is defined to be the dose d_m ∈ {d₁, . . . , d_k}, 1 ≤ m ≤ k such that, d_m = arg min_di Δ(R̂(d_i), θ), i = 1, ..., k. Note that m is a random quantity that depends on R̂(d_i) which are random. However conditional on the data $\mathcal{F}=\{(x_j,y_j),j=1,\dots N\}$ from N patients, then d_m is determined at each step.

It is important to note that the goal of Phase I trials is to focus on a single target level in terms of safety, and unlike preclinical or pharmacokinetic/dynamic studies, the goal is not to estimate the entire dose toxicity curve, which would require us to gather information at dose levels away from the target level. For these reasons, a simple one parameter power model has been shown to be appropriate in this setting [Paoletti and Kramar 2009]. In this paper, we aim to obtain efficacy estimates at the MTD and a nearby level in order to decide which level looks most promising in terms of both safety and efficacy. Such estimates can be obtained via randomization of patients to two levels as illustrated in the next section. Use of the one-parameter model will still provide consistent estimates at the MTD but will generally introduce bias at the other levels, with increased bias the further away we are from the MTD. This bias will be the least at the values adjacent to the MTD. Nonetheless, it could be argued that randomization might be accompanied by a richer model, for example, a two-parameter model or a Bayesian Model Average, or a multiple skeleton model [Yin and Yuan 2011]. At and close to the MTD, we can assume the rate of DLTs to be reasonably approximated by the target rate, for example 0.20. For a sample size of 25 patients, this leads to a standard deviation of 0.08. The bias involved in extrapolating beyond but close to the MTD will typically be less than this. At much higher sample sizes, the bias will remain but the standard deviation will become smaller and eventually be overtaken by the bias [O'Quigley, et al. 2015]. This is a question that could be studied further.

2.1 Prospective expansion guided by toxicity and/or efficacy

Assume that for the patients accrued during the expansion phase, i.e., in a subset of patients, in addition to monitoring their toxicity we also collect some other measures of efficacy or pharmacodynamic / pharmacokinetic endpoints [Pei and Hughes 2008, O'Quigley, Hughes, Fenton, Pei 2010]. For example, there are studies that modify eligibility criteria to require measurable disease or biopsy for patients accrued in the expansion cohort and therefore efficacy is measured on a subset of patients. Accordingly, we re-write the log likelihood function and express it as the sum of two components: 1) the contributions from patients who have toxicity outcomes (all patients), and 2) the contributions of patients who have efficacy measures (the patients accrued during the expansion phase only). Let us denote the true probability of efficacy response as X_j = x_j as: Q(x_j) = Pr (V_j = 1|X_j = x_j), where V_j is a binary random variable denoting efficacy response for patient j. As before, we will use a one-parameter working model $\varphi (d_i,b)={\beta }_i^b$ for Q(x_j) [O'Quigley, Hughes and Fenton 2001], where β_i is a skeleton of initial probabilities of efficacy. We require that for any dose level d_i ∈ {d₁, . . . , d_k} there exists a value of b, such that ϕ(d_i, b_i) = Q(d_i), i = 1, ..., k. We assume that N patients have safety measurements, and J, J ≤ N patients accrued in the expansion have efficacy and safety measurements. Clearly the toxicity and efficacy outcomes are not independent. One way to proceed would be via the use of copula models in conjunction with standard marginal models for the rates of toxicity and efficacy. Dependence on the particular, often arbitrarily chosen, correlation structure for the copula model can be problematic [Cunanan and Koopmeiners 2014] and so our suggestion is to bypass this by making a simple working assumption that the correlation that exists between toxicity and efficacy is essentially captured by the given dose. As a consequence, given the dose, these probabilities can now be treated as conditionally independent. We use that as a working assumption, and, in addition, we carried out extensive simulations to investigate the robustness of the inference to significant departures from that assumption (see Results section and Supplemental Material). The derivatives of the log likelihood with respect to a and b are given by:

$$\begin{array}{cc}\hfill \partial \log L(a,b\mid \mathcal{F})∕\partial a=& \sum _{i=1}^k[t_i\left(N\right)\frac{{\psi }^{\prime }}{\psi }(d_i,a)+(n_i\left(N\right)-t_i\left(N\right))\frac{-{\psi }^{\prime }}{1-\psi }(d_i,a)]\hfill \\ \hfill \partial \log L(a,b\mid \mathcal{F})∕\partial b=& \sum _{i=1}^k[r_i\left(J\right)\frac{{\varphi }^{\prime }}{\varphi }(d_i,b)+(n_{e,i}\left(J\right)-r_i\left(J\right))\frac{-{\varphi }^{\prime }}{1-\varphi }(d_i,b)]\hfill \end{array}$$ (2)

where n_e,i(J) are the number of patients treated at dose i who are also evaluable for efficacy response, and r_i(J) are the number of efficacy responders observed at dose i.

Instead of assigning the next patient systematically at a dose x_j+1 = d_m, we randomize patients to two levels, d_m and the level just above d_m if R̂(d_m) < θ or the level just below d_m if R̂(d_m) > θ. We can base the randomization on a random mechanism by using equal randomization probabilities of 0.50 at the two levels or by using the inverse of the distance to θ. In other words, we randomly select a dose according to a discrete distribution which depends on the available levels and the current estimate of the MTD. On the basis of the data from the first j patients, we assign the (j + 1)^th patient to a dose level as follows:

• If R̂(d_m) ≤ θ < R̂(d_m+1), 1 ≤ m < k, then we randomize the patient to one of two dose levels, x_j+1 = d_m with probability p_m where

  $$p_m=1-\left\{\Delta (\widehat{R}\left(d_m\right),\theta ){\left[\Delta (\widehat{R}\left(d_{m+1}\right),\theta )+\Delta (\widehat{R}\left(d_m\right),\theta )\right]}^{-1}\right\}$$ (3)

  or x_j+1 = d_m+1 with probability p_m+1 = 1 – p_m.

• If R̂(d_k) < θ, we allocate the patient to the highest two levels with randomization probabilities of p_k = p_k–1 = 0.5.

• If R̂(d₁) > θ, allocation is still probabilistic but we ensure the closest level, which is the lowest dose, is chosen with higher probability for safety reasons. For example, we can use the following probabilities for the lowest two levels: p₁ = 0.8 and p₂ = 0.2. Alternatively by design, as long as R̂(d₁) > θ, we could use p₁ = 1.

We continue this algorithm until a fixed number of patients have been accrued during the expansion phase, and at the end of the trial the RP2D is defined as the dose closest to the target rate, as in the definition given for d_m, for the (N +1)^th dose assignment. Randomizing to two levels, say d_m, d_m+1, and assuming the model ψ(d_m, a), then the estimate â will converge almost surely to the value a₀ where U(a₀) = 0 and U(a) is given by:

$$U\left(a\right)=\pi \left(d_m\right)[R\left(d_m\right)\frac{{\psi }^{\prime }}{\psi }(d_m,a)+(1-R\left(d_m\right))\frac{-{\psi }^{\prime }}{1-\psi }(d_m,a)]+[1-\pi \left(d_m\right)][R\left(d_{m+1}\right)\frac{{\psi }^{\prime }}{\psi }(d_{m+1},a)+(1-R\left(d_{m+1}\right))\frac{-{\psi }^{\prime }}{1-\psi }(d_{m+1},a)]$$

where π(d_m) is the stable distribution of patients included at level d_m [O'Quigley 2006].

The goal of Phase I trials remains to find a safe and acceptable dose for the agent being tested, and that is the rationale of following the safety criterion along with randomization for dose allocation. Thus far the RP2D is the dose that is chosen with respect to the probability distribution with p_m (Equation 3). The collection of efficacy data is considered a secondary and often exploratory aim, as in obtaining some initial information on efficacy to design further studies. In the next section we give secondary criteria for the definition of the RP2D. The information at the end of the study might not be enough to distinguish levels based on their efficacy rates, but the idea is that these efficacy rates, predicted separately at each level, will provide additional insight for deciding which is the most promising dose to move forward to a Phase II study.

2.2 Monitoring the expansion cohort

Here we formalize the choice of the RP2D based on hypothesis testing for efficacy. The question we address is whether the chosen dose should move forward for additional testing assuming it has met some efficacy threshold. The efficacy assessment contributes to deciding which dose to take forward as the RP2D as follows. Denote a low efficacy rate, say q₀, and a higher, more clinically interesting rate, q₁, 0 < q₀ < q₁ < 1. We test the hypotheses: H₀ : Q(d_i) ≤ q₀ against H₁ : Q(d_i) ≥ q₁, where Q(d_i) denotes the true, unknown, efficacy rate at level d_i. At each dose level d_i, these hypotheses correspond to H₀ : b ≥ b₀ against H₁ : b ≤ b₁ where b is the parameter that models the dose - efficacy relationship. Since these are composite hypotheses, under H₀ we define the region B₀ to be (b₀, ∞) and similarly under H₁ the region B₁ is (0, b₁). The toxicity contributions involving the parameter a cancel out when the respective integrals cover the regions B₁ and B₀ under the H₁ and H₀, respectively. Specifically, assuming j* patients have been treated at level d_i, with efficacy response for each patient denoted by v_l, l = 1, ..., j*, the test statistic at level d_i is given by:

$$T_1\left(d_i\right)=\frac{{\int }_{B_1}{\prod }_{l=1}^{j^{\ast }}{\beta }_i^{b{v}_l}{(1-{\beta }_i^b)}^{(1-v_l)}g\left(b\right)db}{{\int }_{B_0}{\prod }_{l=1}^{j^{\ast }}{\beta }_i^{b{v}_l}{(1-{\beta }_i^b)}^{(1-v_l)}g\left(b\right)db}$$ (4)

where g(b) is a pre-specified probability distribution for the parameter b. Note that the proposed test statistic is calculated at each dose level separately by including contributions to the likelihood from patients treated at that respective level alone. This test will support H₁ if there is sufficient evidence in support of H₁, ie T₁(d_i) > (1 – ϵ₂)/ϵ₁, where the boundaries depend on the choice of Type I and II error rates denoted as ϵ₁, and ϵ₂, respectively, and on the sequence of efficacy responses. At the end, we might still be indecisive if the test supports continuation of the trial because ϵ₂/(1 – ϵ₁) < T₁(d_i) < (1 – ϵ₂)/ϵ₁. Alternatively if the test supports H₀, ie T₁(d_i) < ϵ₂/(1 – ϵ₁) then the decision might be that no more resources need to be spent with this agent at the current dose level.

As a next step, we simultaneously test for efficacy ie, H₀ : Q(d_i) ≤ q₀ against H₁ : Q(d_i) ≥ q₁ and for an adequate toxicity rate, ie, H₀ : R(d_i) > s₀ against H₁ : R(d_i) ≤ s₁, 0 < s₁ ≤ s₀ < 1; where R(d_i) denotes the true toxicity rate at dose d_i. Let A₁, A₀ denote the restricted space for a under H₁, H₀, and B₁, B₀ denote the space for b under H₁, H₀. Given Ω(j) = {(x₁, y₁, v₁), ..., (x_j, y_j, v_j)}, and assuming j* patients have been treated at level d_i, let

$${\mathcal{H}}_{\{A,B\}}={\int }_B{\int }_A\prod _{l=1}^{j^{\ast }}{\beta }_i^{b{v}_l}{(1-{\beta }_i^b)}^{(1-v_l)}\prod _{l=1}^{j^{\ast }}{\alpha }_i^{a{y}_l}{(1-{\alpha }_i^a)}^{(1-y_l)}{g}_1\left(a\right)g_2\left(b\right)dadb$$ (5)

where g₁(a), g₂(b) denote pre-specified probability distribution functions for the parameters a and b respectively. The sequential test statistic is defined as the ratio of the functions $\mathcal{H}$ when integrated within the respective regions under H₁, H₀, respectively and it is given by $T\left(d_i\right)={\mathcal{H}}_{\{A_1,B_1\}}∕{\sum }_{\mathcal{R}}{\mathcal{H}}_{(A_{\mathcal{R}},B_{\mathcal{R}}\}}$ where $\mathcal{R}$ denotes different regions for the parameters a and b. The regions under the null correspond to different clinical hypotheses and one can modify the region under the null as well as the indifference regions accordingly. As a special case, if we want to test an efficacious and non toxic dose against a non-efficacious and toxic dose, the hypotheses are H₀ : b ≥ b₀ and a ≤ a₀ against H₁ : b ≤ b₁ and a ≥ a₁ and the test statistic equals to ${\left[{\mathcal{H}}_{\{A_0,B_0\}}\right]}^{-1}{\mathcal{H}}_{\{A_1,B_1\}}$. Specifically, the test statistic at level d_i is given by:

$$T_2\left(d_i\right)=\frac{{\int }_{B_1}{\int }_{A_1}\prod _{l=1}^{j^{\ast }}{\beta }_i^{b{v}_l}{(1-{\beta }_i^b)}^{(1-v_l)}\prod _{l=1}^{j^{\ast }}{\alpha }_i^{a{y}_l}{(1-{\alpha }_i^a)}^{(1-y_l)}{g}_1\left(a\right)g_2\left(b\right)dadb}{{\int }_{B_0}{\int }_{A_0}\prod _{l=1}^{j^{\ast }}{\beta }_i^{b{v}_l}{(1-{\beta }_i^b)}^{(1-v_l)}\prod _{l=1}^{j^{\ast }}{\alpha }_i^{a{y}_l}{(1-{\alpha }_i^a)}^{(1-y_l)}{g}_1\left(a\right)g_2\left(b\right)dadb}$$

where A₀ : (0, a₀), A₁ : (a₁, ∞) and B₀ : (b₀, ∞) and B₁ : (0, b₁) are the corresponding regions for the hypotheses given above. Alternatively, we can choose to test for an adequate efficacy rate at level i assuming the value of the toxicity rate is known. The hypotheses will then be H₀ : b ≥ b₀(a) against H₁ : b ≤ b₁(a) conditional on a known value for a, for example the current estimate of a, â. For simplicity we can use the mean of a or the maximum likelihood estimate of a (maximum) as a plug in estimate in Equation 5. In the context of Phase I designs, given the small sample size involved, the operating characteristics provide our main guide to the practical usefulness of such approximations.

In practice, we might approximate the composite hypotheses by using simple point hypotheses rather than composite ones. Integrating over a composite hypothesis amounts to taking a mean, therefore we can approximate this mean (of a function) by the same function of the mean. Assume that at the current level d_i where patient j is being treated, we want to test the hypotheses: H₀ : Q(d_i) = q₀ against H₁ : Q(d_i) = q₁, where q₀, and q₁ denote low and desirable efficacy rates respectively. We can calculate the test statistic after j* patients have been accrued at level d_i given by:

$$T_3\left(d_i\right)=r_i\left(j^{\ast }\right)\log \left(\frac{q_1(1-q_0)}{q_0(1-q_1)}\right)+j^{\ast }\log \frac{(1-q_1)}{(1-q_0)}$$ (6)

where r_i(j*) is the sum of responders treated at d_i who also have efficacy response measured. This test uses the empirical estimate of the number of efficacy responses assuming binomial distribution (O'Quigley et al. 2001). These tests help us decide whether the current dose is efficacious (T₁ or T₃), or efficacious and safe (T₂), which are the secondary criteria used to define the RP2D. All tests use the boundaries given above, i.e. ϵ₂/(1 – ϵ₁), (1 – ϵ₂)/ϵ₁.

2.3 Theoretical Properties

The Average Sample Number (ASN) and Operating Characteristic (OC) function of the proposed tests are of interest from both a theoretical and applied perspectives. Let us denote the probability that the sequential process will terminate with the acceptance of H₀ at dose level i when b is the true value of the parameter as L_i(b). Let E₁ = (1 – ϵ₂)/ϵ₁ and E₂ = ϵ₂/(1 – ϵ₁) be the boundaries for the sequential test T₁. The following lemma is needed for the proof of Theorem 1.

Lemma 1

The Operating Characteristic function L_i(b) is given by $L_i\left(b\right)=[E_1^{h\left(b\right)}-1]∕[E_1^{h\left(b\right)}-E_2^{h\left(b\right)}]$ where for any chosen b > 0, h(b) is the solution of $b=[\log (c^{\ast }(b_1,b_0,h)-1)-\log (c^{\ast }(b_1,b_0,h)-{\beta }_i^{(b_1-b_0)h})][1∕\left(\log \left({\beta }_i\right)\right)]$, where $c^{\ast }(b_1,b_0,h)={[(1-{\beta }_i^{b_1})∕(1-{\beta }_i^{b_0})]}^h$.

Proof

See Appendix A.1.

Theorem 1

The expected value of T₁ is given by

$$\mathbb{E}\left(T_1\left(d_i\right)\right)=L_i\left(b\right)E_2+(1-L_i\left(b\right))E_1.$$

Proof

See Appendix A.1 in Supplementary Materials.

If we assume that all patients in the expansion cohort are treated at the same level, say d_m for example, then the probability to terminate the clinical trial overall will be equal to the probability of terminating the experiment at d_m. However, because experimentation occurs at two levels, the probability of terminating the clinical trial in favor of H₀, L*(b) is given by $L^{\ast }\left(b\right)={\sum }_{i=1}^k\mathrm{Pr}(\text{stop for}{H}_0\mid d_i)\pi \left(d_i\right)={\sum }_{i=1}^k{L}_i\left(b\right)\pi \left(d_i\right)$ where π(d_i) corresponds to the true probability of experimenting at level d_i. It has been shown [O'Quigley 2006] that under certain conditions, as N increases, CRM has the property to converge to the true MTD, say d_m*, where m* denotes the location of the unknown, true MTD (π(d_i) → 0, i ≠ m*, while π(d_i) → 1, for i = m*). In the proposed design, we assume that experimentation will focus at two levels around d_m* as defined in Section 2.1 and the corresponding probabilities will depend on the randomization probabilities accordingly. Thus there exist two levels whose π(d_i) ≠ 0, specifically π(d_m*) > 0 and π(d_{m* +1}) > 0, while for the remaining levels we assume π(d_i) → 0, i ≠ m*, m* + 1. If J, and therefore N, increase without bound, we could approximate these probabilities with the stable distribution of patients included at d_m*. Thus, L*(b) = π(d_m*)L_m*(b) + [1 – π(d_m*)]L_m*+1(b). Numerical approximations for L_i(b) (Supplementary Materials, Appendix A.2) and the expected value of n, which is the number of patients required to reach a decision in favor of H₁, are derived in Appendix B.

3 Applications

3.1 An example of a clinical trial in solid tumors

For illustration we use a published Phase I trial that followed the 3+3 algorithm during the dose escalation phase followed by an expansion cohort [Isambert et al. 2012]. The trial included patients with advanced solid tumors with metastatic or nonresectable cancer. The aim of the study was to find the RP2D of aflibercept when in combination with docetaxel. The trial followed the 3+3 design with modifications and recommended level 4 as the MTD, based on two adverse events of hypertension observed in levels 5 and 6 that met the definition of DLT. Additionally, one patient experienced a hypertension at level 5 that did not meet DLT criteria but was less manageable than hypertension observed at lower dose level, and this was taken into consideration in the RP2D decision. A decision was made to enroll 4 instead of 3 patients at level 1 at the discretion of the investigators. Two additional patients were enrolled at level 5, as the dose level above 9 mg/kg had not been cleared in the parallel phase I single-agent study. These led to slight departures from the 3+3 design. The dose escalation phase consisted of 34 patients, ten of whom were treated at the MTD. An additional 20 patients were treated at the MTD as part of a DEC for a total of 54 (34+20) patients in the trial. The observed DLT rates at each one of the six dose levels that were included in the trial before the DEC were 1/7, 0/3, 0/6, 0/10, 1/5, 1/3, respectively. Although the trial selected level 4 as the MTD, the estimated MTD based on the above model and the data from 34 patients, is level 5. below we illustrate how we could allocate patients to levels during the expansion phase using a model based algorithm sequentially after each patient's response is updated. The toxicity outcomes of the additional patients were simulated using isotonic regression estimates of the observed rates [Ivanova et al. 2006] obtained during the dose escalation phase, resulting in ’true’ rates at levels 5 and 6 of 0.20 and 0.33, respectively. Table 1 shows the estimated dose toxicity parameter â obtained via Equation 2 sequentially. At the end of the study, for an α_i = (0.1, 0.2, 0.3, 0.4, 0.5, 0.6), â = 2.56, b̂ = 2.49. The algorithm without randomization allocated 9 patients to level 5 and 11 patients to level 6, and the observed efficacy rate at level 5 and 6 was 0/9 and 5/11, respectively. The true efficacy rates used in simulation were: 0.07,0.07,0.24,0.24,0.24,0.33 for each level respectively. In this example, the estimated efficacy rate (0.28) is closer to the true rate (0.33) than the observed rate (0.45). The test given by Equation 6 recommends terminating the trial in favor of H₁ after 10 patients and supports adequate efficacy rate of 30% or more at level 6. Note that the recommendation at the beginning of the DEC is to continue the trial, then it switches to evidence favoring H₀ as more patients are treated at level 5 without efficacy responses and then by patient number 10, it reaches a decision in favor of a response rate of 30% for dose level 6. Note that the revised MTD using data from the DEC is not the same as the MTD reached during the dose escalation phase. This is not surprising, and follows not just as a result of the additional data obtained during the DEC, but also because the targeting objective of a model based design is diffierent from that of a 3+3 design which provides a sampling mechanism but not an accurate estimate of the MTD [Shih and Lin 2006].

Table 1.

Illustrative Trial: Parameter estimates and decision rules for a hypothetical expansion cohort of 20 patients enrolled in addition to the 34 patients accrued in the dose escalation trial. The parameter estimate, â, is obtained using safety data and efficacy data are used for T₃(d_i). Type I and II errors ar set at 20% and efficacy rates are set at q₀ = 5% , and q₁ = 30% under H₀, H₁ respectively.

Patient No.	Data: (di,y,v)	â	T3(di)	Decision
35	5 0 0	2.2369	−0.31	continue
36	5 0 0	2.2868	−0.61	continue
37	5 0 0	2.3355	−0.92	continue
38	5 1 0	2.1611	−1.22	continue
39	5 0 0	2.2057	−1.53	acc H0/stop
40	5 0 0	2.2493	−1.83	acc H0/stop
41	5 0 0	2.2919	−2.14	acc H0/stop
42	5 0 0	2.3336	−2.44	acc H0/stop
43	5 0 0	2.3743	−2.75	acc H0/stop
44	6 0 1	2.4264	1.79	rej H0/stop
45	6 0 1	2.4778	3.58	rej H0/stop
46	6 0 1	2.5292	5.38	rej H0/stop
47	6 1 0	2.4050	5.07	rej H0/stop
48	6 0 0	2.4519	4.76	rej H0/stop
49	6 0 0	2.4987	4.46	rej H0/stop
50	6 0 0	2.5456	4.15	rej H0/stop
51	6 0 0	2.5902	3.85	rej H0/stop
52	6 1 1	2.4741	5.64	rej H0/stop
53	6 0 1	2.5169	7.43	rej H0/stop
54	6 0 0	2.5588	7.13	rej H0/stop

3.2 Designing and running a trial

Logistically calculating the test statistic after each patient inclusion is challenging. Instead, we can provide investigators in advance the number of efficacy responses required to make a decision in favor of accepting or rejecting the null hypothesis respectively, and include these numbers in the protocol as shown in Table 2. Investigators need to only count the number of efficacy responses r_i(j); if this number lies in the the interval $(r_1^{\ast }\left(j\right),r_2^{\ast }\left(j\right))$ we continue experimentation, if $r_i\left(j\right)\ge r_2^{\ast }\left(j\right)$ we conclude in favor of H₁, and if $r_i\left(j\right)\le r_1^{\ast }\left(j\right)$ we conclude in favor of H₀. An R code can be provided by the first author to obtain the numbers $r_1^{\ast }\left(j\right),r_2^{\ast }\left(j\right)$ for pre-specified values for Type I, and Type II errors, and rates q₀, q₁. Selecting the values of these errors in an actual trial will depend on the operating characteristics of the sequential probability ratio test (SPRT), which in turn depend on the true underlying parameters, such as the efficacy rates which are unknown. The operating characteristics given in Table 5 help us decide the values of Type I and II errors by examining how many patients it takes to conclude in favor of the H₁. Larger values of Type I and II errors will result in early termination, i.e. smaller ASN. It is not uncommon for Type I and II errors to be set as high as 20% in DEC.

Table 2.

Acceptance and rejection numbers used for trial design, $(r_1^{\ast }\left(j\right),r_2^{\ast }\left(j\right))$ for the test statistics given in Equations 4 and 6.

	ε1 = 0.20, ε2 = 0.20	ε1 = 0.20, ε2 = 0.20
	q0 = 0.05, q1 = 0.30	q0 = 0.15, q1 = 0.30
	$r_1^{\ast }\left(j\right),r_2^{\ast }\left(j\right)$	$r_1^{\ast }\left(j\right),r_2^{\ast }\left(j\right)$
Patient No.	for T1 for T3	for T1 for T3
1	( - , - ) ( - , 1 )	( - , - ) ( - , - )
2	( - , - ) ( - , 1 )	( - , 2 ) ( - , 2 )
3	( - , 2 ) ( - , 2 )	( - , 2 ) ( - , 3 )
4	( - , 2 ) ( - , 2 )	( - , 2 ) ( - , 3 )
5	( - , 2 ) ( 0 , 2 )	( - , 3 ) ( - , 3 )
6	( - , 2 ) ( 0 , 2 )	( 1 , 3 ) ( - , 3 )
7	( - , 2 ) ( 0 , 2 )	( 1 , 3 ) ( - , 4 )
8	( 1 , 2 ) ( 0 , 2 )	( 1 , 3 ) ( 0 , 4 )
9	( 1 , 3 ) ( 0 , 2 )	( 1 , 4 ) ( 0 , 4 )
10	( 1 , 3 ) ( 0 , 3 )	( 1 , 4 ) ( 0 , 4 )
11	( 1 , 3 ) ( 0 , 3 )	( 2 , 4 ) ( 0 , 4 )
12	( 1 , 3 ) ( 1 , 3 )	( 2 , 4 ) ( 1 , 5 )
13	( 1 , 3 ) ( 1 , 3 )	( 2 , 5 ) ( 1 , 5 )
14	( 1 , 3 ) ( 1 , 3 )	( 2 , 5 ) ( 1 , 5 )
15	( 2 , 4 ) ( 1 , 3 )	( 2 , 5 ) ( 1 , 5 )
16	( 2 , 4 ) ( 1 , 3 )	( 3 , 5 ) ( 1 , 6 )
17	( 2 , 4 ) ( 1 , 4 )	( 3 , 6 ) ( 2 , 6 )
18	( 2 , 4 ) ( 1 , 4 )	( 3 , 6 ) ( 2 , 6 )
19	( 2 , 4 ) ( 2 , 4 )	( 3 , 6 ) ( 2 , 6 )
20	( 2 , 4 ) ( 2 , 4 )	( 3 , 6 ) ( 2 , 6)

Table 5.

Proportion of trials deciding in favor of H₁, H₀, or inconclusive (also indicates continuation of the trial) when including patients treated at the MTD under different sample size requirements accrued during the expansion cohort (J = 12,25,50). The four scenarios represent trials simulated under Scheme 3 of Table 3. T₁, T₂, T₃ are defined in Table 4.

		Scenario 1			Scenario 2
Scenario 1	J	H 1	H 0	inconclusive	H 1	H 0	inconclusive
T 1	50	0.06	0.80	0.13	0.71	0.11	0.17
	25	0.06	0.68	0.26	0.55	0.10	0.34
	12	0.05	0.48	0.46	0.37	0.11	0.52
T 2	50	0.07	0.77	0.16	0.73	0.11	0.17
	25	0.08	0.62	0.30	0.60	0.09	0.31
	12	0.09	0.39	0.52	0.45	0.12	0.43
T 3	50	0.05	0.72	0.23	0.68	0.09	0.24
	25	0.04	0.49	0.47	0.49	0.05	0.45
	12	0.02	0.21	0.77	0.29	0.01	0.69
		Scenario 3			Scenario 4
	J
T 1	50	0.39	0.45	0.15	0.77	0.05	0.18
	25	0.33	0.37	0.30	0.58	0.06	0.36
	12	0.25	0.23	0.52	0.37	0.09	0.54
T 2	50	0.39	0.44	0.16	0.79	0.04	0.17
	25	0.34	0.34	0.33	0.63	0.08	0.29
	12	0.31	0.20	0.49	0.47	0.12	0.41
T 3	50	0.37	0.40	0.23	0.75	0.02	0.23
	25	0.28	0.27	0.45	0.54	0.02	0.44
	12	0.15	0.09	0.76	0.30	0.01	0.69

4 Simulation study

4.1 Operating Characteristics

In the simulation study, we assume investigators follow the 3+3 design during the dose escalation phase followed by a DEC of additional J patients. The dose expansion phase is guided by the model following the completion of the 3+3. We assume that the trial established an initial estimate of the MTD using the 3+3 design [Iasonos et al. 2008]. Additional data, such as efficacy or PK response, are obtained during the expansion phase. The DEC could be accrued under the following three schemes: Scheme 1: all patients are treated at the MTD established during the dose escalation phase (3+3). Scheme 2: after the MTD is estimated using the 3+3 algorithm, patients accrued during the expansion phase are randomized to two levels sequentially using Equation 3; d_m might change at each step, based on the estimated toxicity rates R̂(d_m) and the updated toxicity data up to that point (the point of randomization of a new patient). Scheme 3: same as scheme 2, except that the predicted probabilities of DLT are obtained using a bivariate outcome of toxicity and efficacy, simultaneously utilizing all available information from all patients. In this last set of trials we calculated the sequential tests after each patient, using diffierent forms of hypothesis testing as shown in Section 2.2. The parameters used in the simulation study are as follows:

1. The true toxicity and efficacy rates at each dose level are denoted as R_i and Q_i respectively and are shown in Table 3. Scenario 1 denotes a case where there exists a safe dose which is not efficacious and the efficacious level is not safe; in Scenario 2, d₅ is the dose which is safe and simultaneously efficacious. Scenario 3 has two levels that are safe but only one is efficacious. For Scenario 4 the models are following the true rates. and it is used as a theoretical bound of the method’ performance.

2. The skeleton values for toxicity and efficacy for the parameters α_i, β_i are given by skeleton values equal to 0.1, 0.2, 0.3, 0.4, 0.5, 0.6 for the 6 levels respectively.

3. The sample size during the 3+3 stage varies, since the trial stops at any time after observing 2 or more DLTs at a level, and after 6 patients have been treated at the level below and with at most 1/6 DLTs at the MTD. The sample size for the DEC J, varied from 12, 25, 50 when evaluating accuracy of dose recommendation and percent of patients treated. A maximum sample size of 200 is used in order to estimate the average sample number.

4. Type I and Type II errors, ϵ₁, ϵ₂ are set at 10%.

5. For the hypothesis test involved in Section 2.2, the efficacy rates that are considered too low and desirable are q₀ = 10% and q₁ = 30% respectively. The acceptable threshold for toxicity was set at s₁ = s₀ = θ = 30%. Alternatively, one can test the hypotheses H₀ : R(d_i) > s₀ = 0.3 and H₁ : R(d_i) ≤ s₁ = 0.2 so that we can reject levels with DLT rates > 0.3 while considering levels with rates ranging from 0.2-0.3 as supporting further experimentation (s₁ ≤ θ ≤ s₀). The choice of values of s₁, s₀ depend on the individual clinical scenario.

6. The uniform distribution was used for the distribution of g₁(a) and g₂(b) in the test statistics T₁, T₂ with a sensitivity analysis using Gamma distribution with diffierent parameters allowing for larger variance.

Table 3.

Proportion of trials recommending each dose level for the four scenarios for J = 50. Scheme 1: 3+3 design followed by expansion; Scheme 2: expansion is guided by CRM and randomization; Scheme 3: expansion is guided by CRM and randomization using efficacy as well as toxicity. True toxicity and efficacy rates used in the simulation study are denoted with R, Q respectively. MTD is indicated in bold.

Scenario	Levels:	d 0	d 1	d 2	d 3	d 4	d 5	d 6
1	R		0.10	0.15	0.30	0.45	0.50	0.60
	Q		0.05	0.09	0.10	0.30	0.40	0.45
	Scheme 1	0.08	0.19	0.40	0.26	0.06	0.01
	% patients		0.25	0.38	0.25	0.07	0.01	0.00
	Scheme 2			0.11	0.61	0.20	0.01
	% patients		0.10	0.18	0.45	0.20	0.03	0.00
	Scheme 3			0.12	0.61	0.18	0.01
	% patients		0.10	0.18	0.44	0.20	0.03	0.00
2	R		0.05	0.10	0.15	0.20	0.30	0.60
	Q		0.01	0.05	0.09	0.10	0.30	0.40
	Scheme 1	0.03	0.09	0.17	0.23	0.26	0.20	0.01
	% patients		0.14	0.19	0.23	0.23	0.17	0.02
	Scheme 2		0.00	0.00	0.02	0.26	0.63	0.07
	% patients		0.07	0.07	0.11	0.25	0.41	0.08
	Scheme 3		0.00	0.00	0.03	0.28	0.59	0.07
	% patients		0.07	0.07	0.11	0.26	0.40	0.08
3	R		0.05	0.1	0.15	0.27	0.33	0.60
	Q		0.01	0.05	0.09	0.10	0.30	0.40
	Scheme 1		0.10	0.17	0.36	0.20	0.13	0.02
	% patients		0.14	0.19	0.33	0.19	0.11	0.02
	Scheme 2		0.00	0.00	0.06	0.45	0.43	0.04
	% patients		0.06	0.07	0.14	0.34	0.31	0.06
	Scheme 3		0.00	0.0	0.08	0.43	0.43	0.04
	% patients		0.06	0.07	0.15	0.34	0.31	0.05
4	R		0.02	0.06	0.12	0.20	0.30	0.41
	Q		0.02	0.06	0.12	0.20	0.30	0.41
	Scheme 1		0.05	0.13	0.28	0.27	0.20	0.08
	% patients		0.09	0.15	0.27	0.24	0.17	0.07
	Scheme 2		0.00	0.00	0.01	0.20	0.61	0.18
	% patients		0.05	0.06	0.09	0.22	0.42	0.17
	Scheme 3		0.00	0.00	0.01	0.21	0.60	0.18
	% patients		0.05	0.06	0.09	0.22	0.41	0.17

Table 3 provides a summary of the dose recommendation across many simulated trials. We see that following a model based approach during the expansion phase increases the accuracy of finding the true MTD. The increase is on average 40% in absolute percentage points or 35% improvement compared to assigning all patients at the MTD found during the dose escalation phase. The increase in accuracy is apparent across many scenarios regardless of the location of the MTD. This indicates that we ought to take into account the toxicity responses from the additional patients accrued during the expansion phase, and while the efficacy responses are considered secondary in terms of dose allocation, there is no loss in accuracy by estimating efficacy rates simultaneously to the toxicity rates. We recommend updating these rates as the trial is ongoing because this approach is both ethical (since safety remains the primary endpoint) and scientifically informative (since it enables the measurement of efficacy as a secondary objective).

Table 4 shows the results from carrying out sequential probability ratio tests. Each test is calculated at the dose level where the current patient is being treated. For each one of the three tests we have summarized the percent of trials where the decision was in favor of H₁ : R(d_i) ≥ 0.30 at the MTD or at MTD plus or minus a level. The first scenario is a case where there exists a safe dose which is not efficacious, and the dose above this level is unsafe and efficacious. Table 4 shows that all tests correctly accept MTD+1 as an efficacious level, but fail to support MTD as efficacious level, given the fact that 20-24% of the trials decided in favor of H₁ when testing efficacy at MTD. Note that T₂ supports efficacy less frequently than T₁ at MTD+1 since T₂ tests simultaneously for a safe and efficacious level, and MTD+1 fails these requirements for Scenario 1. In Scenario 2, the tests correctly identify the MTD as efficacious and safe dose which is supported by the true rates while again T₂ often rejects MTD+1 based on safety compared to the other two tests. In scenario 3, the MTD falls between dose level 4 or 5 based on safety alone, whereas dose level 5 is more efficacious. Thus the tests are deciding in favor of H₁ at the MTD or/and MTD+1. The last scenario represents a case where the working models follow the true rates and the MTD is efficacious. In this scenario, 95% of trials reached a decision in favor of H₁.

Table 4.

Proportion of trials deciding in favor of H₁ when including patients treated at the MTD, MTD −1, MTD +1 for the four scenarios of Table 3 and trials under Scheme 3. T₁ is based on model based efficacy rates; T₂ is based on an acceptable region of efficacy and toxicity and T₃ is based on the observed efficacy rate. Median Sample size and interquartile range (IQR) in order to make a decision in favor of H₁ at any dose.

	Test :	MTD−1	MTD	MTD+1	Median n (IQR)
Scenario 1
	T 1	0.06	0.20	0.56	35 ( 9, 201)
	T 2	0.18	0.26	0.49	34 (11, 201)
	T 3	0.03	0.17	0.52	60 (17, 201)
Scenario 2
	T 1	0.11	0.84	0.61	17 ( 7, 40)
	T 2	0.25	0.85	0.49	16 ( 8, 36)
	T 3	0.07	0.84	0.56	23 (12, 50)
Scenario 3
	T 1	0.07	0.53	0.60	24 ( 8, 71)
	T 2	0.19	0.58	0.54	21 ( 9, 58)
	T 3	0.04	0.50	0.57	33 (13, 89)
Scenario 4
	T 1	0.43	0.95	0.64	10 (5,21)
	T 2	0.53	0.96	0.62	11 (6,19)
	T 3	0.39	0.94	0.61	15 (9,27)

The sample size required to make a decision in favor of H₁ or H₀ was calculated for each trial (denoted as ASN*). In addition, we calculated the average sample number (ASN) required to make a decision in favor of H₁ separately at each level. Figure 2 shows the distribution of ASN when the test is calculated at any level, regardless if that was the MTD. We see that depending on the scenario and whether there exists a safe and efficacious dose, the tests either terminate in favor of H₁ early as in Scenario 2 or they take longer to reach a decision for H₁ as in Scenario 1, when a level with high efficacy might not be a safe dose. The median sample size is shown in Table 4 and it is substantially smaller with T₂ as compared to the test based on the empirical rates. This supports increase in efficiency by using complete data on both toxicity and efficacy for the cases studied in this paper. Using a model based test, we need on average 20 patients to reach a decision in favor of H₁ which is consistent with current clinical practice. Additional simulations with a scenario where the efficacious dose was highly toxic (R =50%) showed that each test takes longer (larger ASN compared to the cases presented here) to reach a decision in favor of H₁ because there is little experimentation at the efficacious level due to safety concerns while the safe levels are not efficacious.

Figure 2.

Distribution of sample size required to make a decision in favor of H₁ at any level regardless if that was the MTD. Horizontal panels show sequential tests based on T₁, T₂, T₃ for the 4 scenarios respectively.

4.2 Sensitivity analysis

In order to assess whether Type I and Type II errors are controlled and how small sample sizes affect the operating characteristics, we report the decision reached by the three sequential tests when a sample is fixed at 12, 25, or 50 (Table 5) in the context of dose expansion cohorts. The number of trials in favor of H₁ in Scenario 1 is an estimate of the Type I error since the MTD is not efficacious (response rate at MTD is 10%),and we see Type I error is less than the set value of 10%. In Scenario 2 the MTD has an efficacy rate of 30%, so the number of trials in favor of H₀ is an estimate of the Type II error and again it is close to the set value of 10%. A sensitivity analysis for the choice of distribution g(b) can inform us about the influence of the choice of such a distribution. In our sensitivity analysis for the distributions used in T₁,T₂ we assumed Gamma distribution with various shape and scale parameters that result in various mean and variance values. The results show that in certain cases, using a Gamma distribution with small variance can be more informative than a Uniform distribution since the sequential test was reaching a decision early on and a higher number of trials were reaching a decision in favor of H₁ (Table 6). This indicated that the prior was informative when the variance was small (1.25) but was not informative with larger variance (variance of 4 for a and 6 for b). The relative importance of the prior depends on the sample size. Since here we are not only dealing with estimation and finding the location of the MTD but also using sequential tests to guide a decision process of whether to terminate or continue the trial, the influence of the prior matters early on in the trial. If the decision is to stop the trial early, then we will never increase N to recover from that decision. For these reasons we suggest using a non informative prior distribution such as Uniform.

Table 6.

Proportion of trials deciding in favor of H₁ when including patients treated at the MTD, MTD −1, MTD +1 for the four scenarios when using different prior distributions. T₁ is based on model based efficacy rates; T₂ is based on an acceptable region of efficacy and toxicity. Median Sample size (ASN) to make a decision in favor of H₁ at any dose. G : Gamma with parameters (scale,shape).

g(b) in T1					g2(b), g1(a) in T2
Scenario 1	MTD−1	MTD	MTD+1	ASN	Scenario 1	MTD−1	MTD	MTD+1	ASN
Uniform	0.06	0.20	0.56	35	Uniform	0.18	0.26	0.49	34
G(1.5,2)	0.11	0.26	0.59	14	G(1.5,2);G(1,2)	0.17	0.26	0.49	34
G(2,1)	0.15	0.31	0.63	12	G(2,1);G(2,1)	0.17	0.25	0.48	36
G(5, 0.5)	0.49	0.74	0.78	4	G(5, 0.5);G(4,0.5)	0.20	0.29	0.50	30
Scenario 2					Scenario 2
Uniform	0.11	0.84	0.61	17	Uniform	0.25	0.85	0.49	16
G(1.5,2)	0.15	0.84	0.61	12	G(1.5,2);G(1,2)	0.23	0.85	0.48	16
G(2,1)	0.19	0.85	0.61	11	G(2,1);G(2,1)	0.22	0.84	0.48	16
G(5, 0.5)	0.50	0.94	0.72	4	G(5, 0.5);G(4,0.5)	0.26	0.86	0.49	16
Scenario 3					Scenario 3
Uniform	0.07	0.53	0.60	24	Uniform	0.19	0.58	0.54	21
G(1.5,2)	0.10	0.54	0.61	15	G(1.5,2);G(1,2)	0.17	0.58	0.54	21
G(2,1)	0.14	0.58	0.62	13	G(2,1);G(2,1)	0.17	0.57	0.53	22
G(5, 0.5)	0.45	0.79	0.72	4	G(5, 0.5);G(4,0.5)	0.20	0.59	0.54	20
Scenario 4					Scenario 4
Uniform	0.43	0.95	0.64	10	Uniform	0.53	0.96	0.62	11
G(1.5,2)	0.44	0.94	0.66	6	G(1.5,2);G(1,2)	0.52	0.96	0.62	11
G(2,1)	0.49	0.95	0.64	6	G(2,1);G(2,1)	0.52	0.96	0.61	11
G(5, 0.5)	0.69	0.99	0.70	3	G(5, 0.5);G(4,1/2)	0.54	0.97	0.62	11

We assessed the robustness of our proposed approach to the assumption of conditional independence by running additional simulations under various values of correlation parameter(Appendix C of Supplementary Materials). Our results back up the findings of Cunanan and Koopmeiners (2014) who found that a simple model that assumes independence performs just as well as more complex models that model the correlation parameters explicitly. We found that ignoring the dependence structure, even when strong (odds ratio =4), has a negligible impact in terms of the decisions reached by the proposed tests, or model parameter estimation (Supplemental Table 2).

5 Conclusion

In this paper, we outline a methodology to adequately design and monitor DEC in Phase I trials in oncology. This methodology provides initial estimates of efficacy activity, as this is one of the goals of DEC, and aids in providing a go/no go decision rule at the current dose. It is meant to serve as a guide to help clinical investigators decide whether the dose with the best chance for efficacy activity should be selected or whether more patients need to be treated and at which level, versus abandonment of the investigational drug altogether. Given that there is still considerable uncertainty in the selection of the MTD after the dose escalation part of the phase I trial, we propose experimentation at more than a single level during the expansion phase in order to estimate efficacy at more than one dose level. This dose exploration during the expansion phase will provide support to the decision of whether a higher or lower dose is needed with regards to efficacy. The secondary efficacy measure can capture evidence of biomarker expression or tumor absorption, which allows the dose expansion to focus experimentation in this targeted population and help select the appropriate patient population for future trials. Finally, an important feature of the proposed approach is that it does not require toxicity and efficacy endpoints to be obtained at the same time. The sequential equations can be updated at any point, as data become available, making this approach logistically simple to implement.

Sequential tests are efficient in terms of the sample size required to test for a specific hypothesis [Wald 1947, Cheung 2007] and they have been used extensively in other contexts such as randomized Phase II or III studies with multiple looks. For typical Phase II studies with the size of treatment effect comparable to the ones studied in this paper, on average 35 patients are needed (depending on error rates). In the simulation study we presented, when there exists a safe and efficacious dose, on average 16-24 patients are required for the dose expansion phase alone to terminate the study. In certain situations, depending on several factors such as the location of the MTD, the steepness of the dose response curve, and the effect size, sample size savings can be significant when compared to fixed sample tests. Addressing the combined goal of estimating the RP2D and the efficacy at this dose via a single dose finding study plus DEC, may lead to worthwhile savings when compared to two studies, one that establishes the MTD and a more standard Phase II study with a fixed sample test.

In this paper, we followed a 3+3 design prior to adding a DEC. Several authors have shown that model based designs are more accurate in finding the MTD and treat most patients at or around the MTD [Iasonos et al. 2008, Garrett-Mayer 2006, Onar et al. 2009]. For these reasons, it would be preferable to use a model based design from the beginning of the trial. We study this in a related paper showing that the DEC can be incorporated more readily into the trial design and much less is required in the way of further methodology [Iasonos and O'Quigley 2015]. However, the choice of which design to use is up to clinical investigators. Regardless of how we obtain the data, SPRT allows us to select a dose based on promising activity, since it allows us to stop at any point for futility, stop early if there is a strong efficacy signal, or suggest that further experimentation is needed if the results are inconclusive. Such information is crucial before making a decision on whether to embark on a larger, possibly randomized, Phase II or even a Phase III study.