Beyond the classic thermoneutral zone

Abstract

The thermoneutral zone is defined as the range of ambient temperatures where the body can maintain its core temperature solely through regulating dry heat loss, i.e., skin blood flow. A living body can only maintain its core temperature when heat production and heat loss are balanced. That means that heat transport from body core to skin must equal heat transport from skin to the environment. This study focuses on what combinations of core and skin temperature satisfy the biophysical requirements of being in the thermoneutral zone for humans. Moreover, consequences are considered of changes in insulation and adding restrictions such as thermal comfort (i.e. driver for thermal behavior). A biophysical model was developed that calculates heat transport within a body, taking into account metabolic heat production, tissue insulation, and heat distribution by blood flow and equates that to heat loss to the environment, considering skin temperature, ambient temperature and other physical parameters. The biophysical analysis shows that the steady-state ambient temperature range associated with the thermoneutral zone does not guarantee that the body is in thermal balance at basal metabolic rate per se. Instead, depending on the combination of core temperature, mean skin temperature and ambient temperature, the body may require significant increases in heat production or heat loss to maintain stable core temperature. Therefore, the definition of the thermoneutral zone might need to be reformulated. Furthermore, after adding restrictions on skin temperature for thermal comfort, the ambient temperature range associated with thermal comfort is smaller than the thermoneutral zone. This, assuming animals seek thermal comfort, suggests that thermal behavior may be initiated already before the boundaries of the thermoneutral zone are reached.

Introduction

The thermoneutral zone (TNZ) is defined as: ‘the range of ambient temperature at which temperature regulation is achieved only by control of sensible (dry) heat loss, i.e. without regulatory changes in metabolic heat production or evaporative heat loss.’¹ One remarkable feature of the classical TNZ definition is that it only considers autonomic thermoregulatory mechanisms, and omits the influence of thermal behavior. Nevertheless, thermal behavior is considered as the major influencing factor of body temperature homeostasis,² and is driven by thermal comfort.³ The thermal comfort zone (TCZ) is defined in terms of perception and qualifies as the state of mind that expresses satisfaction with the thermal environment.⁴ Furthermore the TCZ is suggested to relate to positive anticipations of the current thermal environment. In other words, thermal discomfort (i.e., negative anticipation) drives a human being to counteract the thermal environment accordingly.

According to their definitions the TNZ and the TCZ are not directly related to each other. However, physiologically, both zones share a common source of information, namely skin and core temperature.⁵ Furthermore, functionally, they may share a common goal, that is to preserve body temperature.⁶ A living body can only maintain a stable core temperature when heat production and heat loss are balanced. That means that heat transport from body core to the skin must equal heat transport from skin to the environment.

This study investigates what combinations of body core, skin and ambient temperature satisfy the biophysical requirements of being in the TNZ for humans. Nevertheless concepts apply to other animals as well. Moreover, we study the consequence of changes in insulation and adding restrictions such as thermal comfort (i.e., derive TCZ). By comparing the ambient temperature ranges associated with the TNZ and the TCZ, the aim is to better understand the link between the two, and discuss practical implications with respect to metabolic research and the built environment.

Methods

This section describes the biophysical model that is used to analyze what combinations of body core temperature (T_c), mean skin temperature (T_s) and ambient temperature (T_a) satisfy the requirements of thermal balance. The section is structured as follows: first the effect size of autonomic and behavioral thermoregulatory mechanisms are described, second the biophysical model is introduced, third the ranges of biological and physical model parameters for 2 scenarios are given, fourthly the equations for T_s and T_c are given. Fifthly, 4 categories are defined that indicate what thermoregulatory action is required to maintain thermal balance. Sixthly, the derivation of T_a ranges associated with the TNZ and TCZ is described.

Thermoregulation within the TNZ: effect size

With respect to mechanisms of thermoregulation within the TNZ, we only consider mechanisms that influence insulation, and do not result in changes in metabolic heat production. With this restriction, the body is able to change total body tissue insulation by changes in blood flow from 0.124 m²°C/W (i.e., maximal vasoconstriction) to 0.031 m²°C/W (i.e., maximal vasodilation) respectively.⁷ Together, through behavioral regulation clothing insulation can be changed from 0 m²°C/W (i.e., nude, 0 Clo) to 0.92 m²°C/W (i.e., arctic clothing, 6 Clo), the airflow and thereby also insulation provided by air can be modified (e.g., draft or breeze) or T_a can be adjusted (e.g., thermostat in building), see Figure 1 for a schematic overview.

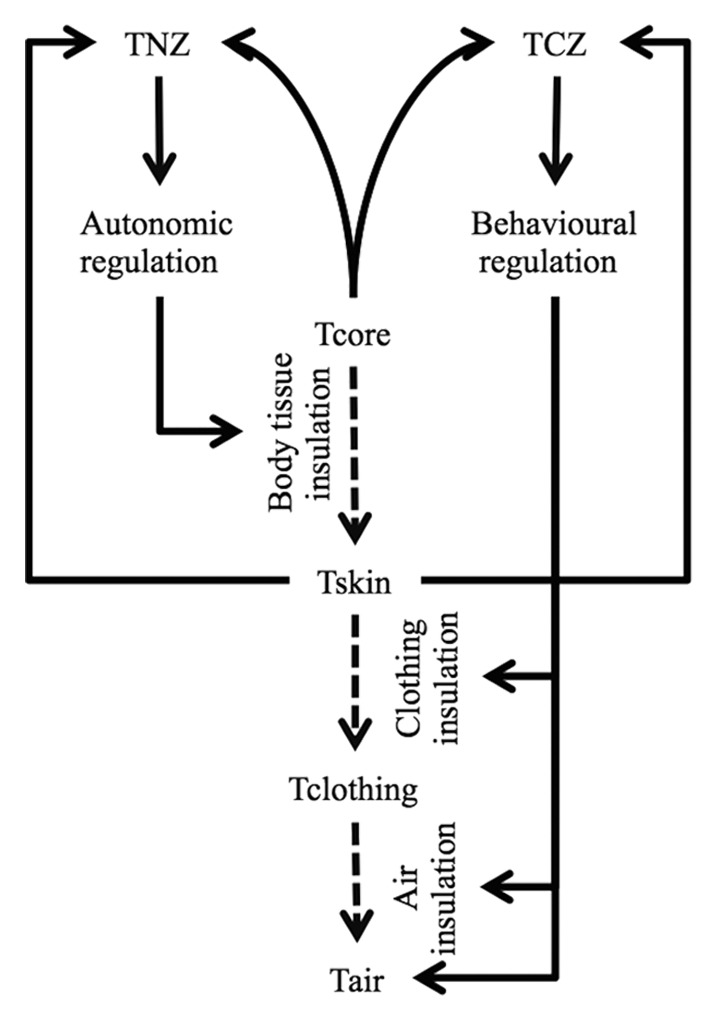
Figure 1. schematic overview of autonomic and behavioral control of thermal insulation. Solid arrows denote relation and/or control and dashed arrows denote heat flow.

Biophysical thermal network model

A biophysical thermal network model was used to calculate T_c and T_s, taking into account metabolic heat production (M), dynamic body tissue insulation (I_body), static clothing insulation (I_cl), static air insulation (I_air) and evaporative heat loss, see Figure 2.

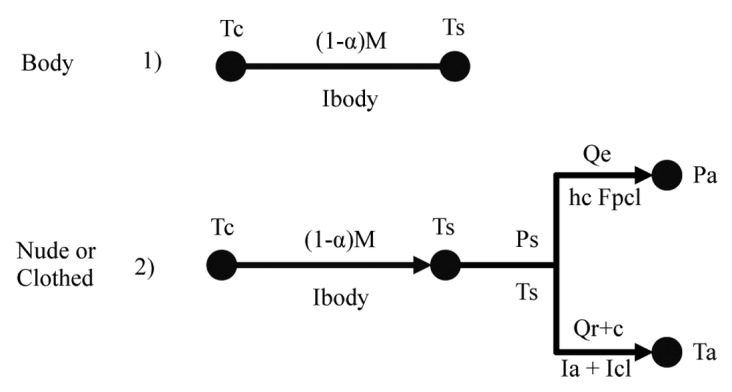
Figure 2. Thermal network to describe heat balance in the thermoneutral zone. Tc: core temperature, T_s: mean skin temperature, T_a: ambient temperature, (1−α)M: metabolic rate corrected for respiratory heat loss, Q_r+c: combined radiative and convective heat loss, Ps: saturated vapor pressure at skin surface, P_a: vapor pressure of the air, Q_e: evaporative heat loss, h_c: convective heat loss coefficient, Fpcl: clothing evaporative permeability coefficient, I_body: body insulation, I_cl: clothing insulation, I_a: air insulation.

1. With the first model (Fig. 2. Body) the range of T_s that satisfy a steady-state thermoneutral condition is calculated for a range of T_c around T_c = 37 °C, a range of M corrected for respiratory heat loss (see Supplemental Material, A2), and a range of (I_body) associated with maximal vasoconstriction and maximal vasodilation. Specific ranges are defined below.

2. With the second model (Fig. 2. Nude or Clothed) steady-state T_c is calculated over a range of ambient temperatures 10°C ≤ T_a ≤ 40 °C and skin temperatures 20 °C ≤ T_s ≤ 40 °C, given low wind speed (air velocity = 0.1 m/s) air insulation, in nude and in clothed condition. I_body is calculated as a function of T_s.

Physiological insulation, anthropometry and metabolic rate

Total body insulation is defined by a passive part: tissue insulation, and an active part: regulation of skin blood flow. In case of total skin vasoconstriction, tissue insulation provided by muscle and fat is about I_body,min = 0.124 m²°C/W for a man with 4 mm subcutaneous fat.⁸ In case of full skin vasodilation, passive tissue insulation is by-passed and reduces I_body to about I_body,min = 0.031 m²°C/W .⁷ Thus, I_body is inversely related to blood flow. Several experiments show a linear relation between T_s, skin blood flow and I_body for a resting man.^7,9 Therefore, we calculate body insulation as a linear function of skin temperature (see E1). The modeled T_s of I_body,max results from the minimal skin temperature (T_s,min) that satisfies steady-state thermoneutral condition with T_c = 36 °C. Likewise, modeled T_s of I_body,min results from the maximal skin temperature T_s,max that satisfies steady-state thermoneutral condition with T_c = 38 °C. Thus the equation for I_body is given by:

$I_{body}=I_{body,\max }+\frac{\left(I_{body,\max }-I_{body,\min }\right)}{\left(T_{s,\min }-T_{s,\max }\right)}\left(T_s-T_{s,\min }\right)$(E1)

Where T_s,min ≤ T_s ≤ T_s,max.

Heat loss from skin to environment scales linearly with body surface area (A). For this study, body surface area is set to correspond to an average man A = 1.86 m².¹⁰

The minimum amount of heat production to sustain life is referred to as the basal metabolic rate (BMR). In literature, BMR for an average man is reported as BMR ≈ 86 W or BMR ≈ 46 W/m².⁴ BMR is significantly related to age, gender, length and height.¹¹ To account for these influences, we consider a 5% range 82 W ≤ BMR ≤ 90 W in this paper. BMR is often measured in physiological laboratory experiments. During such experiments, volunteers are quasi-nude and in supine position. Nevertheless, under daily living conditions, e.g., in office conditions, humans operate seldom in this state. Changes in posture, arousal and activity increase M significantly. For a sitting male, performing office work M ≈ 112W or M ≈ 60 W/m². Similar to the BMR, a range of M is considered in this paper 106 W ≤ M ≤ 118 W.

To model both laboratory and office conditions, 2 scenarios are considered:

1) Classical TNZ: a nude person in supine position at BMR and

2) Functional TNZ: a clothed person in sitting condition at M associated with office work. The insulation provided by clothing is I_cl = 1Clo = 0.155 W/m²°C.

Here, the classical scenario refers to the TNZ as defined in the glossary of terms for thermal physiology;¹ the functional scenario is analogous to the definition of ‘TNZ classical’ with the difference that clothing is worn and M > BMR.

Equations for minimum and maximum T_s as a function of T_c, M, I_body and A

Heat balance between M and heat transport from core to skin minus respiratory heat loss is satisfied when $\left(1-\alpha \right)M=A\left(\frac{\left(T_c-T_s\right)}{I_{body}}\right)$. Here, α = 0.08 is the fraction of M that is accounted for respiratory heat loss (see Supplemental Material, A2 for more details).¹²

Minimum T_s for which M and body heat transport is balanced corresponds to the state where T_c is minimal and M and I_body are maximal and vice versa for maximal T_s. Hence the feasible steady-state T_s range is defined as: $T_{s,\min }=T_{c,\min }-\left(1-\alpha \right)M_{\max }\frac{I_{body,\max }}{A}\le T_s\le T_{c,\max }-\left(1-\alpha \right)M_{\min }\frac{I_{body,\min }}{A}=T_{s,\max }$ (E2).

Equation of T_c as a function of T_s and other heat transfer parameters

The equation for T_c below follows the scheme where M corrected for respiratory heat loss equals heat loss by radiation and convection (Q_r+c) plus evaporative heat loss (Q_e). For brevity, only the final equation for T_c is given in this section, see Supplemental Material for full derivation,

$T_c=T_s+\frac{I_{body}}{\left(1-\alpha \right)}\left(\frac{\left(T_s-T_a\right)}{I_{cl}+I_{air}}+\frac{Q_e}{A}\right)$(E3).

Here T_a is ambient temperature in °C, I_air, is air insulation in m²°C/W, I_body refers to body insulation in m²°C/W, I_cl, is clothing insulation in m²°C/W and Q_e/A is evaporative heat loss in W/m².

Heat balance categories

Solutions for which T_c and T_s remain in steady-state are calculated for 10 °C ≤ T_a ≤ 40 °C, and skin temperature 20 °C ≤ T_s ≤ 40 °C. Constellations of T_a and T_s (solutions) that do not satisfy (36 °C ≤ T_c ≤ 38 °C) are filtered out. Until now, no restrictions on heat flow, other than (1−α)M = Q_r+c + Q_e, are defined; only temperatures are calculated that satisfy heat flow balance with the environment. Categories of body heat deficit, body heat surplus or body heat balance are defined by calculating the actual heat flow for each of the solutions and comparing that to the metabolic rate corrected for respiratory heat loss. The 4 categories are defined as follows:

1) TNZ body: heat loss is balanced relative to metabolic rate:

(1−α)M_min ≤ Q_r+c + Q_e ≤ (1−α)M_max ,

2) SWEAT: there is a heat surplus and evaporation is required to maintain thermal balance: Q_r+c + Q_e ≤ (1−α)M_min,

3) NST: there is a heat deficit and cold induced thermogenesis by non-shivering (M_nst = 0.12M) is sufficient to maintain thermal balance: 
(1−α)M_max ≤ Q_r+c + Q_e ≤ (1−α)(M_max + M_nst),¹³

4) SH⁺NST: there is a heat deficit and cold induced thermogenesis by shivering and non-shivering is required to maintain thermal balance: 
(1−α)(M_max + M_nst) ≤ Q_r+c + Q_e ≤ (M_sh + M_nst),

here maximal heat production through shivering and non-shivering is capped at M_sh + M_nst = 372W, which is the empirical maximum cold-induced heat production in humans.¹⁴

Finding T_a associated with TNZ and TCZ

This section describes how the set of solutions described above (i.e., combinations of T_a and T_s) are further filtered to define the T_a range for the TNZ and the TCZ.

For the TNZ, the T_a range is defined by the subset of solutions for which corresponding T_s satisfy that body heat transport equals M, i.e., T_s,min ≤ T_s ≤ T_s,max.

To find the TCZ the same method is applied, however, the values for T_s,min and T_s,max are different. In this study the main comfortable skin temperature range used is 31.5 °C ≤ T_s ≤ 35.5 °C as reported by Gagge et al.¹⁵ Moreover, a more conservative range 32.8 °C ≤ T_s ≤ 33.8 °C as reported for man in supine position by Weiwei et al. is also considered.¹⁶

Results

The results section is structured as follows: first the TNZ is presented for the classical condition (i.e., not clothed and at basal metabolic rate) and the functional condition (i.e., clothed in business suit and at office work metabolic rate), second the TCZ is presented for both conditions.

Classical TNZ: nude and basal metabolic rate

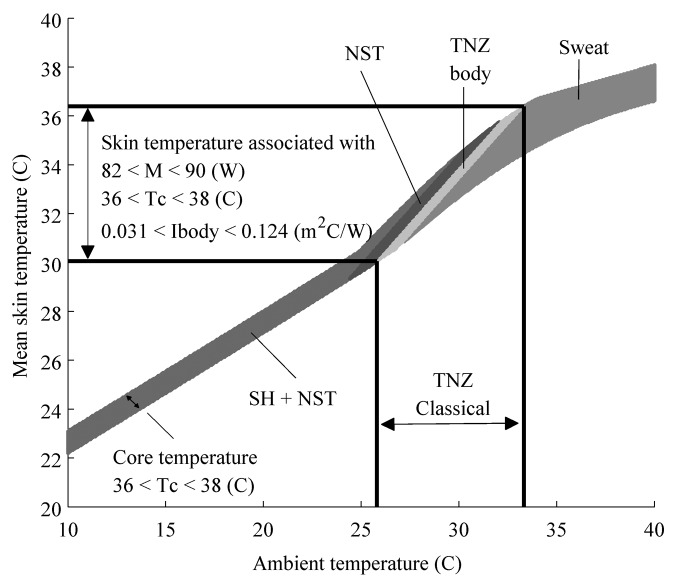
The steady-state T_a range for the TNZ for a person in a nude condition and heat production at BMR as calculated by the model are shown in Figure 3. Each band in Figure 3 depicts for a given T_a the range of T_s in which the equation constraints are satisfied for each category, e.g., ‘TNZ body’, ‘SWEAT’, ‘NST’, ‘SH⁺NST’. The band labeled ‘TNZ body’ depicts that thermal balance is satisfied and heat loss equals BMR. Thus, ‘TNZ body’ indicates for which T_s the ‘TNZ classical’ is supported from the perspective of human body internal heat transport.

Figure 3. The classical thermoneutral zone (denoted by ‘classical TNZ’), is defined as the range of ambient temperature at which temperature regulation is achieved only by control of sensible (dry) heat loss, i.e., without regulatory changes in metabolic heat production or evaporative heat loss. Each band depicts for a given ambient temperature the range of mean skin temperature in which the equation constraints are satisfied for each category, e.g., ‘TNZ body’, ‘SWEAT’, ‘NST’, ‘SH⁺NST’. The light gray area labeled TNZ body depicts solutions that satisfy that internal body heat transport equals external heat loss and core temperature ranges between 36 °C ≤ T_c ≤ 38 °C. In other words, TNZ body indicates where the classical thermoneutral zone is supported from the perspective of the human body. NST: solutions for which steady-state heat loss is between 83 W ≤ Q ≤ 88 W. The body can achieve thermal balance by non-shivering thermogenesis. Shiver+NST: solutions for which steady-state heat loss is between 88 W ≤ Q ≤ 372 W. The body can achieve thermal balance by shivering thermogenesis. SWEAT: solutions for which steady-state heat loss is Q ≤ 83 W. The body can achieve thermal balance by increased evaporation.

Steady-state skin temperature ranges between 30.5 °C ≤ T_s ≤ 36.8 °C. Where T_s = 30.5 °C corresponds to T_c = 36 °C and I_body,max = 0.124 m²°C/W and M_min = 82 W. Vice versa T_s = 36.8 °C corresponds to T_c = 38 °C, I_body,min = 0.031 m²°C/W and M_max = 90 W. Consequently, the slope of body insulation vs. skin temperature is −0.015 m²/W (used in Equation 1).

The area labeled ‘SH+NST’ is narrower than the area labeled ‘SWEAT.’ This is explained by body insulation. In case of ‘SH+NST’ the body is at maximal insulation. This means the body can vary internal heat transport up to 30W, whereas in case of ‘SWEAT’ the body is at maximal conduction, in this case the body internal heat transport can vary up to 120 W. In between maximal vasoconstriction and maximal vasodilation the body gradually changes from an insulator to a conductor, and consequently, for each ambient temperature there is a wider range of skin temperatures that satisfy the steady-state solutions.

It is important to note that the steady-state ambient temperature range associated with the classical TNZ does not guarantee that the body is in thermal balance at basal metabolic rate per se. Instead, depending on the combination of T_s and T_a, the body may require significant increases in heat production or heat loss to maintain core temperature stable within the range 36 °C ≤ T_c ≤ 38 °C (see ‘Sweat’, ‘NST’ and ‘SH⁺NST’ areas within the ‘TNZ classical’ range in Fig. 3) or even will not be able to keep the body in thermal balance (see white region inside ‘TNZ classical’ range in Fig. 3). For example, if skin temperature is T_s = 32°C, the body can remain in thermal balance when 26.8 °C ≤ T_a ≤ 28.9 °C, shivering is required for 26.8 °C ≤ T_a ≤ 27.3 °C, NST is sufficient for 27.3 °C ≤ T_a ≤ 27.9 °C and sweating is required for 28.5 °C ≤ T_a ≤ 28.9 °C. Only if the ambient temperatures range 27.9 °C ≤ T_a ≤ 28.5 °C the body can be in thermoneutral balance for 36 °C ≤ T_c ≤ 38 °C.

Functional TNZ: clothed and performing office work

Relative to the nude case, clothing insulation and increased M shift the TNZ to lower T_a and cause the solution areas to be wider. That is, for each T_a in ‘TNZ functional’ there is a wider range of T_s for which the body can support required heat transport than in ‘TNZ classical’.

The TNZ for a clothed person is (14.8 °C ≤ T_a ≤ 24.5 °C), see Figure 4. The skin temperature ranges between (28.8 °C ≤ T_s ≤ 36.4 °C). The slope of body insulation vs. skin temperature is −0.012 m²/W (used in Equation 1). Core temperature and body insulation ranges are the same as in the laboratory case, however M_min = 106 W and M_max = 118 W and corresponds to the metabolic rate of a sedentary man performing office work.

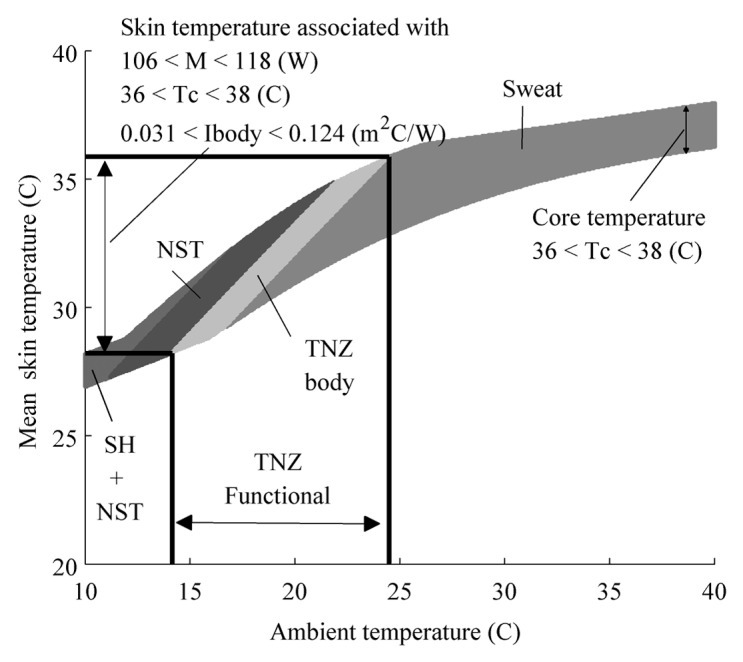
Figure 4. The functional thermoneutral zone is denoted by ‘functional TNZ’ for a person dressed in a business suit and heat production associated with light office work. The definition of ‘TNZ functional’ is analogous to the definition of ‘TNZ classical’ with the difference that the metabolic heat production is greater than the basal metabolic rate. Each band depicts for a given ambient temperature the range of mean skin temperature in which the equation constraints are satisfied for each category, e.g., ‘TNZ body’, ‘SWEAT’, ‘NST’, ‘SH⁺NST’. The light gray area labeled TNZ body depicts solutions that satisfy that internal body heat transport equals external heat loss and core temperature ranges between 36 °C ≤ T_c ≤ 38 °C. In other words, TNZ body indicates where the functional TNZ is supported from the perspective of the human body. NST: solutions for which steady-state heat loss is between 107 W ≤ Q ≤ 118 W. The body can achieve thermal balance by non-shivering thermogenesis. Shiver + NST: solutions for which steady-state heat loss is between 118 W ≤ Q ≤ 372 W. The body can achieve thermal balance by shivering thermogenesis. SWEAT: solutions for which steady-state heat loss is Q ≤ 98 W. The body can achieve thermal balance by increased evaporation.

TCZ: nude and basal metabolic rate

Next we narrow the band of thermoneutral skin temperatures from 30.5°C ≤ T_s ≤ 36.8 °C to the comfortable skin temperature range as reported by Gagge et al. (31.5 °C ≤ T_s ≤ 35.5 °C). This narrows the ambient temperature range of the TNZ: 25.9 °C ≤ T_a ≤ 33.3 °C to the TCZ: 27.5 °C ≤ T_a ≤ 32.3 °C, see Figure 5. Hence the laboratory steady-state TCZ is narrower than the steady-state thermoneutral zone (∆T_a,tnz = 6.9 °C vs. ∆T_a,tcz = 4.8°C). Constraining the comfortable skin temperature range even further to a conservative 32.8 °C ≤ T_s ≤ 33.8 °C as reported by WeiWei et al., the conservative comfortable ambient temperature range is restricted to 29.0 °C ≤ T_a ≤ 30.4 °C.

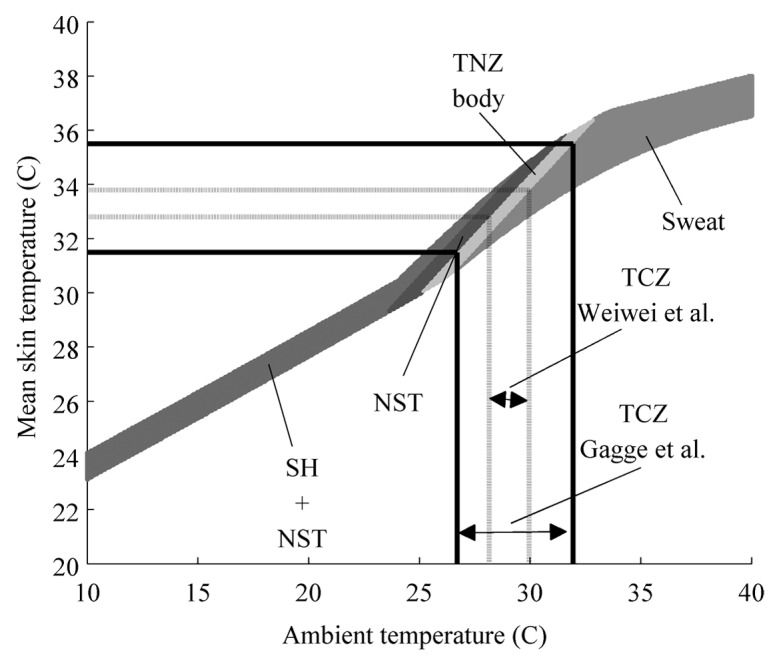
Figure 5. Steady-state ambient temperature ranges of the thermal comfort zone for a nude person. Each band depicts for a given ambient temperature the range of mean skin temperature in which the equation constraints are satisfied for each category, e.g., ‘TNZ body’, ‘SWEAT’, ‘NST’, ‘SH⁺NST’. The light gray area labeled ‘TNZ body’ depicts solutions that satisfy that internal body heat transport equals external heat loss and core temperature ranges between 36 °C ≤ T_c ≤ 38 °C. The Solid lines indicate comfortable mean skin temperature is as reported by Gagge et al.¹⁵ The dashed lines indicate a more conservative range of comfortable mean skin temperature range as reported by Weiwei et al.¹⁶

Interestingly, even the conservative ambient thermal comfort range includes solutions where the body would need to either produce or lose more heat to maintain thermal balance, see Figure 5 areas ‘NST’ and ‘Sweat’ within the dashed lines.

TCZ: clothed and at resting metabolic rate

As with the laboratory case, the comfortable mean skin temperature range 31.5 °C ≤ T_s ≤ 35.5 °C narrows the ambient temperature range from TNZ_clothed: 14.5 °C ≤ T_a ≤ 24.5°C to TCZ_clothed: 17.5 °C ≤ T_a ≤ 24.0 °C, see Figure 6. Hence the laboratory steady-state thermal comfort zone is narrower than the steady-state thermoneutral zone (∆T_a,tnz = 9.7 °C vs. ∆T_a,tcz = 6.5 °C). For the conservative comfortable mean skin temperature range (32.8 °C ≤ T_s ≤ 33.8 °C), the conservative comfortable ambient temperature range is narrowed down to 19.5 °C ≤ T_a ≤ 21.9 °C.

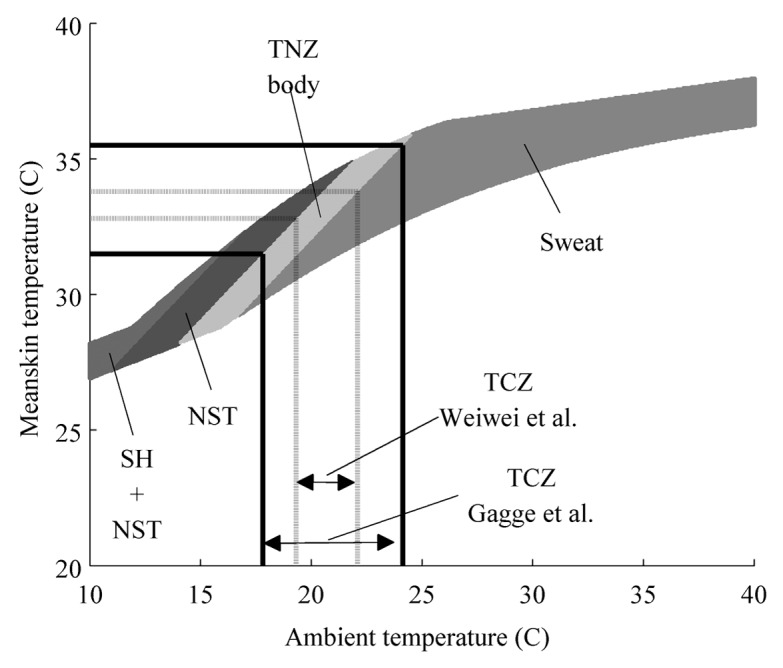
Figure 6. Steady-state ambient temperature range of the thermal comfort zone for a person dressed in a business suit and heat production at resting metabolic rate. Each band depicts for a given ambient temperature the range of mean skin temperature in which the equation constraints are satisfied for each category, e.g., ‘TNZ body’, ‘SWEAT’, ‘NST’, ‘SH⁺NST’. The light gray area labeled TNZ body depicts solutions that satisfy that internal body heat transport equals external heat loss and core temperature ranges between 36 °C ≤ T_c ≤ 38 °C. Comfortable mean skin temperature is as reported by Gagge et al.¹⁵ The dashed lines indicate a more conservative range of comfortable mean skin temperature range as reported by Weiwei et al.¹⁶

Discussion

This study describes what constellations of T_c, T_s, T_a satisfy the biophysical requirements of being in the thermoneutral zone for steady-state conditions. Furthermore, by constraining T_s to a temperature range associated with thermal comfort the thermal comfort zone is derived.

Toward a more accurate definition of the TNZ

The biophysical analysis in this study shows that depending on T_s, the classical definition of the TNZ does not guarantee at all that the body is indeed in a thermoneutral state. As can be seen in Figure 3, only the light gray area denoted as ‘TNZ body’ supports a thermoneutral state. For instance, in the nude condition, when ambient temperature is T_a = 30 °C, thermoneutral mean skin temperature is bound to 33.4 °C ≤ T_s ≤ 33.8 °C. However, body processes other than temperature regulation (e.g., blood pressure regulation, circadian rhythm or disease) may influence skin temperature as well.¹⁷ If T_s exceeds the predefined bounds, increased heat production (in case of higher T_s) or evaporation (in case of lower T_s) is required to maintain heat loss balanced relative to the metabolic rate. In determining the thermoneutral temperature ranges for rats the importance of skin temperature is already taken into account.¹⁸ Therefore, the current definition of the TNZ might require a revision. According to the authors a more accurate definition of the thermoneutral zone would be: ‘the combinations of ambient temperature and mean skin temperature for a given core temperature at which temperature regulation is achieved only by control of sensible (dry) heat loss, i.e. without regulatory changes in metabolic heat production or evaporative heat loss’. This subtle difference has a significant impact on the design of metabolic studies that require a thermoneutral condition, since controlling T_a alone is not sufficient.

The TNZ and experiments

The first study that describes the TNZ in air and in humans is by Hardy and Dubois.¹⁹ They report a lower critical ambient temperature T_a,H&D ≈ 28.5 °C and corresponding skin temperature T_S,H&D = 33.5 °C. At first glance, these values are considerably different than reported in this study (T_a = 26.4 °C and T_s = 30.5 °C). However, Hardy and Dubois did not define where they measured skin temperature and their volunteers also had a lower M ≈ 75W and lower I_body,max ≈ 0.093 m²°C/W. Using these averaged parameters the biophysical model finds for the lower bound T_a = 29.2 °C and T_s = 32.5 °C, which is more in line with the experimental findings. The example above stresses the importance of the M and the capacity of the body to change I_body in relation to the TNZ. Notably, if M increases due to normal behavioral activity, the neutral ambient temperature range is considerably lowered compared with the resting state. This is especially relevant in housing of mice and small rodents for which the housing temperature is crucial to mimic the thermal conditions of humans.²⁰

Thermal comfort and indoor environments

The relation between the TNZ and TCZ is based on mean skin temperature ranges associated with thermal comfort. Two ranges are considered: a relatively wide range as reported by Gagge et al.,¹⁵ and a more conservative, relatively narrow range as reported by WeiWei et al.¹⁶ Both skin temperature ranges associated with thermal comfort are narrower than the skin temperature range associated with the TNZ. Consequently, the derived T_a range of the TCZ is narrower than the thermoneutral zone (compare Figs. 3 and  5). In this study mean skin temperature was considered in relation to thermal comfort in a uniform and steady-state environment. However, several studies show the importance of distal skin temperatures in relation to thermal comfort in non-uniform and transient environments.^21,22 Analysis of non-uniform and transient environments is outside the scope of this study, however, this may require attention in a future study. Likewise, T_c is known to affect thermal comfort as well.^5,23 For instance, relatively low core temperature (T_c = 36 °C), is shown to require relatively high mean skin temperature (T_s ≈ 35 °C) to maintain thermal comfort. The model in this paper does not impose that extra restriction. Adding the restriction could possibly lead to further narrowing of the TCZ.

As thermal comfort is considered as the major driver for thermal behavior,³ results of this study suggest that thermal behavior is likely to be initiated before the bounds of the TNZ are reached. Putting this in perspective of thermal discomfort being the negative anticipation of the thermal environment there is a benefit to preserve the individual being by counteracting a potentially hazardous environment before any harm is done. Nevertheless, as a result of acclimatization (e.g., regular exposure to a thermal challenge), the body may learn that it is able to cope with that environment without harm, and as such, recognize the respective thermal environment as relatively comfortable. Indeed, an acclimation study from our laboratory shows that already after 10 d of regular exposure to a discomfortable cold environment and outside the thermoneutral zone, thermal comfort increases from ‘uncomfortable’ to ‘just comfortable’.²⁴ Thus, the TCZ may be more flexible than the TNZ and, after acclimation, may be extended outside the TNZ.²⁵

Current indoor thermal environment design for thermal comfort is primarily based on PMV (Predicted Mean Vote) criteria, calculated by the PMV/PPD model developed by Fanger.²⁶ The PMV is expressed on a 7-point Thermal Sensation Scale ranging from cold (−3) to hot (+3). This vote can be linked to thermal comfort through the PPD, i.e., the percentage of people who will be dissatisfied with the thermal environment. The PMV/PPD model incorporates clothing, metabolic heat production and heat loss for a person at comfortable skin temperature. This is comparable to the current study approach, except that this study includes the variable thermal insulation of the body itself. For clothed man (1Clo) performing office work (112 W), as in the functional case covered in this study, Fanger assumes as mean skin temperature T_S,F = 34.7 °C and predicts the comfortable ambient temperature range (v_air = 0.1 m/s) between 21.5 °C ≤ T_a,F ≤ 25.1 °C, where ǀPMVǀ ≤ 0.5 . Using the same value for mean skin temperature the biophysical model returns 21.7 °C ≤ T_a ≤ 23.1 °C, which is comparable for the lower part, yet the upper limit of the PMV model is 2 °C higher than the upper limit of our biophysical model. This suggests that humans remain in thermal comfort even while limited increases in evaporation through sweating are required to maintain a stable body temperature.

Although the PMV/PPD model is designed for static thermal environments only, experiments show that the PMV/PPD model can also be applied during small thermal transients.⁴ This can be explained with the physiological aspect of the model described in this paper, that is during a small thermal transient the body may adjust body insulation or skin temperature and remain in the ‘TNZ body’ area (see Fig. 6), and thus does not require increased evaporation, metabolic heat production or any form of thermal behavior in order to preserve body temperature. However, perhaps more interesting, even within the T_a and T_s ranges associated with thermal comfort areas marked as ‘NST’ and ‘SWEAT’ are found. This suggests that a significant increase in metabolic heat production may be possible without losing thermal comfort, which in turn may be beneficial to prevent or counteract metabolic diseases such as obesity and diabetes.

Considerations and limitations

Several model parameters in this biophysical model study were chosen to reflect a human in a resting condition. In this section consequences and limitations of these model choices are considered. Furthermore, it should be noted that although the model parameter values are retrieved from empirical studies, the exercise performed in this manuscript is not an in vivo experiment and thus requires an independent study to validate the finds, both for the TNZ and the TCZ.

First, on physiological parameters, the M was chosen as BMR and that during daily office work, which is slightly higher than the BMR. Increased activity would significantly increase M. As a result the TNZ would become wider (see equation E2) and shift to cooler T_a. Furthermore, values for I_body were obtained from studies on healthy lean male subjects; in case of obesity it is reasonable to assume higher body tissue insulation. Besides M and I_body, body core temperature range used (36 °C ≤ T_c ≤ 38 °C) might not be sufficient to justify the entire range of body tissue insulation in resting man, i.e., there is evidence that maximal vasodilation and minimal tissue insulation are expected at body core temperature above 38 °C.²⁷ Second, on physical and boundary parameters, skin wetness was considered 6% of total skin surface area as proposed for resting man by Gagge et al.²⁸ In case of greater skin wetness, evaporative heat loss would be greater and consequently shift the TNZ to warmer T_a. In contrast, higher relative humidity (ϕ > 50%) would make it harder to evaporate sweat and shift the thermoneutral zone to lower T_a. Furthermore, air velocity was set relatively low (v_air = 0.1 m/s). In case of draft or a breeze convective heat loss would increase and shift the TNZ to lower ambient temperatures.

Conclusion

This study describes what constellations of body core, skin and ambient temperature satisfy the biophysical requirements of being in the thermoneutral zone for steady-state conditions. Furthermore, by constraining mean skin temperature to a temperature range associated with thermal comfort the thermal comfort zone is derived. The biophysical analysis shows that the steady-state ambient temperature range associated with the thermoneutral zone does not guarantee that the body is in thermal balance at basal metabolic rate per se. Instead, depending on the constellation of core temperature, mean skin temperature and ambient temperature, the body may require significant increases in heat production or heat loss to maintain stable core temperature. Therefore, the definition of the thermoneutral zone requires a revision to include core and skin temperature as well. Furthermore, after adding restrictions on skin temperature for thermal comfort, the ambient temperature range associated with thermal comfort is smaller than the thermoneutral zone. This, assuming animals seek thermal comfort, suggests that thermal behavior may be initiated already before the boundaries of the thermoneutral zone are reached.

Glossary

Abbreviations:

BMR

basal metabolic rate

PMV

predicted mean vote

PPD

percentage people dissatisfied

NST

category label indicating body heat deficit relative to basal metabolic rate cold induced thermogenesis by non-shivering is sufficient to maintain thermal balance

SH+NST

category label indicating body heat deficit relative to basal metabolic rate cold induced thermogenesis by shivering and non-shivering is required to maintain thermal balance

SWEAT

category label indicating a body heat surplus increased evaporation is required to maintain thermal balance

TCZ

thermal comfort zone

TNZ

thermoneutral zone

TNZ body

category label indicating body heat loss is balanced relative to metabolic rate this definition of the thermoneutral zone incorporates the combination of mean skin temperature and ambient temperature

TNZ classical

TNZ referring to the classic definition of the thermoneutral zone which only defines the ambient temperature range

TNZ functional

TNZ referring to the classic definition of the thermoneutral zone taking into account clothing insulation and metabolic heat production associated with light office work

_a

ambient

_air

air

_body

referring to the human body

_c

body core

_cl

clothing

_clothed

clothed

_con

convective

_e

evaporative

_H&D

referring to Hardy & Dubois

_F

referring to Fanger

_max

maximal

_min

minimal

_r

radiative

_r+c

radiative + convective

_rsp

respiratory

_s

skin or mean skin

α

fraction of metabolic heat production that is accounted for by respiratory heat loss

A (m²)

body surface area

ϕ

relative humidity

Fpcl

permeation efficiency factor for water vapor evaporated from the skin surface through clothing to the ambient air

γ (mmHg Pa^-1)

conversion factor from Pascal to mmHg

h (W m^-2 °C^-1)

heat transfer coefficient

I (m²°CW^-1)

insulation

λ (°C mmHg^-1)

Lewis relation

M (W)

Metabolic rate

P (mmHg)

saturated vapor pressure

T (°C)

Temperature

Q (W)

heat loss

v (m s^-1)

velocity

w

skin wetness fraction

∆T (°C )

Indicating a temperature range

10.4161/temp.29702

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest are disclosed

Acknowledgments

This work was supported by grants from AgentschapNL (INTEWON: EOSLT10033), TKI Energo and TKI Solar Energy (TEGB|13023).

Supplemental Materials

Supplemental Materials may be found here: www.landesbioscience.com/journals/temnperature/article/29702