3D Printing Variable Stiffness Foams Using Viscous Thread Instability

Abstract

Additive manufacturing of cellular structures has numerous applications ranging from fabrication of biological scaffolds and medical implants, to mechanical weight reduction and control over mechanical properties. Various additive manufacturing processes have been used to produce open regular cellular structures limited only by the resolution of the printer. These efforts have focused on printing explicitly designed cells or explicitly planning offsets between strands. Here we describe a technique for producing cellular structures implicitly by inducing viscous thread instability when extruding material. This process allows us to produce complex cellular structures at a scale that is finer than the native resolution of the printer. We demonstrate tunable effective elastic modulus and density that span two orders of magnitude. Fine grained cellular structures allow for fabrication of foams for use in a wide range of fields ranging from bioengineering, to robotics to food printing.

Additive manufacturing processes are frequently used to produce lightweight and porous cellular structures. In bio-printing applications these structures are beneficial for cellular scaffolding¹,². Porous structures are advantageous for medical implants since they promote cell migration into the implant³. For mechanical applications, cellular structures are valuable for weight reduction in parts⁴, as well as for optimizing static and dynamic mechanical properties.

Printed cellular structures are produced in one of two ways: Either explicitly, through geometric design of the cells themselves, or implicitly through toolpath processing such as volume-filling using crisscrossing paths.

The explicit methodology allows for complex cellular structure but requires the printing process to have a resolution that is significantly higher than the unit cell⁴. Such processes involve the design of a complex cellular structure as a computed geometry⁵. Since each feature must be explicitly defined, the printing process must have a resolution fine enough to reproduce the cell strut and geometry at the desired scale. Explicit cell fabrication requires a print process at least one order of magnitude smaller than the smallest element of the cell⁶,⁷. For example, state-of-the art commercial resolution of 10 microns permits fabrication of cellular structures with unit cell resolution at the scale of millimeters, in order to get sufficient fidelity. Cell size limitations inherently limits the feature size of pores which can be produced using additive manufacturing processes.

Implicit cell fabrication processes produce cells by controlling the directly weave strands into regular patterns such as hexagonal and rectilinear meshes. Strand weaving allows for the production of finer pore sizes such as those used in bio applications, but results in relatively periodic structures limited by the positioning accuracy of the print head¹. Usually, a simple structure is sent to a path planning software, where the paths are placed with a regular spacing⁸. Direct strand control enabled vertical pores that vary between 10% and several hundred percent of the strand width⁹,¹⁰,¹¹. These structures are useful in bio-scaffolding applications because they can have sufficiently small pores relative to the print process resolution, allowing a 10-micron accuracy machine to produce pores on the 10-to-100 micron scales. However, implicit processes are often limiting because they can only produce rectangular pores. Regular porosity patterns are not analogous to biological tissues and that generally have inhomogeneous pore structure.

Alternatively, the pore structure can be encoded into the design of the printing head, where multiple nozzles are spaced at a fixed distance to produce offset strands of material¹². Pathing algorithms can then generate mechanically strong 2D cellular structures extruded vertically (2.5 dimensions), but cannot produce true 3D structures¹³,¹⁴. Such 2.5D structures, such as a height map, contain no overhanging elements¹⁵.

In this work we describe a new method of implicit processing that produces cellular foams with complex structures at a resolution that is finer than that of the native resolution of the printer, by exploiting viscous thread instability (VTI) in the printing process itself.

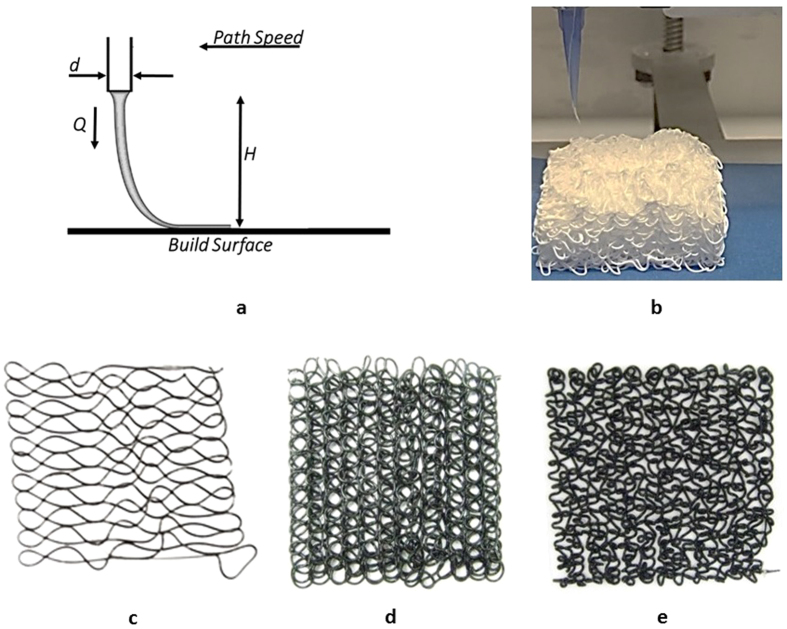
Viscous thread instability (VTI) is a well-characterized effect¹⁶,¹⁷,¹⁸, familiar to anyone who has watched honey drizzle onto a surface. The phenomenon has been studied in the past in 1D and 2D systems where a fluid is allowed to flow from a height over a moving belt. For a certain range of process parameters, a variety of patterns of movement of the strands can be produced. Patterns are classified into shapes such as “W’s”, meanders, alternating loops, and translating coils¹⁷ (Fig. 1). In the past, these meandering motions have been studied for modeling in computer graphics, or for modeling manufacturing processes¹⁹, or studying chaotic systems.

Figure 1.

To induce viscous thread instability, the printer nozzle must be elevated from the build surface (a,b), and the flow rate must be increased. This can induce patterns such as meanders (c), translated coils (d), and alternating loops (e).

In this paper we demonstrate that inducing VTI in a direct writing system can result in controlled variation in the stiffness of the resulting meta-structure. We focus on the alternating loops and translating coils since they produce the greatest amount of interconnectedness between strands. Printing with these patterns allows us to generate nonwoven textiles on a 3D printer and to develop open-celled foam structures that go beyond the traditional ordered cells used in 3D printing processes²⁰. Rather than simply depositing the material under instability conditions as a line, we generated 2D rectilinear path movements that produced complex interconnected structures. These structures are then stacked upon each other in a layered printing process to produce foamed structures. VTI 3D Printing can be performed with a wide range of printable materials, as varied as plastics, silicones and corn dough²¹,²².

Methods

Printing

The printing process involves modifying the material deposition parameters, such as lifting the nozzle above the printer surface, the material flow rate (Q), the movement speed of the head (Ps), the spacing between path movements (Pw), and layer height (Ph). These parameters can all be varied to induce different types of patterns in the print structure. In order to maintain a consistent pattern across layers of a print, we print a single layer of the pattern, record its average layer height, and then offset the next layer by the layer height. Several layers were then printed to confirm the initial estimate of the layer height. The resulting printed structures can radically vary in appearance, as seen in Fig. 2.

Figure 2. Various patterns from the “fluid mechanic sewing machine” can be generated using a direct write 3D printing system.

By applying these patterns in each layer, various complex foam structures can be produced (a–c). These have varying densities, interconnectivity, and stiffnesses. Such structures can be printed into complex shapes such as a space shuttle (d).

In order to characterize the process’s effects on the resulting material, printed 60 different patterns using different combinations of deposition rate, nozzle height, and spacing between strands. Some of the more interesting combinations are listed in the appendix. We then performed mechanical testing to determine the effective elastic modulus of three distinctive patterns, and compared these two solid printed structures. Printing was conducted on a Fab@Home Model 3 system and Seraph Scientist system using a valve head with a 22 gauge tapered tip. The patterns of Dow Corning Silicone 732 were printed in stochastic patterns 29, 39, and 60. As seen in Table 1, these patterns were selected for examination because of the differences in their densities. The process parameters can be seen in Table 2.

Table 1. The printed patterns can reduce the effective stiffness by up to two orders of magnitude while only reducing the density by 50%.

Pattern	Density	Pore size (mircons)	Effective EM in compression (MPa)	SE in compression (MPa)	EM in tension (MPa)	SE in tension (MPA)
Bulk	1040	NA	0.608	0.005	0.79	0.07
Pattern 29	900	100–200	0.38	0.05	0.216	0.003
Pattern 39	700	300–600	0.077	0.004	0.13	0.02
Pattern 60	500	500–1800	0.0092	0.0004	0.102	0.004
50%–50% composite of 29 and 39	800	100–600	0.124	0.003	0.36	0.01

The structures in compression can linearly be added together in different layers to produce a composite of proportional stiffness.

Note: EM = Elastic modulus; SE = Standard error.

Table 2. The printing process parameters for generating the patterns on a robocasting system.

Pattern Name	Path width (mm)	Path speed (mm/s)	Pressure (PSI)	offset height (mm)	Tip diameter (mm)	Path Height (mm)	Strand diameter (mm)
29	1	10	70	3	0.4064	0.85	0.40
39	0.9	20	70	3	0.4064	0.8	0.40
60	0.5	20	70	5	0.4064	1.3	0.35

Bulk silicone has a density of 1040 kg m⁻³, pattern 29 has a density of 900 kg m⁻³, pattern 39 has a density of 700 kg m⁻³, and pattern 60 has a density of 500 kg m⁻³. For all of the tests performed, the force versus displacement was recorded. The average and standard error of the samples values are reported in Table 1. The effective Young’s modulus of each sample was calculated by selectively fitting a linear section to the initial displacement. If there was no linear region, the secant method was used.

Tension Tests

Tensile tests were performed using specimens cut from printed sheets of each pattern of material. These specimens were formed by slicing strips from bulk material. The dimensions of these strips were based loosely on those required by ASTM D882. The specimens were 4 mm thick, 6 mm wide, and 115 mm long. Five specimens were tested from each batch at a rate of 50 mm/min in the XY plane of the print.

Compression Tests

Samples for compression testing were printed and submitted to testing using ASTM standard 575. For each pattern, sample blocks were made to specification using a punch to cut the material from a large printed sheet. Three samples were made from each sheet. This helped ensure consistency in the samples. Each specimen cycled three times through compression and release at a rate of 12 mm/min along the Z axis of the print. The first two cycles conditioned the specimens, and the third was used for analysis. The measurements in the Z direction for compression and the XY direction for tension were done to model the most likely use cases. Foam structures are generally used in compression applications and can be clamped and stressed in the direction perpendicular to their loading.

Results

Printed structures such as pattern 39 and pattern 60 exhibit three distinct regions, as seen in Fig. 3b. The initial linear region represents the force required for the structures to collapse under the displacement; the third region is the sharp increase in slope which denotes that the structure is fully collapsed and the silicone material itself is being compressed. The second (middle) region represents a transition between the other two regions. In sample 29 and the bulk material, there is just one continuous nonlinear region. This is because the structure of pattern 29 is so dense that there is no meaningful strand length to buckle and the material is compressed with the initial displacement.

Figure 3.

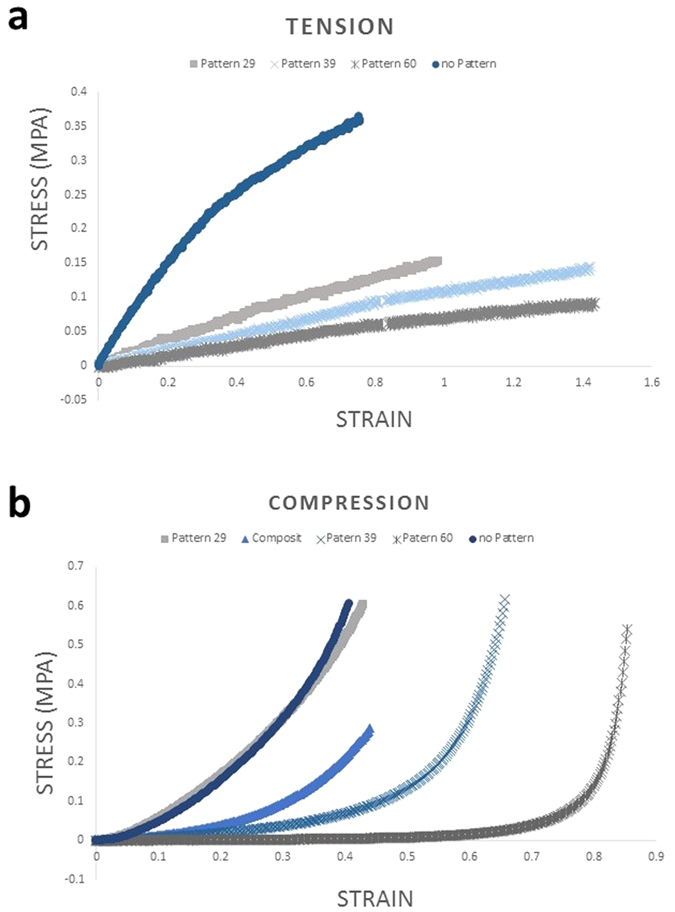
The stress strain curves of various samples in tension (a) and compression (b) show how the different structures can affect the stiffness of the resulting material bulk.

The dual-region effect does not appear in tension (Fig. 3a), most likely because the samples in tension distribute the tension load across the fibers composing the system, causing the entire structure to be in tension.

The composite material combining 50% of pattern 29 and 50% of pattern 39, behaves very differently in tension and compression. The composite was produced with each layer alternating between the two base patterns. Mechanical testing showed that the composite behaved according to the isostress model while in compression. The fused behavior allows a system of known patterns to be used to span a range of effective moduli in compression. In tension, however, the composite pattern was significantly stronger than either of its base components. We believe the increased strength is caused by the pattern generating a greater density of connections between strands in the XY plane while maintaining the density of connections in the Z direction the same. This limits the effective length of the strands, making them significantly stronger in tension in the XY plane.

Discussion

VTI 3D printing process allows for the direct production of soft foam structures. In production environments, foams are often used for mechanical padding, acoustic dampers, energy absorption zones, fluid filtering and absorption, and thermal insulation. This new process of producing foams allows for the production of such structures directly inside of complex printed parts. The low effective elastic modulus we have achieved of 1.5% of the initial bulk modulus of the material allows for the production of soft structures for padding. This is in contrast to the typically hard structures of nylon and metal which are used in industrial 3D printing processes.

The ability to combine characterized patterns layer by layer to produce desired stiffnesses by design can be of great benefit in the customization of padding. Desired stiffnesses in the Z direction can be achieved by printing well-characterized layers of different patterns on top of one another. In the printing plane, patterns can be varied smoothly as function of the X and Y.

The use of VTI in printing systems can produce patterns faster than current direct write technologies. Aside from lowering the density of material printed, often VTI requires that the printer operate at flow rates greater than solid fill printing would demand. High print rates imply more material to be deposited in less time for the same fill volume.

VTI patterns can also be patterned at multiple scales. As seen in Fig. 3c, the coils produced in the printing process can be stitched tightly together, and those rows of coils can then be separated using implicit pathing techniques to generate a second layer to the patterned structure. As seen in Table 1 the scale of the pores generated is of the same order of scale as the print nozzle (406 microns).

Conclusion

Generating foamed structures by 3D printing can have many applications. The complex structures produced can be used to make filters and catalytic substrates. Rather than produce simple extrusions, this system can be used to produce structures with a shorter mean free path than traditional extruded substrates. Additionally, it allows for the production of filters using printers with nozzles diameter on the order of the pore size. For example, a 10-micron filter could be printed using a10 micron accuracy print process rather than a nanometer scale process.

VSI Printing also represents a new method of making scaffolding. Rather than producing rectilinear bio-scaffolds using implied pathing, scaffolding can be generated with more intricate and varied-size pores that more naturally replicate tissue structures. For this application, bio-inks with sufficient viscosity and surface tension will be needed; materials such as alginate hydrogels would not be sufficient. The open cellular matrix also makes it an ideal substrate for printing composite structures. Printed foams could be infused with epoxies and other materials that are difficult to print. The non-rectilinear structure may prevent crack propagation, a concern with regular periodic cellular structures.

VTI-based printing can provide a novel method for producing open cellular structures. It allows for the production of complex printed structures with variable stiffness and complex pores. The use of this new implicit structure generation allows for the printed cells to be significantly smaller than explicit geometric methods, without the complexity limitations of previous methods. Its simplicity as a process allows it to be applied to various direct write systems immediately.

Additional Information

How to cite this article: Lipton, J. I. and Lipson, H. 3D Printing Variable Stiffness Foams Using Viscous Thread Instability. Sci. Rep. 6, 29996; doi: 10.1038/srep29996 (2016).