Thermostability of Enzymes from Molecular Dynamics Simulations

Abstract

Thermodynamic stability is a central requirement for protein function and one goal of protein engineering is improvement of stability, particularly for applications in biotechnology. Herein, molecular dynamics simulations are used to predict in vitro thermostability of members of the bacterial Ribonuclease HI (RNase H) family of endonucleases. The temperature dependence of the generalized order parameter, S, for four RNase H homologs, from psychrotrophic, mesophilic and thermophilic organisms, is highly correlated with experimentally determined melting temperatures and with calculated free energies of folding at the midpoint temperature of the simulations. This study provides an approach for in silico mutational screens to improve thermostability of biologically and industrially relevant enzymes.

Graphical abstract

Understanding protein stability, and more specifically thermostability, has long been of interest in structural biology and biophysics, but also in biotechnology.¹ Thus, thermostable enzymes may be useful catalysts for industrial processes run at relatively high temperatures, which has many advantages, such as increased reaction rate, increased solubility of reactants, and reduced contaminating microbial growth^1–3.

The unfolding, or melting temperature, T_m is a metric for the thermostability of a protein. T_m is the temperature at which the Gibbs free energy G of the folded and unfolded states, and thus their populations, are equal. While attempts have been made to determine T_m by molecular dynamics simulations, computational limitations usually limit the study of complete unfolding processes to very small and fast-folding proteins.^4,5 Computational tools to predict protein stability fall into two main categories. The energy of unfolding (ΔG) is studied using physical, statistical or empirical potentials in the first instance, or using machine-learning methods trained on datasets of experimental unfolding energies in the second^6–8. Promising results have been reported recently by applying a Monte Carlo simulation approach to the bacterial enzyme dihydrofolate reductase.⁹ A high-throughput approach has been developed for finding multiple stabilizing mutations of a protein.¹⁰

Ribonuclease HI (RNase H; EC 3.1.26.4) enzymes, have been studied extensively to shed light on thermostability, because highly conserved structural homologs exist in both psychrotrophic and thermophilic organisms.^11–24 These enzymes nonspecifically cleave the RNA strand of RNA:DNA hybrid substrates,²⁵ and have been implicated in many biological processes, including removal of R-loops, removal of Okazaki fragments, synthesis of multicopy single-stranded DNA, and removal of ribonucleotides misincorporated into the genome.^26,13

To study the influence of temperature on the dynamical behavior of RNase H variants in silico, we conducted Molecular Dynamics (MD) simulations for RNase H enzymes from four different organisms, as shown in Table 1.¹³ The set is composed of proteins from psychrotrophic (soRNH), mesophilic (ecRNH), moderately thermophilic (ctRNH), and thermophilic (ttRNH), bacteria. The protein ctRNH, despite its origins in the proteome of a moderate thermophile, has a melting temperature T_m that is similar to that of the mesophile protein ecRNH.

Table 1.

Ribonuclease H Enzymes.

Protein	PDB ID	Source Organism	Tm (°C)
soRNH	2E4L	Shewanella oneidensis	53.232
ctRNH	3H08	Chlorobium tepidum	68.533
ecRNH	2RN2	Escherichia coli	70.732
ttRNH	1RIL	Thermus thermophilus	8934

The four proteins were simulated for 100 ns at 273, 300 and 340 K. The preparation of the simulations has been described previously.^12,13,27,28 Each trajectory was divided into 10 ns blocks to reflect global tumbling time^12,29 and the squares of the generalized order parameters (S²) for the backbone NH bond vector (henceforth simply “order parameters”) were calculated for each block and then averaged over all blocks. The order parameters describe the orientational fluctuations of the backbone NH vectors and can by measured experimentally by NMR spectroscopy.³⁰ Order parameters for all proteins at the three studied temperatures are shown in the Supporting Figure S1. All order parameters were scaled by ξ = (1.02/1.04)⁶ ≈ 0.89 to account for zero point vibrational motions of the NH bond vectors.^30,31

The temperature dependence of S² is described by the dimensionless parameter Λ, which is directly related to the temperature-dependent effective potential for the fluctuations of the NH bond vector, and together with S² provides information about the contributions of these fluctuations to heat capacity:^35–37

$$\Lambda =\frac{d\mathit{\text{ln }}(1-S)}{d\mathit{\text{ln }}T}$$

The Λ values determined from experimental order parameters for E. coli RNase H and the villin headpiece helical subdomain HP36 exceed simulated values by a factor of about 2^35,36. Even though agreement between experimental and simulated order parameters is typically very good (R = 0.7 – 0.9)¹³, small systematic differences in the order parameter can have a larger influence on Λ, as described previously³⁵. This discrepancy does not affect the approach described herein as long as comparisons are between simulations using identical protocols.

Supporting Figure S2 shows plots of ln(1−S) versus lnT for select residues in E. coli RNase H. Linear regression was used to extract Λ values as the slope of these plots for each residue. The quality of the fit was assessed by the correlation coefficient R. Incorporating simulations at additional temperatures has only minor effects on resulting Λ values (Supporting Figure S3).

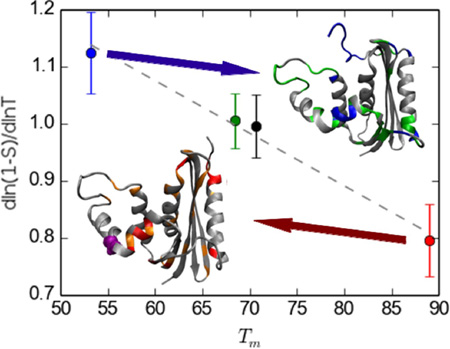
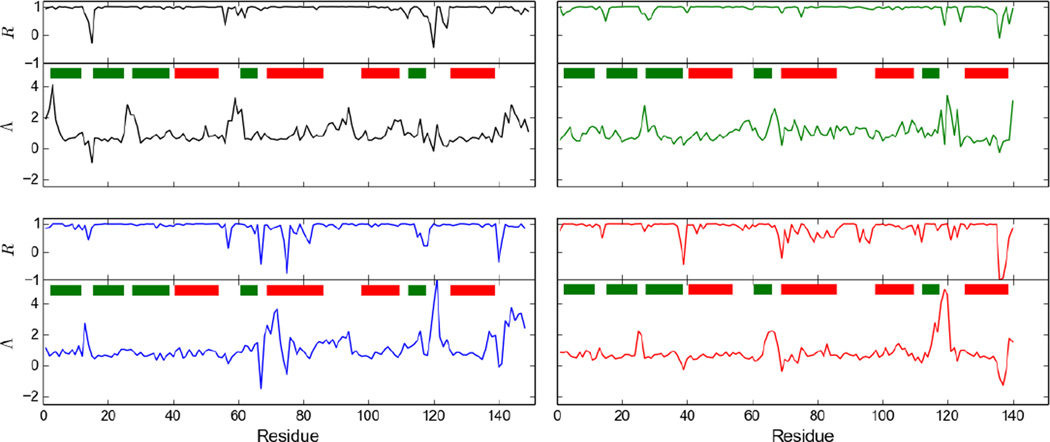
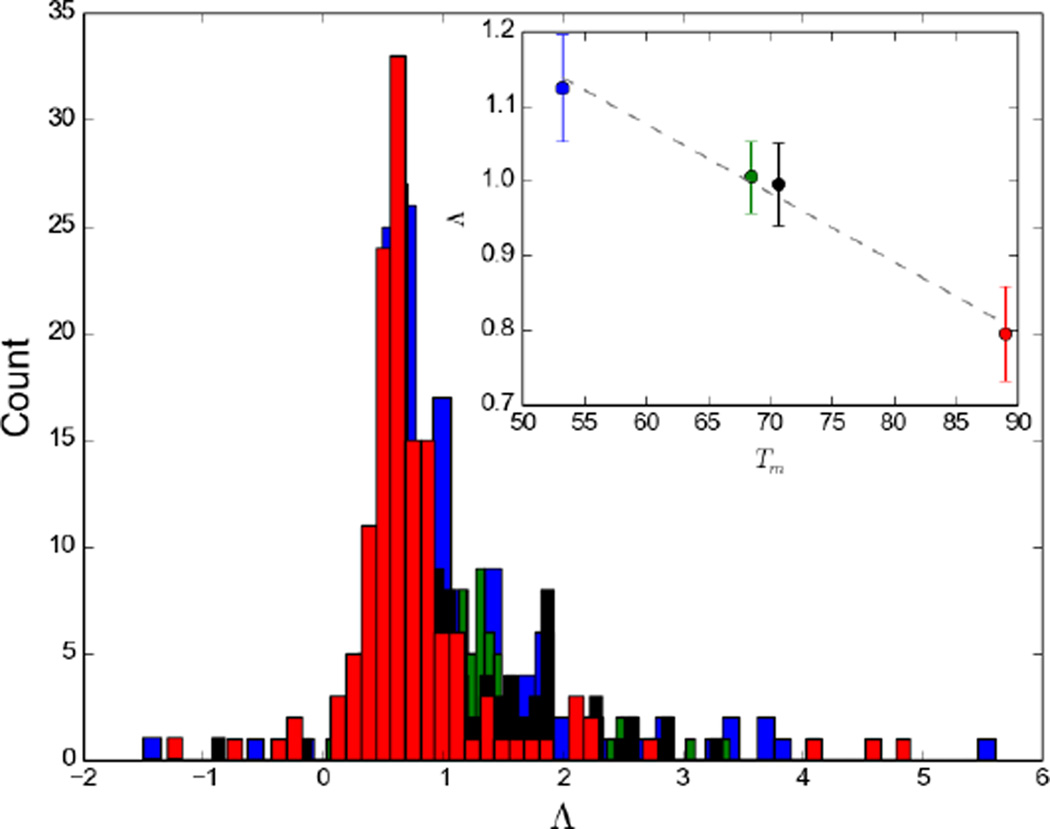
Figure 1 shows Λ and R values as a function of sequence for the four studied proteins. For most residues the linear regression yielded R values close to unity. The majority of the low R values correspond to low Λ values and thus low temperature dependence. Accordingly, the number of residues with R values smaller than 0.8 is much smaller for ecRNH (15 out of 149) than for ttRNH (38 out of 140). The distributions of Λ for the different proteins are compared in Figure 2. A plot of Λ averaged over all residues for each organism against experimental melting temperature T_m is reveals a homomorphic relationship between the two, with a lower average Λ value corresponding to a higher melting temperature (Fig. 2). A similar correlation is observed between Λ and ΔG for folding calculated at 304 K, the midpoint of the investigated temperature range, using the Gibbs-Helmholtz equation (not shown).

Figure 1.

Λ and R values for ecRNH (black), ctRNH (green), soRNH (blue), ttRNH (red). Prolines do not have an NH bond vector and were omitted from the sequences for this figure. Green and red bars represent sheets and helices, respectively.

Figure 2.

Histograms of Λ values for the four organisms with experimentally determined T_m values: soRNH (blue), ctRNH (green), ecRNH (black), ttRNH (red). The inset shows the homomorphic relationship between average Λ values and experimentally determined T_m.

The linear relationship of all four data points is statistically highly significant (p < 0.01 for weighted least squares). Removing Λ values of residues with R values < 0.8 increases the average Λ values in a similar fashion for all proteins, without affecting the qualitative relationship between average Λ and T_m, the slope of the fitted line is −0.008 or −0.009 K⁻¹ with R values of 0.98 or 0.99, if these residues are excluded or included, respectively.

To study the effect of a single thermostabilizing mutation on Λ values, we conducted another set of MD simulations on an E. coli variant with a thermostabilizing Glycine insertion at position 80b (mimicking this position in ttRNH); the simulated order parameters are shown in Supporting Figure 4a. This mutant has been crystallized (PDB: 1GOA) and thermodynamically characterized.^38,39 The insertion has a small thermostabilizing effect and increases T_m by 1.2 K.^38,39 Supplementary Figure 4b and 4c show that the correlation between Λ values for ecRNH and the iG80b mutant are extremely high for the first approximately 60 residues, while they differ quite significantly around and following (in sequence) the insertion. Thus the effects of the insertion are not restricted locally but lead to changes across the protein, presumably through changes in packing (ttRNH has a reduced solvent accessible surface area compared to ecRNH – ca. 8800 Ų vs ca. 9500 Ų -, the iG80b mutant lies in between with ca. 9200 Ų). The average value for Λ decreases slightly from 0.995 to 0.965, agreeing with the increase in T_m of 1.2 K. Supplementary Figure S4d shows that including this fifth datapoint improves the statistical significance of the weighted linear regression further (p < 0.001).

A plot of Λ values averaged separately for α-helices, β-sheets and loops, shows that no particular secondary structure element is dominates the trend versus T_m (Supporting Figure S5). Loop backbone order parameters have on average a greater temperature dependence than secondary structure order parameters. Interestingly, ctRNH has loop Λ values that are closer to those of ttRNH, which could reflect a larger contribution of loop dynamics to heat capacity. ΔC_p of ctRNH has been shown to be closer to that of ttRNH, while the overall melting temperature is closer to that of ecRNH³³.

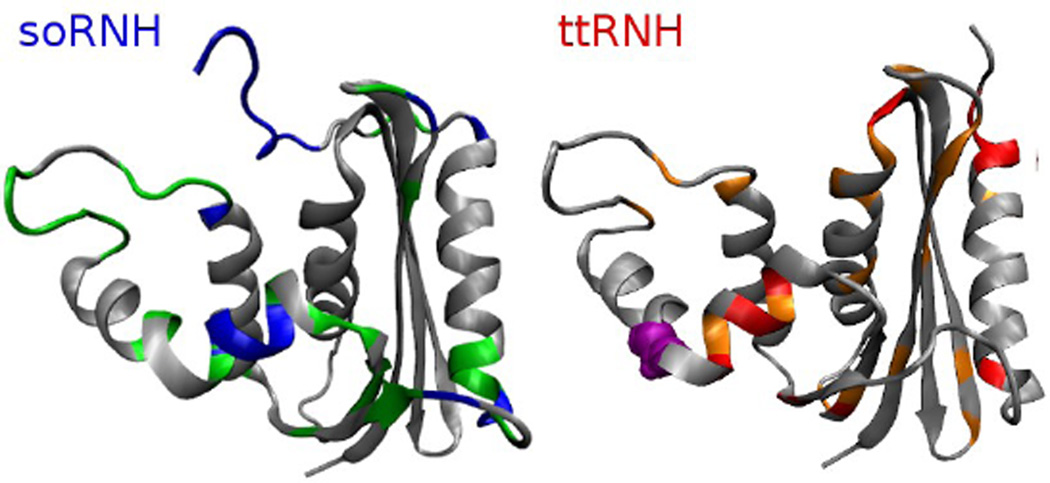
A plot of the Λ values of the four wild-type proteins and the iG80b mutant, accounting for insertions and deletions, (Supporting Figure S6) shows regions with strong differences in Λ values especially for the psychrotrophic (soRNH) and thermophilic (ttRNH) proteins. Figure 3 shows the structures of soRNH and ttRNH with residues with particularly high or low Λ values highlighted. These regions include helix α_B, the handle region and the β₅/α_E-loop, which have all been implicated in substrate binding.^11,12,40 Many of these residues have been implicated in thermostability as well.^40,41 As one example, the octapeptide LKKAFTEG in helix α_B, of ttRNH (comprising the iG80b insertion) has an average Λ value of 0.4±0.2 in ttRNH and an average of 2.2±0.4 for the corresponding heptapeptide MRQGIMT in soRNH. The substitution of the ttRNH octapeptide into the corresponding sequence of ecRNH leads to a ~5 K increase in T_m at pH 5.5.⁴¹ The observation that many of the residues with extreme values of Λ are important for both substrate binding and thermostability may reflect evolutionary trade-offs between activity and stability.

Figure 3.

Structures of soRNH (left) and ttRNH (right). soRNH: Residues with Λ values over 1.2 in green, residues with Λ values over 2 in blue. ttRNH: Residues with Λ values under 0.5 in orange, residues with Λ values under 0.3 in red. The iG80b in ttRNH insertion is shown as purple spheres.

We have shown, at least within one homologous family of enzymes including proteins from psychrotrophic, mesophilic and thermophilic organisms, that a linear homomorphic relationship exists between experimentally determined melting temperature and the average of the simulated parameter Λ, describing the temperature dependence of backbone conformational fluctuations of amide bond vectors. This result suggests that Λ is a good proxy for thermostability within a family of homologous proteins. Lastly, this study suggests the possibility for in silico identification of thermostabilizing mutations within a protein family, without the need to simulate full unfolding events, as an adjunct to other computational approaches for protein design.¹⁰