Feasibility of ¹⁸F-Fluoromisonidazole Kinetic Modeling in Head and Neck Cancer Using Shortened Acquisition Times

Abstract

¹⁸F-fluoromisonidazole dynamic PET (dPET) is used to identify tumor hypoxia noninvasively. Its routine clinical implementation, however, has been hampered by the long acquisition times required. We investigated the feasibility of kinetic modeling using shortened acquisition times in ¹⁸F-fluoromisonidazole dPET, with the goal of expediting the clinical implementation of ¹⁸F-fluoromisonidazole dPET protocols.

Methods

Six patients with squamous cell carcinoma of the head and neck and 10 HT29 colorectal carcinoma–bearing nude rats were studied. In addition to an ¹⁸F-FDG PET scan, each patient underwent a 45-min ¹⁸F-fluoromisonidazole dPET scan, followed by 10-min acquisitions at 96 ± 4 and 163 ± 17 min after injection. Ninety-minute ¹⁸F-fluoromisonidazole dPET scans were acquired in animals. Intratumor voxels were classified into 4 clusters based on their kinetic behavior using k-means clustering. Kinetic modeling was performed using the foregoing full datasets (FD) and repeated for each of 2 shortened datasets corresponding to the first approximately 100 min (SD1; patients only) or the first 45 min (SD2) of dPET data. The kinetic rate constants (KRCs) as calculated with a 2-compartment model for both SD1 and SD2 were compared with those derived from FD by correlation (Pearson), regression (Passing–Bablok), deviation (Bland–Altman), and classification (area-under-the-receiver-operating characteristic curve) analyses. Simulations were performed to assess uncertainties due to statistical noise.

Results

Strong correlation (r ≥ 0.75, P < 0.001) existed between all KRCs deduced from both SD1 and SD2, and from FD. Significant differences between KRCs were found only for FD-SD2 correlations in patient studies. K₁ and k₃ were reproducible to within approximately 6% and approximately 30% (FD-SD1; patients) and approximately 4% and approximately 75% (FD-SD2; animals). Area-under-the-receiver-operating characteristic curve values for classification of patient clusters as hypoxic, using a tumor-to-blood ratio greater than 1.2, were 0.91 (SD1) and 0.86 (SD2). The percentage SD in estimating K₁ and k₃ from 45-min shortened datasets due to noise was less than 1% and between 2% and 12%, respectively.

Conclusion

Using single-session 45-min shortened ¹⁸F-fluoromiso-nidazole dPET datasets appears to be adequate for the identification of intratumor regions of hypoxia. However, k₃ was significantly overestimated in the clinical cohort. Further studies are necessary to evaluate the clinical significance of differences between the results as calculated from full and shortened datasets.

The relationship between tumor hypoxia and poor overall outcome has been demonstrated for several types of human malignancies (1), including head and neck cancer (2–4). Tumor hypoxia can be identified by measuring partial pressure of oxygen using polarographic electrodes (3,5). Another method to characterize tumor hypoxia is by means of immunohistochemical analysis of exogenous (e.g., pimonidazole, etanidazole pentafluoride) or endogenous (e.g., carbonic anhydrase IX, hypoxia-inducible factor 1α) hypoxia markers (6). Both techniques, however, are invasive, require lesions accessible to needle placement, and are subject to undersampling.

PET with ¹⁸F-fluoromisonidazole is a noninvasive imaging technique that has been shown to be clinically feasible for detecting tumor hypoxia (7,8). Because of its lipophilicity, ¹⁸F-fluoromisonidazole passively diffuses out of the vasculature and through cell membranes and is reduced to a nondiffusible charged form by intracellular nitro-reductases (7). Under normoxic conditions, the reduced form of fluoromisonidazole is rapidly oxidized back to its diffusible form, with tissue levels rapidly declining as blood-borne fluoromisonidazole is cleared. Otherwise, the fluoromisonidazole metabolites remain trapped and undergo irreversible reductions to form covalent bonds to macromolecules, leading to progressive accumulation of ¹⁸F within hypoxic cells (7). Previous studies suggested a tumor-to-blood ratio in excess of 1.4 at 2 plus hours after injection to identify hypoxic volumes (7,8). However, a combination of severely hypoxic and necrotic tissues supplied by structurally and functionally abnormal vasculature may lead to low total uptake even at late time points. Conversely, the physiologic clearance of ¹⁸F-fluoromisonidazole from well-perfused normoxic tissue may result in measured activity concentrations comparable to those in hypoxic tumors (9,10). To overcome the foregoing limitations in the interpretation of static ¹⁸F-fluoromisonidazole images, kinetic modeling of dynamic PET (dPET) data has been suggested as a means of reliably characterizing perfusion and identifying hypoxia in tumors (9,10).

A major drawback of such an approach is the long acquisition times typically used to extract the pharmacokinetic parameters of ¹⁸F-fluoromisonidazole. At our institution, the ¹⁸F-fluoromisonidazole dPET protocol consists of 30- to 45-min dPET followed by 10-min static PET acquisitions at approximately 90 min and at approximately 150–180 min after injection. Such lengthy protocols compromise clinical practicality as well as patient compliance and accrual. The aim of the current study was to assess the reproducibility of kinetic rate constants (KRCs) as calculated from shortened ¹⁸F-fluoromisonidazole dPET datasets in a cohort of patients with squamous cell carcinoma of the head and neck (SCCHN) and in a preclinical rodent model. Special attention was paid to kinetic rate constants serving as surrogate metrics of perfusion (K₁) and hypoxia (k₃).

MATERIALS AND METHODS

Clinical Studies

This retrospective study was approved by our Institutional Review Board (IRB 04-070; registered under www.clinicaltrials.gov identifier NCT00606294), and all subjects signed a written informed consent form regarding the examination and use of anonymous data for research and publication purposes. Patients aged 18 years or older with a histologically confirmed diagnosis of SCCHN were eligible for this study. Exclusion criteria included all nasopharyngeal, paranasal sinus, salivary cancer, and thyroid malignancies; prior chemotherapy or radiotherapy within the last 3 y; previous surgical resection for the same disease; any prior radiotherapy to the head and neck region; and pregnancy.

Six male patients (age, 59 ± 10 y) were included in the study (Table 1). All patients were scanned on a flat-top couch insert in a radiotherapy treatment immobilization mask. Intravenous lines in contralateral antecubital veins were inserted for each patient and were used for radiotracer injection.

TABLE 1.

Patient Characteristics

Patient no.	Tumor stage	Tumor site	Lesion	Lesion VOI (cm3)
1	cT1N2b	Left glossal tonsillar sulcus and left base of tongue	1	13.3
			2	3.3
2	T1N2b	Left tonsil	3	24.2
3	cT2N3M0	Left tonsil	4	3.3
4*	cT2N2b	Base of tongue	5	32.9
5†	cT3N2a	Left tonsil and bilateral neck	6	33.0
			7	6.5
6*	T2N2b	Left tonsil	8	11.2

^*Patients for whom list-mode data were not available.

^†Patient whose first ¹⁸F-fluoromisonidazole acquisition was stopped at 40 min.

¹⁸F-FDG PET/CT Protocol

Each patient underwent a baseline ¹⁸F-FDG PET/CT study for radiotherapy simulation. Patients were injected intravenously with 451 ± 18 MBq of ¹⁸F-FDG (range, 437–477 MBq), after a fasting period of 6 h or more. Whole-body PET scans were acquired for 3 min per bed position (70-cm field of view [FOV]), starting at 69 ± 10 min (range, 61–84 min) after injection. Data were acquired on a Discovery STE PET/CT scanner (GE Health-care Inc.), having a resolution of approximately 5.5 mm in full width at half maximum at the center of the FOV. The CT images were acquired with oral contrast using the following settings: 140 kVp, 250 mA, and 3.8-mm slice thickness. PET emission data were corrected for attenuation, scatter, and random events and then iteratively reconstructed into a 256 × 256 × 47 matrix (voxel dimensions, 2.73 × 2.73 × 3.27 mm) using the ordered subset expectation maximization algorithm provided by the manufacturer (2 iterations, 20 subsets, and a gaussian postprocessing filter of 6.0 mm in full width at half maximum).

¹⁸F-Fluoromisonidazole PET/CT Protocol

Each patient underwent ¹⁸F-fluoromisonidazole dPET imaging on a Discovery STE PET/CT scanner 1–3 d after the ¹⁸F-FDG PET/CT. ¹⁸F-fluoromisonidazole was prepared as previously reported (11). Patients received an intravenous bolus injection of 429 ± 41 MBq of ¹⁸F-fluoromisonidazole (range, 364–475 MBq). The dPET acquisition was initiated simultaneously with the injection. ¹⁸F-fluoromisonidazole data were acquired in list-mode for 1 bed position, centered over the lesion, for 45 min (binned into 6 × 30, 7 × 60, and 7 × 300 s frames). Two additional 10-min static image sets were acquired at 96 ± 4 min (range, 90–103 min) and 163 ± 17 (range, 150–186 min) after injection. Patients were allowed a rest period between scans. Before each PET scan, a low-dose CT scan was obtained for attenuation correction and image registration purposes. CT scans were obtained with 120 kVp; 3.8-mm slice thickness; and 40, 10, and 80 mA for the first, second, and third scans, respectively. List-mode PET data of the first 3 min of the dataset was retrospectively rebinned into 36 × 5 s frames to delineate the carotid artery from the internal jugular vein and thereby define the input function (IF) volume of interest (VOI). All ¹⁸F-fluoromisonidazole PET images were reconstructed using the same parameters as for the ¹⁸F-FDG study.

Preclinical Studies

All animal experiments and procedures were approved by our Institutional Animal Care and Use Committee and complied with the National Institutes of Health regulations on the research use of rodents.

Ten rats were included in this study. HT29 human colorectal carcinoma cells (no. HTB-38; American Type Culture Collection) were maintained in Dulbecco modified Eagle medium (MediaTech Inc.) supplemented with 10% fetal bovine serum and 1% penicillin–streptomycin at 37°C in a 5% CO₂ atmosphere. Xenografts were initiated by subcutaneous inoculation of approximately 5.0 × 10⁶ cells in 0.2 mL of phosphate-buffered saline into the right hind limb of each of ten 6- to 8-wk-old female athymic nu/nu rats as previously described (12). Animals (weight, 228 ± 18 g) were anesthetized using 2% isoflurane in air. An activity of 41.3 ± 2.9 MBq (range, 36.7–46.0 MBq) of ¹⁸F-fluoromisonidazole was administered via tail vein injection. Image acquisition was performed with either an R4 or Focus 120 microPET scanner (Siemens Medical Solutions Inc.), with animals prone and the FOV centered on the tumor, using a 350- to 700-keV energy window and 6-ns coincidence timing window. Data were acquired in dynamic mode for a total of 90 min and binned into 4 × 5, 4 × 10, 4 × 30, 7 × 60, 10 × 300, and 3 × 600 s frames. Images were reconstructed using a 3-dimensional maximum a posteriori estimation algorithm into a 128 × 128 × 95 matrix (voxel dimensions, 0.87 × 0.87 × 0.79 mm). The reconstructed image resolution was approximately 1.6 mm in full width at half maximum at the center of the FOV. Measurements performed with a uniformly filled phantom of dimensions comparable to a rat demonstrated adequate uniformity without attenuation and scatter correction. Therefore, no attenuation or scatter correction was applied for the rat image data.

Image Analysis

Reconstructed dPET images were analyzed with PMOD (version 3.504; PMOD Technologies GmbH). For patient studies, 8 lesions were identified on the ¹⁸F-FDG PET/CT scans. In 1 case (patient 5), dynamic ¹⁸F-fluoromisonidazole acquisition was interrupted at 40 min after injection because of the patient’s discomfort and inability to continue. The 2 delayed ¹⁸F-fluoromisonidazole and the ¹⁸F-FDG image sets were spatially registered to the first ¹⁸F-fluoromisonidazole image set using the General Registration tool in the AW Workstation (version 4.6; GE Healthcare). Rigid image registration was performed locally for each lesion using the CT image sets, and the resulting transformation matrices were applied to the corresponding PET image sets. The whole-tumor VOI (wVOI) was delineated on ¹⁸F-FDG images using a 50% of the maximum tumor activity concentration threshold, and the resulting VOI was copied to the corresponding dynamic ¹⁸F-fluoromisonidazole image set. For animal studies, the wVOI was delineated manually on a slice-by-slice basis using the final frame (80–90 min).

Kinetic Modeling

Kinetic modeling of ¹⁸F-fluoromisonidazole dPET images was performed in PMOD, using an irreversible 1-plasma 2-tissue-compartment model (13). In this model, C_p(t), C₁(t), and C₂(t) correspond to the activity concentration as a function of time after injection in the plasma (C_P(t)), in the form of free and otherwise nonhypoxia-localized activity in tissue (C₁(t)), and in the form of hypoxia-localized tracer (C₂(t)). The 4 unknowns estimated are v_B, the fractional vascular volume; K₁, the transfer rate constant from C_P to C₁; K₁/k₂, the distribution volume of C₁; and k₃, the rate of conversion from C₁ to C₂. k₄ was set to 0, assuming irreversible trapping of ¹⁸F-fluoromisonidazole (7). Although v_B and K₁/k₂ are unitless, K₁ and k₃ (assuming unit density tissue) are expressed in min⁻¹.

For patient studies, the input function was derived by segmenting the common carotid artery on the rebinned dPET dataset (i.e., corresponding to the 36 × 5 s time frames). In 2 cases (patients 4 and 6), the list-mode data were not available; because the common carotid artery could not be identified from the original dPET dataset, the IF VOI was defined on the internal jugular vein. For animal studies, the input function was derived by segmenting the descending aorta (identified from a summed image of the first 3 frames [15 s] of the study). All IF time–activity curves were corrected for partial-volume effect by calculating the geometric transfer matrix containing weighting elements w_i,j that represent the fraction of true activity spilled over from VOI_i into VOI_j (14). Neighboring regions were defined using k-means clustering based on the time-weighted Euclidean distance between the voxel time–activity curves (10 clusters, 200 iterations) (15).

Voxels within each wVOI were similarly subclassified into 4 clusters, with k-means clustering performed based on the first 45 min of dPET data. The choice of 4 tumor subvolumes (cVOIs) was made to conceptually represent hypoxic, partially hypoxic, normoxic, and necrotic regions of the tumor. The Levenberg–Marquardt algorithm (16) was used to fit the cVOI-derived time–activity curves to estimate the KRCs (100 random fits, 200 iterations). The target activity concentration at each time frame was weighed by (13):

$$w_i=\frac{1}{{\mathrm{\sigma }}_i^2},{\mathrm{\sigma }}_{\mathrm{i}}=\mathrm{c}\surd \left(\frac{\text{AC}({\mathrm{t}}_{\mathrm{i}})}{\mathrm{\Delta }{\mathrm{t}}_{\mathrm{i}}\times {\mathrm{e}}^{-\mathrm{\lambda }{\mathrm{t}}_{\mathrm{i}}}}\right),$$ Eq. 1

where c is the scaling factor, Δt_i is the frame duration, AC(t_i) is the decay-corrected activity concentration measured at the midframe time t_i, and λ = ln2/T_1/2 is the isotope decay constant. Kinetic modeling was conducted for the full dataset (FD; reference standard), the first approximately 100 min of dPET data (SD1; patients only), and the first 45 min of dPET data (SD2). The input function time–activity curves that were corrected for partial-volume effect were fitted with a 3-term exponential function, using the available temporal data in each case, to obtain a modeled IF as:

$$\text{IF}(\mathrm{t})=\{\begin{array}{ll}\text{Linear}\text{interpolation}\hfill & t<t_0\hfill \\ \sum _{i=1}^3{A}_i{e}^{-(t-t_0)\text{ln}2/T_i}\hfill & t\ge t_0\hfill \end{array},$$ Eq. 2

where IF(t) is the modeled activity concentration in the blood at time t, t₀ defines at what time the model switches from linear to triexponential interpolation between measured values (after the IF peak), and the A_i and T_i terms represent the fitting parameters.

Statistical Analysis

The kinetic rate constants calculated from each of the 2 shortened datasets were compared with those derived from the full dataset in a stepwise approach. First, a Pearson correlation coefficient (r) was computed to calculate the strength and direction of a linear relationship between the KRCs, modeled as:

$$Y=\mathrm{\alpha }+\mathrm{\beta }\mathrm{X}+\mathrm{\epsilon },$$ Eq. 3

where intercept α, slope β, and ε correspond to the systematic, proportional, and random differences. If a strong significant correlation (r ≥ 0.75, P < 0.05) was found, nonparametric Passing–Bablok regression (17) was performed to test for the presence of systematic (95% confidence interval [CI] for α does not include 0) or proportional (95% CI for β does not include 1) differences between the 2 sets of KRCs. A cumulative sum test for linearity was used to validate the applicability of Passing–Bablok analysis (17). Random differences between 2 sets of KRCs were measured using residual SD. If the slope and intercept were not significantly different from 1 and 0, respectively, Bland–Altman analysis (18) was performed to calculate the 95% limits of agreement, after testing for the normality assumption on the differences between 2 sets of KRCs using the Kolmogorov–Smirnov test.

Receiver-operating-characteristics analysis (19) was performed in patient studies to evaluate the reliability of shortened datasets for the task of identifying tumor hypoxia, using a tumor-to-blood ratio greater than 1.2 (4) as a discrimination threshold. The diagnostic performance was assessed on the basis of k₃ and K_i (influx rate constant, defined as K₁k₃/[k₂+k₃], in units of min⁻¹) calculated from shortened datasets, and the area-under-the-receiver-operating characteristics curve was subsequently determined (19). All statistical analyses were performed in MedCalc (version 15.6; MedCalc Software bvba).

Simulations

Modeled time–activity curves (mTACs) were obtained by fitting all 32 cVOI-derived time–activity curves from patients. For each mTAC, 100 samples of noisy time–activity curves were simulated by adding noise consistent to that observed on a cluster level. The noise was estimated as follows: data were acquired on a Discovery STE PET/CT scanner using a National Electrical Manufacturers Association/International Electrotechnical Commission body phantom filled with ¹⁸F-FDG (activity concentration was equivalent to the average tumor ¹⁸F-fluoromisonidazole activity concentration in the ~170-min time point), for 30 min in gated mode (10 bins), as described previously (20). Images were reconstructed using the same parameters as in clinical studies. Fifty nonoverlapping VOIs of 5 × 5 × 5 voxels (corresponding in size to the average patients’ cluster volumes) were drawn on the central axial plane in the phantom image set. For each VOI, a histogram of the average activity concentrations from the 10 gated image bins was constructed and fitted with a normal distribution fit, to calculate the SD of the distribution and deduce the corresponding scaling factor c (as per Eq. 1). The average scaling factor over 50 VOIs was subsequently used to simulate cluster noise on a frame-by-frame basis for each mTAC. Kinetic modeling was conducted using mTACs and input functions as derived from full datasets (mTAC_FD and IF_FD; that is, for SD1 and SD2, mTAC_FD and IF_FD were truncated). The percentage bias and percentage SD were calculated with respect to the true value for each kinetic parameter (13):

$$\%{\mathit{bias}}_i=\left(\frac{{\mathrm{\mu }}_{xi}}{x_i^{\mathit{true}}}-1\right)\times 100,$$ Eq. 4

$$\%{\mathit{stddev}}_i=\left(\frac{{\mathrm{\sigma }}_{xi}}{x_i^{\mathit{true}}}\right)\times 100,$$ Eq. 5

where μ_xi, σ_xi, and $x_i^{\mathit{true}}$ are the sample mean, sample SD, and true value of a kinetic parameter x for i-th cluster. Additionally, Pearson r was calculated for K₁ and k₃ deduced from the 100 noisy time–activity curves using FD and SD1 and SD2, respectively.

RESULTS

Clinical Studies

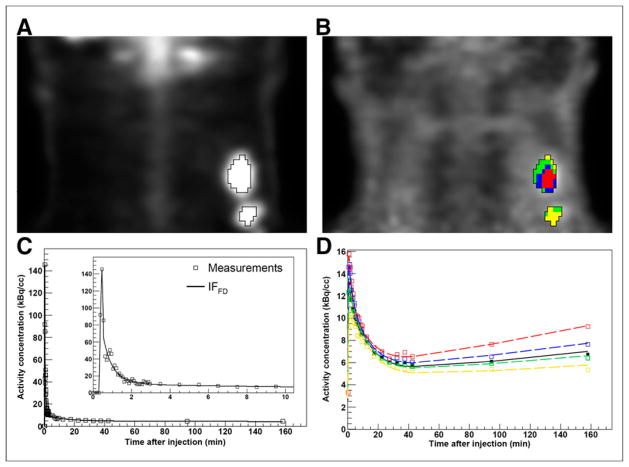
Coronal images for patient 1 are shown in Figures 1A (¹⁸F-FDG PET) and 1B (¹⁸F-fluoromisonidazole PET). The corresponding IF and tumor time–activity curves are shown in Figures 1C and 1D, respectively.

FIGURE 1.

Clinical study of patient 1 (lesion 1). (A) Definition of VOI (wVOI) on ¹⁸F-FDG PET image (coronal view). (B) wVOI is copied to coregistered ¹⁸F-fluoromisonidazole dPET image and subclassified into 4 clusters (cVOIs). (C) Modeled input function based on full dataset (IF_FD), superimposed on measurements. Insert shows initial 10 min of data. (D) Modeled time–activity curves derived from wVOI (solid line) and from 4 cVOIs (dashed lines), superimposed on measured wVOI time–activity curve (■) and cVOI time–activity curves (□). cVOIs are color-coded to those shown in B.

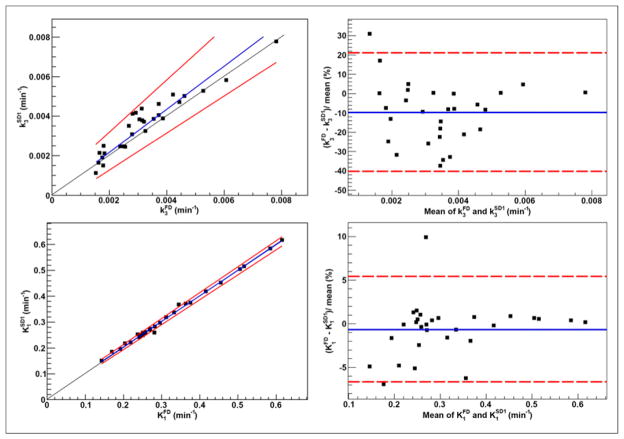
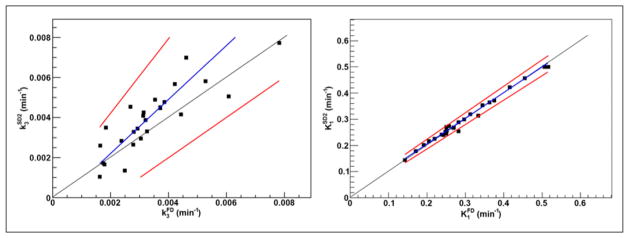
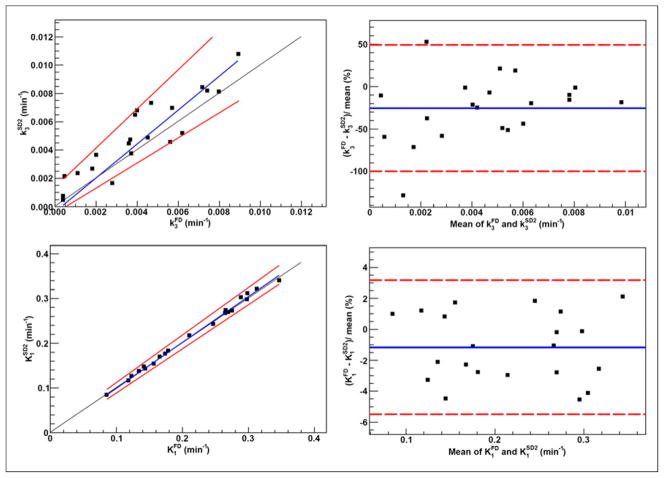
Clusters included 25.0% ± 9.1% of tumor voxels (range, 7.9%–46.0%). The KRCs calculated from the full dataset were 0.0032 ± 0.0015 min⁻¹ (range, 0.00071–0.0078 min⁻¹) for k₃ and 0.33 ± 0.13 min⁻¹ (range, 0.13–0.62 min⁻¹) for K₁. Subsequently, only clusters that resulted in k₃ > 0.001 min⁻¹ (i.e., greater than the value reported for normoxic tumors and normal tissue in head and neck (13)) were included in the analysis, 29 clusters for SD1 and 26 clusters for SD2. The results of correlation, Passing–Bablok, and Bland–Altman analyses are summarized in Figure 2 (FD-SD1), Figure 3 (FD-SD2), and Table 2. Strong correlation (r ≥ 0.75, P < 0.001) was observed between all corresponding KRCs. Passing–Bablok regression for FD-SD1 correlations showed no significant biases. Bland–Altman analysis revealed less than 1% and less than 10% mean differences between the calculated K₁ and k₃, respectively, which were reproducible to within approximately 6% and approximately 30%. However, as proportional bias was observed when comparing FD-SD2, Bland–Altman analysis was not conducted. The analysis was repeated for K_i (data not shown), and no significant biases were identified.

FIGURE 2.

Passing–Bablok regression (left) and Bland–Altman analysis (right) results for k₃ (top) and K₁ (bottom), calculated using full (FD; ~170 min) and ~100 min shortened (SD1) datasets in clinical studies (n = 29). Also displayed are regression line (blue) and its CIs (red) for Passing–Bablok regression and mean percentage difference (blue) with limits of agreement (red) for Bland–Altman analysis.

FIGURE 3.

Passing–Bablok regression results for k₃ (left) and K₁ (right), calculated using full (FD; ~170 min) and 45 min shortened (SD2) datasets in clinical studies (n = 26). Also displayed are regression line (blue) and its CIs (red).

TABLE 2.

Summary of Correlation, Regression, and Deviation Analyses

Dataset combination	KRC	Pearson r (95% CI)	Passing–Bablok				Bland–Altman
							P†	Mean % difference (95% CI)	95% limits of agreement (lower; upper)
			P*	Slope (95% CI)	Intercept (95% CI)	Residual SD (95% CI)
FD-SD1 (clinical) n = 29	k3	0.95 (0.89–0.98)	0.58	1.08 (0.94–1.32)	−6.0E-6 (−6.1E-4 to 5.3E-4)	3.4E-4 (−6.7E-4 to 6.7E-4)	0.20	−10 (−16 to −4)	−40; 21
	K1	1.00 (0.99–1.00)	0.58	0.99 (0.97–1.00)	0.0045 (−1.3E-4 to 0.011)	0.0058 (−0.011 to 0.011)	1.00	−1 (−2 to 1)	−7; 5
FD-SD2 (clinical) n = 26	k3	0.85 (0.69–0.93)	1.00	1.40 (1.01–1.86)	−6.8 E-4 (−0.0020 to 4.7E-4)	6.3E-4 (−0.0012 to 0.0012)	Analysis not conducted	Analysis not conducted	Analysis not conducted
	K1	1.00 (0.99–1.00)	0.86	1.04 (0.99–1.08)	−0.012 (−0.024 to 2.2E-4)	0.0060 (−0.012 to 0.012)	1.00	0 (−2 to 1)	−8; 7
FD-SD2 (preclinical) n = 21	k3	0.91 (0.79–0.96)	0.98	1.10 (0.89–1.38)	5.2E-4 (−5.1E-4 to 0.0013)	8.2E-4 (−0.0016 to 0.0016)	0.82	−26 (−43 to −8)	−100; 49
	K1	1.00 (0.99–1.00)	0.98	1.02 (0.98–1.06)	−0.0013 (−0.0079 to 0.0069)	0.0038 (−0.0075 to 0.0075)	1.00	−1 (−2 to 0)	−5; 3

^*Cumulative sum test.

^†Kolmogorov–Smirnov test.

FD = full dataset (~170 min in clinical, 90 min in preclinical studies); SD1 = first shortened dataset (~100 min); SD2 = second shortened dataset (45 min).

The area-under-the-receiver-operating characteristics values for the classification of cVOIs as hypoxic are given in Table 3. Pearson r between tumor-to-blood ratio and k₃ and K_i, as calculated using FD, were 0.71 and 0.90, respectively (P < 0.001). For classification analyses, all 32 clusters were included.

TABLE 3.

Summary of Classification Analyses

Dataset	KRC	AUC (95% CI; binomial exact)	Associated criterion
SD1, n = 32	k3	0.70 (0.51–0.85)	>0.0021
	Ki	0.91 (0.75–0.98)	>0.0027
SD2, n = 32	k3	0.80 (0.62–0.92)	>0.0034
	Ki	0.86 (0.69–0.96)	>0.0023

AUC = area-under-the-receiver-operating characteristics curve; SD1 = first shortened dataset (~100 min); SD2 = second shortened dataset (45 min).

Preclinical Studies

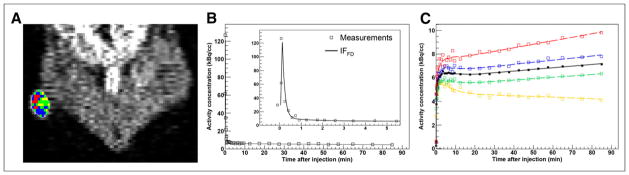
A coronal image for animal 1 (lesion 1) is shown in Figure 4A, and the IF and tumor time–activity curves are shown in Figures 4B and 4C, respectively. The discontinuities in the example clusters may be due to noise propagated by the image reconstruction.

FIGURE 4.

Kinetic modeling in tumor-bearing rodents (animal 1). (A) Definition of wVOI (white contour) on last 10-min frame of ¹⁸F-fluoromisonidazole dPET (coronal view), subclassified into 4 clusters (cVOIs). (B) Modeled input function based on full dataset (IF_FD), superimposed on measured time–activity curves. Insert shows initial 5 min of data. (C) Modeled time–activity curves derived from wVOI (solid line) and from 4 cVOI (dashed lines), superimposed on measured wVOI time–activity curve (■) and cVOI time–activity curves (□). cVOIs are color-coded to those shown in A.

Clusters included 25.0% ± 9.7% of tumor voxels (range, 7.4%–44.2%). Twenty-one clusters were included in the analysis (excluding those for which k₃ = 0). The KRCs calculated from the FD were 0.0040 ± 0.0026 min⁻¹ (range, 0.00041–0.0089 min⁻¹) for k₃ and 0.22 ± 0.076 min⁻¹ (range, 0.085–0.35 min⁻¹) for K₁. The results of correlation, Passing–Bablok, and Bland–Altman analyses are summarized in Figure 5 and Table 2. Strong correlation was observed in all cases. Passing–Bablok analysis revealed no proportional or systematic biases. Bland–Altman analysis revealed less than 1% and less than 25% mean differences between the calculated K₁ and k₃, respectively, which were reproducible to within approximately 4% and approximately 75%.

FIGURE 5.

Passing–Bablok regression (left) and Bland–Altman analysis (right) results for k₃ (top) and K₁ (bottom), calculated using full (FD; 90 min) and 45 min shortened datasets (SD2) in preclinical studies (n = 21). Also displayed are regression line (blue) and its CIs (red) for Passing–Bablok regression and mean percentage difference (blue) with limits of agreement (red) for Bland–Altman analysis.

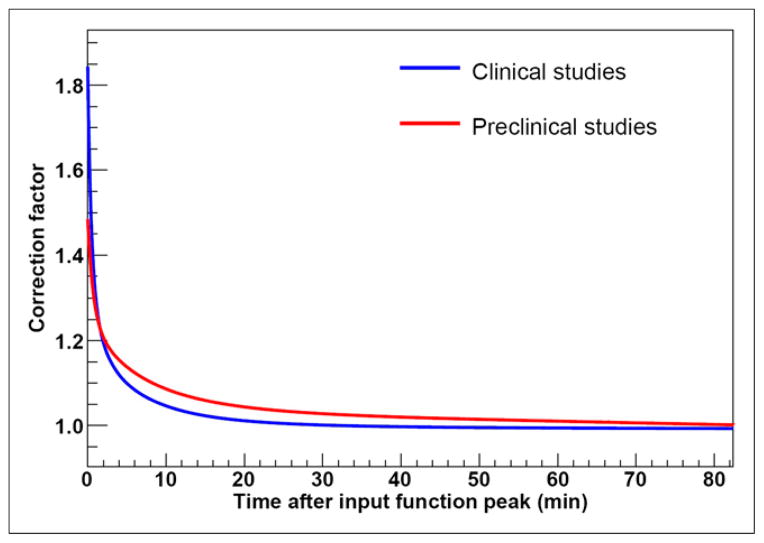
Correction factor to the input function due to partial-volume effect for pooled data from both clinical and preclinical studies is higher at initial times after injection because of the largest differences between activity concentrations of ¹⁸F-fluoromisonidazole in vasculature and surrounding tissue, falling to approximately 1 as ¹⁸F-fluoromisonidazole diffuses from the vasculature (Fig. 6).

FIGURE 6.

Correction factor for input function due to partial-volume effect, for pooled data from clinical and preclinical studies.

Simulations

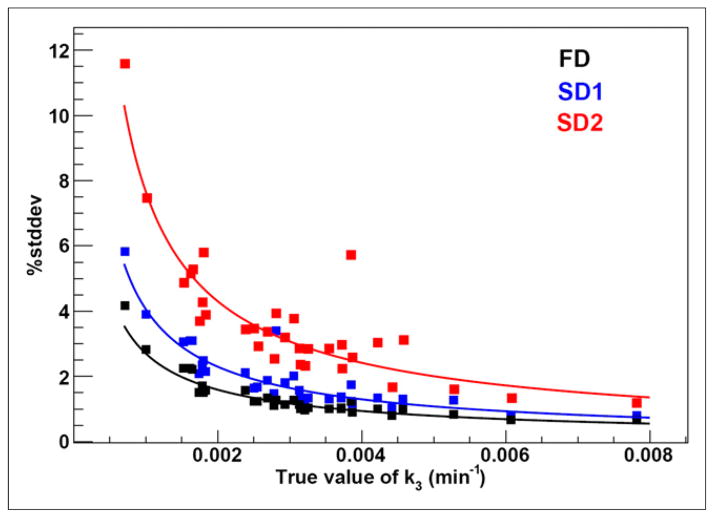
The average scaling factor c over the 50 VOIs was 0.064 ± 0.026. Although no bias was observed, the %stddev in k₃ increased for shorter acquisition times and was inversely proportional to the true value of k₃, ranging from approximately 1%–4%, approximately 1%–6%, and approximately 2%–12% for FD, SD1, and SD2, respectively (Fig. 7). For K₁, both %bias and %stddev were less than 1% in all cases. Correlation between K₁ as calculated using full and shortened noisy time–activity curves was strong (r > 0.90), whereas for k₃ it was lower (r = 0.55 for SD1 and r = 0.19 for SD2). A summary of simulation results is given in Table 4.

FIGURE 7.

Percentage SD in estimating k₃ from simulated data. FD = full dataset (~170 min); SD1 = first shortened dataset (~100 min); SD2 = second shortened dataset (45 min).

TABLE 4.

Summary of Simulation Results

Kinetic rate constant	Metric	Full dataset (~170 min)	First shortened dataset (~100 min)	Second shortened dataset (45 min)
k3	%bias	0.0 ± 0.1	0.0 ± 0.1	0.0 ± 0.2
	%SD	1.4 ± 0.7	2.0 ± 1.0	3.7 ± 2.0
	Pearson r (range)		0.55 ± 0.08 (0.33–0.85)	0.19 ± 0.13 (0.00–0.80)
K1	%bias	0.1 ± 0.1	0.1 ± 0.1	0.1 ± 0.1
	%SD	0.6 ± 0.2	0.6 ± 0.2	0.6 ± 0.2
	Pearson r (range)		0.96 ± 0.10 (0.43–0.99)	0.93 ± 0.09 (0.48–0.99)

DISCUSSION

dPET studies are largely confined to research applications, because the routine acquisition of multisession dPET scans is challenging. Despite reports that additional prognostic information such as the composite assessment of hypoxia and blood flow can be obtained from the analysis of ¹⁸F-fluoromisonidazole dPET data (21,22), static acquisitions at between 2 and 4 h after injection are predominantly used (23). We investigated the feasibility of kinetic modeling of ¹⁸F-fluoromisonidazole dPET using shortened acquisition times as a means of overcoming the limitations of both static and dynamic ¹⁸F-fluoromisonidazole imaging in identifying regions of tumor hypoxia in a clinically practical manner.

Measured uptake values on a voxel level exhibit considerable variations that represent not only differences in metabolic processes, but also noise, which is propagated through image reconstruction and kinetic modeling (10). Misregistration between the 3 ¹⁸F-fluoromiso-nidazole scans may additionally compromise the accuracy of voxel-wise kinetic modeling. Clustering was performed to reduce these effects, while maintaining the ability to study hypoxia and perfusion characteristics of tumor subvolumes.

Strong correlations were found between all corresponding KRCs as calculated using shortened and full datasets (Table 2). In the clinical studies, Passing–Bablok regression revealed no significant differences between the KRCs as calculated from the FD and SD1, implying that using the approximately100-min shortened datasets would not result in a bias in the estimation of KRCs. However, proportional differences were observed for FD-SD2 correlations. An increased residual SD with larger 95% CIs was also measured, showing that kinetic modeling of ¹⁸F-fluoromisonidazole dPET in SCCHN patients will be more prone to errors in determining the KRCs as the duration of the study is further shortened. In contrast, the results from the animal studies revealed no significant differences in the KRCs calculated from SD2 datasets. Narrower 95% CIs for slope, intercept, and residual SD were observed for KRCs calculated from the 45-min datasets in the animal compared with patient studies.

Results indicate that k₃ was overestimated when using shortened datasets. Analyzing kinetically heterogeneous regions with a compartment model designed for homogeneous tissues may result in the overestimation of k₃, the magnitude of which depends on the acquisition period (24,25). Although this effect has been observed previously (26–28), further investigations are necessary to understand its significance in the context of ¹⁸F-fluoromisonidazole dPET.

Causes for the differences in the results between patient and animal studies may be attributed to a variety of factors including the more rapid circulation time and metabolism in rodents compared with man, dissimilarity of pharmacokinetic characteristics of ¹⁸F-fluoromisonidazole in the 2 tumor types, different acquisition lengths for full datasets, the fact that the animals were anesthetized during the acquisition whereas the patients were not, and the increased uncertainty brought about by the need to coregister the piecewise acquisition in human studies. Additionally, list-mode PET data were not available for 2 patients. Thirty-second initial time frames were therefore used, resulting in a lower peak activity concentration of the IF, leading to less stable KRC estimates (13).

The area-under-the-receiver-operating characteristics, calculated to assess the reliability of shortened ¹⁸F-fluoromisonidazole dPET datasets for the task of identifying tumor hypoxia, was high when either k₃ (0.80) or K_i (0.86) values as calculated from 45-min dataset were used. These results suggest that single-session 45-min acquisitions in SCCHN patients may present an attractive alternative when used for identifying the presence of hypoxia on a tumor subvolume level.

Simulations were performed to assess uncertainties in ¹⁸F-fluoro-misonidazole kinetic modeling due to statistical noise and shortened acquisition time. The decrease in %stddev of k₃ with increasing k₃ value is a possible result of the steeper rise in ¹⁸F-fluoromisonidazole uptake that allows a more precise estimation of k₃. K₁ remained accurately estimated using shortened datasets, as observed in both patient and animal studies. As K₁ is predominantly determined from the early parts of time–activity curves, the correlation between K₁ as calculated using full versus shortened noisy time–activity curves was higher than the corresponding correlation for k₃ (which strongly depends on the later parts of time–activity curves). No bias in K₁ or k₃ was observed when shortening the acquisition time, because kinetic modeling for shortened datasets was performed using truncated mTAC_FD and IF_FD. These results indicate that K₁ and k₃ could in principle be calculated accurately from shortened acquisitions. The discrepancy between simulation and clinical results, however, is due to the difference in the shape of time–activity curves as modeled using full or shortened datasets, which in turn highlights kinetic heterogeneity within tumor subvolumes as a potential source of bias (24,25). When the analysis in clinical studies was repeated using IF_FD for all datasets, the overestimation of k₃ was not reduced (data not shown). The potential impact of misregistration between the 3 ¹⁸F-fluoromisonidazole scans on overestimation of k₃ (by means of combining tumor regions with different pharmacokinetic properties) is a subject of an ongoing study.

A limitation of this study was the small sample size. The used statistical methods do not address the clinical significance of the results. The clinical significance of differences between the kinetic rate constants as calculated from shortened and full dPET datasets has not yet been evaluated. Further, a test–retest study will be necessary to investigate the reproducibility of ¹⁸F-fluoromisonidazole kinetic modeling.

CONCLUSION

Using single-session 45-min shortened ¹⁸F-fluoromisonidazole dPET datasets appears to be adequate for the identification of intratumor regions of hypoxia. However, k₃ was significantly overestimated in the clinical cohort. Further studies are necessary to evaluate the clinical significance of differences between the results as calculated from full and shortened datasets.