Conformational Sub-states and Populations in Enzyme Catalysis

Abstract

Enzyme function involves substrate and cofactor binding, precise positioning of reactants in the active site, chemical turnover, and release of products. In addition to formation of crucial structural interactions between enzyme and substrate(s), coordinated motions within the enzyme-substrate complex allows reaction to proceed at a much faster rate, compared to the reaction in solution and in the absence of enzyme. An increasing number of enzyme systems show the presence of conserved protein motions that are important for function. A wide variety of motions are naturally sampled (over femtosecond to millisecond time-scales) as the enzyme complex moves along the energetic landscape, driven by temperature and dynamical events from the surrounding environment. Areas of low energy along the landscape form conformational substates, which show higher conformational populations than surrounding areas. A small number of these protein conformational sub-states contain functionally important structural and dynamical features, which assist the enzyme mechanism along the catalytic cycle. Identification and characterization of these higher-energy (also called excited) sub-states and the associated populations is challenging, as these sub-states are very short-lived and therefore rarely populated. Specialized techniques based on computer simulations, theoretical modeling and nuclear magnetic resonance (NMR) have been developed for quantitative characterization of these substates and populations. This chapter discusses these techniques and provides examples of their applications to enzyme systems.

1. Introduction

A number of factors contribute to an enzyme’s ability to accelerate a biochemical reaction by several orders of magnitude as compared to the reaction in water (Benkovic & Hammes-Schiffer, 2003; Agarwal, 2006). It is well known that enzymes achieve this acceleration by providing special structural and electrostatic environments suitable for the chemical reaction to occur (Warshel, et al., 2006). The designated function of an enzyme molecule is, therefore, to provide an environment that is considerably different from the bulk-solution, and which favors the reaction to proceed at a much faster rate than otherwise possible. A wealth of information is available about the role of structure in enzyme function (Knowles, 1991), and it is also widely acknowledged that enzymes provide electrostatic and structural stabilization of the transition state and other intermediates during the reaction (Benkovic, 1992). Recent investigations show that even if these two are taken into account, the catalytic efficiency cannot be fully explained for a large number of enzymes (Agarwal, 2005). Emerging evidence indicates that enzyme rates may be closely tied to ability of enzymes to sample through a number of alternate structures (or conformational sub-states) such that it allows the reactive environment to achieve structural and electrostatic complementarity to the transition state (and other intermediate states) along the reaction (Ramanathan, Savol, Burger, Chennubhotla, & Agarwal, 2014).

In the more familiar paradigm, the catalytic cycle involves the binding of substrate(s), and if required cofactor(s), and the positioning of these into the correct orientation into the active site. This is followed by the actual chemical step or substrate turnover. Then, the product(s) and spent cofactor are released (Boehr, McElheny, Dyson, & Wright, 2006). Inherently, the movement of various molecules in and out of the active site would require enzyme motion; such passive motions could be considered as a consequence of these binding/release events. However, evidence continues to build strongly in favor of some of the protein motions playing a much more active or promoting role in the catalytic cycles of enzymes. Protein motions occur over 12 orders of magnitude in time, allowing enzymes to sample vastly different conformations. Large-scale motions or conformational fluctuations at long time-scales enable the sampling of high energy intermediates or a group of conformations (conformationalsub-state ). Experimental evidence continues to indicate that the rate of sampling of correct motions is somehow connected to the time-scale (or rate) of the various events in the enzyme cycle (Boehr, Dyson, & Wright, 2006; K. A. Henzler-Wildman, et al., 2007). In particular, if the rate-limiting event of enzyme cycle requires a conformational motion of the enzyme, then the catalytic efficiency is directly tied to the sampling of the conformational sub-state and conformations transitions into this substate (Ramanathan, et al., 2014).

Investigations indicate that sampling of these conformational sub-states is an intrinsic property of an enzyme, and is observed even in the apo form of the enzyme (Eisenmesser, Bosco, Akke, & Kern, 2002). In a number of nuclear magnetic resonance (NMR) experiments it has been observed that an enzyme does not necessarily experience a unique structural signature (corresponding to a homogeneous population) at each sub-step along the catalytic cycle (Boehr, McElheny, et al., 2006). Rather, it is much more likely that the enzyme samples not only the majority of conformations in a single sub-states but that it also samples the minor conformations associated with the neighboring sub-states. Overall, this is an indication of the fact that the enzyme landscape is full of conformational states, which are sampled over different time-scales (Ramanathan, Savol, Langmead, Agarwal, & Chennubhotla, 2011).

To understand the catalytic efficiency of the full enzyme cycle as well as to understand the relevance of motions and conformational sub-states along the catalytic cycle, it is important to quantitatively characterize the sub-states and the conformational transitions along the landscape (Ramanathan, et al., 2014). Experimental information has been difficult to obtain because the time-scales involved can vary several orders of magnitude (see Figure 1) (Kleckner & Foster, 2011), while each experimental technique has an inherent limitation of time-scale(s)/resolution. It has been recently suggested that a joint effort between computational and experimental techniques can provide much more useful ways of obtaining data and deciphering the information. In this chapter, we discuss computational and theoretical techniques that allow the characterization of the dynamics and the associated conformational sub-states. Discussion is also presented regarding the current methodologies to extract information on conformational sub-states using NMR relaxation dispersion experiments. Finally, we provide two illustrative examples on how these techniques are applied to enzyme catalysis.

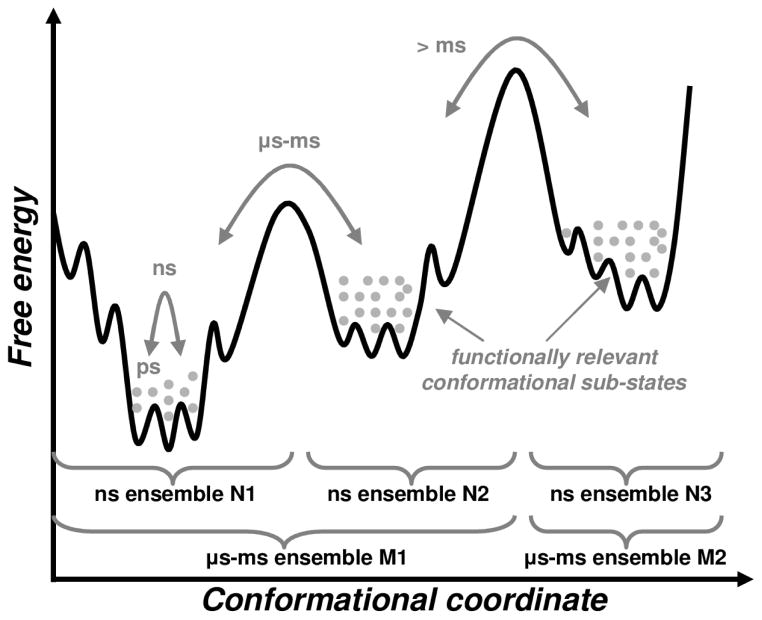
Figure 1. Conformational sub-states in enzyme landscape.

Protein motions allow an enzyme to sample a variety of conformational sub-states. Motions within sub-states occur on fast time-scales (ps-ns) and conformational fluctuations at longer time-scales (μs-ms and >ms) allow overcoming large barriers, enabling access to other sub-states in the conformation hierarchy. Gray dots indicate unique conformations. The conformations within each well (sub-state) form ns ensembles (N1, N2 and N3), while μs-ms ensembles would correspond to wider areas (M1 and M2). This figure is partially is based on information from ref. (Kleckner & Foster, 2011).

2. Theoretical Concepts

Proteins, including enzymes, sample distinct conformations enabled by internal motions on a wide range of time scales (Frauenfelder & Leeson, 1998; Kleckner & Foster, 2011). The motions within proteins range from bond vibrations that occur on femtosecond time-scales to slow conformational fluctuations of domains that occur on microsecond (or longer) time-scales. In the intermediate time-scales are movements of loops and coordinated movements of beta-sheets. As depicted in Figure 1, the various low energy regions of the protein energy landscape (valleys or energy wells) are separated by barriers associated with conformational changes on the microsecond-millisecond (μs-ms) or longer (>ms) time-scale, while within-well sampling operates at faster picosecond-nanosecond time-scales (ps-ns) (K. Henzler-Wildman & Kern, 2007). Thermodynamic sampling governs sub-state populations and their transitions according to temperature and energy barrier height. Some energy wells have more population (densely populated) while others may be less populated (scarcely populated). Emerging evidence suggests that protein function (such as enzyme catalysis) is facilitated by conformational sub-states that promote specific interactions between reactants at various stages in the catalytic cycle (Boehr, McElheny, et al., 2006; Eisenmesser, et al., 2002; Goodey & Benkovic, 2008; K. A. Henzler-Wildman, et al., 2007).

Experimental investigations and computer simulations show that protein internal motions generate a distribution, or ensemble, of structures. Depending upon the experimental technique used or time-scale of computer simulations, data on different types of ensemble can be collected. For example, in Figure 1, N1, N2 and N3 correspond to ps-ns ensembles, while M1 and M2 correspond to μs-ms ensembles. Thermo-dynamical sampling allows enzymes to visit many of these alternative conformations; therefore, during analysis it would not be possible to assign catalytic relevance a priori to a single conformation and ignore functional characteristics of all others. On the contrary, these alternative conformations, or conformational sub-states (and their transitions) are increasingly understood as promoting function (Fraser, et al., 2009; Fraser, et al., 2011). In this new paradigm, the internal protein motions are critical to, not a byproduct of, enzyme function.

The challenge associated with characterizing the conformational sub-states partially arises from the fact that the protein conformational landscape is multi-dimensional and the conformational sub-states involve multiple dimensions (or variables). Therefore, techniques are required to reduce the multi-dimensional representation into lower dimensional space (with limited variables). In the past, several definitions of conformational sub-states or intermediates have been used where classification of conformations is based on geometrical quantities from active sites (such as important inter-atomic distances or angles) or based on other quantities such as orientation of a few residues or loop regions. However, this requires an assumption and/or prior knowledge of the importance of residues. In reality, the conformational sub-states are defined by thermo-dynamical sampling; therefore, any technique that proposes to identify correct conformational sub-states should also be able to provide clear energetic separation in the landscape. In this chapter, we use a fundamentally different definition of conformational substates, which is based on identification of functionally relevant conformational fluctuations, and does not require prior knowledge of the mechanism or important residues. This is an automated process and one of the advantages is that it can achieve consistency with internal energy-based separation. This is discussed in more detail in section 5 below.

3. Ascertaining conformational sub-states and populations from relaxation-dispersion NMR

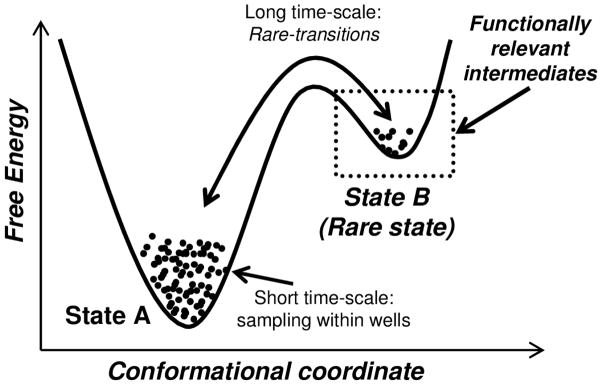
Enzyme active sites achieve transition state stabilization by forming critical interactions with substrate(s). At transition state, the enzyme structures themselves are under strain and a part of higher energy conformations. Figure 2 shows a schematic of how an enzyme in ground state A samples another state B with higher energy conformations, enabled by conformational transitions that occur on slow time-scales (milliseconds). Sub-state B could contain functionally relevant conformations that stabilize the transition state and therefore promote the enzyme reaction. Due to the higher energy of state B, the population in this state is lower and sampled infrequently. When enzymes are investigated using techniques such as NMR (either in apo or substrate-bound forms), the resulting dynamic equilibrium ensemble data is populated by a mix of conformational populations, with the major population represented by the ground state A and the minor excited population by state B. The minor population of state B has been referred to as hidden or invisible, as it is masked by the major population of state A.

Figure 2. Conformational transitions enable enzymes to sample higher energy sub-states.

In a hypothetical case where enzyme samples two states A and B. State A is in lower energy and has higher population and state B is higher in energy and has lower population. State B contains conformations that are functionally relevant; therefore, in this case the sampling of conformation transitions at long time-scale (and its rate) that enable access to state B will be important for function as well.

Experimental NMR relaxation investigation allows one to decompose this NMR data into information about the two states A and B and the populations associated with them. Spin-relaxation rates, especially those of transverse (R₂) magnetization, have been particularly useful to characterize the rate of conformational exchange between such states on the millisecond time-scale, further providing quantifiable information on the equilibrium site populations (p_A and p_B). In recent years, the relaxation-compensated Carr-Purcell-Meiboom-Gill (rcCPMG) and R_1ρ experiments have been extensively used to characterize functionally relevant conformational exchange at specific local and/or global atomic sites within enzymes, specifically because they sample the millisecond time-scale of catalysis (k_cat) in most enzyme systems (Kleckner & Foster, 2011; Lisi & Loria, 2016; Palmer, 2015). The rcCPMG experiment has been the method of choice to probe a two-site chemical exchange experienced by ¹H-¹⁵N backbone amide vectors (¹⁵N-CPMG), providing a precise atomic-scale measure of the millisecond dynamics experienced by nearly every residue on a given enzyme. Despite considerable experimental improvements in recent years – especially with respect to higher molecular weight systems (Kay, 2015) – routine ¹⁵N-CPMG analysis remains dependent on the lack of resonance overlap and overall quality of the two-dimensional ¹H-¹⁵N heteronuclear single quantum coherence (HSQC) spectra of enzymes under study. Analyzing the line shape, width and chemical shift of the ¹H-¹⁵N HSQC resonances allows one to extract information on residues experiencing conformational exchange, providing quantifiable data on the invisible excited states rarely populated in solution (p_B). The theory and experimental implementation of the rcCPMG experiment is beyond the reach of the present review and has been treated in detail elsewhere (Ishima, 2014; Palmer, Kroenke, & Loria, 2001). Here, we provide a quick overview of the type of information obtained from multiple-field fits of the R₂ relaxation data measured as a function of the spacing τ_CP between successive π pulses in a CPMG echo sequence. Useful parameters extracted from such experiments include the weight of equilibrium populations (p_A and p_B), the chemical shift differences between each state ω_A and ω_B (Δω), and the rate of conformational exchange (k_ex) between each state.

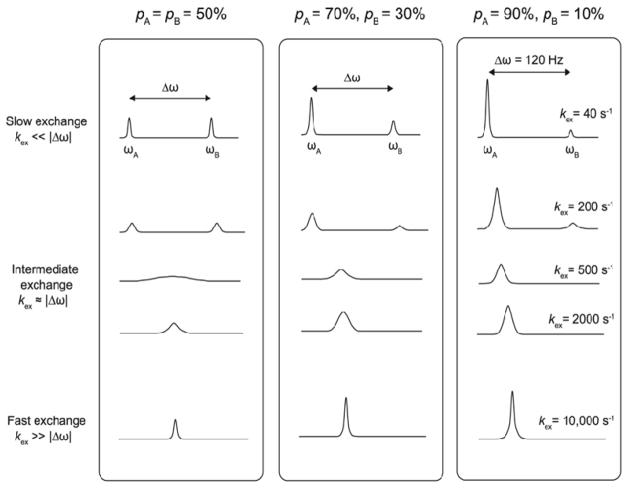
NMR is particularly well suited to study subtle structural changes occurring in proteins, since distinct populations A and B arising from slow structural transitions between two or more states give rise to magnetically distinct line shapes and chemical shift resonances in NMR spectra (e.g. ω_A and ω_B in a two-site exchange system) (Figure 3). This is particularly obvious for systems where the exchange rate (k_ex) between the two states A and B occurs on a slow time-scale (k_ex≪ Δω), and for approximately equal population ratios (e.g. 50% p_A and p_B), or slightly skewed population ratios (e.g. 70% p_A and 30% p_B). Note that k_ex corresponds to the arrow that goes between the two states in Figure 2. While this ideal situation provides structural information on populated states exchanging on a time-scale slow enough to allow the appearance of individual line shapes for each populated state, it does not provide any functional information on the rarely populated (p_B < 5–10%), higher energy conformers exchanging on a much faster time-scale (e.g. k_ex > 1000 s⁻¹). This situation is typical of enzyme systems experiencing conformational exchange between highly skewed populations on the fast NMR regime (k_ex ≫ Δω), where the functionally relevant, higher-energy conformer B is so rarely populated that it is often invisible (i.e. displaying a highly broadened line shape) in the NMR spectrum, despite it being potentially involved in stabilizing a transition state, positioning a specific reactant, and/or releasing a reaction product. Figure 3 presents theoretical examples where the rcCPMG method provides the theoretical means to extract, analyze and quantify these hidden, low-populated states experiencing conformational exchange on the millisecond time-scale, which often overlaps with the rate of catalysis (k_cat) in many enzyme systems.

Figure 3. Two-site conformational exchange experienced by a ¹H-¹⁵N amide vector sampling distinct weighted populations of states A and B on various NMR time-scales.

All three columns report on simulated two-state chemical exchange where the populations of each state (p_A and p_B) are skewed, with Δω = 120 Hz and k_ex = 40, 200, 500, 2000 or 10,000 s⁻¹. For clarity, values of Δω and k_ex are only labeled in the right column. Slow exchanging populations sampling states A and B give rise to two distinct line shapes corresponding to magnetically distinct conformers of equal weight (column 1, ω_A and ω_B), separated by chemical shift difference Δω. Resonance signal broadening results from increased rates of chemical exchange between each state (local dynamics) on the intermediate and fast time-scale regimes, where a single weighted-average chemical shift population is observed (k_ex > 500 s⁻¹ in this particular example). A single, sharper signal with distinct intensity and line width is observed on faster time-scales. A similar behavior is observed when the p_A and p_B population ratio is significantly skewed in favor of ground state A (columns 2 and 3). While excited state B is invisible on intermediate and fast time-scales, the shape and chemical shift of the resulting NMR signal is proportional to each population state. Relaxation-dispersion NMR experiments such as the rcCPMG and R_1ρ methods provide the theoretical means to extract, analyze and quantify these hidden, low-populated states experiencing conformational exchange on the millisecond time-scale, which often overlaps with the rate of catalysis (k_cat) in many enzyme systems. Adapted from ref. (Kempf & Loria, 2004).

4. Obtaining conformational sub-states from simulations

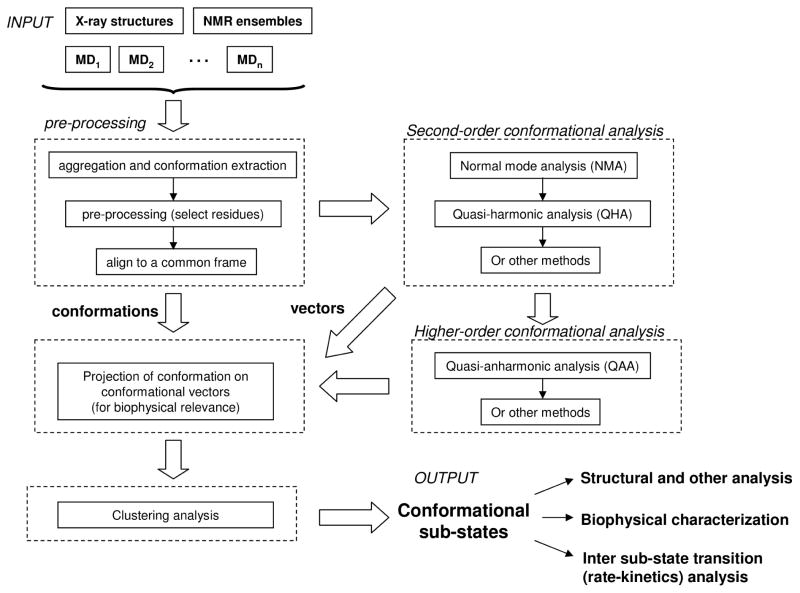
The general scheme used for identification and characterization of the conformational sub-states is described in Figure 4. The protein conformational landscape is highly multi-dimensional (hundreds to thousands of dimensions correspond to the number of atoms and internal degrees of motion). It is not practical to inspect each dimension (or even two or three at a time) for characterization of the full landscape. For visualization and interpretation, methods are required to find alternate representation that reduce this complex multi-dimensional conformational landscape to a simple representation. Typically, this is done by finding a set of a limited number of alternate variables (typically ranging between 3 and 10) where the entire conformational data set can be visualized at a time. A number of techniques have been used to identify such variables or independent coordinates based on the use of principal component analysis (PCA) or related second-order methods. These methods provide eigenvectors corresponding to large-scale protein and enzyme motions, and the conformations can then be projected on these independent coordinates to identify the locations of various sub-states along the conformational landscape. A number of second-order methods are available to obtain the protein motions from individual protein structures (conformation) or a collection of conformations. These are briefly described below.

Figure 4. Protocol for extraction of conformational sub-states and populations.

The input to the method is a set of structures or conformations (from X-ray, NMR or MD simulations), which after preprocessing are used to obtain second-order conformational vectors. For more accurate characterization higher-order methods are used. The obtained vectors are used for projecting the conformations from initial set of conformations. The results are analyzed by clustering method to classify the conformations into sub-states.

4.1 Normal mode analysis (NMA)

This method computes vibrational modes of a molecular system by diagonalization of the Hessian matrix (Leach, 2001; Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems, 2005). Assuming the molecular system has N atoms, the Hessian matrix is a 3N × 3N matrix. The elements of the matrix are the second-order energy derivatives with respect to the displacement of atomic positions in the x, y, z directions. The elements can be computed analytically (for small systems) or computationally (for larger systems like enzymes). Once the Hessian matrix is computed, it is diagonalized to solve for the eigenvectors and eigenvalues.

$${\mathrm{\epsilon }}_{\mathrm{i}}\mathit{F}={\mathrm{\epsilon }}_{\mathrm{i}}{\mathrm{\omega }}_{\mathrm{i}}$$ (1)

The time-scale of molecular vibration is determined by taking the inverse square root of the eigenvalues (ε) obtained after diagonalization. The eigenvector (ω) corresponding to the eigenvalue represents the vibrational modes, which are a set of displacement vectors for the atoms in the molecular or the protein conformation.

4.2 Time-averaged normal coordinate analysis (TANCA)

This method is similar to NMA in the sense that the vibrational modes of a protein (or protein vibrational modes) are obtained by diagonalization of the Hessian matrix (Hathorn, Sumpter, Noid, Tuzun, & Yang, 2002; Tuzun, Noid, Sumpter, & Yang, 2002). However, NMA suffers from some limitation when considering a highly flexible molecular system such as a protein. NMA uses a reference structure and the eigenvalues and eigenvectors thus obtained are only relevant to the reference starting structure. The method therefore weights highly toward the high frequency motions and less toward the low frequency motions. Moreover, the low frequency obtained using NMA are not reliable for molecular conformations that differ considerably from the reference structure for NMA. In enzyme function the low frequency motions are more important as they are required for overcoming the high-energy barriers. Techniques such as TANCA can partially overcome this problem by diagonalization of the Hessian matrix which has been constructed numerically by averaging the elements over time (from multiple structures). This allows the fast frequency motions to be removed by averaging providing more accurate low frequency modes that are relevant for enzyme function (Ramanathan & Agarwal, 2009).

4.3 Quasi-harmonic analysis (QHA)

This method computes protein vibrational modes from a set of protein conformations that are sampled using either the molecular dynamics (or Monte-Carlo) type simulations (Perahia, Levy, & Karplus, 1990). QHA is a powerful method in obtaining protein vibrational modes that are representative of longer time-scales or the low frequency vibrations, by utilizing the information from a set of structures, which may be separated by a long time scale – or from different parts of the protein conformational space. The vibrational modes are obtained by diagonalization of the atomic fluctuation matrix. For a protein with N atoms, the atomic fluctuation matrix, F is a symmetric 3N × 3N matrix with term F_αβdefined as:

$${\mathit{F}}_{\alpha \beta }=\langle {m_{\alpha }}^{1/2}(x_{\alpha }-\langle x_{\alpha }\rangle ){m_{\beta }}^{1/2}(x_{\beta }-\langle x_{\beta }\rangle )\rangle$$ (2)

where α,β run through the 3N degrees of freedom in Cartesian space and m_α is the mass of atom corresponding to the αth degree of freedom and x_α are the Cartesian coordinates of the atom corresponding to the αth degree of freedom. Quantities in ‹› denote an average determined from molecular dynamics (MD) simulation. To obtain the eigenmodes (vibrational modes), diagonalization of the atomic fluctuation matrix is performed (see Eq. 1). The time-scale of protein vibration is determined by taking the inverse square root of the eigenvalues (ε) obtained after diagonalization. The eigenvector (ω) corresponding to the eigenvalue represents the protein vibrational modes, which are a set of displacement vectors for the atoms in the protein confirmation. Note one of the benefits of QHA is that multiple MD trajectories can be combined to construct the atomic fluctuation matrix – thus allowing vibrational modes to be computed that represent conformational changes between different areas of the protein conformational space.

4.4 Elastic anisotropic network models (ANM)

This type of calculation uses coarse-grained normal mode analysis to obtain protein conformational modes (Doruker, Jernigan, & Bahar, 2002; Haliloglu, Bahar, & Erman, 1997). These calculations use a simple parameter harmonic potential for the particles in the system. The eigenmodes are obtained by the diagonalization of Kirchhoff’s matrix, which is similar to the Hessian matrix, but uses a reduced model of the protein and treats the protein motions as Gaussian-type motions.

For an enzyme-based system, only the coordinates of enzyme, substrate and cofactor are used for calculating the vibrational modes. Typically non-reactive ions and solvent molecules are excluded from this analysis. Each of the methods discussed above provides a set of vector (or independent vectors), each 3N in length, corresponding to x, y, z displacement vectors for N atoms. In addition to identification of vectors the other requirement to obtain conformational sub-states is a set of enzyme conformations. The conformations are usually collected from MD simulations. A single trajectory or multiple trajectories can be used. In addition, it is also possible for conformations from NMR ensembles and a collection of X-ray structures to be used for projection and subsequent analysis.

Typically a small number of vectors (3–10) are used for further analysis, as they can capture a large fraction of the protein motion (in terms of variance). The first few vectors correspond to the slowest motions that occur at slow time-scales. Using these vectors, the conformations from the ensemble are projected on each of these vectors. Once the conformations (MD and/or X-ray/NMR based) are projected, a clustering method is used for identification of the sub-states. Well-defined clusters represent sub-states while diffused conformations over landscape (where it is difficult to define clusters) correspond to a flat landscape with little possibility of sub-states. It should also be noted that the inability to get proper clusters (substates) could also be an indication of the limitation of the underlying computational methodology used for the vector extraction. Note that the same set of conformations can be used as input to obtain the independent coordinates (vectors) and then to obtain the projections on the vectors.

5. Anharmonic conformational analysis (ACA)

The techniques discussed in the previous section are second-order methods based on the assumption that the protein sub-states and overall landscape can be described by harmonic or quasi-harmonic wells (H, Q in Figure 5). However, a number of experiments, including the one combining neutron scattering experiments with computational modeling on protein thermophilic rubredoxin, indicate that the protein motions are anharmonic and that the onset of anharmonic structural changes activates functionally relevant motions (Borreguero, et al., 2011).

Figure 5. Protein energy landscape.

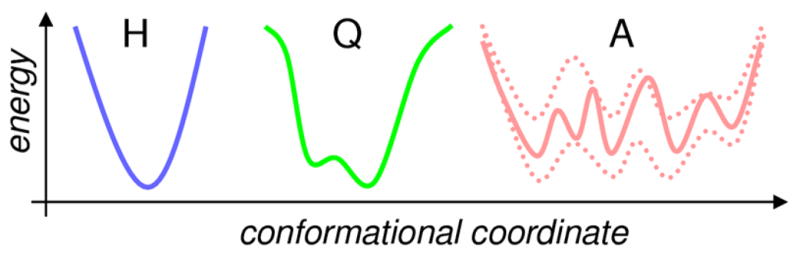
(along individual conformational coordinates) can be classified as harmonic (H), quasi-harmonic (Q) or anharmonic (A). Harmonic landscapes with a single sub-state (well) can be well described by second-order methods. Quasi-harmonic landscapes can be approximated by second-order methods depending on how well a harmonic function is able to fit into the multiple sub-states. Anharmonic landscapes with multiple substates are poorly approximated by second-order methods and require higher-order methods for accurate characterization.

This assumption of second-order motions has an important consequence. It can lead to inaccurate characterization of protein conformational sub-states in that heterogeneous conformers are incorrectly grouped into a single conformational sub-state (Figure 6). Neighboring conformations in a conformational sub-state are expected to have similar energy and functionally relevant geometrical/kinetic properties. When the protein motions are anharmonic with multiple wells in the conformational landscape, the use of higher order methods is necessary for identifying them.

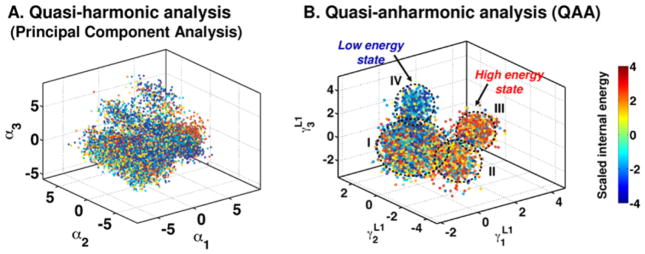
Figure 6. The benefit of using a higher-order statistical method allows identification of conformational sub-states with homogeneous properties.

Conformational sub-states identification for protein ubiquitin was performed using two different methods. (A) The conformational sub-states identified by second-order methods such as quasi-harmonic analysis and principal component analysis do not achieve clear of separation and the population of the conformation show mixed properties. (B) Using a higher-order method such as quasi-anharmonic analysis (QAA) allows identification of sub-states that are clearly separated and conformations have homogeneous properties. In both panels, each dot corresponds to a single conformation and the coloring is by scaled internal conformational energy.

5.1 Quasi-anharmonic analysis (QAA)

To quantify the anharmonic time-dependent conformational changes (A in Figure 5), we have introduced an approach called quasi-anharmonic analysis (V. M. Burger, et al., 2012; Ramanathan, Agarwal, Kurnikova, & Langmead, 2010; Ramanathan, Savol, Agarwal, & Chennubhotla, 2012; Ramanathan, et al., 2011; Savol, Burger, Agarwal, Ramanathan, & Chennubhotla, 2011). QAA uses fourth-order statistics (for analytical convenience) to describe the atomic fluctuations and summarizes the internal motions using a small number of dominant anharmonic modes. We have successfully demonstrated this approach in the context of protein functions such as molecular recognition (ubiquitin and lysozyme) and enzyme catalysis (human cyclophilin A) (Ramanathan, et al., 2011). An emergent property of QAA is that by characterizing anharmonicity in positional fluctuations, our method discovers energetically homogeneous conformational sub-states. Note that emergent implies that the discovered homogeneity is achieved without any prior knowledge of the internal energy of the systems.

After aligning the MD ensemble, the QAA approach is to use a small set of anharmonic basis vectors to represent the positional deviation vectors of each conformer:

$$\mathrm{\delta }\mathbf{x}=\mathbf{A}\mathrm{\gamma }$$ (3)

Here, δx denotes the positional deviation vector of size (3N × 1), where N is the number of atoms, A is a matrix of size (3N × m) (where m ≪ 3N) derived from an approximate diagonalization of a tensor built to hold the fourth-order statistics of positional deviations δx. The anharmonic modes of motion, which are the columns of A, are sorted in the decreasing order of their norms for convenience. Each anharmonic basis vector a_i in the matrix A has an excitation coefficient γ_i. Just like PCA, A fully decorrelates the input ensemble, i.e., there are no second-order dependencies between the elements of γ. In addition, matrix A is guaranteed to reduce fourth-order dependencies. By construction, A can be non-orthogonal (unlike the PCA modes), meaning that exciting anharmonic mode a_i can also effect a_j because of non-orthogonal coupling between the basis vectors. By design, QAA ignores any non-linear coupling that may exist in the fluctuations between different parts of a protein.

The various steps involved in performing QAA are (see Figure 4):

1. Apply Gaussian-weighted root mean square deviations (RMSD) superposition algorithm on the MD ensemble to identify rigid and flexible residues (Ramanathan, et al., 2012).

2. Use rigid residues to iteratively align the MD ensemble. Find the positional deviations from the iteratively derived mean conformer.

3. Build a low-dimensional representation for the fluctuations of the backbone or C_α atoms using PCA.

4. Choose a low-dimensional subspace m (say 50 or so) that captures 90–95% of overall variance. This initial projection onto the top m PCA bases reduces the dimensionality of the problem from 3N to m and helps speed up convergence of the learning algorithm for QAA.

5. Learn the QAA matrix A, sort the anharmonic modes in decreasing order of their magnitude. For visualization, build a (dimension-reduced) anharmonic space of coefficients: γ₁, γ₂, and γ₃.

6. To gain additional insights into the conformational landscape, label (or color) each triplet in the anharmonic space by either experimental or computational features such as scaled internal energy, inter-domain distance, etc.

5.2 Identifying conformational sub-states

Observe that neighboring conformers in QAA space have biophysically relevant coordinates (Figure 6), and this coherence is an emergent property of the QAA representation. Based on this observation, we hypothesize that nearest neighbors in the QAA space can be hierarchically clustered to form dynamically and kinetically related metastable states.

To this end, we consider each frame in the trajectory as a node in an undirected graph constructed in the m-dimensional QAA space. We connect each node to a small number of its nearest Euclidean neighbors. The edges weights are binary (either 0 or 1), denoting either the presence or absence of an edge. We then cluster this network using a hierarchical Markov diffusion framework that we have proposed previously (V. Burger & Chennubhotla, 2012; V. M. Burger, et al., 2012; Chennubhotla & Bahar, 2007a, 2007b; Savol, et al., 2011). First, we initiate a Markov chain to propagate on the network and identify a set of putative cluster centers. The total number of clusters is automatically determined by the algorithm, with the rule that every node in the network has some Markov probability of transitioning into at least one of the putative cluster. Second, a Markov transition matrix is built using this reduced representation based on the principle that Markov chains initiated on both the fine scale and coarse scale representations of the network should reach stationary distributions simultaneously. This principle in turn helps build a hierarchical representation of the network and promotes formation of meta-stable clusters in the data. We expect that fine-grained hierarchy levels will produce many small clusters containing close neighbors in the QAA space; that is, within each such cluster most members will be drawn from the same, narrow time-window. As Markov diffusion progresses (fine-grained to coarse-grained), conformers that are more distant neighbors will be connected by edges in the diffused network and will therefore be assigned to the same cluster. Thus, the hierarchical clustering can highlight dynamical connections between conformers at different timescales.

QAA is one component of a larger suite of tools that we developed, termed as anharmonic conformational analysis (ACA), to probe molecular recognition pathways (Savol, et al., 2011) and to reveal intermediate states in intrinsically disordered proteins (V. M. Burger, et al., 2012).

6. Examples of conformational sub-states in enzyme catalysis

6.1 Hydride transfer catalyzed by dihydrofolate reductase

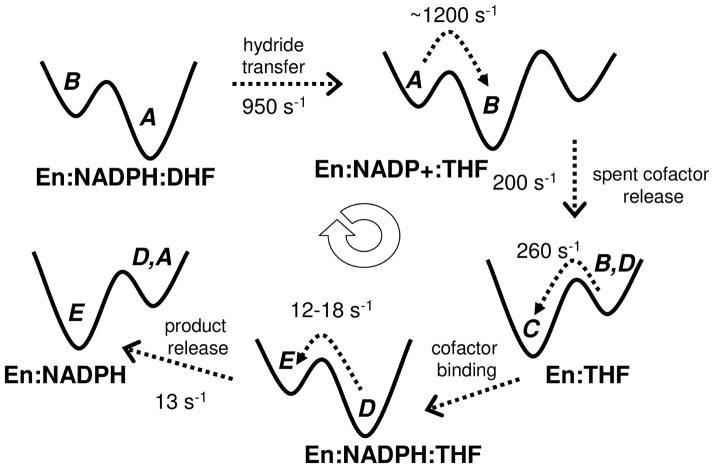
The enzyme dihydrofolate reductase (DHFR) catalyzes the conversion of substrate dihydrofolate (DHF) to tetrahydrofolate (THF) and uses nicotinamide adenosine dinucleotide phosphate (NADPH) as a cofactor. The catalytic cycle of Escherichia coli DHFR (EcDHFR) consists of at least five sub-states corresponding to intermediates associated with the substrate (DHF) and cofactor (NADPH) binding, the chemical step of hydride transfer and the product (THF) and spent cofactor (NADP⁺) release. Using ¹⁵N spin-relaxation NMR techniques (mostly the rcCPMG described above), Wright and co-workers discovered that at each intermediate along the catalytic cycle represents sampling of populations from multiple conformational sub-states (Figure 7) (Bhabha, Biel, & Fraser, 2015; Boehr, Dyson, et al., 2006; Boehr, McElheny, et al., 2006).

Figure 7. Conformational sub-states associated with the catalytic activity of enzyme E. coli DHFR.

The enzyme DHFR (En) catalytic cycle consists of 5 intermediate states associated with binding and release of cofactor NAPDH, substrate DHF, spent substrate NADP+ and product THF. Each of these intermediate sample multiple enzyme conformations sub-states (A, B, C, D, or E). The available rates of conversion between the intermediates and the conformational exchange between sub-states are labeled. Note that for each of these intermediate states the lower energy well will have higher population and the higher energy wells will have much lower conformational populations. Adapted from (Boehr, McElheny, et al., 2006).

Each intermediate samples the majority of conformational populations relevant to the current state; however, a small fraction of the population also samples the neighboring sub-states (Boehr, McElheny, et al., 2006). The conformational sub-states are stabilized by interactions with the substrate and cofactor. Therefore, the minority of conformations sampled in the present state over time become the major conformations for the subsequent intermediate in the cycle. The rate of the conversion between different intermediate states was observed to coincide with the rate of sampling of inter-conversion between the majority and minority of conformational states (see dashed arrows in Figure 7). For example, the maximum rate of hydride transfer step (the rate-limiting step of the EcDHFR mechanism at pH > 8.5) the maximum rate is measured to be 950 s⁻¹. The time-scale of this event coincides with the rate of conformational exchange between its reactant and product conformational intermediates, which has been measured to be about 1200 s⁻¹. The explanation for this observation is that the conformational sampling allows the enzyme in the reactant ground state (protonated DHF+NADPH) to sample conformations that favor the product state (THF+NAPD⁺). Once the enzyme reaches the product-favoring conformational state, the hydride transfer occurs. (There is a proton transfer that accompanies hydride transfer, which is considered to precede hydride transfer and occurs almost instantly; therefore, protonated DHF is considered as the reactive species in the ground state for the chemical step.) The overall rate of the reaction is controlled by the slowest step in the reaction. Under normal conditions the slowest event is product (THF) release, which occurs roughly at 13 s⁻¹, while the rate of conversion of the conformation sub-states is 12–18 s⁻¹.

The details about the fraction of major and minor population in the DHFR catalytic cycle are not fully available from this study. It is proposed that R₂ relaxation dispersion experiments can generally only characterize higher energy conformations that make up at least 1 to 2% of the ensemble. Therefore minor state populations in EcDHFR would be of similar order. Further, there may be additional excited states that are not accessible to the R₂ relaxation dispersion experiments. Alternate techniques are required to obtain more detailed information about the conformational populations.

6.2 Cis/trans isomerization catalyzed by cyclophilin A

The computational technique QAA has been successfully used to identify conformational sub-states associated with the cis/trans isomerization reaction catalyzed by the enzyme human cyclophilin A (CypA) (Ramanathan, et al., 2011). This enzyme belongs to the class of enzymes known as peptidyl-prolyl isomerases (PPIases), and catalyzes the rotation of amide bond preceding to proline residues in a wide variety of substrates, including peptides and proteins (Agarwal, 2004; Agarwal, Geist, & Gorin, 2004). MD simulations in conjunction with reaction pathway sampling were used to sample conformations along the reaction pathway. The dihedral angle associated with the amide bond was used as a reaction coordinate and umbrella sampling was used to collect 18,500 conformations along the enzyme reaction catalyzed by CypA in a representative substrate. QAA was then used to identify multi-scale hierarchy characterization of protein landscape both in time- and length-scales. Results are depicted in Figure 8. The conformational landscape is characterized and separated into a number of conformational sub-states (marked by ellipses). The conformations are colored according to the reaction coordinate (amide bond dihedral angle).

Figure 8. Computational method QAA allows identification of multi-scale hierarchy associated with catalysis by enzyme CypA.

(a) Multi-level (2 levels shown) hierarchy of conformational sub-states, each dot is a conformations. Each colored dot represents a single sampled conformation; ellipses indicate sub-states; TS′, TS″, and T indicate transition state area. (b) the free energy profile and conformations in (a) are colored according to reaction coordinate, (c) conformational change between sub-states corresponding to black arrow in (a), and (d) impact of identified motions on CypA’s mechanism. Adapted from (Ramanathan et al., 2011).

The characterization of the conformational snapshots along the CypA reaction with QAA reveals the following results:

1. QAA correctly identifies the sub-state that corresponds to the transition state (TS) area. In Figure 8, this corresponds to the highest point in the free energy profile (and green colored conformations). The first iteration of QAA (called Level I) identifies conformational sub-states associated with the reactant, product, and in the vicinity of TS (labeled as TS′) as well as a mixed energy state (labeled as cluster I). Note that QAA is a way to represent the data in lower dimensional space; therefore, it allows identification of different sub-states in multiple iterations. The mixed cluster is then further characterized (Level II), which allows identification of the more accurate conformational sub-state associated with the TS (TS″). It is very important to note that the information about the reaction coordinate is not an input to the QAA method. Therefore, the identification of the functionally relevant reactant, product and TS sub-states is an emergent property.

2. The conformations within the sub-states are sampled at fast time-scales and the transitions at long time-scales enable access to functionally important sub-states with higher energy. Without requiring any prior knowledge, the transition from lower to TS sub-state [black arrows in sub-panel (a)] indicates the reaction promoting intrinsic protein dynamics with implications for the mechanism [panel (c) and (d)]. Therefore, the theoretical foundation of QAA provides us with a unique methodology to bridge the gaps in time-scales as well as length-scales. Note that this is related to the short-lived hidden conformational sub-states that have been discovered using X-ray and NMR techniques, and influence enzyme catalysis in CypA (Fraser, et al., 2009).

3. The conformational transitions that enable access to the TS sub-state (and other substates) can be identified by drawing an arrow between various centers of mixed clusters and the sub-state (see black arrow) and the conformations along this arrow provides detailed atomic level information about the fluctuations in various parts of the enzyme (lower panel Figure 8). Interestingly, this information from CypA coincides with the NMR spin-relaxation experiments. Further, the identification of highly flexible regions and the conserved hydrogen bonds between these regions provides information about a network of residues that promote catalysis.

Overall, for results for CypA indicate that the enzyme spends most of its time sampling lower energy states (ground states), including the reactant and product sub-states. Over long time-scales, the conformational fluctuations based on the topology of the enzyme allow sampling of the rare-intermediate states or the functionally relevant sub-states. These sub-states contain the correct geometric and dynamical properties for the formation of transition state and thus for promoting the reaction mechanism.

QAA offers a number of advantages over alternate approaches: (1) QAA allows automatic separation of the conformation into sub-states that capture global to local motions (length-scales) and varying over fast to slow time-scales; (2) A unique advantage of QAA is that without any prior knowledge of functionally related coordinates, it identifies intermediate substates with functionally important structural and dynamical features; and (3) Comparison of the functionally relevant sub-states provides insights into the reaction promoting intrinsic enzyme dynamics as well as a network of coupled motions (or enzyme residue networks) that enable solvent-enzyme thermo-dynamical coupling.

7. Summary and Conclusions

Enzymes sample a wide variety of conformations in solution. Only a small fraction of these conformations contain the correct structural and dynamical features that allow the stabilization of the various intermediates during the enzyme mechanism. The sampling of alternate conformations is an intrinsic property of enzymes, enabled by the topology and driven by temperature and the surrounding environment. Identification and characterization of these conformational sub-states can be achieved though the use of experimental techniques such as NMR and computer simulations.

New techniques are required to process the experimental data and simulations data. NMR relaxation-dispersion experiments such as the rcCPMG methodology allow the extraction of useful conformational exchange information related to the functional behavior of apo and ligand-bound enzymes in solution, including the weight of equilibrium populations sampled by the enzyme (p_A and p_B), the chemical shift differences between each state ω_A and ω_B (Δω), and the rate of conformational exchange (k_ex) between the ground (p_A) and excited (p_B) population states. Atomic-scale analysis of these parameters in conjunction with computer simulations provides a wide range of information on the importance of these excited sub-states in enzyme function and catalysis. For computer simulations, the conformational fluctuations are identified using second-order or more accurate higher-order methods. The projections of the conformations on the fluctuations (or vectors) allow the identification of conformational sub-states. Characterization of these states with various biophysical properties (energy, reaction coordinate and other parameters) provides detailed information on the reaction mechanism.

The current challenge with these techniques remains the validation of the conformational sub-states identified, as they are rarely populated and only last for very short durations. Joint efforts between experimental and computational techniques would enable more accurate characterization of these functionally relevant conformers. For example, m in QAA can be selected such that it reproduces p_A and p_B obtained from NMR. This would allow validation of the computational methodology, and as a benefit detailed and quantitative information will then be available about conformational sub-states and populations associated with enzyme catalysis.