Abstract
The particle-particle random phase approximation (pp-RPA) and the particle-particle Tamm-Dancoff approximation (pp-TDA) are applied to the challenging conical intersection problem. Since they describe the ground and excited states on the same footing and naturally take into account the interstate interaction, these particle-particle methods, especially the pp-TDA, can correctly predict the dimensionality of the conical intersection seam as well as describe the potential energy surface in the vicinity of conical intersections. Though the bond length of conical intersections is slightly underestimated compared with the complete-active-space self consistent field (CASSCF) theory, the efficient particle-particle methods are promising for conical intersections and non-adiabatic dynamics.
Graphical abstract
The conical intersection1,2 is an important concept in nonadiabatic dynamics. They occur at a set of molecular geometries where two electronic states are degenerate and the potential energy surfaces intersect. Conical intersections are ubiquitous and play a vital role in many nonadiabatic processes related to energy transfer, charge transfer, and ultrafast photochemical transitions.2,3
Multireference wave function methods are most frequently used to describe conical intersections. Among these methods are the complete-active-space self-consistent field (CASSCF), the complete-active-space second-order perturbation theory (CASPT2), and the multireference configuration interaction (MRCI). These methods are able to provide accurate results for conical intersections with a proper choice of the active space, however, their computational cost also quickly grows with the size of the active space, which is usually not affordable for complex systems.
Density functional theory (DFT) and linear-response time-dependent density functional theory (LR-TDDFT, or TDDFT for brevity) are widely used for ground state and excited states calculations thanks to their good balance of accuracy and efficiency.4,5 However, they completely fail to describe those conical intersections involving the ground state and an excited state.5,6 This is because the excited states, which are described by TDDFT, have no state interaction with the ground state described by DFT. Therefore, although the conical intersections should occur in a subspace of Nint − 2 dimension, with Nint the internal degree of freedom,2 the dimension of this intersection space is incorrectly expanded by 1 with TDDFT.5,6
In the past few years, many DFT-based methods have been developed to circumvent this problem by introducing the state interaction between the ground state and excited states.7 Li et al. directly introduced a configuration interaction coupling element to the matrix of TDDFT within the Tamm-Dancoff approximation to break the unphysical degeneracy.8 Van Voorhis’s group developed configuration interaction based constrained density functional theory (CDFT-CI)9 and well described the conical intersections with some prior knowledge on the target system.10 Based on a spin-restricted ensemble construction of the Kohn-Sham DFT (REKS) and a state-averaged (SA) energy functional, Huix-Rotllant et al. suggested a state interaction element in the SI-SA-REKS method, which also properly describes the conical intersections and yields the correct dimensionality.11,12 A natural introduction of the interaction is from the spin-ip (SF) TDDFT.13,14 It starts from a high-spin state and targets the low-spin ground and excited states by a spin-ip operator. The state interaction element between the ground and excited states are naturally built in the SF-TDDFT matrix and therefore the dimensionality of intersection space is also correct. Furthermore, the SFTDDFT has been applied to locate the geometries of conical intersections.12,15
In this communication, we will apply the recently developed DFT-based particle-particle random phase approximation (pp-RPA) and particle-particle Tamm-Dancoff approximation (pp-TDA)16–18 to the description of conical intersections. The pp-RPA in combination with the Hartree-Fock (HF) reference has been a text-book method for describing correlation energy in nuclear physics for a long time,19 but it was not combined with DFT until very recently by van Aggelen et al.16 in electronic structure calculations. The pp-RPA and pp-TDA were also further applied to excited states calculations including both excitation energy calculation17 and geometry optimization.20 These pp methods start from a two-electron defficient (N-2) reference, and target the neutral (N) states by adding two electrons, thus describing the ground and excited states on the same footing. Similar to SF-TDDFT, the interaction between ground and excited states are naturally taken into consideration. Therefore, it is expected that the pp methods can also describe conical intersections with a relatively low (O(N4)) computational cost.21
The basic working equation for pp-RPA is
| (1) |
with
| (2) |
where a, b, c, d are virtual orbital indices and i, j, k, l are occupied orbital indices with the restrictions that a > b, c > d, i > j and k > l. The brackets are defined as
| (3) |
and 〈pq‖rs〉 ≡ 〈pq|rs〉 − 〈pq|sr〉. The eigenvectors describe the pairing matrix response to a pairing field of adding or removing electron pairs, and the corresponding eigenvalues are two-electron addition or two-electron removal energies. Starting from an N-2 reference, the energy of the neutral ground and excited states can be obtained by20
| (4a) |
| (4b) |
where 0 and n denote the ground and excited states, respectively.
The pp-TDA is even simpler than pp-RPA. It can be obtained simply by setting the matrix B in Eq. (1) to be 0 and only solving on the eigenvalue problem for matrix A
| (5) |
Note here, it is known that methods with non-Hermitian Hamiltonian in principle cannot describe all conical intersections with possible complex eigenvalues.22,23 As a result, methods based on coupled cluster theory may face challenges for accidental same-symmetry conical intersections.22,23 Here before we go into the detailed performances of pp methods, we briey comment on the Hermiticity of the pp methods. The matrices A and C in Eqs (1) and (5) are both Hermitian. Therefore, mathematically speaking, the pp-TDA eigenvalue problem is guaranteed to be stable with only real eigenvalues. In contrast, because of the special metric [I, 0; 0, −I] in Eq (1), the pp-RPA in principle can have imaginary eigenvalue problems. However, till now we have never encountered this problem in regular systems thanks to the physical fact that the two-electron addition and two-electron removal processes are well decoupled. In other words, the pp-RPA solutions preserve the stability of molecules with respect to the spontaneous disproportionation reactions into two-electron addition and removal products, leading to real eigenvalues in the pp-RPA solutions. But we cannot guarantee it to also perform well for challenging accidental same-symmetry conical intersections. Therefore, although in later sections we present results both from pp-RPA and pp-TDA, we tentatively recommend pp-TDA for general conical intersection problems.
The pp calculations are performed with QM4D.24 TDDFT and CASSCF calculations are performed with Gaussian09.25 The B3LYP functional is used in pp-RPA and TDDFT calculations. Trihydrogen (H3) and ammonia (NH3) are employed as test systems. The 6-31G basis set is used for H3 and the aug-cc-pVDZ basis set is used for NH3. The active space in CASSCF is chosen to be (3,6) for H3 and (6,6) for NH3. To overcome the convergence problem for regular CASSCF, SA-CASSCF is used in NH3, which averages over the lowest two states. Because H3 is an open-shell doublet species, the pp methods based on unrestricted N-2 calculations generates two set of spin-contaminated data, and we average the two series to reduce the spin contamination.17,26
Previously, H3 has been used to demonstrate the problem of TDDFT as well as the success of CDFT-CI in describing conical intersections.6,10 For this open-shell doublet system, a seam of symmetry-required conical intersections between the lowest two doublet states is located at equilateral geometries where the singly occupied molecular orbital (SOMO) and the lowest unoccupied molecular orbital (LUMO) are degenerate. However, if we fix two atoms and only move the third one, the higher D3h symmetry will reduce to lower C2υ or Cs symmetries and hence break the orbital and state degeneracy. Therefore, as was done in Ref. 6, we fix two atoms on the y axis with coordinates being (0, 0.409) and (0, −0.409), and place the third atom initially at (0.708, 0) with the D3h symmetry and then move it along the x and y directions for scanning purpose.
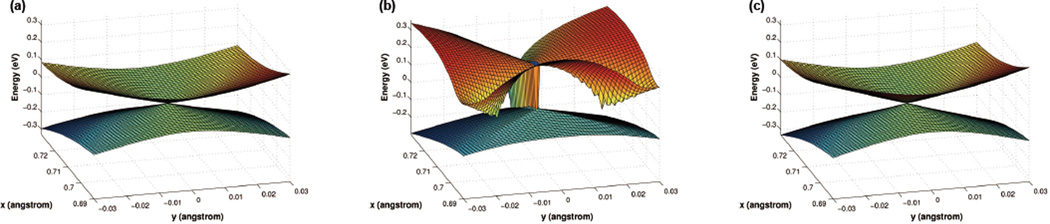
The results are shown in Figure 1a–c. The reference potential energy surfaces are obtained from CASSCF(3,6)/6-31G, which is essentially a full active-space calculation within the selected basis set. The surfaces display a double-cone feature. TDDFT on top of a ground state DFT calculation provides a buttery-like surface. The two “wings” have unphysical basins that occur at Cs symmetry. The “body” originates from the instability problem, which yields imaginary TDDFT eigenvalues that are plotted as negative ones in the figure. In contrast to TDDFT, the pp methods yield results that closely resemble the CASSCF calculations in terms of both the potential energy surface shape and the transition energy amplitude. Note that the pp-RPA reduces to the pp-TDA for this three-electron system since the dimension of B and C are both 0. The accurate double-cone surfaces indicate that the pp methods can also yield good numerical results in the vicinity of conical intersections.
Figure 1.
Potential energy surfaces of H3 around a conical intersection by (a) CASSCF(3,6), (b) TDDFT-B3LYP, (c) pp-RPA/TDA-B3LYP. Two atoms are fixed on the y axis at (0, 0.409) and (0, −0.409), respectively, while the position of the third atom is varied along the x and y axes. TDDFT gives an unphysical buttery shape for the excited state surface, while the pp-RPA, which reduces to the pp-TDA in this three-electron case, correctly describes the conical intersection with potential energy surfaces closely resembling CASSCF.
NH3 is another well studied model system.8,27–29 Many conical intersections can be located at planar geometries.27 We first study the one with the D3h symmetry. Unlike H3, whose D3h geometries are all in the seam of conical intersections, there is only one point of degeneracy for NH3. At this point, the closed-shell state and the open-shell state are degenerate. We locate this point simply by scanning over symmetric bond stretching. Afterwards, the potential energy surfaces are scanned by extending the degree of freedom to β, which is the angle between any N-H bond and the vector that trisects the solid angle spanned by the three N-H bonds. The D3h symmetry is essentially reduced to C3υ and the two states involved are both reduced 1A1 when β deviates from 90°.
The results are plotted in Figure 2a–d. CASSCF, pp-RPA and pp-TDA all predict a sloped conical intersection, whereas TDDFT in combination with ground state DFT predicts a curved line of intersections due to the absence of state interaction. TDDFT also suffers from instability issues with imaginary eigenvalues when the bond length gets longer, and displays an unphysical valley because the imaginary values are plotted as negative values. For the pp methods, although their potential energy surfaces look similar to the CASSCF results, the locations of conical intersections differ from CASSCF. With the aug-cc-pVDZ basis set, CASSCF predicts a conical intersection with bond length equal to 1.487 Å, while pp-RPA and pp-TDA predicts 1.397 Å and 1.391 Å, respectively. The bond length predicted by pp methods is smaller than that predicted by CASSCF, and in fact this is true with any given basis set. While the reason could partially lie in the fact that CASSCF lacks some dynamic correlation, it is also probable that the pp methods have some errors. It has been known that pp-RPA and pp-TDA often underestimate the equilibrium bond lengths for ground and excited states.20 Therefore, it seems that the pp methods tend to underestimate the bond lengths at which chemical phenomena occur. The reason might be that the pp methods start with an N-2 SCF calculation, whose molecular orbitals are overly contracted due to the less screening of the electron-nuclei attraction compared to the neutral species. Nonetheless, it is possible that this problem may be overcome with a better choice of reference orbitals, such as using the orbitals from the neutral reference system (e.g. the HF* reference in Ref. 17).
Figure 2.
Potential energy surfaces of NH3 around the conical intersection with D3h symmetry by (a) CASSCF(6,6), (b) TDDFT-B3LYP, (c) pp-RPA-B3LYP, (d) pp-TDA-B3LYP. Radius denotes the bond length of the three N-H bonds, and β is the angle between any N-H bond and the vector that trisects the solid angle spanned by the three N-H bonds. TDDFT completely fails and predicts a line of intersections. In contrast, the pp methods correctly predict the double-cone feature, although the bond length of the conical intersection is shorter compared to the CASSCF result.
The energy differences between the D3h conical intersection geometry and the ground state geometry are also briey investigated. The results are shown in the supporting information. It suggests that for NH3, the pp methods perform well for the energy differences, though more general performances await further studies on more systems.
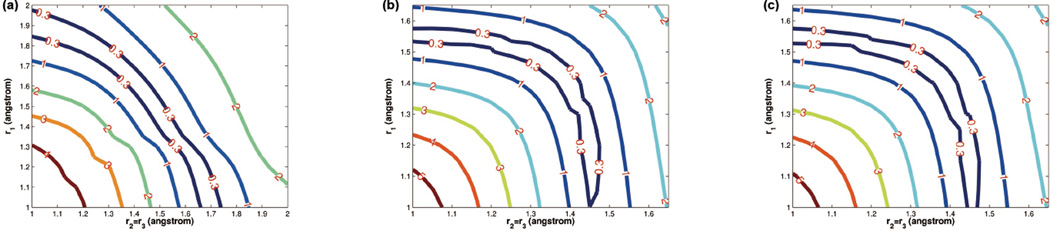
We also studied the conical intersections for NH3 with a C2υ symmetry. One bond (r1) can be freely stretched while the other two are always kept equal (r2 = r3). The bond angles are all fixed to be 120°. The contour plots in Figure 3a–c show the energy splitting between the two potential energy surfaces. The seam of conical intersections lies in between the two lines marked with 0.3 eV. Again, we can see that CASSCF and the pp methods predict similar chemical phenomena within different bond length scales. The results for pp-RPA and pp-TDA with bond length 1–1.6 Å have a roughly similar landscape as CASSCF with bond length 1–2 Å.
Figure 3.
Contour plot of potential energy surface splitting (in eV) near the seam of conical intersections for NH3 with C2υ symmetry by (a) CASSCF(6,6), (b) pp-RPA-B3LYP, (c) pp-TDA-B3LYP. Bond angles are fixed at 120°. The plot is with respect to r1 and r2(= r3). The seam of conical intersections lies in between the pair of lines marked with 0.3 eV. The results from the pp methods are very similar, and with bond length 1–1.6 Å, they have a roughly similar landscape as the CASSCF results with bond length 1–2 Å.
In summary, the pp methods can correctly describe the dimensionality of the conical intersection space. The potential energy surfaces in the vicinity of conical intersections are also well depicted. This is due to the fact that the pp methods are essentially multi-configuration approaches that describe the ground and excited states on the same footing, and naturally take into account the interstate interaction without any ad hoc correction elements. In this sense, it is similar to SF-TDDFT. From a quantitative perspective, the pp-RPA and pp-TDA may underestimate the bond lengths for conical intersections as a result of the contracted N-2 molecular orbitals, a shortcoming that might be overcome with different reference orbitals. Nonetheless, as an efficient DFT-based approach, the pp methods, especially the pp-TDA which in principle will never suffer from instability problems, are promising in possible applications to conical intersections and non-adiabatic dynamics.
Supplementary Material
Acknowledgments
Y.Y. has been supported by the National Science Foundation (CHE-1362927), L.S. by the National Institute of Health (R01 GM061870-13), D.Z. and W.Y. by the Center for the Computational Design of Functional Layered Materials, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Award # DE-SC0012575. Y.Y. and W.Y. initiated the project, all participated in the research design, Y.Y. carried out the calculations and wrote the first draft, all contributed to analyzing the results and finishing the writing.
Footnotes
Supporting Information Available
Summary of energetics for NH3 at equilibrium geometry and the D3h conical intersection. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Yarkony DR. Diabolical Conical Intersections. Rev. Mod. Phys. 1996;68:985–1013. [Google Scholar]
- 2.Yarkony DR. Conical Intersections: The New Conventional Wisdom. J. Phys. Chem. A. 2001;105:6277–6293. [Google Scholar]
- 3.Worth GA, Cederbaum LS. Beyond Born-Oppenheimer: Molecular Dynamics through a Conical Intersection. Annu. Rev. Phys. Chem. 2004;55:127–158. doi: 10.1146/annurev.physchem.55.091602.094335. [DOI] [PubMed] [Google Scholar]
- 4.Parr R, Yang W. Density-Functional Theory of Atoms and Molecules. New York: Oxford University Press; 1989. [Google Scholar]
- 5.Ullrich CA. Time-Dependent Density-Functional Theory: Concepts and Applications. Oxford: Oxford University Press; 2012. [Google Scholar]
- 6.Levine BG, Ko C, Quenneville J, Martínez TJ. Conical Intersections and Double Excitations in Time-Dependent Density Functional Theory. Mol. Phys. 2006;104:1039–1051. [Google Scholar]
- 7.Huix-Rotllant M, Nikiforov A, Thiel W, Filatov M. Density-Functional Methods for Excited States. Heidelberg: Springer; 2015. pp. 445–476. [Google Scholar]
- 8.Li SL, Marenich AV, Xu X, Truhlar DG. Configuration Interaction-Corrected Tamm–Dancoff Approximation: A Time-Dependent Density Functional Method with the Correct Dimensionality of Conical Intersections. J. Phys. Chem. Lett. 2014;5:322–328. doi: 10.1021/jz402549p. [DOI] [PubMed] [Google Scholar]
- 9.Wu Q, Cheng C-L, Van Voorhis T. Configuration Interaction Based on Constrained Density Functional Theory: A Multireference Method. J. Chem. Phys. 2007;127:164119. doi: 10.1063/1.2800022. [DOI] [PubMed] [Google Scholar]
- 10.Kaduk B, Van Voorhis T. Communication: Conical Intersections Using Constrained Density Functional Theory–Configuration Interaction. J. Chem. Phys. 2010;133:061102. doi: 10.1063/1.3470106. [DOI] [PubMed] [Google Scholar]
- 11.Huix-Rotllant M, Filatov M, Gozem S, Schapiro I, Olivucci M, Ferre N. Assessment of Density Functional Theory for Describing the Correlation Effects on the Ground and Excited State Potential Energy Surfaces of a Retinal Chromophore Model. J. Chem. Theory Comput. 2013;9:3917–3932. doi: 10.1021/ct4003465. [DOI] [PubMed] [Google Scholar]
- 12.Gozem S, Melaccio F, Valentini A, Filatov M, Huix-Rotllant M, Ferre N, Frutos LM, Angeli C, Krylov AI, Granovsky AA, et al. Shape of Multireference, Equation-of-Motion Coupled-Cluster, and Density Functional Theory Potential Energy Surfaces at a Conical Intersection. J. Chem. Theory Comput. 2014;10:3074–3084. doi: 10.1021/ct500154k. [DOI] [PubMed] [Google Scholar]
- 13.Shao Y, Head-Gordon M, Krylov AI. The Spin-Flip Approach Within Time-Dependent Density Functional Theory: Theory and Applications to Diradicals. J. Chem. Phys. 2003;118:4807–4818. [Google Scholar]
- 14.Wang F, Ziegler T. Time-Dependent Density Functional Theory Based on a Noncollinear Formulation of the Exchange-Correlation Potential. J. Chem. Phys. 2004;121:12191–12196. doi: 10.1063/1.1821494. [DOI] [PubMed] [Google Scholar]
- 15.Minezawa N, Gordon MS. Optimizing Conical Intersections by Spin-Flip Density Functional Theory: Application to Ethylene. J. Phys. Chem. A. 2009;113:12749–12753. doi: 10.1021/jp908032x. [DOI] [PubMed] [Google Scholar]
- 16.van Aggelen H, Yang Y, Yang W. Exchange-Correlation Energy from Pairing Matrix Fluctuation and the Particle-Particle Random Phase Approximation. Phys. Rev. A. 2013;88:030501. doi: 10.1063/1.4865816. [DOI] [PubMed] [Google Scholar]
- 17.Yang Y, van Aggelen H, Yang W. Double, Rydberg and Charge Transfer Excitations from Pairing Matrix Fluctuation and Particle-Particle Random Phase Approximation. J. Chem. Phys. 2013;139:224105. doi: 10.1063/1.4834875. [DOI] [PubMed] [Google Scholar]
- 18.Peng D, van Aggelen H, Yang Y, Yang W. Linear-Response Time-Dependent Density-Functional Theory with Pairing Fields. J. Chem. Phys. 2014;140:18A522. doi: 10.1063/1.4867540. [DOI] [PubMed] [Google Scholar]
- 19.Ring P, Schuck P. The Nuclear Many-Body Problem. Berlin: Springer; 1980. [Google Scholar]
- 20.Zhang D, Peng D, Zhang P, Yang W. Analytic Gradients, Geometry Optimization and Excited State Potential Energy Surfaces from the Particle-Particle Random Phase Approximation. Phys. Chem. Chem. Phys. 2015;17:1025–1038. doi: 10.1039/c4cp04109g. [DOI] [PubMed] [Google Scholar]
- 21.Yang Y, Peng D, Lu J, Yang W. Excitation Energies from Particle-Particle Random Phase Approximation: Davidson Algorithm and Benchmark Studies. J. Chem. Phys. 2014;141:124104. doi: 10.1063/1.4895792. [DOI] [PubMed] [Google Scholar]
- 22.Hättig C. Structure Optimizations for Excited States with Correlated Second-Order Methods: CC2 and ADC (2) Adv. Quantum Chem. 2005;50:37–60. [Google Scholar]
- 23.Köhn A, Tajti A. Can Coupled-Cluster Theory Treat Conical Intersections? J. Chem. Phys. 2007;127:044105. doi: 10.1063/1.2755681. [DOI] [PubMed] [Google Scholar]
- 24.An In-house Program for QM/MM Simulations ( http://www.qm4d.info) [Google Scholar]
- 25.Frisch M, Trucks G, Schlegel HB, Scuseria G, Robb M, Cheeseman J, Scalmani G, Barone V, Mennucci B, Petersson Ge, et al. Gaussian 09. 2009 [Google Scholar]
- 26.Yang Y, Burke K, Yang W. Accurate Atomic Quantum Defects from Particle-Particle Random Phase Approximation. Mol. Phys. 2016;114:1189–1198. [Google Scholar]
- 27.Yarkony DR. Exploring Molecular Complexity: Conical Intersections and NH3 Photodissociation. J. Chem. Phys. 2004;121:628–631. doi: 10.1063/1.1772351. [DOI] [PubMed] [Google Scholar]
- 28.Nangia S, Truhlar DG. Direct Calculation of Coupled Diabatic Potential-Energy Surfaces for Ammonia and Mapping of a Four-Dimensional Conical Intersection Seam. J. Chem. Phys. 2006;124:124309. doi: 10.1063/1.2168447. [DOI] [PubMed] [Google Scholar]
- 29.Li ZH, Valero R, Truhlar DG. Improved Direct Diabatization and Coupled Potential Energy Surfaces for the Photodissociation of Ammonia. Theor. Chem. Acc. 2007;118:9–24. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.