Abstract
Goal
This study aims at a systematic assessment of five computational models of a birdcage coil for magnetic resonance imaging (MRI) with respect to accuracy and computational cost.
Methods
The models were implemented using the same geometrical model and numerical algorithm, but different driving methods (i.e., coil “defeaturing”). The defeatured models were labeled as: specific (S2), generic (G32, G16), and hybrid (H16, H16fr-forced). The accuracy of the models was evaluated using the “Symmetric Mean Absolute Percentage Error” (“SMAPE”), by comparison with measurements in terms of frequency response, as well as electric (||E⃗||) and magnetic (||B⃗||) field magnitude.
Results
All the models computed the ||B⃗|| within 35 % of the measurements, only the S2, G32, and H16 were able to accurately model the ||E⃗|| inside the phantom with a maximum SMAPE of 16 %. Outside the phantom, only the S2 showed a SMAPE lower than 11 %.
Conclusions
Results showed that assessing the accuracy of ||B⃗|| based only on comparison along the central longitudinal line of the coil can be misleading. Generic or hybrid coils – when properly modeling the currents along the rings/rungs – were sufficient to accurately reproduce the fields inside a phantom while a specific model was needed to accurately model ||E⃗|| in the space between coil and phantom.
Significance
Computational modeling of birdcage body coils is extensively used in the evaluation of RF-induced heating during MRI. Experimental validation of numerical models is needed to determine if a model is an accurate representation of a physical coil.
Index Terms: Safety, finite difference time domain, validation, field probes, SMAPE
I. INTRODUCTION
Magnetic Resonance Imaging (MRI) is a radiological imaging technique widely used in clinical practice, with over 30 million examinations a year [1]. The success of MRI is due to its clinical versatility, the use of non-ionizing radiation, and the high soft-tissue contrast [2]. Birdcage body coils are the most common type of radiofrequency (RF) coil used in MRI in the clinical environment and have been shown to provide a highly homogeneous field [3–6]. Birdcage body coils are typically driven by a two or four-port excitation with the power sources placed in one of the two end-rings of the birdcage [4].
An accurate characterization of the electromagnetic field generated by the RF coil is needed to assess RF-induced heating of tissue during MRI [7, 8]. Hence, an accurate assessment of the overall or local specific absorption rate (SAR) is extremely important for the safety of the patient [9–16] or in patients with conductive medical devices that are totally [1, 8, 17–22], or partially implanted, or in contact with the skin [7, 23]. In this context, computational modeling allows systematic and faster analysis of many variables affecting RF-induced heating, which cannot be accounted for experimentally [24, 25]. Over the past 20 years computational modeling has been increasingly used to address the RF safety issue [9–11, 17–20]. Several models of RF birdcage coil have been implemented following different levels of complexity, that here we categorized as: specific, generic, and hybrid. Specific models [11–13, 21, 26–29] replicate the number and position of the input excitation in the real physical coil by the presence of lumped elements (i.e., resistors and capacitors) representing the input impedance of the ports. This allows reproducing the physical input and reflected power. The importance of using a specific model was emphasized, for example, by Ibrahim et al. [11, 27] in order to correctly replicate the electromagnetic coupling between the coil and its load. A generic model [9, 10, 14, 30–34] makes use of a multiport excitation and forces currents inside the coil to a specific amplitude and phase, without the implementation of lumped elements. Liu et al. [10] supported the use of a generic model because of its low computational cost (i.e., no tuning required). Generic models were shown to well replicate the homogeneity of the magnetic field, electric field, and SAR distribution inside the ASTM phantom [26], the cylindrical phantom [35], and the human body models [10]. Lastly, a hybrid model [15, 35–37] includes both the multiport excitation and presence of lumped elements, the convenience of such an approach, over a specific model, is the independence of the frequency response from the loading conditions [22].
There are several studies that compared the different approaches [10, 26, 35] as well as studies that compared the models against measurements [17, 27, 30, 36]. However the comparison between simulated and measured electric and magnetic field magnitude (||E⃗|| and ||B⃗||, respectively) has been mostly performed along one-dimensional lines through the isocenter of the coil.
In this study, we aimed to evaluate the effect of “defeaturing” the numerical model with respect to the computational cost of the simulations as well as accuracy against measurements. The term “defeaturing” was used to indicate that the birdcage model systems were implemented using different driving methods, while maintaining the same geometrical model and the same numerical algorithm. Five numerical models were implemented: one specific (i.e., S2) [11, 13, 20, 28], two generic (i.e., G32 [9, 10, 32], G16 [30, 31, 33]), and two hybrid (i.e., H16 [15, 35], H16fr-forced [37]). The assessment of accuracy vs. defeaturing was performed by comparing each numerical model with a physical coil in terms of frequency response, as well as ||E⃗|| and ||B⃗||. In line with literature, as a first step ||E⃗|| and ||B⃗|| were compared along the longitudinal central line. Furthermore, the state-of-the-art approach was extended by including the evaluation of the fields performed for different planes both inside the phantom and in the space between phantom and coil. The field inside the phantom is of interest for SAR assessment with or without implanted conductive devices, while the space between phantom and coil must be characterized in presence of conductive devices partially implanted or in contact with the skin. Therefore, the region of interest, where the model accuracy must be evaluated is dependent on the specific target of the study.
Section II. A describes the geometrical specifications of the physical coil and the setup used to perform the measurements (i.e., frequency response, ||E⃗|| and ||B⃗||). Section II. B presents the five computational models and the numerical setup. Section II. C shows the method used to quantify the accuracy of each model with respect to the physical coil. Section III presents the results on frequency response (III. A), power requirements (III. B), ||E⃗|| and ||B⃗|| (III. C). Section IV presents a discussion of the study including its limitations, and final conclusions.
II. MATERIALS and METHODS
A. Measurements
1) Birdcage coil specifications
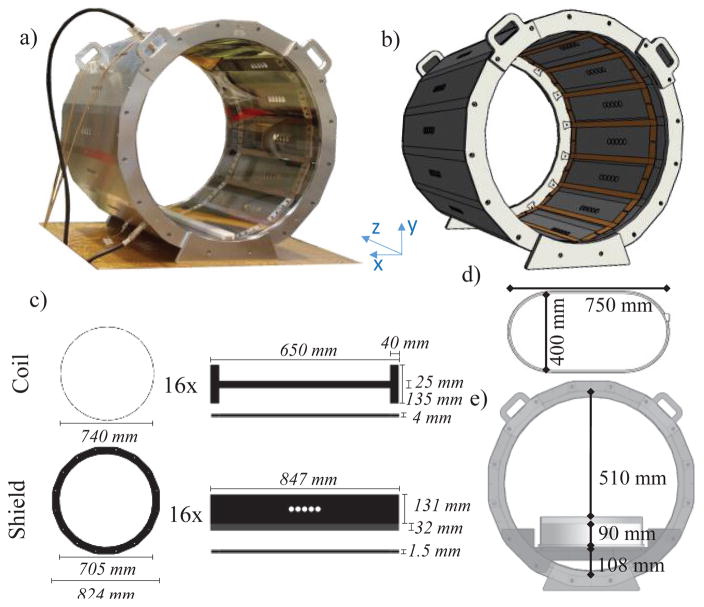
A commercially available high-pass birdcage body coil (MITS1.5, Zurich Med Tech, Zurich, Switzerland) was used for the measurements (Fig. 1a). The coil is composed of 16 rectangular strips (rungs) 570 mm long, which are laid out with cylindrical symmetry (diameter = 746 mm). The rungs are connected at each end by 16 distributed capacitors composed of a 40 mm wide strip. The coil is shielded by a 16-sided regular polygonal enclosure (Fig. 1c). The coil was driven at two ports (I and Q, located 90° apart) in quadrature mode (i.e., equal amplitude with a 90° phase shift between each port excitation) by two AN8102-08 RF power amplifiers (Analogic Co., Peabody, MA). Two baluns were present at the entrance of the sources to assure a low reflected power to the amplifiers. The nominal resonant frequency of the physical coil was fr,ph = 63.5 MHz ± 0.5 MHz. The net input power was set to obtain B1rms of:
| (1) |
where ||B⃗(xc, yc, zc)|| is the root mean square (RMS) value of ||B⃗|| at the isocenter of the coil (xc, yc, zc) = (0,0,0). Custom-made software included with the system was used to control and modify the settings of the input signal.
Fig. 1.
Geometry characterization of the system (a) MITS1.5 physical coil (b) 3D view of the computational model as implemented in the software. The computational RF body coil system was modeled to match the physical coil geometry (c). During measurements a superellipse-shaped phantom (d) was placed in the bottom of the coil (e). The physical phantom was filled to a depth of 90 mm with a 2.5 g/L saline solution with a conductivity of 0.47 S/m
2) Measurements setup
Data of ||E⃗|| and ||B⃗|| were collected using a robotic measurement system (DASY 5NEO, SPEAG, Zurich, Switzerland) [22, 38, 39] with two ||E⃗|| probes (ER3DV6 and EX3DV4 for measurements in air and saline, respectively) and a ||H⃗|| probe (H3DV7) (SPEAG, Zurich, Switzerland). For each measurement point the probes returned three RMS values – one for each field component x, y, and z. The total magnitude was than computed based on the quadratic norm (i.e., ||·||). The values of ||H⃗|| were then converted to ||B⃗|| based on the following relation:
| (2) |
where μ0 is the permeability of vacuum. A superellipse-shaped phantom was used for the measurements (Fig. 1d). The phantom consisted of a plexiglass container (6 mm thick, 750 mm long and 400 mm wide) supported by a plexiglass table (Fig. 1e). The physical phantom was filled to a depth of 90 mm with a 2.5 g/L saline solution with a conductivity σ = 0.47 S/m at room temperature [40, 41]. The conductivity was measured with the YSI model 30 conductivity meter (YSI Incorporated, Yellow Springs, Ohio 45387 USA). Measurements were carried out with the coil loaded with the phantom as shown in Fig. 1e. Spatial calibration between the robot-guided field probes and the birdcage coil was achieved by importing a 3D CAD model of the coil into the DASY-5NEO software, defining three points on the coil model, and manually aligning the field probes with corresponding points on the physical coil. Experimental data of ||E⃗|| and ||H⃗|| were collected with a spatial resolution of 1 cm:
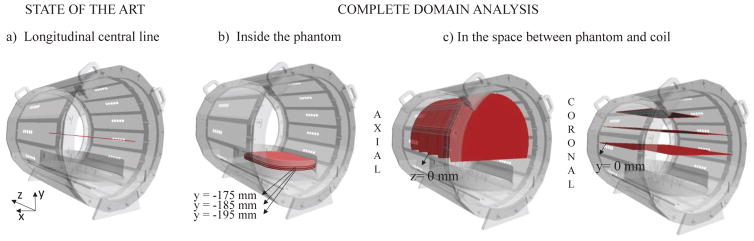
along the longitudinal central line in (xc, yc) (Fig. 2a).
inside the phantom (Fig. 2b), at three saline depths of 35, 40, and 45 mm within an elliptical area of 2025, 1995 and 1935 cm2, respectively.
Outside the phantom, in the space between phantom and coil (Fig. 2c): i) in five axial planes at z = −279, −141, 0, 141, and 279 mm within an area of 2270 cm2; and ii) in three coronal planes at y = 0, 126, and 252 mm within an area of 5184 cm2, 4492 cm2, and 2322 cm2, respectively.
Fig. 2.
||E⃗|| and ||B⃗|| were measured and computed both in air and in saline. In line with literature a first analysis was performed along the central longitudinal line of the coil (a). As complete domain analysis, measurements inside the phantom were performed in three coronal planes at three different saline depths of 35, 40, and 45 mm (corresponding to the absolute coordinates of y = −175 mm, −185 mm, −195 mm) (b). Measurements in the space between phantom and coil were performed in air (c) in five axial planes (i.e. z = −279 mm, −144 mm, 0 mm, 144 mm, 279 mm), and three coronal planes (i.e. y = 0 mm, 126 mm, 252 mm). For each plane the ξ index was calculated
The dimensions of the measurement planes were such to avoid possible collision of the probe with the coil and/or the phantom.
B. Computational modeling
1) Electromagnetic numerical implementation
EM simulations were implemented with the commercially available software xFdtd (Remcom Inc., State College, PA) which has been extensively used in literature for MRI RF-safety evaluation [16, 18, 42, 43].
The computational model of the birdcage coil was based on a reverse engineering approach, because the specific electronic characteristics of the physical coil were unknown. The model matched the geometry of the physical coil (Fig. 1b). Twenty cells of free space padding (20×20×20 mm3) were added to ensure free propagation of the field outside the coil volume without reflection [27]. Additionally, eight absorbing layers were set as boundary conditions [29, 44]. The mesh grid was optimized based on the PrOGrid tool included in XFdtd [45] ensuring a finer grid resolution near the boundaries of good conductors. A finer isotropic resolution (2.5×2.5×2.5 mm3) was imposed for the phantom to accurately resolve the measurement grid. The model included over 52 million cells and the simulation time-step used to ensure FDTD Courant–Friedrich–Levy stability [46], proportional to the smallest cell size, was 4 ps. Simulation run on a PC Intel(R) Core(TM) i7-4930K CPU @ 3.40GHz, with 64 GB of RAM and NVIDIA Tesla K40c graphic processing units.
2) Computational models of the birdcage coil and the phantom
Simulations were performed with the coil loaded with a superellipse-shaped phantom with same dimensions of the physical phantom. Both the coil and the shield were modeled as copper (σ = 58.13·106 S/m). The table supporting the phantom and the phantom case were modelled as plexiglass (σ = 0 S/m, and εr = 3.2). Finally, the load of the phantom was modeled as saline solution (σ = 0.47 S/m, εr = 80, and ρ = 1050 kg/m3).
As described below, five different approaches of simulating a birdcage coil were implemented. The distributed capacitors present in the physical coil were modeled as two conductive rectangular slabs connected by numerically defined lumped elements, as in [22]. The two baluns present at the physical sources were not modeled in the numerical coils.
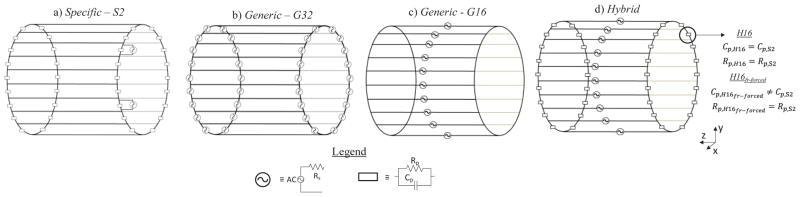
(Fig. 3a): the rings were interrupted by a 5 mm gap centered between two adjacent rungs. A lumped element composed of a resistor Rp in parallel with a capacitor Cp was placed in each gap. Additionally, two ports were set in two gaps of one of the two rings, 90° spatially apart, as in the physical coil. The ports were placed on one of the two rings on one side of the phantom, and with respect to the iso-center in the negative part of the z-axis.
Fig. 3.
Five electrical models implemented: (a) Specific 2port (S2), (b) Generic 32port (G32), (c) Generic 16port (G16), (d) Hybrid 16port (H16) and Hybrid 16port frequency forced (H16fr-forced). Model a) to c) were representative of a high pass body model wile model d) was representative of a low pass body model.
(Fig. 3b): the rings were interrupted by a 5 mm gap centered between two adjacent rungs; each gap included a port; no lumped elements were used.
(Fig. 3c): the rungs were interrupted in the middle by a 5 mm gap; each gap included a port; no lumped elements were used, following a “low-pass” design type [3].
(Fig. 3d): the rings were interrupted by 5 mm gaps centered between each two adjacent rungs with a lumped element composed of a resistor Rp in parallel with a capacitor Cp placed in each gap; each of the 16 rungs was interrupted in the middle by a 5 mm gap containing the driving port; the lumped elements used were the same as in the S2 model.
frequency forced (Fig. 3d): the location of the ports was the same as for the H16. For each lumped element, the resistor was the same as for the S2, whereas the capacitor was changed to force one of the S11 minima to 63.5 MHz.
In all models, the ports were modeled as a voltage source with a resistor Rs = 50 Ω in series (Fig. 3). For the S2 model the voltage input at the two sources was:
| (3) |
Where and are the total net input power at Q (i.e., 0° shifted), and I (i.e., 90° shifted) port of the physical coil respectively.
For the other four models the voltage input at the sources was 1 V. The results for all five models were normalized as in equation (1). The phase of the signal feeding the source was equal to its azimuthal position (i.e. 0° and 90° for the S2, 22.5° for each source in the 16port, G16 and G32). Additionally for the G32, the ports at the same azimuthal position in the two rings were 180° out of phase.
3) Simulation setup
For each model, two sets of simulations were performed with different voltage excitations: i) a broadband excitation with a cutoff frequency at 1 GHz, and ii) a sinusoidal excitation at 63.5 MHz.
In the first set, the frequency response of the models was studied by feeding a single port with a broadband waveform while the other/s port/s was/were connected to a 50 Ω load. Additionally, the S2 broadband simulations were used to calculate the final values of Cp and Rp to replicate both the tuning and matching conditions of the physical coil. A similar approach was followed for the H16fr-forced, albeit only applied to Cp (i.e., Rp,H16fr–forced = Rp,H16). The final values were: Rp,S2 = 1940 Ω, Cp,S2 = 72.8 pF, and Cp,H16fr–forced = 16 pF. With the 4 ps timestep the virtual computing time needed to reach convergence of the frequency response was 0.8 μs (i.e., 2·105 steps.) Different tests were performed changing the resistor value of the lumped element to verify whether or not the coil matching would affect the electromagnetic field results.
In the second set, all the ports were fed simultaneously with a sinusoidal waveform at 63.5 MHz with a phase shift equal to the azimuthal position of the port inside the coil. A total computing time of 30 periods was enforced to ensure a convergence of the field higher than 30 dB within two computation cycles.
Convergence level was chosen to assure that a steady-state condition was reached for both frequency response and field distribution.
C. Accuracy of numerical models vs. measurements
Experimental validation of the computational coils was performed by comparing the frequency response of the models, as well as ||E⃗|| and ||B⃗|| generated by the physical coil. For each simulation the field values were computed inside a three-dimensional sensor including the coil and the phantom. Numerical results were returned as three complex values – one for each field component x, y, and z – at each point of the predefined sensor. In order to compare the numerical data with the measurements, the total RMS magnitude of the field was then computed based on the quadratic norm accordingly to:
| (4) |
Where the symbol * represent the complex conjugate of the complex field – E⃗ or B⃗ – and the subscripts x, y, and z the spatial component of the field. As done in [11, 26, 30] a comparison was first performed on the profile of ||B⃗|| along the central longitudinal axes of the coil (xc = 0 mm, yc = 0 mm). This analysis was then herein extended to the ||E⃗|| [17]. An additional comparison was performed computing the “Symmetric Mean Absolute Percentage Error” (“SMAPE”) [47] (ξ) between simulated and measured values
| (5) |
where Xk and Yk are the value of ||E⃗(x,y,z)|| or ||B⃗(x,y,z)|| in the kth voxel of the area considered for the measured (Xk) and simulated (Yk) data, respectively. ξ was calculated along the longitudinal central line and in the planes described in section II.A.2 and displayed in Fig. 2b–d. In addition, as a term of comparison between the models, the mean SMAPE ξ̄ was evaluated for each plane.
| (6) |
where N number of voxels inside the plane.
III. Results
A. Power requirements
Comparing the loaded coil with the unloaded condition, the field polarization at the isocenter was highly affected by the presence of the phantom. In the loaded condition, the physical coil required a total net input power of 219 W to obtain a ||B⃗|| = 3 μT at the isocenter, with and . The available power (i.e., the power injected into each port) was the same for both I and Q ports, however the Q port had less reflected power. This was caused by the phantom being closer to the Q port and thus loading the coil asymmetrically. The polarization was clockwise with respect to the sources and elliptical with a ratio of the field components equal to 0.63. Conversely, in the unloaded case, the polarization was clockwise with respect to the sources and circular with a ratio of the field components equal to 0.9. The simulations performed with different resistor values confirmed that the matching affected only the overall power requirements, generating fields linearly proportional in magnitude to the net input power [48].
B. Frequency response
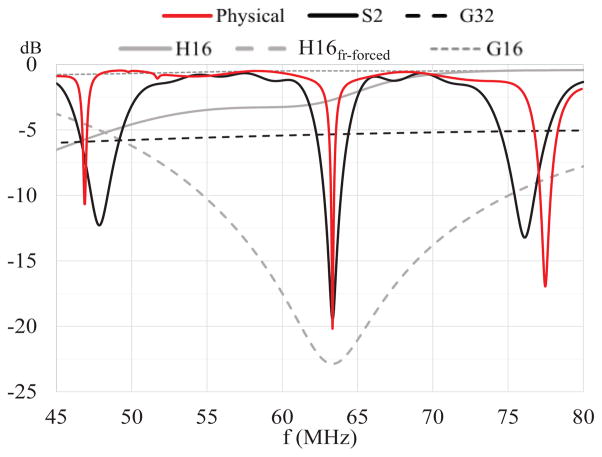
For the physical coil, the S11 at fr,ph = 63.5 MHz was −18.9 dB (see Fig. 4, red trace) with a Q-factor of 800. As reported in Fig. 4, the five computational models gave different results in terms of scattering parameters. The S2 and H16fr-forced showed a resonance peak at fr = 63.5 MHz of −19.1 dB and −22.9 dB, respectively. The Q-factor for the S2 and the H16fr-forced were 160 and 14, respectively. The H16 presented an almost flat frequency response of −3.2 ± 2.4 dB in the frequency range selected (i.e., from 40 to 80 MHz). Around fr,ph, the G32 and the G16 presented also a flat response of −6.3 dB and −0.8 dB respectively.
Fig. 4.
Scattering parameters (i.e., S11) of the physical coil and five computational models. The resonance frequency of the physical coil was captured only by the S2 and H16fr-forced models. The G32, H16 and G16 showed a flat frequency response around 63.5 MHz.
C. EM fields
1) Longitudinal central line
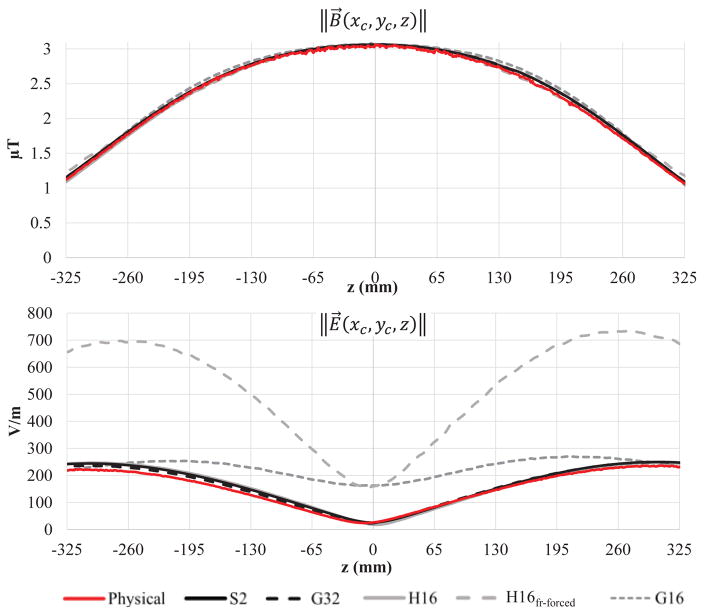
As shown in Fig. 5, all the models were able to replicate the measured values of ||B⃗|| along the central longitudinal line of the coil. For the five models, the maximum ξ for the magnetic field ||B⃗(xc,yc,z)|| compared to the measured values was less than 5%. Conversely two of the models showed significantly different profiles of measured ||E⃗|| when compared to the physical coil, with values of ξ̄ up to 147 % for both the H16fr-forced and G16. Finally, in the physical coil, the value of ||E⃗|| along the longitudinal line was the smallest at 10 mm from the isocenter with a magnitude of 24 V/m. Conversely, the H16, the S2, and the G32 showed a minimum at the isocenter with a magnitude of 17 V/m, 26 V/m and 23 V/m, respectively, whereas H16fr-forced and G16 showed a minimum of 160 V/m.
Fig. 5.
||E⃗|| and ||B⃗|| along the longitudinal axis z in the center of the coil (i.e., xc = yc = 0 mm). The figure shows the values measured in the physical coil as well as simulated. The five computational models were able to model the measured profile of ||B⃗||. Conversely, ||E⃗|| was accurately modeled only by the S2, G32 and H16. ||E⃗|| was about three-fold higher along the entire axis for the H16fr-forced, while it was up to seven-fold higher at the measured minimum (i.e., z = −10 mm) for both the H16fr-forced and G16. Values were normalized accordingly to equation 1.
2) Inside the phantom
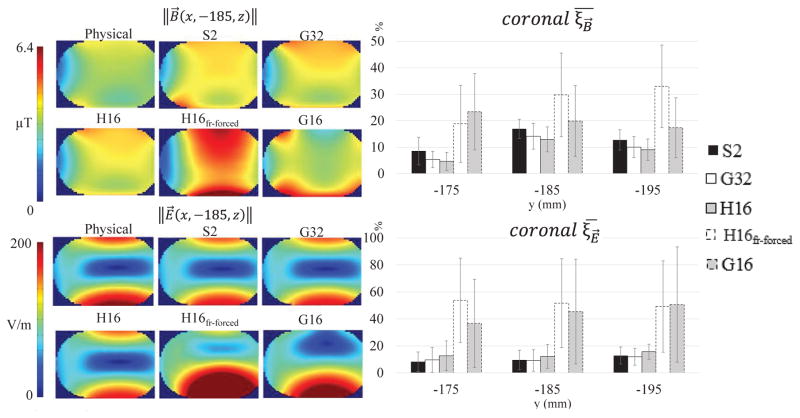
As shown in Fig. 6, the values of ||E⃗|| and ||B⃗|| simulated by the five models were significantly different when compared to each other and to the measured data inside the phantom. In particular, only the S2, G32, and H16 were able to accurately replicate ||E⃗|| and ||B⃗|| inside the phantom:
Fig. 6.
||E⃗|| and ||B⃗|| on coronal planes inside the phantom. For each plane the mean SMAPE ξ̄ value (equation 6) is reported in the histogram. In all three planes, ||E⃗|| and ||B⃗|| of the physical coil were well replicated only by the S2, G32, and H16 models, with a ξ less than 17 % for both. Conversely, models H16fr-forced and G16 reported an ξ between 17 % and 32 % for ||B⃗|| and between 37 % and 54 % for ||E⃗||. This result exemplifies how the analysis of the central longitudinal line (Fig. 5) is not sufficient to assess how well a model replicates the magnetic field of a physical coil.
For ||B⃗||, the ξ̄ was always better than 14 % for the S2, G32, and H16, while for H16fr-forced and G16 was worse than18 % %.
For ||E⃗||, the ξ̄ was always better than 16 % for the S2, G32, and H16, while for H16fr-forced and G16 was worse than 37 %.
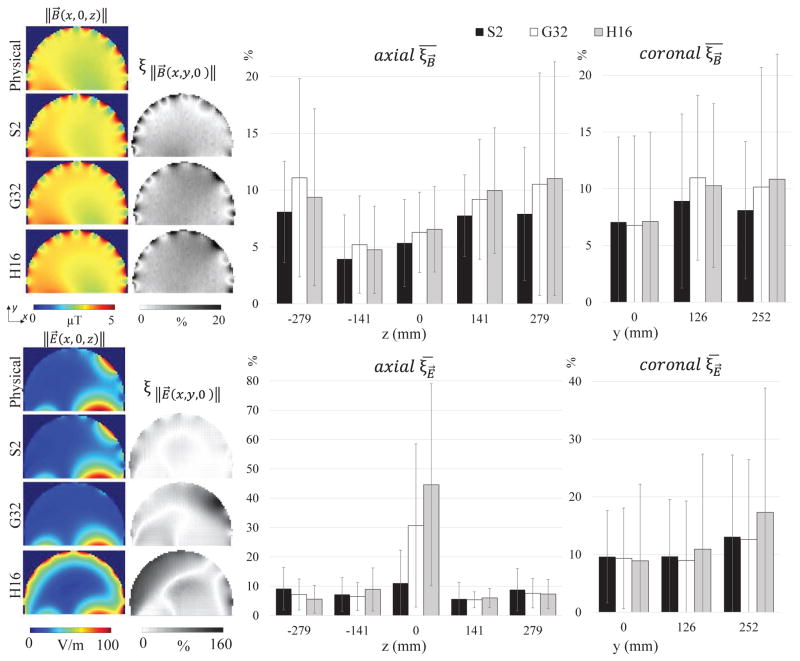
3) In the space between phantom and coil
The field data outside the phantom are reported only for the S2, G32, and H16 because these models were the only ones able to accurately replicate ||E⃗|| and ||B⃗|| (see IV.C). Outside the phantom similar values of ξ̄ (i.e., between 3.9 % and 11.1 % for the axial planes, and between 6.8 % and 17.3 % for the coronal planes) were obtained in all the planes, except for the central axial plane. The ||E⃗|| throughout the central axial plane was only accurately modeled by the S2, with a ξ̄ equal to 11 % and maximum ξ of 58 % on the left of the map (Fig. 7). Conversely, the G32 did not show any field peak while the H16 was affected by the presence of the multiport excitation. The G32 showed values of ξ up to 158 % (i.e., ||E⃗|| 80 V/m lower compared to the measurements in proximity of the source) and an overall ξ̄ of 31 %. The H16 showed a local ξ up to 134 % (i.e., ||E⃗|| up to 80 V/m higher compared to the measurements on the left of the map in Fig. 7), and an overall ξ̄ of 45 % (Fig. 7). On the other axial planes, ξ̄ was always der 9.15 % when evaluating both the planes farther (i.e., 279 mm) and closer (i.e., −279 mm) to the physical sources. Additionally, ξ̄ for ||B⃗|| was always lower than 11 % for the three models in both axial and coronal planes.
Fig. 7.
||B⃗|| (top) and ||E⃗|| (bottom) maps on the central axial planes (i.e., z = 0 mm) in air for the physical coil and the three numerical model S2, G32, and H16. The ξ (SMAPE) maps (equation 5) are reported on the right side of the field maps. On the right, the calculated ξ̄ (equation 6) and the relative standard deviation are reported for the five axial and three coronal planes measured. In all the planes, ||B⃗|| of the physical coil was well replicated by the three computational models with ξ̄ always less than 11 %. In the central axial plane, only the S2 model was able to replicate the ||E⃗|| peak due to the ports position, whereas the G32 showed a uniform ||E⃗|| and the H16 model was highly affected by the multiport excitation - increasing the ξ̄ of the plane up to 45 %
The distribution of ||E⃗|| was asymmetric with respect to the isocenter, with values 12 % higher in the planes far from the sources. This result is in line with the measured field along the central longitudinal line (Fig. 5b) where the field showed a 7 % asymmetry between the two maxima. The same asymmetry in the axial planes was well replicated by the S2 (i.e., 10 %), while it was less pronounced for the G32 (i.e., 6 %), and for the H16 (i.e., 4 %).
Discussion
The main contribution of this study is the characterization, against measurements from a physical coil, of five different computational coil models representative of the three main modeling approaches available in the scientific literature: generic, specific and hybrid coils. All of the coil models represented different implementations of the same physical birdcage body coil. Three quantities were taken into account for the comparison: frequency response, ||E⃗||, and ||B⃗||.
The fields were analyzed both inside the phantom and in the space between the phantom and the coil. Different applications may require different levels of field accuracy in specific locations. An accurate assessment of the electromagnetic field inside the phantom is important when evaluating SAR levels as overall safety of the patient [9–16] or the RF-induced heating in patients with conductive medical devices that are fully implanted in the body [22] like deep brain stimulators [8, 17, 18] or pacemakers [1, 20, 21]. Conversely, an accurate representation of ||E⃗|| in the space between the coil and the load is important when evaluating safety in patients with conductive medical devices that are partially implanted or in contact with the skin [7, 23]. High temperature changes in gel were reported in presence of external devices that are in contact with the skin, such as electroencephalography leads [49–51], electrocardiography leads [52–54], catheters in interventional MRI [55, 56], and orthopedics external fixators [37, 57]. Data presented in this paper were normalized based on the ||B⃗|| magnitude at the isocenter of the coil. This choice is in accordance to the state of the art to compare ||B⃗|| along the longitudinal central line (Fig. 5), and because the maximum ||B⃗|| occurs at the isocenter of the coil. Different normalization procedures could be considered. As an additional test, results were also compared with a normalization based on the mean of the ||B⃗|| in the central plane of the phantom (i.e., y = - 185 mm). Comparison between models showed the same the overall behavior of the results (data not shown).
The choice of performing the comparison of the numerical models with the simulations based on the SMAPE relied on its definition. The SMAPE is self-limited – by definition - to an error rate of 200%, reducing the influence of the low items such as low value of the field. Conversely, when calculating error normalized to a single value, low values can be problematic because they could have infinitely high errors that skew the overall error rate (e.g., data in central axial plane, where the value of the field magnitude values are very low).
In this study, three of the five models (i.e. G32, H16, and G16) were characterized – by definition – by a flat frequency response, whereas the two additional models (i.e., H16fr-forced and S2) were implemented to be tuned at the resonance frequency of the physical coil. Out of these latter models, the H16fr-forced was adjusted to replicate the tuning characteristics of the physical coil, while the S2 replicated both the tuning [58] and the matching characteristics, by adjusting the losses via the resistor of the lumped elements. The Q-factor of the S2 was lower compared to the physical coil possibly due to the presence of components generating loss of energy (e.g., in the resistor of the numerical model). Nevertheless, this did not affect the overall field at the single excitation frequency used to generate ||B⃗|| and ||E⃗|| (second settings in section II.B.3), given that the results were normalized with respect to ||B⃗||, as previously done in literature [27, 30].
Measuring ||B⃗|| and ||E⃗|| inside the phantom was considered essential for the numerical models validation. The position chosen for the study was due to physical constraints set by the DASY measurement system (e.g., minimum distance needed between the physical probe and the coil.) and it allowed field measurements inside the phantom.
When simulating using an FDTD approach, the biggest advantage of using either a generic or a hybrid model was related to the computational cost of the simulation. The latter could be reduced in terms of: i) time required for each simulation, or ii) number of simulations required to obtain the final solution. When using a multiport excitation, the simulation time was reduced by approximately one third, because forcing the currents inside the model allowed reaching the steady-state convergence with a smaller number of periods. Therefore, with the system used, simulating a multiport excitation would reduce the simulation time of approximately 1 hour and 20 minutes. Furthermore, the number of simulations was reduced since tuning and matching of the model were not required. Indeed, while one simulation (i.e., the excitation only) was needed for the generic model, at least two – one for tuning and one for the excitation (see section II.B.3) – were needed for the specific model. Both computing time and number of simulations can be reduced for a generic model, whereas only the computing time was reduced for a hybrid model, which is thus more computationally intensive. In fact a hybrid model relies on the specific model to assess the lumped element values to be used.
The analysis of ||E⃗|| and ||B⃗|| performed in this study suggests that: i) an accurate representation of the frequency response does not guarantee an accurate estimation of ||E⃗|| and ||B⃗||; ii) assessing the accurate modeling of ||B⃗|| based only on the results along the central longitudinal line of the coil can be misleading; iii) when defeaturing a hybrid type of coil, the proper selection of lumped element values is crucial to assure a good representation of ||E⃗|| and ||B⃗|| inside the phantom; iv) simplified models via proper defeaturing still allow accurate modeling of ||E⃗|| and ||B⃗|| inside the phantom.
An accurate representation of the frequency response does not guarantee an accurate estimation of ||E⃗|| and ||B⃗||
This is proven by comparing the results of the S2 and H16fr-forced. Both models showed a resonance profile similar to the physical coil, however only the S2 was able to accurately model ||E⃗|| and ||B⃗|| inside and outside the phantom with ξ̄ less than 17 %. Conversely, the G32 and the H16 were able to accurately model ||E⃗|| and ||B⃗|| even though they did not show a resonance profile. Thus the accurate representation of the frequency response is neither a necessary nor sufficient condition for an accurate estimation of ||E⃗|| and ||B⃗||.
Assessing the accurate modeling of ||B⃗|| based only on the results along the central longitudinal line of the coil can be misleading
In previous studies [11, 26, 30] models were compared by analyzing the profile of ||B⃗|| along the central longitudinal line. The results of this study show how this analysis may not ensure the accuracy of the models. This is directly deductible from the comparison of magnetic field graphs vs. plane maps (see Fig. 5 vs. Fig. 6). While all of the models simulated the same ||B⃗|| along the longitudinal line (Fig. 5), neither H16fr-forced nor G16 were able to accurately model the ||B⃗|| of the physical coil (Fig. 6), with a mean SMAPE higher than 20%. Hence, a comparison based only on ||B⃗|| may not be sufficient to validate a computational model. Low-pass and high-pass coils have different distribution of ||E⃗|| and ||B⃗|| field inside the coil. As a consequence, the G16 showed a ||E⃗|| outside (Fig. 5) and inside (Fig. 6) the phantom up to seven-fold different compared to the high pass physical coil.
When defeaturing a hybrid type of coil, the proper selection of lumped element values is crucial to assure a good representation of ||E⃗|| and ||B⃗|| inside the phantom
When comparing a generic to a hybrid model (i.e., H16 and H16fr-forced, Fig. 3), the values of ||E⃗|| were significantly different, depending on the specific value of capacitance used for the lumped element. Specifically, the H16 showed a high pass behavior with a SMAPE within a few % compared to the S2 (see Figs. 5–7). The H16fr-forced generated results similar to the low pass G16 (see Figs. 5 and 6). Hybrid models are designed to reproduce ||E⃗|| and ||B⃗|| of a specific model by forcing the currents along the coil. However, the frequency response of a hybrid model cannot be directly compared to the one of a specific model, because of the different feeding conditions. Thus a S11 minimum of a hybrid model cannot be considered equivalent to a resonance mode of a specific model. The implementation of a model such as the H16fr-forced is equivalent to changing the frequency response of the original specific model, causing a different current distribution inside the coil. As a consequence, the H16fr-forced and the S2 will in fact represent two different coils, thus generating different ||E⃗|| and ||B⃗||.
Simplified models via proper defeaturing still allow for accurate modeling of ||E⃗|| and ||B⃗|| inside the phantom
The S2, G32 and H16 all showed similar results inside the phantom with ξ̄ lower than 17 % for both ||E⃗|| and ||B⃗||. This was already shown by different studies comparing specific and hybrid [17, 35] or generic models [10, 26, 30]. However, when comparing the field outside the phantom in the space between the coil and the load — which was not done in previous studies — differences among these three models were more evident. On the central axial plane, the S2 was the only one able to replicate the ||E⃗|| peak of the source (Fig. 7), with a mean SMAPE of less than 11 %. The ||E⃗|| peak in the central axial plane is due to the current distribution along the rung, which is higher at the center. The G32 showed a uniform ||E⃗|| around the coil underestimating the measured field of up to 80 V/m, while the H16 exhibited high values of ||E⃗|| all around the coil generated by the multiport excitation in the middle of the rungs, causing an overestimation of the field of up to 80 V/m. This effect was reduced in points farther from the sources. As such, this study suggests the need of additional work to assess whether or not a fully featured S2 may be necessary to accurately evaluate the safety of the conductive medical devices that are partially implanted or in contact with the skin.
A. Limitations
The analysis conducted in this study focused only on ||E⃗|| and ||B⃗||, because the available measurement system was not capable of measuring the phase of the fields. A complete analysis of the phase of E⃗ and B⃗ fields may be important to assess the safety of an implant, because the coupling of the implant with the field is both dependent on the magnitude and phase of the radiated field. Additionally, a full uncertainty analysis, both numerical and experimental, will be performed as a second step of the validation work [22, 59, 60].
IV. Conclusions
We evaluated five computational models of a birdcage body coil, including one specific (S2), two generic (G32, G16) and two hybrid (H16, H16fr-forced). The computed results were compared against a physical coil at 63.5 MHz. The comparison was based on the frequency response, and on ||E⃗|| and ||B⃗|| in the coil loaded with a phantom. Depending on the specific application, different level of accuracy may be needed inside or outside the phantom. Thus, in this study the fields were evaluated both inside the phantom and in the space between phantom and coil. All the coil models computed ||B⃗|| within 35 % relative to the measured results. However, only the S2, G32, and H16 were able to accurately model ||E⃗|| and ||B⃗|| of the physical coil inside the phantom, with a maximum mean SMAPE ξ̄ of 16 %. Additionally, outside the coil only the S2 was able to accurately simulate the ||E⃗|| in proximity of the feeding port in the central axial plane, with ξ̄ equal to 11 %. Conversely the G32 and the H16 showed ξ̄ equal to 31 % and 45 %, respectively. In conclusion: i) all the models were able to accurately model ||B⃗|| along the longitudinal line; ii) the generic G16 and the hybrid H16fr-forced were not able to model either ||E⃗|| nor ||B⃗|| inside the phantom; iii) the generic G32 and the hybrid H16 were able to accurately model ||E⃗|| inside the phantom; and iv) only the S2 was able to accurately model ||E⃗|| both inside and outside the phantom. Because computational modeling of birdcage body coils is extensively used in the evaluation of RF-induced heating during MRI, experimental validation of numerical models is recommended to determine if a model is an accurate representation of a physical coil.
Acknowledgments
This work was supported in part by the Research Participation Program at the Center for Devices and Radiological Health administered by the Oak Ridge Institute for Science and Education through an interagency agreement between U.S. Department of Energy and the U.S. Food and Drug Administration (FDA), and in part by a Cooperative Research and Development Agreement between Imricor Medical Systems and the Center for Devices and Radiological Health (CDRH), FDA, and in part by the Office of Women’s Health, U.S. FDA.
The authors thank the following colleagues: Howard Bassen, Brian Beard, Eugenia Cabot, Giovanni Calcagnini, Myles Capstick, Daniel X. Hammer, Victor Krauthamer, Niels Kuster, Eugenio Mattei, Manuel Murbach, Alessandra Paffi, Emanuele Piuzzi, Sunder Rajan, Amir Razjouyan, Peter Serano, Earl Zastrow.
The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.
Biographies

Elena Lucano received the M.S. degree in Biomedical Engineering in 2012, from the University of Rome Sapienza (Rome, Italy). Since April 2013, she has been enrolled in a research participation program at U.S. Food and Drug Administration (FDA), Center for Devices and Radiological Health (CDRH), Office of Science and Engineering Laboratories (OSEL), (Silver Spring, MD, US). Since November 2013 she is a PhD student in electronic engineer at the University of Rome “Sapienza” in the Department of Information Engineering, Electronics and Telecommunications. Her research interests are electromagnetic compatibility of medical devices, and numerical modeling of RF sources.

Micaela Liberti (M’04) received the Laurea degree in electronic engineering and doctorate degree from Sapienza University of Rome, in 1995 and 2000, respectively. In 2002, she became an Assistant Professor with the Department of Electronic Engineering, Sapienza University. Since 2008, she has being a member of the Scientific Council of the European Bioelectromagnetic Association (EBEA) and since 2011, she has being serving as its scientific secretary. Since 2012, she has been the national supplent representative of COST TD1104: “European network for development of electroporation-based technologies and treatments”. Her scientific interests include theoretical modeling in bioelectromagnetics, microdosimetry, exposure systems dosimetry and design.

Gonzalo G. Mendoza received the B.S. degree in Biomedical Engineering from the Central University of Cochabamba (Cochabamba, Bolivia) in 1997. He obtained the M.Sc. degree in Biomedical Engineering from The Catholic University of America (Washington DC, USA) in 2002. From 2000 to 2003 Mr. Mendoza was a Research Assistant and then a Research and Development Biomedical Engineer at The Catholic University of America. Since 2003, he has been a Biomedical Engineer Contractor with the FDA, CDRH, OSEL. Mr. Mendoza research interest are in the field of electromagnetic compatibility and human subject safety, in which he has authored several journal articles and conference proceedings.
Tom Lloyd received a MS in Electrical Engineering from Iowa State University. He has over 10 years of medical device and MRI compatibility experience. Mr. Lloyd is currently the Vice President of Research at Imricor and a U.S. appointed expert in the fields of MRI safety and the compatibility of implanted and interventional products in MRI.

Maria Ida Iacono received her Master Degree in 2007 and Ph.D. in 2011 in biomedical engineering from the Polytechnic of Milan (Milan, Italy). In 2010 she was awarded a Rocca Foundation doctoral fellowship at Massachusetts Institute of Technology (MIT) to join the Martinos Center For Biomedical Imaging, Massachusetts General Hospital, MIT-Harvard Medical School, from 2010 to 2012. Since 2012 she has been with the FDA, CDRH, OSEL where she was first a Postdoctoral Fellow and became a Scientist in 2014. She is currently author of 10 peer-reviewed journal articles, and 28 conference proceedings. Her research interests include medical imaging, in particular MRI, image processing, computational modeling, radio-frequency safety of medical devices in MRI, and brain stimulation.

Francesca Apollonio (M’06) received the Laurea degree (cum laude) in electronic engineering and doctorate degree from Sapienza University of Rome, in 1994 and 1998, respectively. In 2000, she became Assistant Professor at the Department of Electronic Engineering, Sapienza University. Since 2011 she is member of the National Scientific Commision CNR-URSI, Commission K “Electromagnetics in Biology and Medicine”. Since 2012 she is part of the Board of Directors of the Bioelectromagnetic Society (BEMS). Her research interest focuses on the interaction between electromagnetic fields and biological systems using both theoretical and experimental approaches.

Steve Wedan received a BS in Electrical Engineering from Michigan Technological University, summa cum laude, and an MS in Electrical Engineering from Marquette University. He has over 20 years of medical device experience, including design engineering of MRI and ultrasound systems for GE Healthcare, as well as Vice President and Chief Technology Officer for Applied Biometrics Inc. Prior to co-founding Imricor, Mr. Wedan founded and operated a consulting company, Wedan Technologies Inc., from 2000–2006. Mr. Wedan is a U.S. appointed expert in the fields of MRI safety and the compatibility of implanted and interventional products in MRI.

Wolfgang Kainz received the M.S. Degree in Electrical Engineering and Ph.D. Degree in Technical Science from the Technical University of Vienna, Austria, in 1997 and 2000, respectively. He is currently Research Biomedical Engineer at the FDA, CDRH, OSEL and has published over 160 peer-reviewed articles and book chapters. He is a member of the Administrative Committee of the IEEE International Committee on Electromagnetic Safety and member of many International Standards Committees. His research interest is currently focused on the safety and effectiveness of medical devices and safety of humans in electromagnetic fields. This includes computational electrodynamics for safety and effectiveness evaluations using anatomical models of the human anatomy; magnetic resonance imaging (MRI) safety; performance and safety of wireless technology used in medical devices; electromagnetic compatibility of medical devices; dosimetric exposure assessments from DC to light; and novel methods to computationally assess the safety and effectiveness of neuroprosthetics and therapeutic stimulation methods. In 2004, Dr. Kainz initiated the Virtual Family Project in co-operation with IT’IS and Prof. Ji Chen from the University of Houston.

Leonardo M. Angelone received the Laurea in electronic engineering from the University of Rome “La Sapienza,” Rome, Italy, in 2001. In 2008, he received the Ph.D. degree in biomedical engineering from Tufts University, Medford, MA, USA. Dr. Angelone has completed two Research Fellowships at the Department of Radiology, Massachusetts General Hospital, Harvard Medical School (2001–2003 and 2008–2014). He was a Postdoctoral Consultant with the Research and Development Department, Surgical Products Division, Hologic Inc., from 2008 to 2009. Since 2009, he has been a Research Biomedical Engineer with the FDA, CDRH, OSEL. He has authored more than 80 peer-reviewed journal articles and conference proceedings. His research interests include the assessment of energy deposition and heating induced in the human body by medical devices using electromagnetic energy.
Contributor Information
Elena Lucano, Sapienza University of Rome (Rome, Italy) and with the U.S. FDA, CDRH, Office of Science and Engineering Laboratories, Division of Biomedical Physics.
Micaela Liberti, Sapienza University of Rome (Rome, Italy).
Gonzalo G. Mendoza, U.S. FDA, CDRH, Office of Science and Engineering Laboratories
Tom Lloyd, Imricor Medical Systems.
Maria Ida Iacono, U.S. FDA, CDRH, Office of Science and Engineering Laboratories.
Francesca Apollonio, Sapienza University of Rome (Rome, Italy).
Steve Wedan, Imricor Medical Systems.
Wolfgang Kainz, U.S. FDA, CDRH, Office of Science and Engineering Laboratories.
Leonardo M. Angelone, U.S. FDA, CDRH, Office of Science and Engineering Laboratories.
V. References
- 1.Sutton R, et al. Safety of magnetic resonance imaging of patients with a new Medtronic EnRhythm MRI SureScan pacing system: clinical study design. Trials. 2008;9:68. doi: 10.1186/1745-6215-9-68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Blamire AM. The technology of MRI--the next 10 years? The British Journal of Radiology. 2008 Aug;81:601–17. doi: 10.1259/bjr/96872829. [DOI] [PubMed] [Google Scholar]
- 3.Hayes CE. The development of the birdcage resonator: A historical perspective. NMR in Biomedicine. 2009;22:908–918. doi: 10.1002/nbm.1431. [DOI] [PubMed] [Google Scholar]
- 4.Hayes CE, et al. An efficient, highly homogeneous radiofrequency coil for whole-body NMR imaging at 1.5 T. Journal of Magnetic Resonance (1969) 1985;63:622–628. [Google Scholar]
- 5.Boissoles P, Caloz G. Magnetic field properties in a birdcage coil. archives-ouvertes.fr 2006 [Google Scholar]
- 6.Tropp J. The theory of the bird-cage resonator. Journal of Magnetic Resonance (1969) 1989;82:51–62. [Google Scholar]
- 7.Atalar E. Radiofrequency safety for interventional MRI procedures. Academic radiology. 2005;12:1149–57. doi: 10.1016/j.acra.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 8.Carmichael DW, et al. Functional MRI with active, fully implanted, deep brain stimulation systems: safety and experimental confounds. NeuroImage. 2007;37:508–17. doi: 10.1016/j.neuroimage.2007.04.058. [DOI] [PubMed] [Google Scholar]
- 9.Oh S, et al. Experimental and numerical assessment of MRI-induced temperature change and SAR distributions in phantoms and in vivo. Magnetic resonance in medicine. 2010;63:218–23. doi: 10.1002/mrm.22174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu W, et al. Calculations of B1 Distribution, Specific Energy Absorption Rate, and Intrinsic Signal-to-Noise Ratio for a Body-Size Birdcage Coil Loaded with Different Human Subjects at 64 and 128 MHz. Appl Magn Reson. 2005 Mar;29:5–18. doi: 10.1007/BF03166953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ibrahim TS, et al. B1 field homogeneity and SAR calculations for the birdcage coil. Physics in medicine and biology. 2001 Feb;46:609–19. doi: 10.1088/0031-9155/46/2/324. [DOI] [PubMed] [Google Scholar]
- 12.Wolf S, et al. SAR simulations for high-field MRI: how much detail, effort, and accuracy is needed? Magnetic resonance in medicine. 2013;69:1157–68. doi: 10.1002/mrm.24329. [DOI] [PubMed] [Google Scholar]
- 13.Hand JW, et al. Numerical study of RF exposure and the resulting temperature rise in the foetus during a magnetic resonance procedure. Physics in medicine and biology. 2010;55:913–30. doi: 10.1088/0031-9155/55/4/001. [DOI] [PubMed] [Google Scholar]
- 14.Amjad A, et al. Power Deposition Inside a Phantom for Testing of MRI Heating. IEEE Transactions on Magnetics. 2005;41:4185–4187. [Google Scholar]
- 15.Murbach M, et al. Local SAR enhancements in anatomically correct children and adult models as a function of position within 1.5 T MR body coil. Progress in biophysics and molecular biology. 2011;107:428–33. doi: 10.1016/j.pbiomolbio.2011.09.017. [DOI] [PubMed] [Google Scholar]
- 16.Kainz W, et al. Calculation of induced current densities and specific absorption rates (SAR) for pregnant women exposed to hand-held metal detectors. Physics in medicine and biology. 2003;48:2551–60. doi: 10.1088/0031-9155/48/15/319. [DOI] [PubMed] [Google Scholar]
- 17.Cabot E, et al. Evaluation of the RF heating of a generic deep brain stimulator exposed in 1.5 T magnetic resonance scanners. Bioelectromagnetics. 2013 Feb;34:104–13. doi: 10.1002/bem.21745. [DOI] [PubMed] [Google Scholar]
- 18.Angelone LM, et al. Analysis of the Role of Lead Resistivity in Specific Absorption Rate for Deep Brain Stimulator Leads at 3T MRI. IEEE transactions on medical imaging. 2010;29:1029–1038. doi: 10.1109/TMI.2010.2040624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pisa S, et al. Interaction between the RF Field of MRI Apparatus and Pacemakers. INTECH Open Access Publisher; 2011. [Google Scholar]
- 20.Mattei E, et al. Numerical Model for Estimating RF-Induced Heating on a Pacemaker Implant During MRI: Experimental Validation. IEEE Transactions on Biomedical Engineering. 2010;57:2045–2052. doi: 10.1109/TBME.2010.2043102. [DOI] [PubMed] [Google Scholar]
- 21.Pisa S, et al. Power Absorption and Temperature Elevation Produced by Magnetic Resonance Apparatus in the Thorax of Patients With Implanted Pacemakers. IEEE Transactions on Electromagnetic Compatibility. 2010;52:32–40. [Google Scholar]
- 22.Neufeld E, et al. Measurement, simulation and uncertainty assessment of implant heating during MRI. Physics in medicine and biology. 2009;54:4151–69. doi: 10.1088/0031-9155/54/13/012. [DOI] [PubMed] [Google Scholar]
- 23.Carmichael DW, et al. Feasibility of simultaneous intracranial EEG-fMRI in humans: a safety study. NeuroImage. 2010;49:379–90. doi: 10.1016/j.neuroimage.2009.07.062. [DOI] [PubMed] [Google Scholar]
- 24.Simunić D, et al. Spatial distribution of high-frequency electromagnetic energy in human head during MRI: numerical results and measurements. IEEE Transactions on Biomedical Engineering. 1996;43:88. doi: 10.1109/10.477704. [DOI] [PubMed] [Google Scholar]
- 25.Shellock FG. Radiofrequency energy-induced heating during MR procedures: a review. Journal of Magnetic Resonance Imaging. 2000 Jul;12:30–6. doi: 10.1002/1522-2586(200007)12:1<30::aid-jmri4>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 26.Mattei E, et al. Numerical FDTD models of electromagnetic field generated by the RF coil of an MRI scanner: comparison among different solutions. Proceedings of the Sixth IASTED International Conference on Biomedical Engineering. 2008:187–192. [Google Scholar]
- 27.Ibrahim TS, et al. Computational analysis of the high pass birdcage resonator: finite difference time domain simulations for high-field MRI. Magnetic resonance imaging. 2000 Sep;18:835–43. doi: 10.1016/s0730-725x(00)00161-2. [DOI] [PubMed] [Google Scholar]
- 28.Aussenhofer SA, Webb AG. Design and evaluation of a detunable water-based quadrature HEM11 mode dielectric resonator as a new type of volume coil for high field MRI. Magnetic Resonance in Medicine. 2012 Oct;68:1325–31. doi: 10.1002/mrm.24451. [DOI] [PubMed] [Google Scholar]
- 29.Duan Y, et al. Assessment of a PML Boundary Condition for Simulating an MRI Radio Frequency Coil. International Journal of Antennas and Propagation. 2008;2008:1–10. [Google Scholar]
- 30.Alecci M, et al. Radio frequency magnetic field mapping of a 3 Tesla birdcage coil: Experimental and theoretical dependence on sample properties. Magnetic Resonance in Medicine. 2001;46:379–385. doi: 10.1002/mrm.1201. [DOI] [PubMed] [Google Scholar]
- 31.Liu W, et al. Effects of end-ring/shield configuration on homogeneity and signal-to-noise ratio in a birdcage-type coil loaded with a human head. Magnetic resonance in medicine. 2004;51:217–21. doi: 10.1002/mrm.10683. [DOI] [PubMed] [Google Scholar]
- 32.Jin JM, et al. Computation of electromagnetic fields for high-frequency magnetic resonance imaging applications. Physics in medicine and biology. 1996;41:2719–38. doi: 10.1088/0031-9155/41/12/011. [DOI] [PubMed] [Google Scholar]
- 33.Angelone LM, et al. Metallic electrodes and leads in simultaneous EEG-MRI: specific absorption rate (SAR) simulation studies. Bioelectromagnetics. 2004;25:285–95. doi: 10.1002/bem.10198. [DOI] [PubMed] [Google Scholar]
- 34.Gandhi OP, Chen XB. Specific absorption rates and induced current densities for an anatomy-based model of the human for exposure to time-varying magnetic fields of MRI. Magnetic resonance in medicine. 1999;41:816–23. doi: 10.1002/(sici)1522-2594(199904)41:4<816::aid-mrm22>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 35.Ruoff J, et al. Resolution adapted finite element modeling of radio frequency interactions on conductive resonant structures in MRI. Magnetic resonance in medicine. 2012;67:1444–52. doi: 10.1002/mrm.23109. [DOI] [PubMed] [Google Scholar]
- 36.Van den Berg CaT, et al. The use of MR B+1 imaging for validation of FDTD electromagnetic simulations of human anatomies. Physics in medicine and biology. 2006;51:4735–46. doi: 10.1088/0031-9155/51/19/001. [DOI] [PubMed] [Google Scholar]
- 37.Liu Y, et al. Computational and Experimental Studies of an Orthopedic Implant : MRI-Related Heating at 1 . 5-T / 64-MHz and 3-T / 128-MHz. Journal of Magnetic Resonance Imaging. 2013;497:491–497. doi: 10.1002/jmri.23764. [DOI] [PubMed] [Google Scholar]
- 38.Bassen HI, Mendoza GG. In-vitro mapping of E-fields induced near pacemaker leads by simulated MR gradient fields. Biomedical engineering online. 2009;8:39–39. doi: 10.1186/1475-925X-8-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kainz W, et al. Dosimetric comparison of the specific anthropomorphic mannequin (SAM) to 14 anatomical head models using a novel definition for the mobile phone positioning. Physics in medicine and biology. 2005;50:3423–45. doi: 10.1088/0031-9155/50/14/016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sammet CL, et al. RF-related heating assessment of extracranial neurosurgical implants at 7T. Magnetic resonance imaging. 2013;31:1029–1034. doi: 10.1016/j.mri.2012.10.025. [DOI] [PubMed] [Google Scholar]
- 41.A F2182-11a. Standard Test; Method for Measurement of Radio Frequency Induced Heating On or Near Passive Implants During Magnetic Resonance Imaging 2011 [Google Scholar]
- 42.Collins CM, Smith MB. Signal-to-noise ratio and absorbed power as functions of main magnetic field strength, and definition of “90 degrees “ RF pulse for the head in the birdcage coil. Magnetic resonance in medicine. 2001;45:684–91. doi: 10.1002/mrm.1091. [DOI] [PubMed] [Google Scholar]
- 43.Bit-Babik G, et al. Simulation of exposure and SAR estimation for adult and child heads exposed to radiofrequency energy from portable communication devices. Radiation research. 2005;163:580–590. doi: 10.1667/rr3353. [DOI] [PubMed] [Google Scholar]
- 44.Berenger J-P. A perfectly matched layer for the absorption of electromagnetic waves. Journal of computational physics. 1994;114:185–200. [Google Scholar]
- 45.R. XFDTD), “6.4, User’s Manual,” ed.
- 46.Kunz KS, Luebbers RJ. The finite difference time domain method for electromagnetics. CRC press; 1993. [Google Scholar]
- 47.Armstrong JS. Long-Range Forecasting: From Crystal Ball to Computer. Wiley; 1985. [Google Scholar]
- 48.Lucano E, et al. Building a computational model of a transmit body coil: considerations for RF safety,” in. Proc Intl Soc Mag Reson Med. 2014:4903. [Google Scholar]
- 49.Chou C, Guy A. Carbon-loaded Teflon electrodes for chronic EEG recordings in microwave research. The Journal of microwave power. 1979;14:399–404. doi: 10.1080/16070658.1979.11689175. [DOI] [PubMed] [Google Scholar]
- 50.Lemieux L, et al. Recording of EEG during fMRI experiments: patient safety. Magnetic Resonance in Medicine. 1997;38:943–952. doi: 10.1002/mrm.1910380614. [DOI] [PubMed] [Google Scholar]
- 51.Angelone LM, et al. On the effect of resistive EEG electrodes and leads during 7 T MRI: simulation and temperature measurement studies. Magnetic resonance imaging. 2006;24:801–812. doi: 10.1016/j.mri.2006.01.006. [DOI] [PubMed] [Google Scholar]
- 52.Kugel H, et al. Hazardous situation in the MR bore: induction in ECG leads causes fire. European radiology. 2003;13:690–4. doi: 10.1007/s00330-003-1841-8. [DOI] [PubMed] [Google Scholar]
- 53.Lange S, Nguyen QN. Cables and electrodes can burn patients during MRI. Nursing. 2006;36:18. doi: 10.1097/00152193-200611000-00012. [DOI] [PubMed] [Google Scholar]
- 54.Niendorf T, et al. Electrocardiogram in an MRI environment: clinical needs, practical considerations, safety implications, technical solutions and future directions. INTECH Open Access Publisher; 2012. [Google Scholar]
- 55.Konings MK, et al. Heating around intravascular guidewires by resonating RF waves. Journal of magnetic resonance imaging. 2000;12:79–85. doi: 10.1002/1522-2586(200007)12:1<79::aid-jmri9>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 56.Nitz WR, et al. On the heating of linear conductive structures as guide wires and catheters in interventional MRI. Journal of magnetic resonance imaging : JMRI. 2001;13:105–14. doi: 10.1002/1522-2586(200101)13:1<105::aid-jmri1016>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 57.Luechinger R, et al. Safety Evaluation of Large External Fixation Clamps and Frames in a Magnetic Resonance Environment. Journal of Biomedical Materials Research Part B: Applied Biomaterials. 2006:17–22. doi: 10.1002/jbm.b.30699. [DOI] [PubMed] [Google Scholar]
- 58.Doty FD, et al. Practical aspects of birdcage coils. Journal of magnetic resonance. 1999;138:144–54. doi: 10.1006/jmre.1998.1703. [DOI] [PubMed] [Google Scholar]
- 59.Chen X-L, et al. Analysis of human brain exposure to low-frequency magnetic fields: a numerical assessment of spatially averaged electric fields and exposure limits. Bioelectromagnetics. 2013;34:375–84. doi: 10.1002/bem.21780. [DOI] [PubMed] [Google Scholar]
- 60.Schmidt C, et al. Influence of uncertainties in the material properties of brain tissue on the probabilistic volume of tissue activated. IEEE transactions on bio-medical engineering. 2013;60:1378–87. doi: 10.1109/TBME.2012.2235835. [DOI] [PubMed] [Google Scholar]