Growth mindset tempers the effects of poverty on academic achievement

Significance

This study is the first, to our knowledge, to show that a growth mindset (the belief that intelligence is not fixed and can be developed) reliably predicts achievement across a national sample of students, including virtually all of the schools and socioeconomic strata in Chile. It also explores the relationship between income and mindset for the first time, to our knowledge, finding that students from lower-income families were less likely to hold a growth mindset than their wealthier peers but that those who did hold a growth mindset were appreciably buffered against the deleterious effects of poverty on achievement. These results suggest that mindsets may be one mechanism through which economic disadvantage can affect achievement.

Abstract

Two largely separate bodies of empirical research have shown that academic achievement is influenced by structural factors, such as socioeconomic background, and psychological factors, such as students’ beliefs about their abilities. In this research, we use a nationwide sample of high school students from Chile to investigate how these factors interact on a systemic level. Confirming prior research, we find that family income is a strong predictor of achievement. Extending prior research, we find that a growth mindset (the belief that intelligence is not fixed and can be developed) is a comparably strong predictor of achievement and that it exhibits a positive relationship with achievement across all of the socioeconomic strata in the country. Furthermore, we find that students from lower-income families were less likely to hold a growth mindset than their wealthier peers, but those who did hold a growth mindset were appreciably buffered against the deleterious effects of poverty on achievement: students in the lowest 10th percentile of family income who exhibited a growth mindset showed academic performance as high as that of fixed mindset students from the 80th income percentile. These results suggest that students’ mindsets may temper or exacerbate the effects of economic disadvantage on a systemic level.

Socioeconomic background is one of the strongest, best established predictors of academic achievement (1, 2). It is well-known that economic disadvantage can depress students’ academic achievement through multiple mechanisms, including reduced access to educational resources, higher levels of stress, poorer nutrition, and reduced access to healthcare (3–5). Nonetheless, students with the same economic background clearly vary in their academic outcomes, and researchers have long suggested that students’ beliefs, such as locus of control, may temper or exacerbate the effects of economic disadvantage on academic achievement (6–9). However, there has been a lack of clarity as to what these beliefs are or how they interact with structural factors, like economic disadvantage, on a systemic level. The current research identifies a belief—students’ mindset about intelligence—that is systematically associated with economic disadvantage and moderates its effects on achievement. Importantly, it is also a belief that is potentially amenable to change (10–14).

Numerous studies have found that students fare better if they believe that their intellectual abilities can be developed—a belief called growth mindset—than if they believe that their intellectual abilities are immutable—a belief called fixed mindset (15). These studies have documented numerous ways in which mindsets influence behaviors that impact academic achievement (16–18). Students with a fixed mindset tend to avoid situations in which they might struggle or fail because these experiences undermine their sense of their intelligence. In contrast, students who have a growth mindset tend to see difficult tasks as a way to increase their abilities (11) and seek out challenging learning experiences that enable them to do so (16, 17). As a consequence, students who have a growth mindset tend to earn better grades than students who hold a fixed mindset (11, 17, 18), especially in the face of difficulty. Additionally, a number of field experiments have now shown that growth mindset plays a causal role in achievement. These field experiments, including two blinded, randomized, controlled studies conducted with over 1,500 participants each, have shown that targeted interventions can help students start to develop a growth mindset and that such interventions can lead to higher achievement for students facing greater adversity (10–14).

However, because previous research was conducted with unrepresentative samples and lacked socioeconomic data, it has been impossible for researchers to address fundamental questions about the relationship between mindset and socioeconomic achievement gaps. Is the relationship between mindset and academic achievement a lawful pattern that can be observed reliably across an entire nation, and is it strong enough to be practically meaningful when measured against canonical structural factors, like family income? Is there evidence that economic disadvantage reinforces the fixed mindset? Finally, is a fixed mindset even more deleterious to economically disadvantaged students because they must overcome greater obstacles to succeed? We systematically investigate these questions for the first time, to our knowledge, using a national dataset containing all 10th graders in Chile.

Materials and Methods

This work uses a dataset of all 10th grade public school students in Chile to address these questions on a national scale. The Chilean Government administers standardized tests to measure the mathematics and language skills of all 10th graders in the country every other year. It also surveys each student, each student’s family, and each school. The 2012 student survey for the first time, to our knowledge, measured students’ mindsets about the malleability of intelligence using a short version of the standard instrument used by Dweck (15). Students who agreed or strongly agreed with statements suggesting that intelligence cannot be changed (i.e., “intelligence is something that cannot be changed very much” and “you can learn new things, but you can’t change a person’s intelligence”) were categorized as having a fixed mindset, those who disagreed or strongly disagreed were categorized as having a growth mindset, and those who were uncertain were categorized as having a mixed mindset. A categorical system was used in graphical presentations for clarity, whereas a continuous standardized score was used in analyses. The details, including the Spanish translation of the items, are provided in SI Materials and Methods.

The analyses include all public school students who answered at least one mindset item and completed at least one standardized test (n = 168,203 and n = 168,553 for mathematics and language, respectively). These students represent 75% of all 10th graders from Chile’s public schools, and the schools represent 98% of all 2,392 public schools. A detailed description of the population as well as the imputation methods that were used for missing data are available in SI Materials and Methods. The descriptive statistics for variables on the whole population and the analytical sample are listed in Table S1.

Table S1.

Statistics for all student and school variables used

Variable	Public school students			Analytical sample
	N	Mean	SD	N	Mean	SD
Student-level variables
Test scores
Mathematics score	189,107	−0.102	0.954	167,605	−0.080	0.958
Language score	189,265	−0.073	0.979	167,605	−0.043	0.975
Mindset score	170,977	−0.031	0.994	167,605	−0.025	0.995
Female	225,394	50%		167,605	51%
Native	130,220	14%		119,864	14%
Monthly family income (2012 CLP)	141,414			129,962
Reference: less than $100,000	10,461	7%		9,333	7%
$100,000–$200,000	37,494	27%		34,141	26%
$200,000–$300,000	31,355	22%		28,848	22%
$300,000–$400,000	18,232	13%		16,863	13%
$400,000–$500,000	12,230	9%		11,348	9%
$500,000–$600,000	9,045	6%		8,383	7%
$600,000–$800,000	7,911	6%		7,371	6%
$800,000–$1,000,000	5,493	4%		5,119	4%
$1,000,000–$1,200,000	2,874	2%		2,680	2%
$1,200,000–$1,400,000	1,878	1%		1,749	1%
$1,400,000–$1,600,000	1,224	1%		1,142	1%
$1,600,000–$1,800,000	768	1%		722	1%
$1,800,000–$2,000,000	724	1%		673	1%
$2,000,000–$2,200,000	469	0%		434	0%
More than $2,200,000	1,256	1%		1,156	1%
Maximum education completed by mother	140,593			129,265
Reference: less than elementary school	17,761	13%		16,030	12%
Elementary school	17,430	12%		15,788	12%
High school incomplete	20,614	15%		18,838	15%
High school	52,210	37%		48,298	37%
Some vocational higher education	5,265	4%		4,872	4%
Vocational higher Education	3,067	2%		2,838	2%
Some college	15,537	11%		14,450	11%
College	8,018	6%		7,503	6%
Postgraduate	691	1%		648	1%
Maximum education completed by father	135,389			124,503
Reference: less than elementary school	16,794	12%		15,099	12%
Elementary school	18,348	14%		16,793	14%
High school incomplete	20,295	15%		18,529	15%
High school	48,034	36%		44,410	36%
Some vocational higher education	4,818	4%		4,457	4%
Vocational higher Education	4,484	3%		4,165	3%
Some college	11,672	9%		10,839	9%
College	9,666	7%		9,015	7%
Postgraduate	1,278	1%		1,196	1%
Has a computer	141,071	85%		129,684	86%
Has internet at home	132,850	67%		122,268	67%
Books at home	142,763			131,181
Reference: no books	4,050	3%		3,556	3%
Less than 10	31,230	22%		28,276	22%
10–50	70,681	50%		65,146	50%
51–100	23,226	16%		21,601	17%
More than 100	13,576	10%		12,602	10%
People at home
Mother	225,394	57%		167,605	70%
Father	225,394	39%		167,605	49%
Stepmother	225,394	1%		167,605	1%
Stepfather	225,394	5%		167,605	6%
Siblings	225,394	47%		167,605	58%
Grandparents	225,394	11%		167,605	13%
Relatives (other)	225,394	5%		167,605	6%
Nonrelatives	225,394	2%		167,605	2%
No member reported	225,394	37%		167,605	22%
School-level variables
2010 School mathematics score	215,580	−0.218	0.843	161,063	−0.139	0.852
2010 School language score	225,394	−0.196	0.884	167,605	−0.110	0.870
School size	225,368	142.450	108.744	167,605	143.199	111.972
Classroom size	225,394	36.606	6.706	167,605	36.887	6.563
Poverty concentration	223,992	0.661	0.166	166,834	0.646	0.169
Rural	225,368	4%		167,605	4%
School SES group	225,337			167,605
Low	66,088	29%		44,230	26%
Medium low	85,758	38%		62,047	37%
Medium	52,340	23%		43,379	26%
Medium high	20,496	9%		17,425	10%
High	655	0%		524	0%
Independent (reference: governmental)	225,368	60%		167,605	61%
Geographical region	225,368			167,605
1	3,214	1%		2,229	1%
2	4,630	2%		3,438	2%
3	8,130	4%		5,826	4%
4	4,329	2%		3,173	2%
5	10,227	5%		7,741	5%
6	22,089	10%		15,982	10%
7	12,270	5%		9,289	6%
8	14,540	7%		11,055	7%
9	28,165	13%		20,440	12%
10	14,377	6%		11,136	7%
11	5,731	3%		4,492	3%
12	11,440	5%		8,889	5%
13	1,374	1%		1,082	1%
14	2,145	1%		1,735	1%
15	82,707	37%		61,098	37%
Student self-beliefs and expectations
I am smart	173,967	3.281	0.651	166,621	3.288	0.647
I am good at mathematics	174,753	2.661	0.746	167,267	2.667	0.747
I like mathematics	174,621	2.467	0.955	167,167	2.473	0.956
I am good at language	174,482	2.677	0.675	167,039	2.680	0.674
I like language	174,716	2.749	0.774	167,228	2.752	0.774
Student expectations	165,728			158,765
Reference: drop out	919	1%		754	1%
High school graduate	20,781	13%		18,988	12%
Vocational degree	41,963	25%		39,963	25%
College degree	102,065	62%		99,060	62%
Parent expectations	137,394			126,292
Reference: will not finish high school	841	1%		706	1%
High school (vocational)	19,786	14%		17,455	14%
High school (preparatory)	6,043	4%		5,362	4%
Vocational higher education	28,152	21%		25,670	20%
College	67,729	49%		63,180	50%
Postgraduate	14,843	11%		13,919	11%
Total schools	2,392			2,339
Total students	225,394			167,605

Public school students data refer to all available data. Analytical sample data refer to data available after removing students who were missing language, mathematics, and mindset scores (these data were used in the analyses). As evidenced by the similarities between the two samples, conclusions drawn from the analytical sample can be generalized to all public school students. All variables in this table are included in the models of Column 4 in Table 2, with the exception of the last seven variables (student self-beliefs and expectations), which are added later as a way to test for reverse causation. CLP, Chilean pesos; SES, socioeconomic status.

Results

First, we sought to determine whether the relationship between mindset and academic achievement constitutes a lawful pattern that can be observed reliably across an entire nation and whether it is strong enough to be practically meaningful when measured against canonical structural factors, like family income. Consistent with prior findings (1, 19), canonical predictors of academic achievement, such as family income and parents’ education, were correlated with test scores in our sample (Table 1). Importantly, the relationship between student mindsets and achievement was comparably strong and held across all students in Chile. Student mindset explained 11.8% of variance (r = 0.343) in a composite average of mathematics and language scores, and the top student-level socioeconomic predictor explained 11.3% (r = 0.336). The difference between these correlations was statistically significant: Fisher’s r to Z = 2.29; P = 0.02 (20). Among school-level socioeconomic variables, the poverty concentration index was the strongest predictor of test scores (explaining 26.2% of variance), whereas the average mindset at the school—or “school mindset”—was again on par with this variable (explaining 26.6% of the variance). This difference was not statistically significant: Fisher’s r to Z = 1.58; P = 0.11.

Table 1.

Unconditional Pearson correlations between key variables and standardized achievement test scores

Variable	Language	Mathematics	Average language and mathematics
Student-level variables
Mindset	0.333	0.292	0.343
Family income	0.226	0.301	0.289
Natural log of family income	0.249	0.331	0.319
Mother years of education	0.275	0.338	0.336
Father years of education	0.269	0.326	0.326
School-level variables
Average mindset in school	0.427	0.513	0.516
Poverty index	−0.412	−0.520	−0.512
SES quintile	0.402	0.508	0.500
School mathematics 2010	0.486	0.625	0.610
School language 2010	0.525	0.528	0.578

All values reported are significant (P < 0.001). Details about each variable are in SI Materials and Methods. SES, socioeconomic status.

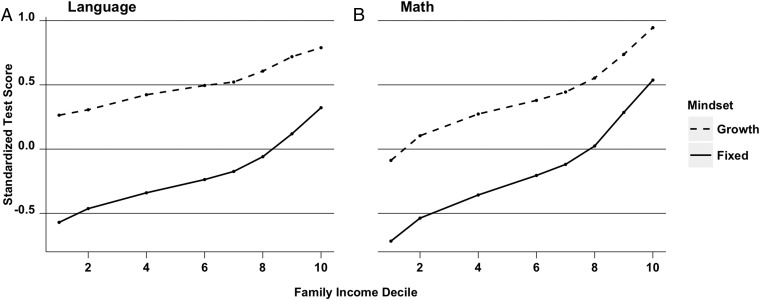
Second, we sought to determine the robustness and generalizability of this relationship. We found that the relationship between mindset and achievement could be observed across the socioeconomic spectrum and even when controlling for an extensive list of important student- and school-level factors. As Fig. 1 shows, students who subscribed to a growth mindset outperformed their peers at each family income level. Furthermore, mindset remained a highly significant predictor of achievement across a series of hierarchical linear regression models (21) controlling for all available canonical predictors of achievement (1, 19, 22). Table 2 presents the results, showing that the relationship between mindset and test scores still holds in each of these models. To start, column 2 in Table 2 shows this analysis for standardized mathematics and language scores without any covariates. Column 3 in Table 2 controls for student-level characteristics, including gender, ethnic origin, family income, mother’s and father’s educations, the presence of household assets (e.g., books, computer), and family structure. Column 4 in Table 2 further adds school-level variables, including the socioeconomic level of the school, school enrollment, average class size, type of administration, urbanicity, geographic region, and the school’s 2010 average mathematics and language test scores. With all of these important covariates included, the model accounted for almost all of the variability of scores between schools (93–95% depending on the subject) and 36–44% of the total variance; however, the estimate of the mindset effect on achievement remained significant (B = 0.203; SE = 0.002; P < 0.001 for language and B = 0.138; SE = 0.002; P < 0.001 for mathematics). The estimated coefficients suggest that, on average, the academic growth associated with a student who changes from having a fixed mindset to a mixed mindset or from a mixed mindset to a growth mindset is 0.2 SDs on language test scores and 0.13 SDs on mathematics test scores.

Fig. 1.

Average standardized mathematics and language test scores for students with growth and fixed mindsets by family income decile. A shows language scores, and B shows mathematics scores. Dashed lines represent students with growth mindset, and solid lines represent students with fixed mindset. For clarity, only fixed mindset and growth mindset (not mixed mindset) students are included. However, we note that mixed mindset students consistently fell in between the two other groups.

Table 2.

Language and mathematics test scores predicted by mindset score (standardized) when controlling for student- and school-level variables

Variables	Test score predicted by mindset with no other controls	Test score predicted by mindset and student-level variables	Test score predicted by mindset and both student- and school-level variables
Language score
Mindset regression coefficient	0.214*	0.206*	0.203*
SE	0.003	0.002	0.002
Student controls		Included	Included
School controls			Included
No. of students	168,552	168,552	168,552
No. of schools	2,339	2,339	2,339
Mathematics score
Mindset regression coefficient	0.146*	0.140*	0.138*
SE	0.002	0.002	0.002
Student controls		Included	Included
School controls			Included
No. of students	168,203	168,203	168,203
No. of schools	2,339	2,339	2,339

Each column describes a maximum likelihood hierarchical linear model with students nested in schools. Column 2 presents mindset standardized regression coefficients without any control variables. Column 3 adds student-level controls. Column 4 adds school-level controls. Full list of controls is available in SI Materials and Methods, Table S1.

^*Regression coefficients are P < 0.01.

We also considered the possibility of reverse causation—perhaps doing well in school leads to a growth mindset rather than the other way around. That is, students who do well may hold positive self-perceptions, such as believing themselves to be intelligent, accomplished students. It is plausible that these positive self-perceptions could lead to other positive beliefs, such as the belief that their intellectual ability can grow over time. To test for reverse causation, we ran the previous model and added controls for a variety of beliefs and expectations that could play a role in this reverse causal process. These beliefs included students’ self-assessments of their intelligence and their ability in each subject, such as agreement with the statements “I am smart,” “I am better than the majority of my classmates on mathematics tests,” and “I do well in language arts.” We also controlled for student’s and parents’ expectations of the student’s academic attainment and the degree to which the student liked each subject area and thought that it was important. The relationship between mindsets and achievement remained highly significant when controlling for these factors (B = 0.171; P < 0.001 for language and B = 0.119; P < 0.001 for mathematics). Thus, our effect is not because of the fact that students who see themselves as doing well simply observe their academic growth and come to the conclusion that intelligence can be developed.

An additional model was created to assess the reliability of the relationship between mindset and achievement across each individual school. To calculate a range of plausible values for the mindset effect per school, the model included a school-level random component for the mindset coefficient as well as all student- and school-level control variables. Through this analysis, we estimate a positive association between mindset and achievement for each of 2,339 schools included in the sample (the 95% plausible value range for the association between mindset and language per school was 0.077–0.261, and the 95% plausible value range for the association between mindset and mathematics per school was 0.038–0.200). Details are in SI Materials and Methods.

Consistent with prior experimental studies, our results show that, for students with the same observable characteristics, those with a growth mindset achieved at higher levels than those with a fixed mindset. Furthermore, these results show for the first time, to our knowledge, that this relationship is comparably strong with that between family income and achievement and that it holds true systemically—across an entire nation’s socioeconomic spectrum and across virtually all of its schools.

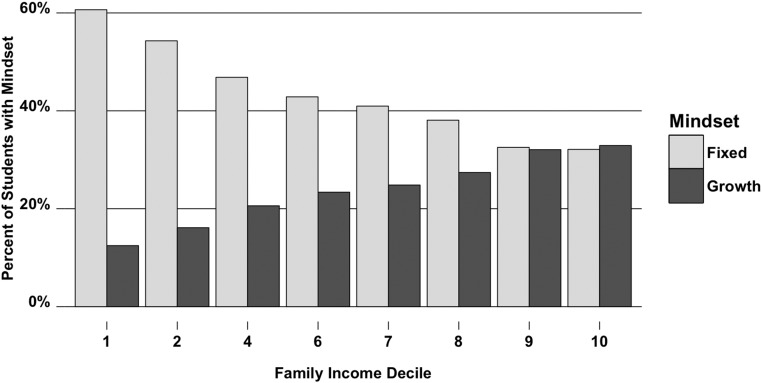
A final series of models investigated the prevalence of mindsets as a function of income as well as the relationship between income and achievement as a function of mindset. First, we tested the possibility that economic disadvantage and the limited structural opportunities associated with it could themselves reinforce a fixed mindset. A simple correlation revealed that students’ mindsets and family income were, indeed, linked (r = 0.17; P < 0.001). At the extremes, students from the lowest-income families were twice as likely to endorse a fixed mindset as students from the top-income families and schools (Fig. 2).

Fig. 2.

Percentage of students with fixed and growth mindsets as a function of family income. Percentages do not add up to 100 at each income decile because, for clarity, only fixed mindset and growth mindset (not mixed mindset) students are included. However, we note that the percentage of mixed mindset students consistently fell in between the two other groups. Families reported their income by selecting one income range from a list. Some income deciles are missing because on the questionnaires, parents were not offered an income choice corresponding to that decile.

Second, we tested whether a fixed mindset was even more harmful to the academic achievement of economically disadvantaged students because those students, lacking the resources of higher-income students, would need to overcome greater obstacles to succeed. A negative interaction between family income (standardized) and mindset in predicting test scores (B = −0.020; P < 0.001 and B = −0.018; P < 0.001 for language and mathematics, respectively, which is shown in SI Materials and Methods, Table S2) suggested that lower income magnifies the deleterious effects of a fixed mindset or, conversely, that a growth mindset may help mitigate the negative effects of economic deprivation on academic achievement. This difference is illustrated in Fig. 1, where we observe that, strikingly, students from low-income families (the lowest 10%) who had a growth mindset showed comparable test scores with fixed mindset students whose families earned 13 times more (80th percentile).

Table S2.

Language and mathematics test scores predicted by mindset, income, and their interaction

Variable	Language standardized score (SD)		Mathematics standardized score (SD)
	Without controls	With controls	Without controls	With controls
Mindset	0.221*	0.208*	0.150*	0.141*
SE	0.003	0.002	0.002	0.002
Standardized income	0.037*	−0.013*	0.056*	0.003
SE	0.003	0.003	0.002	0.003
Mindset × standardized income	−0.022*	−0.020*	−0.024*	−0.018*
SE	0.002	0.002	0.002	0.002
Student-level controls		Included		Included
School-level controls		Included		Included
No. of students	130,508	130,508	130,357	130,357
No. of schools	2,234	2,234	2,234	2,234

The negative interaction shows that students from lower-income families benefit more from a growth mindset. Each column describes a maximum likelihood hierarchical linear model with students nested in schools. Columns 3 and 5 control for all student and school covariates included in models of Column 4 in Table 2. Students included in these models are those included in the analytical sample who were not missing income information. SEs are clustered by school.

^*P < 0.01.

Discussion

The results of this study speak to researchers, educators, and policymakers interested in understanding equality of opportunity. We document for the first time, to our knowledge, on a national scale a robust relationship between students’ mindsets about intelligence and their academic performance. Our research shows that, at every socioeconomic level, those who hold more of a growth mindset consistently outperform those who do not—even after holding constant a panoply of socioeconomic and attitudinal factors. The relationship between mindset and achievement holds true across all of Chile’s schools and across all levels of family income. In other words, for any two students with equal characteristics, the one endorsing a growth mindset is more likely to enjoy higher academic achievement, suggesting that the benefit of having a growth mindset holds widely. Furthermore, these robust, nation-level correlations are complemented by multiple prior randomized field experiments showing that a growth mindset has a causal impact on achievement (10–14).

These findings also document for the first time, to our knowledge, a relationship between mindsets and economic disadvantage. The lowest-income Chilean students were twice as likely as the highest-income students to report a fixed mindset, and their mindset was an even stronger predictor of success for these low-income students. Although existing data cannot explain why low-income students were more likely to endorse a fixed mindset, this finding does suggest that economic disadvantage may lead to poorer academic outcomes, in part by leading low-income students to believe that they cannot grow their intellectual abilities. The observation that mindset is a more important predictor of success for low-income students than for their high-income peers is novel, although it is consistent with prior research, which has found that a fixed mindset is more debilitating (and a growth mindset is more protective) when individuals must overcome significant barriers to succeed (13, 14).

To be clear, we are not suggesting that structural factors, like income inequality or disparities in school quality, are less important than psychological factors. Nor are we saying that teaching students a growth mindset is a substitute for systemic efforts to alleviate poverty and economic inequality. Such claims would stand at odds with decades of research and our own data. Rather, we are suggesting that structural inequalities can give rise to psychological inequalities and that those psychological inequalities can reinforce the impact of structural inequalities on achievement and future opportunity. As such, research on psychological factors can help illuminate one set of processes through which economic disadvantage leads to academic underachievement and reveal ways to more effectively support students who face additional challenges because of their socioeconomic circumstances.

SI Materials and Methods

A. Materials.

The data analyzed in this study come from five national datasets collected by the Chilean Department of Education in 2012. These datasets include measures of performance on mathematics and language standardized tests, mindset, and socioeconomic background of the 10th grade Chileans (244,826 students in 2,772 schools), and they are part of the Chilean System for Measurement of Educational Quality (SIMCE; in Spanish). The SIMCE administers standardized assessments of mathematics and language to all Chilean 10th grade students every other year. In addition, students, parents, and teachers complete a questionnaire that covers a wide range of information. Included in the 2012 students’ questionnaire for the first time, to our knowledge, was an adapted version of the mindsets about intelligence scale (15) described in detail in SI Materials and Methods, section C.

The SIMCE datasets are available to researchers through a short application process (www.agenciaeducacion.cl/simce/bases-de-datos-nacionales/). Additional school demographics data were obtained from a public dataset available from the Department of Education (www.junaeb.cl/ive; 2012 dataset Prioridades 2012 con IVE-SINAE Oficial Básica y Media).

B. Study Population.

The population included in the analysis corresponds to all 10th grade public school students in 2012 who completed at least one national test and answered at least one mindset item.

Chilean public schools.

We use public schools to refer to all Chilean schools that receive funding from the government. These schools can be owned by the central government, the local government (called municipal schools), or private organizations (schools called subvencionados). Public school students account for all Chilean 10th grade students other than the 8% who attend private schools that receive no public funding. We excluded these privately funded schools from our analysis because the government does not calculate poverty rates for them (a key measure for predicting achievement) and because their structure and student bodies systematically differ from the rest of the education system.

Final sample.

Fifteen percent of 10th grade students did not have either mathematics or language test scores in the dataset. Students may not have scores for different reasons: a student missed the day of the test, materials were lost, tests were blank, or the test was waived because of a learning disability. These students were dropped from our sample. Students with missing mindset scores were not included in our analysis, but their test scores and other information (such as income) were used for standardizations and calculations of deciles if available. The final sample in the main analysis represents 75% of all 10th grade public school students in Chile distributed across 98% of all 2,392 public schools (n = 168,203 and n = 168,552 for mathematics and language, respectively).

Missing data.

There are some missing data in most of the variables used in the analysis, and the missing data are not random. For example, family income is missing predominantly at low socioeconomic schools (45% of students from these schools had missing income data, whereas only 26% of students from richer schools did). To include these students in the analyses, we followed two procedures for dealing with missing data. In cases in which we could use the variable as categorical, we created a missing category. For the rest of the variables, we coded the missing value as zero and created the corresponding missing dummy. We ran all analyses with both the imputed sample and a limited sample (with no imputed variables), and conclusions do not vary (results are equally significant and of similar magnitude). The section below describes the imputation used for each variable.

C. Overview of Variables.

The primary outcome variables are mathematics and reading standardized test scores. Summary statistics for the variables used in the analysis are displayed in Table S1.

Scores.

Mathematics and language scores provided in the SIMCE dataset for each student were standardized across the full national population (M = 0.0; SD = 1; range = −2.398–2.510 for mathematics and −2.453–2.488 for language). A third score was calculated as the mean of the standardized mathematics and language scores (M = −0.061; SD = 0.879; range = −2.426–2.503).

Mindset.

The 2012 SIMCE student questionnaire included two items to measure the students’ mindset. The items were selected from the “theory of intelligence” scale (15). The items asked students about their level of agreement with the Spanish translation of the following statements: “intelligence is something that cannot be changed very much” and “you can learn new things, but you can’t change a person's intelligence.” Students marked their answers on a six-point Likert scale from strongly agree to strongly disagree (Cronbach’s α = 0.86). The exact wording in the Spanish items is the following: “La inteligencia es algo que no se puede cambiar mucho” and “Se pueden aprender cosas nuevas, pero no se puede cambiar la inteligencia de una persona,” with the scale points labeled Muy de acuerdo, De acuerdo, Un poco de acuerdo, Un poco en desacuerdo, En desacuerdo, and Muy en desacuerdo. Items were coded so that lower scores are associated with a lower growth mindset. Responses with more than one mark are considered as missing.

Because of space limitations, the survey could only include two mindset items. We chose fixed mindset items rather than growth mindset items because growth items sometimes create an acquiescence bias. This decision is consistent with those made in other recent investigations of mindset (13, 14). Because the mindset score is lower for low-income students (i.e., they were more likely to agree to the fixed mindset statements), we checked to ensure that low-income students did not show more acquiescence bias than students from other groups, and there is no evidence of it. Low-income students were as likely as high-income students to disagree on the questions that immediately followed the measures of mindset.

A mindset score was calculated by averaging the two mindset items or using only one if the other was missing. The final averaged score was standardized across all available students (M = 0.0; SD = 1; range = −1.239–1.824). A categorical variable was created based on the mindset score to use in graphical representations of the data. For simplicity, students were classified into three distinct mindset categories: “fixed mindset” refers to students who scored from 1 to 2 (i.e., agree or strongly agree), “growth mindset” refers to those who scored from 5 to 6 (i.e., disagree or strongly disagree), and “mixed mindset” refers to those who scored between 2.1 and 4.9, with 46.79%, 21.25%, and 31.96% falling into each category, respectively. Although we present only the clear growth and fixed mindset groups in our graphs, we note that the mixed mindset group typically fell in between the other two on the achievement measures, and this relationship held true across income levels.

Student background.

Information about students’ background was retrieved mostly from the parent questionnaire. Parents or guardians responded to paper questionnaires by hand. We coded the responses following government guidelines and previous studies (22, 23). Results do not vary when using these variables as categorical or continuous.

Variables representing student background include the following variables.

• i)Monthly family income: Parents or guardians reported their family monthly income by selecting one of 15 ranges (for example, between CL$400,001 and CL$500,000 or above CL$2,200,000 for the last category). In regressions, this information was used as a categorical variable, with dummy codes for each range and an additional category for missing income. In the analyses that required income as a continuous variable (such as the correlation calculations), we used the conversion table provided by the Chilean Department of Education (23) to replace the ranges with the value in the middle of the range. Results do not vary when using each type of variable. These responses were also used to compute each child’s family income decile. Some income deciles are missing because on the questionnaires, parents were not offered an income choice corresponding to that decile.
• ii)Mother’s and father’s level of education: Parents or guardians reported the highest level of education reached by each parent. Categorical variables mother education and father education were created with the following categories: less than elementary school, elementary school completed, less than high school, high school completed, some higher education incomplete, technical or vocational higher education completed, college completed, postgraduate degree, and an extra category for missing values. To create a continuous variable (used for correlations), this information was translated into years of education following the conversion table provided by the Chilean Government (23).
• iii)Books at home: Parents or guardians selected one of these categories: none, less than 10, between 10 and 50, between 51 and 100, or more than 100. This variable was coded categorically (with dummy codes), with a category for missing value.
• iv)Computer at home and internet at home: Each of these was dummy-coded, with an additional category for missing value.
• v)Family composition: Parents or guardians selected the members of the family who lived at home from a list. One dummy variable represents each answer (mother, father, siblings, grandparents, other relatives, or other nonrelatives), and an additional dummy code indicated that both parents live at home with the child. A missing family dummy was added when no member of the family was selected as living at home and for all students with no parent questionnaire.
• vi)Native origin: Parents or guardians indicated whether the father or mother of the student was a member of one of Chile’s indigenous peoples. It was coded as a dummy variable, indicating that at least one parent was of native origin.
• vii)Female: Dummy code indicating that the student was a female. This variable was provided with students’ scores directly from the government and had no missing data.

School socioeconomic information.

School-level data were retrieved from both the SIMCE dataset and a school demographics dataset publicly available from the Department of Education (www.junaeb.cl/ive; 2012 dataset Prioridades 2012 con IVE-SINAE Oficial Básica y Media).

• i)Poverty concentration index (IVE-SINAE in Spanish): This index reports the percentage of students in the school who are labeled as priority because of their low socioeconomic status. This index is calculated by the Chilean Department of Education to determine the recipients of free lunch and other benefits every year. All public schools have this index.
• ii)Socioeconomic level of the school: This variable is defined and calculated by the Chilean Department of Education, and it is a composite of several socioeconomic characteristics. It classifies each school into one of five socioeconomic categories: low, medium low, medium, medium high, and high. The analytical procedure to develop the composite value is described by the Chilean Government (23). In its calculation, it uses responses from the 2012 parents’ questionnaire (mother and father education level and monthly family income) and the poverty concentration index.
• iii)Rural (vs. urban): Designation was provided by the Department of Education. A dummy-coded variable indicated that the school was in a rural area.
• iv)School size: A continuous variable describing the number of students enrolled in the school with no missing data.
• v)Administration type: Public schools in Chile vary by administration. Privately administrated schools subsidized with public funding are labeled as independent in this analysis; publicly funded schools administrated by a governmental agency are labeled as government. A dummy variable indicates whether the school is independent.
• vi)Mathematics and language whole-school score from 2010: The most recent previous time that each school was assessed in mathematics and language in 10th grade was in 2010. We retrieved this score through the data provided by the SIMCE, and we standardized the scores for the whole dataset. Schools that were missing an average score from 2010 were assigned a zero, and we included separate dummy variables to indicate that the school was missing a 2010 mathematics or language score.

Other student variables (self-beliefs and expectations).

The student surveys included several measures of attitudes and beliefs. Unless otherwise noted below, these variables are coded as continuous. Students with missing responses are coded as zero, and a dummy variable is included to indicate that they are missing responses.

• i)Self-rated intelligence: Students responded to the item “I am smart” on four-point Likert scale (from agree a lot to disagree a lot).
• ii)Self-rated mathematics ability: Students answered four questions on a four-point Likert scale (from agree a lot to disagree a lot). Questions included “I am better than the majority of my classmates in math,” “I do math exercises pretty well,” “I am good at math,” and “I get good results in math class.”
• iii)Self-rated language ability: Students answered two questions on a four-point Likert scale (from agree a lot to disagree a lot). Questions included “I am good at reading” and “I get good results in language class.”
• iv)Academic enjoyment: Students reported the level of enjoyment for each subject’s class and activities. A separate variable was calculated for mathematics and language, each averaging the answers to the corresponding two four-point Likert items [e.g., “I like doing math exercises” and “I like the math class” (reliability α = 0.62 and 0.85, respectively)].
• v)Importance of subject: The students agreed or disagreed with the statements “math is important,” and “reading is important” on a four-point scale (from agree a lot to disagree a lot). A separate variable was created for each subject.
• vi)Expectations of educational attainment: Students selected the highest educational level that they expected to complete from these options: dropping out before graduating from high school, graduating from high school, attending vocational school, or attending college. A missing category was added.
• vii)Parents’ expectations: Parents or guardians indicated whether they expected their child to not graduate high school, only graduate high school, attend vocational school, or attend college. A missing category was added.

D. Analyses.

Simple correlations.

We investigated whether our mindset measure was related to performance on the mathematics and language achievement tests. Initially, we calculated the correlation between mindset and achievement and compared it with other canonical predictors of achievement (Table 1). Then, to rule out the possibility that students’ mindset scores were simply a reflection of their family or school background factors or their interests and perceived ability, we also tested a series of models that controlled for these factors.

Hierarchical models.

We assume that test scores vary as a function of student and school characteristics. To represent the hierarchical nature of the data, we modeled them using a hierarchical linear model with students nested within schools (21). This model allows the mindset coefficient to vary across schools, while simultaneously accounting for schools’ characteristics. The most complete specification is shown below, where we control for student- and school-level characteristics and add a random component to the mindset coefficient:

level 1 model (student):

$${\text{SCORE}}_{ij}={\mathrm{\beta }}_{0j}+{\mathrm{\beta }}_{1j}\times \left({\text{MINDSET}}_{ij}\right)+{\mathit{X}}_{\mathit{ij}}^{\mathit{\prime }}\mathbf{\delta }+r_{ij}$$

and level 2 model (school):

$$\begin{array}{c}{\mathrm{\beta }}_{0j}={\mathrm{\gamma }}_{00}+{\mathit{S}}_{\mathit{j}}^{\mathit{\prime }}{\mathbf{\gamma }}_{\mathbf{0}}+u_{0j}\hspace{0.17em}\text{and}\\ {\mathrm{\beta }}_{1j}={\mathrm{\gamma }}_{10}+u_{1j}.\end{array}$$

At level 1, SCORE_ij is the standardized test score of student i in school j in mathematics or language. MINDSET_ij is the student’s standardized mindset score. X_ij is a vector of the student-level covariates, β_0j is the intercept of the regression set to vary from school to school, β_1j is the regression coefficient indicating the strength of the association between mindset and achievement scores within school j; δ is a vector of the regression coefficients accompanying vector X_ij (fixed across schools), and r_ij is a random error of the linear prediction representing individual differences of students; it is assumed to be normally distributed within schools, with mean = 0 and variance σ².

At level 2, the dependent variables are the intercept and the mindset slope from level 1. The intercept β_0j is modeled as predicted by school-level covariates S_j and a random component u_0j that varies per school (assumed to be normally distributed, with mean = 0 and variance τ₀₀², independent of each other); γ₀₀ is the intercept, and it also represents the grand mean of the test scores across all schools when all characteristics are set to zero. Finally, β_1j is also set to have a fixed component γ₁₀ (representing the average association between mindset and scores across schools) and an independent random component u_1j per school normally distributed, with mean = 0 and variance τ₁₁² across schools.

The coefficient of interest is γ_10. It represents the predicted average increase in test score (in SDs) by an increase of 1 SD in the mindset score, leaving everything else equal. A 1-SD increase in mindset approximately represents an increase from a mixed mindset to a growth mindset or from a fixed mindset to a mixed mindset. Therefore, the predicted average increase in test scores from a change of a fixed mindset to a growth mindset can be approximated as 2 × γ₁₀ (and 2 × β_1j for a particular school j).

We ran different specifications for this model, starting from a simple version in which we set the mindset coefficient-β_1j to be the same for all schools (i.e., we set β_1j = γ₁₀ by forcing u_1j = 0 for all j) and included no student- or school-level controls. To it, we successively added student- and school-level variables. The results of these models enabled us to observe the stability of the coefficient representing the relationship between mindset and test scores. It changed little in strength across models as shown in Table 2.

In addition, we ran a school fixed effects model (i.e., u_0j is replaced by a constant for each school and u_1j = 0), which allows accounting for the sorting of students into schools. The relationship between mindsets and achievement is similar to that in the previous models (B = 0.203; P = 0.002 for language and B = 0.137, P = 0.002 for mathematics controlling for student-level covariates).

This analysis shows that the relationship between mindset and achievement is essentially unaffected by controlling for important covariates at the student and school levels. The covariates included are powerful predictors of test scores, but they lead to only small changes in the estimated mindset effect.

Heterogeneity of the mindset effect.

The heterogeneity of the mindset–achievement relationship (β_1j) across schools and students was assessed in two ways. It was first modeled with a random residual (u_1j) on the mindset coefficient. This approach allows the hierarchical model to estimate a different relationship between mindset and achievement per school. A likelihood ratio test rejects the hypothesis that the relationship is the same at all schools (L = 139.12; P < 0.001). The model estimates the variance of this relationship, with which we can calculate a 95% plausible value range. The estimated mean and SD for the association between mindset and achievement per school are M = 0.204; SD = 0.055 for language and M = 0.139; SD = 0.045 for mathematics. Therefore, the 95% plausible value ranges are 0.097–0.311 and 0.051–0.227, respectively. These ranges suggest that the relationship between mindset and test scores at any school is expected to be positive.

A second set of analyses revealed that the variability of the mindset coefficient can be partially explained by individual family income. To the models reported in Table 2 (Columns 2 and 4), we added an interaction between mindset and income in the level 1 regression. Income was standardized and continuous. Students with missing income were not included in this model. Table S2 shows the results. The results show that the lower the family income, the more powerful the relationship between mindset and achievement.