Boosting medical diagnostics by pooling independent judgments

Significance

Collective intelligence is considered to be one of the most promising approaches to improve decision making. However, up to now, little is known about the conditions underlying the emergence of collective intelligence in real-world contexts. Focusing on two key areas of medical diagnostics (breast and skin cancer detection), we here show that similarity in doctors’ accuracy is a key factor underlying the emergence of collective intelligence in these contexts. This result paves the way for innovative and more effective approaches to decision making in medical diagnostics and beyond, and to the scientific analyses of those approaches.

Abstract

Collective intelligence refers to the ability of groups to outperform individual decision makers when solving complex cognitive problems. Despite its potential to revolutionize decision making in a wide range of domains, including medical, economic, and political decision making, at present, little is known about the conditions underlying collective intelligence in real-world contexts. We here focus on two key areas of medical diagnostics, breast and skin cancer detection. Using a simulation study that draws on large real-world datasets, involving more than 140 doctors making more than 20,000 diagnoses, we investigate when combining the independent judgments of multiple doctors outperforms the best doctor in a group. We find that similarity in diagnostic accuracy is a key condition for collective intelligence: Aggregating the independent judgments of doctors outperforms the best doctor in a group whenever the diagnostic accuracy of doctors is relatively similar, but not when doctors’ diagnostic accuracy differs too much. This intriguingly simple result is highly robust and holds across different group sizes, performance levels of the best doctor, and collective intelligence rules. The enabling role of similarity, in turn, is explained by its systematic effects on the number of correct and incorrect decisions of the best doctor that are overruled by the collective. By identifying a key factor underlying collective intelligence in two important real-world contexts, our findings pave the way for innovative and more effective approaches to complex real-world decision making, and to the scientific analyses of those approaches.

Collective intelligence, that is, the ability of groups to outperform individual decision makers when solving complex cognitive problems, is a powerful approach for boosting decision accuracy (1–7). However, despite its potential to boost accuracy in a wide range of contexts, including lie detection, political forecasting, investment decisions, and medical decision making (8–14), little is known about the conditions that underlie the emergence of collective intelligence in real-world domains. Which features of decision makers and decision contexts favor the emergence of collective intelligence? Which decision-making rules permit this potential to be harnessed? We here provide answers to these important questions in the domain of medical diagnostics.

Our work builds on recent findings on combining decisions, a research paradigm known as “two heads better than one” (15–20). In their seminal study, Bahrami et al. (15) showed that two individuals permitted to communicate freely while engaging in a visual perception task, achieved better results than the better of the two did alone. Koriat (17) subsequently demonstrated that this collective intelligence effect also emerges in the absence of communication when the “maximum-confidence slating algorithm” (hereafter called confidence rule) is used and the decision of the more confident dyad member is adopted. Importantly, in both studies, combining decisions led to better outcomes only when both individuals had similar levels of discrimination ability, suggesting that similarity in the discrimination ability of group members is a crucial factor in predicting whether groups can outperform their best member. At present, however, it is unclear whether these findings can help to understand the emergence of collective intelligence in real-world decision-making contexts, where stakes are high and decisions are made by experts with a long history of training.

We address this issue in the domain of medical diagnostics. In the United States alone, an estimated 200,000 patients die each year from preventable medical errors (21), including a large proportion of diagnostic errors (22, 23). Reducing the frequency of diagnostic errors is thus a major step toward improving health care (24, 25). Previous research on collective intelligence in medical diagnostics has yielded conflicting results: Some studies have found that group decision making boosts diagnostic accuracy (9, 12, 26, 27), whereas others have found null or even detrimental effects (28, 29).

We here investigated whether similarity in doctors’ diagnostic accuracy explains whether combining the independent decisions of multiple doctors improves or deteriorates diagnostic accuracy. We examined this question in two medical domains in which diagnostic errors are rife: breast and skin cancer diagnostics (30, 31). Within each domain, our approach was to use a simulation study that draws on previously published datasets where a large number of medical experts had independently diagnosed the same medical cases. For all cases, the correct diagnosis (i.e., cancerous, noncancerous) was available. In particular, the breast cancer dataset on which we drew comprises 16,813 diagnoses and subjective confidence estimates made by 101 radiologists of 182 mammograms (32), with a mean individual sensitivity ± SD = 0.766 ± 0.112 and specificity = 0.665 ± 0.113 (SI Appendix, Fig. S1); the skin cancer dataset comprises 4,320 diagnoses and confidence estimates made by 40 dermatologists of 108 skin lesions (33), with a mean individual sensitivity ± SD = 0.833 ± 0.130 and specificity = 0.835 ± 0.070 (SI Appendix, Fig. S1). These datasets allowed us to investigate the performance of collective intelligence rules that are based on aggregating the independent judgments of multiple doctors, and how this performance depends on the similarity in doctors’ diagnostic accuracy (a discussion of approaches based on direct interactions between doctors is provided in Discussion).

Results

We investigated the performance of virtual groups of diagnosticians using either of two collective intelligence rules: the confidence rule (17, 20) and the majority rule (34, 35). For any particular group evaluating any particular case, the confidence rule adopts the judgment of the most confident diagnostician, whereas the majority rule adopts the judgment receiving the most support within that group. For any of our groups, we compared the performance of these two rules with the performance of the best diagnostician in that group in terms of (i) sensitivity, (ii) specificity, and (iii) Youden’s index (J). The last is a composite measure of accuracy that combines sensitivity and specificity (J = Sensitivity + Specificity − 1) (36, 37).

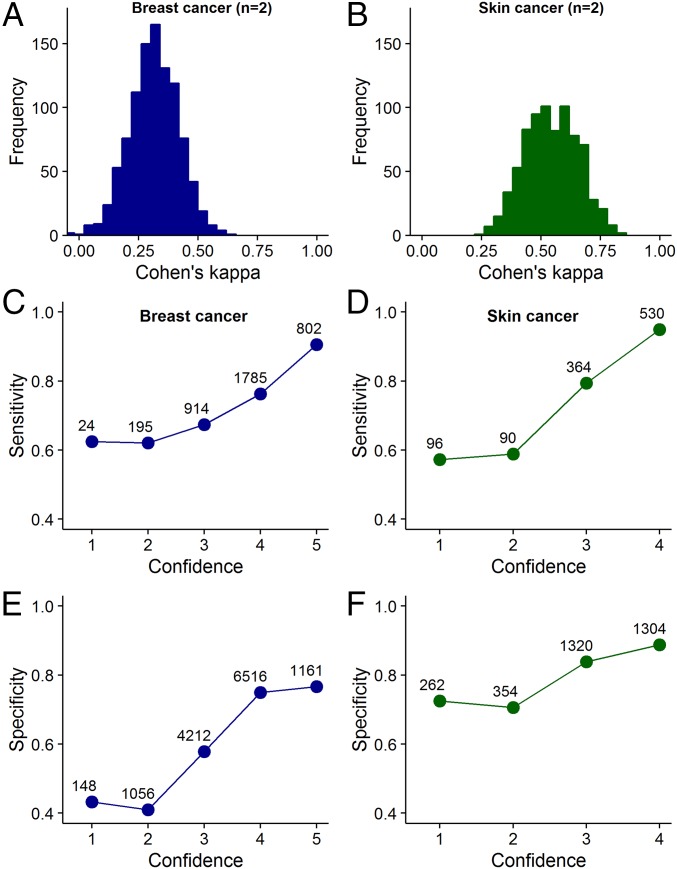
Pooling the independent judgments of multiple diagnosticians with the confidence or the majority rule can only promote collective intelligence when two conditions are fulfilled. First, the judgments of different diagnosticians must not be perfectly correlated with each other (if different diagnosticians give identical judgments on all cases, there is no scope for collective intelligence). Second, in case of the confidence rule, there has to be a positive correlation between confidence and accuracy levels. Initial analyses of our datasets showed that both conditions are fulfilled in both diagnostic contexts (Fig. 1).

Fig. 1.

Two basic conditions underlying collective intelligence. (A and B) Frequency distribution of Cohen’s kappa values for unique groups of two diagnosticians, randomly sampled from our datasets. A kappa value of 1 indicates complete agreement of judgments among diagnosticians (i.e., identical judgments on all cases), whereas a kappa value of 0 or lower indicates low levels of agreement (i.e., few identical judgments). Although there is substantial variation in the kappa values between groups, overall, there is a substantial amount of disagreement among diagnosticians. SI Appendix, Fig. S2 shows that with decreasing kappa value, the ability of a group to outperform its best diagnostician increases. (C–F) Relationship between confidence and sensitivity/specificity. The more confident the diagnosticians were of their diagnosis, the higher were their levels of sensitivity (C and D) and specificity (E and F) in both diagnostic contexts. Symbol labels indicate the sample size. SI Appendix, Fig. S3 shows that this positive relationship between confidence and sensitivity/specificity holds for the best-performing, midlevel-performing, and poorest performing diagnosticians.

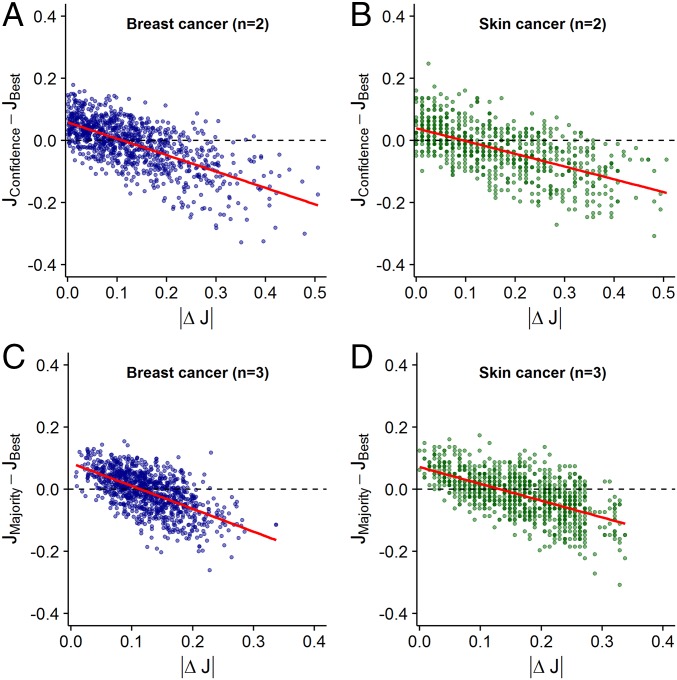
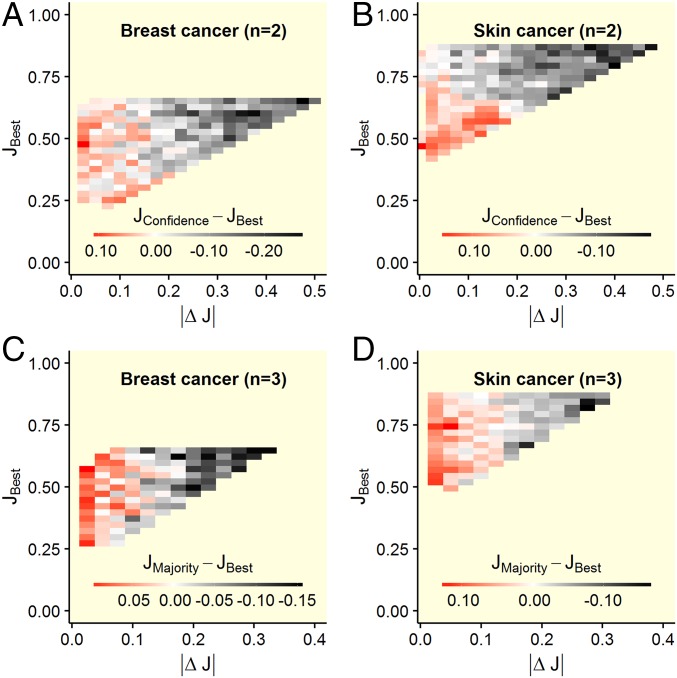
We first considered groups of two diagnosticians using the confidence rule. In both diagnostic contexts, we found that as the difference in accuracy levels between two diagnosticians increases, their joint ability to outperform the better diagnostician decreases [breast cancer: estimate (est) ± SE = −1.03 ± 0.04, t = −24.9, P < 0.001, Fig. 2A; skin cancer: est ± SE = −0.55 ± 0.03, t = −20.1, P < 0.001, Fig. 2B]. When diagnosticians’ accuracy levels were relatively similar (|ΔJ| < 0.1), the confidence rule outperformed the better diagnostician (Fig. 2 A and B). In contrast, for relatively dissimilar groups, the better diagnostician outperformed the confidence rule. This effect was largely independent of the accuracy level of the better diagnostician (Fig. 3 A and B), the accuracy level of the poorer diagnostician (SI Appendix, Fig. S4 A and B), and the average accuracy level within groups (SI Appendix, Fig. S5 A and B). When we analyzed the effects of similarity in accuracy on collective sensitivity and specificity, the same pattern emerged: In both diagnostic contexts, combining decisions using the confidence rule led to higher sensitivity and specificity (relative to the better individual), but only when the two diagnosticians’ accuracy levels were similar (SI Appendix, Fig. S6). Moreover, independent of similarity, the confidence rule consistently outperformed the average individual performance within the group (SI Appendix, Fig. S7). When considering groups of three and five diagnosticians using the confidence rule, we find that the above results generalize to these larger group sizes (SI Appendix, Fig. S8).

Fig. 2.

Performance difference between the confidence/majority rule and the best diagnostician in a group as a function of the difference in accuracy levels (i.e., |ΔJ|) between diagnosticians. Results are shown for groups of two diagnosticians using the confidence rule (A and B) and for groups of three diagnosticians using the majority rule (C and D). Each dot represents a unique combination of two (or three) diagnosticians. Values above 0 indicate that the confidence/majority rule outperformed the best individual in the group. Values below 0 indicate that the best individual outperformed the confidence/majority rule. Red lines are linear regression lines. In both breast cancer (A and C) and skin cancer (B and D) diagnostics, the confidence/majority rule outperformed the best individual only when the diagnosticians’ accuracy levels were relatively similar (|ΔJ| < 0.1).

Fig. 3.

Performance difference between the confidence/majority rule and the best diagnostician in a group as a function of the difference in accuracy levels between diagnosticians and the accuracy level of the best diagnostician. Shown are results for groups of two diagnosticians using the confidence rule (A and B) and for three diagnosticians using the majority rule (C and D). Red areas indicate that the confidence/majority rule outperformed the best diagnostician within that group, white areas indicate no performance difference, and gray and black areas indicate that the best diagnostician outperformed the confidence/majority rule. Shown are averaged values based on (maximally 1,000) randomly drawn unique groups. The confidence/majority rule outperformed the best diagnostician only when the diagnosticians’ accuracy levels were relatively similar (i.e., left part of the heat plots). This effect was independent of the accuracy level of the best diagnostician.

Similarly, when considering groups of three diagnosticians using the majority rule, we found that as the differences in accuracy levels across the three diagnosticians increase, the group’s joint ability to outperform the best diagnostician decreases in both diagnostic contexts (breast cancer: est ± SE = −1.26 ± 0.05, t = −27.7, P < 0.001, Fig. 2C; skin cancer: est ± SE = −0.68 ± 0.03, t = −23.3, P < 0.001, Fig. 2D). As in the case of the confidence rule, the majority rule outperformed the best diagnostician in that group only when the three diagnosticians’ accuracy levels were relatively similar (|ΔJ| < 0.1). Again, this effect was largely independent of the performance of the best diagnostician (Fig. 3 C and D), the performance of the poorest diagnostician (SI Appendix, Fig. S4 C and D), and the average performance within groups (SI Appendix, Fig. S5 C and D), and it held for both sensitivity and specificity (SI Appendix, Fig. S9). Moreover, independent of diagnostic similarity, the majority rule consistently outperformed the average individual performance within the group (SI Appendix, Fig. S10). When considering groups of five diagnosticians using the majority rule, we find that the above results generalize to this larger group size (SI Appendix, Fig. S11). SI Appendix, Fig. S12 provides a direct comparison of the confidence and the majority rule for different group sizes.

To further understand the mechanisms underlying the above findings, we developed simplified analytical models of the two most basic scenarios investigated above, namely, two diagnosticians using the confidence rule and three diagnosticians using the majority rule (model details are provided in SI Appendix). To illustrate, consider two diagnosticians using the confidence rule. From the point of view of the better (i.e., more accurate) diagnostician, employing the confidence rule has two effects: The poorer diagnostician may overrule incorrect judgments of the better diagnostician (positive effect), and the poorer diagnostician may overrule correct judgments of the better diagnostician (negative effect). Importantly, our model shows that the strength of both effects depends on the similarity in accuracy levels between the two diagnosticians (SI Appendix). As similarity decreases (assuming constant average accuracy), the better diagnostician gets better and the poorer gets worse, thereby decreasing the positive effect (the better diagnostician makes fewer incorrect judgments and the poorer makes fewer correct judgments) and increasing the negative effect (the better diagnostician makes more correct judgments and the poorer makes more incorrect judgments). As a consequence, and in line with our main findings above (Fig. 2), the model predicts that as similarity decreases, the ability of the group to outperform its better member also decreases. An analogous trend holds for the situation where three diagnosticians use the majority rule (SI Appendix).

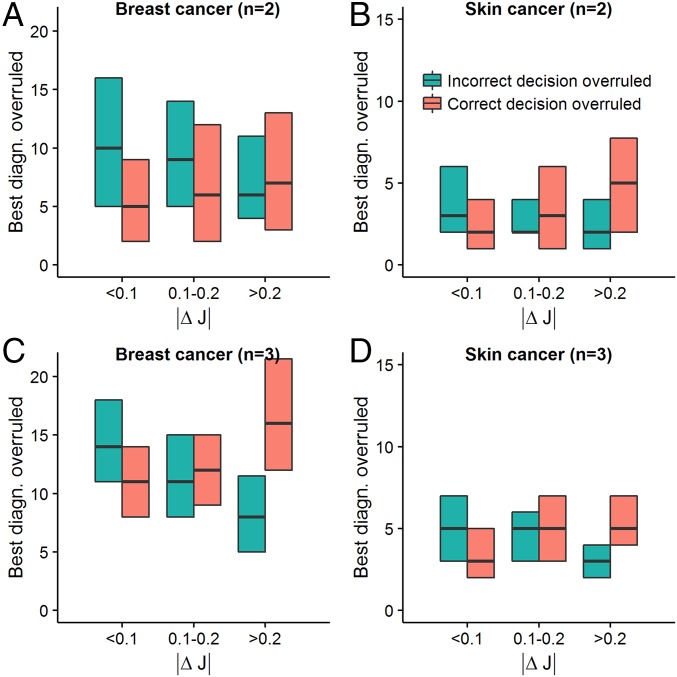
Further analyses of our datasets showed that in both diagnostic contexts and for both the confidence and the majority rule, the number of correct and incorrect judgments of the best diagnostician that are overruled is fully in line with the prediction from the above modeling analysis. In particular, we find that as similarity decreases, (i) the positive effect above decreases (i.e., the number of incorrect judgments of the best diagnostician that were overruled by the poorer diagnostician/the majority decreases; Fig. 4, green bars) and (ii) the negative effect above increases (i.e., the number of correct judgments of the best diagnostician that were overruled by the poorer diagnostician/the majority increases; Fig. 4, red bars). Moreover, while the positive effect outweighs the negative effect for relatively high levels of similarity (|ΔJ| < 0.1), the reverse is true for relatively low levels of similarity (|ΔJ| > 0.2), thereby explaining why only relatively similar groups can successfully use the confidence and majority rule to outperform their best member.

Fig. 4.

Number of correct/incorrect decisions of the best diagnostician overruled by the confidence/majority rule as a function of the difference in accuracy levels between diagnosticians. Green box plots correspond to the number of cases where an incorrect decision of the best diagnostician (diag.) within a group was overruled by the more confident diagnostician (A and B) or the majority (C and D). Red box plots correspond to the number of cases where a correct decision of the best diagnostician within a group was overruled by the more confident diagnostician (A and B) or the majority (C and D). Shown are averaged values based on (maximally 1,000) randomly drawn unique groups, using either of the two collective intelligence rules. Box plots show medians and interquartile ranges. As predicted from our modeling analysis (SI Appendix), with decreasing similarity in accuracy levels (i.e., higher |ΔJ|), the number of incorrect decisions by the best individual that were overruled decreased and the number of correct decisions by the best individual that were overruled increased.

Discussion

Although collective intelligence has the potential to transform decision making in a wide range of domains, little is known about the conditions that underlie its emergence in real-world contexts. Drawing on large real-world datasets, involving more than 140 doctors performing more than 20,000 diagnoses, we have identified similarity in decision accuracy as a key factor underlying the emergence of collective intelligence in breast and skin cancer diagnostics. In particular, we have found that when a group of diagnosticians is characterized by relatively similar accuracy levels, combining their independent judgments improves decision accuracy relative to the best diagnostician within that group. In contrast, when accuracy levels become too disparate, combining independent judgments leads to poorer diagnostic outcomes relative to those diagnostic outcomes achieved by the best diagnostician. This result is highly robust and holds across different performance levels of the best diagnostician, different group sizes, and different collective intelligence rules (confidence rule and majority rule).

To reap the benefits associated with collective intelligence, we need to know which characteristics of decision makers and decision contexts favor the emergence of collective intelligence and which decision-making rules allow this potential to be harnessed. We have here provided answers to both questions in the domain of medical diagnostics. In particular, and in contrast to current practice, our findings strongly suggest that similarity in diagnostic accuracy should be a key criterion for assembling groups in medical diagnostics, such as in the context of independent double reading of mammograms, a standard practice in Europe (38). Our analyses suggest that groups of diagnosticians with similar accuracy levels can use simple algorithmic approaches (i.e., confidence rule, majority rule) to achieve a performance that is superior to their best member. At a group size of two, the confidence rule can be employed to outperform the best diagnostician. For a group size of three onward, the majority rule tends to outperform the confidence rule (SI Appendix, Fig. S12).

Future studies should address at least three issues. First, we have focused on combining independent diagnostic judgments, thus not investigating situations in which diagnosticians directly communicate with each other. Therefore, one open question is the extent to which our findings generalize to face-to-face interactions and discussions within medical teams. Previous work in nonmedical contexts has shown that similarity in accuracy is a prerequisite for collective intelligence to arise during group discussions (15), suggesting that it may also matter in interacting medical teams. Second and more generally, it remains unknown how these two collective intelligence mechanisms (aggregation of independent judgments versus group discussions) compare in medical diagnostics (19). Group discussions are known to be a double-edged sword (39). Phenomena such as group think, interpersonal competition, social loafing, and obedience to authority can compromise group accuracy (40–42), yet groups are known to outperform individuals across a range of tasks (7, 43). It will thus be important to compare the relative gains (or declines) in accuracy that these mechanisms afford across medical diagnostic contexts. Third, improving decision accuracy is of prime importance across a wide range of contexts (e.g., economic decision making, political decision making). Future work should investigate whether and to what extent similarity in decision accuracy is a key enabling factor of collective intelligence in these contexts.

Materials and Methods

Our analyses are based on the two previously published datasets outlined below.

Breast Cancer Dataset.

The breast cancer dataset comprises 16,813 interpretations of 182 mammograms made by 101 radiologists (mean number of mammograms evaluated per radiologist = 166, range: 161–173) and is one of the largest mammography datasets available (32). Mammograms included in the test set were randomly selected from screening examinations performed on women aged 40–69 y between 2000 and 2003 from US mammography registries affiliated with the Breast Cancer Surveillance Consortium (BCSC; Carolina Mammography Registry, New Hampshire Mammography Network, New Mexico Mammography Project, Vermont Breast Cancer Surveillance System, and Group Health Cooperative in western Washington). Radiologists who interpreted mammograms at facilities affiliated with these registries between January 2005 and December 2006 were invited to participate in this study, as well as radiologists from Oregon, Washington, North Carolina, San Francisco, and New Mexico. Of the 409 radiologists invited, 101 completed all procedures and were included in the data analyses. Each screening examination included images from the current examination and one previous examination (allowing the radiologists to compare potential changes over time), and presented the craniocaudal and mediolateral oblique views of each breast (four views per woman for each of the screening and comparison examinations). This approach is standard practice in the United States (32). Women who were diagnosed with cancer within 12 mo of the mammograms were classified as cancer patients (n = 51). Women who remained cancer-free for a period of 2 y were classified to be noncancer patients (n = 131; i.e., 28% prevalence).

Radiologists viewed the digitized images on a computer (home computer, office computer, or laptop provided as part of the original study). The computers were required to meet all viewing requirements of clinical practice, including a large screen and high-resolution graphics (≥1,280 × 1,024 pixels and a 1280MB video-card with 32-bit color). Radiologists saw two images at the same time (i.e., the left and right breasts) and were able to alternate quickly (≤1 s) between paired images, to magnify a selected part of an image, and to identify abnormalities by clicking on the screen. Each case presented craniocaudal and mediolateral oblique views of both breasts simultaneously, followed by each view in combination with its prior comparison image.

Cases were shown in random order. Radiologists were instructed to diagnose them using the same approach they used in clinical practice (i.e., using the breast imaging reporting and data system lexicon to classify their diagnoses, including their decision that a woman be recalled for further workup).

Radiologists evaluated the cases in two stages. For stage 1, four test sets were created, with each containing 109 cases (32). Radiologists were randomly assigned to one of the four test sets. For stage 2, one test set containing 110 cases was created and presented to all radiologists. Some of the cases used in stage 2 had already been evaluated by some of the radiologists in part 1. To avoid having the same radiologist evaluating a case twice, we excluded all cases from part 2 that had already been viewed by that radiologist in part 1. This procedure resulted in a total of 161 unique cases for radiologists in test sets 1 (n = 25 radiologists) and 2 (n = 30 radiologists) and 173 unique cases for radiologists in test sets 3 (n = 26 radiologists) and 4 (n = 20 radiologists), resulting in a total of 16,813 unique readings. Between the two stages, radiologists were randomly assigned to one of three intervention treatments. Because there were no strong treatment differences (44), we pooled the data from stages 1 and 2. For all group simulation analyses, radiologists were always grouped within the four test sets (because radiologists in the same test set had evaluated the same images).

In our analysis, we treated the recommendation that a woman should be recalled for further examination as a positive test result. After providing each final diagnosis, radiologists rated their confidence in it on a five-point scale.

Skin Cancer Dataset.

The skin cancer dataset comprises 4,320 diagnoses by 40 dermatologists of 108 skin lesions and was collected as part of a consensus meeting via the internet, called the Consensus Net Meeting on Dermoscopy (33). Skin lesions were obtained from the Department of Dermatology, University Frederico II (Naples, Italy); the Department of Dermatology, University of L’Aquila (Italy); the Department of Dermatology, University of Graz (Austria); the Sydney Melanoma Unit, Royal Prince Alfred Hospital (Camperdown, Australia); and Skin and Cancer Associates (Plantation, FL). The lesions were selected based on the photographic quality of the clinical and dermoscopic images available. The goal of the study was to diagnose whether a skin lesion was a melanoma, the most dangerous type of skin cancer. Histopathological specimens of all skin lesions were available and judged by a histopathology panel (melanoma: n = 27, nonmelanoma: n = 81; i.e., 25% prevalence).

All participating dermatologists had at least 5 y of experience in dermoscopy practice, teaching, and research. They first underwent a training procedure in which they familiarized themselves with the study’s definitions and procedures in web-based tutorials with 20 sample skin lesions. They subsequently evaluated 108 skin lesions in a two-step online procedure. First, they used an algorithm to differentiate melanocytic from nonmelanocytic lesions. Whenever a lesion was evaluated as melanocytic, the dermatologist was asked to classify it as either melanoma or a benign melanocytic lesion, using four different algorithms. Here, we focus on the diagnostic algorithm with the highest diagnostic accuracy which is also the one most widely used for melanoma detection: pattern analysis (33). It uses a set of global (textured patterns covering most of the lesion) and local features (representing characteristics that appear in part of the lesion) to differentiate between melanomas and benign melanocytic lesions.

We treated the decision to classify a lesion as melanoma as a positive test result. After providing each final diagnosis, dermatologists rated their confidence in it on a four-point scale.

Ethics Statement.

The breast cancer data were assembled at the BCSC Statistical Coordinating Center (SCC) in Seattle and analyzed at the Leibniz Institute of Freshwater Ecology and Inland Fisheries in Berlin (IGB), Germany. Each registry, the SCC and the IGB, received institutional review board approval for active and passive consent processes or were granted a waiver of consent to enroll participants, pool data, and perform statistical analysis. All procedures were in accordance with the Health Insurance Portability and Accountability Act. All data were anonymized to protect the identities of women, radiologists, and facilities. The BCSC holds legal ownership of the data. Information regarding data requests can be found at breastscreening.cancer.gov/work/proposal_data.html.

For the skin cancer data, the review board of the Second University of Naples waived approval because the study did not affect routine procedures. All participating dermatologists signed a consent form before participating in the study. The skin cancer dataset has been included in Dataset S1.

Collective Intelligence Rules.

Both datasets include the judgments of experts who independently evaluated the same cases and rated their confidence in each diagnosis. We created virtual groups of diagnosticians who evaluated the cases “together” using two collective intelligence rules: the confidence rule (17, 20) and the majority rule (34, 35).

Confidence rule.

Separately for both datasets, we created virtual groups (for group sizes of two, three, and five diagnosticians). For each group size, we set an upper limit of 1,000 randomly drawn unique groups. The confidence rule stipulates that the diagnosis of the most confident diagnostician in the group is adopted for the case in question. Given a group size of two, for example, the confidence of both diagnosticians was compared for the case in question and the decision of the more confident diagnostician was adopted. All cases were evaluated in this way. If both diagnosticians were equally confident, one of the two decisions was chosen randomly. We calculated the performance of the confidence rule for each group in terms of (i) sensitivity, (ii) specificity, and (iii) Youden’s index (J). The last is a composite measure of accuracy, combining sensitivity and specificity (J = Sensitivity + Specificity − 1) (36, 37). The value of J ranges from −1 to 1, a perfect test has J = 1 (i.e., sensitivity = specificity = 1) and lower values correspond to lower discriminatory power. We then compared the performance of the confidence rule (i) with the performance of the best diagnostician in that particular group and (ii) with average individual performance in that particular group.

Majority rule.

Separately for both datasets, we created 1,000 unique groups with sizes of three and five (odd numbers to avoid the use of a tie-breaker rule) and evaluated the performance of the majority rule in each group. The majority rule stipulates that the decision that received the most votes is adopted, irrespective of the confidence associated with those decisions. We classified each case as “cancerous” or “noncancerous” depending on which of the two diagnoses received more votes among the group members. We then evaluated the performance of the majority rule for each group in terms of (i) sensitivity, (ii) specificity, and (iii) Youden’s index (J). Finally, we compared the performance of the majority rule with the (i) performance of the best diagnostician in that particular group and (ii) average individual performance in that particular group.

Statistical Analyses.

To determine the similarity in accuracy between group members, we calculated J for each group member and then used the mean pairwise absolute deviation (MPAD) to calculate the similarity in J among group members. MPAD $=\frac{2}{n\left(n-1\right)}·{\displaystyle \sum _{i<j}}|J_i-J_j|$, where n is the number of diagnosticians i and j. For a group size of two, this measure is simply the absolute difference in J between the two group members. For a group size of three or more, this measure is the expected absolute difference in J between two randomly chosen group members. We analyzed the effect of similarity in accuracy on a group’s ability to outperform its best and average individual(s) using general linear models in R (version 3.2.2). Significance levels were derived from the t values and associated P values.