Uncovering edge states and electrical inhomogeneity in MoS₂ field-effect transistors

Significance

The performances of devices based on transition metal dichalcogenides (TMDs) are far from their intrinsic limits, presumably due to various disorders in these 2D crystals. To date, little is known about the magnitude and characteristic length scale of electrical inhomogeneity induced by the disorders in TMDs. In this paper, strong mesoscopic (submicrometer) electrical inhomogeneity in MoS₂ flakes, which reveals the potential fluctuations, was observed by a unique technique termed microwave impedance microscopy. The local conductance of edge states and its contribution to the transport were also resolved and analyzed experimentally for the first time, to our knowledge. The results provide a comprehensive understanding of the potential landscape in TMDs, which is very important for the improvement of device performance.

Abstract

The understanding of various types of disorders in atomically thin transition metal dichalcogenides (TMDs), including dangling bonds at the edges, chalcogen deficiencies in the bulk, and charges in the substrate, is of fundamental importance for TMD applications in electronics and photonics. Because of the imperfections, electrons moving on these 2D crystals experience a spatially nonuniform Coulomb environment, whose effect on the charge transport has not been microscopically studied. Here, we report the mesoscopic conductance mapping in monolayer and few-layer MoS₂ field-effect transistors by microwave impedance microscopy (MIM). The spatial evolution of the insulator-to-metal transition is clearly resolved. Interestingly, as the transistors are gradually turned on, electrical conduction emerges initially at the edges before appearing in the bulk of MoS₂ flakes, which can be explained by our first-principles calculations. The results unambiguously confirm that the contribution of edge states to the channel conductance is significant under the threshold voltage but negligible once the bulk of the TMD device becomes conductive. Strong conductance inhomogeneity, which is associated with the fluctuations of disorder potential in the 2D sheets, is also observed in the MIM images, providing a guideline for future improvement of the device performance.

Electrostatic gating in the field-effect transistor (FET) configuration has played an essential role in the blooming field of semiconducting transition metal dichalcogenides (TMDs) such as MoS₂ and WSe₂ (1). The electrical control of carrier densities in these naturally formed 2D sheets is crucial for the realization of many intriguing phenomena, such as the metal−insulator transition (2–6), novel spin and valley physics (7–12), and superconducting phases (13–15). In addition, the carrier modulation provides an ideal tuning parameter to study the screening effect, which is particularly important for charge transport in 2D materials that are highly susceptible to local variations of the disorder potential (2–5, 16, 17). As a result, a complete understanding of the electronic properties of TMD FETs at all length scales, i.e., from local defects in the atomic scale, to electronic inhomogeneity in the mesoscale, to device performance in the macroscale, is imperative for both fundamental research on and practical applications of these fascinating materials.

Transport and most optical measurements on TMD FETs are inherently macroscopic in nature, in which the sample response is averaged over large areas. TMD films in actual devices, however, are far from electronically uniform. Due to the relatively large amount of intrinsic defects and the inevitable charged states in the substrates, mesoscopic electrical inhomogeneity is not uncommon in TMDs, leading to hopping transport and percolation transition in the devices (6, 16–19). Little is known, however, about the magnitude and characteristic length scale of such conductance fluctuations. For layered van der Waals materials, another unique feature occurs at the sample edges, where the broken crystalline symmetry and the presence of dangling bonds introduce additional electronic states to the bulk band structure. To date, edge states in TMDs are theoretically studied by first-principles calculations (20–22) and experimentally probed by scanning tunneling microscopy (STM) and spectroscopy (20, 23), whereas their contribution to the overall charge transport has not been fully addressed. Spatially resolved conductance maps are therefore highly desirable for the understanding of electrical inhomogeneity and edge channels in TMD FETs.

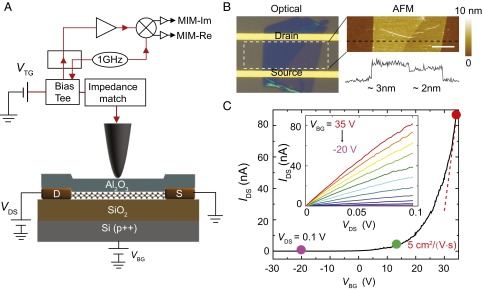
In this paper, we report the microwave impedance microscopy (MIM) (24, 25) study on the nanoscale conductance distribution during the normal operation of MoS₂ FETs. The experimental setup for our simultaneous transport and MIM measurements is schematically illustrated in Fig. 1A. The MoS₂ FETs and the MIM tip are mounted on the sample stage and the z scanner of a commercial atomic force microscope (AFM), respectively. During the contact-mode AFM scans, a low-power (∼10 μW) 1-GHz microwave signal is delivered to the shielded cantilever tip (26) through the impedance match section. A dc bias can also be coupled to the tip using a bias tee. The reflected signal is then amplified and demodulated to form the MIM-Im and MIM-Re signals, which are proportional to the imaginary and real parts, respectively, of the small changes of tip−sample admittance in the measurement. Using the standard finite element analysis (FEA) modeling (24), the local sample conductivity can be mapped out with a spatial resolution determined by the tip diameter (on the order of 100 nm) rather than the free-space wavelength (λ = 30 cm) of the 1-GHz microwave. The conductance fluctuation in this mesoscopic regime is particularly important for macroscopic device performance.

Fig. 1.

Experimental setup and device characterization. (A) Schematic diagram of the device and the MIM setup. The 1-GHz microwave signal is guided to the tip through an impedance match section, and the reflected signal is detected by the MIM electronics. The carrier density can be either globally tuned by the back-gate voltage V_BG or locally modulated by the dc bias on the tip V_TG. (B) Optical and the zoom-in AFM images of an exfoliated MoS₂ FET device. (Inset) A line profile across the surface. (Scale bar, 5 μm.) (C) Transfer characteristics of the device at V_DS = 0.1 V. The dashed line is a linear fit to the curve for V_BG > 30 V, from which the field-effect mobility μ_FE ∼ 5 cm²/(V⋅s) can be deduced. The solid circles (purple, green, and red) match the color coding in Fig. 5. (Inset) The output characteristics from V_BG = 35 V to −20 V with 5-V steps.

Results and Discussion

The starting materials of our FETs are few-layer exfoliated and monolayer (ML) chemical vapor deposited (CVD) MoS₂ flakes. The samples were transferred to or directly grown on SiO₂ (285 nm)/Si substrates, after which the source and drain contacts (20 nm Ag/30 nm Au) were formed via conventional electron beam (e beam) lithography and deposition (27, 28). To avoid direct contact between the metallic tip and the 2D sheets, which would strongly perturb the semiconducting MoS₂, we covered the device by the e-beam deposition of a thin (15 nm) layer of Al₂O₃. As a result, the carrier density in MoS₂ can be either globally modulated by the heavily doped Si back gate or locally tuned by the tip as a scanning top gate. Thanks to the capacitive tip−sample interaction, the MIM is capable of preforming subsurface electrical imaging (29–32) on the buried MoS₂ nanosheets.

Multiple exfoliated and CVD MoS₂ devices were investigated in this work, all of which exhibited similar behaviors. Fig. 1B shows the optical and the close-up AFM images of a typical FET fabricated on an exfoliated flake. The sample consists of two distinct regions with thicknesses of 2.1 nm and 2.8 nm, corresponding to three and four MLs, respectively, of MoS₂. Excluding several wrinkles from the exfoliation, the surface roughness of the sample is about 0.4 nm, presumably due to the fabrication process and Al₂O₃ deposition. The linear output characteristic I_DS−V_DS curves in Fig. 1C, Inset at different back-gate voltages (V_BG) are indicative of the good Ohmic contacts between Ag and MoS₂ (27). From the n-type transfer characteristics in Fig. 1C, the field effect mobility can be extracted by using the expression ${\mu }_{\text{FE}}=\left(\text{d}{I}_{\text{DS}}/\text{d}{V}_{\text{BG}}\right)\mathrm{\cdot }\left(L/W\right)\mathrm{\cdot }{C}_{\text{ox}}^{-1}\mathrm{\cdot }{V}_{\text{DS}}^{-1}\mathrm{\approx }5\hspace{0.17em}{\text{cm}}^2/(\text{V}.\text{s})$, where C_ox is the parallel-plate capacitance of the SiO₂ layer, and L and W are the channel length and width, respectively. Note that, although the room temperature mobility is comparable to that of most back-gated devices reported in the literature (3, 5, 6, 16, 17), it is much lower than the theoretical phonon-limited value (33), suggesting the presence of considerable disorder in this device, which will be explored by the MIM study below.

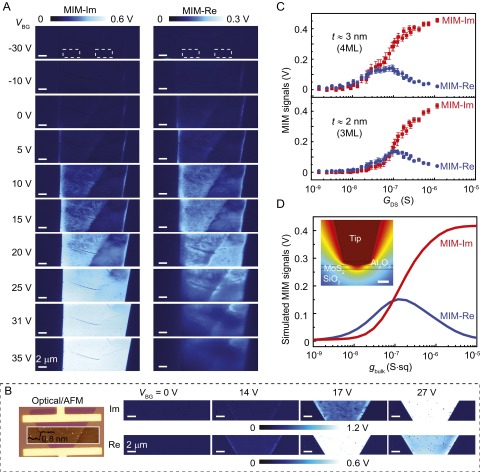
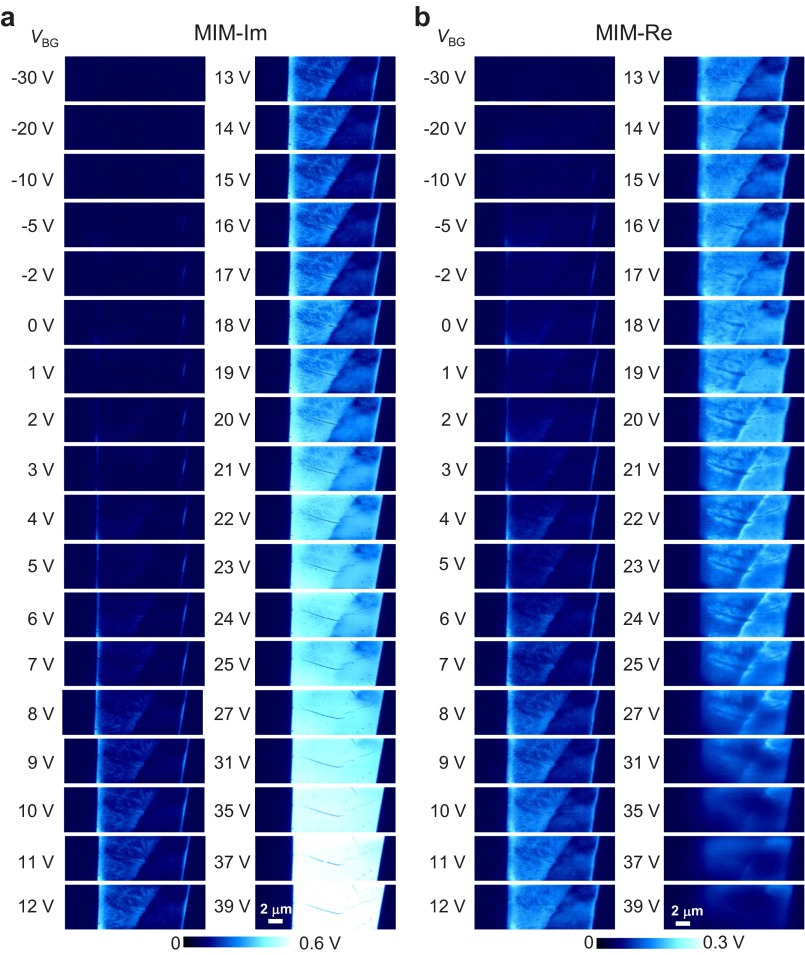
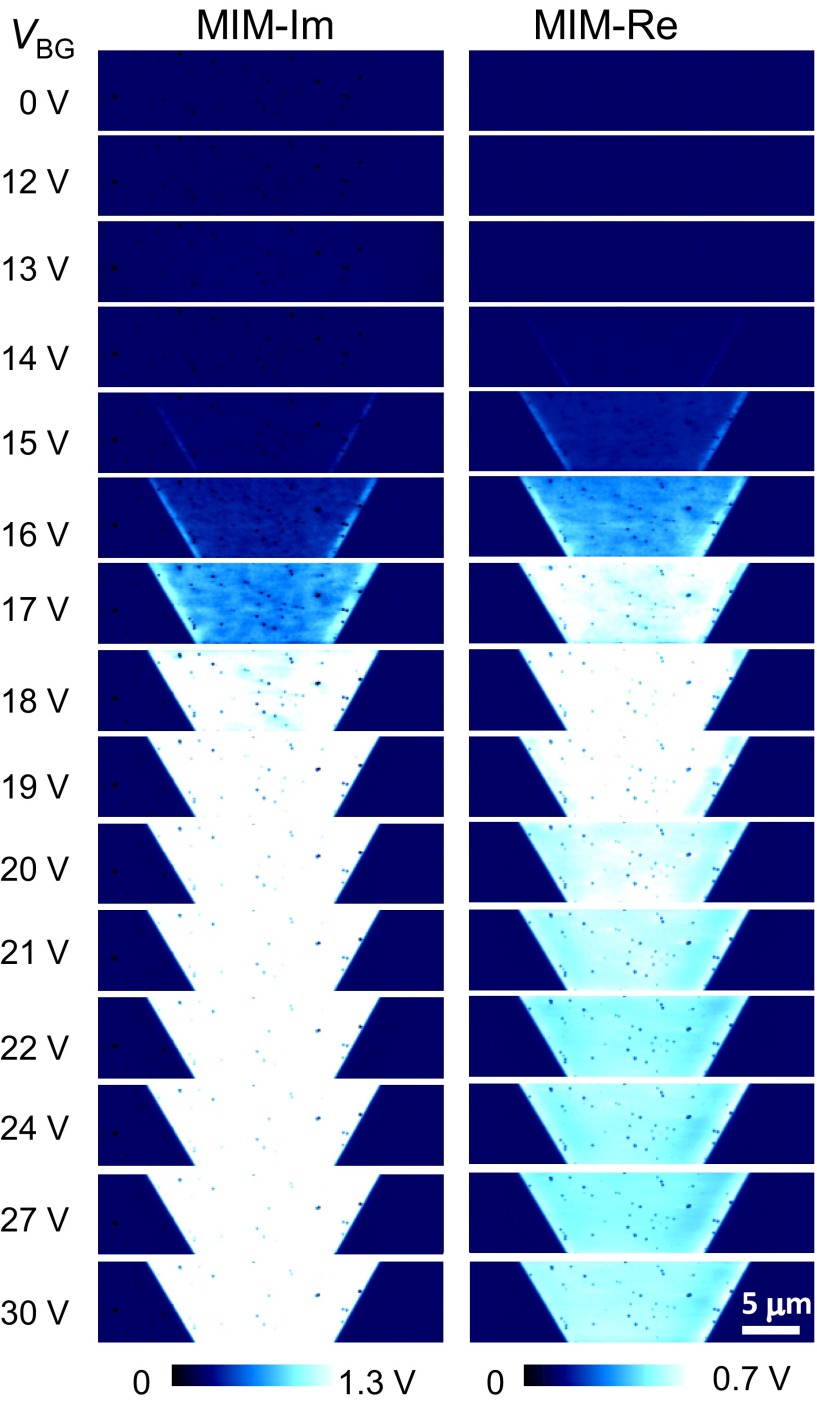
Fig. 2A displays selected MIM images within the channel region of the device in Fig. 1B as a function of V_BG. The complete set of data and a video clip showing the gate dependence can be found in Fig. S1 and Movie S1, respectively. The evolution of local conductance maps vividly demonstrates the insulator-to-metal transition induced by the electrostatic field effect. When the flake is in the insulating limit at V_BG = −30 V, there is virtually no electrical contrast between MoS₂ and the substrate. As V_BG gradually goes up to 0 V, the contrast first emerges at the edges of the flake and then in the interior of the sample. Note that the MIM-Im signals are always higher on the four-ML region, with slightly smaller band gap (34) and higher mobility (35) than the three-ML part. For increasing V_BG toward 20 V, strong inhomogeneity is observed in both MIM output channels. At the same time, the MIM signals at the edges gradually merge into the bulk and become indistinguishable with the rest of the flake for V_BG > 20 V. For even higher back-gate voltages, the sample appears uniformly bright in MIM-Im and dim in MIM-Re. During the entire process, the MIM-Im signals on the MoS₂ flake rise monotonically as increasing V_BG, whereas the MIM-Re signals reach a peak at V_BG ∼20 V and diminish afterward. Similar MIM data are observed by gradually ramping up the dc tip bias V_TG during the scans, as shown in Fig. S2. The local gating, on the other hand, results in a complex in-plane potential gradient away from the tip (36) and therefore will not be analyzed in detail here. We emphasize that the same trend of MIM response has been seen in all six MoS₂ FETs in this study. Fig. 2B shows the optical, AFM, and MIM images of a CVD-grown ML MoS₂ device (complete set of data included in Fig. S3), with the overall behavior similar to that in Fig. 2A. In the following, we will focus on the exfoliated sample in Fig. 1 for quantitative analysis of the MIM data.

Fig. 2.

Overall MIM response during the insulator-to-metal transition. (A) MIM-Im and MIM-Re images in the channel region (zoom-in image in Fig. 1B) of the device at selected back-gate voltages. (B) Optical, AFM (Inset), and MIM images of another FET device fabricated on a CVD-grown ML MoS₂ flake (see Fig. S3 for details). (A and B scale bars, 2 μm.) (C) Average MIM signals inside the white dashed boxes in A as a function of the source−drain conductance G_DS. (D) Simulated MIM signals as a function of the bulk sheet conductance g_bulk, showing very good agreement with the measured data in C. (Inset) The modeling geometry and the quasi-static potential distribution when the MoS₂ layer is insulating. (Scale bar, 50 nm.)

Fig. S1.

Complete set of MIM data at different back-gate voltages. (A) MIM-Im and (B) MIM-Re images of the device channel. A video showing the evolution is provided in Movie S1.

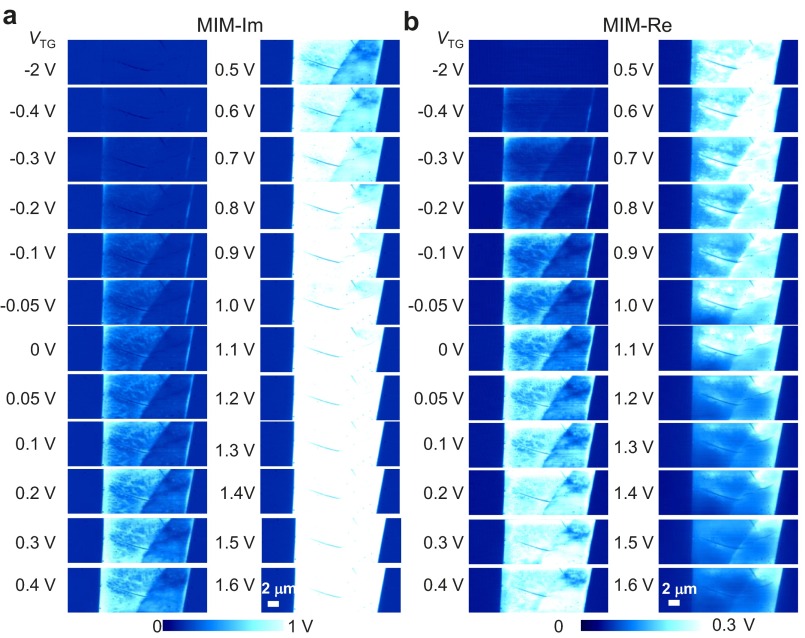
Fig. S2.

MIM images at different top-gate voltages. (A) MIM-Im and (B) MIM-Re images on the same area of the device as in Fig. 2A. The features are similar to that of the back-gated data. As V_TG increases from −2 V to 1.6 V, MIM-Im signals increase monotonically, whereas MIM-Re signals reach a peak around V_TG = 1.5 V and then diminish. The bright edges are also observed at low V_TG before the bulk becomes conductive. Significant electrical inhomogeneity is visualized, as well, before the saturation of MIM signals.

Fig. S3.

MIM-Im (Left) and MIM-Re (Right) images of a device fabricated on a CVD-grown MoS₂ flake at different back-gate voltages. The overall evolution of MIM signals as a function of V_BG, the emergence of edge states (e.g., at V_BG = 14 V), and the conductance inhomogeneity (e.g., at V_BG = 17 V) are again observed in this sample. Note that different color scales compared with the data of exfoliated sample are adopted here for better visualization, because a different MIM tip was used and the MIM contrasts were different. For different tips, a calibration on standard sample and Im/Re are used for quantitative analysis (46).

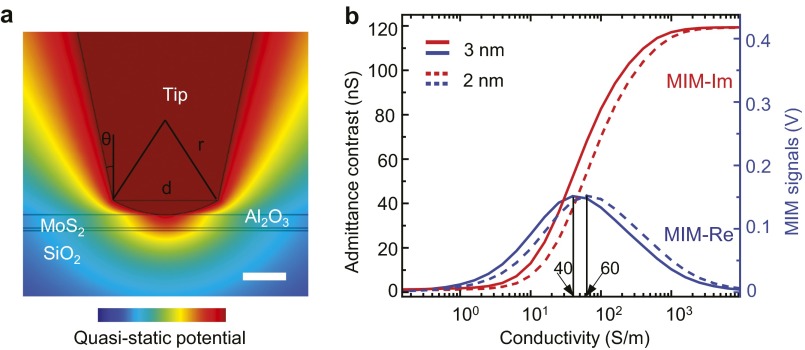
The average MIM-Im/Re signals within two 4 μm × 2 μm areas (white dashed boxes in Fig. 2A) on the four-ML and three-ML segments are shown in Fig. 2C, where the x axis is converted from V_BG to the two-terminal source−drain conductance (G_DS) by using the transfer curve in Fig. 1C. To quantitatively interpret the MIM signals as local conductance, we have calculated the MIM response curves as a function of the bulk MoS₂ sheet conductance g_bulk using FEA (24). Details of the FEA modeling and justification of the simulation parameters are included in Fig. S4. As shown in Fig. 2D, the simulated MIM-Im signal, which is proportional to the tip−sample capacitance, increases monotonically as increasing g_bulk and saturates at both the insulating (g_bulk < 10⁻⁹ Siemens·sq or S⋅sq) and conducting (g_bulk > 10⁻⁵ S⋅sq) limits. The MIM-Re signal, on the other hand, represents the effective loss in the tip−sample interaction and peaks at an intermediate g_bulk of ∼10⁻⁷ S⋅sq. Note that G_DS ≈ g_bulk⋅W/L if the source/drain contact resistance is relatively small compared with the channel resistance. An excellent agreement between the experimental data and our modeling result can be obtained by comparing the averaged MIM signals in Fig. 2C and the simulation in Fig. 2D. The MIM images thus provide a quantitative measure of the mesoscopic conductance distribution in the MoS₂ FET.

Fig. S4.

FEA using COMSOL 4.4 for MoS₂ thin films. (A) Modeling geometry and quasi-static potential distribution when the MoS₂ layer is insulating (3D conductivity σ = 10⁻² S/m). (Scale bar, 50 nm.) (B) Simulated admittance contrast and MIM signals as a function of MoS₂ conductivity σ for both 2- and 3-nm-thick MoS₂ films. Because all of the relevant dimensions here are much smaller than the free-space wavelength (30 cm) at 1 GHz, the interaction is in the extreme near-field regime and can be modeled as lumped elements. The MIM-Im and MIM-Re signals are proportional to the imaginary and real parts, respectively, of tip−sample admittance change. We have calibrated the impedance match section and the MIM electronics and shown that an admittance contrast of 1 nS corresponds to an MIM output signal of 3.5 mV (46). Because the width of the MoS₂ film is much larger than the MIM tip diameter, the 2D axisymmetric model can be used in this case. The shape of the MIM tip in A (r = 120 nm; d = 120 nm; θ = 12°; tip height h = 1 µm) is determined by its signals on standard calibration samples (46). Other parameters are as follows: for MoS₂, t = 2 nm or 3 nm in thickness, 8 μm in width, and dielectric constant ε = 7 (6, 46, 47); for SiO₂, 285 nm in thickness and ε = 3.9; for heavily doped Si, conductivity σ = 10⁵ S/m; and for Al₂O₃, 15 nm in thickness and ε = 9. The MIM response curves for the 2-nm-thick MoS₂ film are very similar to those of the 3-nm-thick MoS₂ film, except that they are laterally shifted by a factor of 1.5, as shown in B. In other words, the MIM response is effectively invariant with respect to the 2D sheet conductance g_bulk = σ_bulk⋅t, as long as t is much smaller than the tip diameter. As a result, we only quote the sheet conductance in Fig. 2D.

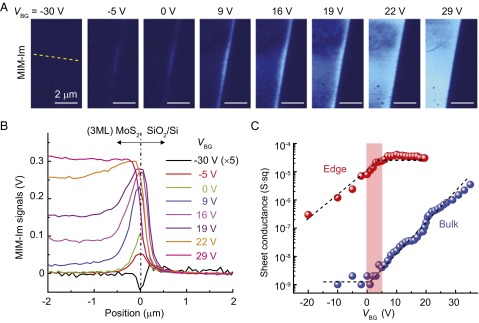
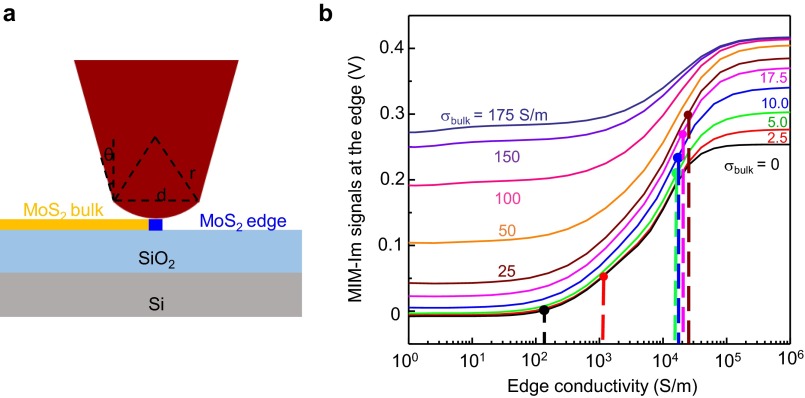
A prominent feature in Fig. 2A is the emergence of conductive edge states before the bulk of the sample is populated by conduction electrons. The presence of localized edge channels on the boundary of a 2D system is one of the most intriguing phenomena in condensed matter physics (37). In the case of TMDs, both density functional theory (DFT) calculations (20–22) and STM measurements (20, 23) have revealed the metallic (semiconducting) states at the zigzag (armchair) edges, whereas their influence on the device performance has not been experimentally probed. The MIM-Im images on the three-ML side of the sample at selected V_BG are shown in Fig. 3A, with the line profiles across the sample edge (yellow dashed line) plotted in Fig. 3B. Note that the apparent width of ∼200−300 nm at different locations of the boundary is determined by the spatial resolution or the tip diameter d rather than the actual width w_edge of the edge states. To quantify the edge conductance, we performed 3D FEA modeling of the MIM response, in which a narrow conductive channel with w_edge = 5 nm is situated in between the insulating substrate and the MoS₂ bulk. Because w_edge << d, the simulation result is invariant with respect to the product of w_edge and the sheet conductance of the edge g_edge. Details and justifications of the modeling parameters are shown in Fig. S5. The edge and bulk conductance values determined by comparing the 3D FEA and the MIM data are plotted in Fig. 3C. As V_BG increases from −30 V to 0 V, g_edge rapidly increases for more than two orders of magnitude, whereas the bulk conductance g_bulk stays below our sensitivity limit of ∼10⁻⁹ S⋅sq. For 0 V < V_BG < 5 V, g_edge levels off and g_bulk starts to rise above the noise floor. For V_BG above 5 V, g_edge saturates around 4 × 10⁻⁵ S⋅sq, whereas g_bulk continues to increase as V_BG increases. The quantitative mapping of g_edge signifies the fundamental difference between the topologically trivial edge states in TMDs and the nontrivial quantum Hall (QH) (37) or quantum spin Hall (QSH) (38, 39) edges. The TMD edges in our case can be treated as a normal 1D conductor, where the carriers experience the usual scattering events. Given the FET channel length L ≈ 10 μm in this sample, the maximum contribution of the edge states to the total conduction G_edge = g_edge⋅w_edge/L is on the order of 10⁻⁸ S, which is negligible once the FET is turned on. The QH or QSH edge channels, on the other hand, are dissipationless due to the suppression of backscattering and are responsible for the transport quantization when the bulk is insulating. Indeed, in our previous MIM studies on both QH (30) and QSH (31) systems, the highly conductive edges display maximum MIM-Im and zero MIM-Re signals, in sharp contrast to the finite signals in both channels for the MoS₂ edges.

Fig. 3.

Edge state conductance of MoS₂. (A) Selected MIM-Im images on the rightmost region of the flake. (Scale bars, 2 μm.) (B) Selected profiles (averaged over 20 lines) along the yellow dashed line in A. The physical boundary of the three-ML MoS₂ is centered in the plot. (C) Effective edge and bulk conductance as a function of V_BG. The shaded column marks the onset of bulk conduction and the saturation of edge conduction. The dashed lines are guides to the eyes.

Fig. S5.

The 3D FEA modeling for MoS₂ with edge states. (A) Schematic of the tip−sample geometry of the 3D modeling. (B) Computed MIM-Im signals of the edge state as a function of the edge conductivity at various bulk conductivity values. Because the width of MoS₂ edge states is much smaller than the tip diameter, we can no longer use the 2D axisymmetric model to simulate the edge states. A shows the 3D FEA geometry, in which the MoS₂ edge states are modeled as a thin wire with a width of w_edge = 5 nm. Note that, although the actual w_edge can be anywhere from subnanometer to a few nanometers (23), its exact value is not important here, because the simulation is invariant with respect to g_edge⋅w_edge. As V_BG changes, both the bulk and edge conductivity will change accordingly. Moreover, to deduce the edge conductivity, the bulk conductivity should be first determined from the 2D FEA. B shows a series of simulated MIM-Im curves with different σ_bulk from 0 S/m to 175 S/m. The edge conductivity σ_edge at a certain V_BG can thus be extracted from the corresponding curve. The sheet conductance of edges (g_edge) in Fig. 3C is then calculated as g_edge= σ_edge⋅h, where h = 2 nm is the film thickness.

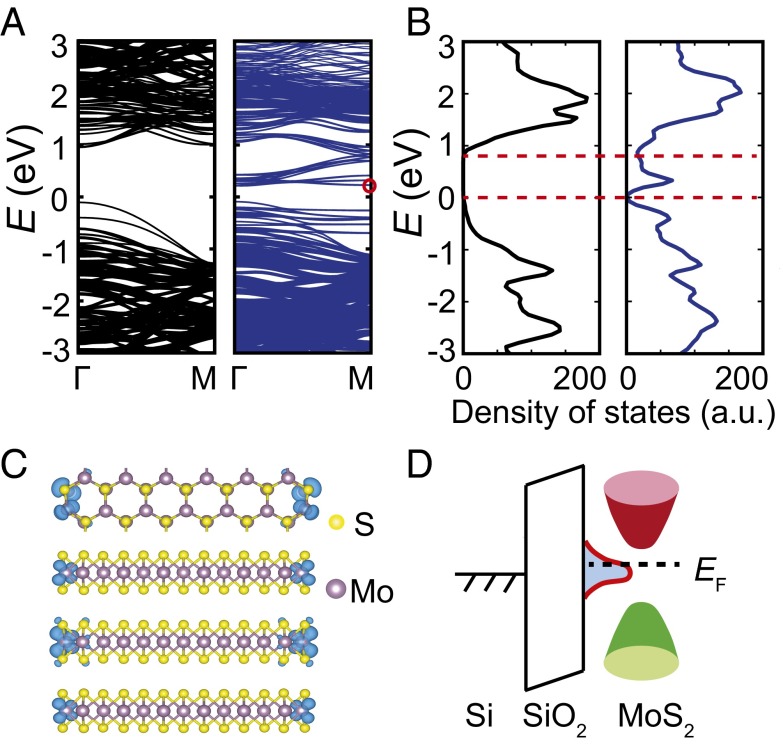
For further investigations of the observed edge states, we carried out first-principles DFT calculations (Methods) on one-ML and three-ML MoS₂ nanosheets. Fig. 4A shows the computed energy bands of an infinite 2D sheet and a nanoribbon with armchair edges of three-ML MoS₂. Compared with the bulk band structure, multiple bands appear within the bulk gap for the nanoribbon, reducing its energy gap from the bulk value of ∼1.1 eV to ∼0.3 eV, as also indicated by the density of states (DOS) plots in Fig. 4B. The charge density of additional electronic states at the M point of the Brillouin zone, circled in Fig. 4A, is well localized at boundary atoms in Fig. 4C, confirming that the additional bands in Fig. 4A are associated with the edge states. For a nanoribbon with zigzag edges, there are also edge states within the band gap, which connect the bulk conduction and valence bands as shown in Fig. S6 (18–20). For completeness, we have also included the DFT results of one-ML MoS₂ in Fig. S6, showing similar characteristics to the three-ML MoS₂. In reality, the edges in our devices may be a mixture of armchair and zigzag configurations, and the dangling bonds are usually terminated by foreign molecules from the environment. Nevertheless, the additional DOS inside the bulk band gap will be retained, leading to the topologically trivial edge states at the sample boundary (20, 22). As schematically illustrated in Fig. 4D, electrons will first populate the edge states with increasing V_BG. After these in-gap states are completely filled and g_edge is saturated, the further increase of V_BG will then raise the Fermi level E_F into the bulk conduction band, resulting in the upturn of g_bulk. Compared with the bulk bands, the edge bands are relatively flat, suggestive of higher effective mass and possibly lower mobility of the edge states. Consequently, once the bulk states participate in the transport at high gate voltages, the contribution of the edge states to the overall conductance becomes negligible. Such a physical picture nicely matches the evolution of local conductance maps deduced from the MIM data in Fig. 3C.

Fig. 4.

DFT calculations of three-layer MoS₂ edge states. (A) Calculated band structures of the three-ML bulk MoS₂ (Left) and a 1.9-nm-wide MoS₂ nanoribbon with armchair edges (Right). (B) Total DOS of the same bulk (Left) and nanoribbon (Right) MoS₂. (C) Top view (Uppermost Row) and side view (Lower Three Rows) of the electron wave functions for selected orbitals, circled in A. The edge states are mainly localized at the boundary atoms. (D) Cartoon of edge and bulk band structures. As the Fermi level E_F moves upward, the edge states will be populated before the bulk states.

Fig. S6.

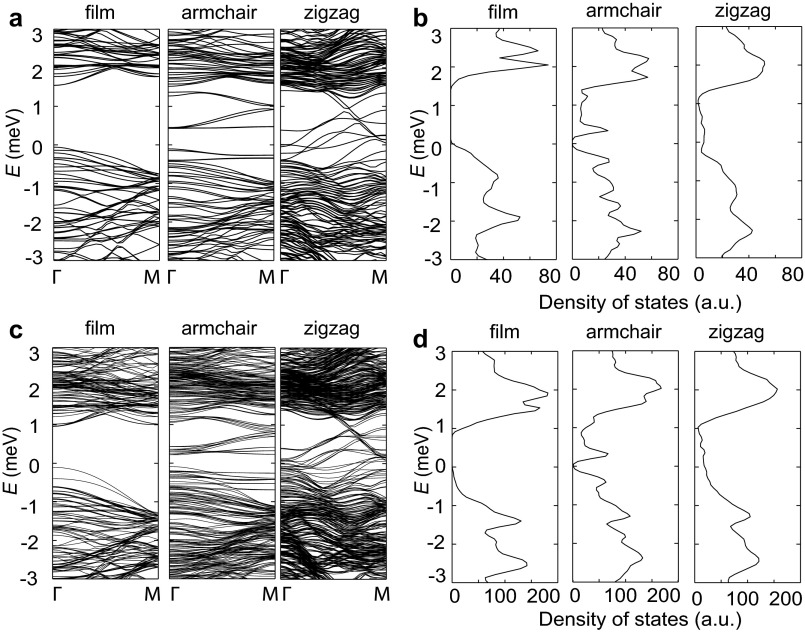
The one-ML and three-ML MoS₂ edge states by DFT calculations. (A) Calculated band structures of the one-ML bulk MoS₂ (Left), 1.9-nm-wide MoS₂ armchair nanoribbons (Middle), and 3.1-nm-wide zigzag nanoribbons (Right). For all of the configurations, the edge atoms are not saturated by extra atoms, as shown in Fig. 4. (B) Corresponding DOS for MoS₂ in A. Calculated band structure (C) and corresponding DOS (D) for three-ML MoS₂. Compared with bulk band structure, multiple bands emerge within the band gap for both armchair and zigzag nanoribbons. For the armchair nanoribbons, the energy gaps, ∼0.5 eV for one ML and ∼0.3 eV for three ML, are reduced from the bulk values, ∼1.6 eV for one ML and ∼1.1 eV for three ML. In contrast, the edge bands of zigzag nanoribbons seamlessly connect the bulk conduction and valence bands. Note that the SOC is considered for both cases. SOC reduces the degeneracy of energy bands but does not change the main features of band structures (21).

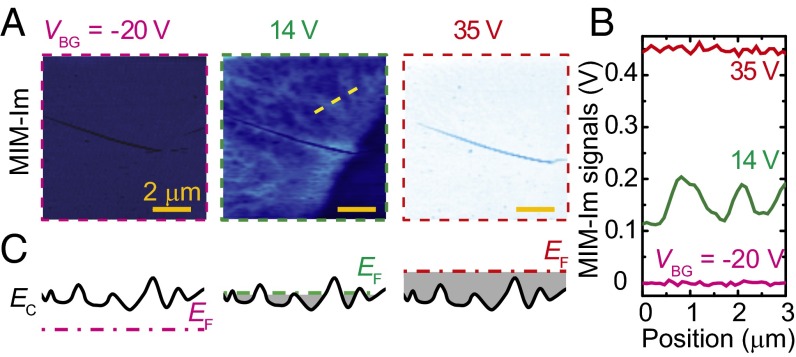
From the onset of bulk conduction at V_BG = 5 V to the saturation of MIM signals around V_BG = 25 V, pronounced spatial inhomogeneity with submicrometer length scale can be observed inside the MoS₂ flake. Both the strengths and spatial dimensions of the conductance fluctuations in this subthreshold regime are of critical importance for the device performance. We emphasize that the large variation of MIM signals cannot be accounted for by the surface roughness of the Al₂O₃ capping layer, as analyzed in Fig. S7. In Fig. 5A, the zoom-in MIM-Im images are displayed at V_BG = −20 V, 14 V, and 35 V, together with the corresponding line profiles in Fig. 5B. The variation of MIM signals at V_BG = 14 V corresponds to local fluctuations of g_bulk from 5 × 10⁻⁸ S⋅sq to 2 × 10⁻⁷ S⋅sq in the four-ML region. Admittedly, the MIM-Im response (Fig. 2C) is also highly sensitive in this intermediate conductance range. Because the transistor is completely turned off for V_BG = −20 V (E_F below the bulk conduction band minimum E_C) and on for V_BG = 35 V (E_F well above E_C), as shown in Fig. 1C, it is reasonable to expect much weaker spatial conductance variations under these two conditions. On the other hand, electrical inhomogeneity is most significant when E_F intersects the spatially fluctuating E_C, as schematically shown in Fig. 5C. The MIM maps thus provide both quantitative measurements and direct visualization of the mesoscopic potential landscape in the sample (32), which is the combined effect from defects within the MoS₂ layer, charges inside the substrate and the capping layer, and impurities across the interface. The percolation network is vividly demonstrated in the subthreshold regime, which was only indirectly inferred from atomic scale or macroscale studies (18, 19). Note that a similar technique, the alternating current STM (40), can be applied to study the atomic-scale defects in MoS₂, which would provide complementary information to our MIM work.

Fig. S7.

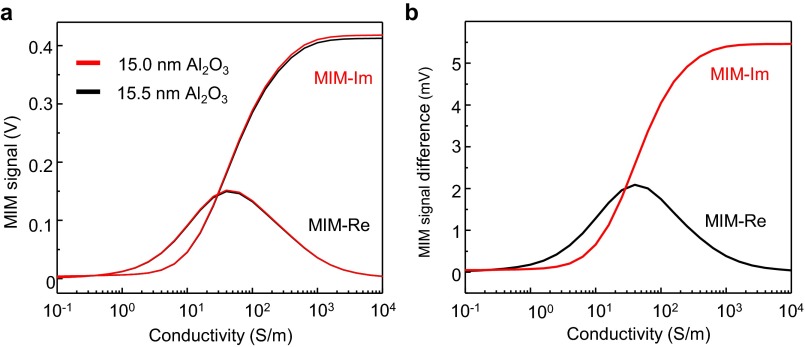
Influence of Al₂O₃ roughness on MIM signals. (A) Computed MIM signals as a function of the MoS₂ conductivity for Al₂O₃ thicknesses of 15.0 nm and 15.5 nm. (B) Difference between the MIM signals for the two cases in A. The influence of the surface roughness (∼0.4−0.5 nm) of the Al₂O₃ layer is minimal (<6 mV) and cannot explain the large electrical inhomogeneity observed in the MIM images around the subthreshold regime.

Fig. 5.

Electrical inhomogeneity in the MoS₂ FET device. (A) Close-up MIM-Im images in the center of the flake at V_BG = −20 V, 14 V, and 35 V. (Scale bars, 2 μm.) (B) Line cuts along the orange dashed line in A at the three V_BG as in A. (C) Schematics of the relative positions between E_F and the spatially fluctuating E_C at the same V_BG as in A and B. The color coding (purple, green, and red) matches the solid circles in Fig. 1C.

In summary, we demonstrate the local conductance mapping of functional MoS₂ FETs by MIM. We find that, during the insulator-to-metal transition, electrons induced by the electrostatic field effect first populate the edge states before occupying the bulk of the 2D sheets, a scenario further corroborated by our first-principles calculations. The results unambiguously confirm that the contribution of edge states to the channel conductance is significant under the threshold voltage but negligible once the bulk becomes conductive. The magnitude and spatial dimensions of mesoscopic electrical inhomogeneity in the subthreshold regime are also visualized from the MIM data. The simultaneous macroscopic transport and mesoscopic imaging experiments on TMD FETs are critically important for both fundamental research and practical applications on these fascinating materials.

Methods

Transport Measurements.

Output and transfer characteristic curves are measured at the ambient condition with a semiconductor analyzer Keithley 4200.

MIM Measurements.

The MIM in this work is based on an AFM platform (Park AFM XE-70). The customized shielded cantilevers are commercially available from PrimeNano Inc. FEA is performed using the commercial software COMSOL 4.4.

DFT Calculations.

Density functional theory calculations are performed using the Vienna Ab Initio Simulation Package with the projector augmented wave method and Perdew−Burke−Ernzerhof exchange-correlation functional (41–43). For three-ML MoS₂, the interlayer van der Waals interactions are taken into account by Grimme's D2 correction (44). A plane wave cutoff of 400 eV and a k-point spacing smaller than 0.2 Å⁻¹ along each periodic direction are used. A vacuum layer of larger than 15 Å is adopted to minimize the interaction between MoS₂ nanoribbon/sheet and its periodic images. Atomic structures are fully relaxed, with the force on each atom less than 0.01 eV/Å. The spin−orbit coupling (SOC) is included in the calculation of electronic properties, given a giant spin−orbit-induced spin splitting in MoS₂ layers (45). Denser k meshes and a Gaussian smearing of 0.1 eV are applied in the calculation of DOS. For an infinite sheet of one-ML and three-ML MoS₂, we construct supercells with a similar structure to corresponding armchair nanoribbons but without edges, which can be easily compared with the results of armchair nanoribbons.