Conservation law for self-paced movements

Significance

Most of our day-to-day movements are carried out spontaneously at a comfortable pace. A leading theory for how movements are generated cannot model such self-paced movements because it requires external factors to determine the pace, such as reward or a deadline to complete a movement. We show that the dual form of this existing theory implies a conserved quantity, called “drive,” that accounts for the regular features in self-paced movements without assuming any external factors. Drive complements the current theory based on external tasks by formalizing the influence of internal motivation on biological motor control.

Abstract

Optimal control models of biological movements introduce external task factors to specify the pace of movements. Here, we present the dual to the principle of optimality based on a conserved quantity, called “drive,” that represents the influence of internal motivation level on movement pace. Optimal control and drive conservation provide equivalent descriptions for the regularities observed within individual movements. For regularities across movements, drive conservation predicts a previously unidentified scaling law between the overall size and speed of various self-paced hand movements in the absence of any external tasks, which we confirmed with psychophysical experiments. Drive can be interpreted as a high-level control variable that sets the overall pace of movements and may be represented in the brain as the tonic levels of neuromodulators that control the level of internal motivation, thus providing insights into how internal states affect biological motor control.

Optimality principles accurately predict many regularities observed in biological movements (1). In addition to minimizing the cost of making a movement, however, optimal control models must also restrict the duration of the movement (2–7), or introduce motor tasks that encourage faster movements (8–15); otherwise, the minimum cost could be achieved by simply decreasing the overall movement speed. Consequently, this approach neglects biological movements that are generated in a self-paced manner (i.e., in the absence of external task contingencies that can affect the pace of movements).

We present here a theoretical framework that is dual to optimal control theory, based on an internal conserved quantity called “drive”: The constancy of drive characterizes the regularities within a movement, whereas the level of drive sets the overall pace, which is shared between movements. This bridges the conventional distinction between local regularities within individual movements and global regularities across multiple movements. Drive formalizes the influence of internal motivation on the planning and execution of movements, providing a new perspective on biological motor control processes.

Results

Self-paced movements can be modeled as time-invariant control processes: The body dynamics model, $\dot{q}=f\left(q,u,t\right)$, and cost function, $\mathrm{ℒ}\left(q,u,t\right)$, where q is state and u is control, do not explicitly depend on time. In physics, time invariance is fundamentally associated with conservation of energy, which is the dual variable of time (16). The analogous conserved quantity for control theory is the partial time derivative of the minimal integrated cost, which we call “drive” (Materials and Methods, Drive)

$$\mathcal{D}\left(t\right)\equiv -\frac{\partial }{\partial t}\underset{\left\{u\left(\tau \right)\right\}}{\text{min}}{\displaystyle {\int }_0^t\mathrm{ℒ}\left(q,u,\tau \right)d\tau .}$$ [1]

Drive is related to the Hamiltonian function (17)

$$\mathrm{\mathscr{H}}\left(p,q,u,t\right)=p\cdot f\left(q,u,t\right)-\mathrm{ℒ}\left(q,u,t\right),$$ [2]

where p is a Lagrange multiplier to ensure that movements satisfy the dynamical equations, $\dot{q}=f$ (Materials and Methods, Least Action Principle of Motor Control). Along an optimal movement trajectory, drive has the same value as the Hamiltonian, $\mathcal{D}=\mathrm{\mathscr{H}}$, and evolves as $\dot{\mathcal{D}}={\mathrm{\mathscr{H}}}_t=p\cdot f_t-{\mathrm{ℒ}}_t$, where dots represent total time derivatives and subscripts denote partial time derivatives. Thus, time invariance of the model ($f_t=0$, ${\mathrm{ℒ}}_t=0$) implies conservation of drive: $\dot{\mathcal{D}}=0.$

Drive conservation is valid for any time-invariant optimal control models. As a concrete example, we analyze drive conservation on minimum-jerk control, an optimal control model that accurately reproduces a wide range of hand movements (7, 18–20). This model assumes a linear time-invariant model of the limb dynamics and a quadratic cost of the control that can be represented as squared-jerk, $\mathrm{ℒ}={\Vert \ddot{\overrightarrow{\upsilon }}\Vert }^2/2$, where jerk is the second-order time derivative of hand velocity. Drive associated with minimum-jerk control is

$$\mathcal{D}=\frac{1}{2}{\Vert \ddot{\overrightarrow{\upsilon }}\Vert }^2-\dot{\overrightarrow{\upsilon }}\cdot \stackrel{⃛}{\overrightarrow{\upsilon }}+\overrightarrow{\upsilon }\cdot \stackrel{⃜}{\overrightarrow{\upsilon }},$$ [3]

whose time derivative is $\dot{\mathcal{D}}=\overrightarrow{\upsilon }\cdot {\overrightarrow{\upsilon }}^{\left(5\right)}$ (Materials and Methods, Minimum-Jerk Drive).

Local Regularities.

Drive conservation (Eq. 3) and minimum-jerk control have identical solutions, which can be analytically solved for straight and circular hand movements.

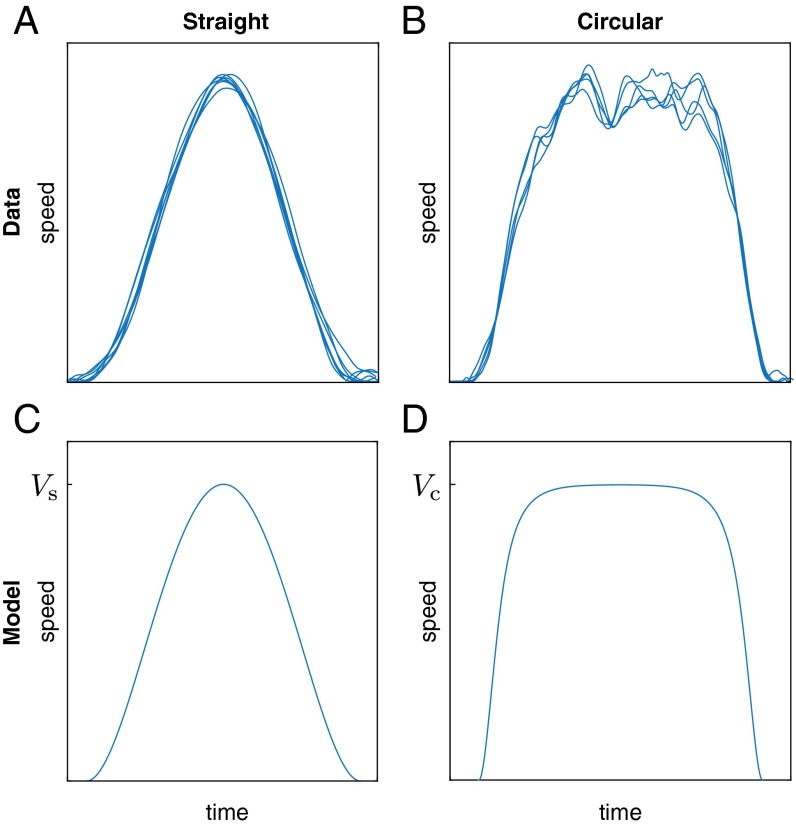
For a straight hand movement, they predict a smooth bell-shaped speed profile (7): $\upsilon \left(t\right)=16\hspace{0.17em}{V}_{\text{s}}{\left(t/T\right)}^2{\left(1-t/T\right)}^2$, where $V_{\text{s}}=15L/8T$ is the peak-speed, L is the length, and T is the duration (Fig. 1C). Despite the time-varying speed, the movement satisfies ${\overrightarrow{\upsilon }}^{\left(5\right)}=0$, thus conserving the drive. This result closely approximates the speed profiles observed in human reaching movements (Fig. 1A) (7, 21).

Fig. 1.

Local regularities within individual self-paced movements. (A) Bell-shaped speed profiles for straight hand movements and (B) plateau-shaped speed profiles during circular drawing movements ($\mathrm{\Theta }=4\pi$). Trajectories from several trials are aligned and overlaid. The plateau speed exhibits fluctuations due to the imperfect shape of the circular trajectories. (C and D) Model predictions from minimum-jerk control and drive conservation (Eq. 3).

For a circular hand movement, they predict a speed profile that is constant except near the end points where the speed starts and finishes at zero, as observed in human movements (Fig. 1 B and D) (22). During the circular motion, the speed is approximately $\upsilon \left(t\right)=V_{\text{c}}\approx R\mathrm{\Theta }/T$, where R is the radius, and $\mathrm{\Theta }$ is the angular distance. Despite the time-varying direction, $\overrightarrow{\upsilon }$ and ${\overrightarrow{\upsilon }}^{\left(5\right)}$ maintain orthogonality, which conserves the drive.

Note that the level of drive is directly related to movement variables, such as the overall length and duration of a straight movement

$$\mathcal{D}=1800\frac{L^2}{T^6},$$ [4]

or the radius, angular length, and duration of a circular drawing movement

$$\mathcal{D}\approx \frac{5}{2}\frac{R^2{\mathrm{\Theta }}^6}{T^6},$$ [5]

which can be derived from Eq. 3 (Materials and Methods, Straight Hand Movements and Circle-Drawing Movements).

Global Regularities.

As illustrated above, local regularities within the trajectories of individual movements are equivalently described by both drive conservation and optimal control models. Unless a motor task is given that determines the movement pace, however, optimal control models cannot predict the global regularities that occur across multiple movements, because each movement is considered a separate optimization problem.

In contrast, drive conservation extends seamlessly across time-invariant movements (Materials and Methods, Time Invariance and Conservation of Drive)

$${\mathcal{D}}_1={\mathcal{D}}_2=\cdots =\text{constant},$$ [6]

where ${\mathcal{D}}_i$ is the drive level of the i-th movement. Thus, self-paced movements share a common level of drive. This result is equivalent to the combined optimal solution that minimizes the total cost of multiple movements.

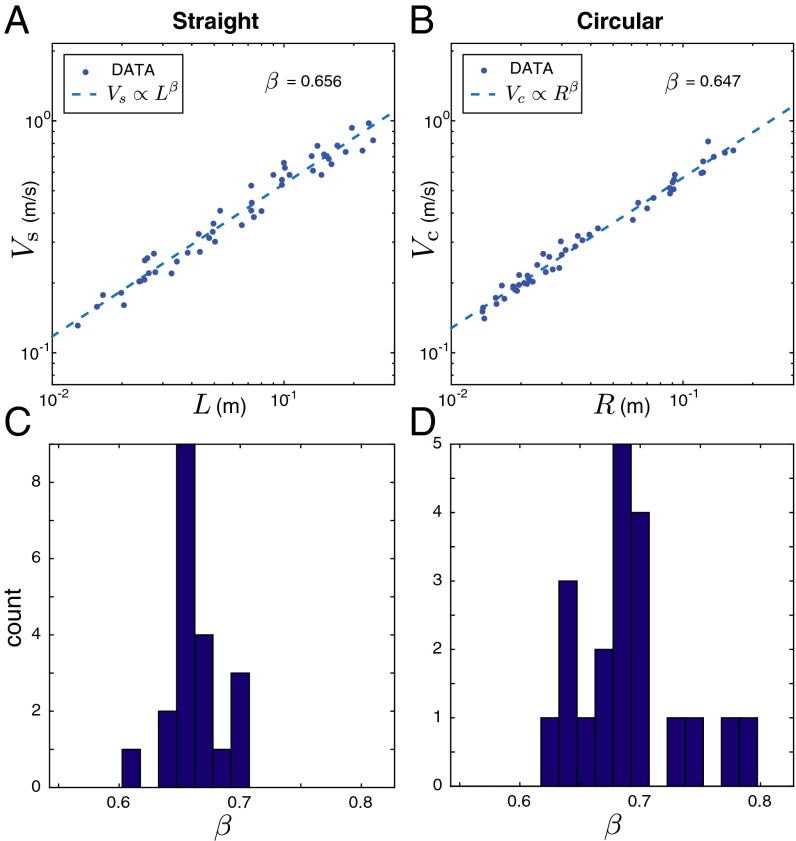
Drive conservation (Eq. 6) predicts correlations between global movement variables across trials. According to Eq. 4, the duration of straight movements at a constant drive level should scale with the length as $T\propto L^{1/3}$, and therefore the peak speed should scale as $V_{\text{s}}\mathrm{\propto }L/T\propto L^{2/3}$. For circle-drawing movements, Eq. 5 predicts that the duration scales as $T\propto R^{1/3}\mathrm{\Theta }$, and therefore the overall speed should scale with the radius as $V_{\text{c}}\approx R\mathrm{\Theta }/T\propto R^{2/3}$, independent of the angular distance.

We confirmed these power law predictions with psychophysical studies in which subjects made self-paced straight and circular drawing movements. In straight movements, the peak speed and length of movements exhibited the predicted scaling relationship, $V_{\text{s}}\propto L^{\beta }$, with exponent $\beta =0.69\pm 0.07$ (mean $\pm$ SD, $N=10$) (Fig. 2A). For circle-drawing movements, the predicted scaling relationship was found between the overall speed and radius of movements, $V_{\text{c}}\propto R^{\beta }$, with exponent $\beta =0.71\pm 0.08$ (mean $\pm$ SD, $N=10$) (Fig. 2B).

Fig. 2.

Global regularities in the scaling relationship between the overall size and speed of self-paced movements. (A) The length–speed relationship for straight hand movements and (B) the radius–speed relationship for circle-drawing movements of one subject. (C and D) Histograms of the measured power law exponent pooled from all subjects and sessions.

These scaling power laws hold generally across movements that are scaled versions of the same trajectory shape, such as ellipse-drawing movements of various sizes (Fig. 3C) (23). These can be intuitively understood by dimensional analysis: Because drive is the partial time derivative of the minimal integrated cost, it has the same dimensions as the cost function itself, which, for the minimum-jerk control, is

$$\left[\mathcal{D}\right]=\left[\mathrm{ℒ}\right]=\frac{{\left[length\right]}^2}{{\left[time\right]}^6}=\frac{{\left[speed\right]}^6}{{\left[length\right]}^4}.$$ [7]

The same 1:3 ratio between the exponents of the length and time dimensions is also found in the cost functions of many optimal control models, including the muscular-force-change cost (2, 3), the joint-torque-change cost (4), and the squared-control cost for third-order dynamics models (5, 6). Therefore, drive conservation applied to these models should also predict the same two-thirds power law between overall size and speed of movements.

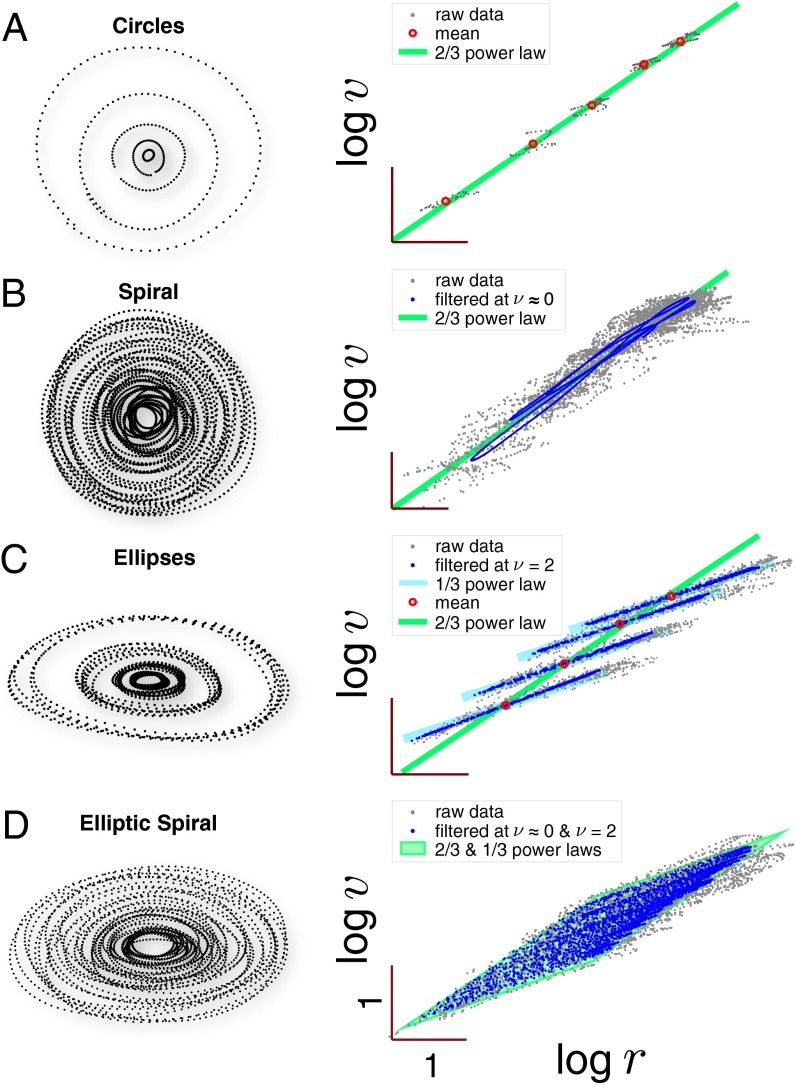
Fig. 3.

Local and global regularities in curve-drawing movements. (A) Circle-drawing movements, (B) a spiral-drawing movement, (C) ellipse-drawing movements, and (D) an elliptic spiral-drawing movement. (Left) Movement traces and (Right) log-radius of curvature vs. log-speed plots. Gray dots indicate raw data. Red dots indicate average radius of curvature, R, and average speed, V. Blue dots indicate band-pass-filtered data at the desired frequencies of spiral ($\nu \approx 0$) and/or elliptic shape ($\nu =2$) to average out deviations (see ref. 20). Data from ref. 20. (Scale bar: 1.0.)

Curvature–Speed Relationship.

The global scaling relationship also explains the origin of a well-known regularity observed in handwriting and curve-drawing movements, which exhibit high correlations between instantaneous speed, $\upsilon \left(t\right)$, and radius of curvature, $r\left(t\right)$ (18, 22, 23).

In a logarithmic spiral trajectory, an arbitrary arc of the trajectory can be scaled to match any other part of the trajectory, because of its self-similar shape. Therefore, if the scaling relationship were to apply between arbitrary arc pairs of the movement, it must apply at every instant in the movement so that $\upsilon \left(t\right)\propto r{\left(t\right)}^{2/3}$. Empirically, spiral-drawing movements do exhibit the predicted two-thirds power law between radius of curvature and speed (Fig. 3B) (20), consistent with the global scaling relationship (Fig. 3A). This consistency is compelling evidence that the regularities within individual movements and across trials are indeed governed by the same underlying principle of drive conservation.

For nonspiral movements, the instantaneous curvature–speed relationship varies with the shape of the curved trajectory. The general relationship can be predicted by analyzing the drive Eq. 3 in the rotating frame representation (24)

$$\mathcal{D}=\frac{{\upsilon }^6}{r^4}g\left(z\prime ,l\prime ,\cdots \right),$$ [8]

where $g(\cdots )$ is a dimensionless function of the derivatives of log speed, z, and log radius of curvature, l (Materials and Methods, Curved Hand Movements). The ${\upsilon }^6/r^4$ term induces the two-thirds power law for both the local curvature–speed relationship and the global scaling between overall size, R, and overall speed, V, but the local relationship is further modified by the derivative terms, which dampens high-frequency fluctuations of movement speed (20). For instance, Eq. 8 yields the well-established, local one-third power law for ellipse drawing movements, $\upsilon \left(t\right)/V\approx {\left(r\left(t\right)/R\right)}^{1/3}$ (22), as well as the global two-thirds power law, $V\propto R^{2/3}$, across the movements (Fig. 3C) (23). Moreover, it predicts that these power laws intermix for more complex movement shapes, such as elliptic-spiral movements, whose curvature–speed relationship exhibits features of both the one-third and the two-thirds power laws (Fig. 3D) (20, 22). Therefore, drive conservation bridges the distinction between global and local regularities.

Discussion

Drive and its conservation law provide a critical framework for understanding biological motor control. Drive quantifies the internal motivation level for generating movements. It maintains a constant level throughout various self-paced movements and determines the scaling relationship between the overall size and speed of movements.

Drive conservation provides a new perspective for understanding movement regularities. In the optimal control framework, modeling the global regularities requires auxiliary motor tasks that motivate faster movements, such as maximizing the reward rate (8, 10) or minimizing the time cost with an accuracy constraint (11, 12) or a total-cost constraint (13), or without any constraint (14, 15). Despite their pertinence for externally motivated movements, such as lever pressing (8) and fast reaching movements (25), however, these models are not applicable to most spontaneous movements that are produced in the absence of reward or time pressure, such as comfortably paced reaching movements (26) and curved hand movements (18). In contrast, in the drive-based framework, global regularities are explained by the same conservation principle that governs local regularities, without the need for any external motor tasks.

In curved movements, the global perimeter-duration regularity, called global isochrony, has been extensively studied along with the local one-third power law (18, 27). However, the origin of global isochrony and its relationship with the local power law have not been understood: Previously, the mixed appearance of both regularities within a movement (Fig. 3D) led to the hypothesis that complex movements are produced in a segmented manner, with the local power law in effect within each segment, and the global isochrony applying across the segments (18, 28). In the drive-based framework, these regularities are in fact inseparable, originating from the same conservation principle (Eq. 8).

Drive is defined as the dual variable of time for motor control. This duality can be understood in analogy with thermodynamic duals, such as the volume and pressure of a gas. Time, like volume, is an extensive property, which increases additively as more constituents are involved. Drive, like pressure, is an intensive property, which does not add but instead shares a common value among the constituents. The dual relationship also implies that each of these variables can be used interchangeably as the independent control variable. However, they have different causal implications: When time is used as the control, one moves fast because time is short; when drive is used, the movement concludes quickly because one moves fast. Time is the master in time-based control scenario, whereas in the other case the driver is in control. Ultimately, the choice of control variable depends on the perspective of the modeler.

Time is the control variable in the optimal control framework, which is natural from an experimenter’s point of view: The experimenter decides the desired duration of the motor task, either with an explicit time limit or by implicitly encouraging faster movements. In contrast, drive is a natural control variable from the perspective of the person performing the movements, who sets the internal motivation level. Time-based control has an undesirable implication that the subject has to preplan the entire course of movements to satisfy the task requirements, which can be problematic for a lengthy sequence of movements or a single, prolonged movement, such as doodling. Drive-based control resolves the planning problem: The apparent dependencies between self-paced movements are the consequences of generating them with a constant drive level, not due to a carefully planned choreography. Similarly, self-paced doodling under constant drive (Eq. 8) only requires short-term planning of $\approx 1$ rad of angular coordinate (20). In this respect, drive-based control shares similarities with receding-horizon control, which optimizes the solutions only up to a short horizon ahead.

The biological basis of drive can be sought in brain systems that modulate the overall pace of movements. A previous study has suggested that tonic dopamine levels may regulate movement pace by representing the average net reward rate in a repetitive task (8). However, the average only summarizes past movement trials, and, moreover, does not generally apply to nonrepetitive or non-reward-driven movements. Instead, tonic dopamine could represent drive, which directly controls the current pace of movements, independently of the previously estimated expected reward. This can be tested in experiments that vary pace while controlling for reward. Clinical support for this prediction can be found in neural disorders with reduced dopamine levels, such as Parkinson’s disease, where the overall speed of movements is decreased (29). Drugs that reduce dopamine activity, such as chlorapromazine and holoperidol (30), also reduce movements. In contrast, increased dopamine activity occurs in Tourette’s syndrome (31), marked by fast, hyperkinetic movements, and early stages of Huntington’s disease (32), characterized by choreiform movements.

The neuromodulator noradrenaline is another candidate for drive. Recent studies indicate that the activity of noradrenergic neurons reflects the effort needed to perform goal-directed actions (33, 34): The higher the activity of the noradrenergic neurons in the locus coeruleus, the stronger the action. Amphetamine, which activates both dopamine and adrenergic receptors, greatly enhances movement activity. The eye pupil size is tightly linked to the level of cortical activity (35) and to the levels of noradrenaline, which might be a way to monitor the level of drive during a motor task.

The drive-based framework can be generalized to movements whose pace is affected by external factors. Indeed, many optimal control models with external tasks can be shown to be time-invariant and thus conserve drive. It will be worth investigating how such tasks influence the internal drive level. More generally, humans can also generate movements that do not conserve drive by intentionally changing the pace or by responding to time-varying motor tasks or internal states, such as emotions, hunger and fatigue. A generalized drive-based control theory for time-varying drive is needed to account for the wide range of behaviors observed in nature, which could be coupled with physiological experiments to explore how the brain plans and executes such movements.

Materials and Methods

Least Action Principle of Motor Control.

Consider an optimal control problem involving a dynamical model of the body, $\dot{q}=f\left(q,u,t\right)$, and a cost function $\mathrm{ℒ}\left(q,u,t\right)$ in the time range $\left[t_o,t_f\right]$, where q is the body state and u is the control signal. Define the action of a state-control trajectory pair from $t_o$ up to $\overline{t}$ as the integrated cost ($t_o\le \overline{t}\le t_f$)

$$\mathcal{A}\left({\left\{q,u\right\}}_{t_o}^{\overline{t}}\right)\mathrm{\equiv }{\displaystyle {\int }_{t_o}^{\overline{t}}\mathrm{ℒ}\left(q,u,t\right)dt,}$$

subject to the constraint that the state-control trajectory satisfies the body dynamics: $\dot{q}=f$. The constraint can be explicitly expressed via Lagrange multipliers

$$\mathcal{A}\left({\left\{p,q,u\right\}}_{t_o}^{\overline{t}}\right)={\displaystyle {\int }_{t_o}^{\overline{t}}\left(p\cdot \dot{q}-\mathrm{\mathscr{H}}\left(p,q,u,t\right)\right)dt,}$$ [9]

where p is the Lagrange multiplier, called the momentum, and

$$\mathrm{\mathscr{H}}\left(p,q,u,t\right)\equiv p\cdot f\left(q,u,t\right)-\mathrm{ℒ}\left(q,u,t\right)$$ [10]

is called the Hamiltonian (17). The augmented trajectory set ${\left\{p,q,u\right\}}_{t_o}^{\overline{t}}$ is optimal only if the change of the action caused by arbitrary infinitesimal variations ${\left\{\delta p,\delta q,\mathit{\delta }u\right\}}_{t_o}^{\overline{t}}$ vanishes

$$\begin{array}{c}\delta \mathcal{A}=\mathcal{A}\left({\left\{p+\delta p,q+\delta q,u+\delta u\right\}}_{t_o}^{\overline{t}}\right)-\mathcal{A}\left({\left\{p,q,u\right\}}_{t_o}^{\overline{t}}\right)\\ \approx {\displaystyle {\int }_{t_o}^{\overline{t}}\left(\left(\dot{q}-{\mathrm{\mathscr{H}}}_p\right)\cdot \delta p-\left(\dot{p}+{\mathrm{\mathscr{H}}}_q\right)\cdot \delta q-{\mathrm{\mathscr{H}}}_u\cdot \delta u\right)dt}\\ +\overline{p}\cdot \delta \overline{q}-p_o\cdot \delta q_o,\end{array}$$ [11]

where the subscripts denote partial differentiation. Integration by parts is used for ${\displaystyle {\int }_{t_o}^{\overline{t}}p\cdot \delta \dot{q}}=-{\displaystyle {\int }_{t_o}^{\overline{t}}\dot{p}\cdot \delta q+\overline{p}\cdot \delta \overline{q}-p_o\cdot \delta q_o}$, where $q_o$, $p_o$ and $\overline{q}$, $\overline{p}$ are the state and momentum at time $t_o$ and $\overline{t}$, respectively. Therefore, the necessary condition for the optimal augmented trajectory set is summarized by the following Hamilton–Pontryagin equations:

$$\dot{q}={\mathrm{\mathscr{H}}}_p=f$$ [12]

$$-\dot{p}={\mathrm{\mathscr{H}}}_q=p\cdot f_q-{\mathrm{ℒ}}_q$$ [13]

$$0={\mathrm{\mathscr{H}}}_u=p\cdot f_u-{\mathrm{ℒ}}_u,$$ [14]

which reduces Eq. 11 to

$$\delta {\mathcal{A}}^{\text{*}}=\overline{p}\cdot \delta \overline{q}-p_o\cdot \delta q_o.$$ [15]

This implies the optimal action ${\mathcal{A}}^{\text{*}}$ only depends on the boundary times and states

$${\mathcal{A}}^{\text{*}}\left(t_o,\overline{t},q_o,\overline{q}\right)={\displaystyle {\int }_{t_o}^{\overline{t}}\mathrm{ℒ}\left(q,u,t\right)dt,}$$ [16]

where the integration is along the optimal state-control trajectory. For notational simplicity, we denote $\overline{t},\overline{q}$ as $t,q$, that is, ${\mathcal{A}}^{\text{*}}\left(t_o,t,q_o,q\right)$.

Note that if the dynamics is simply given by $\dot{q}=u$, then Eqs. 10 and 14 reduce to the Legendre transform between the Lagrangian and the Hamiltonian formulations of classical mechanics and Eqs. 12 and 13 reduce to Hamilton’s equations.

Drive.

Drive is defined as the dual variable of time, that is, the partial time-derivative of the optimal action

$$\mathcal{D}\left(t\right)\equiv -{\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial t}|}_{q,q_o,t_o},$$ [17]

which has the same numerical value, but a different functional form, as the Hamiltonian

$$\mathcal{D}=\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial q}\cdot \dot{q}-\frac{d{\mathcal{A}}^{\text{*}}}{dt}=p\cdot f-\mathrm{ℒ}=\mathrm{\mathscr{H}},$$ [18]

because according to Eqs. 15 and 16

$$p=\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial q},\hspace{1em}\hspace{1em}\mathrm{ℒ}=\frac{d{\mathcal{A}}^{\text{*}}}{dt}=\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial q}\cdot \dot{q}+\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial t}.$$

The total time derivative of drive is (from Eqs. 12–14)

$$\dot{\mathcal{D}}=\dot{\mathrm{\mathscr{H}}}={\mathrm{\mathscr{H}}}_t+{\mathrm{\mathscr{H}}}_p\cdot \dot{p}+{\mathrm{\mathscr{H}}}_q\cdot \dot{q}+{\mathrm{\mathscr{H}}}_u\cdot \dot{u}.={\mathrm{\mathscr{H}}}_t.$$ [19]

Time Invariance and Conservation of Drive.

For time-invariant control problems, the Hamiltonian Eq. 10 reduces to $\mathrm{\mathscr{H}}\left(p,q,u\right)=p\cdot f\left(q,u\right)-\mathrm{ℒ}\left(q,u\right)$, which leads to conservation of drive

$$\dot{\mathcal{D}}={\mathrm{\mathscr{H}}}_t=p\cdot f_t-{\mathrm{ℒ}}_t=0.$$

Now consider an extended formulation in which the total action of multiple movements is minimized as a combined optimization problem

$${\mathcal{A}}_{\text{all}}^{\text{*}}\left(T_{\text{all}}\right)=\min \left[{\displaystyle \sum _{\text{movements}}^{\text{multiple}}{\displaystyle \int \mathrm{ℒ}\hspace{0.17em}dt}}\right]=\underset{T_1,\cdots ,T_N}{\text{min}}\left[{\displaystyle \sum _{i=1}^N{\mathcal{A}}_i^{\text{*}}\left(T_i\right)}\right],$$

where N is the number of movements under consideration. Because of time invariance, the individual action, ${\mathcal{A}}_i^{\text{*}}$, depends on duration rather than explicit start–end times. The total duration, $T_{\text{all}}={\displaystyle {\sum }_{i=1}^N{T}_i}$, is considered an independent control variable of the problem. The optimality condition is

$${\displaystyle \sum _{i=1}^N{\mathcal{D}}_i\hspace{0.17em}\delta T_i}=0$$ [20]

for arbitrary variations of duration $\delta T_i$ that satisfy the constraint ${\displaystyle {\sum }_{i=1}^N\delta T_i}=0$, where ${\mathcal{D}}_i\equiv -\partial {\mathcal{A}}_i^{\text{*}}/\partial T_i$ is the drive level of movement i. Because $\delta T_N=-{\displaystyle {\sum }_{i=1}^{N-1}\delta T_i}$, Eq. 20 can be expressed as ${\displaystyle {\sum }_{i=1}^{N-1}\left({\mathcal{D}}_i-{\mathcal{D}}_N\right)\delta T_i}=0,$ which leads to drive conservation across movements

$${\mathcal{D}}_1={\mathcal{D}}_2=\cdots ={\mathcal{D}}_N.$$ [21]

Note that this formulation regards the total duration as a control variable, which leads to the planning problem that all N movements must be planned together to match $T_{\text{all}}$. This problem vanishes if instead drive is the control variable.

Minimum-Jerk Drive.

We apply the above formulation to the case of minimum-jerk control, which considers a simple third-order linear dynamical model and a quadratic control cost

$$\dot{q}=f\left(q,u\right)=Aq+Bu,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{ℒ}\left(q,u\right)=u^2/2,$$

where

$$q=\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\end{array}\right),\hspace{0.17em}A=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right),\hspace{0.17em}B=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right),$$

and $q_1=x$ is the hand position. This is equivalent to the more familiar form of the model: $\mathrm{ℒ}={\stackrel{⃛}{x}}^2/2$ (7). Denoting the momentum vector as $p=\left(p_1,p_2,p_3\right)$, the Hamiltonian of the control problem (Eq. 10) is

$$\mathrm{\mathscr{H}}\left(q,p,u\right)=p\cdot f-\mathrm{ℒ}=p_1\cdot q_2+p_2\cdot q_3+p_3\cdot u-{\left|\left|u\right|\right|}^2/2.$$ [22]

The optimal state-momentum dynamics (Eqs. 12 and 13) is

$$\left(\begin{array}{c}{\dot{q}}_1\\ {\dot{q}}_2\\ {\dot{q}}_3\end{array}\right)={\mathrm{\mathscr{H}}}_p=\left(\begin{array}{c}{q}_2\\ q_3\\ u\end{array}\right)\text{and}\left(\begin{array}{c}{\dot{p}}_1\\ {\dot{p}}_2\\ {\dot{p}}_3\end{array}\right)=-{\mathrm{\mathscr{H}}}_q=\left(\begin{array}{c}0\\ -p_1\\ -p_2\end{array}\right),$$

and the optimal control is $u=p_3$ (Eq. 14). Therefore, the components of the state-momentum vectors are identified as

$$\left(\begin{array}{c}{q}_1\\ q_2\\ q_3\end{array}\right)=\left(\begin{array}{c}x\\ \dot{x}\\ \ddot{x}\end{array}\right)\text{and}\left(\begin{array}{c}{p}_1\\ p_2\\ p_3\end{array}\right)=\left(\begin{array}{c}{x}^{\left(5\right)}\\ -\stackrel{⃛}{x}\\ \stackrel{⃜}{x}\end{array}\right).$$

Then, the drive can be calculated from the Hamiltonian Eq. 22 to be $\mathcal{D}={\stackrel{⃛}{x}}^2/2-\ddot{x}\hspace{0.17em}\stackrel{⃜}{x}+\dot{x}{x}^{\left(5\right)}.$ For multidimensional movements, this result generalizes to

$$\mathcal{D}=\frac{1}{2}{\Vert \ddot{\overrightarrow{\upsilon }}\Vert }^2-\dot{\overrightarrow{\upsilon }}\cdot \stackrel{⃛}{\overrightarrow{\upsilon }}+\overrightarrow{\upsilon }\cdot \stackrel{⃜}{\overrightarrow{\upsilon }},$$ [23]

where $\overrightarrow{\upsilon }\equiv \dot{\overrightarrow{x}}$ is the hand velocity. Note that $\dot{\mathcal{D}}=\overrightarrow{\upsilon }\cdot {\overrightarrow{\upsilon }}^{\left(5\right)}$.

Straight Hand Movements.

For a straight movement, $\overrightarrow{\upsilon }$ and ${\overrightarrow{\upsilon }}^{\left(5\right)}$ are parallel. Thus, $\dot{\mathcal{D}}=\overrightarrow{\upsilon }\cdot {\overrightarrow{\upsilon }}^{\left(5\right)}=0$ is satisfied only if the speed profile is a fourth-order polynomial in time, that is, the well-known bell-shaped speed profile (7)

$$\upsilon \left(t\right)=30\frac{L}{T}{\left(\frac{t}{T}\right)}^2{\left(\frac{T-t}{T}\right)}^2,\hspace{0.17em}\hspace{0.17em}\left(0\le t\le T\right),$$ [24]

where L and T are the length and duration of the movement, respectively. The jerk profile is $\ddot{\upsilon }\left(t\right)=30L/T^3\left(2-12t/T+12t^2/T^2\right)$. Therefore, the minimal action is

$${\mathcal{A}}^{\text{*}}\left(L,T\right)={\displaystyle {\int }_0^T\frac{1}{2}{\left(30\frac{L}{T^3}\left(2-12\frac{t}{T}+12\frac{t^2}{T^2}\right)\right)}^2}dt=360\frac{L^2}{T^5},$$

whose time differentiation yields the drive

$$\mathcal{D}\left(L,T\right)=-\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial T}=\frac{1800L^2}{T^6}.$$ [25]

This result can also be obtained directly from Eqs. 23 and 24.

Circle-Drawing Movements.

For a circle-drawing movement, $\dot{\mathcal{D}}=\overrightarrow{\upsilon }\cdot {\overrightarrow{\upsilon }}^{\left(5\right)}=0$ is satisfied by a constant speed profile, which keeps $\overrightarrow{\upsilon }$ and ${\overrightarrow{\upsilon }}^{\left(5\right)}$ orthogonal

$$\upsilon \left(t\right)=V_{\text{c}}=\frac{R\mathrm{\Theta }}{T},\hspace{0.17em}\hspace{0.17em}\left(0\le t\le T\right),$$

where $R,T,\mathrm{\Theta }$ are the radius, duration, and angular distance of the movement, respectively. The jerk profile is $\Vert \ddot{\overrightarrow{\upsilon }}\Vert =V_{\text{c}}^3/R^2=R{\mathrm{\Theta }}^3/T^3.$

Integrating the jerk cost yields the minimal action

$${\mathcal{A}}^{\text{*}}\left(R,\mathrm{\Theta },T\right)={\displaystyle {\int }_0^T\frac{1}{2}{\left(\frac{R{\mathrm{\Theta }}^3}{T^3}\right)}^2}dt=\frac{R^2{\mathrm{\Theta }}^6}{2T^5},$$

whose time differentiation yields the drive

$$\mathcal{D}\left(R,\mathrm{\Theta },T\right)=-\frac{\partial {\mathcal{A}}^{\text{*}}}{\partial T}=\frac{5}{2}\frac{R^2{\mathrm{\Theta }}^6}{T^6}=\frac{5}{2}\frac{V_{\text{c}}^6}{R^4}.$$ [26]

Curved Hand Movements.

Curved movements on a 2D plane can be represented in the Frenet–Serrett frame, whose basis vectors rotate along the trajectory as $\widehat{t}\prime =\widehat{n}$, $\widehat{n}\prime =-\widehat{t}$, where $\widehat{t},\widehat{n}$ are the unit tangent and normal vectors, and the prime symbol denotes differentiation with respect to the angle coordinate, θ, that is, the orientation of the tangent vector (24). By representing velocity and its time derivatives in this frame

$$\overrightarrow{\upsilon }=\upsilon \widehat{t},\hspace{1em}\hspace{1em}\dot{\overrightarrow{\upsilon }}=r^{-1}{\upsilon }^2\left(z\prime \widehat{t}+\widehat{n}\right),\hspace{1em}\ddot{\overrightarrow{\upsilon }}=\cdots ,$$

the drive Eq. 23 of curved movements can be reexpressed as

$$\begin{array}{c}\mathcal{D}={\Vert \ddot{\overrightarrow{\upsilon }}\Vert }^2/2-\dot{\overrightarrow{\upsilon }}\cdot \stackrel{⃛}{\overrightarrow{\upsilon }}+\overrightarrow{\upsilon }\cdot \stackrel{⃜}{\overrightarrow{\upsilon }}\\ ={\upsilon }^6/2r^4(5+2z\prime \prime \prime \prime -30z\prime \prime +10l\prime \prime -25l^{\prime 2}+40{\mathrm{z\prime }}^4+15{\mathrm{z″}}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-82z^{\prime 3}l\prime +z″\prime \left(20z\prime -12l\prime \right)+z\prime \prime \left(82{\mathrm{z\prime }}^2-90l\prime z\prime -8l\prime \prime +22l^{\prime 2}\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\mathrm{z\prime }}^2\left(-20l\prime \prime +55l^{\prime 2}-75\right)+z\prime \left(-2l\prime \prime \prime +14l\prime \prime l\prime +90l\prime -12l^{\prime 3}\right),\end{array}$$ [27]

where $z\equiv \log \left(\upsilon /V\right)$, $l\equiv \text{log}\left(r/R\right)$ are, respectively, the log-speed and the log-radius of curvature ($V,R$ are the overall speed and radius), and time differentiation is converted to angle differentiation via the conversion factor, $d\theta /dt=\upsilon /r$. An equivalent result was derived in ref. 20 in terms of curvature, $\kappa \equiv 1/r$, and log-curvature, $h\equiv -l$.

For logarithmic spiral paths, $r\left(\theta \right)=R{e}^{a\theta }$, Eq. 27 is exactly solved by the two-thirds power law, $\upsilon \left(t\right)\propto r{\left(t\right)}^{2/3}$, yielding

$$\mathcal{D}=\frac{{\upsilon }^6}{r^4}\frac{\left(5+5a^2/3+4a^4/81\right)}{2}.$$

For simple curved paths with a single frequency component (i.e., a sinusoidal log-radius of curvature profile), $l=\mathit{ϵ}\sin \left(\nu \theta \right)$, low-order perturbation analysis of Eq. 27 yields

$$\mathcal{D}=\frac{5V^6}{2R^4},\hspace{1em}\left(0\text{th}\hspace{0.17em}\text{order}\right)$$ [28]

$$z=\beta \hspace{0.17em}l,\hspace{1em}\left(1\text{st}\hspace{0.17em}\text{order}\right),$$ [29]

which describe the global two-thirds power law, $V\propto R^{2/3}$, and the instantaneous power law, $\upsilon \left(t\right)/V={\left(r\left(t\right)/R\right)}^{\beta }$, respectively. The exponent β is a decreasing function of frequency ν

$$\beta \left(\nu \right)=\frac{2}{3}\left(\frac{1+{\nu }^2/2}{1+{\nu }^2+{\nu }^4/15}\right).$$ [30]

Spiral movements are characterized by the zero frequency limit, $\nu \to 0$, and elliptic movements are characterized by frequency $\nu =2$, which exhibits the one-third power-law: $\beta \left(2\right)=30/91\approx 1/3$. Derivation and experimental confirmation of the above results, as well as the mixtures of power laws for general complex curved movements, are shown in refs. 20 and 24.

Experimental Method.

The study was approved by the University College London institutional ethics committee. Ten healthy subjects were recruited for the study and provided written informed consent. We recorded movements from the subjects using a Wacom Cintiq 24 digitizing tablet. The subjects had initial practice sessions to familiarize themselves to the tablet setup and the task, followed by two experimental sessions, each comprised of 25 straight- and 25 circle-drawing movements with brief break periods in between. The tasks did not require accurate tracing. Before each movement onset, the subjects were briefly shown a straight or circular shape of random size that guided them to explore a wide range of movement size. We used thick/fuzzy lines to emphasize the absence of accurate tracing requirement. The instruction for circle drawing was “Draw a circle: 2–5 counter-clockwise rotations. Do not make fine corrections, but try to get the overall size right.” The instruction for line drawing was “Draw a horizontal line. Do not make fine corrections, but try to get the overall length right.” See ref. 20 for the detailed method and the analysis of the curve-drawing movements.