Significance
How nanometer-sized proteins produce micron-scale subcellular organization is poorly understood. Here we study the spatial organization of the ras-related nuclear protein (Ran) pathway in mitosis. Our results reveal that whereas the upstream components of this pathway are well described as a reaction-diffusion system the downstream components exhibit more complex behaviors in which their association with microtubules causes them to be enriched in the spindle region. Because the Ran pathway influences the nucleation of microtubules, this suggests the presence of feedback based on spatial localization, in which the Ran pathway generates the microtubules that localize it. We argue that such feedback between soluble signaling pathways and the cytoskeleton have functional consequences with general implications for subcellular organization.
Keywords: RanGTP gradient, spatial organization, microtubule nucleation, feedback loop, spindle size
Abstract
Concentration gradients of soluble proteins are believed to be responsible for control of morphogenesis of subcellular systems, but the mechanisms that generate the spatial organization of these subcellular gradients remain poorly understood. Here, we use a newly developed multipoint fluorescence fluctuation spectroscopy technique to study the ras-related nuclear protein (Ran) pathway, which forms soluble gradients around chromosomes in mitosis and is thought to spatially regulate microtubule behaviors during spindle assembly. We found that the distribution of components of the Ran pathway that influence microtubule behaviors is determined by their interactions with microtubules, resulting in microtubule nucleators being localized by the microtubules whose formation they stimulate. Modeling and perturbation experiments show that this feedback makes the length of the spindle insensitive to the length scale of the Ran gradient, allows the spindle to assemble outside the peak of the Ran gradient, and explains the scaling of the spindle with cell size. Such feedback between soluble signaling pathways and the mechanics of the cytoskeleton may be a general feature of subcellular organization.
Cells exhibit internal order over a range of length scales (1). The manners in which nanometer-sized proteins specify micrometer-scale subcellular organization remain poorly understood. Either mechanics or chemistry could in principle produce order at length scales of cellular dimensions. The simplest mechanical phenomena result from the cytoskeleton: Filaments can be microns long and thus their individual lengths may even be sufficient to specify large-scale subcellular organization. Chemical processes can produce large, defined length scales through the interplay between diffusion and reactions (2). The simplest reaction–diffusion phenomenon, which has been widely discussed in the context of subcellular organization, is a scenario in which a signaling molecule is phosphorylated at one location in a cell and diffuses away and gradually dephosphorylates (3). Simple mathematical models of such source-sink scenarios predict that the resulting steady-state profile will be an exponentially decreasing gradient of the phosphorylated form around the source, with a length scale of , where is the diffusion coefficient of the signaling molecule and is the rate of dephosphorylation (3). is the average distance a molecule diffuses before it is dephosphorylated.
Although mechanics and chemistry are individually sufficient to give rise to structure at micrometer-length scales, increasing evidence suggests that the joint contribution of both of them leads to novel phenomena that might be important for subcellular organization: The interactions of diffusible molecules with the cytoskeleton can alter their mobility and localization, greatly modifying reaction–diffusion processes (4–8); large-scale patterns can arise if signaling molecules are advected by the motors they regulate (9) or if they recruit factors that further activate them (10); and a shallow reaction–diffusion signaling gradient can produce a sharp concentration gradient in a downstream factor if the signaling molecule regulates the cooperative association of the downstream factor (11). Thus, there is a plethora of mechanisms capable of generating subcellular organization from mechanics, chemistry, or a combination of the two, but it is unclear how prevalent these different possibilities are in cells.
The ras-related nuclear protein (Ran) pathway forms gradients around chromosomes in mitosis that are believed to control the spatial regulation of microtubule nucleation and dynamics (12–14) and has been hypothesized to contribute to spindle length (15, 16) and the kinetics of chromosome capture (17). The small GTPase Ran is the most upstream component of the Ran pathway. Soluble gradients in Ran activity are believed to be established by a reaction–diffusion process in which generation of a localized source is followed by diffusion and degradation (7, 8, 12, 13, 18): The conversion of the GDP-bound form of Ran (RanGDP) to the GTP-bound form of Ran (RanGTP) by nucleotide exchange is catalyzed by regulator of chromatin condensation 1 (RCC1), which localizes to chromosomes, whereas Ran GTPase-activating protein (RanGAP), a soluble protein, enhances the hydrolysis of RanGTP to RanGDP throughout the cytoplasm. RanGTP activates spindle assembly factors (SAFs) that control microtubule nucleation and other aspects of microtubule behaviors (18). Previous work demonstrated that the Ran pathway is essential for proper spindle assembly in meiosis II and mitosis (12, 13, 18–23), but the importance of the spatial organization of the Ran pathway remains unclear. Förster resonance energy transfer (FRET) biosensors have been used to show that RanGTP forms soluble gradients around chromosomes (12, 13), and because RanGTP regulates microtubule nucleation (12, 13, 20), it has been proposed that the Ran gradient controls the spatial distribution of microtubule nucleation (12, 13) and hence is a major determinant of spindle length (15, 16).
However, the observation that spindles can form away from the peak of the RanGTP gradient in cells undergoing mitosis with unreplicated genomes (MUG) demonstrates that the position of the RanGTP gradient is not the sole determinant of the spatial regulation of microtubule nucleation (24). Furthermore, the length of the spindle is not affected when RanGTP is perturbed by modifying RCC1 expression (19) or through use of the mutant RanT24N (25), which acts to inhibit RCC1. As discussed above, mathematical models predict that the length scale of the gradient should be determined by the distance RanGTP diffuses before it is converted to RanGDP and by the hydrolysis rate of RanGTP, which depends on the concentration of RanGAP, and the diffusion coefficient of RanGTP (3). These mathematical models predict that altering the source (i.e., the rate of RanGTP production, which is governed by RCC1 activity) should influence the magnitude of the Ran gradient but should not affect the length scale of the Ran gradient (3). Thus, although previously published results argue that altering the magnitude of the RanGTP gradient does not affect the length of the spindle, it is not known whether the length scale of the RanGTP gradient influences the length of the spindle.
Results and Discussion
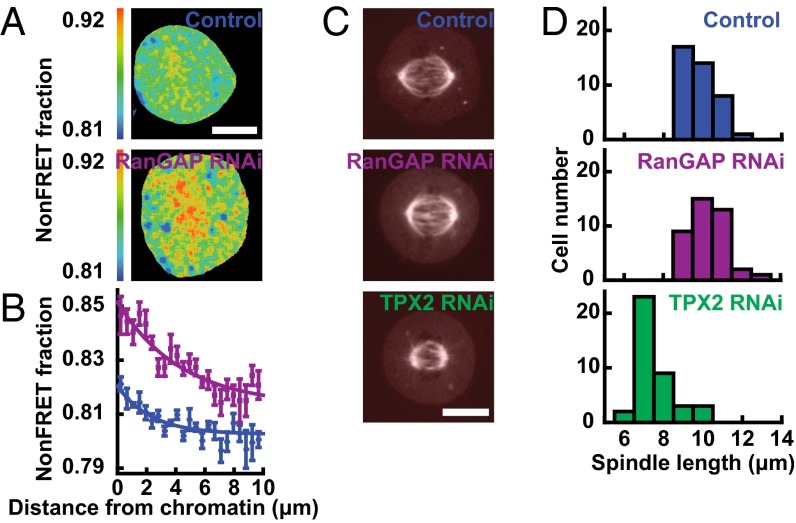
We sought to explore whether perturbing the length scale of the RanGTP gradient affects the length of the spindle. We thus used RNAi to knock down RanGAP in human tissue culture cells and visualized the RanGTP gradient by fluorescence lifetime imaging microscopy (FLIM) measurements of the FRET biosensor (pSG8 RBP-4) (19) (Fig. 1A). We found that knocking down RanGAP nearly doubled the length of the RanGTP gradient, increasing it from 2.3 ± 0.3 µm in control cells to 4.4 ± 0.5 µm in cells with RanGAP RNAi (Fig. 1B). Thus, RanGAP is a major determinant of the length scale of the RanGTP gradient, as predicted by mathematical models (3, 7, 8, 12). Despite the large change in the length of the RanGTP gradient, the RanGAP knockdown did not significantly affect the morphology of the spindle (Fig. 1C) and produced no significant change in spindle length, which was 9.80 ± 0.83 (SD) µm in control spindles and 10.23 ± 0.90 (SD) µm with RanGAP RNAi (Fig. 1D) (SI Text). We next examined the effect of perturbing a downstream component of the Ran pathway, TPX2, which is implicated in Ran-regulated microtubule nucleation (20, 26). Knocking down TPX2 with RNAi reduced the spindle length to 7.55 ± 0.95 (SD) µm (Fig. 1D), consistent with previous results arguing that Ran-regulated, TPX2-mediated microtubule nucleation contributes to setting spindle length (27). Taken together with previous results, these data demonstrate that spindle length is not influenced by the amplitude of the RanGTP gradient (19, 25) or the length scale of the RanGTP gradient, despite the importance of the Ran pathway for spindle assembly and spindle length (12, 13, 18–23). It is unclear how RanGTP could regulate microtubule nucleation (12, 13, 20) without the spatial organization of RanGTP influencing spindle morphology. To gain insight into this issue, we sought to further characterize the spatial organization of the Ran pathway in mitosis.
Fig. 1.
Spindle length is insensitive to the length of the RanGTP gradient but sensitive to the concentration of a Ran-regulated SAF. (A) FLIM images of the RanGTP in mitotic cells visualized with the FRET biosensor pSG8 RBP-4 in a control cell (Top) and in a RanGAP-knockdown cell (Bottom). (Scale bar: 10 µm.) (B) RanGTP activity, measured by fraction of nonFRETing biosensor, as a function of distance from chromosomes in control cells (blue circles, n = 6 cells) and in RanGAP-RNAi cells (purple squares, n = 8 cells), with exponential fits (lines) giving length scales of 2.3 ± 0.3 µm and 4.4 ± 0.5 µm, respectively. (C) Images of mCherry-tubulin in a control cell (Top), in a RanGAP-RNAi cell (Middle), and in a TPX2-RNAi cell (Bottom). (Scale bar: 10 µm.) (D) Histograms of spindle length in control cells (Top, blue, n = 40 cells), RanGAP-RNAi cells (Middle, purple, n = 40 cells), and TPX2-RNAi cells (Bottom, green, n = 40 cells).
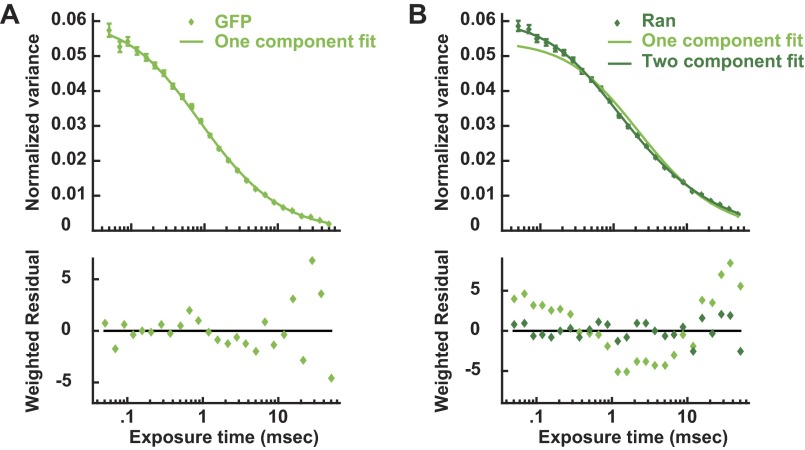
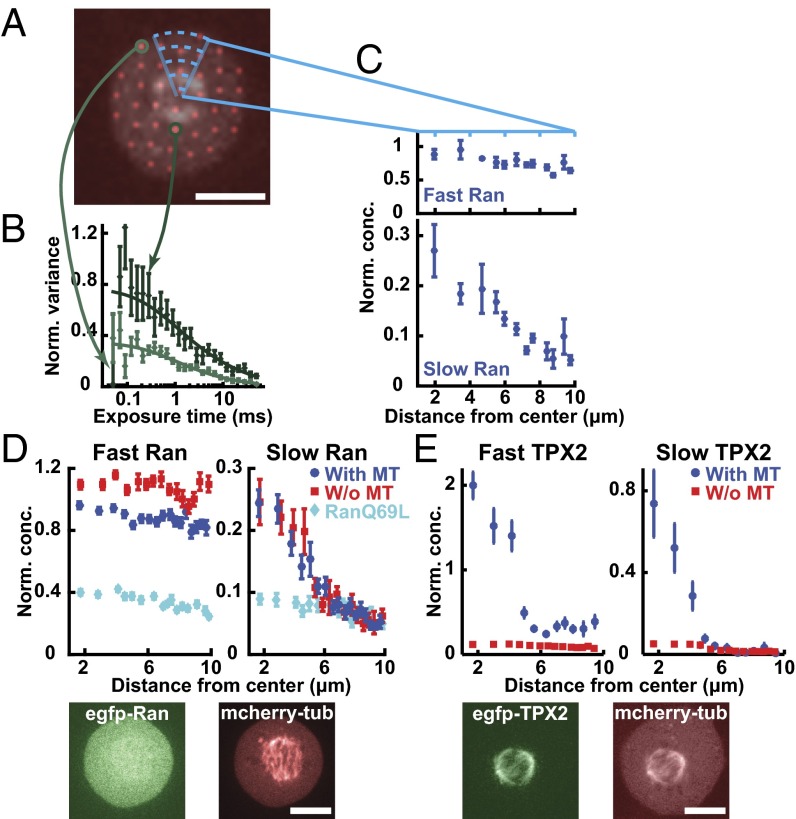
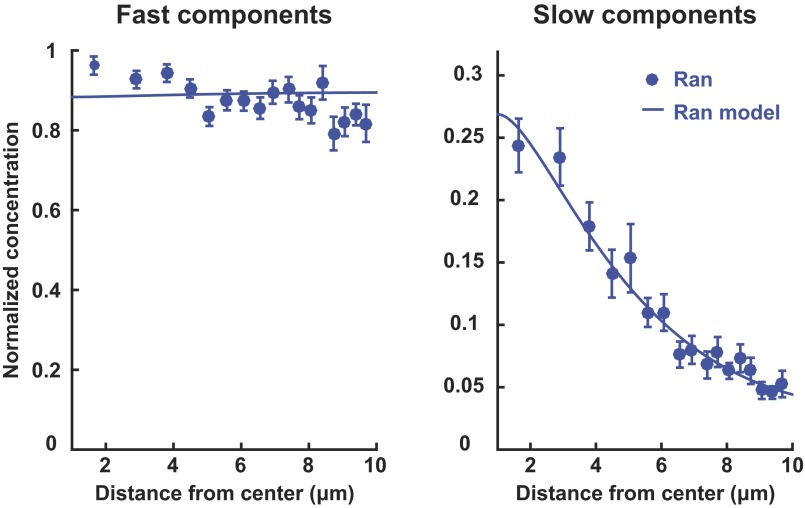
As the Ran gradient is believed to be established by reaction-diffusion processes (7, 8, 12, 13, 18), we examined spatial variations in the behavior of soluble proteins in the Ran pathway in mitotic cells using a recently developed multipoint fluorescence fluctuation spectroscopy technique: time-integrated multipoint moment analysis (TIMMA) (28). TIMMA uses measurements of the first and second moments of intensity fluctuations, at time scales from tens of microseconds to tens of milliseconds, to determine the concentration and diffusion coefficient of fluorescently labeled proteins at hundreds of locations throughout a sample. Because insoluble proteins are nearly static on these timescales, they do not contribute to the measured fluctuations, and thus TIMMA only probes the dynamics of soluble proteins (28). We first investigated the dynamics of soluble Ran, which, at all locations, is well described by two components: a fast species with a diffusion coefficient of 31.7 ± 2.0 µm2/s and a slow species with a diffusion coefficient of 1.4 ± 0.3 µm2/s (Fig. S1). The slow species of Ran likely corresponds to Ran in a complex, but the value of the diffusion coefficient cannot be used to quantitatively infer the size of the Ran complex, because diffusion coefficients of soluble proteins inside cells are strongly influenced by their transient interactions with other cellular components (29). The fast species of Ran is likely to be predominantly freely diffusing Ran, because its diffusion coefficient is similar to that of GFP (40.3 ± 1.4 µm2/s), which diffuses as a single component (Fig. S1). Ran is known to form a wide variety of complexes in cells (30), so the two species resolved by TIMMA are almost certainly extremes of a continuous distribution. TIMMA simultaneously provides ∼50 separate measurements in each mitotic cell (Fig. 2A). The concentrations of fast and slow species were determined for each of these locations (Fig. 2B), allowing spatial variations of the behaviors of soluble Ran to be investigated in single cells: Whereas the concentration of the fast component is spatially uniform, that of the slow component is enriched around chromosomes (Fig. 2C). Because the measured concentration of the species of Ran depends on the expression level of EGFP-Ran, which varies from cell to cell, we normalized the data in each cell to make the average concentration of soluble Ran equal to one. We averaged results from multiple cells to better visualize the spatial variations in soluble Ran (Fig. 2D, dark blue), whose slow component is approximately fourfold higher concentration in solution near chromosomes than at the cell periphery. This observation is consistent with expectations from reaction–diffusion models of the Ran pathway (7, 8) that predict that slowly diffusing Ran complexes should be enriched in solution around chromosomes, as confirmed by a comparison between these experimental results and a simple mathematical model (SI Text and Fig. S2). To test whether the enrichment of Ran around chromosomes is caused by the local production of RanGTP at that location, we investigated the behavior of RanQ69L, a hydrolysis-dead mutant of Ran. RanQ69L exhibits fast- and slow-diffusing species, similar to Ran, but the slow species of RanQ69L is spatially uniform (Fig. 2D, cyan), demonstrating that the gradient requires the cycling of RanGTP to RanGDP as expected. Taken together, these results show that the diffusion and spatial organization of Ran are consistent with previously proposed reaction–diffusion mechanisms in which RanGTP and large complexes are produced near chromosomes and then diffuse away and dissipate.
Fig. S1.
TIMMA variance curves of EGFP and EGFP-Ran in mitotic cells. (A) Variance curve of EGFP in mitotic cells (circles) with a single component fit (line). Averaging the normalized variance curves throughout cells reveals that the dynamics of EGFP can be well described as a single diffusing species with a diffusion coefficient of 40.3 ± 1.4 µm2/s. (B) Variance curve of EGFP-Ran in mitotic cells (circles) with single- (light-green line) and two-component (dark-green line) fits. The diffusion of EGFP-Ran cannot be described as a single diffusion species but is well fit by a model with two components: a fast species with a diffusion coefficient of 31.7 ± 2.0 µm2/s and a slow species with a diffusion coefficient of 1.4 ± 0.3 µm2/s.
Fig. 2.
Contrasting Ran and TPX2 in mitotic cells. (A) A mitotic cell with the spindle viewed by imaging mCherry-tubulin, overlaid with pinhole locations. (Scale bar: 10 µm.) (B) Two individual variance curves of EGFP-Ran from the corresponding locations with the fit curves. (C) Concentration profiles of the fast (Top) and slow (Bottom) components of Ran as a function of distance from the spindle center for this cell. To correct for different levels of expression of EGFP-Ran between cells, the average concentration of Ran in the cell was normalized to a value of one. (D) Concentration profiles of the fast (Top Left) and slow (Top Right) components of Ran (blue circles, n = 13 cells), Ran with microtubules disassembled (i.e., with nocodazole) (red squares, n = 10 cells), and RanQ69L (cyan diamonds, n = 6 cells) in wild-type cells. Fluorescence images of a mitotic cell with EGFP-Ran (Bottom Left) and from mCherry-tubulin (Bottom Right). (Scale bar: 10 µm.) To compare gradients in cells with different expression levels and under different conditions, the concentration of Ran was normalized such that the slow component overlapped with the control in the region outside the spindle (between 7–10 μm from the center). (E) Concentration profiles of the fast (Top Left) and slow (Top Right) components of TPX2 in wild-type cells (blue circles, n = 7 cells) and with microtubules disassembled (i.e., with nocodazole) (red squares, n = 7 cells). Fluorescence images of a mitotic cell with EGFP-TPX2 (Bottom Left) and mCherry-tubulin (Bottom Right). (Scale bar: 10 µm.) To compare gradients in cells with different expression levels and under different conditions, the concentration of TPX2 was normalized such that the slow component overlapped with the control in the region outside the spindle (between 7–10 μm from the center).
Fig. S2.
Comparison of the Ran reaction–diffusion model (Eqs. S5–S7) from simulations (solid line) and the concentration profiles of the fast and slow components of Ran measured with TIMMA (blue circles, n = 13 cells).
We next sought to characterize the diffusion and spatial organization of SAFs, to compare with those of Ran. We first studied the behaviors of TPX2. Like Ran, TPX2 is well described by two components (Fig. S3), a fast species and a slow species. TPX2 is also known to form a wide variety of complexes in cells (20, 21, 31), so, as with Ran, the two species resolved by TIMMA are almost certainly extremes of a continuous distribution. Unlike with Ran, the two species of TPX2 both form soluble gradients, which are highly enriched in solution around chromosomes (Fig. 2E, blue). TPX2, the downstream component of the Ran pathway, displays a more dramatic gradient than Ran (compare Fig. 2D, blue and 2E, blue), the upstream component. Such behavior is not predicted to occur in simple, linear reaction–diffusion models of signaling cascades (7). TPX2 binds to microtubules (21) and strongly associates with the spindle (Fig. 2E, Bottom). As noted above, TIMMA only probes the behavior of soluble proteins and thus does not directly provide information on TPX2 that is bound to the spindle. However, we hypothesized that the binding of TPX2 to spindle microtubules might influence the distribution of soluble TPX2, leading to its steep gradient around chromosomes. To test this possibility, we depolymerized microtubules in spindles by exposing them to 6 µM nocodazole for 2 h and found that the enrichment of TPX2 in solution around chromatin was greatly reduced (Fig. 2E, red). Thus, the soluble gradient of TPX2 depends on the presence of microtubules, consistent with it arising from the interactions between TPX2 and microtubules. In contrast, Ran is not strongly associated with the spindle (Fig. 2D, Bottom), and depolymerizing spindle microtubules does not significantly influence the Ran gradient (Fig. 2D, red).
Fig. S3.
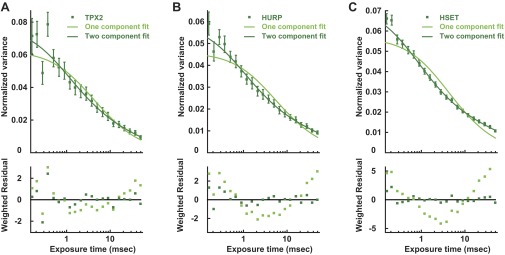
TIMMA variance curves of EGFP-SAFs in mitotic cells. (A) Variance curve of EGFP-TPX2 in mitotic cells (dark-green squares) with single- (light-green line) and two-component (dark-green line) fits. In the two-component fit, a fast species with a diffusion coefficient of 26.0 ± 6.1 µm2/s and a slow species with a diffusion coefficient of 1.0 ± 0.5 µm2/s. (B) Variance curve of EGFP-HURP in mitotic cells (dark-green squares) with single- (light-green line) and two-component (dark-green line) fits. In the two-component fit, a fast species with a diffusion coefficient of 41.6 ± 7.9 µm2/s and a slow species with a diffusion coefficient of 0.6 ± 0.2 µm2/s. (C) Variance curve of EGFP-HSET in mitotic cells (dark-green squares) with single- (light-green line) and two-component (dark-green line) fits. In the two-component fit, a fast species with a diffusion coefficient of 38.5 ± 3.7 µm2/s and a slow species with a diffusion coefficient of 0.4 ± 0.1 µm2/s.
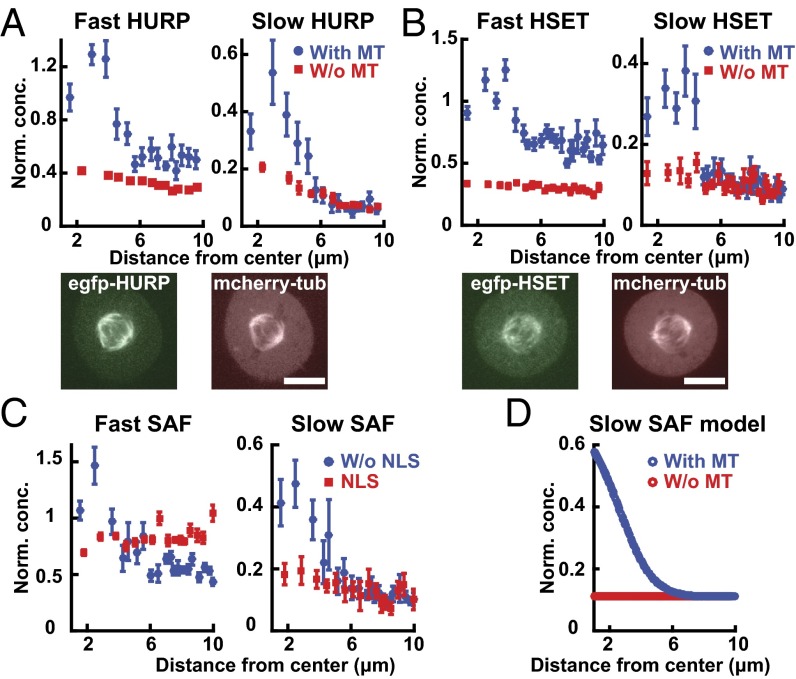
To test whether microtubule-dependent localization is unique to TPX2, or is a property of Ran-regulated SAFs more generally, we investigated the behaviors of two other SAFs: HURP, which is reported to be involved in Ran-dependent microtubule bundling and nucleation (22), and HSET, a Ran-regulated motor protein (23). Both HURP and HSET diffuse as two soluble components (Fig. S3) and are known to form a wide variety of complexes in cells (22, 23), suggesting that, as with Ran and TPX2, the two species resolved by TIMMA are extremes of a continuous distribution. HURP and HSET display soluble gradients around chromosomes (Fig. 3 A and B, blue) and localize to the spindle (Fig. 3 A and B, Bottom), and their soluble gradients are strongly reduced when microtubules are depolymerized (Fig. 3 A and B, red). Therefore, TPX2, HURP, and HSET display concentration gradients in their soluble and bound populations in the presence of microtubules of the spindle (Fig. S4) and are spatially uniform in the absence of microtubules.
Fig. 3.
Spatial organization of the SAFs HURP and HSET in mitotic cells. (A) Concentration profiles of the fast component (Top Left) and slow component (Top Right) of HURP in wild-type cells (blue circles, n = 7 cells) and microtubule-disassembled cells (red squares, n = 6 cells). Fluorescence images of a mitotic cell with EGFP-HURP (Bottom Left) and from mCherry-tubulin (Bottom Right). (Scale bar: 10 µm.) (B) Concentration profiles of the fast component (Top Left) and slow component (Top Right) of HSET in wild-type cells (blue circles, n = 10 cells) and microtubule-disassembled cells (red squares, n = 6 cells). Fluorescence images of a mitotic cell with EGFP-HSET (Bottom Left) and mCherry-tubulin (Bottom Right). (Scale bar: 10 µm.) (C) Concentration profiles of the fast component (Left) and slow component (Right) of HSET without an NLS sequence (blue circles, n = 7 cells) and the NLS sequence of HSET without the microtubule-binding region (red squares, n = 6 cells). (D) Simulated soluble gradients of a SAF that interacts with microtubules in the presence (blue circle) or absence (red circle) of microtubules.
Fig. S4.
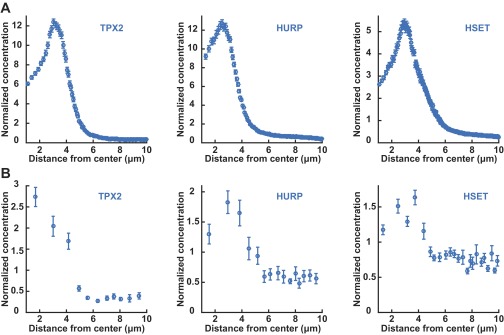
Comparisons of the total intensity distributions of EGFP-labeled SAFs obtained from spinning-disk confocal microscopy, with the soluble distribution of those factors obtained by TIMMA. (A) Intensity profile of EGFP-TPX2 (Left, blue circles), EGFP-HURP (Middle, blue circles), and EGFP-HSET (Right, blue circles) as a function of distance from the spindle center. (B) Concentration profile of the total soluble components of EGFP-TPX2 (Left, blue circles), EGFP-HURP (Middle, blue circles), and EGFP-HSET (Right, blue circles) as a function of distance from the spindle center. The relative normalization of concentrations between total (from imaging) and soluble (from TIMMA) SAFs was set by assuming that all SAFs far removed from the spindle (7–10 μm from the center) were soluble.
We hypothesized that the microtubule-dependent soluble gradients of SAFs are caused by the binding of SAFs to microtubules in the spindle and not Ran regulation per se. To test this possibility, we studied HSET mutants. An HSET construct that contains its nuclear localization sequence (NLS), and thus interacts with the Ran pathway, but that lacks its microtubule-interacting domain diffuses as two components, similar to full-length HSET, but is not significantly enriched around chromosomes (Fig. 3C, red). In contrast, a mutant of HSET that contains its microtubule-interacting domain but lacks an NLS, and is thus not regulated by the Ran pathway, displays soluble gradients around chromosomes similar to wild-type HSET (Fig. 3C, blue). Thus, the soluble gradients of HSET require interactions with microtubules and are not dependent on direct regulation by Ran.
Taken together, our experimental results argue that the binding of SAFs to microtubules in the spindle not only localizes the bound SAFs but also causes strong gradients in soluble SAFs. We sought to further explore the validity of this explanation by constructing a computational model of the behaviors of a SAF diffusing and interacting with the microtubules of the spindle (Fig. S5). Using realistic parameters (Tables S1 and S2), this model produces a strong gradient of a soluble SAF in the presence of microtubules (Fig. 3D, blue) and a nearly uniform distribution in their absence (Fig. 3D, red). Thus, the binding of SAFs to microtubules is not only sufficient to localize bound SAFs to the spindle but also creates large concentrations of soluble SAFs in the spindle region as well (Fig. 4A).
Fig. S5.
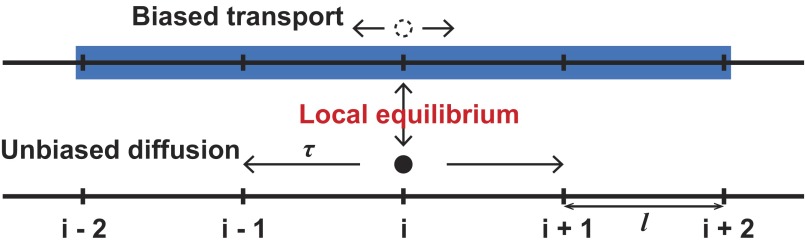
Microscopic model of biased random walk on a lattice. The random walker is in local equilibrium between soluble and microtubule-bound forms and can hop with a discrete step of duration, τ, between consecutive sites separated by a distance, l. It can move by unbiased diffusion, stay at the current site, or move in a biased fashion along microtubules.
Table S1.
Modeling parameters of Ran behaviors
| Species | DRanGTP, µm2/s | DRanGDP, µm2/s | DRancomp, µm2/s | kh, s−1 | kc, s−1 | khc, s−1 | ke, µm/s | C0, µM |
| Ran | 30* | 30* | 1.5* | 5.5 (1.2)† | 0.1‡ | 0.45§ | 15¶ | 6# |
Obtained from TIMMA through fits to Eq. S1 (and rounded for use in the simulations).
Calculated from the length scale of decay of RanGTP activity, measured with FLIM FRET (Fig. 1), and the diffusion coefficient of Ran, measured with TIMMA. This value is similar to that previously measured in vitro: 2.1 s−1 (54) and 10.6 s−1 (55). The change of kh from 5.5 s−1 to 1.2 s−1 upon RNAi of RanGAP reproduces the measured change in the RanGTP gradient (Fig. 1B).
Obtained by fitting the ratio of fast to slow population and the spatial variations in the slow population measured from TIMMA (Fig. S2).
Determined to be >0.1 s−1 in vitro (56) and obtained by fitting the spatial variations in the slow population measured from TIMMA (Fig. S2).
From ref. 54.
From ref. 57.
Table S2.
Modeling parameters of SAF behaviors
| Species | D0, µm2/s | Dinact, µm2/s | aac, µM−1 | bac, µm2 µM−1 s−1 | kca, µM−1⋅s−1 | kci, s−1 | C0, µM |
| SAF (Fig. 3D) | 0.4* | 0.4* | 0.024† | 0.003‡ | 2§ | 0.05§ | 0.1¶ |
| Nucleator SAF (Figs. 4C, 5, and 6) | 0.4 | 0.4 | 0.02 (0)# | 0.011 | 2 | 0.05 (2)# | 0.2 |
Obtained from TIMMA through fits to Eq. S1 (and rounded for use in the simulations).
Obtained from TIMMA through measurements of the relative ratio of mobile to immobile fractions. The immobile fraction was determined using the procedure of ref. 46.
Obtained by fitting the spatial variations measured from TIMMA (Fig. 3D).
The ratio of kca and kci determines the fraction of active nucleators at steady state.
From ref. 20.
aac is set to 0 in the model without interactions between SAFs and microtubules, in which case kci is adjusted to 2 to keep the spindle length the same.
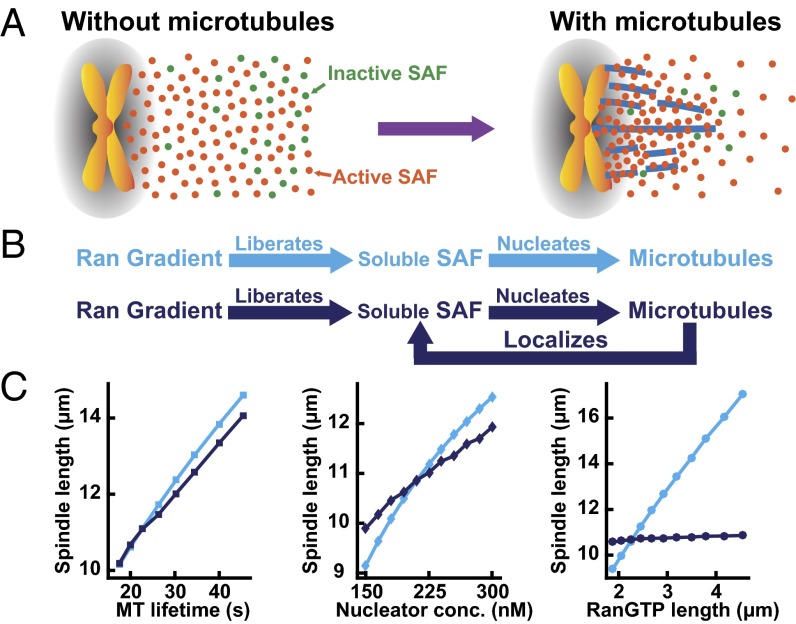
Fig. 4.
The localization of SAFs by spindle microtubules implies a feedback based on spatial localization. (A) A cartoon showing the distribution of activated (orange circles) and inactivated cargoes (green circles) when microtubules are absent (Left) and when microtubules are present (Right) in a mitotic cell. (B) In the absence of microtubule interactions, the Ran pathway would be linear (Top, cyan). The interaction between SAFs and microtubules leads to a feedback based on spatial localization because SAFs that nucleate microtubules localize where microtubules are present (Bottom, dark blue). (C) (Left) Simulated spindle length as a function of microtubule lifetime without (cyan squares) and with (dark-blue squares) the interaction of the SAF with microtubule. (Middle) Simulated spindle length as a function of nucleator concentration without (cyan diamonds) and with (dark-blue diamonds) the interaction of the SAF with the microtubule. (Right) Simulated spindle length as a function of the length of the RanGTP gradient without (cyan circles) and with (dark-blue circles) the interaction of the SAF with the microtubule.
Our results demonstrate that the interactions between SAFs and microtubules lead to large concentration gradients of SAFs around spindles. We wondered whether the localization of SAFs by microtubules might explain why the length of the spindle is not influenced by the length of the Ran gradient (Fig. 1), even though the Ran pathway regulates microtubule nucleation and is required for proper spindle assembly (12, 13, 18–23). SAFs are known to regulate microtubule nucleation and other behaviors of microtubules (12–14). In the absence of interaction with microtubules, SAFs freely diffuse, implying a linear organization of the Ran pathway in which the Ran gradient liberates SAFs from karyopherins, allowing the freed SAFs to nucleate microtubules (Fig. 4B, cyan). In contrast, the influence of microtubules on the localization of both soluble and bound SAFs implies the existence of a feedback loop in which SAFs are localized by the microtubules they nucleate (Fig. 4B, dark blue). To explore the consequences of this feedback, which results solely from spatial localization, we constructed a computational model of spindle assembly in which microtubules are nucleated by a Ran-regulated SAF, rapidly grow and shrink, and interact with each other via molecular motors and passive cross-linkers, and we either include or exclude the binding of SAFs to microtubules (SI Text). Both the linear and feedback models are able to generate a spindle of appropriate size with realistic parameters (Tables S1 and S2). Both models predict that spindle length is approximately proportional to the lifetime of microtubules in the spindle (Fig. 4C, Left), consistent with previous models of spindle assembly (15, 16) and previous experimental data showing that spindle length is influenced by factors that affect microtubule stability (32, 33), such as MCAK (34), katanin (35), and XMAP215 (16). Similarly, both models predict that spindle length is approximately proportional to the concentration of microtubule nucleators (Fig. 4C, Center), consistent with the observed reduction in spindle length upon knocking down TPX2 (Fig. 1D) (27) and previous models of spindle assembly (15, 16).
However, the role of the Ran gradient is very different in these two models. In the absence of microtubule interactions, the extent of the Ran gradient determines the size of the region in which microtubule nucleation occurs (12), such that the size of the spindle is predicted to increase approximately linearly with the length of the Ran gradient (Fig. 4C, Right, cyan), as also seen in previous models of spindle assembly (15, 16). In contrast, with microtubule interactions, the location of a microtubule-nucleating SAF is determined by its association with microtubules. With realistic parameters (Tables S1 and S2), this model predicts that spindle length does not significantly change as a function of the RanGTP gradient (Fig. 4C, Right, dark blue), in agreement with experiments (Fig. 1). To investigate the robustness of these results, we performed additional simulations increasing or decreasing the parameters by a factor of two and observed the same trend irrespective of the specific parameter values used (Table S3). Therefore, the localization of SAFs by microtubules is sufficient to account for the insensitivity of spindle morphology to the length scale of the Ran gradient.
Table S3.
Sensitivity analysis of the spindle length with respect to the modeling parameters
| With microtubule interaction | Without microtubule interaction | |||||
| Parameters* | Control | RanGAP RNAi | Ratio | Control | RanGAP RNAi | Ratio |
| ke, µm⋅s−1 | ||||||
| 7.5 | 10.61 | 10.89 | 0.97 | 8.85 | 14.30 | 0.62 |
| 15 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 30 | 10.70 | 10.74 | 1.00 | 11.93 | 19.08 | 0.63 |
| kc, s−1 | ||||||
| 0.225 | 10.69 | 10.82 | 0.99 | 10.94 | 19.45 | 0.56 |
| 0.45 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.9 | 10.64 | 10.87 | 0.98 | 10.05 | 14.26 | 0.70 |
| khc, s−1 | ||||||
| 0.05 | 10.67 | 10.87 | 0.98 | 10.32 | 15.53 | 0.66 |
| 0.1 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.2 | 10.69 | 10.77 | 0.99 | 10.77 | 17.98 | 0.60 |
| kca, µM−1⋅s−1 | ||||||
| 1 | 10.46 | 10.92 | 0.96 | 7.92 | 11.86 | 0.67 |
| 2 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 4 | 10.70 | 10.70 | 1.00 | 13.35 | 19.59 | 0.68 |
| kci, s−1 | ||||||
| 0.025 (1) | 10.63 | 10.69 | 0.99 | 13.40 | 19.50 | 0.69 |
| 0.05 (2) | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.1 (4) | 10.68 | 11.02 | 0.97 | 7.90 | 11.85 | 0.67 |
| knuc, µM⋅s−1 | ||||||
| 5 | 6.00 | 6.20 | 0.97 | 8.74 | 14.53 | 0.60 |
| 10 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 20 | 10.86 | 10.76 | 1.01 | 12.94 | 19.75 | 0.66 |
| csig, µM | ||||||
| 0.125 (0.02) | 12.83 | 12.94 | 0.99 | 14.47 | 18.03 | 0.80 |
| 0.25 (0.04) | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.5 (0.08) | — | — | — | 6.49 | 9.44 | 0.69 |
| ca, µM | ||||||
| 0.0075 | 10.70 | 10.83 | 0.99 | 10.34 | 16.49 | 0.63 |
| 0.015 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.03 | 10.69 | 10.84 | 0.99 | 11.35 | 16.90 | 0.67 |
| D, µm2⋅s−1 | ||||||
| 0.02 | 8.89 | 8.93 | 1.00 | 10.21 | 16.29 | 0.63 |
| 0.04 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 0.08 | 12.58 | 12.92 | 0.97 | 11.01 | 17.87 | 0.62 |
| ε, µm | ||||||
| 0.25 | 11.11 | 11.21 | 0.99 | 10.80 | 17.41 | 0.62 |
| 0.5 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 1 | 9.37 | 9.48 | 0.99 | 10.40 | 16.70 | 0.62 |
| M0, µM | ||||||
| 50 | 15.46 | 16.38 | 0.94 | 12.94 | 19.75 | 0.66 |
| 100 | 10.68 | 10.86 | 0.98 | 10.61 | 17.04 | 0.62 |
| 200 | 3.39 | 3.45 | 0.98 | 8.74 | 14.53 | 0.60 |
| aac, µM−1 | ||||||
| 0.01 | 13.04 | 13.79 | 0.95 | |||
| 0.02 | 10.68 | 10.86 | 0.98 | |||
| 0.04 | 7.78 | 7.70 | 1.01 | |||
| bac, µm2⋅µM-1⋅s−1 | ||||||
| 0.0055 | 13.09 | 13.88 | 0.94 | |||
| 0.011 | 10.68 | 10.86 | 0.98 | |||
| 0.022 | 7.33 | 7.53 | 0.97 | |||
Numbers in parentheses were used in simulations without interactions between SAFs and microtubules.
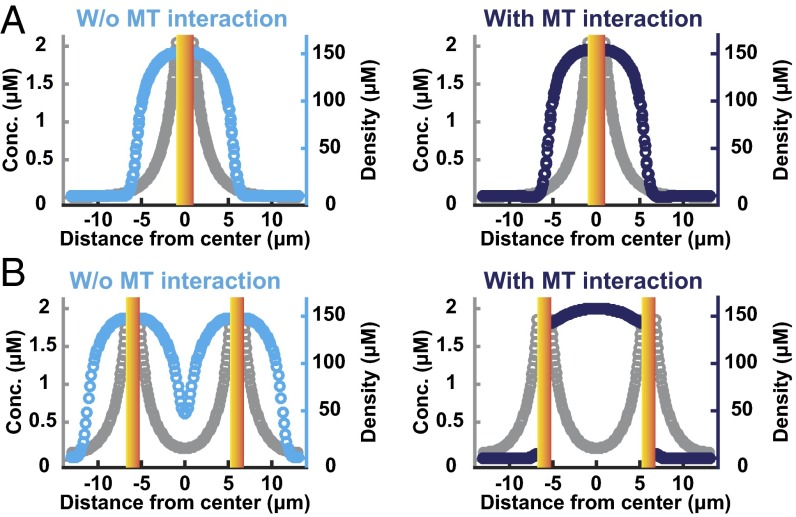
In cells undergoing MUG, the bulk of chromosomes detach from kinetochores and centromeric DNA. It has previously been found that in these cells the detached chromosome mass localizes to the periphery of the spindle, and thus the spindle is outside the peak of the Ran gradient, which emanates from the chromosomes (24). This result demonstrates that the location of the Ran gradient is not the sole determinant of the location of microtubule nucleation. We next investigated whether our simulations are consistent with these results from MUG cells. In simulations of control cells, with chromosomes localized to the cell center, spindles form around the peak of the Ran gradient in both the absence and the presence of interactions between SAFs and microtubules (Fig. 5A), as expected. To model MUG cells, we performed simulations with the chromosomes split into two masses located 12 μm apart. In simulations without interactions between SAFs and microtubules, microtubules form around the peak of the two Ran gradients (Fig. 5B, Left), in disagreement with experiments. In simulations incorporating the localization of SAFs by microtubules, the spindle assembles between the two chromosomes masses, away from the peaks of the Ran gradient (Fig. 5B, Right), as observed experimentally (24). The assembly of the spindle between the chromosome masses results from the positive feedback between the generation of microtubules by SAFs and the localization of SAFs by microtubules: SAFs activated by one chromosome mass can bind to microtubules nucleated by SAFs from the other chromosome mass, leading to more microtubules being generated between the two chromosome masses, which then bind more SAFs. Because this feedback is based on SAF localization, not further activation of SAFs, it causes microtubules to localize between chromosomes but does not result in a significant change in the total amount of microtubules generated. Thus, the localization of SAFs by microtubules is sufficient to explain the observation that spindles assemble outside the peak of the Ran gradient in MUG cells.
Fig. 5.
The localization of SAFs by microtubules enables spindle assembly away from the peak of the Ran gradient, as observed in cells undergoing MUG. (A) Simulated microtubule density (cyan and dark blue) and RanGTP concentration (gray) with chromosomes (graded yellow bars) in the center of the cell. In both models without (Left) and with (Right) interactions between SAFs and microtubules, the spindle is centered on the chromosomes, at the peak of the RanGTP gradient. (B) To mimic MUG cells, simulations were performed with chromosomes (graded yellow bars) split into two masses, 12 μm apart. In simulations without interactions between SAFs and microtubules (Left), microtubules still assemble around chromosomes, at the peaks of the RanGTP gradient. In simulations with interactions between SAFs and microtubules (Right), microtubules assemble between the chromosomes, away from the peaks of the RanGTP gradient.
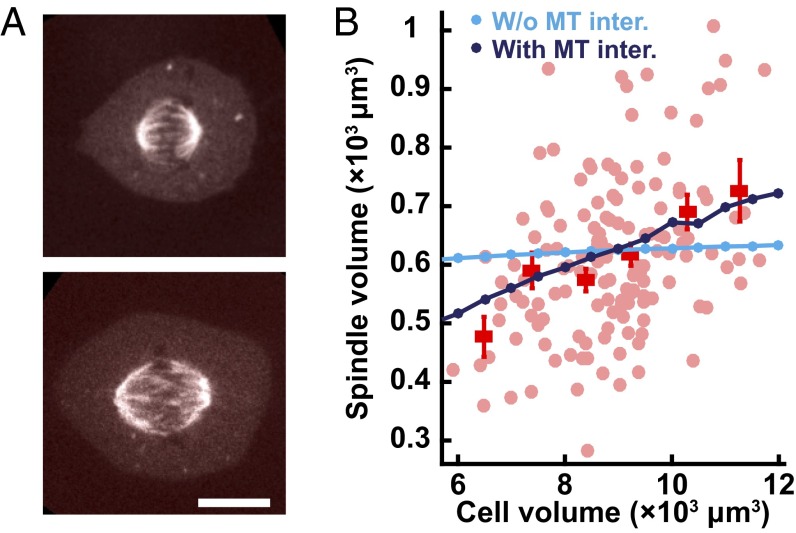
It has previously been shown that the size of the spindle is correlated with cell size during changes in early development (36–39), between different species (39, 40), between genetically different individuals within a species (40), and when spindles are assembled in vitro in cell extracts encapsulated in droplets (41, 42). To our knowledge, the scaling of the spindle with cell size has not been investigated in human tissue culture cells such as were used in this study. To probe the possible connection between cell size and spindle size in this system, we used the endogenous variation that exists in tissue culture cells, where cell size and spindle size clearly differ for different cells (Fig. 6A). We performed 3D imaging of 140 cells expressing mCherry-tubulin and for each cell measured the cell volume and the spindle volume and found that they are significantly correlated (Fig. 6B). We next sought to determine whether our model could provide insight into this scaling of the spindle with cell size. In simulations without interactions between SAFs and microtubules, varying cell volume by a factor of two does not substantially change the size of the spindle (Fig. 6B, cyan). Thus, in the absence of interactions between SAFs and microtubules, the size of the spindle is strongly influenced by microtubule stability, the concentration of microtubule nucleators, and the length scale of the Ran gradient (Fig. 4) but is insensitive to cell size, in disagreement with experiments (Fig. 6B). In contrast, in simulations with interactions between SAFs and microtubules there is a strong dependence of spindle size on cell size, consistent with experimental observations (Fig. 6B, dark blue). The scaling of spindle size with cell size arises because the strong association of SAFs to the spindle causes a substantial fraction of SAFs in the cell to localize to the spindle. This results in SAFs acting as a limiting component for spindle size (43): Larger cells (with the same concentration of SAFs) have a larger number of SAF molecules, allowing more SAFs to localize to the spindle, which then nucleate more microtubules and produce larger spindles. Thus, the localization of SAFs by microtubules is sufficient to explain the scaling of spindle size with cell size.
Fig. 6.
The localization of SAFs by microtubules gives rise to a scaling of spindle size with cell size, as observed experimentally. (A, Top) The fluorescence image of a smaller spindle within a mitotic U2OS cell is presented. (Bottom) The image of a larger spindle within a mitotic U2OS cell is presented. (Scale bar: 10 µm.) (B) Light-red circles show spindle volume plotted vs. cell volume for 140 individual cells, measured by z-stack imaging of U2OS cells expressing mCherry-tubulin. Average spindle volumes for different cell sizes are indicated (red squares with SE). Simulations without interactions between SAFs and microtubules (cyan circles) predict that spindle size should be insensitive to cell size, in disagreement with observations. Simulations with interactions between SAFs and microtubules (dark-blue circles) predict a scaling of spindle size with cell size, consistent with experiments.
This study shows that whereas Ran exhibits spatial gradients due to a reaction–diffusion-type system, the downstream components of the Ran pathway display more complex behaviors in which the association of SAFs with spindle microtubules causes both soluble and microtubule-bound SAFs to be highly enriched in the spindle region. Thus, the spatial distributions of microtubule nucleation, and other processes controlled by the Ran pathway, are not solely governed by soluble gradients set up by reaction–diffusion processes. Rather, the association of SAFs with microtubules strongly influences their localization, and thus where they carry out their activities. This picture is consistent with the previous finding that RanGTP and TPX2 promote the growth of microtubules off of other microtubules in meiotic Xenopus egg extracts (26). The localization of SAFs by microtubules has functional consequences: In the absence of interactions between SAFs and microtubules, doubling the length scale of the Ran gradient would double the length of the spindle, but the presence of SAFs–microtubule interactions is predicted to make the length of the spindle insensitive to the length of the Ran gradient, as observed experimentally. The localization of SAFs by microtubules can also account for the ability of spindles to assemble away from the peak of the Ran gradient in MUG cells (24) and the scaling of the spindle with cell size and provides a mechanism that might explain the insensitivity of spindle morphology to other perturbations in the Ran pathway and how cells can reliably proceed through mitosis despite large cell-to-cell variations in gradients in upstream components of the Ran pathway (19). More generally, because SAFs are involved in nucleating microtubules and are also localized by microtubules, this interaction implies a feedback based on spatial localization (Fig. 4A), not biochemical activity, which has been more typically considered. Feedback between reaction–diffusion systems of soluble proteins and the cytoskeleton may play a general role in subcellular organization and cell signaling (2).
Materials and Methods
See SI Text for details.
Materials.
U2OS Cell lines were cultured in DMEM supplemented with 10% (vol/vol) FBS and maintained at 37 °C in 5% (vol/vol) CO2. For sample preparation, cells were seeded on microscope cover glass and transfected with plasmids that express genes of interest. For RNAi experiments, shRNA (RanGAP) or siRNA (TPX2) transfection was used to knock down the target gene in the U2OS cell line. Samples were transferred into a custom-made heating stage and kept at 37 °C during experiments.
Methods.
Spinning-disk confocal images were taken with an electron multiplying CCD (EMCCD) camera of 512 × 512 pixels. TIMMA data were obtained with an EMCCD camera of 128 × 128 pixels with the spinning disk fixed. FLIM experiments were performed using two-photon confocal microscopy. A time-correlated single photon counting (TCSPC) system was used to collect and process FLIM data.
SI Text
Cell Lines and Plasmids.
The U2OS cell line was purchased from American Type Culture Collection. The U2OS cell line stably expressing mCherry-tagged tubulin was provided by A. Hyman, Max Planck Institute, Dresden, Germany. The U2OS cell lines with RanGAP1 RNAi were produced by harnessing shRNA. Four sets of DNA oligonucleotide sequence targeting human RanGAP1 gene were purchased (Hmi414528, Hmi414529, Hmi414530, and Hmi414531, Block-iT miRNA RNAi select oligos; Life Technologies) and cloned into pcDNA6.2-GW/miR vector following the manufacturer’s protocol (4935-00, Block-iT Pol II miR RNAi expression vector kit; Life Technologies). Cells were transfected with the expression clones by FuGENE HD protocol (E2311, FuGENE HD transfection reagent; Promega Corp.). Transfected cells were selected by 2 µg/mL blasticidin (R210-01, Blasticidin S HCl; Life Technologies) for at least 3 wk. TPX2 RNAi was conducted by transfecting siRNA (4427037, assay ID s22745, Silencer select predesigned siRNA; Life Technologies), following the manufacturer’s protocol, with 48 h of incubation.
pEGFP-Ran and pEGFP-RanQ69L were gifts from P. Clarke, University of Dundee, Dundee, United Kingdom. pEGFP-TPX2 was a gift from T. Mitchison, Harvard Medical School, Boston. pEGFP-HURP was a gift from M. Koffa, Democritus University of Thrace, Alexandroupolis, Greece. pEGFP-HSET was a gift from C. Walczak, Indiana University, Bloomington, IN. These constructs have been previously validated (22, 26, 44, 45) and TIMMA measurements indicate that they were expressed at concentrations of ∼20 nM, far below the endogenous concentrations of these proteins, which range from 100 nM to 6 μM. pEGFP-NLS(HSET) was created by amplifying NLS (AAGAGGAGGCCTGACCAGATGGAAGATGGCCTGGAGCCTGAGAAGAAACGG)-containing sequence from the pEGFP-HSET plasmid and cloned into a linearized vector fragment prepared from the pEGFP-HSET plasmid by Gibson assembly protocol (E2611S, Gibson assembly master mix; New England Biolabs). Similarly, pEGFP-HSET without NLS region was created by the Gibson protocol.
pSG8-mTFP1-RBP-dsREACh (pSG8 RBP-4) was constructed by assembly reaction of mTFP1-RBP-dsREACh sequence amplified from pLenti-RBP-4 (pK234), a gift from P. Kaláb, National Institutes of Health, Bethesda, into pSG8 vector fragment amplified from pSG8-mTFP1-linker-dsREACh (pK364), a gift from P. Kaláb by in-fusion protocol (638916, In-Fusion HD cloning plus CE; Clontech Laboratories).
Cell Culture and Sample Preparation.
All experiments were performed on U2OS cells cultured in DMEM (high glucose, l-glutamine, and phenol red, 11965; Life Technologies) supplemented with 10% (vol/vol) FBS (16000, certified, one shot, US origin; Life Technologies) and maintained at 37 °C in 5% (vol/vol) CO2. For U2OS cell lines of RanGAP1 RNAi, DMEM also contained 2 µg/mL blasticidin. For the sample preparation, cells were seeded in six-well culture plate containing microscope cover glasses of 25-mm diameter (0117650, no. 1.5H, high-precision microscope cover glasses; Paul Marienfeld GmbH & Co. KG). After one day, cells were transfected with plasmids including genes of interest by using a transfection reagent (SL100489-OS, GenJet in vitro DNA transfection reagent for U2OS cells; Signagen Laboratories) using the manufacturer’s protocol. Twelve hours after transfection, the culture media was changed into RPMI 1640 depleted of riboflavin (RR060070L1, l-glutamine, non-GMP formulation; Life Technologies) or FluoroBrite DMEM (A1896701; Life Technologies). From 12 to 24 h later, the cover glasses inside the wells were transferred into a custom-made heating stage. Then, the stage was placed in Nikon Eclipse TE2000-E (TIMMA or fluorescence imaging) or Nikon Eclipse Ti microscope (FLIM). During the experiments, samples were kept in RPMI 1640 or FluoroBrite DMEM media at 37 °C.
Quantitative Real-Time PCR.
Total RNA from the cells grown on a 25-cm2 tissue culture flask with monolayer coverage was collected by using RNeasy kit protocol (74104; Qiagen). From the RNA sample, cDNA was synthesized by using SuperScript III first-strand synthesis protocol (18080; Life Technologies). Then, the real-time PCR was run on an Applied Biosystems 7900HT by using Taqman fast advanced protocol (4444556; Life Technologies). The Taqman probe (4331182, Hs00610049_m1; Life Technologies) was used to detect RanGAP cDNA. The endogenous control was β-actin (4333762F; Life Technologies) or GAPDH (4333764T; Life Technologies). Compared with the wild-type U2OS cell line, the 4 RNAi cell lines showed ∼0.2–0.5 relative quantitation of RanGAP cDNA. We chose the cell line showing the lowest RanGAP quantitation (antisense target sequence: TCCACCTGCCGCAAGGTCTTC) for the experiments involving RanGAP knockdown.
TIMMA.
Single cells in mitosis expressing a protein of interest were selected by wide-field fluorescence microscopy. The previous described experimental setup and data acquisition (28) were used with minor modifications. The experiments were performed on the Nikon Eclipse TE2000-E microscope with an apochromat 60× water immersion objective lens and 1.5× magnifying optics. The samples were excited by 488-nm laser (Cyan 488 laser; Spectra-Physics). The excitation was modulated by AOTF switching in laser merge module (LMM5; Spectral Applied Research). The fluorescence fluctuation intensities were acquired on the iXon 860 EMCCD camera of 128 × 128 pixels (Andor Technology) through the Yokogawa CSU-X1 spinning-disk unit (Yokogawa Electric Corp.). The exposure times were determined from 50 µs to 50 ms by logarithmic scale. The total measurements were split by 15 cycles to minimize the effects from photobleaching. Per each acquisition cycle, during the measurements background intensities were obtained from camera pixels that were not on the spinning-disk pinhole locations. All of the data acquisition and postanalysis procedures were performed using homemade Labview codes (National Instruments).
Spinning-Disk Confocal Microscopy.
The epifluorescence images were acquired on the EMCCD camera of 512 × 512 pixels (ImageM enhanced C9100-13; Hamamatsu Pphotonics) mounted in the spinning-disk confocal microscope. The images were acquired using Metamorph (Molecular Devices) or μManager software (Vale laboratory at University of California, San Francisco). Z-stack images were acquired by high-speed piezo-Z scanner (P-725 PIFOC; Physik Instrumente). Images were analyzed by home-written MATLAB routines (The MathWorks, Inc.) or ImageJ software (NIH).
Measurements of Cell and Spindle Volume.
Z-stack 3D images, with 1-µm intervals, were taken for U2OS cells expressing mCherry-tubulin. Throughout a Z-stack image, cell area was estimated from each 2D image and integrated to calculate cell volume. Spindle poles were spotted throughout the Z-stack image and the length between them was calculated based on right triangle trigonometry. Spindle width was estimated from the image showing the maximum distance. Spindle volume was calculated assuming ellipsoidal geometry with the measured length and width.
FLIM.
The experimental system was implemented on the Nikon Eclipse Ti microscope. The samples were excited by a mode-locked Ti:sapphire laser (Mai Tai Deepsee; Spectra-Physics) and scanned by DCS 120 confocal scanner (Becker & Hickl GmbH). The fluorescence from the sample was collected on HPM-100-40 hybrid detector and processed by TCSPC 152 module (Becker & Hickl GmbH). The Becker & Hickl SPCM software package was used to control the data acquisition procedures. The spatially resolved lifetime analysis of the data was performed using home-written MATLAB routines and Fluofit software (Picoquant).
Quantitative Analysis of TIMMA Data.
The calculated first-order (mean) and second-order central moments (variance) of fluorescence fluctuation intensities were fit to model functions based on a 3D free diffusion model of fluorophores (28). For a single species, the variance curve is given by
| [S1] |
where N is the average number of molecules in the observation volume, r = wz/wxy is the ratio of the observation volume’s axial width to its radial width, τD = wxy2/4D is the residence time it takes a particle to diffuse through the observation volume, which is determined by the particle’s diffusion coefficient, D, λ is the brightness per unit time for an individual molecule, and γ is the second moment of the observation volume. For two species, the variance curve is a sum of two terms of the similar forms, with different values of N, τD, and D for each species. The system was calibrated as described previously (28).
Generation of Normalized Concentration Curves.
The concentration obtained from fitting to the 3D free diffusion model (Eq. S1) is in error if the long tail of the point spread function of the spinning-disk microscope extends beyond the cell periphery. Therefore, the concentration needs to be corrected for such geometric effects. We used free EGFP in mitotic U2OS cells to obtain a standard curve for geometric calibration. The single-component fitting was performed on the average moment curve for the multiple observation volumes (n ≅ 300) throughout multiple cells (n = 7) expressing free EGFP. The diffusion time of EGFP was determined from the fitting. We obtained a calibration curve of particle number by fitting the curve of normalized EGFP number as a function of distance from the cell center to a polynomial function. Assuming apparent deviations in EGFP concentration are caused solely by geometric effects, the concentration after the calibration becomes
| [S2] |
where g(x) is the calibration function. Measurements of immobile fractions and corresponding corrections were performed as described previously (46). After the calibrations, the concentration curves are normalized to be unity for the entire soluble components in wild-type experiments. For the comparison of different curves, the concentrations in the region (between 7–10 µm from the center) were normalized into the control curves.
FLIM FRET Analysis.
Photons were binned as a function of distance from chromosomes and a biexponential decay, convoluted with the instrument response function (independently measured using a urea crystal), was used to measure the fraction of FRETing and nonFRETing biosensors:
| [S3] |
where τ1 (∼0.48–0.54 ns) and τ2 (∼2.41–2.46 ns) are the lifetimes of FRETing and nonFRETing species. The RBP-4 biosensor was used in mitotic U2OS cells. The nonFRETing fraction, which decreases exponentially to a plateau value, was fit to
| [S4] |
where r is the length scale of the RanGTP gradient.
Computational Modeling
All computations were performed with Comsol Multiphysics software (v. 5.0; Comsol). Two-dimensional axisymmetric space was harnessed to model the rotationally symmetric 3D geometry and the extra-fine option was chosen for finite element analysis. General Form PDE mode was used to describe model equations, boundary conditions, and initial conditions. Simulations were performed in time-dependent mode with an interval of 0.1 s for 1,000 s, which was confirmed to be sufficient to reach steady state.
Unless otherwise noted, the simulations were performed in a spherical cell with a radius of 13 μm, with the chromosomes represented as a sphere of 1-μm radius, located at the cell center.
Modeling Ran Cycling in Mitosis.
Ran was modeled as existing in three forms, free RanGTP, free RanGDP, and Ran in a large complex:
| [S5] |
| [S6] |
| [S7] |
where kh, kc, and khc are the reaction constants of GTP hydrolysis, RanGTP complexation, and GTP hydrolysis in complex (see Tables S1 and S2 for parameter values). At chromosomes, RanGDP is converted to RanGTP by nucleotide exchange, leading to the boundary condition
| [S8] |
where ke is the reaction constant of GDP to GTP exchange. Thus, in the simulations, this reaction converting RanGDP to RanGTP is set to occur at the surface of the chromosomes. We used a no-flux boundary condition at the cell periphery. For the initial condition, all Ran exists as RanGDP.
Modeling of SAFs and Their Interactions with Microtubules.
We model SAFs being converted from an inactive form, SAFinact, to an active form, SAFact, by RanGTP. The mobility of the active form is modified by interactions with microtubules, which have a spatially varying density, represented by the spatial varying concentration of tubulin in polymer (i.e., microtubules), ρ. The resulting dynamics of SAFs is given by
| [S9] |
| [S10] |
where kca and kci are the reaction constants of SAF activation and deactivation and Dac(ρ) and uac(ρ) are diffusion coefficient and drift velocity of the active SAF, which explicitly depend on microtubule density, ρ.
We used a microscopic lattice model to derive the appropriate functional form of Dac(ρ) and uac(ρ). Our derivation closely mirrors standard derivations of the diffusion equation, which also frequently start with a lattice model and then take the continuum limit (47, 48). We consider a model in which proteins randomly diffuse and bind microtubules, whose density spatially varies, whereas proteins that are bound to microtubules can remain stationary or move in a directed fashion and unbind microtubules. We first consider a one-dimensional model in which space is divided into discrete lattice sites separated by a distance, l, and time is divided into discrete steps of duration, τ (Fig. S5). For simplicity, we assume that binding and unbinding is much more rapid than movement, so the ratio between soluble and microtubule-bound proteins is always locally in equilibrium. The resulting master equation is
| [S11] |
where P(x,t) is the probability of the protein’s being at location x at time t, r(x) is the probability of the protein’s being unbound at location x, f(x) is the probability of a bound protein to be transported to the minus x direction, and w is the probability that a bound protein remains stationary.
Taylor-expanding Eq. S11, dropping higher-order terms in l, and using that w is near one (because diffusion is locally much more rapid than transport on microtubules), this reduces to
| [S12] |
where r(x) is the fraction of unbound proteins at location x. If unbound proteins bind microtubules with an association constant ka and bound proteins unbind with a rate kd, then the assumption of local equilibrium between bound and unbound proteins implies
| [S13] |
where cfree and cbound are the concentrations of unbound and microtubule-bound proteins. Thus,
| [S14] |
where aac (=ka/kd) is a measure of the association of the proteins with microtubules.
f(x) is the directional bias of transport of bound proteins, defined to be 1/2 for equal movement in both directions, 0 for uniform movement in the positive x direction, and 1 for uniform movement in the negative x direction. Because we do not explicitly model microtubule polarity, we expect that the directional bias would arise from changes in microtubule density, the simplest form of which is
| [S15] |
The intuition behind Eq. S15 is that a spatial variation in microtubule density implies a spatial variation in microtubule ends, which would produce a directional bias to transport for proteins that move directionally along microtubules.
Combining Eqs. S12, S14, and S15, and generalizing to higher dimensions, gives an equation of motion for the proteins:
| [S16] |
where D0 = l2/2τ is the diffusion coefficient of unbound proteins and bac = m⋅l(1 – w)/τ is a measure of the net transport speed of bound proteins. The microscopic lattice spacing, l, and time step, τ, should be not thought of as real, physical variables that can be experimentally measured; rather, the only parameters that can be observed, and thus the only ones that need to be specified (Tables S1 and S2), are those that appear in Eq. S16: D0, aac, and bac. Eq. S16 is a diffusion and drift equation for the motion of the proteins with local concentration, c, with a diffusion coefficient that depends on microtubules density
| [S17] |
and a drift velocity that depends on microtubule density
| [S18] |
Thus, in our simulation, the full equations for SAFs are given by Eqs. S9 and S10, with Eqs. S17 and S18. We used a no-flux boundary condition for both active and inactive SAFs at the surface of the cell and chromosomes. For initial conditions, we took all SAFs to be inactive.
Modeling of Microtubules.
We first consider an SAF with (or without) a fixed distribution of microtubules, taken to be a shifted error function (Fig. 3D):
| [S19] |
where ρ0, the peak tubulin concentration in the spindle, is 160 µM, xl, the half-length of the spindle, is 5 µm, and σ determines the sharpness of the microtubule profile in the spindle, and is taken to be 3 µm.
We next considered the case where all microtubules are generated by an SAF that is a microtubule nucleator (Fig. 4). The dynamics of the SAF is described by Eqs. S9, S10, S17, and S18. We model the microtubules as being nucleated by the active SAF, polymerizing and depolymerizing, and interacting via bundling proteins and motors, using the equation
| [S20] |
The left-hand side of Eq. S20 is the Cahn–Hilliard equation, which we use to describe the motion and interactions between microtubules. The Cahn–Hilliard equation has been extensively used in many areas of material science and physics to model the behavior of objects with attractive interactions that result in phase separation (49, 50) and has recently been shown to even apply for nonequilibrum “active” materials (51), and is thus a reasonable model of microtubules that aggregate due to the activity of bundling proteins and molecular motors. The third-order term can be viewed as a chemical potential, arising from the derivative of a Landau free energy. D is a measure of the mobility of microtubules (0.04 µm2/s), ε is the interface thickness separating the inside of the high-density spindle from the rest of the cytoplasm (0.5 µm), and M0 is the microtubule density that motors and bundling try to achieve in the spindle region (100 µM).
The right-hand side of Eq. S20 describes microtubule nucleation and turnover. The second term arises from microtubule polymerization and depolymerization dynamics, where kmtd is a measure of the rate of microtubule turnover (0.05 s−1) (52). Because microtubule nucleation depends on factors that are not Ran-regulated, as well as Ran-regulated SAFs (53), the microtubule nucleation rate is expected to be a saturating function of active SAF, consistent with experimental observation (12, 13), as represented by the first term on the right-hand side. knuc is the maximum rate of microtubule nucleation (10 µM⋅s−1), csig is the half-maximum concentration of SAF for nucleation (0.25 µM), and ca determines how rapidly the nucleation reaction saturates with changing active SAF concentration (0.015 µM). To simulate the absence of SAF–microtubule interactions, aac in Eqs. S17 and S18 was set to zero and csig was adjusted to 0.040 µM to replicate the size and tubulin density of the spindle.
For simulations, the chemical potential in the Cahn–Hilliard equation is taken as a dummy variable. No flux is applied as the boundary condition at the surface of the cell and chromosomes. For the initial condition, the microtubule is distributed as Gaussian peaked at the chromosome surface with 155 μM and 3.5 μm width. For the MUG simulation, chromosomes were taken to exist in two masses with radii of 0.8 μm, located 12 μm apart with the same initial condition for microtubule density.
Acknowledgments
We thank Aaron Groen and Tim Mitchison for helpful conversations; Bodo Stern, Tim Mitchison, Alex Schier, and Andrew Murray for comments on the manuscript; Anthony Hyman, Paul Clarke, Tim Mitchison, Maria Koffa, Claire Walczak, Keisuke Hasegawa, and Petr Kaláb for providing materials; Dann Huh and Tae Yeon Yoo for assistance in gene cloning; and Tim Peterson for assistance in quantitative RT-PCR. This work was supported by National Science Foundation Grants DBI-0959721 and DMR-0820484 and United States–Israel Binational Science Foundation Grant BSF 2009271.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1607498113/-/DCSupplemental.
References
- 1.Alberts B, et al. Molecular Biology of the Cell. 5th Ed Garland; New York: 2007. [Google Scholar]
- 2.Howard M. How to build a robust intracellular concentration gradient. Trends Cell Biol. 2012;22(6):311–317. doi: 10.1016/j.tcb.2012.03.002. [DOI] [PubMed] [Google Scholar]
- 3.Kholodenko BN. Cell-signalling dynamics in time and space. Nat Rev Mol Cell Biol. 2006;7(3):165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chen J, Lippincott-Schwartz J, Liu J. Intracellular spatial localization regulated by the microtubule network. PLoS One. 2012;7(4):e34919. doi: 10.1371/journal.pone.0034919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen J, Liu J. Spatial-temporal model for silencing of the mitotic spindle assembly checkpoint. Nat Commun. 2014;5:4795. doi: 10.1038/ncomms5795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shi C, Channels WE, Zheng Y, Iglesias PA. A computational model for the formation of lamin-B mitotic spindle envelope and matrix. Interface Focus. 2014;4(3):20130063. doi: 10.1098/rsfs.2013.0063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stelling J, Kholodenko BN. Signaling cascades as cellular devices for spatial computations. J Math Biol. 2009;58(1-2):35–55. doi: 10.1007/s00285-008-0162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lipkow K, Odde DJ. Model for protein concentration gradients in the cytoplasm. Cell Mol Bioeng. 2008;1(1):84–92. doi: 10.1007/s12195-008-0008-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bois JS, Jülicher F, Grill SW. Pattern formation in active fluids. Phys Rev Lett. 2011;106(2):028103. doi: 10.1103/PhysRevLett.106.028103. [DOI] [PubMed] [Google Scholar]
- 10.Wedlich-Soldner R, Altschuler S, Wu L, Li R. Spontaneous cell polarization through actomyosin-based delivery of the Cdc42 GTPase. Science. 2003;299(5610):1231–1235. doi: 10.1126/science.1080944. [DOI] [PubMed] [Google Scholar]
- 11.Lee CF, Brangwynne CP, Gharakhani J, Hyman AA, Jülicher F. Spatial organization of the cell cytoplasm by position-dependent phase separation. Phys Rev Lett. 2013;111(8):088101. doi: 10.1103/PhysRevLett.111.088101. [DOI] [PubMed] [Google Scholar]
- 12.Caudron M, Bunt G, Bastiaens P, Karsenti E. Spatial coordination of spindle assembly by chromosome-mediated signaling gradients. Science. 2005;309(5739):1373–1376. doi: 10.1126/science.1115964. [DOI] [PubMed] [Google Scholar]
- 13.Kaláb P, Pralle A, Isacoff EY, Heald R, Weis K. Analysis of a RanGTP-regulated gradient in mitotic somatic cells. Nature. 2006;440(7084):697–701. doi: 10.1038/nature04589. [DOI] [PubMed] [Google Scholar]
- 14.Athale CA, et al. Regulation of microtubule dynamics by reaction cascades around chromosomes. Science. 2008;322(5905):1243–1247. doi: 10.1126/science.1161820. [DOI] [PubMed] [Google Scholar]
- 15.Loughlin R, Heald R, Nédélec F. A computational model predicts Xenopus meiotic spindle organization. J Cell Biol. 2010;191(7):1239–1249. doi: 10.1083/jcb.201006076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reber SB, et al. XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. Nat Cell Biol. 2013;15(9):1116–1122. doi: 10.1038/ncb2834. [DOI] [PubMed] [Google Scholar]
- 17.Wollman R, et al. Efficient chromosome capture requires a bias in the ‘search-and-capture’ process during mitotic-spindle assembly. Curr Biol. 2005;15(9):828–832. doi: 10.1016/j.cub.2005.03.019. [DOI] [PubMed] [Google Scholar]
- 18.Kalab P, Heald R. The RanGTP gradient - a GPS for the mitotic spindle. J Cell Sci. 2008;121(Pt 10):1577–1586. doi: 10.1242/jcs.005959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hasegawa K, Ryu SJ, Kaláb P. Chromosomal gain promotes formation of a steep RanGTP gradient that drives mitosis in aneuploid cells. J Cell Biol. 2013;200(2):151–161. doi: 10.1083/jcb.201206142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gruss OJ, et al. Ran induces spindle assembly by reversing the inhibitory effect of importin alpha on TPX2 activity. Cell. 2001;104(1):83–93. doi: 10.1016/s0092-8674(01)00193-3. [DOI] [PubMed] [Google Scholar]
- 21.Wittmann T, Wilm M, Karsenti E, Vernos I. TPX2, A novel xenopus MAP involved in spindle pole organization. J Cell Biol. 2000;149(7):1405–1418. doi: 10.1083/jcb.149.7.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Koffa MD, et al. HURP is part of a Ran-dependent complex involved in spindle formation. Curr Biol. 2006;16(8):743–754. doi: 10.1016/j.cub.2006.03.056. [DOI] [PubMed] [Google Scholar]
- 23.Ems-McClung SC, Zheng Y, Walczak CE. Importin alpha/beta and Ran-GTP regulate XCTK2 microtubule binding through a bipartite nuclear localization signal. Mol Biol Cell. 2004;15(1):46–57. doi: 10.1091/mbc.E03-07-0454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.O’Connell CB, Lončarek J, Kaláb P, Khodjakov A. Relative contributions of chromatin and kinetochores to mitotic spindle assembly. J Cell Biol. 2009;187(1):43–51. doi: 10.1083/jcb.200903076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maresca TJ, et al. Spindle assembly in the absence of a RanGTP gradient requires localized CPC activity. Curr Biol. 2009;19(14):1210–1215. doi: 10.1016/j.cub.2009.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Petry S, Groen AC, Ishihara K, Mitchison TJ, Vale RD. Branching microtubule nucleation in Xenopus egg extracts mediated by augmin and TPX2. Cell. 2013;152(4):768–777. doi: 10.1016/j.cell.2012.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bird AW, Hyman AA. Building a spindle of the correct length in human cells requires the interaction between TPX2 and Aurora A. J Cell Biol. 2008;182(2):289–300. doi: 10.1083/jcb.200802005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Oh D, Zidovska A, Xu Y, Needleman DJ. Development of time-integrated multipoint moment analysis for spatially resolved fluctuation spectroscopy with high time resolution. Biophys J. 2011;101(6):1546–1554. doi: 10.1016/j.bpj.2011.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elowitz MB, Surette MG, Wolf PE, Stock JB, Leibler S. Protein mobility in the cytoplasm of Escherichia coli. J Bacteriol. 1999;181(1):197–203. doi: 10.1128/jb.181.1.197-203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nachury MV, et al. Importin beta is a mitotic target of the small GTPase Ran in spindle assembly. Cell. 2001;104(1):95–106. doi: 10.1016/s0092-8674(01)00194-5. [DOI] [PubMed] [Google Scholar]
- 31.Ma N, Titus J, Gable A, Ross JL, Wadsworth P. TPX2 regulates the localization and activity of Eg5 in the mammalian mitotic spindle. J Cell Biol. 2011;195(1):87–98. doi: 10.1083/jcb.201106149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Goshima G, Wollman R, Stuurman N, Scholey JM, Vale RD. Length control of the metaphase spindle. Curr Biol. 2005;15(22):1979–1988. doi: 10.1016/j.cub.2005.09.054. [DOI] [PubMed] [Google Scholar]
- 33.Mitchison TJ, et al. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol Biol Cell. 2005;16(6):3064–3076. doi: 10.1091/mbc.E05-02-0174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ohi R, Burbank K, Liu Q, Mitchison TJ. Nonredundant functions of Kinesin-13s during meiotic spindle assembly. Curr Biol. 2007;17(11):953–959. doi: 10.1016/j.cub.2007.04.057. [DOI] [PubMed] [Google Scholar]
- 35.Loughlin R, Wilbur JD, McNally FJ, Nédélec FJ, Heald R. Katanin contributes to interspecies spindle length scaling in Xenopus. Cell. 2011;147(6):1397–1407. doi: 10.1016/j.cell.2011.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wühr M, et al. Evidence for an upper limit to mitotic spindle length. Curr Biol. 2008;18(16):1256–1261. doi: 10.1016/j.cub.2008.07.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Greenan G, et al. Centrosome size sets mitotic spindle length in Caenorhabditis elegans embryos. Curr Biol. 2010;20(4):353–358. doi: 10.1016/j.cub.2009.12.050. [DOI] [PubMed] [Google Scholar]
- 38.Hara Y, Kimura A. Cell-size-dependent spindle elongation in the Caenorhabditis elegans early embryo. Curr Biol. 2009;19(18):1549–1554. doi: 10.1016/j.cub.2009.07.050. [DOI] [PubMed] [Google Scholar]
- 39.Crowder ME, et al. A comparative analysis of spindle morphometrics across metazoans. Curr Biol. 2015;25(11):1542–1550. doi: 10.1016/j.cub.2015.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Farhadifar R, et al. Scaling, selection, and evolutionary dynamics of the mitotic spindle. Curr Biol. 2015;25(6):732–740. doi: 10.1016/j.cub.2014.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hazel J, et al. Changes in cytoplasmic volume are sufficient to drive spindle scaling. Science. 2013;342(6160):853–856. doi: 10.1126/science.1243110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Good MC, Vahey MD, Skandarajah A, Fletcher DA, Heald R. Cytoplasmic volume modulates spindle size during embryogenesis. Science. 2013;342(6160):856–860. doi: 10.1126/science.1243147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Goehring NW, Hyman AA. Organelle growth control through limiting pools of cytoplasmic components. Curr Biol. 2012;22(9):R330–R339. doi: 10.1016/j.cub.2012.03.046. [DOI] [PubMed] [Google Scholar]
- 44.Moore W, Zhang C, Clarke PR. Targeting of RCC1 to chromosomes is required for proper mitotic spindle assembly in human cells. Curr Biol. 2002;12(16):1442–1447. doi: 10.1016/s0960-9822(02)01076-x. [DOI] [PubMed] [Google Scholar]
- 45.Cai S, Weaver LN, Ems-McClung SC, Walczak CE. Kinesin-14 family proteins HSET/XCTK2 control spindle length by cross-linking and sliding microtubules. Mol Biol Cell. 2009;20(5):1348–1359. doi: 10.1091/mbc.E08-09-0971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Skinner JP, Chen Y, Müller JD. Fluorescence fluctuation spectroscopy in the presence of immobile fluorophores. Biophys J. 2008;94(6):2349–2360. doi: 10.1529/biophysj.107.115642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nelson P. Biological Physics. Freeman; New York: 2013. [Google Scholar]
- 48.Phillips R, Kondev J, Theriot J, Garcia H. Physical Biology of the Cell. 2nd Ed Garland; New York: 2012. [Google Scholar]
- 49.Bray AJ. Theory of phase-ordering kinetics. Adv Phys. 2002;51(2):481–587. [Google Scholar]
- 50.Desai RC, Kapral R. Dynamics of Self-Organized and Self-Assembled Structures. Cambridge Univ Press; Cambridge, UK: 2009. [Google Scholar]
- 51.Stenhammar J, Marenduzzo D, Allen RJ, Cates ME. Phase behaviour of active Brownian particles: The role of dimensionality. Soft Matter. 2014;10(10):1489–1499. doi: 10.1039/c3sm52813h. [DOI] [PubMed] [Google Scholar]
- 52.Needleman DJ, et al. Fast microtubule dynamics in meiotic spindles measured by single molecule imaging: Evidence that the spindle environment does not stabilize microtubules. Mol Biol Cell. 2010;21(2):323–333. doi: 10.1091/mbc.E09-09-0816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Scrofani J, Sardon T, Meunier S, Vernos I. Microtubule nucleation in mitosis by a RanGTP-dependent protein complex. Curr Biol. 2015;25(2):131–140. doi: 10.1016/j.cub.2014.11.025. [DOI] [PubMed] [Google Scholar]
- 54.Klebe C, Bischoff FR, Ponstingl H, Wittinghofer A. Interaction of the nuclear GTP-binding protein Ran with its regulatory proteins RCC1 and RanGAP1. Biochemistry. 1995;34(2):639–647. doi: 10.1021/bi00002a031. [DOI] [PubMed] [Google Scholar]
- 55.Görlich D, Seewald MJ, Ribbeck K. Characterization of Ran-driven cargo transport and the RanGTPase system by kinetic measurements and computer simulation. EMBO J. 2003;22(5):1088–1100. doi: 10.1093/emboj/cdg113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Floer M, Blobel G, Rexach M. Disassembly of RanGTP-karyopherin beta complex, an intermediate in nuclear protein import. J Biol Chem. 1997;272(31):19538–19546. doi: 10.1074/jbc.272.31.19538. [DOI] [PubMed] [Google Scholar]
- 57.Bischoff FR, Ponstingl H. Mitotic regulator protein RCC1 is complexed with a nuclear ras-related polypeptide. Proc Natl Acad Sci USA. 1991;88(23):10830–10834. doi: 10.1073/pnas.88.23.10830. [DOI] [PMC free article] [PubMed] [Google Scholar]