Differences in the emergent coding properties of cortical and striatal ensembles

Abstract

The function of a given brain region is often defined by the coding properties of its individual neurons, yet how this information is combined at the ensemble level is an equally important consideration. In the present study, multiple neurons from the anterior cingulate cortex (ACC) and the dorsal striatum (DS) were recorded simultaneously as rats performed different sequences of the same three actions. Sequence and lever decoding was remarkably similar on a per-neuron basis in the two regions. At the ensemble level, sequence-specific representations in the DS appeared synchronously but transiently along with the representation of lever location, while these two streams of information appeared independently and asynchronously in the ACC. As a result the ACC achieved superior ensemble decoding accuracy overall. Thus, the manner in which information was combined across neurons in an ensemble determined the functional separation of the ACC and DS on this task.

INTRODUCTION

A fundamental goal in neuroscience is to determine the specific function and information processing capabilities of anatomically distinct brain regions. A common approach to this problem is to infer function based on the sensory, motor or cognitive events that evoke neural responses in a given region. While this approach has been invaluable in advancing our understanding of sensory areas, it can be problematic for regions such as the frontal cortex, which is comprised of neurons that are highly multi-modal^1,2. Furthermore, single neuron correlates in frontal regions are often very similar to those found in its efferent targets, such as the dorsal striatum. Perhaps in this case further insight could be gained by considering how neurons collectively respond rather than what they respond to.

How a neuron responds is determined by many factors including its biophysical properties, the input it receives, as well as the structure of the local microcircuit. In the neocortex, pyramidal neurons form massive, interconnected networks with interneurons exerting relatively weak inhibition^3,4. This arrangement favors recurrent excitation and with it, persistent activity patterns through time. Overall, cortical ensemble patterns are usually well-balanced with equal numbers of neurons slightly increasing or decreasing their response to any given event^5,6. By contrast, local regions of the striatum receive strong excitatory inputs from the cortex, which generate responses that are temporally restricted by powerful and widespread inhibition produced by local interneurons^7–9. Accordingly, when recorded from behaving animals, striatal neurons tend to be activated transiently and synchronously^10,11. This synchronized activity may be an asset in the context of movement generation and learning^10,12, but may also be a detriment if it concurrently amplifies variability or ‘noise’ in the neural responses over time¹³. By understanding how these differences might influence the way in which neural ensembles within the frontal cortex versus striatum encode the same information, we hope to gain new insight into their unique functions of these two interrelated brain regions.

To address this issue, we used bundles of tetrodes to simultaneously record from neurons in the anterior cingulate cortex (ACC) and the central portion of the dorsal striatum (DS)^14,15 while rats performed a sequential action task. Although there is already a rich literature on the responses of individual frontal cortex and striatal neurons on such tasks ^16–30, our aim was to better understand how coherent ensemble representations emerged from the activity of single neurons. The task required rats to presses three levers in different temporal orders (termed ‘sequence blocks’ below) to receive reward. We found that even though single neurons in the ACC and DS represented information about sequences and lever presses with similar overall accuracy, the unique way this information was combined across the neurons through time in the ACC yielded far superior overall ensemble sequence decoding accuracy than we observed in the DS.

RESULTS

Behavior

The experimental apparatus is depicted schematically in Fig. S1a and the task structure in Fig. S1b. Different sequences of actions (referred as ‘sequence blocks’) consisted of presses on the same physical levers in different temporal orders. Each lever was distinguished by specific cues temporarily affixed to the area immediately surrounding the levers. The sequence of cues was always the same for a given rat, but the cues were moved to different lever locations for each of the two or three sequence blocks. This task design permitted an examination of the manner in which the two regions encoded objective information about discrete lever press actions versus more abstract information about ‘sequences’ of actions. The rats were required to perform three different sequences of operant responses in a single session, and did so with a high degree of accuracy (% correct response: mean ± SD: 89.2 ± 5.4%). Overall behavioral performance across different sequences in all sessions did not differ (1-way ANOVA, F_2,48=0.22, p=0.80). Across all trials in all sequence blocks, the latencies from the first to the second lever, and those from the second to the third lever were also equivalent (unpaired t-test, t₁₁₀₂=0.89, p=0.38).

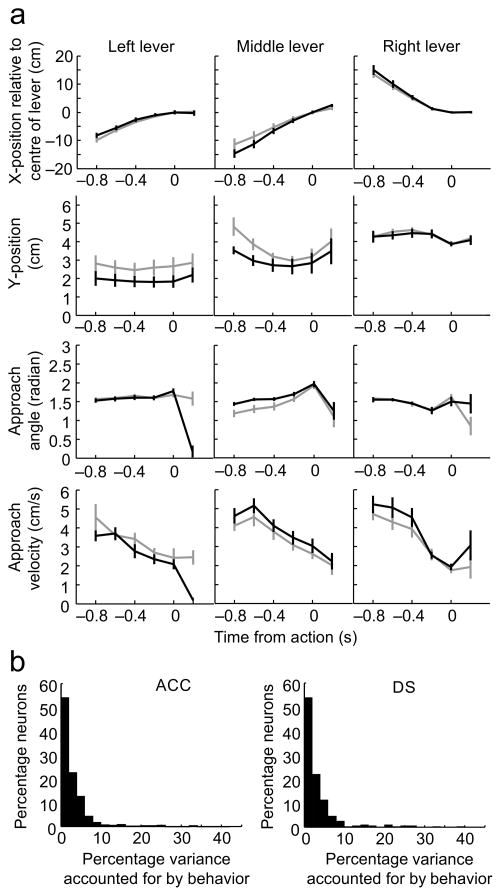
The neural analysis described below will compare neural activity associated with presses on the same physical lever in different sequence blocks. Even though we will focus on presses on the identical physical lever, the lever may be approached at a different body angle, along a different trajectory or at a different velocity in each sequence block. This could be problematic because differences in movements or movement paths leading up to an action can affect ACC activity^31,32. In an attempt to minimize the behavioral variability across sequence blocks, we focused on ‘common segment’ elements. ‘Common segments’ consist of presses on the same lever when approached from the same preceding lever in two sequence blocks. As shown in Fig. 1a, the average X,Y trajectories, the angle of approach to the lever and the approach velocity were similar for common segment lever presses performed in different sequence blocks. None of the behavioral measurements differed significantly across sequence blocks (repeated-measures ANOVA, no effect of sequence for x-position: F_1,78=1.24, p=0.27; for y-position: F_1,78=3.37, p=0.07; for approach angle: F_1,78=0.0063, p=0.94; for approach velocity: F_1,78=0.055, p=0.82; no interaction between time and sequence: for x-position: F_5,390=0.061, p=1; for y-position: F_5,390=0.49, p=0.79; for approach angle: F_5,390=1.91, p=0.093; for approach velocity: F_5,390=1.18, p=0.32).

Figure 1.

Behavior was similar for common segment lever presses in different sequence blocks. a) Values of the behavioral variables for matched pairs of common-segments lever presses. Common-segments involved presses on the same two levers occurring as part of two different sequence blocks (black vs. gray). Each column represents a different physical lever while the 4 rows display the animal’s x-coordinate, y-coordinate, lever approach angle and lever approach velocity in the 6 bins surrounding each lever press (the lever press occurred at time 0 in each panel). The two lines in each panel correspond to the value of each of these variables in one of the two sequence blocks. During these intervals, the animals’ location and movement were highly similar across sequence blocks but were quite different across the three physical levers. Error bars indicate s.e.m. b) Distributions of the percentage of firing rate variance accounted for when the behavioral variables shown in (a) were used as factors in a multiple linear regression analysis, performed on all ACC neurons (left panel) or all DS neurons (right panel). The residual matrices represent the iFR values that remained after the impact of these behavioral variables has been removed. These matrices will be used in the analyses shown in subsequent figures.

While similar, they were not completely overlapping and in order to determine whether this remaining behavioral variability may have impacted the neuronal responses, the behavioral variables shown in Fig. 1a were used as factors in a multi-linear regression model performed individually on each neuron (see Methods). The analysis revealed that the total amount of variability in firing rate that could be accounted for by the 5 factors was on average 3.04% for ACC neurons and 3.39% for DS neurons. In fact, in only 3.99% of the ACC neurons and 5.64% of DS neurons did the behavioral variables collectively account for more than 10% of firing rate variance during the common segment lever press periods (Fig. 1b). Among these neurons, the percentages of variance accounted for by the model did not differ (unpaired t-test, t₃₉= −1.21, p=0.23). While this percentage would likely be larger if all task periods had been considered, at least for the common segment lever press periods, any impact of the differences in behavior across sequence blocks was relatively small for most individual neurons.

Single neuron correlates of sequence differentiation

The selectivity of single ACC and DS neurons for sequences was assessed using signal detection approach by calculating for each neuron a selectivity index (see Methods). The SI for ‘sequence’ was calculated by comparing the firing rates in the 6 bins surrounding common segment lever presses performed in different sequence blocks. Even though the effects of behavioral variability on instantaneous firing rates (iFRs) were small for the common segment periods (Fig. 1b), we nevertheless tested whether they could impact SI-based sequence discrimination. We re-calculated the SI values using the residual firing rate matrix generated from the multi-linear regression analysis performed above since in the residual matrix, the impact of these variables had theoretically been regressed off.

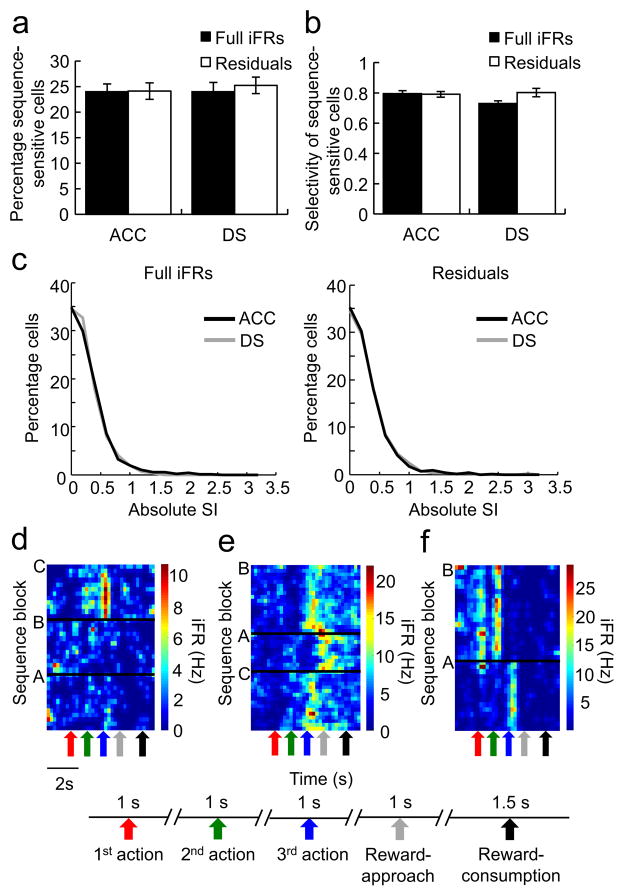
Across all neurons recorded (N_ACC=637, N_DS=351), 24.0% of individual ACC neurons and 24.0% of individual DS neurons were selective for sequence (i.e. had absolute SI values >=0.5), a difference which was not statistically significant (2-way ANOVA, no effect of region: F_1,60=0.11, p=0.74, unequal N HSD test: ACC vs. DS: p=1; Fig. 2a). When the calculation of SIs was repeated using the residual matrices, 24.1% of ACC neurons and 25.2% of DS neurons were found to be sequence selective. The differences in the number of sequence-selective neurons detected using the full versus residual matrices were not significant for the ACC (2-way ANOVA, no effect of regression: F_1,60=0.17, p=0.69, unequal N HSD test: ACC original vs. residuals: p=1), or the DS (unequal N HSD test: p=0.96). In order to test the strength of the sequence signals, we compared the SIs of all the neurons possessing SI values >=0.5. The average SIs of these putatively sequence-selective neurons did not differ between the two regions (ACC=0.79; DS=0.73; 2-way ANOVA, F_1,916=1.34, p=0.25, unequal N HSD test: ACC vs. DS: p=0.34; Fig. 2b). Furthermore, the mean SI values of these neurons were similar if they were calculated using the full or residual matrices (unequal N HSD test, original vs. residuals for ACC: p=1; for DS: p=0.24; Fig. 2b). These results implied that the ACC and DS had remarkably similar numbers of neurons that were equally selective for sequence differentiation. The extraordinary similarity in the distribution of SI sequence values for the two regions is evident from Fig 2c. Examples of two ACC neurons and a DS neuron that exhibited significant sequence selectivity are shown in Fig. 2d, e and f respectively.

Figure 2.

No regional differences in the way individual neurons responded to presses in different sequence blocks or on different physical levers. a) The ACC and DS had a similar proportion of neurons showing significant responsiveness for sequences calculated using the original iFR matrices (left, ACC: black bar, DS: white bar) or the residual iFR matrices (right, ACC: black bar, DS: white bar). Error bars indicate s.e.m. b) Sequence-sensitive neurons from the ACC (black) and the DS (white) had similar absolute selectivity indices (SI), calculated either using the full iFR matrices (left, ACC: black bar, DS: white bar) or the residual iFR matrices (right, ACC: black bar, DS: white bar). Error bars indicate s.e.m. c) The distributions of absolute SIs based on either the full iFR matrices (left) or the residual iFR matrices (right) across the neuronal populations in the ACC (black) and DS (gray) overlap. d) Heat relief iFR plot of an example neuron from the ACC that responded to only one type of lever press in one sequence block. e) An example ACC neuron that responded to the 3^rd lever press (and reward) in a sequence-dependent manner. f) Heat relief iFR plot of an example neuron from the DS that responded to only one type of lever press in one sequence block. Note that presses on the middle lever in one sequence block (as the 1^st action) consistently elicited responses from the neuron, whereas presses on the same lever in the other sequence block (as the 2^nd action) did not.

Sequence information by neurons versus ensembles

Next we asked how single neurons compared to ensembles in terms of sequence differentiation and whether this relationship varied between the two regions. To compare the sequence decoding properties of single neurons versus ensembles on an equal footing, a modified Receiver Operator Characteristic (ROC) analysis approach was employed. The ROC analysis has an advantage in situations where the distributions are unknown because it assesses performance over a range of threshold values rather than being forced to evaluate differences at a single threshold level relative to some theoretical distribution. The signal detection characteristics of individual ACC and DS neurons were investigated by creating for each neuron a sequence-specific template for the 1.4s period leading up to and including a common segment lever press in half of the trials in one sequence block. As the data were binned at 200ms, the template was a vector of 7 instantaneous firing rate (iFRs) values for each single neuron. The template was then moved through both sequence blocks and bin by bin correlations were calculated. This process was repeated using templates created from different groups of trials and the results averaged. A ‘true positive’ or ‘hit’ occurred when a correlation score larger than a threshold value was found in the lever press interval of the remaining half of trials of the sequence block from which the original template was constructed. A ‘false alarm’ occurred when a correlation score larger than the threshold value was found between the template and the ‘common segment’ lever presses performed in the alternate sequence block. If hits and false alarms occur at the same rates at all thresholds, the ROC curve would be a straight-line with a 45° slope, with an area-under-the-curve (AUC) of 0.5.

In order to compare ensembles to single neurons using this approach, a similar analysis was performed, except in this case rather than the vectors being 7 iFR values, they were N × 7 iFR values, with N being the number of recorded neurons per session. Because the templates were much larger than those of any individual neuron, one would expect a low probability of recurrence of a similar ensemble activity state pattern, thereby reducing false alarm rates. Concurrently, the larger templates would be equally disadvantageous as it is equally unlikely that a match between the template and activity patterns during the remaining half of the trials in the same sequence block (i.e. hits) would ever occur. Because the ROC analysis weighs hits versus false alarms in this way, it is an effective means to directly compare signal detection of single neurons versus ensembles. It is important to emphasize that simply having a larger template confers no advantage on its own. As proof of this, the performance of the ensembles following random time block shuffles is given by the thick dashed lines in each panel (Fig. 3a, b) which are essentially at 45°.

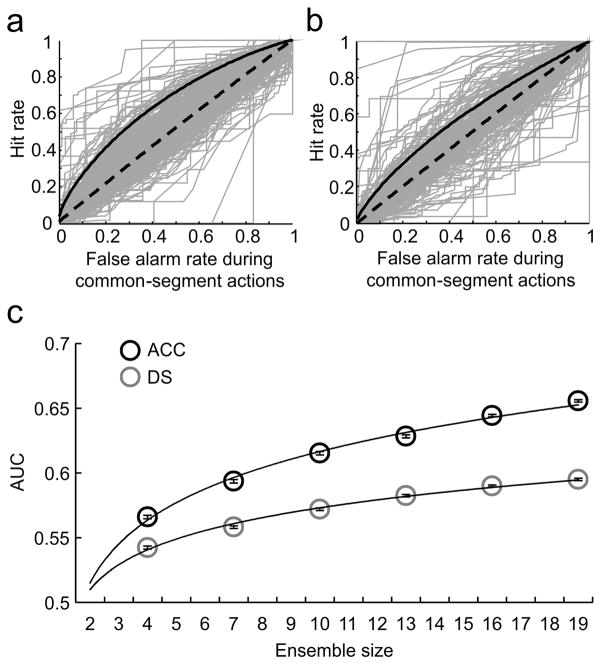
Figure 3.

Comparison of the signal detection characteristics of single neurons versus ensembles. a) ACC single unit ROCs (gray curves) were constructed from hit and false-alarm rates during the ‘common-segment’ periods for each neuron. Hits and false-alarms were based on running correlations between a neural activity template derived from half of the trials in one sequence block and activities in the remaining half trials in the same sequence-block (‘hits’) or with activities in the alternate sequence-block (‘false alarms’). The ensemble ROC (solid black line) detected the correct sequence better than the majority of the single units or the time-bin shuffled ensemble controls (dashed black line). b) DS single unit ROCs (gray curves) were constructed from hit and false-alarm rates during the common-segments using the same methods as in (a). The ensemble ROC (solid black line) detected the correct sequence better than its shuffled control (dashed black line) but was eclipsed by many more single units than in the ACC. c) Ensemble decoding performance improved with increasing ensemble size in both the ACC and DS, but at a much higher rate in the ACC. Ensembles of different sizes were randomly drawn from ACC and DS neuronal populations, and the AUCs were calculated from the sequence signal-detection ROCs. This process was repeated 100 times at each ensemble size for each region, and the mean and s.e.m. are plotted (ACC: black circles, DS: gray circles). The best fitting trend lines were power functions (ACC: top, DS: bottom), which explained more than 99% of the variance.

For sequence decoding, as shown in Fig. 3a, the hit:false alarm ratios for ACC ensembles (solid black curve) were higher than 96.77% of individual neurons (gray curves) during the ‘common segment’ periods of the two sequence blocks. In contrast, only 9.12% of individual DS neurons (gray curves, Fig. 3b) were superior to the DS ensembles for the same periods (solid black curve, Fig. 3b). Overall, single DS neurons were superior to DS ensembles significantly more often than was the case for single ACC neuron compared to ACC ensembles (Pearson’s chi-square: χ² =12.1, df=1, p=0.0005). It is clear from Fig. 3a, b that the reason for this difference is not that DS neurons were superior to ACC neurons on a single neuron basis, in fact they were not (independent-sample t-test: t₉₄₁=1.59, p=0.11), instead, when DS neurons were combined into ensembles, their performance was significantly worse than when ACC neurons were combined into ensembles (independent-sample t-test: t₃₁=4.44, p=1.1×10⁻⁴).

To examine the relative superiority of ACC ensembles for sequence decoding in greater detail, neurons were selected randomly from the population of 637 ACC and 351 DS neurons to create ensembles of different sizes and then we performed the ROC analysis on each ensemble. Every data point shown in Fig. 3c is the average of 100 draws. This analysis reveals that the ACC ensembles achieved superior signal detection across all ensemble sizes. Additionally, the steeper ACC curve, in comparison to the DS curve, indicated that signal detection improved progressively as more ACC neurons were added. Based on the functions fit to the data, we extrapolate that on average a randomly drawn ensemble of 112-neurons would be required for the DS to achieve the same level of sequence-signal detection as an ensemble of 19 neurons drawn randomly from the ACC. This is quite striking when one considers that individual neurons in the two areas performed equally on a per neuron basis (Fig. 2a–c). Paradoxically, the DS is at a disadvantage when its neurons are combined into ensembles for sequence decoding.

Unique activity states represent sequence information

In order to understand how ACC ensembles achieved better ROC performance, we probed more deeply into the nature of the ensemble codes themselves. Fig. 4a and b show 3-dimensional representations of the multiple single unit activity (MSUA) spaces from representative ACC and DS ensembles respectively. As illustrated in these plots, ensemble activity states during lever presses in one sequence block were tightly clustered but shifted to another region of the MSUA space when the same lever was pressed as part of a different sequence block. A shift in the MSUA space means that the ensembles entered a distinct activity state pattern for each sequence block.

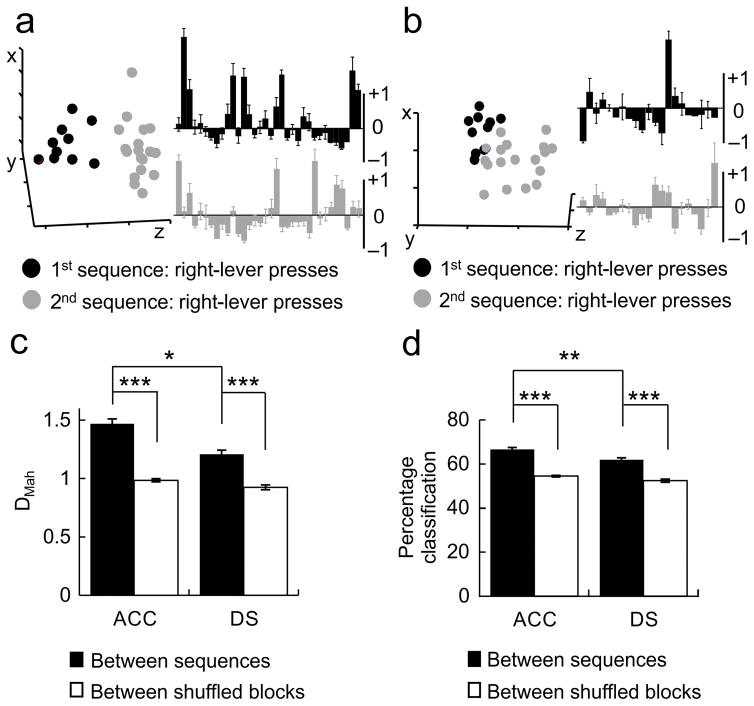
Figure 4.

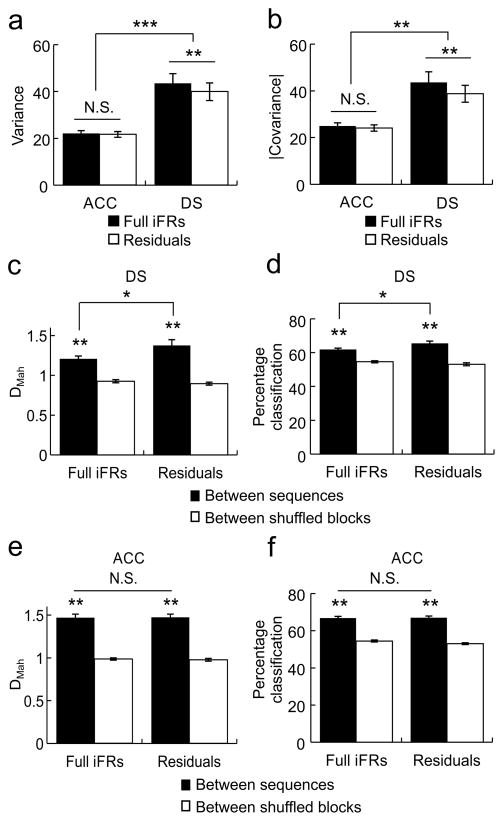
Sequence information is represented as differences in ensemble activity state patterns in both the ACC and DS. a) (Left) An example multiple single-unit activity (MSUA) space constructed from the iFRs of all 34 ACC neurons recorded during a single session, visualized in 3 dimensions using multidimensional scaling. Each dot represented a population vector containing the activities of the entire ensemble during right-lever presses. Dots were colored black if the activities were associated with one sequence block, gray if associated with the alternate sequence block. (Right) The average or prototypical activity of ACC neurons recorded during right lever presses in the two sequence blocks. Each bar represents the average normalized iFR for each neuron across all right lever presses in sequence block A (top, black bars) or sequence block B (bottom, gray bars). Mean ± s.e.m. b) (Left) An example MSUA space constructed from the iFRs of all 20 DS neurons recorded simultaneously during the same session as in (a). (Right) The prototypical activity of DS neurons recorded during right lever presses in the two sequence blocks. c) When common-segment lever press periods were examined, the average separation (D_Mah in MSUA space) between lever presses performed during different sequence blocks (black bars) were significantly larger than shuffled control blocks (white bars). d) A leave-one-out prediction procedure based on D_Mah was used to classify trials as belonging to one of two sequence blocks. Classification accuracy for the actual data (black bars) was significantly better than for trial shuffled data (white bars) for both the ACC and DS, although ACC ensembles performed significantly better than DS ensembles. *p<0.05, ** p<0.001, *** p<0.00001.

In order to quantify the differences in firing patterns associated with different sequence blocks, the Mahalanobis distance (D_Mah) ^5,33 was calculated between population vectors in the MSUA spaces. The D_Mah between the activity states associated with common-segment lever presses in different sequence blocks was significantly larger than the D_Mah between shuffled control blocks (Kruskal-Wallis test: F_3,140=96.34, p=9.5×10⁻²⁰), for both the ACC (Tukey’s test, p=0) and the DS (Tukey’s test, p=1.0×10⁻⁶; Fig. 4c). Once again the ACC was superior, as the D_Mah between the neural patterns associated with presses on the same lever occurring in different sequence blocks was significantly larger for ACC ensembles than for DS ensembles (Tukey’s test, p=0.023).

In order to show that these activity state patterns functionally important for sequence decoding, a leave-one-out variant of the D_Mah analysis was applied to the common-segment lever press periods. Using this form of Mahalanobis discriminant analysis (MDA), the correct sequence-block could be accurately predicted in 66.6% of cases for ACC ensembles and in 61.9% of cases for DS ensembles both of which were significantly better than when the procedure was repeated using shuffled sequence-block assignments (2-way ANOVA, main effect of sequence F_1,140=204.89, p=1.8×10⁻²⁹, main effect of region F_1,140=20.53, p=1.3×10⁻⁵; Fig. 4d). More importantly, ACC ensembles classified each specific sequence with higher accuracy than did DS ensembles (Tukey’s test, p=0.00022).

Regional differences in ensemble variance/covariance

The sequence classification and decoding measures used above weigh differences between the patterns (i.e. the ‘signal’) relative to the variance and covariance in the patterns across time. Therefore, ACC ensembles could be superior to DS ensembles either in terms of the strength of their ‘signals’ or because they exhibited less variance/covariance through time. In order to disambiguate these two possibilities we examined each separately.

In order to assess potential difference in ‘signal’ strength we calculated the Euclidean distance (D_Euc) rather than the D_Mah between points in the MSUA spaces associated with each sequence block. D_Euc and D_Mah both measure the distance between the sets of points in the MSUA space but differ in that D_Euc is a simple measure of the geometric distances between the centers of clusters, whereas D_Mah weighs these distances relative to the individual variances and pooled covariance of the two sets of points. Therefore, D_Euc represents a pure measure of the ensemble signal independent of variance/covariance. Unlike D_Mah, D_Euc between common-segments in different sequence blocks did not differ between the ACC and the DS ensembles (independent-sample t-test: t₇₀ = −1.09, p=0.28) suggesting that the difference between the ACC and DS was not due to differences in the sequence ‘signal’. This was not unexpected given the similarities in sequence differentiation by single ACC and DS neurons described above.

Therefore, the differences in decoding accuracy must be related to the differences in the variance/covariance between the two areas. Accordingly, the variance across bins within a trial was indeed higher in the DS than the ACC (post hoc Tukey’s test, p=0.00015; Fig. 5a, dark bars) as was the absolute covariance (post hoc Tukey’s test, p=0.00017; Fig. 5b, dark bars).

Figure 5.

Consistency of sequence encoding in the ACC and DS within behavioral epochs. a) Ensemble variance calculated based on activities during the time bins within each pair of common-segment lever presses was higher in the DS than in the ACC. Ensemble variance calculated on the residual iFR matrices (right, white) was smaller than the variance calculated from full iFR matrices (right, black) in the DS, but the two were equivalent in the ACC (left bars). b) Ensemble covariance was also greater in the DS (right) than in the ACC (left). Ensemble covariance calculated on the residual iFR matrices (white) was smaller than the covariance calculated from full iFR matrices (black) in the DS, but the two were equivalent in the ACC. c) In ACC ensembles, between-sequence D_Mah calculated using the residuals from the initial behavioral regression was equivalent to that calculated using the full iFRs, and both were greater than shuffled controls. d) In ACC ensembles, between-sequence leave-one-out MDA using the residual iFR matrices (right) was equivalent to that calculated using the full iFR matrices (left). e) In contrast to the ACC, in DS ensembles, D_Mah calculated using the residual iFR matrices from the initial behavioral regression (right) was greater than that calculated using the full iFR matrices (left), although both the full iFRs and the residuals still contained robust sequence information. f) In DS ensembles, sequence classification using the residual iFR matrices (right) was more accurate than when calculated using the full iFR matrices (left). Error bars indicate s.e.m. *p<0.05, ** p<0.001, *** p<0.00001

In addition, we found that a significant portion of the variance and covariance was related to the coordinated firing in response to behavioral events in the DS because variance (repeated measures ANOVA, main effect of regression: F_1,70=18.3, p=5.8×10⁻⁵, Tukey’s test: p=0.00017; Fig. 5a, right bars) and covariance (repeated measures ANOVA, effect of regression: F_1,70=19.7, p=3.4×10⁻⁵; Tukey’s test: p=0.00017; Fig. 5b, right bars) were both lower in the residual matrices than in the full iFR matrices. In contrast, this was not true for the ACC, as the variance (Tukey’s test: p=0.88) and covariance (Tukey’s test: p=0.77) were both similar in the full and residual matrices from the behaviorally derived multi-linear regression discussed previously (Fig. 5a,b, left bars). Thus the responses of DS neurons to the behavioral variables contained more coordinated variation throughout a given action than did ACC neurons.

The higher degree of covariance in the responses of DS neurons to the behavioral variables may have contributed to the poorer performance of the DS on the ensemble measures of sequence decoding. To test this possibility we repeated the sequence discrimination analysis above using the residual matrices. This indeed improved the performance of DS ensembles as it led to a significant increase in the D_Mah between common segment lever presses (repeated-measures ANOVA and post hoc Tukey’s test: residuals>full matrix: p=0.00039; Fig. 5c) and improved sequence decoding accuracy using MDA (repeated-measures ANOVA and post hoc Tukey’s test: residuals>full matrix: p=0.015; Fig. 5d). In contrast, repeating the same analysis using the residual ACC matrices had no effect on the ability of ACC ensembles to separate common segments lever presses in different sequence blocks (repeated-measures ANOVA and post hoc Tukey’s test: residuals=full matrix: p=0.82; Fig. 5e) nor did it have any effect on MDA based decoding accuracy (repeated-measures ANOVA and post hoc Tukey’s test: residuals=full matrix: p=0.99; Fig. 5f). Therefore, the firing rate variance of DS neurons associated with the measures of behavioral variability shown in Fig. 1 contributed to its inferior sequence decoding at the ensemble level. This makes intuitive sense given that the levers being compared in the two sequence blocks were identical and therefore the stronger the neurons encoded this commonality, the less likely they would be able to differentiate between the two sequence blocks.

Regional differences in lever press action encoding

The previous analysis suggested that relative to the ACC, DS ensembles more strongly tracked the commonalities associated with pressing the same physical levers in different sequence blocks. In order to test whether the spatial lever decoding ability, the same type of ROC-based analysis described above was again employed. In this case, a template was created by randomly selecting half of all presses on a given physical lever. A ‘hit’ occurred when a correlation score larger than a threshold value was found in the remaining half responses on the same lever, while a ‘false alarm’ occurred when a correlation score larger than the threshold value was found between the template and the presses performed on a different lever. This procedure was performed both on single units as well as ensembles as outlined above for the case of sequence decoding.

In support of the prediction, the decoding of spatial lever identity by DS neurons was indeed superior to that of ACC neurons on a single-neuron basis (2-way ANOVA, main effect of region: F_1,2853=29.78, p=5.3×10⁻⁸). Yet surprisingly, in spite of this, ACC ensembles nevertheless matched DS ensembles in lever-decoding ROC performance (2-way ANOVA, no effect of region: F_1,93=0.70, p=0.40). Likewise the D_Mah between population vectors associated with responses on the 3 different levers were similar between regions (2-way ANOVA, no effect of region: F_1,194 =1.08, p=0.30; both regions discriminated among the 3 levers significantly better than shuffled controls, 2-way ANOVA, F_1,194 =497.3, p=2.0×10⁻⁵⁵). Similar results were also obtained using MDA (2-way ANOVA: F_1,194=770.4, p=1.8×10⁻⁶⁹; post hoc Tukey’s test: DS=ACC, p=0.63). Therefore, even though DS neurons were indeed better than ACC neurons in terms of their ability to differentiate unique lever press actions, this advantage did not translate to the ensemble level. It would appear that on this task, the signals carried by individual neurons tended to be less synergistic when combined in the DS relative to the ACC.

ACC vs. DS in the timing of sequence and lever signals

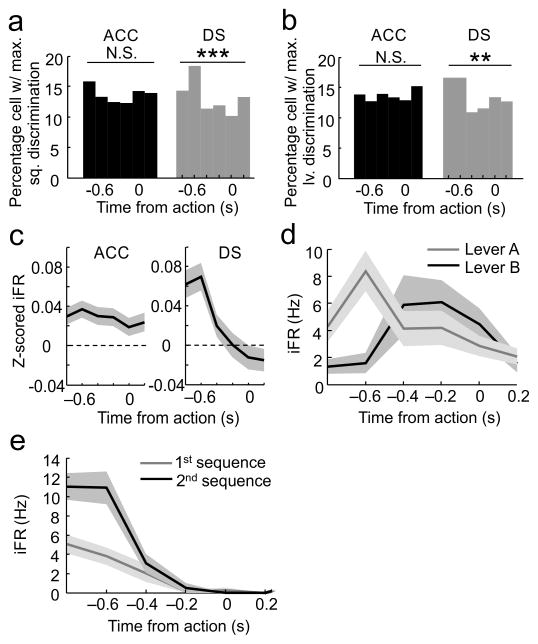
What is it about the DS that resulted in this type of counteractive ensemble effect? One factor may relate to the timing of different signals. To explore this issue, a rolling F-statistic was used to find the proportions of neurons that exhibited their maximal firing differentiation of sequence versus lever identity within each trial. The proportions of ACC neurons differentiating sequences (Pearson’s Chi-square: χ²=9.28, df=5, p=0.098; Fig. 6a, left bars) or lever presses (Pearson’s Chi-square: χ²=4.79, df=5, p= 0.44; Fig. 6b, left bars) was equal for all time bins within a trial. Furthermore, there was no relationship between the bins in which the maximal differentiation among levers and the bins where the maximal discrimination between sequences occurred within a trial (Spearman’s rho: r=0.024, p=0.36). In other words, the sequence and lever press signals evolved independently in the ACC within each trial.

Figure 6.

Comparison of the timing of maximal sequence and lever differentiation in ACC and DS ensembles. a) The strength of sequence discrimination (based on rolling F-statistic) fluctuated across bins in the DS population (right bars), where the largest proportion of neurons exhibited maximal sequence specific firing differentiation around 0.6s prior to lever press while the smallest proportion exhibited sequence specific firing differentiation at around the actual lever press response itself. Such was not the case in the ACC (left bars), where an equal percentage of neurons exhibited maximal sequence-specific firing differentiation in each of the 6 bins. b) The strength of lever discrimination (based on rolling F-statistic) fluctuated across bins in the DS (right bars), where the largest proportion of neurons exhibited maximal lever differentiation 0.6s prior to lever press. Such was not the case in the ACC (left bars), where an equal percentage of neurons exhibited maximal lever-specific firing differentiation in each of the 6 bins. c) Average level of activity across time bins leading up to all lever presses in all sequence blocks and sessions, in all ACC neurons (left) and all DS neurons (right) respectively. d) An example of a DS neuron displaying maximal differentiation between sequences at approximately 0.6s prior to presses on the same lever. e) An example of a DS neuron reaching maximal differentiation between levers at approximately 0.6s prior to lever presses within the same sequence block. Shading in c–e indicates s.e.m. *p<0.01, **p<0.001, *** p<0.0001.

In marked contrast, the proportions of DS neurons maximally differentiating between sequences (Pearson’s Chi-square: χ²=21.62, df=5, p=0.00062; Fig. 6a, right bars) or between levers (Pearson’s Chi-square: χ²=17.98, df=5, p=0.0030; Fig. 6b, right bars) were highly non-uniform across the bins within each trial. More importantly, there was a small but significant correlation between the bins where the greatest proportions of DS neurons maximally differentiated sequences and lever press actions (Spearman’s rho: r=0.097, p=0.013). Specifically, the maximal point of differentiation for both sequences and lever press actions occurred concurrently at ~600ms prior to the actions in the DS (Fig. 6a, b). This was also close to the point where generalized activity was also highest (Fig. 6c). This effect can be seen in the example DS neuron responses shown in Fig. 6d,e.

Collectively, these results can be summarized as follows. In order to make a correct choice on this task a rat must maintain a representation of the overall sequence block as well as the actual physical lever to be pressed. DS neurons collectively exhibited large firing rate fluctuations in response to the specific lever press actions and this coherent fluctuation appeared at the same point within each trial where the ensembles maximally differentiated sequence blocks. Because the two streams of information were at odds during common segment lever presses of this task, the decoding accuracy for each stream suffered. In contrast, ACC ensembles excelled not because they had more neurons selectively coding the correct action or sequence block, but because the two streams of information remained independent across neurons through time.

DISCUSSION

Previous studies have observed robust responses of single neurons in the frontal cortex and striatum during actions^{16–22,24,27,34,35}. The present study focused on how information about sequential actions carried by single neurons was combined into ensemble codes and whether this differed in the ACC versus the DS. The results showed that the key factor that separated the two regions was the manner in which information was combined across the population through time rather than specific responses of single neurons.

At the single neuron level, ACC and DS neurons consistently performed similarly across various measures including single neuron sequence selectivity and single neuron ROC performance. However, DS neurons performed more poorly on almost all ensemble-based measures of sequence differentiation, including the separation of the sequence activity state patterns based on D_Mah, MDA and ROC performance. The one exception was the separation of the activity state clusters using D_Euc. This was the only measure of pure sequence differentiation (i.e. ‘signal’) that was completely independent of variance/covariance across time. DS neurons tended to exhibit larger variance and covariance and respond more as a collective. The point where the largest proportion of DS neurons tended to maximally differentiate sequence identity was also the point where most neurons differentiated lever identity and this coincided with the point of maximal overall activity. Since in our task, the sequences were different yet the actual physical levers pressed were identical across the two sequence blocks, if sequence and lever signals emerged simultaneously but transiently across the ensemble, the decoding of either would suffer. By contrast in ACC ensembles, information about the physical lever was functionally independent from the information about the overall sequence (Fig. 5e, f) and as a result, sequence and lever differentiation in the ACC remained high across all 6 bins rather than being concurrently maximal in just one or two. It is also important to emphasize that this uniformity through time was not a result of persistent firing in individual ACC neurons that has been well characterized in the frontal cortex. Rather it was because the neurons had mutually independent time courses and were thereby able to tile all seven time bins as a population. The asynchrony in the ACC population allowed multiple conflicting sources of information to co-exist, while the synchronous nature of DS activity pitted different representations against each other within a small time window. Of course these differences between the two areas were not absolute, but were nevertheless large enough to significantly impact the accuracy of the representations that emerged at the ensemble level.

While generally disadvantageous in terms of sequence and lever decoding on this particular task, the inherent synchrony in the DS is vitally important for functions mediated by the DS such as movement generation and learning^12,36. The differences in persistence and synchrony between the ACC and DS are therefore functionally important and likely reflected the general properties of the two regions. The larger synchrony of DS over ACC neurons¹⁰ may be related to the local circuitry within the striatum itself that is able to transform tonic excitatory cortical drive into alternating and synchronized activity patterns³⁷. In addition, because a small pool of interneurons are able to exert powerful control over many medium spiny neurons (MSNs), it is possible that changes in a single interneuron can effectively turn off a large group of MSNs⁸. A second important difference we observe between the ACC and DS is the long-tailed firing rate distributions exhibited by populations of DS neurons (Fig. S3, gray curve). Long-tailed distributions are consistent with firing at low rates interspersed with brief periods of very high activity. This activity profile is likely a consequence of the biophysical properties of MSNs that require large synchronous inputs from the cortex in order to fire since they possess hyperpolarized resting potentials and strong K+ currents that suppress all but the strongest synchronous inputs^38,39. The firing characteristics we observed in the DS population are therefore consistent with the known physiology and anatomy of the region.

The increased variance and covariance across DS neurons may help tune DS neurons to promote a single coherent but intermixed signal at a very specific point in time prior to an action. In contrast the ACC may persistently maintain a conceptual representation of the general plan or action strategy that can be independent from the actual actions involved. Therefore both regions are endowed with features that work together to allow the animal to consider the entirety of ongoing experience and yet respond in a decisive manner.

METHODS

Animals

Four experimentally naïve male Long-Evans rats (450–550g) were housed in a facility with 12hr light-dark cycle, with all training and recording taking place during the light cycle. For the duration of the behavioral experiments, the rats were food-restricted to just below 90% of their free-feeding weights. Feeding took place in the home cage after their daily training/recording sessions, and water was available ad libitum in the cages at all times. The animals were single-housed to accommodate the food restriction procedures, recovery from surgery and maintenance of the implant. All procedures were carried out in accordance with the Canadian Council of Animal Care and the Animal Care Committee at the University of British Columbia.

Apparatus

Within a large Plexiglas box (25″×18″), a main panel was installed with 3 levers designated Lever1 to 3 from right to left (Fig. S1A). On any given day of sequence training, a unique tactile object (velcro, cardboard or soft foam) was stuck to the lever panel (but not on the lever itself) and the area on the floor immediately in front of the lever panel to symbolize the order in which the 3 levers should be pressed. An area of 25″×13″ was left for the rat to move freely. On the opposing-side wall, a food cup was located at the centre, with each delivery of reward accompanied by a pure tone. Retractable levers and pellet dispenser were controlled and recorded with a PC via a Med Associate interface system (St.Albans, VT, USA).

Sequence task

All training and recording took place during the light cycle. The naïve subjects were first trained on an FR1 schedule to press each of the 3 levers. A minimum of 60 presses within 0.5hrs, with no less than 15 presses on each lever was required prior to the rat moving on to the next stage of training. After 3–5d of FR1 training, the rats were trained on sequence A: Right Lever→Middle Lever→Left Lever. Thereafter they were trained on sequence B (Middle Lever→Left Lever→Right Lever) and finally sequence C (Left Lever→Right Lever→Middle Lever). In each case food reward was given after the correct lever press in the sequence. A lever retracted only when it was pressed in the correct order, and remained extended in the event of an error. For training on all sequences, the percentage of correct response on the 3rd item of the sequence had to reach 75% before moving on to the next trained sequence. The order of lever presses in each sequence was given by tactile objects placed on the panel and the floor in front of the levers. For a given animal, each object consistently designated a single serial position. At any one of the 3 stages of single-sequence training, if after 3 days of training, the animal still hadn’t reached criterion and if day-to-day improvement ceased, a delay-punishment protocol was introduced to extinguish errors made on the 3^rd lever of the given sequence. Specifically, if the 3^rd lever was pressed before the 1^st lever, all levers retracted and a 10-s time-out period ensued. This training continued until the animal reached criterion performance. When the criterion had reached criteria on all 3 sequences, the rat was surgically implanted and allowed 10d to recover. After recovery, 2–3 refresher sessions on each sequence were given before the first multi-sequence test day.

On the multi-sequence test days, the animals had to perform a minimum of 10 trials on each sequence at or above criterion, and switch from sequence to sequence in one of three possible orders pseudo-randomly: Sequence C→Sequence B→Sequence A, Sequence B→Sequence A→ Sequence C, or Sequence A→Sequence C→Sequence B. In-between sequences, the animals were taken out of the box to allow for rearrangement of the tactile objects. Because the task was self-paced, and because it always took the animals more than 1s between lever presses, we defined each lever-press epoch with reference to the time stamp of the lever press. In all but the ROC analysis, we used six 200-ms time bins, including four bins prior to the LP bin, the LP bin itself, plus one bin after the LP. In the ROC analysis, we included one more bin after the 6-bin epoch to have 7 numbers for the purpose of having meaningful and reliable correlation coefficients. In addition, after the last lever-press epoch in each trial, a 1-s period was defined as the ‘reward approach’ period, during which the animals ran from the last lever towards the food cup, prior to consuming the reward. Neural activities during reward approach and consumption were shown in single neuron examples (Fig.2d–f) but were not used in any analyses.

Surgery

Stereotaxic surgeries were performed with sterilized-tip procedures under anesthesia by isoflurane. NSAIDs analgesic, antibiotic, and a local anesthetic, were given before incision. One elliptical-shaped craniotomy was made centered at: AP: +3.2mm, ML: +1.0mm, and another craniotomy was made centered at AP: +1.2mm and ML: +3mm. Once the dura mater was retracted, the bottoms of the two bundles of 8 30-gauge tubes, containing a total of 16 tetrodes, were placed on the cortical surface. The bundles were of cylindrical shape with a bottom radius of ~0.4mm, and were angled medially by ~15 degrees. The implants were fixed with bone screws and dental acrylic. At the end of the surgery, tetrodes in the anterior bundle were extended by ~1.4mm into the brain to enter the anterior cingulate cortex (ACC), and tetrodes in the posterior bundle were extended by ~3mm to enter the dorsal striatum (DS). Animals were given 10d to recover. Prior to each recording session, small adjustments were made with the hyperdrives to maximize the number of neurons recorded.

Acquisition of electrophysiological data

For data acquisition, EIB-36TT with pre-amplifier (Neuralynx Inc., Bozeman, MT, USA), connected to the extracellular electrodes, were plugged into HS-36 headstages and tether cables (Neuralynx Inc., Bozeman, MT). Signals were converted by a Digital Lynx 64 channel system (Neuralynx Inc., Bozeman, MT) and sent to a PC workstation, where electrophysiological and behavioral data were read into Cheetah 5.0 software (Neuralynx Inc., Bozeman, MT). Files were then read into Offline Sorter (Plexon Inc., Dallas, TX) for spike sorting, based on visually dissociable clusters in 3D projections along multiple axes for each electrode of a tetrode (peak and valley amplitudes, peak-to-valley ratio, principal components and area). Sorting was confirmed by examining auto- and cross-correlations, and ANOVAs were conducted from the 2D and 3D projections. Spike timestamps were then read into Matlab (Mathworks Inc., Natick, MA) for all further analysis.

Histology

At the end of the studies, the animals were deeply anesthetized using urethane i.p. injection, and a 100μA current was passed through the electrodes for 30s. Animals were then perfused with a solution containing 250ml 10% buffered formalin, 10ml glacial acetic acid, and 10 g of potassium ferrocyanide. This solution causes a Prussian blue reaction, which marks with blue the location of the iron particles deposited by passing current through the electrodes. The brains were then removed and stored in a 10% buffered formalin/20% sucrose solution for at least 1 week, before being sliced and mounted to determine precise electrode locations. Since multiple sessions were recorded from individual animals the precise recording locations could not be derived from electrode lesions, but all electrode tracks were inferred between the entrance point and the dyed spot. Representative recording sites are shown in Fig. S2a, c, and the ranges of recording are shown in Fig. S2b, d.

Analysis

Instantaneous firing rate (iFR)

A total of 33 large ensembles were collected from 4 rats that acquired all 3 sequences and successfully switched among them within a given session. To obtain an estimate of the neural firing rate for each isolated cell i as a function of time bin t, r_i(t), for each spike train in each 200-ms bin, the instantaneous firing rates (iFRs) were calculated as the reciprocals of the inter-spike intervals, convolved with 20-ms Gaussian kernels and then averaged ^5,40. Neurons firing less than 0.14 Hz were excluded from further analysis, because the sample of spikes was too small (250 or less) to be reliably representative of the cell’s activity in relation to behavior. Each lever-press epoch included the 1-s period centered at the moment of lever-press, while the reward-approach period was the 1-s period immediately after the 3^rd lever-press epoch.

Multiple Linear Regression (MLR)

A model with 5 factors that characterized the animals’ spatial location and movements were used to isolate the effect of behavioral variability on neural activities during the ‘common-segment’ pairs. A linear model was employed simply because we could not specify any type of consistent non-linear relationship between the firing rate of the neurons and changes in the behavioral variables. Nevertheless linear regression was appropriate since for each neuron the residuals and the predicted values produced by the model were uncorrelated, indicating that the iFRs indeed had a linear relationship with the behavioral predictors. All behavioral analyses were performed using the common segment LPs. Common segments included instances where the same two levers were pressed in the same order, but as part of two different sequences. 18 out of the 19 sessions had satisfactory tracking of behaviors and thus were included in MLR and other analyses involving the residual matrices (see below). In 12 out of the 18 sessions, the rats performed 3 sequences, and we used all 3 possible pairs of common-segments. In 6 out of 18 sessions the rats performed 2 sequences, so only one pair of common-segments existed in each of these sessions, and was used in the analysis.

Behavioral variables were constructed based on video tracking data. Since the video rate was 1 frame/33.3ms, we averaged 6 frames to synchronize the video with the 200ms iFR bins. The first two factors extracted from the video tracking data were the ‘X’ and ‘Y’ position of the animals in the chamber. For visualization purposes in Fig 1a, these positions were given with reference to the center of each lever. However, for the model, the positions were given with reference to a single fixed point (i.e. the right wall) across the three levers. To generate the next two factors in the model, we calculated the vector created between the animal’s current position and its position 200ms prior. The third factor ‘A’ was the approach angle, or the angle between this vector and the lever. The fourth factor ‘V’ was the bin-by-bin velocity of the animal during lever approach and was simply the length of this vector at each time step (converted into cm/s). The fifth factor ‘T’ was the time (in seconds) since the previous lever press:

$$F(t)=b_{\mathit{0}}+b_{\mathit{1}}X(t)+b_{\mathit{2}}Y(t)+b_{\mathit{3}}A(t)+b_{\mathit{4}}V(t)+b_{\mathit{5}}T(t)+\mathrm{\epsilon }(t),$$ (eq. 1)

For a given time bin t, F(t) represented the neuron’s normalized iFR within that bin. We then examined the distribution of the percentage of variance accounted for by the model (the R² statistic) for each neuron (Fig. 1b). The residual matrix resulting from the regression in each session was used to perform a series of control analyses, including D_Mah, D_Mah-based leave-one-out error, and ensemble variance and covariance (see sections below). By comparing the results from these residual-based analyses with those from the full iFR matrices, the effect of behavioral variability on sequence decoding was elucidated.

Selectivity index

To examine whether individual units were responsive to sequence, the selectivity for each unit i with respect to each pair of common segments—both of which were associated with the same lever but belonged to two different sequence blocks—was obtained by grouping the firing rates into two classes: the iFRs of a given neuron during one common segment were assigned to Class A, whereas the iFRs of the same neuron during the other common segment in the pair were assigned to Class B. The index was then computed as:

$$d_i^{\prime }=\frac{\left|\langle \{r_i(t)\mid t\in A\}\rangle -\langle \{r_i(t)\mid t\in B\}\rangle \right|}{\sqrt{{\sigma }_{i,t\in A}^2+{\sigma }_{i,t\in B}^2}}$$

where 〈·〉 denotes the mean.

Receiver operating characteristic (ROC) curve and statistics

The ROC method was used to test classification performance of single neurons and ensembles. ROC analysis has an advantage in situations where the distributions are unknown because it assesses performance over a range of threshold values rather than being forced to evaluate differences at a single threshold level relative to some theoretical distribution. In a simple example, if a detector’s sensitivity level is set to 0.5, signals (or observations) stronger than this level are reported as positives (or ‘1’) and below as negatives (or ‘0’). Out of all positives, the proportion of incidents when the target was truly present would be the ‘hit rate’ and the remaining proportion would be ‘false-alarm rate’. Each threshold level yields a single dot in the ROC curve. In the present study, an ROC analysis was run on correlation scores as described in the text, for the classification of both sequences and lever locations. Because correlation coefficients are on a continuous scale, a large number of thresholds were used to produce the detailed ROC curves. We used the area-under-curve (AUC) from each individual curve for statistical analysis. Because a 45-degree straight-line with an AUC=0.5 indicates a lack of signal-noise differentiation, the AUCs can be tested for significance by a simple one-sample t-test against a normal distribution with mean = 0.5 and unknown variance. In the case where AUCs from ensembles and from single-units were compared, an independent-sample t-test was used. In all of the cases involving multiple groups, a 2-way ANOVA was also used with 2 control groups—random normal distributions with the same sample size and the same variance and mean = 0.5. The relative numbers of neurons in each region were not different from those obtained using the Bonferroni-corrected one-sample t-test.

In order to analyze the effect of ensemble size on the between-sequence separation of activity states, ensemble AUCs were calculated between pairs of common-segments (i.e. lever responses that differed only in their sequence identity) based on randomly selected ensembles with varying sizes (n=4, 7, 10, 13, 16 and 19). For each ensemble size, 100 random draws of n neurons were performed for each session and the resulting AUC averaged, for a complete representation of the whole data set. For both the ACC and the DS, the average AUCs at each ensemble size were plotted (Fig. 3d) and a power function was fitted for each region. The power function was selected as it accounted for more than 99% of the variance.

Multiple-single unit activity (MSUA) analysis

For population analysis, population vectors r(t) = [r₁(t) … r_N(t)] were constructed, with N equal to the number of single units isolated from a given recording session. The term MSUA space refers to the N-dimensional space spanned by all recorded units and populated by these vectors r(t). Each dot in the MSUA space represents the state of the entire recorded ensemble within one 200 ms bin. All points corresponding to different 200ms bins within the epochs of the same behavior are shown in the same color. All statistical analyses were performed in the full space of all recorded units. For the purpose of visualization, multi-dimensional scaling (MDS) was applied to reduce dimensionality.

To quantify the effects of sequence and lever location on network activity, the Mahalanobis distances (D_Mah) were computed between the sets of N-dimensional vectors associated with task epochs of interest. To control for differences in MSUA space dimensionality (i.e. ensemble size) in D_Mah comparisons, a normalization procedure was employed: N_min was the minimum number of units recorded in any of the data sets to be compared, and K_min was the minimum number of time bins. For data sets with N and K greater than N_min and K_min, N_min units and K_min data points were selected at random and D_Mah was computed. This procedure was repeated 1000 times and the results averaged to make full use of all units and data points recorded. The resultant normalized D_Mah averages were used in various statistical analyses. In order to determine the significance level of a given D_Mah value, between-sequence separation was compared to within-sequence separation (Fig. 4c), and between-lever separation was compared to within-lever separation. To calculate average D_Mah within a sequence block, bootstrap surrogate blocks were created by randomly shuffling 1-s blocks of the iFR matrices. The distance between the 2 shuffled blocks therefore represents the separation between activities during random behavioral events. The process was repeated 100 times and the D_Mah values averaged. We also used the residual matrices from the linear regression (see above) to calculate the D_Mah, and compared the results to the D_Mah calculated from the full iFR matrix in order to reveal the influence of the behavioral variables on sequence decoding (Fig. 5c, e).

The calculation of D_Mah incorporates 3 aspects of ensemble activity: the difference in mean firing rates (i.e., Euclidean distance or D_Euc), the variance in each neuron’s activity and covariance between any 2 cells in the ensemble. We focused on the bin-by-bin variance and covariance, calculated among neurons after averaging across all trials for each time bin within the lever-press epochs. In order to better understand the difference between ACC and DS in sequence encoding on the ensemble level observed in D_Mah, we also analyzed D_Euc, variance and covariance separately. From each session, 19 cells were randomly drawn and the total covariance was calculated and summed, and the process was repeated for 100 times before the results were averaged for each session. Thus the ensemble bin-to-bin variance was the average of summed variance in a typical 19-cell (i.e. Nmin) ensemble (Fig. 5a), and the ensemble covariance shown in Fig. 5b was the summed absolute covariance between each cell pair in an ensemble, since we were concerned with the magnitude of the covariance rather than its direction. We also used the residual matrices from the linear regression (see above) to calculate the ensemble variance and covariance in order to examine the effect of behavioral variation (Fig. 5a and b).

Leave-one-out Mahalanobis discriminant analysis (MDA)

In the analysis above, D_Mah was calculated between clusters. The leave-one-out prediction uses another variant of D_Mah: dot-to-cluster distance. In each distance calculation, a ‘dot’ is the ensemble iFR vector of a single time-bin recorded during a common-segment action. When all the dots for each sequence block are plotted together, there are two clusters in the MSUA space. If the D_Mah from the dot to its home sequence-cluster is shorter than that to the alternative sequence-cluster, then a correct classification is counted. The final performance is shown in percentage of correct classifications out of all time-bins tested (Fig. 4d). In order to have a control for the classification performance, bootstrap surrogate blocks were created by randomly shuffling 1-s blocks of the iFR matrices. The distance between the 2 shuffled blocks therefore represents the separation between activities during random behavioral events. The process was repeated 100 times and the leave-one-out errors averaged. Two-way ANOVA was then used to test the performance of ensembles from both regions (Fig. 4d). Additionally, the residual matrices from the linear regression (see above) were used to calculate the leave-one-out errors and their results were compared the results to those calculated from the full iFR matrix (Fig. 5d and f).

F-statistic for sequence discrimination and for lever discrimination

The F-statistic was calculated separately for sequence classification and lever discrimination. To characterize the cells’ temporal profile of sequence discrimination (Fig. 6a), for each neuron, the F-statistic was calculated between the iFRs during each pair of common segments (from 2 different sequence-blocks) in each of the 6 time bins, covering the interval from 900ms prior to a given action to 300ms after the action. In other words, the F-statistic for sequence was the between-sequence variance divided by the within-sequence variance in a given time bin. We then plotted the frequency distribution of the time bin in which a cell achieved its maximum F-statistic for each region (Fig. 6a).

To characterize the level of lever discrimination throughout the lever-press epoch, F-statistics were also calculated among each cell’s activities associated with responses on the 3 levers within each sequence block. The F-statistic for lever presses was the between-lever variance divided by the within-lever variance in a given time bin, in a given sequence. The frequency distribution of the time bin in which a cell achieved its maximum F-statistic is plotted in Fig. 6b.

A supplementary methods checklist is available.