The vestibular nerve comprises two neuronal groups that are identified by differences in the regularity of their spontaneous discharge. The mechanisms driving this hallmark difference have long been debated but remain poorly understood. We use a point-neuron model to test if variation in the density of low-voltage-gated potassium currents can account for spike-timing regularity. The model predicts how ion channels and morphology may work together to shape the responses of vestibular afferents.
Keywords: vestibular ganglion neurons, low-voltage-activated potassium currents, regularity
Abstract
The vestibular nerve is characterized by two broad groups of neurons that differ in the timing of their interspike intervals; some fire at highly regular intervals, whereas others fire at highly irregular intervals. Heterogeneity in ion channel properties has been proposed as shaping these firing patterns (Highstein SM, Politoff AL. Brain Res 150: 182–187, 1978; Smith CE, Goldberg JM. Biol Cybern 54: 41–51, 1986). Kalluri et al. (J Neurophysiol 104: 2034–2051, 2010) proposed that regularity is controlled by the density of low-voltage-activated potassium currents (IKL). To examine the impact of IKL on spike timing regularity, we implemented a single-compartment model with three conductances known to be present in the vestibular ganglion: transient sodium (gNa), low-voltage-activated potassium (gKL), and high-voltage-activated potassium (gKH). Consistent with in vitro observations, removing gKL depolarized resting potential, increased input resistance and membrane time constant, and converted current step-evoked firing patterns from transient (1 spike at current onset) to sustained (many spikes). Modeled neurons were driven with a time-varying synaptic conductance that captured the random arrival times and amplitudes of glutamate-driven synaptic events. In the presence of gKL, spiking occurred only in response to large events with fast onsets. Models without gKL exhibited greater integration by responding to the superposition of rapidly arriving events. Three synaptic conductance were modeled, each with different kinetics to represent a variety of different synaptic processes. In response to all three types of synaptic conductance, models containing gKL produced spike trains with irregular interspike intervals. Only models lacking gKL when driven by rapidly arriving small excitatory postsynaptic currents were capable of generating regular spiking.
NEW & NOTEWORTHY
The vestibular nerve comprises two neuronal groups that are identified by differences in the regularity of their spontaneous discharge. The mechanisms driving this hallmark difference have long been debated but remain poorly understood. We use a point-neuron model to test if variation in the density of low-voltage-gated potassium currents can account for spike-timing regularity. The model predicts how ion channels and morphology may work together to shape the responses of vestibular afferents.
the vestibular afferent nerve is characterized by two broad groups of neurons with striking differences in the timing of their spontaneous spike patterns; in one group, the interspike intervals of spontaneous spiking are highly regular, whereas in the other, the interspike intervals are highly variable with irregular Poisson-like statistics (Fernández et al. 1988; Goldberg et al. 1990). Among sensory neurons, the vestibular nerve is unique in the range of spike-timing regularity seen across the population, so much so that the regularity of interspike intervals is often used as a shorthand feature to group neurons that also differ in their response gain and phase (reviewed in Goldberg and Fernández 1979). Moreover, regularity of spike timing may in itself be important for representing sensory information along parallel streams, with one stream representing information as a rate code and the other representing information as a temporal code (Sadeghi et al. 2007). Given its crucial role in organizing vestibular information, understanding how differences in spike-timing regularity arise is an important first step toward understanding the basis of sensory coding in the vestibular periphery.
Even though vestibular afferents are remarkably heterogeneous in their morphology, early work showed that the correspondence between afferent morphology and spike-timing regularity is not strong. Such correspondence is clear in only a subgroup of the afferent population. For example, afferents whose terminals exclusively engulf the entire sensory hair cell (pure calyx) are predominantly found in central zones of the sensory epithelium where irregularly firing afferents make their connections with hair cells. In contrast, afferents that exclusively make numerous small boutonlike terminals with many hair cells (pure bouton) are found in the peripheral zones of the epithelium where regularly firing afferents make their connections (Fernández et al. 1988; Lysakowski et al. 1995). Although the association between spike-timing regularity and region of innervation is clear, this apparent association between afferent morphology and regularity fails for the vast majority of vestibular afferents, which have mixed morphologies (dimorphic). Dimorphic afferents have complex terminal morphologies with any particular afferent making both calyx and bouton terminals. They are also found throughout the sensory epithelia. Thus they can be similar in their morphology and yet differ in their spike-timing regularity (Baird et al. 1988; Goldberg et al. 1990). Such weak correspondence between terminal morphology and regularity of dimorphic afferents suggests that morphology alone cannot explain differences in spike-timing regularity.
These observations, combined with early conceptual (e.g., Highstein and Politoff 1978) and phenomenological (Smith and Goldberg 1986) models, lead to the idea that differences in spike-timing regularity come from differences in the afferents' ion channel composition. The ion channel properties of vestibular afferent neurons are different enough to support this notion. Whole cell patch-clamp recordings show that the cell bodies of vestibular afferents (referred to here as afferent somata and/or vestibular ganglion neurons, VGN) are diverse in their complements of ion channels (e.g., Almanza et al. 2012; Brugeaud et al. 2006; Cervantes et al. 2013; Limón et al. 2005; Risner and Holt 2006; Vega et al. 2009). Although spikes do not originate at the somata of these bipolar neurons, ample immunohistochemical and electrophysiological evidence suggests that similar groups of ion channels are found both at the cell body and within the neuroepithelium, closer to the spike initiation zones of bipolar sensory neurons (Black et al. 2012; Hossain 2005; Lysakowski et al. 2011; Rose et al. 2013; Rutherford et al. 2012; Wooltorton et al. 2006; Yi et al. 2010). Moreover, emerging electrophysiological evidence from calyx terminals suggests that the ion channel properties of vestibular afferents differ based on the region of the epithelium they innervate (e.g., Meredith and Rennie 2015; Songer and Eatock 2013).
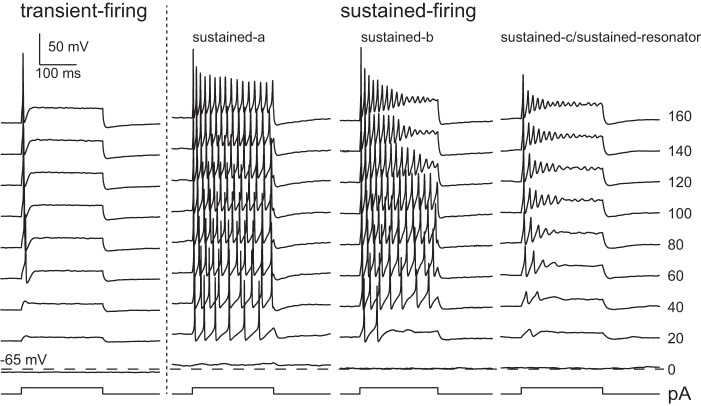
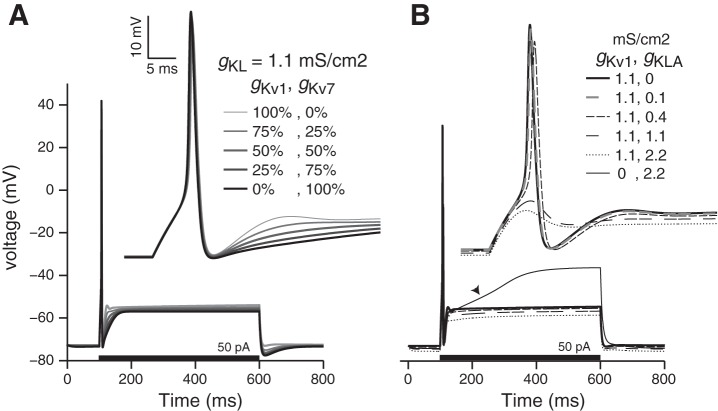
As a consequence of differences in their ion channel composition, VGN somata respond to injected currents with different spike thresholds (Risner and Holt 2006) and firing patterns (Iwasaki et al. 2008; Kalluri et al. 2010; Yoshimoto et al. 2015). Based on their responses to current steps, the somata of vestibular ganglion neurons fall into two broad groups (Fig. 1): one group fires only once at the onset of injected step currents (transient firing), whereas the second group fires with a train of action potentials (sustained firing) (Kalluri et al. 2010). Neurons within each group also share other electrophysiological features; neurons with transient responses have lower resting potentials, larger current thresholds, and faster membrane time constants than do neurons with sustained responses. Neurons in the sustained-firing group also show considerable variability in the number and size of their action potentials. Some neurons fire long trains of action potentials with various rates of accommodation (sustained-a and sustained-b), whereas others fire one or two small action potentials followed by long-lasting voltage oscillations (sustained-c or sustained resonators). Based on pharmacological blocking, previous studies have shown that somata with transient-firing patterns have larger low-voltage-gated potassium currents (IKL) than do somata with sustained-firing patterns (Iwasaki et al. 2008; Kalluri et al. 2010).
Fig. 1.
Dissociated VGN in rat are classified by the adaptation in their current step-evoked firing patterns (in vitro, perforated patch); patterns range from neurons that fire only at the onset of the current step (transient) to neurons that spike long trains of action potentials (sustained-a), short trains of action potentials (sustained-b), and one action potential followed by oscillations in membrane potential (sustained-c). In addition to the qualitative difference in spike-train adaptation, previous in vitro studies showed that the 2 groups also differ in their resting potential, current threshold, and membrane time constants (not shown). The difference in resting potential between the 2 categories is evident in these examples: the membrane voltage of the transient neuron at 0 pA is hyperpolarized below the dashed line and is above the line for all 3 sustained neurons. [Modified from Kalluri et al. 2010.]
Heterogeneity in ion channels and associated differences in step-evoked firing patterns lend evidence to the idea that ion channel heterogeneity may be important for shaping the remarkable range of regularity seen in the in vivo responses of vestibular afferents. By examining the response of VGN somata to artificially injected synaptic noise (pseudosynaptic currents), Kalluri et al. (2010) proposed that IKL is important for producing irregularly timed spiking in vestibular afferents. The purpose of the present study is to examine this hypothesis in a model in which the density of IKL and the parameters of the stimulus could be systematically varied. Such careful examination of ion channel function was not possible empirically because of the experimental constraints of time and inadequate pharmacological manipulation of ion channels. Our goal in the present study was to test the extent to which differences in the density of low-voltage-gated potassium currents (in the absence of other morphological and ion channel differences) can account for the responses of VGN neurons to both step-evoked and pseudosynaptic stimuli. We validated the model by comparing simulated responses against in vitro data collected with similar stimuli (Kalluri et al. 2010).
METHODS
Model Framework
We implemented a single-compartment, conductance-based model with three nonlinear voltage-dependent currents representative of those known to be present in vestibular ganglion neurons. These currents included a transient sodium current (INa) whose properties were based on characterizations of standard neuronal sodium channels, a low-voltage-gated potassium current (IKL) with activation kinetics representative of a Kv1-type ion channel, and a high-voltage-gated potassium current (IKH) to which we attributed all potassium currents that were not associated with IKL. The model also included a passive leak current (Ileak) whose properties were linear and fixed in all simulations, and a capacitive current (CmSdV/dt) to represent the charge redistribution induced by changes in voltage (dV/dt) across the lipid bilayer of the cell membrane. The specific membrane capacitance (Cm) was fixed at 0.9 μF/cm2, and cell surface area (S) was fixed to yield a net capacitance of 10 pF. Although VGN have a wide range of somatic sizes, the net capacitance used in this study is within the range reported for both sustained- and transient-firing categories of VGN. By fixing the cell surface area to a value that was reasonable for both sustained- and transient-firing VGN, our models examine the exclusive influence of ion channels on response characteristics such as current threshold and membrane time constant. To drive spiking, the model included either a current source (Iinj) to represent an externally applied current step, or a synaptic current (Iepsc) to represent the stimulus provided by hair cells.
The single-compartment model was implemented in MATLAB as a differential equation in which the net current across the neuronal membrane was modeled as the sum of currents flowing through individual circuit elements connected in parallel (Eq. 1):
| (1) |
Simulations consisted of solving for the membrane voltage (V) in response to either injected current steps (Iinj) or synaptic currents (Iepsc) as applied through a synaptic conductance. When the model was run to simulate step-evoked responses, Iepsc was set to zero, and vice versa. In either case, V(t) was numerically solved by a backward difference method in MATLAB. The resulting voltage responses were compared with in vitro recordings from the somata of VGN. Spikes evoked by current steps were easy to identify visually and by applying a criterion based on a voltage crossing a threshold value. Because discriminating between spikes and large excitatory postsynaptic potentials (EPSPs) was more difficult when synaptic conductances were applied, for those simulations we used a custom spike detection algorithm (see Analysis of Spike Trains) to detect spikes.
Defining the Currents
The four voltage-dependent currents IKL, IKH, INa, and Iepsc were described by
| (2) |
where the ion channel conductance (gi) was voltage dependent, and the driving force was the difference between the instantaneous voltage (V) and the equilibrium voltage for the ionic species (Ei) passed through the respective conductance. For example, the equation governing the ion channel conductance for the low-voltage-gated potassium current was
| (3) |
where ḡKL represents the maximum conductance density (e.g., mS/cm2) and the variables w4 and z represent the voltage-dependent activation and inactivation kinetics, respectively, of channel gating for a Kv1-type ion channel.
The parameters describing the activation and inactivation kinetics of gKL, gKH, and gNa were based on models that have incorporated similar conductances in auditory neurons (Rothman and Manis 2003b; see appendix a for detailed equations). The maximum conductance densities, equilibrium voltages, and half-maximum activation voltages were tailored for VGN and recording conditions. Because VGN continue to mature during the first 2 postnatal weeks, wherever possible we used the ion channel properties characteristic of VGN from the second postnatal week. Table 1 summarizes the literature surveyed to assign channel properties. We chose to emphasize the second postnatal week to match the age range of the in vitro recordings with which the model responses are compared. Table 2 summarizes the range of conductance values used in the model, and the rationale for these choices is further discussed below.
Table 1.
Model parameters for sodium and potassium conductances selected from literature
| gmax, mS/cm2 | V1/2, mV | k (slope) | |
|---|---|---|---|
| Sodium conductance | |||
| Cochlear nucleusa,b | |||
| gNa | 75 | −38 | 7 |
| P3-6 VGN micec | |||
| gN (act.) (TTX) | 4.2 | −46 | 4.5 |
| gNa(inact.) (TTX) | −69 | ||
| P0-5 VGN miced | |||
| gNa(act.) (TTX) | 1.7 | −53 | |
| gNa(inact.) (TTX) | −65 | 2.4 | |
| Potassium conductance | |||
| Cochlear nucleusa,b | |||
| gKH | 11 | −15 | 5 |
| gKL | 0–15 | −48 | 6 |
| P5-8 VGN micee | |||
| gK (TEA) | 1.7 | −14.5 | |
| gKL (DTX) | 0.8 | −51.2 | |
| P5-7 VGN ratf | |||
| gKL (α-DTX) | −44.8 | 8.4 | |
| gKL + gKH (phasic) | 2.6 | ||
| gKH (tonic) | 1.8 | ||
| P8-16 VGN ratg | |||
| gKL (α-DTX) | 0.2 | −44 | |
Literature was surveyed to select model parameters for sodium (gNa) and potassium (gKL, gKH) conductances. Wherever possible, the pharmacological blocker or response property used to characterize conductance is indicated in parentheses. gmax, maximum conductance; V1/2, half voltage of activation (act.) or inactivation (inact.); α-DTX, α-dendrotoxin; TTX, tetrodotoxin; VGN, vestibular ganglion neurons. Sources:
Rothman and Manis (2003a); bRothman and Manis (2003b); cChabbert et al. (1997); dRisner and Holt (2006); eChabbert et al. (2001); fIwasaki et al. (2008); gKalluri et al. (2010).
Table 2.
Model parameters
| gmax, mS/cm2 | V1/2, mV | Slope | |
|---|---|---|---|
| gKH | 2.8 | −15 | 5 |
| gKL | 0–1.1 | −44.5 | 8.8 |
| gNa (act.) | 8–20 | −38 | 7 |
| gNa (inact.) | −65 | 6 | |
| gleak | 0.03 |
| Additional parameters | |
|---|---|
| EK | −81 mV |
| ENa | 82 mV |
| Eleak | −65 mV |
| Cm | 0.9 pF/cm2 |
Low- and high-voltage-gated potassium conductance.
Two potassium conductances were modeled, one to represent the characteristic time and voltage dependence of low-voltage-gated potassium conductance (gKL) and another with the characteristics of a high-voltage-gated potassium conductance (gKH) to represent the remaining potassium currents. The equations governing the voltage dependence and kinetics of IKL were based on published models for Kv1-type ion channels (Rothman and Manis 2003b; see appendix a for equations). The model equations were consistent with the activation properties of the α-dendrotoxin-sensitive component of IKL (likely to be some combination of Kv1.1, Kv1.2, or Kv1.6) as characterized in VGN. Model responses were simulated with maximum conductance density, ḡKL, varying from 0 to 1.1 mS/cm2; this range is consistent with reported values from second postnatal week VGN (Iwasaki et al. 2008; Kalluri et al. 2010). The high-voltage-gated potassium conductance (gKH) was modeled as a separate channel with a more depolarized activation range (see appendix a for equations based on gKH in Rothman and Manis 2003b). The conductance density of gKH for the present VGN simulations was fixed at 2.8 mS/cm2. This value was derived from the pharmacological data of Iwasaki et al. 2008 coupled with the following three assumptions. First, all potassium currents that remain after gKL is blocked (e.g., Iwasaki et al. 2008) flow through gKH. Second, the steady-state potassium current in transient/phasic-firing neurons comprises IKL plus IKH, whereas the steady-state current in sustained/tonic-firing neurons contains only IKH. Third, IKL accounts for no more than 30% of the total potassium current.
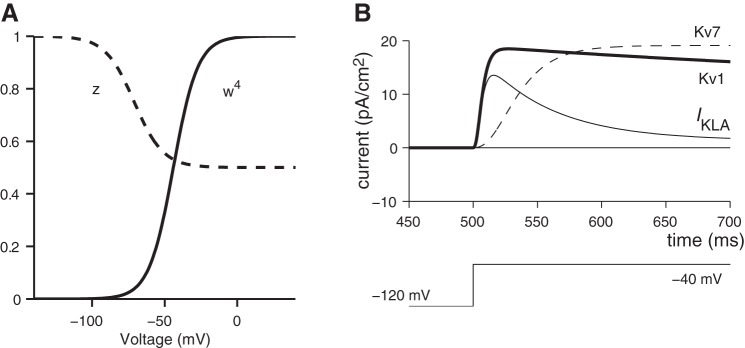
Although the gKL model presented in results contains only the Kv1 component, previous electrophysiological and immunocytochemical studies have shown that IKL in the cell bodies of VGN is likely to be conducted through both Kv1 and Kv7 (KCNQ) channels (Kalluri et al. 2010; Pérez et al. 2009). We excluded the Kv7 component on the basis of the following rationale. The currents carried by Kv7 (M-like currents) are smaller than those carried by the Kv1 component (around 20% of total IKL at the age range studied). In supplementary versions of the model (details described in appendix b), we examined how the proportion of Kv1 vs. Kv7 components influenced the response of modeled neurons. The simulations showed that the qualitative influence of Kv1 and Kv7 currents on transient vs. sustained spiking is similar. Replacing Kv1 with Kv7 produced a subtle elongation in the afterhyperpolarization trajectory, but even these subtle differences were obscured when Kv1 and Kv7 were mixed at the 8:2 ratio that is typical for VGN. At these ratios, the faster kinetics of the Kv1 component dominated the response. As a result, we simplified our representation of gKL by only including the Kv1 component.
Previous recordings in VGN and emerging evidence from calyx terminals of vestibular afferents also suggest that the potassium currents in vestibular afferents vary in their inactivation kinetics (Eatock et al. 2008; Meredith and Rennie 2015; Risner and Holt 2006). By adding an inactivating component to IKL, we explored the influence of rapidly inactivating potassium currents on the firing patterns of modeled VGN (see appendix b). Our results suggest that although these currents can influence the response of modeled VGN, these currents are not necessary to account for the transient vs. sustained firing pattern distinctions seen in VGN. Also, the rate of sustained spiking was sensitive the details of how the inactivating current was modeled. In the present formulation of the transiently inactivating current, the firing patterns started with voltage oscillations and then built up into a fully sustained spike train. Such “buildup-and-fire” responses are present in auditory brain stem neurons and have been attributed to the action of rapidly activating potassium currents (Kanold and Manis 1999), but such patterns have not been reported in VGN. Since the rapidly inactivating potassium current was not necessary to account for the essential difference between transient-firing and sustained-firing categories of VGN, the results presented in the main text were again simplified to only include the Kv1 component of the low-voltage gated conductance.
Sodium conductance.
Sodium conductance was generalized as a single conductance with maximum values ranging between 7 and 50 mS/cm2. The values we used are substantially larger than published values for sodium conductance density in first postnatal week VGN (∼1.7 to 4.3 mS/cm2; Chabbert et al. 1997; Risner and Holt 2006). The adjusted values for sodium conductance density were important because when ḡNa from the first postnatal week and ḡKL from the second postnatal week were used, the model failed to generate robust action potentials. We justified the use of larger conductances based on our expectation that sodium currents also grow with age like many other ionic currents do in the VGN (e.g., IKL and IKH). Also, a reanalysis of previously published data supported this expectation and showed that sodium current densities are at least two- to fourfold greater in the second postnatal week than in the first (data shown in appendix d). Even these higher values of ḡNa may underestimate true sodium conductance density, because the previous study was not designed to study sodium currents, did not isolate currents with channel blockers, and used perforated-patch techniques, which typically have high series resistance electrodes. The latter recording technique combined with the rapid onset and offset of sodium currents may result in an underestimation of the current. A more detailed study of the development and characteristics of sodium and other currents in VGN is an important next step toward refining the representation of this important component of the model.
Synaptic conductance.
The synaptic conductance was defined by reorganizing Eq. 2 to yield
| (4) |
where Iespc stands for the excitatory postsynaptic current (EPSC) trains that were modeled using a stochastic representation of synaptic drive. To generate gs(t) (whose voltage dependence is linear), the EPSC was scaled by the corresponding difference potential between typical membrane potentials (V = −97 mV; Glowatzki and Fuchs 2002; Grant et al. 2010) and the reversal potential for an AMPA-type receptor (Es = 3 mV; Glowatzki and Fuchs 2002). The shapes of the EPSCs are discussed separately below.
To define the random arrival times and amplitudes of Iepsc, we first defined an impulse train, e(t), with randomly sized and spaced impulses. Pulse sizes were drawn from a Gaussian distribution with a nominal mean of 150 pA (SD ±115 pA), and interpulse arrival times were drawn from an exponential distribution with 3-ms average intervals. The nominal values are representative of EPSC amplitudes and rates measured from spiral ganglion terminals that are voltage-clamped to near −97 mV. Iepsc(t) was then constructed by convolving the impulse train with one of three predefined EPSC shapes (s1, s2, or s3) whose amplitudes were uniformly normalized by their maximum values.
| (5) |
DEFINING THE EPSC SHAPE.
We modeled EPSCs with three shapes (Fig. 2). The decision to modify synaptic conductance to yield three EPSC shapes was based on the rationale that variations in EPSC shape could originate from a variety of factors, including differences in AMPA receptor subunits (Matsubara et al. 1999), NMDA receptors (Ishiyama et al. 2002), glutamate accumulation in the synaptic cleft (e.g., Otis et al. 1996), and multiphasic EPSCs (Grant et al. 2010; Songer and Eatock 2013), and/or to represent the attenuation and slowing of synaptic events that might result from EPSPs propagating along extended dendritic arbors. Recent observations that synaptic ribbons and postsynaptic receptors are not directly opposed in calyx terminals (Sadeghi et al. 2014) suggest that glutamate “spillover” can additionally influence the kinetics of synaptic events in the vestibular periphery. We conjectured that regardless of the origin of EPSC shape differences, neurons with different ion channel properties may be differently sensitive to the kinetics of synaptic events and that examining this differential sensitivity within a model would be useful. We did not attempt to model more complex synaptic signaling mechanisms, including proton-based (Highstein et al. 2014) and non-quantal modes of transmission that also have been observed at calyx terminals (Songer and Eatock 2013; Yamashita et al. 1990).
Fig. 2.
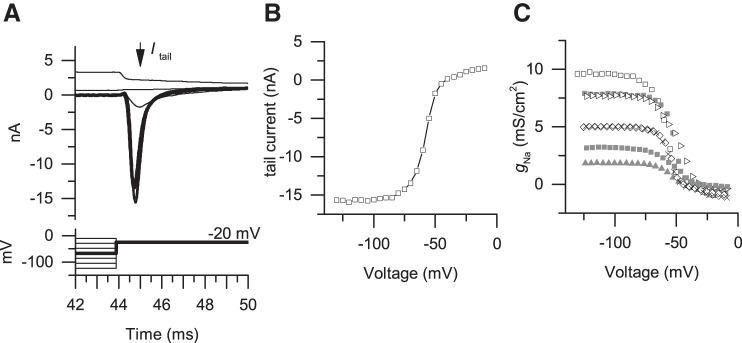
Three EPSC shapes were used to examine the impact of EPSC shape on spike response patterns. The first shape, s1(t), was derived by fitting an alpha function to the synaptic currents recorded from the terminals contacting inner hair cells (e.g., Glowatzki and Fuchs 2002; Grant et al. 2010); these shapes are similar to most events from calyx terminals (Sadeghi et al. 2014). The second shape, s2(t), had a fast onset time [same as s1(t)] but an elongated decay. Such shapes could result from glutamate accumulation and other complexities related to the unique synaptic cleft of calyx terminals. The third shape, s3(t), had a long onset and decay phase that could result from a variety of factors, including the slowing and attenuation of synaptic events via dendritic filtering. Detailed description and equations are provided in the text.
The first EPSC shape, s1(t), was described by a standard alpha function
| (6) |
where α = 0.4 defined the duration of an individual EPSC. The value α = 0.4 was determined by fitting the alpha function to recordings of EPSCs from inner hair cell terminals (Glowatzki and Fuchs 2002; Grant et al. 2010). This shape is similar to the majority of synaptic events recorded in calyx terminals (Sadeghi et al. 2014). This basic EPSC shape was subsequently modified to create two additional EPSC shapes, s2(t) and s3(t). The second shape had the same fast-onset time course as s1(t) but with a longer decay time (Eq. 7). This type of elongated EPSC has been recorded in calyx terminals and could result from glutamate accumulation at the tight cleft formed between the hair cell and calyx and/or from longer diffusion times that may result from an indirect apposition between synaptic ribbons and postsynaptic receptors (Sadeghi et al. 2014).
| (7) |
The third EPSC shape, s3(t), had slower onset and decay times and is given by Eq. 8:
| (8) |
The slower kinetics could result from a variety of different mechanisms. First, slow-onset multiphasic events that have been measured from calyx and inner hair cell terminals may come from the superposition of temporally dispersed events (Grant et al. 2010; Songer and Eatock 2013). Second, we assumed that the attenuation and slowing of synaptic drive as EPSPs propagate along extended dendrites could be represented by slow-onset EPSCs. Finally, we know little about the nature of synaptic events at vestibular bouton terminals; the inclusion of slow synaptic events serves as a parameter variation to juxtapose against the very fast-onset events that appear to be characteristic of EPSCs from terminals such as inner hair cell and calyx endings where temporal precision might be important.
To drive spiking at different rates, we modified either the mean amplitude of the EPSC train or the average interval of EPSC arrival times. We refer to the simulations in which EPSC amplitude was varied while EPSC interval was held constant as “pseudosynaptic paradigms” to be consistent with the nomenclature used in Kalluri et al. 2010, where similar stimuli were applied in vitro. We refer to the more general cases in which EPSC amplitude, rate, and shapes are parametrically varied as “simulated synaptic paradigms.”
Analysis of Spike Trains
Spike detection.
Spikes elicited by Iepsc were detected using a spike detection algorithm as follows. A spike was detected at time t = to if the membrane potential, V(t), satisfied four conditions, including a 0.35-ms refractory period, a threshold criterion (Eq. 9), a requirement that the voltage be at a local maximum (Eq. 10), and a requirement that the rising and falling flanks of the spike be sufficiently fast (Eq. 11).
| (9) |
| (10) |
| (11) |
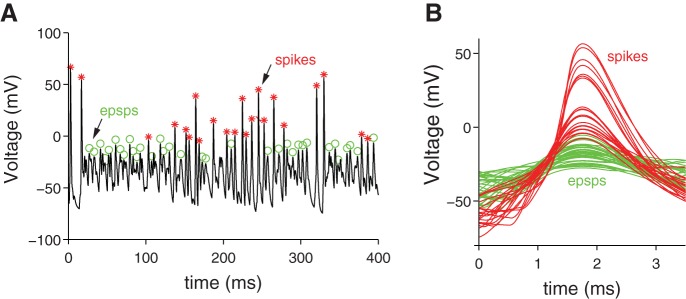
In Eq. 11, the criterion values for “sufficiently fast” (C1 and C2) were empirically tuned (nominally −12 and 11 mV, respectively) to reliably detect by algorithm the events that were visually identified as spikes. The tuning process was particularly important when spike trains evoked by high-magnitude synaptic conductance were analyzed. The tuning allowed us to differentiate between small spikes and large EPSCs. In Fig. 3A, we show examples of the events detected by the algorithm when the criterion values were set at C1, C2 = ±30 mV versus when the criterion value was set at C1, C2 = ±5 mV. The higher criterion values are more selective for spikes, whereas the lower criterion values detect both spikes and EPSPs. The waveforms of spikes vs. EPSPs are shown for comparison in Fig. 3B. For most stimulus conditions, the nominal criterion values were sufficient to reliably identify spikes. At very high-magnitude synaptic conductance (as shown in the example), many spike trains exhibited periods of depolarization block and/or burst spiking during which action potential amplitudes were highly variable. These conditions made it increasingly difficult to confidently set criterion values. Simulations were terminated when such bursts and/or non-monotonic (i.e., non-increasing spike rate) behaviors were detected.
Fig. 3.
Spike detection algorithm at work on a spike train exhibiting periods of depolarization block and burst spiking (same spike train appears at top of Fig. 7). A: green circles indicate EPSPs and red asterisks indicate spikes. B: spikes vs. EPSPs were distinguished by changing the “steepness” criteria C1 and C2 in Eq. 11 from ±30 to ±5 mV. The waveforms of the “shallow” EPSPs are green and the “steeper” spikes are red.
Analysis of regularity.
Simulations with synthetic synaptic stimuli at any particular combination of EPSC amplitude, rate, and shape were run in 1,000-ms blocks. For each simulation block, the EPSC train was redefined by drawing new EPSC amplitudes and times from the random distributions that defined these features. The spike times detected within each block were stored and new simulations conducted until enough spikes were collected such that the standard error of the mean spike interval was <1% of the mean spike interval. The resulting total simulation time needed to generate well-sampled histograms was larger for EPSC parameter combinations that evoked lower rate spiking.
To quantify the regularity of spike timing, we computed the coefficient of variation (CV) as the standard deviation of the interspike interval divided by the mean interspike interval. However, CV depends on spike rate (Goldberg et al. 1984). In vivo, this rate dependence of CV is dealt with by assigning to each neuron a rate-equalized or “normalized” value called CV*. CV* is typically the value of CV (or the extrapolated value) when afferents are driven to spike at an average interval of 15 ms (e.g., Baird et al. 1988). In room temperature recordings, in vitro VGN do not fire this fast (Kalluri et al. 2010). To account for the dependence of CV on spike rate, we drove each simulated neuron to spike at different rates and only compared CVs when neurons were spiking at similar rates.
RESULTS
The results are presented in two sections. In the first, we describe the ability of the conductance-based model to represent the range of step-evoked firing patterns that were observed in vitro (shown in Fig. 1 and described in the Introduction). In the second, we present responses of models in which we tested the extent to which spike-timing regularity can be shaped by the density of gKL. Spiking was driven by synaptic conductances whose activation mimicked the random timing of neurotransmitter release from hair cells. Although vestibular afferents do not directly receive synapses at their somata, we placed synaptic conductance onto the modeled somata based on emerging evidence (see discussion) that similar groups of ion channels are found at both the cell body and at the peripheral terminals of bipolar sensory neurons. In essence, our approach uses the somata of VGN as proxies for their spike initiation zones. Model responses were compared with in vitro experiments where real VGN were similarly driven by currents trains that mimic the shape and random timing of EPSCs provided by synaptic ribbons (Kalluri et al. 2010).
Model Responses to Simple Current Steps
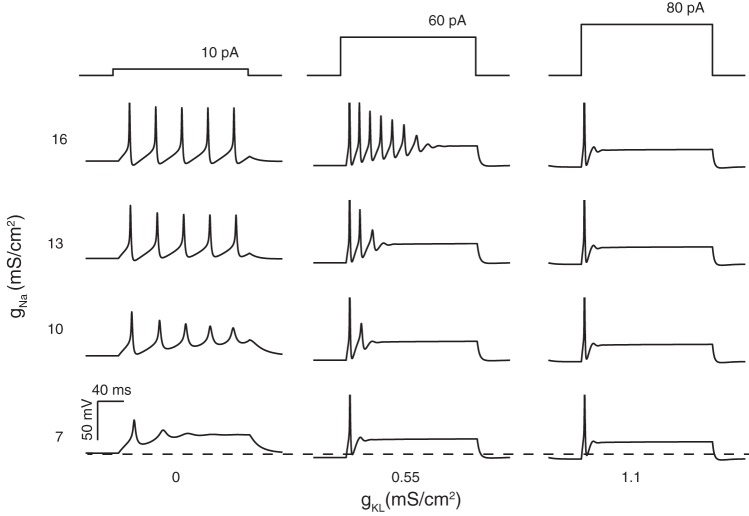
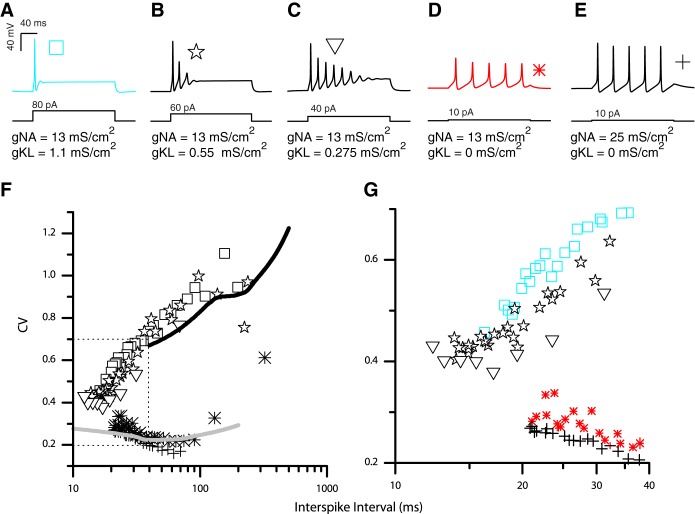
We independently varied ḡKL and ḡNa to determine the extent to which these parameters could account for firing patterns evoked in vitro (i.e., the full range of patterns comprising the transient and sustained categories). Nine simulations with varying ḡKL and ḡNa are shown in Fig. 4. Simulations were started with an initial transmembrane voltage set near the resting or equilibrium potential. The membrane voltage was allowed to reach steady state before current steps were applied in 5-pA increments. For each set of model parameters, voltage responses are shown at the current step (±5 pA) where the first action potential was elicited. As ḡKL was increased, the current step required to generate the first action potential increased (from 10 to 80 pA), and firing patterns transitioned from long trains of action potentials to just one action potential (i.e., from a sustained to a transient response). Intermediate concentrations of gKL yielded intermediate spike patterns with closely spaced multiple spikes that did not continue throughout the depolarization step. When ḡKL = 0, the action potential was short and broad for the lowest value of ḡNa, but as ḡKL increased (for the same value of ḡNa), the action potential became larger, faster, and better defined. Increasing ḡKL while holding ḡNa constant also hyperpolarized resting potentials. More hyperpolarized resting potentials can relieve sodium channel inactivation. This may be the reason why the same sodium channel density yielded robust spiking in the simulations that included gKL but resulted in near spike failure when gKL was missing.
Fig. 4.
Modeled neurons have current-step evoked firing patterns that depend on the maximum conductance of gKL and gNa. Responses are shown at the lowest current step (current threshold ±0.5 pA) that yielded an action potential. Left column: models with gKL = 0 exhibited continual spiking throughout the duration of the current step. Smaller values of gNa produced shorter action potentials. At the lowest value of gNa (bottom row), full action potentials did not form and the modeled neuron responded with sustained voltage oscillations. Interspike/interoscillation intervals varied little during the simulation time and averaged ∼40 ± 0.5 ms (14 intervals were pooled across all responses in left column). Middle column: adding gKL to the model produced accommodation to the firing patterns with the amplitude and number spikes generated decreasing with continued current injection. At any fixed value for gNa (e.g., 10 mS/cm2), the addition of gKL hyperpolarized the resting membrane potential and increased the current amplitudes needed to initiate spiking (across all 3 columns, current threshold increased from 10 to 80 pA). The presence of gKL also made the first action potential larger and faster and the timing between adjacent action potentials shorter than in left column, where gKL was missing. On average, the interspike/interoscillation intervals were 16 ± 0.4 ms (13 intervals were pooled across all responses in middle column). Right column: at gKL=1.1 mS/cm2 (the largest value used), the model responded with a single action potential for all current steps applied.
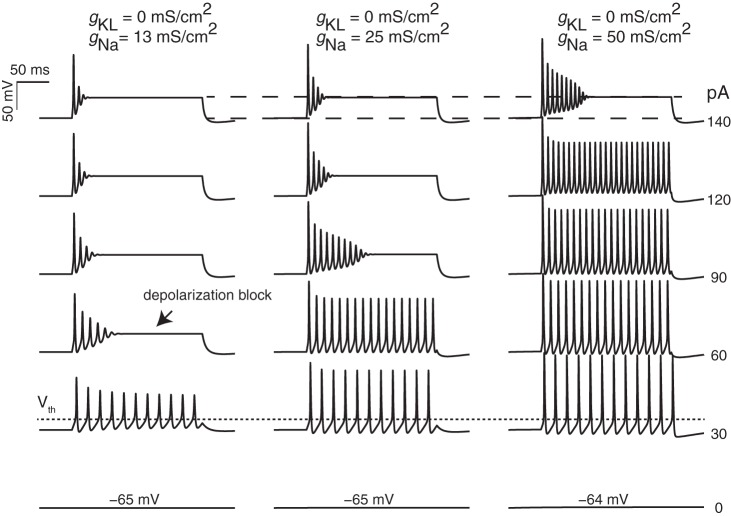
Increasing ḡNa in the absence of ḡKL also influenced the number and size of action potentials (Fig. 4, left column, and Fig. 5). For example, when ḡNa was increased, firing patterns transitioned from a small, ringing spike at the onset of the current step to many spikes (Fig. 4, left column). Although this response also occurs only at the onset of the current step, the presence of the extended voltage oscillations/ringing makes it qualitatively different from transient spiking. To determine whether a simple change in the density of sodium channels could also account for the different resting potential and current thresholds that were previously noted between transient-firing and sustained-firing neurons, we examined model responses as a function of gNa density and current-step amplitude (where ḡKL was fixed at 0 mS/cm2; Fig. 5). Current threshold (within ±5 pA) did not change as ḡNa was increased (not shown), nor did the presence of larger sodium current significantly change the timing between action potentials. However, varying ḡNa did qualitatively account for the range of in vitro responses that comprise the sustained-firing category (compare sustained-a, -b, and -c in Fig. 1). Models with the smallest gNa densities produced responses with the voltage oscillations or “ringing” that is characteristic of the sustained-c/sustained-resonant category. As ḡNa increased, oscillations became full-fledged action potentials and the current step needed to observe depolarization block of spiking also increased. Although varying ḡNa had a robust influence on the number and size of spikes, the timing between action potentials was not very sensitive to ḡNa (compare spacing between action potentials across the columns in Figs. 1 and 5). In contrast, increasing ḡKL yielded larger action potentials but also reduced the spacing between the action potentials (for additional comparisons, see left and middle columns in Fig. 4).
Fig. 5.
Influence of maximum gNa on firing pattern. Responses are shown for simulations with gKL fixed to 0 mS/cm2 and gNa varying (columns). Current-step amplitudes ranged from 0 to 140 pA. As sodium channel density increased, the size of the second and subsequent spikes became larger, the depth of the second and subsequent AHPs became larger, and the current step at which depolarization block occurs (arrow) was also larger. Resting potential (voltage at 0 pA injection), spike threshold (short-dashed line), and steady-state depolarization potential (between the 2 long-dashed lines) were not significantly influenced by the sodium current density. For the 3 columns, the average spike intervals at the 30-pA current steps are 18.1 ± 0.22, 18.1 ± 0.19, and 17.9 ± 0.17 ms, respectively.
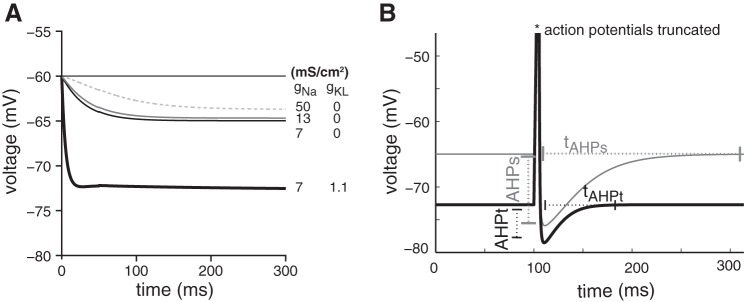
To gain insight into how gKL and gNa might influence spike timing, we examined the time course over which transmembrane voltage recovers after a depolarization. Here the simulations were started at an initial voltage of −60 mV, and the simulation was run until the membrane voltage recovered to its natural equilibrium or resting potential. Figure 6A plots the voltage recovery in four models, each with different combinations of ḡKL and ḡNa. When released from −60 mV, the model with ḡKL > 0 approached its final resting potential more quickly than did the other three models, in which ḡKL = 0. The final resting potential of the model with ḡKL > 0 was also more hyperpolarized than it was for the other three models. In contrast, increasing ḡNa had a mild but opposite influence; the time course for recovering to resting potential was slower and the resting potential was more depolarized than for smaller values of ḡNa.
Fig. 6.
A: influence of gKL and gNa on resting potential and membrane recovery time. The simulation tracks membrane potential after neuron is released from an initial condition of −60 mV. The simulation was run on 4 model neurons; 3 had gKL fixed at 0 mS/cm2 but contained variable amounts of gNa (dashed, gray, and thin black lines), whereas the fourth contained some gKL (thick line). The membrane potential of all 4 neurons settled to a final value (resting potential) that was more negative than −60 mV. The neuron model that included gKL had a more hyperpolarized resting potential and recovered from membrane depolarization faster than the 3 model versions without gKL. In contrast, increasing gNa alone had a more modest (but opposite) impact: membrane recovery time become a little longer, and resting potential became slightly more depolarized. B: afterhyperpolarization depth (AHP) and duration (tAHP) of spikes evoked by a short 1-ms-long pulse are compared for models that otherwise respond to long-duration steps with transient (black line; gNa = 13 mS/cm2, gKL = 1.1 mS/cm2) and sustained firing patterns (gray line; gNa = 13 mS/cm2, gKL = 0 mS/cm2). The modeled sustained-firing VGN has deeper and longer AHPs than the modeled transient-firing VGN.
Differences in the density of gKL also caused the magnitude and time course of the after hyperpolarization potential (AHP and tAHP, respectively) to differ between sustained- and transient-firing neurons (Fig. 6B). We defined the AHP magnitude as the voltage difference between the resting potential and the most negative voltage created by the downstroke of the action potential evoked by a 5-ms current pulse. Similarly, tAHP was the time it took for the voltage to return to rest after the downstroke. The larger and longer AHP of the sustained neurons results largely from their having a more depolarized resting potential rather than from having a deeper hyperpolarization or slower rate of depolarization.
In summary, increasing maximum density of gKL resulted in more negative resting potentials, increased current thresholds, and shortened membrane recovery times. In contrast, increasing gNa strengthened spike amplitude and reduced depolarization block of action potentials but had a less potent influence on resting potential, current threshold, or membrane recovery times. Together, the data in Figs. 4–6 suggest that although differences in gNa may be helpful for controlling the range of firing patterns comprising the sustained category, a difference in gKL was necessary to account for sustained vs. transient firing patterns and the associated differences in resting potential, current threshold, membrane recovery time, and AHPs between the two groups.
Model Responses to Synaptic Conductance
Below we describe how VGN somata with different ion channel properties respond to stimuli that mimic the stochastic timing of real synapses. We evaluated the ability of the present model to account for the responses of VGN when driven by the stochastic timing of realistic inputs. When Kalluri et al. (2010) injected pseudosynaptic currents into vestibular ganglion somata, they found that transient-firing neurons had more irregular interspike intervals than did sustained-firing neurons. Because the in vitro experiments were limited in the range of synaptic rates, amplitudes, and synaptic shapes that could be examined, in the present study we performed two groups of simulations to examine the combined influence of gKL and synaptic conductance on spike-timing regularity. The EPSC trains in the first set of simulations mimicked the pseudosynaptic stimuli used in the in vitro experiments in that the mean EPSC rate was fixed and the mean EPSC amplitude was increased to drive spiking at higher rates. This paradigm allowed us to directly compare the performance of the model against the in vitro data. In the second set of simulations (referred to as simulated synaptic stimuli to distinguish them from the above-described pseudosynaptic stimuli), we parametrically varied the mean amplitude and rate of EPSCs. Moreover, the simulated synaptic paradigm examined the influence on spike-timing regularity of three different EPSC shapes, each with different onset and offset kinetics.
Responses to pseudosynaptic stimuli with varying magnitudes.
Figure 7 shows an example of one modeled neuron responding to the pseudosynaptic stimuli. The average EPSC arrival time interval was fixed at Δti = 3 ms, and the average EPSC amplitude was varied to induce the modeled neuron to spike at different rates. For this case, the average EPSC amplitude varied from 1.5 to 450 pA (denoted on plots as 0.01× and 3×, respectively, relative to a nominal amplitude of 150 pA). We detected spikes using the spike detection algorithm described in methods. At the highest stimulus amplitudes, the spike rate did not continue to increase systematically, but instead started to experience bouts of graded depolarization and burstlike spiking (Fig. 7, arrowhead).
Fig. 7.
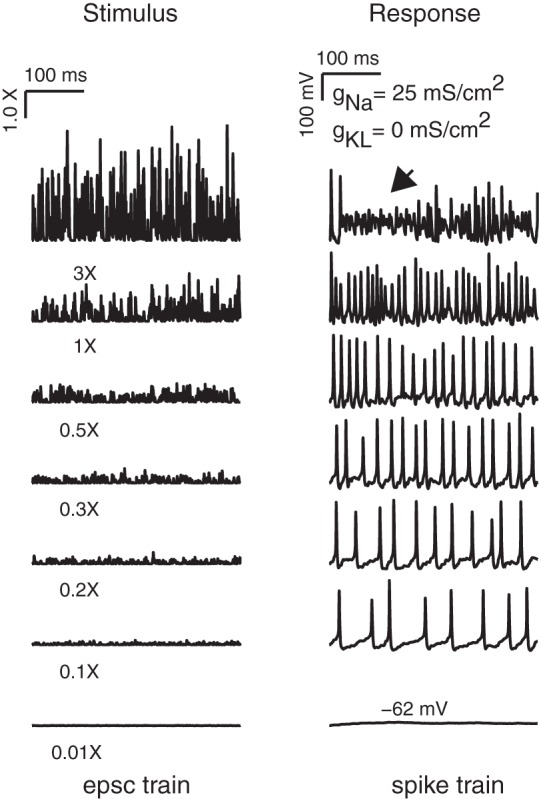
Pseudosynaptic stimuli evoked irregular firing in an example neuron. The mean inter-EPSC interval was fixed at 1 ms. To drive spiking at different rates, the neuron was stimulated with EPSCs whose average amplitude ranged from 0.01 to 3 (relative to a nominal amplitude of 150 pA; i.e., corresponding to EPSCs ranging from 1.5 to 450 pA). Periods of nonspiking, depolarization block, and burst spiking were detected at the highest stimulus amplitudes.
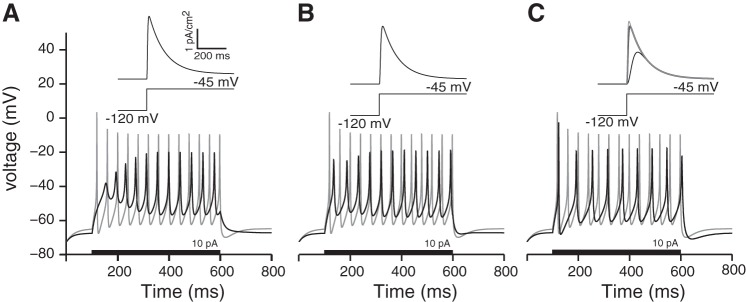
Next, we examined the regularity of the firing patterns in response to the pseudosynaptic stimuli in five modeled neurons whose step-evoked firing patterns ranged from fully transient to fully sustained (Fig. 8, A–E). We drove each of the five models to fire at a range of rates and computed the CV of each spike train (Fig. 8F plots the CV of the interspike interval as a function of mean firing interval). For neurons in Fig. 8, A–C (each of which contained gKL), the CV became smaller as the interspike interval decreased (spike rate increased). When compared at equal firing rates, each of these neurons consistently responded with more irregular firing patterns (higher values of CV) than did neurons in Fig. 8, D and E, which lacked gKL. Among the modeled neurons that contained gKL, those with larger ḡKL had more irregular firing patterns (compare the CV of the square, diamond, and triangle symbols in the zoomed image of Fig. 8G). Among the modeled neurons that lacked gKL, an increase in gNa also influenced the CV by making responses more regular (compare asterisks with cross symbols in Fig. 8G). However, this influence on spike regularity was less dramatic compared with the influence of adding gKL.
Fig. 8.
Modeled responses to pseudosynaptic currents compared with in vitro responses. A–E: current-step evoked responses of models with varying conductance densities. Different symbols represent models with different combinations of gKL and gNa. F: modeled neurons with gKL(as in A) fire more irregularly to EPSC event trains than do model neurons without gKL. G: among neurons with gKL (transient response), those with more gKL have higher CVs than those with less gKL.
The biophysical properties of the modeled neurons are effective at representing the response properties of real VGN. The CVs evoked by pseudosynaptic stimuli from real VGN somata in vitro are very similar to those evoked from our simulated somata (compare simulation results to in vitro trend lines in Fig. 8). In both the models and the recordings from VGN, the CV of transient-spiking neurons was very sensitive to the rate of spiking and decreased as the neuron had lower interspike intervals (higher rates). In contrast, the CV of sustained-spiking neurons was less dependent on rate of spiking, at least for low-magnitude EPSCs, which drove the lowest rates of spiking. As EPSC magnitudes were increased to elicit faster rates of spiking, CVs started to increase as the neurons' responses began to be dominated by the underlying irregularity in the timing of the stimulus. Although EPSC amplitude, spike rate, and concentration of gNa had an influence on spike timing regularity, the dominant trend was that neurons with gKL responded with more irregular firing patterns than did neurons without gKL.
Model responses to simulated synaptic stimuli with varying rates and shapes.
Next, we explored how the shape and arrival time of EPSCs influenced the regularity of interspike intervals. We chose two sets of model parameters to represent the transient and sustained neurons (gKL, gNa, and gleak = 1.1, 13, and 0.03 mS/cm2 and 0, 13, and 0.03 mS/cm2, respectively). The key difference between the two models was the presence of gKL in the transient-firing model. We examined the response properties of each model as a function of EPSC arrival time and the EPSC shape. To examine the influence of stimulus shape, we chose three EPSC shapes that differed in their onset and offset kinetics. These shapes abstractly represent the many complexities that can influence the kinetics of the stimulus provided to a spike generator (refer to Fig. 2 and methods for details).
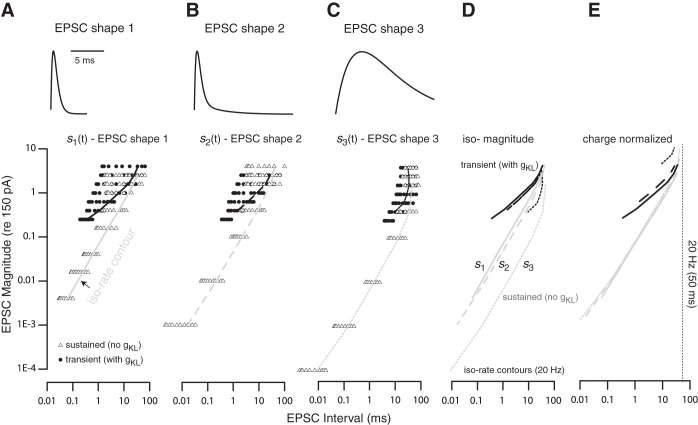
To determine if the likelihood of generating action potentials was influenced by the shape of the EPSCs, we generated three response maps (one for each EPSC shape) for each somatic model as follows (Fig. 9, A–C, a different panel for each shape). A symbol (triangle for the sustained-firing model and circle for the transient-firing model) was drawn on each plot if a particular combination of average EPSC interval and amplitude evoked spiking at an average rate of 10 Hz or greater. Stimulus conditions that evoked spiking slower than 10 Hz were not explored. At any EPSC amplitude, the algorithm incrementally increased the EPSC rate until the spike rate saturated or ceased to increase monotonically. Once a saturation or non-monotonicity in spike rate was detected, the simulation set was terminated and a new simulation set with a new combination of EPSC amplitude and rate was initiated.
Fig. 9.
Activity response maps. Graphs show the combination of EPSC amplitude and rates that induced spiking in modeled sustained-firing neurons (gKL = 0 mS/cm2, gNa = 13 mS/cm2; triangles) and transient-firing neurons (gKL = 1.1 mS/cm2, gNa = 13 mS/cm2; circles). A–C: differences in the response maps for each of 3 different EPSC shapes (insets at top) show that the magnitudes and intervals necessary to evoke firing activity depend on EPSC shape. Black and gray lines drawn on the response maps of transient-and sustained-firing neurons, respectively, indicate the EPSC magnitude and interval combinations that evoked an average spike rate of 20 Hz (iso-rate contours). D: comparison of the iso-rate contours from A–C. At any fixed EPSC interval, the transient-firing model neuron required larger EPSC magnitudes to respond with the same average rate. This current threshold was not greatly influenced by the shape of the EPSC. For the sustained-firing model, the EPSC magnitude required to induce spiking was smaller for s2(t) and s3(t) than for s1(t). E: iso-rate contours for s2(t) and s3(t) are scaled by 1.5 and 10 (shifted up the y-axis) to account for the difference in charge between them and the EPSC defined by s1(t). Note that the units of the abscissa in A should be read as a charge-normalized scale relative to charge in s1(t) for E. Iso-rate contours for the sustained-spiking model largely overlap, whereas the contours for the transient-spiking model are nonoverlapping and contract for the temporally extended stimuli.
Regardless of EPSC shape, the transient-firing model could not be excited by an EPSC train whose average event amplitudes were smaller than 15 pA. These smaller events could not evoke adequate spiking even when EPSC rate was increased, suggesting that the transient-firing model was not successful at integrating and firing. The sustained-spiking model, however, was excitable by both slowly arriving large EPSCs and rapidly arriving small EPSCs. These results suggest that the sustained-spiking models were successful at responding after integrating multiple EPSCs.
The difference between the sustained-firing and transient-firing neurons in their tendency to integrate and fire is better illustrated by examining their iso-rate (curves on Fig. 9, A–C). The iso-rate contours indicate the combination of parameters that evoked spiking at ∼20 Hz (or 50-ms interspike intervals). When directly compared (Fig. 9D), the contours for the transient-firing model (black lines) occupy a much smaller range of EPSC magnitude and intervals than do the contours of the sustained-firing model (gray lines). Also, for the transient-firing model, the contour line for s1(t) is longer and extends to shorter EPSC intervals (faster rates) than do the contour lines for either s2(t) or s3(t). In contrast, for s2(t) and s3(t), the contours for the sustained-spiking models are longer and extend to lower magnitudes and smaller EPSC intervals.
The same result can be alternately viewed by transforming the data in Fig. 9D to consider the net charge that evokes a constant rate of spiking (Fig. 9E). When the three EPSC shapes have the same magnitudes, they have a different total charge; s2(t) and s3(t) have 1.5 times and 10 times more charge than does s1(t). To account for this difference in charge, in Fig. 9E we shifted the iso-rate contours for s2(t) and s3(t) by this 1.5- and 10-fold difference in charge. These charge-normalized contour curves for the sustained-spiking model (gray curves in 9E) largely overlap with a unitary slope (except at the largest stimulus amplitudes when single events are large enough to drive spiking). The unitary slope means that the sustained-spiking model will spike at 20 Hz if the total charge delivered by the stimulus is kept constant (a 10-fold increase in EPSC amplitude must be counteracted by a 10-fold increase in EPSC interval to maintain the same charge transfer and spike rate). In contrast to the sustained-spiking model, the transient-spiking model is more sensitive to the temporal brevity of the stimulus. When driven by s2(t) [which is more temporally extended than s1(t)], both the transient-firing and sustained-firing models required smaller EPSCs to generate spiking. However, for the transient-spiking model, this advantage had a tradeoff in reducing the overall response area (note that the contour no longer extended to shorter EPSC intervals). The longer duration EPSCs of s2(t) increased the likelihood that adjacent EPSCs will overlap, creating fewer temporally distinct events to trigger spiking. Moreover, when the charge-normalized contour curves are compared, we can see that s2(t)and s3(t) required more charge transfer per event to trigger spiking at the same rate. These results suggest that the sensitivity of the transient-spiking model's response relies on both fast onsets and temporal brevity of synaptic events. Overall, these results are consistent with the idea that neurons with gKL preferentially respond to suprathreshold EPSCs with fast onsets, whereas in the absence of gKL, neurons can respond to slow depolarization and are thus successful at integrating multiple small synaptic events to generate spiking.
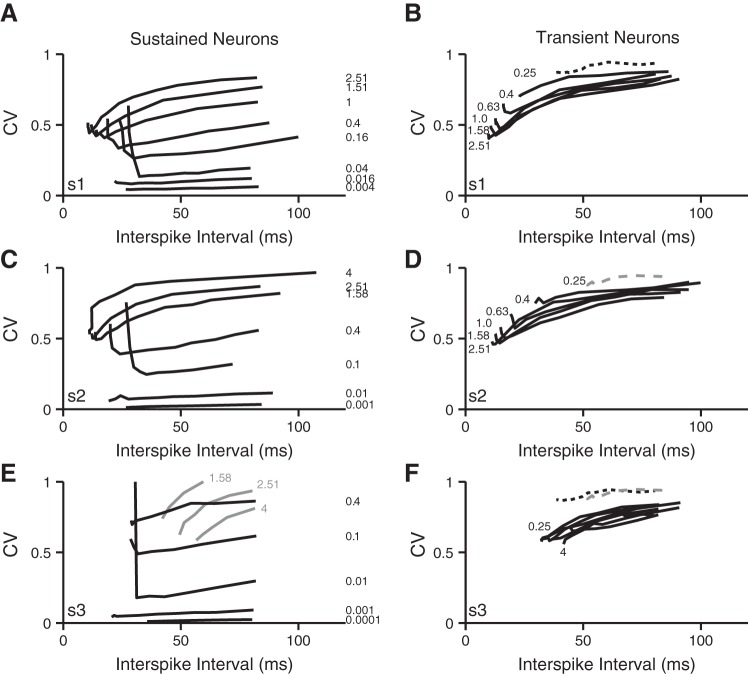
To examine the combined influence of gKL and synaptic drive on spike-timing regularity, the CV values of the same data presented in Fig. 9 are plotted and compared in Fig. 10. The evoked neural activity is grouped together by EPSC shape plus firing pattern category and parametrized by mean EPSC amplitude. Single lines represent the CV of interspike intervals as a function of mean interval. In response to each of the different EPSC shapes, the sustained-firing model produced spike trains with a wide range of regularity (CV <0.01 to CV >0.9). The most regular firing (CV ∼0.01) occurred for rapidly arriving, small-amplitude EPSCs. Although the amplitude and rate combinations producing the most regular firing are smaller and faster than reported at either vestibular calyx or inner hair cell terminals, such events could be representative of the summative activity of hundreds of synapses found on the extended terminal arbors of bouton/dimorphic afferents. In contrast, for all three EPSC shapes, the firing patterns of the transient-firing model were consistently irregular with CV >0.4, suggesting that neurons containing gKL are robust in reflecting irregularity in the timing of synaptic events.
Fig. 10.
Spike-timing regularity. Graphs show the CV of interspike intervals for the spike trains evaluated in Fig. 8. In each panel, individual lines are drawn for monotonic increases in evoked firing that accompanied increases in EPSC rate for a given a fixed mean EPSC magnitude. The magnitude scale factor (relative to a mean magnitude of 150 pA) is shown next to each line. A, C, and E show the responses of the sustained-firing neuron model to the 3 EPSC shapes, respectively. B, D, and F show the response of the transient-firing neuron model to the same 3 EPSC shapes. For comparison, the responses to the EPSC trains with a ×0.25 scale factor (plotted in B and D with dashed black and gray lines, respectively) are reproduced in F.
For both the sustained- and transient-spiking models, the firing patterns became more regular as the spike rate increased (interspike interval decreased), except at the highest rates at which many of the CV curves turned upwards, indicating that the firing patterns first became more regular as the spike rate increased but that as spike rates continued to increase, they changed their behavior to become irregular. A qualitatively similar emergence of irregularity at high spike rates is seen in recordings from in vitro VGN (Kalluri et al 2010) and in the in vivo responses of vestibular afferents (reviewed in Goldberg 2000). Although we did not explore the origin of this irregularity further, it is possible that it is an intrinsic property related to the refractory period of spike generation rather than an irregularity imposed by an extrinsic factor like synaptic timing (O'Gorman et al. 2009). However, although qualitatively similar to the upward deflection seen in vivo, in the present simulations the upturn takes place at much longer intervals (or lower rates) than seen in vivo. This difference might arise (at least in part) by the slower kinetics of ion channels at room temperature than at body temperature. Consistent with this idea, VGN spike considerably slower at room temperature than they do closer to body temperature (Kalluri et al. 2010). Faster spike rates at body temperature may also translate to more regular firing than seen in vitro.
DISCUSSION
Influence of gKL on Step-Evoked Firing Patterns
The simulations presented show that a low-voltage-gated potassium conductance (gKL) can have a potent influence on the response of modeled VGN neurons. Adding gKL changed the current-step induced firing pattern from sustained firing with a train of action potentials to transient firing with a single action potential at the onset of the step. The modeling results are consistent with the experimental observations that pharmacologically blocking gKL converted the step-evoked firing patterns of disassociated VGN from transient spiking to sustained spiking (Iwasaki et al. 2008; Kalluri et al. 2010). The presence of gKL also accounted for the more negative resting potential, higher current thresholds, faster membrane time constants, and the shorter/faster AHPs of transient-firing neurons relative to sustained-firing neurons.
Previous studies have shown that gKL partly comprises KCNQ channels in addition to KV1 channels (Kalluri et al. 2010; Pérez et al. 2009). Since the density of KCNQ channels varies by epithelial zone, afferent type, and developmental age (Hurley et al. 2006; Meredith and Rennie 2015), these channels could be important for shaping regional and developmental differences in afferent spike patterns. When we included both Kv1 and KCNQ components to IKL, the larger and faster Kv1 currents dominated the responses of modeled neurons. Incorporating a mix of KCNQ-like components and Kv1 components did not substantially influence responses (at least over the timescale examined); similar transient spiking was produced when the KCNQ-like conductance was replaced by a larger Kv1-like conductance. Although our simulations suggest that the addition of the slowly activating and noninactivating KCNQ-like component did not significantly influence the firing patterns of VGN, the ability to control the size of IKL (e.g., by efferent modulation of KCNQ channels; Pérez et al. 2009) remains a powerful potential method for controlling the responses of afferent neurons. Such influence may also depend on afferent type or epithelial location and should be considered in models of vestibular neurons that focus on regional differences in such modulatory processes.
Our results suggest that it may be possible to further refine the classification of VGN firing patterns by introducing small amounts gKL to a sustained-firing model. Adding a small amount of noninactivating gKL to a sustained-firing model reduced the interval between spikes. However, this addition also made firing patterns more phasic and hyperpolarized resting potentials. Adding a small amount of a rapidly inactivating gKL (see appendix a) had the opposite effect in that it increased the intervals between spikes. Depending on the size of the current, the addition of the rapidly inactivating current also created a “buildup-and-fire” pattern that has not been observed in VGN. Whole cell voltage-clamp recordings from sustained-firing VGN suggest that these somata may have small amounts of both rapidly inactivating potassium currents and noninactivating linopirdine-sensitive currents (Eatock et al. 2008; Kalluri et al. 2010, respectively), although the size of the former may have been exaggerated by the lack of voltage clamp during sodium channel activation. The present simulations provide a framework to test if the broadly defined group of sustained-firing neurons can be further subclassified.
Influence of gNa and Other Inward Currents on Step-Evoked Firing Patterns
Previous in vitro studies showed that the sustained-firing category is a broad group with some neurons firing long trains of action potentials (sustained-a) and other neurons firing only one action potential followed by voltage oscillations (sustained-c). Although the spike patterns of the sustained category are varied, the group shares similar resting potentials, input resistances, and current thresholds (Kalluri et al. 2010). The present modeling suggests that these shared properties originate from sustained-firing neurons having little gKL. In contrast, varying the density of transient gNa produced only small changes to current threshold, resting potential, or membrane time constant. Despite having little influence on the shared properties of sustained-spiking VGN, variations in the density of gNa successfully accounted for the sustained-a,-b, and -c firing patterns. For example, when the density of the sodium current was increased (in the absence of gKL), the firing patterns of the model changed from a short spike followed by voltage oscillations (sustained-c) to long trains of action potentials (sustained-a).
With the ion channel combinations modeled here, sustained spiking was achieved by excluding gKL but also by using sufficiently large gNa to produce robust spiking. Our analysis of transient inward currents from previously published whole cell currents suggested that sodium current densities from second postnatal week VGN are nearly fourfold larger than the currents from the first postnatal week (data shown in appendix d). That inward currents grow during development is not surprising since other currents in VGN also grow during the first 2 postnatal weeks (e.g., Almanza et al. 2012; Chabbert et al. 1997; Chambard et al. 1999; Iwasaki et al. 2008). However, in constructing the present model, we assumed that only sodium channels modeled here contribute to the upstroke of action potential generation. Real VGN have other ion channels that also could contribute [for instance, T-type calcium channels (Chambard et al. 1999; Limón et al. 2005), a variety of sodium channel subunits (Liu 2012), and HCN channels (Almanza et al. 2012)]. Thus the present predictions about the influence of sodium currents on firing patterns may be better viewed as a general prediction about the net influence of depolarizing currents. Incorporating other inward conductances in future models might make the use of very large sodium conductances unnecessary.
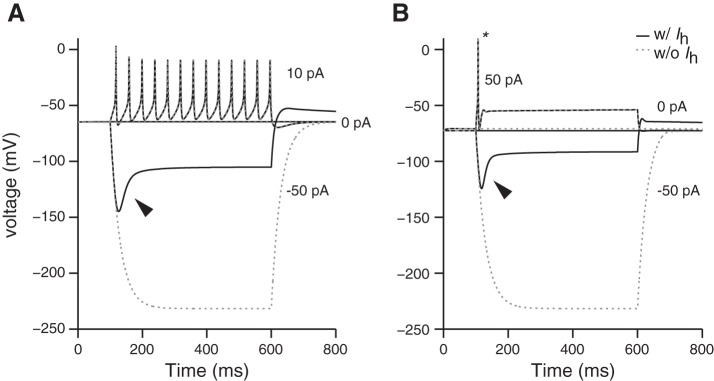
In many neuronal systems, the inward currents of HCN-mediated channels (Ih) not only amplify the depolarizing phase of action potentials but also produce highly regular spiking (reviewed in Accili et al. 2002; DiFrancesco 2010; Maccaferri and McBain 1996). The present model suggests that the activation range of Ih in isolated/cultured VGN is too negative to shape the neurons' in vitro spike patterns (see appendix c and Almanza et al. 2012; Chabbert et al. 2001). Consistent with this characterization, in vitro isolated VGN and modeled VGN do not spike spontaneously. This prediction is consistent with several previous studies in VGN (Almanza et al 2012; Chabbert et al. 2001), which showed that blocking Ih had little effect on VGN spike patterns. These results are at odds with a recent study (Yoshimoto et al. 2015) in which the HCN channel blocker ZD7288 had a potent influence on the firing patterns of isolated VGN. One explanation is that ZD7288 can also block T-type calcium channels and some types of sodium channels (Felix et al. 2003; Wu et al. 2012). Both of these channel types are known to be present in VGN and could participate in triggering spikes. Alternatively, the difference across studies may result from variations in experimental conditions. For example, the activation range of HCN channels can shift depending on the intracellular concentration of cAMP (e.g., by efferent modulation of cyclic nucleotide-dependent mechanisms, reviewed in Almanza et al. 2012; Horwitz et al. 2011). Such modulatory processes could make the current more physiologically available under different conditions. Indeed, recent recordings from the calyx terminals of dimorphic afferents suggest that Ih currents shape postsynaptic events (Meredith et al. 2012) and are important for spontaneous spiking (in the absence of hair cell input) and contribute to spike-timing regularity (Horwitz et al. 2014). Since the influence of Ih on spiking activity depends on several factors including developmental age, cell type, recording conditions, and intracellular concentration of cAMP and other second messengers, the mechanisms underlying its influence on the responses of VGN and on vestibular afferents in vivo requires further study.
Significance of Somatic Ion Channels
We placed synaptic conductances onto our models of VGN somata based on the assumption that ion channels found on the cell bodies of vestibular afferents could serve as proxies for the groups of ion channels found at their spike initiation zones. Emerging immunohistochemical and electrophysiological evidence supports this assumption (also discussed in Kalluri et al. 2010). Antibody labeling locates relevant ion channels in both the somata and peripheral terminals of vestibular afferents (Hurley et al. 2006; Lysakowski et al. 2011; Rutherford et al. 2012; Wooltorton et al. 2006). Other bipolar neurons (e.g., dorsal root ganglion and spiral ganglion) also express in their somata the same ion channels believed to be important in shaping responses at their peripheral terminals (e.g., Black et al. 2012; Hossain 2005; Rose et al. 2013; Yi et al. 2010). Recent recordings from vestibular and auditory afferent terminals are confirming that the ion channels found at the cell body are relevant for shaping neuronal responses at the terminals (Meredith and Rennie 2015; Songer and Eatock 2013; Yi et al. 2010). Therefore, although the action potentials of vestibular afferents in vivo do not originate at the cell body, the ion channels found there are likely to be similar to those found at vestibular terminals near the spike initiation zone.
Influence of gKL on Spike-Timing Regularity
We demonstrated that the presence/absence of gKL was sufficient to account for a significant difference in spike-timing regularity. Simulated VGN that had gKL responded to synaptic noise with irregular spike patterns, whereas simulated VGN that did not have gKL responded with more regular patterns. In the presence of gKL, modeled neurons responded to pseudosynaptic events with highly irregular spike patterns, whereas those without gKL responded with more regular patterns. When modeled somata were injected with pseudosynaptic stimuli similar to those applied experimentally (Kalluri et al. 2010), the observed dependence of CV on spike interval was remarkably consistent with that seen for real VGN. Thus the ability of the model to capture the response features of VGN to both simple step-evoked stimuli and more complex pseudo-synaptic stimuli is strong validation that the ion channel properties modeled in this study captured the dominant biophysical mechanisms underlying the diversity of firing patterns in VGN.
To explore how extrinsic factors related to the stimulus influence spike timing when coupled to somata with different ion channel properties (as proxies for the spike initiation zones), we drove our models with a variety of different synaptic conductances. The tendency for irregular spiking by the model that included gKL did not differ with modifications in synaptic rate, onset time course, or duration of synaptic events. However, modeled VGN with gKL were less likely to fire action potentials when driven by small or slower onset synaptic events. They were more likely to spike when synaptic events had rapid onsets. Extended decays also helped simulated neurons reach threshold. These simulations reinforced the idea that gKL is important for encoding rapid onsets to preserve the temporal fidelity of synaptic events. Similar ideas about the role of gKL in encoding rapid onsets have been long proposed in the auditory system (e.g., Ferragamo and Oertel 2002). In keeping with similar suggestions in the timing pathways of the auditory system (reviewed in Trussell 1999), efficient temporal encoding in vestibular terminals may require a complimentary coupling between a fast-synaptic conductance, low-voltage-gated potassium current and a synaptic morphology that is electronically close to the synapse. It would be hard to initiate spiking from a spike initiation zone that contains gKL if the input is provided by electrotonically distant synapses whose events would slow down and attenuate as EPSPs propagate through the dendritic arbor. This suggestion is consistent with the observation that irregular spiking originates from the central zones of the vestibular epithelia, where the most compact dendritic arbors in the vestibular epithelia are found. Indeed, immunolabeling and electrophysiological evidence indicate that the complex calyces of striolar afferents (which clearly correspond to irregularly firing afferents) have gKL and respond to current steps with transient-spike patterns (Lysakowski et al. 2011; Songer and Eatock 2013). Consistent with the prediction that neurons with gKL may benefit from a close coupling between synapse and spike initiation zone, the first heminodes of striolar calyces begin immediately below the cup of the calyx, whereas the first heminodes of peripheral calyces are located farther from their hair cells (Lysakowski et al. 2011).
In the absence of gKL (i.e., for the sustained-spiking model), the regularity of simulated firing patterns depended on the amplitude of EPSCs. In response to small-amplitude synaptic events, the simulated VGN reached threshold only after integrating events that arrived in rapid succession. Such integration drove spiking that was more regular than the underlying timing of the stimulus. The most regular firing patterns (those with CVs <0.2) were evoked only when the sustained-spiking models were driven by small, rapidly spaced EPSCs. Although the size of these events was considerably smaller than that of those reported at calyx terminals (<1 pA compared with the 10- to 60 pA mini EPSCs of Sadeghi et al. 2014), spatially and temporally dispersed events such as those provided by distant boutons may have the same net influence. This idea is consistent with a previous observation from canal afferents showing greater numbers of bouton terminals in regularly firing dimorphic afferents that terminate in the more peripheral regions of the cristae (e.g., Lysakowski et al. 1995). Similarly, intra-axonal recordings from bouton-bearing afferents of turtle suggest that the synaptic events driving irregular firing are larger and arrive at slower intervals than the synaptic events driving regular firing (Goldberg and Holt 2013). In simulations that used larger magnitude EPSCs, modeled neurons that lacked gKL reached threshold more frequently in response to individual large-amplitude synaptic events. In these cases, some of the random timing of the synaptic drive was reflected in the irregularity of the resulting spike pattern. These simulations suggest that the absence of gKL alone is not sufficient to account for highly regular spiking but that such responses require a combination of small-conductance, high-rate synaptic drive and ion channel properties that enable the neuron to integrate across multiple EPSCs.
The secondary dependence of spike-timing regularity on the features of the synaptic input suggests that although the presence of gKL is sufficient to account for highly irregular firing, highly regular spiking requires both the lack of gKL and something more. The discrepancy between in vitro and in vivo responses could be partially accounted for by the faster ion channel kinetics at the higher body temperatures of in vivo recordings. Such increases in temperature would increase firing rates and consequently produce more regular spiking. For example, a CV of 0.20 at an average spike interval between 50 and 70 ms corresponds to a rate-normalized CV (CV*) between 0.1 and 0.05. These values are well within the expected range for the regular-firing group in vivo. However, there are alternative/additional mechanisms that may also bridge the gap. The present model's finding that sustained-spiking models can fire with a wide range of CVs depending on the features of the stimulus is interesting. Heterogeneity in electrotonic distance, as might result from diverse dendritic morphologies, seems like an intuitive mechanism for creating synaptic events with variable size, shape, and rate. However, previous computational studies concluded that such synaptic attenuation would not be significantly different between vestibular dimorphs from central and peripheral zones of the sensory epithelia (see discussion in Goldberg 2000). An alternative and not mutually exclusive hypothesis is that other currents (e.g., Ih as suggested by Horwitz et al. 2014) can push afferents that lack gKL to fire with extreme regularity. The addition of such currents may make it unnecessary to use extremely fast and small EPSCs to generate highly regular firing. Future work is needed to explore whether an additional ion channel can push the firing patterns of sustained-spiking models into the highly regular range.
Comparison to an Earlier Model
Early observation of the subthreshold activity of vestibular afferents' firing patterns suggested that their ion channels shape their responses. A key observation was that the afterhyperpolarization trajectory (AHP; the voltage trajectory after the downstroke of an action potential) of firing patterns with irregular spike timing was shorter and noisier than the afterhyperpolarization trajectory of firing patterns with regular timing. This observation led to the idea (central to this study) that spike-timing regularity might be shaped by the ion channel properties of the neuron (Highstein and Politoff 1978; Schessel and Highstein 1981). An influential phenomenological model based on these ideas showed how simple differences in a hypothetical “afterhyperpolarization potassium current” can shape the spike-timing regularity of vestibular neurons (Smith and Goldberg 1986). When the Smith and Goldberg model included the AHP current, the modeled neurons fired regularly spaced action potentials in response to synaptic noise. These responses had the deep and long-duration AHPs characteristic of the regular-firing responses observed in vivo. When the AHP current was removed from the model, the simulated neurons fired irregularly spaced action potentials (Smith and Goldberg 1986). The present model is similar to the Smith and Goldberg model in its suggestion that a difference in potassium currents contributes to differences in spike-timing regularity, but the present model differs in its key prediction. In the present model, irregular firing (not regular firing) was driven by the presence of persistent low-voltage-gated potassium channels (gKL). The increased resting conductance that comes from having open gKL channels also accounted for the short and rapidly recovering AHPs that are characteristic of irregularly firing afferents in vivo.
In summary, although the true milieu of ion channels present in vestibular ganglion neurons may be very complex, this model demonstrated that a simple difference in the density of gKL can go a long way toward accounting for many hallmark features of vestibular ganglion and vestibular afferent responses. By incorporating the biophysical properties representative of actual channels known to be present in these neurons, this model takes a first step toward understanding how specific ion channels shape responses in the vestibular nerve.
GRANTS
This research was supported by National Institute on Deafness and Other Communication Disorders Grant R03DC012652 (to R. Kalluri), the House Research Institute, and the Department of Otolaryngology at the University of Southern California.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
A.E.H. and R.K. performed experiments; A.E.H. and R.K. analyzed data; A.E.H. and R.K. interpreted results of experiments; A.E.H. and R.K. prepared figures; A.E.H. and R.K. drafted manuscript; A.E.H. and R.K. edited and revised manuscript; A.E.H. and R.K. approved final version of manuscript; R.K. conception and design of research.
ACKNOWLEDGMENTS
We thank R. A. Eatock, R. L. Goldsworthy, and the anonymous reviewers for valuable discussion and comments on previous versions of the manuscript.
APPENDIX A: KINETIC EQUATIONS FOR CONDUCTANCES
The kinetic equations describing the four currents IKL, IKH, INA, and Ileak are based on the descriptions of these currents from Rothman and Manis (2003b) with minor variations in the parameters used for the sodium conductance and with maximum conductance values ḡKL, ḡKH, ḡNa, and ḡleak chosen to be within the physiological range for vestibular ganglion neurons. The equations are summarized below for completeness.
Low-Voltage-Gated K+ Current
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Modifications to Represent Kv7 and Rapidly Inactivating Components of IKL
To represent the activation and inactivation kinetics of KV1, KV7, and rapidly inactivating potassium currents (IKLA), we made the following modifications to the equations governing the voltage-dependent kinetics of IKL. The outcome of the modifications was to generate three versions of the current. Each version activated and inactivated over similar voltage ranges (as in Fig. A1A) but with different activation and inactivation time courses (Fig. A1B). The first is the formulation for the Kv1 component of IKL. It activated quickly and inactivated to half its maximum value over a relatively slow time course (Fig. A1B, thick solid line; see also Eq. 15). For the second version, we modified the activation time course τw (Eq. 15) with τwkv7 (Eq. 17) to represent the slower activation of Kv7-type currents (Fig. A1B, dashed line).
| (17) |
Fig. A1.
Voltage dependence and kinetics of IKL. A: voltage dependence of channel activation (w∞4; solid line) and inactivation (z∞; dashed line). B: IKL simulated for a voltage-clamp step that depolarizes the cell from an initial voltage of −140 mV (outside the activation range of IKL) to −45 mV (within the activation range for IKL). Simulations show 3 currents: the first is a Kv1-type current that activates fast and inactivates slowly but only partially (thick solid line), the second is a KCNQ-type current with slow activation and no inactivation (Kv7; dashed line), and the third is a transient current that activates fast and inactivates fast and completely (IKLA; thin solid line).
To simulate the lack of inactivation in the Kv7-like version, we made z∞ equal to zero in Eq. 14.
Rapidly inactivating potassium currents have been reported in VGN (e.g., Risner and Holt 2006; Eatock et al. 2008) and in vestibular calyx terminals (Meredith and Rennie 2015). Some of this current in VGN may have been the result of inadequate voltage clamp in the presence of sodium current. Nevertheless, given its observation under different experimental conditions, we decided to explore how such inactivation kinetics might influence spike patterns. Thus, in a third version of IKL, we retained the fast activation of the Kv1-type current while making the current completely inactivate. This was accomplished by making the variable γ in Eq. 14 equal to zero and modifying τz into τzA (see Eq. 18 and Fig. A1B). Although such inactivation kinetics are similar to the inactivation expected for different types of transient potassium currents (A-type currents) as described in models of auditory neurons (e.g., Rothman and Manis 2003b), the present model of the current is based on a modification of IKL rather than an explicit model of the physiological current found in VGN. Thus we refer to it here as IKLA.
| (18) |
High-Voltage-Gated K+ Current
| (19) |
| (20) |
| (21) |
Fast Na+ Current: Standard
| (22) |
| (23) |
| (24) |
APPENDIX B: HOW THE KINETICS OF OTHER IKL COMPONENTS SHAPE FIRING PATTERNS
To examine how IKL containing Kv1-like and Kv7-like components in different proportions influenced spiking, we simulated responses with IKL governed by the following equation:
| (25) |
The parameters γkv1 and γkv7 defined the proportion of the total current carried by the two components, respectively. The equations governing the activation and inactivation parameters (wi and zi, respectively) for each type of current are described together with other currents in appendix a.
Changing the proportions of the Kv1 vs. Kv7 components of IKL did not significantly affect resting potential, action potential amplitude, shape, or the number of action potentials evoked by a current step (Fig. A2A). However, the relative balance between the Kv1 and Kv7 components did influence the trajectory of the afterhyperpolarization (AHP); the transmembrane voltage recovered faster when IKL was composed of larger proportions of Kv1. Also, when IKL was primarily composed of Kv1-like currents, the AHP was followed by a short depolarization. In contrast, when IKL was composed only of Kv7-like currents, the AHP was slower and did not have the overshooting depolarization.
On the basis of in vitro recordings, we estimate that the Kv7 component of IKL accounts for at ∼20% of the total IKL in transient-firing VGN (Kalluri et al. 2010). The present simulations suggest that at these ratios, the different kinetics of Kv7 component have little influence on the distinction between transient and sustained firing patterns (Fig. A2A) and only a small influence on the shape of the AHP (see Fig. A2A, inset). On the basis of these results, we concluded that the Kv7 component of IKL is likely to be most potent when the size of the total current is affected by modulating Kv7 channels (e.g., by efferent activity). Because the dominant effect of IKL (in making spike patterns transient) is captured by a pure Kv1 component, we simplified our representation of IKL by removing the Kv7 component from subsequent simulations.
Fig. A2.
Different IKL components. A: firing patterns and AHPs (inset) when the relative balance between Kv1 and KCNQ-like currents is varied. Black horizontal bars show the duration of the 100-pA current step used to evoke spiking. Models with larger Kv1 had faster AHPs. Models with larger KCNQ have a longer AHP without overshoot. B: spike patterns when a rapidly inactivating potassium conductance (gKLA) was added to a transient spiking model (gKL = 1.1 mS/cm2, gNa = 13 mS/cm2).
Next, we examined whether adding a rapidly inactivating conductance (gKLA) to gKL influences spiking. First, we simulated model responses when IKL was defined as the sum of two components: IKL + IKLA = (ḡKLwkv14zkv1 + ḡKLAwkvA4zkvA)S(V − EK). The first component had the fast activation and slow inactivation kinetics of Kv1, whereas the second component had the fast activation kinetics of Kv1 but inactivated rapidly and completely. The equations governing the inactivation kinetics of gKLA are defined in appendix a.
Adding gKLA to the transient-firing model did not substantially change the firing pattern; i.e., transient firing patterns did not become sustained firing patterns (Fig. A2B). Even doubling the total potassium conductance yielded only a modest change to the steady-state potentials (e.g., the resting potential) because even when present, IKLA inactivated rapidly and substantially (as in Fig. A1B). As IKLA was increased, the model required larger current steps to reach spike threshold (note in Fig. A2B that the model is not spiking for the larger values of IKLA).
IKLA also influenced the time course of the AHP. Initially, the combined potassium conductance produced a deep AHP and rapid recovery. However, as IKLA inactivated during prolonged current injection, a second, slower phase to the afterhyperpolarization emerged. However, this second phase was most obvious when simulations contained IKLA but no other persistent components of IKL (i.e., when IKLA was added to sustained-spiking models; Fig. A2B, arrowhead). We decided to exclude the IKLA component from our representative model of transient-spiking neurons based on the reasoning that the current either has a small influence on the rapid recovery time of transient-spiking neurons or that if present in large amounts, it would have created a biphasic AHP trajectory that has not been reported in VGN.
To understand how IKLA influenced firing patterns in the absence of other IKL components, we simulated firing patterns in a sustained-spiking model with the addition of IKLA. We examined how the onset kinetics of IKLA influenced spiking (Fig. A3, A–C, insets). Overall, the addition of IKLA to the sustained-firing model affected the onset of spiking and slowed the spike rate. The initial inhibition of spiking seen in Fig. A3A is similar to the “buildup-and-fire” patterns seen in some auditory neurons. Our results are consistent with models of auditory neurons in which such buildup-and-fire responses have been attributed to the action of transient potassium currents (Kanold and Manis 1999, 2001). In this case the buildup phase depended on the kinetics of IKLA activation (compare Fig. A3, A–C). As the activation time course slowed, the inactivation began before the current fully activated. As a result, the peak transient current became smaller and had less influence on the onset of the spike pattern. In such cases, the buildup pattern was less prominent and the presence of IKLA appeared to slow the rate of spiking. As these simulations illustrate, the influence of rapidly inactivating potassium currents on the sustained-spiking model can be complex and can depend on the detailed representation of the current. Because we have not observed buildup-and-fire patterns in whole cell recordings from disassociated VGN and IKLA was not a dominant contributor toward creating the distinction between sustained vs. transient-firing patterns, we excluded this current from subsequent simulations.
Fig. A3.
Effect of rapidly inactivating potassium currents on sustained spiking. In A–C, the firing pattern of the baseline sustained-spiking model (gray line; gNa = 13 mS/cm2, gKL = 0 mS/cm2) is compared with the firing pattern after addition of a rapidly inactivating conductance (black line; gKLA = 1.1 mS/cm2). Firing patterns are shown in response to a 10-pA current step. Three versions of gKLA were modeled, each with fast, moderate, and slow activation kinetics (A, B, and C, respectively; see insets for representative voltage-clamp responses). A: when gKLA had rapid activation and inactivation, the beginning of the spike train was suppressed to create an overall “buildup-and-fire” response pattern. B: responses had shorter buildup times when the activation kinetics were slower. C: for the slowest activation kinetics, the response does not have a notable buildup time. In this case the presence of gKLA also slowed the overall spike rate. As the activation kinetics of gKLA slowed down, the net low-voltage-gated current became smaller because the current did not fully activate before rapid inactivation began (comparison of 3 currents in voltage clamp is shown in C, inset).
APPENDIX C: ADDING Ih DID NOT INFLUENCE RESPONSES OF THE PRESENT MODEL
In a preliminary version of the model, we also included a hyperpolarization-activated cationic current to be consistent with the observation that VGN show prominent Ih-mediated voltage sags. We used ongoing recordings in our laboratory (preliminary results presented in Ventura and Kalluri 2014) together with literature (Almanza et al. 2012; Rothman and Manis 2003b) to represent the activation range, kinetics, and conductance density of Ih (Eqs. 26–28).
| (26) |
| (27) |
| (28) |
The firing patterns of modeled transient-firing and sustained-firing VGN were not significantly influenced by the inclusion of hyperpolarization-activated cationic currents (Fig. A4, A and B). Although including the current created the hyperpolarization-induced voltage sag characteristic of Ih (arrowheads), the resting potential, spike shapes, and firing patterns evoked by depolarizing currents remained nearly identical to those in the simulations without Ih (compare dashed lines with solid lines). In the model, the very negative activation range of Ih accounts for this lack of influence, because although the current was capable of creating voltage sags in response to deep hyperpolarization, very little current was available near resting potential to influence spiking. Thus we excluded the Ih current from the main simulations based on the rationale that the activation range of the current was too negative to influence spiking activity in the in vitro experiments that served as the referent against which this model was validated (Kalluri et al. 2010).
Fig. A4.
Firing patterns with and without Ih. A: response patterns of a modeled transient-firing VGN when driven by a series of hyperpolarizing and depolarizing current steps. Solid lines show responses without (w/o) Ih, and dashed lines show responses with (w/) Ih. B: same as A, but for a modeled sustained-firing VGN. Although hyperpolarizing steps reveal the voltage sag characteristic of Ih, the current does not significantly influence resting potentials, AHPs, or depolarization-induced firing patterns.
APPENDIX D: SODIUM CURRENT DENSITY GROWS DURING DEVELOPMENT
To estimate a range for sodium conductance density in second postnatal week VGN, we measured the voltage dependence of sodium current inactivation from whole cell voltage-clamp recordings. These recordings were from cells that were previously characterized as firing with sustained or transient firing patterns (Kalluri et al. 2010). To characterize the sodium channel inactivation, we applied a series of 40-ms-long prepulses that held that cell at voltages ranging from −120 to 0 mV in 5-mV increments. After the prepulse, the cell was depolarized to −20 mV. This depolarization induced an inward transient current that we attribute to sodium channels (time point indicated by arrow in Fig. A5A). The peak current evoked by the step to −20 mV (the tail current) plotted as a function of the prepulse potential shows the voltage dependence of sodium current inactivation in this example cell (Fig. A5B). Next, we computed the instantaneous conductance of the sodium current by normalizing the current with the estimated driving force [−20 to +87 mV (the estimated reversal potential for sodium currents in this preparation)]. The resulting conductance values were normalized by the cell surface area (as estimated by the cell capacitance) to estimate the sodium conductance density in seven individual VGN (Fig. A5C; each curve represents 1 cell). The conductance densities ranged from ∼2 to 10 mS/cm2. The latter value is at least two times greater than the estimates based on first postnatal week recordings in the literature (e.g., Chabbert et al. 1997; Risner and Holt 2006). The sample size used in this case was too small to reveal if there were differences in sodium conductance between transient- and sustained-firing neurons (Fig. A5C, black vs. gray symbols). Overall, these data suggest that sodium current densities can be larger in the second postnatal week than in the first week. Moreover, these data are likely to underestimate the true sodium conductance density because they are based on the inactivated sodium current and on recording methods (e.g., perforated-patch methods that produce electrodes with large series resistance) that were not optimized for characterizing sodium currents.
Fig. A5.
Sodium currents inferred from whole cell recordings of second postnatal week VGN. Data were collected at the same time as the data reported in Kalluri et al. 2010. A: transient inward currents induced by a series of voltage steps (bottom). B: the voltage dependence of sodium channel inactivation is characterized by plotting the maximum inward current measured during the −20-mV step as a function of the prepulse voltage. C: sodium conductance density computed by dividing the voltage-dependent sodium inactivation curves (as in B) by an estimate of sodium driving force (−20 to 87 mV, where −87 mV is the estimated reversal potential for sodium channels in this preparation). Conductance curves are shown for 7 VGN ranging in age from P11 to P14 (solid vs. open symbols indicate neurons with sustained vs. transient firing patterns).
REFERENCES
- Accili EA, Proenza C, Baruscotti M, DiFrancesco D. From funny current to HCN channels: 20 years of excitation. News Physiol Sci 17: 32–37, 2002. [DOI] [PubMed] [Google Scholar]
- Almanza A, Luis E, Mercado F, Vega R, Soto E. Molecular identity, ontogeny, and cAMP modulation of the hyperpolarization-activated current in vestibular ganglion neurons. J Neurophysiol 108: 2264–2275, 2012. [DOI] [PubMed] [Google Scholar]
- Baird RA, Desmadryl G, Fernández C, Goldberg JM. The vestibular nerve of the chinchilla. II. Relation between afferent response properties and peripheral innervation patterns in the semicircular canals. J Neurophysiol 60: 182–203, 1988. [DOI] [PubMed] [Google Scholar]
- Black JA, Frézel N, Dib-Hajj SD, Waxman SG. Expression of Nav1.7 in DRG neurons extends from peripheral terminals in the skin to central preterminal branches and terminals in the dorsal horn. Mol Pain 8: 82, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brugeaud A, Gaboyard-Niay S, Puel JL, Chabbert C. Hypergravity affects the developmental expression of voltage-gated sodium current in utricular hair cells. Neuroreport 17: 1697–1701, 2006. [DOI] [PubMed] [Google Scholar]
- Cervantes B, Vega R, Limón a Soto E. Identity, expression and functional role of the sodium-activated potassium current in vestibular ganglion afferent neurons. Neuroscience 240: 163–175, 2013. [DOI] [PubMed] [Google Scholar]
- Chabbert C, Chambard J, Valmier J. Voltage-activated sodium currents in acutely isolated mouse vestibular ganglion neurones. Neuroreport 8: 1253–1256, 1997. [DOI] [PubMed] [Google Scholar]
- Chabbert C, Chambard JM, Valmier J, Sans A, Desmadryl G. Hyperpolarization-activated (Ih) current in mouse vestibular primary neurons. Neuroreport 12: 2701–2704, 2001. [DOI] [PubMed] [Google Scholar]
- Chambard JM, Chabbert C, Sans a., Desmadryl G. Developmental changes in low and high voltage-activated calcium currents in acutely isolated mouse vestibular neurons. J Physiol 518: 141–149, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiFrancesco D. The role of the funny current in pacemaker activity. Circ Res 106: 434–446, 2010. [DOI] [PubMed] [Google Scholar]
- Eatock RA, Xue J, Kalluri R. Ion channels in mammalian vestibular afferents may set regularity of firing. J Exp Biol 211: 1764–1774, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felix R, Sandoval A, Sánchez D, Gómora JC, De La Vega-Beltrán JL, Treviño CL, Darszon A. ZD7288 inhibits low-threshold Ca2+ channel activity and regulates sperm function. Biochem Biophys Res Commun 311: 187–192, 2003. [DOI] [PubMed] [Google Scholar]
- Fernández C, Baird a R, Goldberg JM. The vestibular nerve of the chinchilla. I. Peripheral innervation patterns in the horizontal and superior semicircular canals. J Neurophysiol 60: 167–181, 1988. [DOI] [PubMed] [Google Scholar]
- Ferragamo MJ, Oertel D. Octopus cells of the mammalian ventral cochlear nucleus sense the rate of depolarization. J Neurophysiol 87: 2262–2270, 2002. [DOI] [PubMed] [Google Scholar]
- Glowatzki E, Fuchs P. Transmitter release at the hair cell ribbon synapse. Nat Neurosci 5: 147–154, 2002. [DOI] [PubMed] [Google Scholar]
- Glowatzki E, Grant L, Fuchs P. Hair cell afferent synapse. Curr Opin Neurobiol 18: 389–395, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JM. Afferent diversity and the organization of central vestibular pathways. Exp Brain Res 130: 277–297, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JM, Fernández C. Vestibular mechanisms. Annu Rev Neurosci 2: 265–289, 1979. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Holt JC. Discharge regularity in the turtle posterior crista: comparisons between experiment and theory. J Neurophysiol 110: 2830–2848, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg JM, Lysakowski A, Fernández C. Morphophysiological and ultrastructural studies in the mammalian cristae ampullares. Hear Res 49: 89–102, 1990. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Smith CE, Fernández C. Relation between discharge regularity and responses to externally applied galvanic currents in vestibular nerve afferents of the squirrel monkey. J Neurophysiol 51: 1236–1256, 1984. [DOI] [PubMed] [Google Scholar]
- Grant L, Yi E, Glowatzki E. Two modes of release shape the postsynaptic response at the inner hair cell ribbon synapse. J Neurosci 30: 4210–4220, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Highstein SM, Holstein GR, Mann MA, Rabbitt RD. Evidence that protons act as neurotransmitters at vestibular hair cell-calyx afferent synapses. Proc Natl Acad Sci USA 111: 5421–5426, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Highstein SM, Politoff AL. Relation of interspike baseline activity to the spontaneous discharges of primary afferents from the labyrinth of the toadfish,. Brain Res 150: 182–187, 1978. [DOI] [PubMed] [Google Scholar]
- Horwitz GC, Risner-Janiczek JR, Holt JR. Mechanotransduction and hyperpolarization-activated currents contribute to spontaneous activity in mouse vestibular ganglion neurons. J Gen Physiol 143: 481–497, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horwitz GC, Risner-Janiczek JR, Jones SM, Holt JR. HCN channels expressed in the inner ear are necessary for normal balance function. J Neurosci 31: 16814–16825, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hossain WA. Where is the spike generator of the cochlear nerve? Voltage-gated sodium channels in the mouse cochlea. J Neurosci 25: 6857–6868, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurley KM, Gaboyard S, Zhong M, Price SD, Wooltorton JRA, Lysakowski A, Eatock RA. M-like K+ currents in type i hair cells and calyx afferent endings of the developing rat utricle. J Neurosci 26: 10253–10269, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishiyama G, Lopez I, Williamson R, Acuna D, Ishiyama A. Subcellular immunolocalization of NMDA receptor subunit NR1, 2A, 2B in the rat vestibular periphery. Brain Res 935: 16–23, 2002. [DOI] [PubMed] [Google Scholar]
- Iwasaki S, Chihara Y, Komuta Y, Ito K, Sahara Y. Low-voltage-activated potassium channels underlie the regulation of intrinsic firing properties of rat vestibular ganglion cells. J Neurophysiol 100: 2192–2204, 2008. [DOI] [PubMed] [Google Scholar]
- Kalluri R, Xue J, Eatock RA. Ion channels set spike timing regularity of mammalian vestibular afferent neurons. J Neurophysiol 104: 2034–2051, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanold PO, Manis PB. Transient potassium currents regulate the discharge patterns of dorsal cochlear nucleus pyramidal cells. J Neurosci 19: 2195–2208, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanold PO, Manis PB. A physiologically based model of discharge pattern regulation by transient K+ currents in cochlear nucleus pyramidal cells. J Neurophysiol 85: 523–538, 2001. [DOI] [PubMed] [Google Scholar]
- Limón A, Pérez C, Vega R, Soto E. Ca2+-activated K+-current density is correlated with soma size in rat vestibular-afferent neurons in culture. J Neurophysiol 94: 3751–3761, 2005. [DOI] [PubMed] [Google Scholar]
- Liu XP. Sodium Channel Diversity in the Vestibular Ganglion: Evidence for NaV1.5-Like and NaV1.8-Like Currents. Cambridge, MA: Harvard–MIT Program in Health Sciences and Technology, 2012. [Google Scholar]
- Lysakowski A, Gaboyard-Niay S, Calin-Jageman I, Chatlani S, Price SD, Eatock RA. Molecular microdomains in a sensory terminal, the vestibular calyx ending. J Neurosci 31: 10101–10114, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lysakowski A, Minor LB, Fernández C, Goldberg JM. Physiological identification of morphologically distinct afferent classes innervating the cristae ampullares of the squirrel monkey. J Neurophysiol 73: 1270–1281, 1995. [DOI] [PubMed] [Google Scholar]
- Maccaferri G, McBain CJ. The hyperpolarization-activated current (I) and its contribution to pacemaker activity in rat CA1 hippocampal stratum oriens-alveus interneurones. J Physiol 497: 119–130, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsubara A, Takumi Y, Nakagawa T, Usami S, Shinkawa H, Ottersen OP. Immunoelectron microscopy of AMPA receptor subunits reveals three types of putative glutamatergic synapse in the rat vestibular end organs. Brain Res 819: 58–64, 1999. [DOI] [PubMed] [Google Scholar]
- Meredith FL, Benke TA, Rennie KJ. Hyperpolarization-activated current (Ih) in vestibular calyx terminals: characterization and role in shaping postsynaptic events. J Assoc Res Otolaryngol 13: 745–758, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meredith FL, Rennie KJ. Zonal variations in K+ currents in vestibular crista calyx terminals. J Neurophysiol 113: 264–276, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Gorman DE, White JA, Shera CA. Dynamical instability determines the effect of ongoing noise on neural firing. J Assoc Res Otolaryngol 10: 251–267, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otis T, Zhang S, Trussell LO. Direct measurement of AMPA receptor desensitization induced by glutamatergic synaptic transmission. J Neurosci 16: 7496–7504, 1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez C, Limón A, Vega R, Soto E. The muscarinic inhibition of the potassium m-current modulates the action-potential discharge in the vestibular primary-afferent neurons of the rat. Neuroscience 158: 1662–1674, 2009. [DOI] [PubMed] [Google Scholar]
- Risner JR, Holt JR. Heterogeneous potassium conductances contribute to the diverse firing properties of postnatal mouse vestibular ganglion neurons. J Neurophysiol 96: 2364–2376, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose KE, Lunardi N, Boscolo A, Dong X, Erisir A, Jevtovic-Todorovic V, Todorovic SM. Immunohistological demonstration of CaV3.2 T-type voltage-gated calcium channel expression in soma of dorsal root ganglion neurons and peripheral axons of rat and mouse. Neuroscience 250: 263–274, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothman JS, Manis PB. Differential expression of three distinct potassium currents in the ventral cochlear nucleus. J Neurophysiol 89: 3070–3082, 2003a. [DOI] [PubMed] [Google Scholar]
- Rothman JS, Manis PB. The roles potassium currents play in regulating the electrical activity of ventral cochlear nucleus neurons. J Neurophysiol 89: 3097–3113, 2003b. [DOI] [PubMed] [Google Scholar]
- Rutherford MA, Chapochnikov NM, Moser T. Spike encoding of neurotransmitter release timing by spiral ganglion neurons of the cochlea. J Neurosci 32: 4773–4789, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadeghi SG, Chacron MJ, Taylor MC, Cullen KE. Neural variability, detection thresholds, and information transmission in the vestibular system. J Neurosci 27: 771–781, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadeghi SG, Pyott SJ, Yu Z, Glowatzki E. Glutamatergic signaling at the vestibular hair cell calyx synapse. J Neurosci 34: 14536–14550, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schessel D, Highstein S. Is transmission between the vestibular type I hair cell and its primary afferent chemical? Ann NY Acad Sci 374: 210–214, 1981. [DOI] [PubMed] [Google Scholar]
- Smith CE, Goldberg JM. A stochastic afterhyperpolarization model of repetitive activity in vestibular afferents. Biol Cybern 54: 41–51, 1986. [DOI] [PubMed] [Google Scholar]
- Songer JE, Eatock RA. Tuning and timing in mammalian type I hair cells and calyceal synapses. J Neurosci 33: 3706–3724, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trussell LO. Synaptic mechanisms for coding timing in auditory neurons. Annu Rev Physiol 61: 477–496, 1999. [DOI] [PubMed] [Google Scholar]
- Vega R, Rodríguez U, Soto E. Acid-sensing ionic-channel functional expression in the vestibular endorgans. Neurosci Lett 463: 199–202, 2009. [DOI] [PubMed] [Google Scholar]
- Ventura C, Kalluri R. Current density differences between action potential firing patterns in vestibular ganglion neurons. Assoc Res Otolaryngol Abs: PS-205, 2014. [Google Scholar]
- Wooltorton JRA, Gaboyard S, Hurley KM, Price SD, Garcia JL, Zhong M, Lysakowski A, Eatock RA. Developmental changes in two voltage-dependent sodium currents in utricular hair cells. J Neurophysiol 97: 1684–1704, 2006. [DOI] [PubMed] [Google Scholar]
- Wu X, Liao L, Liu X, Luo F, Yang T, Li C. Is ZD7288 a selective block of hyperpolarization-activated cyclic nucleotide-gated channel currents? Channels (Austin) 6: 438–442, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita M, Yamashita M, Ohmori H, Ohmori H. Synaptic responses to mechanical stimulation in calyceal and bouton type vestibular afferents studied in an isolated preparation of semicircular canal ampullae of chicken. Exp Brain Res 80: 475–488, 1990. [DOI] [PubMed] [Google Scholar]
- Yi E, Roux I, Glowatzki E. Dendritic HCN channels shape excitatory postsynaptic potentials at the inner hair cell afferent synapse in the mammalian cochlea. J Neurophysiol 103: 2532–2543, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshimoto R, Iwasaki S, Takago H, Nakajima T, Sahara Y, Kitamura K. Developmental increase in hyperpolarization-activated current regulates intrinsic firing properties in rat vestibular ganglion cells. Neuroscience 284: 632–642, 2015. [DOI] [PubMed] [Google Scholar]