Silent Expectations: Dynamic Causal Modeling of Cortical Prediction and Attention to Sounds That Weren't

Abstract

There is increasing evidence that human perception is realized by a hierarchy of neural processes in which predictions sent backward from higher levels result in prediction errors that are fed forward from lower levels, to update the current model of the environment. Moreover, the precision of prediction errors is thought to be modulated by attention. Much of this evidence comes from paradigms in which a stimulus differs from that predicted by the recent history of other stimuli (generating a so-called “mismatch response”). There is less evidence from situations where a prediction is not fulfilled by any sensory input (an “omission” response). This situation arguably provides a more direct measure of “top-down” predictions in the absence of confounding “bottom-up” input. We applied Dynamic Causal Modeling of evoked electromagnetic responses recorded by EEG and MEG to an auditory paradigm in which we factorially crossed the presence versus absence of “bottom-up” stimuli with the presence versus absence of “top-down” attention. Model comparison revealed that both mismatch and omission responses were mediated by increased forward and backward connections, differing primarily in the driving input. In both responses, modeling results suggested that the presence of attention selectively modulated backward “prediction” connections. Our results provide new model-driven evidence of the pure top-down prediction signal posited in theories of hierarchical perception, and highlight the role of attentional precision in strengthening this prediction.

SIGNIFICANCE STATEMENT Human auditory perception is thought to be realized by a network of neurons that maintain a model of and predict future stimuli. Much of the evidence for this comes from experiments where a stimulus unexpectedly differs from previous ones, which generates a well-known “mismatch response.” But what happens when a stimulus is unexpectedly omitted altogether? By measuring the brain's electromagnetic activity, we show that it also generates an “omission response” that is contingent on the presence of attention. We model these responses computationally, revealing that mismatch and omission responses only differ in the location of inputs into the same underlying neuronal network. In both cases, we show that attention selectively strengthens the brain's prediction of the future.

Introduction

Recent neuroscientific advances have generated new theoretical understanding about the broadly construed notion that the human brain is an adaptive prediction engine (Wolpert and Ghahramani, 2000; Lee and Mumford, 2003; Friston, 2009; Clark, 2013). There is a growing consensus that this engine is realized by a hierarchy of successively complex neural processes that feedforward prediction errors and feedback predictions to maintain a constantly updated model of the world (Friston, 2008). According to this proposal of brain function, neural predictions about future events, generated by constantly updated models of the external environment, are thought to flow down a hierarchy of cortical processing layers. Each layer in this hierarchy has a model that tries to predict (i.e., explain away) the neural representations in the layer below. The prediction errors between these predictions and neural activity from the layer below (e.g., from sensory inputs) trigger updates in the models themselves. Within this framework, attentional control is seen as the cognitive manifestation of the precision of these neural predictions (Friston, 2009). Specifically, it is implemented by synaptic gain modulation that generates precision-weighted prediction errors (Feldman and Friston, 2010).

This predictive framework has provided elegant interpretations of “mismatch” responses recorded with electroencephalography (EEG) in auditory paradigms, where the mismatch can occur at successive levels of predictive complexity (Ritter et al., 1999; Wacongne et al., 2011; Chennu et al., 2013). Indeed, computational instantiations of this framework have been fitted to the well-known mismatch negativity (MMN) event-related potential (ERP), considered to be a marker of prediction error (Garrido et al., 2008, 2009; Wacongne et al., 2012; Phillips et al., 2015). The MMN is most commonly elicited by a relatively infrequent sound that differs in its acoustic properties (pitch, loudness, etc.) from a monotonous sequence of preceding, frequent sounds (Näätänen et al., 1978, 2007). An interesting variant of this approach to measuring prediction is to occasionally omit the frequent sound, which is known to produce brain responses time-locked to the expected temporal onset of the omitted sound (Raij et al., 1997; Yabe et al., 1997; Bendixen et al., 2009; Wacongne et al., 2011; SanMiguel et al., 2013). This omission ERP has been proposed to correspond to the pure top-down prediction signal emitted by higher-order cortical areas, and hence serves as a clear test of the predictive coding framework (Wacongne et al., 2011; SanMiguel et al., 2013). However, there is as yet no computationally explicit account of how both the mismatch and the omission responses can be explained by common predictive coding framework.

To address this, we apply dynamic causal modeling (DCM) of evoked responses (David et al., 2006) to test the hypothesis that neural predictions reflected in the omission response are generated in higher-order cortical areas within the same hierarchical framework that also generates the mismatch response. To do so, we combined EEG data and magnetoencephalography (MEG) data with an experimental design derived from the well-established local-global paradigm (Bekinschtein et al., 2009), which orthogonally manipulates the presence versus absence of bottom-up auditory stimuli and top-down attentional control. We use this factorial design to test a common set of computational models representing hierarchically organized neural networks for auditory perception, but with distinct patterns of information flow underpinning the mismatch response and omission response. Going further, we also use DCM to model the effect of attention on this information flow, explicating its role in hierarchical auditory prediction. Our findings generate important new evidence of a pure top-down prediction signal posited by theories of hierarchical prediction, and suggest a clear role for attentional mechanisms in tuning the precision of predictions.

Materials and Methods

Participants.

Twenty neurologically healthy right-handed adults (mean ± SD age, 27.9 ± 5.72 years; 13 females) participated in the study, which was approved by the Cambridge Psychology Research Ethics Committee (2005:08). They gave written informed consent and were paid for their participation.

Stimuli.

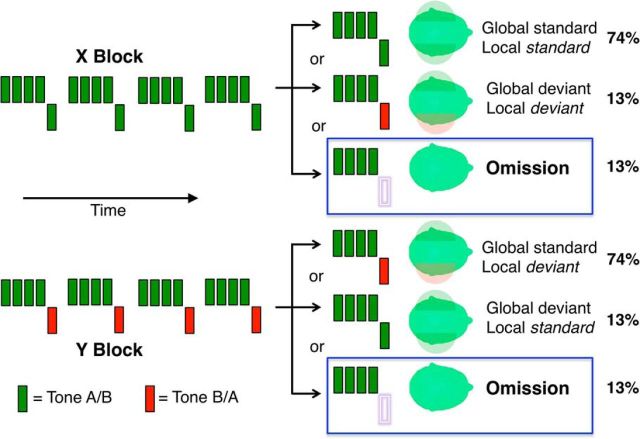
In each experimental condition, a participant was presented 10 blocks of stimuli, with breaks between blocks. Eight of these were experimental blocks, whereas two were control blocks. Audible monaural tones 50 ms long were presented in grouped sequences of 4 or 5 tones, with short gaps of 100 ms. Individual tones were one of two mixtures of three sinusoids, Type A (500, 1000, and 2000 Hz) or Type B (350, 700, and 1400 Hz), following previous research using similar paradigms (Bekinschtein et al., 2009; Wacongne et al., 2011; Chennu et al., 2013). As visualized in Figure 1, sequences consisted of five identical tones (AAAAA or BBBBB), four identical tones, and a final one of the other type (AAAAB or BBBBA), or just four identical tones with the fifth one omitted (AAAA_ or BBBB_). Hence, tone sequences could either be temporally local standards, that is, where the fifth tone's frequency was identical to the previous four (AAAAA and BBBBB); local deviants, where the last tone differed in frequency (AAAAB and BBBBA); or omissions, where the last tone was not presented. The fifth tone in each of these sequences was always presented to the opposite ear from the previous four, unless it was omitted. This allowed us to measure responses to frequency deviance on top of a laterality deviance that we have previously shown to generate a robust mismatch response (Chennu et al., 2013).

Figure 1.

Experimental design. Auditory stimuli consisted of sequences of five monaural tones of frequency Type A or B, presented in experimental blocks of Type X or Y, which were later collapsed together. In X blocks, standard sequences (74%) consisted of 4 repetitions of the same tone in one ear, followed by a fifth one in the opposite ear. These were interspersed with rare, unpredictable deviant sequences where the fifth tone was either different in frequency type (13%) or was omitted (13%). Y blocks were similar, except that the standard sequences had a fifth tone differing in frequency type. This effectively created an orthogonal contrast between temporally local versus global deviance in the pattern of tones. Omission sequences were unexpected in experimental blocks. These were contrasted with predictable repetitions of four-tone omission sequences in two additional control blocks.

Approximately 135 sequences were presented in each block, lasting ∼3.2 min. The interval between consecutive sequences was randomly sampled from a uniform distribution between 700 and 1000 ms. Each experimental block began with a habituation phase, consisting of a 3 s pause followed by the 20 presentations of a 5 tone sequence that would occur commonly throughout the rest of the block, termed the global standard sequence. This was immediately followed by the test phase, consisting of 115 sequences. Of these, 85 (∼74%) were the global standard. The remaining were rare, global deviant sequences, which were either 5 tone sequences or omissions with equal probability. There were 15 (∼13%) of each kind of deviant sequence in a block, pseudorandomly interspersed among the global standards. Between 2 and 5 global standards were always presented between one deviant sequence and the next, with 80% of deviants preceded by 2 or 3 global standards.

Figure 1 illustrates the structure of X and Y block types, which together enable the well-established local-global paradigm, first introduced by Bekinschtein et al. (2009), to create orthogonal local and global contrasts of predictability across 8 experimental blocks. In this paradigm, global standard sequences in X blocks were also local standards, whereas global standards in Y blocks were local deviants. This meant that the tone sequence that served as the global standard in an X block was the global deviant in the complementary Y block, and vice versa. In this way, by collapsing trials appropriately across the X and Y blocks, we were able to contrast local standards (by averaging global standard trials in X blocks and global deviant trials in Y blocks) against local deviants (by averaging global deviant trials in X blocks and global standard trials in Y blocks) to examine the mismatch response. Orthogonally, global standards (averaged over global standard trials in X and Y blocks) could be contrasted against global deviants (global deviant trials in X and Y blocks). Omissions were always locally and globally deviant in experimental blocks, which were averaged and contrasted against those presented in control blocks (see below).

The dominant tone type (A or B) and laterality of the sequences presented within each block were counterbalanced, resulting in the 8 experimental blocks listed in Table 1. So for example, in the L-A-X block (Table 1, first row; see Fig. 1, left column), the locally standard AAAAA sequence was also the global standard. Rare global deviants in this block were also locally deviant, either the sequence AAAAB, or the omission sequence AAAA_ where the fifth tone was omitted. By contrast, in the R-B-Y block (Table 1, third row; see Fig. 1, right column), the locally deviant BBBBA sequence was now the global standard. Global deviants in this block were either the locally standard BBBBB sequence or the BBBB_ omission sequence. The 8 blocks were presented in pseudorandom order such that the first block was always an X block, and no more than two X or two Y blocks were presented consecutively.

Table 1.

Structure of experimental blocks

Laterality	Tone type	Block type	Global standard	Global deviant	Omission
L	A	X	AAAAA	AAAAB	AAAA_
L	B	X	BBBBB	BBBBA	BBBB_
L	A	Y	AAAAB	AAAAA	AAAA_
L	B	Y	BBBBA	BBBBB	BBBB_
R	A	X	AAAAA	AAAAB	AAAA_
R	B	X	BBBBB	BBBBA	BBBB_
R	A	Y	AAAAB	AAAAA	AAAA_
R	B	Y	BBBBA	BBBBB	BBBB_

Two additional control blocks were randomly interspersed among the experimental blocks. These blocks had 120 sequences each, one-half of which were omissions, and the other half were 5 tone sequences presented in the experimental blocks. However, unlike in the experimental blocks, omission sequences in control blocks were entirely predictable, as they were all presented together, one after the other. Hence, the responses to omissions in the control blocks, referred to as omission controls, served as a baseline for comparing with omissions in experimental blocks. The two control blocks contained 60 repetitions of the AAAA_ and BBBB_ omission sequences, respectively.

Experimental task.

Participants were comfortably seated and asked to remain still while fixating on a white cross presented on a gray background to minimize eye movements. They were tested in two main experimental conditions: attend-auditory and attend-visual. The order of the conditions was counterbalanced across participants. The attend-auditory consisted only of auditory stimulation, where participants were asked to attend to the tone sequences and count any rare/uncommon sequences. At the end of each block, they were asked to report this count before continuing with the experiment. Thus, in this condition, participants were expected to attend to and extract the global rule that characterized deviant sequences.

In the attend-visual condition, the auditory stimulation was the same as in the attend-auditory condition, but in addition, participants were asked to perform a demanding visual task intended to divert their attention away from the auditory stimuli. Colored letters (A, E, J, P, or T in red, green, blue, yellow, or magenta) were presented in random order at a rate of ∼1 per second, with an on-screen time of 150 ms followed by an 850 ms blank interval. At the beginning of each block, participants were asked to count the number of occurrences of a randomly selected colored letter designated as the target for that block. There were between 8 and 11 targets in each block. At the end of the block, they were asked to report this count before continuing. Onset times of auditory and visual stimuli were uncorrelated by virtue of selecting the temporal gaps between neighboring auditory and visual stimuli randomly from a uniform distribution with a mean of 0 ms and a SD of 290 ms. Hence, responses to visual stimuli were averaged out in the ERPs time-locked to auditory stimuli.

EEG and MEG data collection.

Simultaneous EEG-MEG data were collected while participants performed the above task, using 70 EEG sensors, 102 magnetometers, and 204 planar gradiometers combined in a multichannel MEG/EEG setup (Elekta Neuromag Oy) and sampled at 1000 Hz. An electrode on the nose tip served as the EEG reference, while a pair of vertical and horizontal electrooculogram (EOG) channels were recorded to monitor eye movements. The participant's head position relative to the MEG sensor array was recorded using 5 head position indicator coils attached to the scalp. A Fastrak system (Polhemus) was used to digitise the 3D positions of these coils and the EEG electrodes relative to the participant's nasion and preauricular points.

Data analysis.

The temporal extension of signal-space separation algorithm (tSSS, as implemented in Maxfilter 2.2 software, Elekta Neuromag (Taulu et al., 2005) was used to perform bad channel interpolation, head movement correction, and external artifact removal on the MEG data. Using SPM12 (Penny et al., 2011) for further analyses, EMEG data were downsampled to 200 Hz and bandpass filtered between 0.5 and 25 Hz using a two-pass Butterworth filter. After discarding the data from the habituation phase of each block of stimuli (see above), the continuous data were epoched from −200 ms to 1300 ms relative to the onset of each tone sequence.

Epochs containing egregious artifacts were discarded by visual inspection, and the retained epochs were submitted to independent components analysis. Components were sorted by the correlation of their time courses with the EOG channels. Components related to eye movements, in addition to those capturing muscle movements, were identified by visual inspection and projected out of the data. The cleaned epochs were baseline-corrected relative to −200 ms to 0 ms before the onset of the fifth tone in a 5 tone sequence, or to the time point where the fifth tone would have occurred, in an omission sequence. EEG data were rereferenced to the common average.

Forward modeling.

Anatomical T1-weighted magnetic resonance images (MRI) of each participant were obtained with a 3-T Siemens MRI scanner (Tim Trio, Siemens AG), with a resolution of 1 × 1 × 1 mm. The locations of the nasion, preauricular points, and the head position coils were used for the coregistration of the T1 images with the MEG sensors and digitized EEG channel locations. The T1 image was segmented and warped to match a canonical brain in MNI standard space, and the inverse of the warps applied to a set of canonical meshes for the scalp, outer skull, inner skull, and cortex to map them back into the individual brain space. A forward model mapping from the 8192 vertices on the cortical mesh to the sensors was estimated using a three-shell Boundary Element Model for the EEG channels, and the single-shell Boundary Element Model fitted to the inner skull for the MEG sensors.

Statistical parameter mapping.

EEG-derived ERPs and MEG-derived event-related fields (ERFs) for 6 conditions of interest (i.e., local standard, local deviant, global standard, global deviant, omission, and omission control) were separately averaged for attend-auditory and attend-visual contexts, resulting in 12 conditions in total. The ERP/ERF topographies between 50 and 650 ms were converted to 3D images by projecting the sensors to a 2D plane and interpolating their data across a 32 × 32 grid, and then tiling these topographies along the third dimension of time (Shtyrov et al., 2012). For each participant, the 12 images were then used to fit a general linear model at each voxel, using a single pooled error estimate for all conditions, whose nonsphericity was estimated using Restricted Maximum Likelihood as described by Friston et al. (2002). Statistically significant clusters of activation, as defined by an initial threshold of p < 0.001 uncorrected, were defined after family-wise correction of cluster size over space and time using random field theory with a p < 0.05 cluster-level FWE threshold (Flandin and Friston, 2015).

DCM.

We used DCM in SPM12 (v6470) to identify the effective coupling between cortical sources that could explain differences between the observed ERPs/ERFs (David et al., 2006). We used neuronal models and parameters similar to previous approaches to modeling ERPs (Garrido et al., 2009; Dietz et al., 2014), where DCM nodes were modeled as distinct cortical sources consisting of laminar subpopulations of excitatory pyramidal cells, spiny stellate cells, and inhibitory interneurons (Jansen and Rit, 1995). Excitatory forward and backward connections modeled between these cortical sources conformed to their known laminar origins (Felleman and Van Essen, 1991; David et al., 2006). The forward projections of these sources to the sensors were modeled using equivalent current dipoles (David et al., 2006). The locations of the dipoles were fixed, based on the coordinates used by Garrido et al. (2009), but no constraints were placed on their orientation or symmetry. Following Garrido et al. (2009), data were detrended and reduced to 8 spatial modes to reduce computational load before model fitting.

We instantiated DCMs of underlying changes in effective connectivity to explain the differences between sets of evoked responses. To do so, we varied the connections between a fixed set of cortical dipoles, across a set of models. To identify the most likely model of the observed differences, each model was fitted to each participant's responses using variational Bayesian inference (Friston et al., 2007). Evoked responses to all conditions being modeled were fit simultaneously, with the modulatory connections capturing any differences between conditions (as specified with a contrast vector [0 1] for standards and deviants, respectively). This procedure estimated the posterior density of the strengths of connections in a model, and the marginal likelihood of the model (i.e., the model evidence). In keeping with previous approaches (Garrido et al., 2009; Dietz et al., 2014; Phillips et al., 2015), the fitted DCMs were then compared with Bayesian Model Selection (BMS) (Penny et al., 2004), starting with a uniform prior over the model space (i.e., assigning equal a priori plausibility to the models considered). The model selection procedure used a fixed-effects (FFX) approach under the assumption that all subjects have the same model architecture but potentially different connection strengths (Stephan et al., 2009). The log Bayes factor was used to compare the relative amount of evidence for each model. A value of ≥3 is conventionally regarded as strong evidence for a particular model, whereas a posterior probability >0.95 that it is the winning model is regarded as informative (Kass and Raftery, 1995; Stephan et al., 2010). We verified that there were no outlier participants in terms of their model evidences. Inference over model parameters was conducted using Bayesian Model Averaging (BMA) with 10,000 iterations (Penny et al., 2010), to derive weighted posterior expectations and SDs of the parameters, which were then used to assess their statistical significance.

Results

Behavior

We examined the reported counts of deviant sequences in the attend-auditory condition and visual targets in the attend-visual condition. Participants reported the correct number with an average accuracy of 90% (SD 8%) for auditory targets in the attend-auditory condition and 93% (SD 4%) for visual targets in the attend-visual condition, confirming that they complied with the attentional manipulation and attended to task-relevant information in the designated sensory modality.

Mismatch response

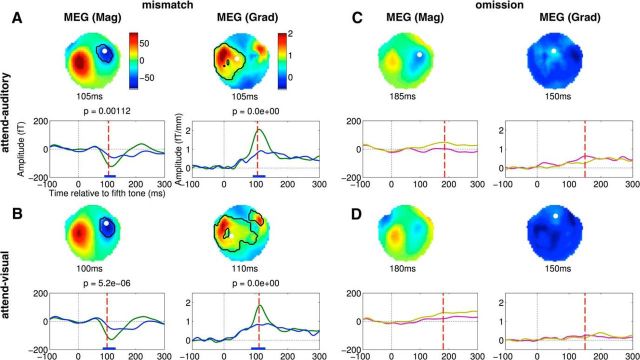
We established that the 5 tone auditory sequences in our experimental design, collapsed across X and Y block types (Fig. 1; see Materials and Methods), elicited evoked components related to the mismatch response. For the condition in which auditory stimuli were attended (attend-auditory), the comparison of local standards versus local deviants (corresponding to the local effect in Bekinschtein et al., 2009) revealed a clear early, short-lived MMN ∼100 ms (Fig. 2A; cluster size k = 513, p = 1.3e-06), immediately followed by a P200 positivity ∼200 ms (Fig. 2C; k = 1361, p = 8.3e-11). We confirmed that the magnetic equivalent of this mismatch response (termed MMNm or MMF, mismatch field) was also robust in both MEG sensor types (see Fig. 3A; MEG mag k = 25, p = 0.00112; MEG grad k = 1354, p < 2.2e-16).

Figure 2.

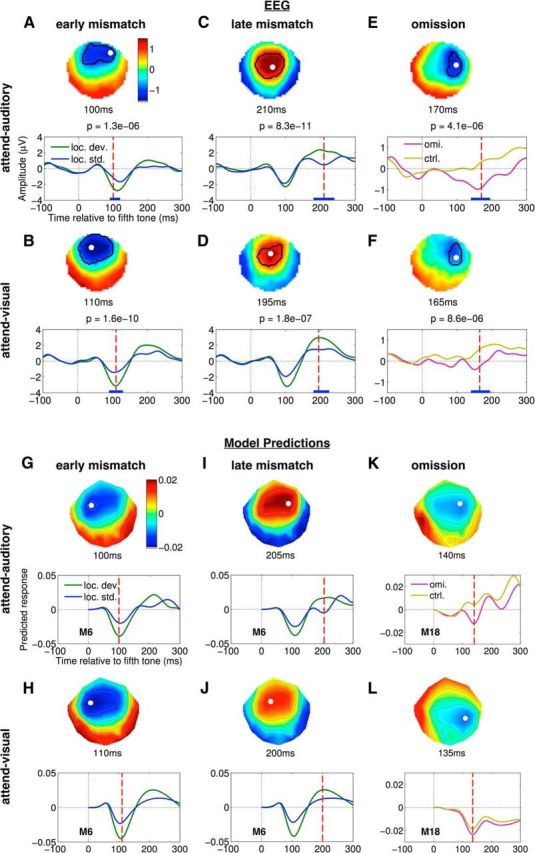
Data and modeling of auditory attention on mismatch and omission effects in EEG. A–F, Top half (each panel), Topography of a spatiotemporal cluster in SPM, at the time point when the F-statistic of the contrast between the pair of ERPs indicated in the legend was maximal. White dot indicates the spatial location of this maximal F-statistic. Bottom half (each panel), Average evoked response across participants at this spatial location. Thick blue horizontal line on the time axis indicates the temporal extent of the cluster. Red dashed vertical line indicates the time point at which topography above is plotted. This time point is also specified in the title above, along with the FWE-corrected cluster-level p value. A, C, Early and late clusters obtained in the contrast between local deviants and local standards in the attend-auditory condition. B, D, Same for the attend-visual condition. E, F, Clusters obtained in the contrasts between unexpected omissions in experimental blocks and expected omissions in the control blocks, for the two attention conditions. G, H, Top half (each panel), Difference between topographies of responses predicted by the winning model, at the time point when the contrast between these responses was maximal. White dot indicates the spatial location of the channel with the maximal difference in the predicted response. Bottom half (each panel), Predicted responses averaged across subject-wise fits of the winning model. Red dashed vertical line indicates the time point at which topography above is plotted. This time point is also specified in the title above. G, I, Early and late components of the local deviant and standard responses predicted by winning model M6 in the attend-auditory condition. H, J, Same for the attend-visual condition. K, L, Omission and omission control responses predicted by winning model M18, in the two attention conditions.

Figure 3.

Effect of auditory attention on mismatch and omission effects in MEG. A, B, Clusters obtained in the magnetometer and (root mean squared) gradiometer contrasts between local deviants and local standards, for the attend-auditory and attend-visual conditions, respectively. C, D, Same for the contrast between omissions and omission controls in the two attention conditions. For interpretation of details depicted in each panel, see Figure 2.

The mismatch response survived the absence of attention to the auditory stimuli (in the attend-visual condition) with no evident detriment in the MMN (Fig. 2B; k = 1293, p = 1.6e-10), P200 (Fig. 2D; k = 667, p = 1.8e-07), or the MEG data (Fig. 3B; MEG mag k = 509, p = 5.2e-06; MEG grad k = 1647, p < 2.2e-16). When testing the main effect of attention, or its interaction with the mismatch response, we found no clusters that survived correction for the whole scalp-time space. However, when adopting a more focused analysis, at the electrode (Cz) where this response is typical maximal, and within the 150–250 ms window during which the P200 ERP is known to peak (O'Donnell et al., 2004; Sur and Sinha, 2009), the P200 was enhanced in the attend-auditory condition. As a result, the interaction between attention and the late mismatch effect was significant (F_(1,19) = 9.7, p = 0.006).

We also confirmed that our attentional manipulation affected other components in the data, even if not addressed here, such as the global effect (i.e., the contrast between global deviants vs standards, encompassing the P300 component), which was contingent on auditory attention in all three modalities.

Omission response

To measure the omission effect, we compared contextually unexpected, rare omissions in experimental blocks, to the predictable omissions in control blocks. That is, in contrast to the mismatch effect, the omission effect represented a comparison between a pair of conditions in both of which the fifth tone in the auditory sequence was omitted, the only difference being whether or not the omission was expected. Figure 2E, F plots the contrast between these conditions (i.e., omissions vs omission controls), revealing a significant omission effect in the ERPs in both attention conditions, from ∼150 to 200 ms (Fig. 2E: k = 434, p = 4.1e-06; Fig. 2F: k = 383, p = 8.6e-06). Further, we also found that the omission ERP effect was smaller in the absence of attention, with the effect of attention on omissions being significant between 160 and 190 ms (k = 36, p = 0.01). The omission effect produced no spatiotemporal clusters of differences in either of the MEG sensor types (Fig. 3C,D) and did not differ between the X and Y blocks in any sensor type.

DCM

Model instantiation

Figure 4B visualizes the set of 18 temporal and temporofrontal DCMs that we instantiated. The cortical locations of the sources modeled, which were taken from Garrido et al. (2009), are shown in Figure 4A, and their MNI coordinates are listed in Table 2. The first 8 DCMs, indicated by the shaded box, are the same as those in Garrido et al. (2009), who previously applied these models to EEG data to evaluate the relative evidence for model adjustment (Winkler et al., 1996) versus adaptation (Jääskeläinen et al., 2004) accounts of the MMN. Specifically, models M1, M3, M5, and M7 represent increasing complexity in terms of the cortical areas included, from bilateral auditory cortices (A1), superior temporal gyri (STG), right inferior frontal gyrus (IFG) and bilateral IFG. Models M2, M4, M6, and M8 are identical to the previous four, except for the addition of intrinsic feedback connectivity in A1. Model M1, the most parsimonious, is effectively a null model that cannot account for any change in effective connectivity to explain the mismatch response. As highlighted by Garrido et al. (2008), model M2 instantiates the adaptation theory of MMN generation (May et al., 1999; Jääskeläinen et al., 2004; May and Tiitinen, 2010), whereas models M3, M5, and M7 instantiate the alternative model adjustment theory (Winkler et al., 1996; Näätänen and Winkler, 1999; Sussman and Winkler, 2001). Models M4, M6, and M8 incorporate elements of both theories.

Figure 4.

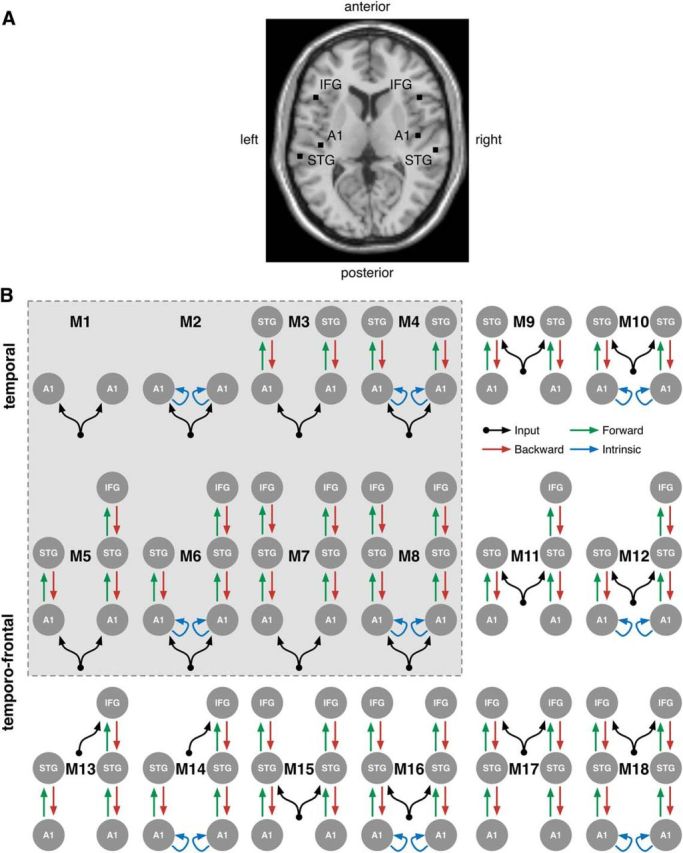
Dynamic causal models. A, Locations of the cortical dipoles in the DCMs visualized in B, which were instantiated to model the mismatch and omission effects. B, Shaded box highlights models of the MMN reproduced from Garrido et al. (2009). For MNI coordinates of the dipoles, see Table 2.

Table 2.

MNI coordinates of dipole locations used for DCM

Source name	Source location (MNI)
	Left	Right
A1	−42, −22, 7	46, −14, 8
STG	−61, −32, 8	59, −25, 8
IFG	−46, 20, 8	46, 20, 8

We tested a further set of 10 models, beyond those in Garrido et al. (2009), to explore plausible alternative sources of downward predictions that could explain the omission effect. Following Phillips et al. (2015), we posited inputs in DCM as representing internally generated higher-order predictions feeding into a model, in addition to the conventional notion of externally generated sensory inputs. The additional models instantiated (see Fig. 4B) were either temporal (M9–12) or temporofrontal (M13–18), and had driving inputs going either into both STGs (M9–12, M15, and M16), right IFG only (M13 and M14, given that Garrido et al., 2009 found evidence for right IFG only) or both IFGs (M17 and M18). In addition, these models also instantiated versions with and without intrinsic feedback connectivity in primary auditory cortex.

Model fitting and selection

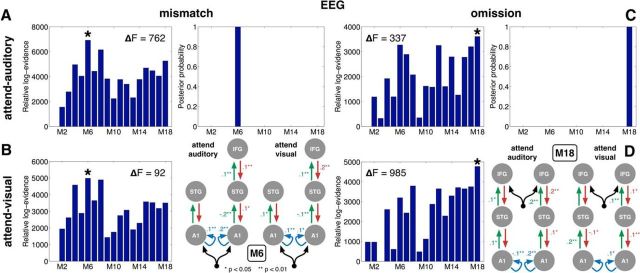
We first fit the whole set of 18 DCMs in Figure 4B to the contrast between local standards and deviants within 0–300 ms relative to the onset of the fifth tone in sequences, using the ERP and ERF data in the attend-auditory and then the attend-visual condition (Figs. 2A,B, 3A,B). We then used FFX BMS to identify the model that best explained the differences that encapsulated the mismatch response. The model evidence and BMS results for the EEG data are shown in Figure 5A, B (for MEG data, see Fig. 6). Model M6, which had driving inputs into bilateral A1, with intrinsic connectivity in A1, and included a right IFG node, had the highest relative log-evidence and posterior probability under both attention conditions and for all three sensor types (EEG, magnetometers, and gradiometers). BMA highlighted many connections in model M6 that were significantly modulated by the mismatch effect in both attention conditions (Fig. 5B, right). Visual examination of the local standard and deviant responses predicted by model M6, averaged over all the subject-wise fits, demonstrated an excellent match to the average scalp ERP data in both attention conditions (compare Fig. 2G–J with Fig. 2A–D), reinforcing the quality of the model fit.

Figure 5.

Model evidence for the mismatch and omission effects. A, B, Left, Relative log-evidence and results of FFX BMS over the DCMs in their ability to model the mismatch effect ERP contrast in the attend-auditory and attend-visual conditions, respectively (Fig. 2, left panels). *The model with the highest log-evidence. The difference between log-evidence of models with highest and second-highest evidence (ΔF) is shown in each case. A ΔF of 5 is equivalent to a Bayes factor of 150 in favor of the winning model. C, D, Left, Log-evidence of the same DCMs, but for modeling the omission effect ERP contrast in the attend-auditory and attend-visual conditions (Fig. 2, right panels). Among the DCMs instantiated and tested (Fig. 4), model M6 (B, right) was the winning model of the mismatch effect (A, right), whereas model M18 (D, right) was the winning model of the omission effect (C, right), in both attention conditions. For connections in the winning models that were significantly modulated by these effects in each attention condition, the posterior expectations of the strength of this modulation calculated with BMA are indicated alongside.

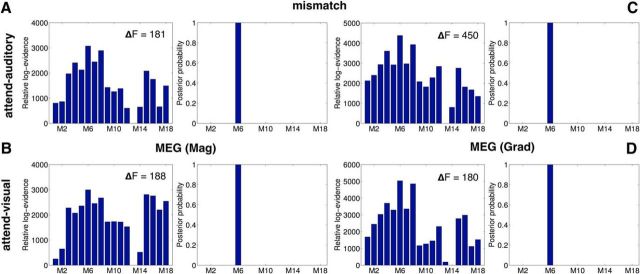
Figure 6.

DCM of the mismatch effect ERFs. Panels plot the relative log-evidence and results of FFX BMS over the DCMs in Figure 4B in their ability to model the mismatch effect contrast in the MEG data (A, B, magnetometers; C, D, gradiometers), in the attend-auditory and attend-visual conditions, respectively (Fig. 3). As with the EEG data, model M6 was the winning model of the mismatch effect in both MEG modalities and attention conditions.

Furthermore, we found consistency in the connection strengths of this winning model across the EEG and MEG data. Specifically, we calculated across-subject correlations between the estimates of the connection weights when model M6 was fit to each subject's mismatch response in EEG, in MEG magnetometers and in MEG gradiometers, for each attention condition. The Pearson correlation was significant between EEG and magnetometer responses (attend-auditory: Pearson's ρ = 0.13, p = 0.08; attend-visual ρ = 0.46, p = 8.4e-10), and between EEG and gradiometer responses (attend-auditory: Pearson's ρ = 0.2, p = 0.009; attend-visual ρ = 0.33, p = 1.5e-05).

It is worth noting that M6 has been found to be the winning model of the MMN in many previous DCM studies (Garrido et al., 2008; Garrido et al., 2009; Phillips et al., 2015), although they used different experimental designs. Importantly, we also found that the M6 was the winning model of the mismatch response (Fig. 2B), even in the absence of auditory attention (Fig. 5B). Together, these findings corroborate the idea that the mismatch response is best explained by a combination of adaptation in primary auditory cortex, in addition to model adjustment in a neural hierarchy that includes superior temporal and inferior frontal areas.

Going beyond previous modeling efforts, we then tested the same 18 models against the omission effect contrast (i.e., omissions vs omission controls; Fig. 2E,F). For this modeling, we only fit the EEG data because the MEG data for the omission effect were relatively weak. The results visualized in Figure 5C, D demonstrate that model M18, a symmetric temporofrontal model with bilateral inputs into IFG, was now the winning model of the omission effect, in both attention conditions. BMA results again showed that multiple connections in M18 were significantly modulated by the omission effect in both attention conditions (Fig. 5D, right). Furthermore, the average scalp-level omission responses predicted by model M18 largely reproduced the observed data (compare Fig. 2K,L with Fig. 2E,F). This suggested that the response to unexpected omissions can be interpreted as being driven by top-down predictions. However, it is worth nothing that the data fit was not as close as for the mismatch response, suggesting that M18 could represent a local optimum in model space with scope for further refinement (see Discussion).

Modeling of interactions

In the DCM analyses above, we fit the attend-visual and attend-auditory conditions separately and found that the same model won in both cases, for both mismatch and omission responses. Yet the ERP/ERF analyses showed that both mismatch and omission responses differed as a function of attention, in particular during the later time window from 150 to 250 ms. We therefore explored how attention modulated the effective connectivity (DCM parameters) within the winning model, when model M6 was applied simultaneously all four mismatch conditions (deviant/control × attend-auditory/attend-visual), and model M18 was applied simultaneously to all four omission conditions (omission/control × attend-auditory/attend-visual). To this end, we created 8 new models derived from M6 or M18, in which different set of connections that were allowed to be modulated. Because we found no significant main effect of attention in the 0–300 ms time window modeled in our DCMs, we only included the main effect of deviance, and the interaction between deviance and attention, as modulations. Therefore, in the model comparisons below, we refer to the interaction between attention and deviance (i.e., modulations that allow the size of the mismatch/omission response to vary with attention).

The set of models M6.1-M6.8 derived from M6 are shown in Figure 7A. In model M6.1, all connections were fixed, representing no interaction between attention and the mismatch response. M6.8 represented the other extreme, where attention modulated all forward and backward connections in M6. The intermediate models represented plausible intermediate alternatives where attention modulated all forward connections only (M6.2), all backward connections only (M6.3), all forward connections plus backward connections between lower (M6.4) and higher (M6.5) layers only, and all backwards connections plus forward connections between lower (M6.6) and higher (M6.7) layers only. The FFX BMS results are shown in Figure 7B, suggesting that model M6.3 was the most likely DCM of the attention-mismatch interaction. That is, auditory attention modulated only backward connections in winning model M6. Corroborating this result, BMA suggested that some backward connections in M6.3 were significantly modulated by the interaction.

Figure 7.

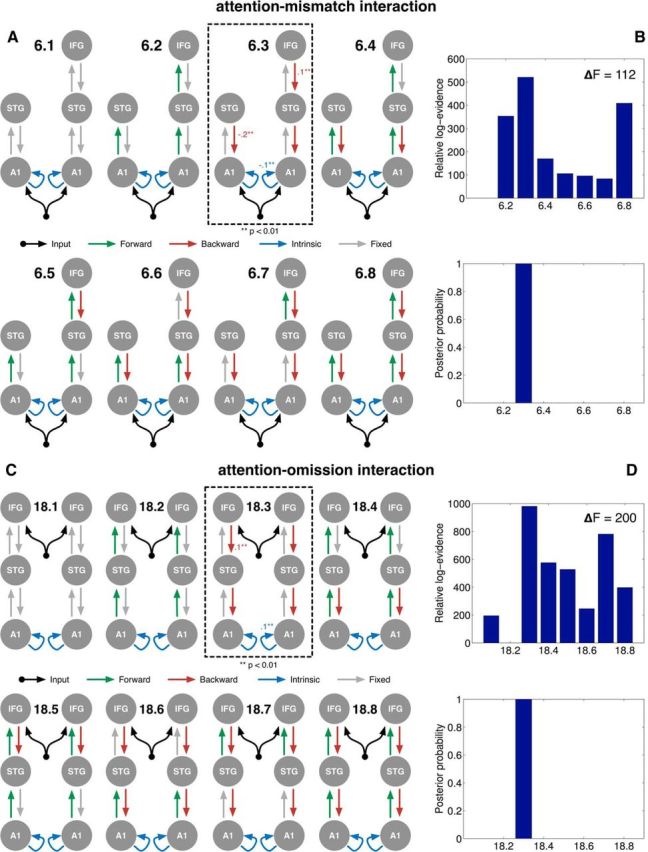
DCM of the interaction between mismatch and omission effects and attention. A, DCM variants of winning model M6 from Figure 4B, which were instantiated to model the interaction contrast between attention and the mismatch effect. B, Results of FFX BMS to compare the fits of the DCMs in A to the interaction. Model M6.3 (A, dashed box) was the winning model for the attention-mismatch interaction. Similarly, C, DCM variants of winning model M18 instantiated to model the interaction between attention and the omission effect. D, Results of FFX BMS of their fits to the interaction. Model M18.3 (C, dashed box) was found to be the winning model of the attention-omission interaction. For connections in the winning models that were significantly modulated by the respective interactions, the posterior expectations of the strength of this modulation calculated with Bayesian model averaging are indicated alongside.

To similarly test the interaction between attention and deviance on the omission response, we tested an analogous set of 8 variations of the winning omission model M18, These models, M18.1–18.8 (Fig. 7C), represent the same set of hypotheses as above about the effective connectivity modulated by attention. The BMS results, shown in Figure 7D, suggested that model M18.3, analogous to M6.3 above, was the most likely DCM. That is, the auditory attention again only modulated backward connections in M18. As with the mismatch effect, BMA again showed that backward connections in M18.3 were indeed significantly modulated by the attention-omission interaction, in keeping with FFX-based BMS.

Discussion

The findings presented here are an exposition of the potential mechanistic bases of sensory prediction in auditory cortex. We have used a well-validated empirical and modeling framework to identify the most likely neural model of predictive information flow in auditory perception, as measured by electromagnetic neural dynamics. In particular, our experimental design allowed us to independently manipulate bottom-up stimulus input (mismatch vs omission) and top-down attention (attend-auditory vs attend-visual). This enabled us to explore a predictive coding framework that could simultaneously explain both the mismatch and omission effects. The DCMs we instantiated represented hypotheses about specific brain areas and causal interactions between them, as potential neural underpinnings of the statistically significant mismatch and omission effects in our data. These DCMs built on prior research into modeling the MMN (Garrido et al., 2009), which we extended with the assumption that the omission effect would activate similar brain areas to those activated by the mismatch effect.

The face validity of these data and modeling results is affirmed by the replication of previous DCM findings relating to the best model of the conventional mismatch response (Garrido et al., 2009). Importantly, our DCM results go further by demonstrating that the same neural architecture can explain mismatch responses with and without attention. Indeed, consistent with other results by Auksztulewicz and Friston (2015), we found that the effect of attention is to specifically modulate backward connections within this architecture, the dynamical consequences of which are that early components (MMN) are not affected as much by attention as are later components.

Most importantly, our results extend to the modeling of the omission effect and its sensitivity to attention. Wacongne et al. (2011) have proposed that the omission effect represents a key test of an active prediction system in the brain. Here, we used DCM to instantiate this proposal computationally and explain the brain response produced by this unexpected absence of a stimulus. Eliminating the interference from neural processing of any stimulus from this observable response has allowed us to elicit and study the dynamics of top-down expectation itself, alongside independent modulation of attention. From a predictive coding perspective, a response to the absence of predicted sensory input during an unexpected omission sequence should directly reflect the strength of downward prediction. Hence, in contrast to the mismatch response, where the bottom-up inputs are generated by auditory stimuli activating primary auditory cortex, the omission response should instead be driven by top-down driving inputs into higher-order cortical areas, which are uncovered when there is an unexpected silence due to the absence of predicted inputs. It is important to note that our DCM results are conditional on the top-down inputs for the omission response (e.g., to frontal cortex) having the same temporal dynamics (a gamma function with mode of 60 ms) as the bottom-up sensory inputs for the mismatch response. This seemed the simplest assumption to make to constrain the present analyses, but future studies could explore (using the DCM model evidence) a wider range of dynamics for the top-down inputs, in case they do differ, perhaps informed by more direct evidence of the nature of such top-down expectation signals.

The role of attention in generating the mismatch response has been the subject of much debate (Woldorff et al., 1991, 1998; Kathmann et al., 1999), and frequency deviance has been claimed to be relatively unaffected by attention (Näätanen et al., 2007). However, attentional modulation of the omission response has been less well studied. Our DCMs of the interaction between attention and the mismatch and omission effects inform this debate, clarifying the role of attention within a predictive coding framework. Indeed, our findings provide direct modeling evidence in support of attention as the mechanism that modulates the strength and precision of downward predictions, as also recently suggested by Auksztulewicz and Friston (2015).

We collected both EEG and MEG data in this study to find potentially complementary information in the two modalities. However, we did not find this to be the case, although there was agreement between the modalities in the mismatch response. In this context, a practical aspect of our empirical findings worth noting was the relatively weak omission effect in the MEG data. Based on the DCM results from the EEG data, we speculate that a potential reason for this could be that activity in the frontal sources, the site of the driving inputs suggested by DCM model 18, did not produce a strong magnetic signal at the MEG sensors. This may reflect the typical head position (which tends to be further from the sensors at the front of the MEG helmet than those at the back), in contrast the close proximity of MEG sensors to the lateral temporal areas that respond strongly to the auditory stimuli generating the mismatch effect. Alternatively, the frontal current sources could have a large radial component, which MEG sensors cannot detect. Future evidence from intracranial EEG would help address this question of the precise sources underlying the omission response.

From a computational perspective, forward and backward connections have distinct implementations and interpretations in DCM. The consequent dynamics are distinct in terms of temporal activation and map onto activations of distinct neuronal populations that generate hierarchical prediction error and prediction in the brain. Our findings here have enabled us to combine empirical and computational evidence to describe these cortical signals, and examine the role of attention in modulating them.