Abstract
Seed traits have been targeted by human selection during the domestication of crop species as a way to increase the caloric and nutritional content of food during the transition from hunter-gather to early farming societies. The primary seed trait under selection was likely seed size/weight as it is most directly related to overall grain yield. Additional seed traits involved in seed shape may have also contributed to larger grain. Maize (Zea mays ssp. mays) kernel weight has increased more than 10-fold in the 9000 years since domestication from its wild ancestor, teosinte (Z. mays ssp. parviglumis). In order to study how size and shape affect kernel weight, we analyzed kernel morphometric traits in a set of 10 maize-teosinte introgression populations using digital imaging software. We identified quantitative trait loci (QTL) for kernel area and length with moderate allelic effects that colocalize with kernel weight QTL. Several genomic regions with strong effects during maize domestication were detected, and a genetic framework for kernel traits was characterized by complex pleiotropic interactions. Our results both confirm prior reports of kernel domestication loci and identify previously uncharacterized QTL with a range of allelic effects, enabling future research into the genetic basis of these traits.
Keywords: introgression population, kernel weight, kernel size and shape, quantitative trait loci (QTL), domestication, Multiparent Advanced Generation Inter-Cross (MAGIC), multiparental populations, MPP
In cereal crops, seeds are the primary products for consumption, and seed size is one of the most important agronomic traits for yield. Seed size is also a vital component of evolutionary fitness in plants. It is believed that larger seeds accumulate sufficient nourishment for germination and have better tolerance to abiotic stresses, while smaller seeds are more efficient at dispersal and colonization (Westoby et al. 2002; Moles et al. 2005). Seed shape traits often govern market classes in some crops, such as long vs. short grain rice (Luo et al. 2004; Huang et al. 2013).
Researchers studying Old World archeological data (Fuller 2007) believe that larger grain size emerged before the loss of shattering during domestication, and that increased seed size compared to progenitors could be found in nearly every domesticated species. Grain shape was involved in a second step of crop improvement and diversification following domestication. Grain shape changes during domestication can also be dramatic (Abbo et al. 2014), although species would still be considered domesticated in the absence of grain shape changes, and the changes are often found in only a subset of domesticates (Gross and Olsen 2010). This is one possible reason why grain shape does not appear to have been a major component of the domestication syndrome in wheat (Gegas et al. 2010). Grain size and shape were both under strong selection during rice (Oryza sativa) domestication (Kovach et al. 2007).
Besides being important in domestication, kernel size and shape are crucial attributes for determining the market value of rice due to their close relationship to quality and yield. For example, studies indicated that larger and more spherical grains could increase the milling yield in wheat (Evers et al. 1990; Evers 1995) and are associated with cooking quality in rice (Luo et al. 2004; Huang et al. 2013). Thus, grain size and shape have attracted significant attention not only in cereal crop breeding programs, but also in genetic studies because of their contributions to yield, quality, and domestication. Understanding the genetic basis of these traits is crucial from both an evolutionary and applied perspective.
The mechanism by which grain crops determine their seed size and shape has remained largely unknown at the gene level and beyond. Most studies on seed size and shape have only identified QTL for grain size and shape in plants ranging from Arabidopsis to various crop plants (Liu et al. 2014; Zhang et al. 2015), which indicate that grain size and shape are quantitative traits. Recently, several genes/QTL controlling seed/fruit size and shape have been cloned in tomato and rice (Frary et al. 2000; Fan et al. 2006; Song et al. 2007; Shomura et al. 2008; Weng et al. 2008; Wang et al. 2012) or identified using mutant strategies in Arabidopsis (Garcia et al. 2005; Zhou et al. 2009). These studies revealed that ubiquitin pathway (Song et al. 2007; Li et al. 2010a), transcription factors (Garcia et al. 2005), G-protein signaling (Fan et al. 2006; Huang et al. 2009), hormone signaling (Jiang et al. 2013; Liu et al. 2015), and epigenetics (Song et al. 2015) are involved in controlling seed/fruit size and shape in plants.
Maize (Zea mays ssp. mays) was domesticated from its progenitor teosinte (Z. mays ssp. parviglumis) about 9000 years ago in southern Mexico (Matsuoka et al. 2002; Piperno et al. 2009). The process of domestication involved artificial selection that resulted in radically different plant, ear, and kernel morphologies between teosinte and maize (Beadle 1939; Doebley and Stec 1993). As is the case for all domesticated crop species, humans had selected for maize plants that were easier to harvest: reduced number of harvest units (ears in the case of maize), ears that did not naturally disperse their seeds by shattering, larger seed size, etc. These attributes collectively are referred to as the domestication syndrome (Harlan 1971; Hammer 1984). However, there are surprisingly few reports on the genetic control of kernel shape in maize (Liu et al. 2014), though QTL mapping has been applied to mine the genomic regions related to kernel shape in other crop plants. To date, studies on the genetics of maize kernel traits have focused mostly on kernel composition, such as oil, protein, and starch content (Goldman et al. 1993; Clark et al. 2006; Flint-Garcia et al. 2009; Cook et al. 2012), and seed weight (Beavis et al. 1994; Messmer et al. 2009; Liu et al. 2016). Thus, there is a need to investigate the genetics of kernel shape in maize.
In the current study, we used a population of teosinte NILs (Liu et al. 2016) derived from 10 parviglumis accessions in the B73 background to investigate the genetic architecture of kernel weight and shape traits. Grain samples from replicated trials were subjected to image analysis to estimate kernel shape parameters. We conducted joint linkage mapping for each trait separately and then on traits derived from a principal component (PC) analysis. We then focused on pleiotropic relationships between kernel weight and shape traits.
Materials and Methods
Genetic materials and field trials
Ten NIL populations were derived from geographically diverse parviglumis accessions by backcrossing into the B73 background as previously described (Liu et al. 2016). Briefly, parviglumis pollen was crossed onto B73 ears, and a single F1 plant was used to derive each population by backcrossing four times. BC4 plants were self-pollinated two generations prior to seed increase by sib-mating. One of the BC4 populations (Z031) was also inbred via doubled haploid technology (AgReliant Genetics, Westfield, IN).
Field trials were conducted at Genetics Farm (two replicates) and Bradford Farm (one replicate) locations near Columbia, MO in 2009 and at Aurora, NY (two replicates) in 2010. The experiments consisted of 694 lines from eight populations in 2009, and 858 lines from all 10 populations in 2010. Plants were planted in single row plots, where lines were randomized within population and populations were randomized within replicates. B73 was planted as a check entry at a rate of 5%.
Phenotypic data collection
Ears were harvested at physiological maturity, and dried at 37° for 5 d, followed by long-term storage at low humidity at 4° for at least 1 yr. The weight of 50 kernels (Wt50k) was obtained from three ears per plot.
Kernel size and shape were obtained using a bulk of kernels from each row grown in Columbia in 2009 and Aurora in 2010, and analyzed with PAX-it (MIS, Inc.) digital imaging software. Specifically, about 50 kernels per ear were scanned on an HP Scanjet G4050 Photo Scanner (Hewlett-Packard). Kernel area, perimeter, length, width, and roundness were calculated by the software after images were captured. The ratio of length and width (L/W) and the factor form density (FFD) were calculated from the raw data. FFD describes the differences in grain density and is calculated as grain weight divided by the product of grain length and grain width in wheat (Giura and Saulescu 1996). Because we have accurate kernel area values, we modified the FFD in our study to mean kernel weight divided by kernel area, based on the differences in size and shape parameters between maize and wheat.
Genotyping and genetic linkage map
The NILs were genotyped via a GoldenGate assay (Illumina, San Diego, CA) with 728 polymorphic SNPs from the NAM marker set (McMullen et al. 2009), with an average of 553 polymorphic SNPs per NIL population as previously described (Liu et al. 2016). Because the BC4 population structure does not permit genetic map construction, we used the NAM genetic map as a framework for marker order (Supplemental Material, Table S1).
The SNP genotypes were converted to 0, 1, and 2 to represent homozygous B73, heterozygous, and homozygous teosinte, respectively. Missing genotypic data (primarily monomorphic markers in specific populations) were imputed based on flanking marker data as previously described (Liu et al. 2016).
Statistical analysis
Descriptive statistics analysis and normality tests on the phenotypic data were performed with SAS software (SAS 9.2, SAS Inc.). Heritability was calculated according to Holland et al. (2003) in SAS (SAS Institute Inc., Cary, NC). LSMeans across environments were calculated in SAS using PROC MIXED with entry, environment, environment by entry, and replicates within environment as random effects. LSMeans are provided in Table S2. PC analysis (PCA) was performed in SAS using the PROC PRINCOMP procedure. The correlation matrix-based method was used for PC extraction, and only PCs with eigenvalues equal to or greater than 1 were retained (Field 2009).
Joint linkage mapping
LSMeans across environments were used for joint linkage QTL analysis by employing the PROC GLMSELECT in SAS as previously described (Buckler et al. 2009; Tian et al. 2011; Liu et al. 2016). Briefly, a stepwise regression model was used to fit the population term, and markers nested within population. Where an individual population lacked an introgression covering the test SNP, no test was conducted for that population. The significance level for entry in, and exit out, of the stepwise model was determined by 1000 permutations. PROC GLM was used to fit an additive model, where the allelic effects were considered fixed effects. Significant alleles were determined by a t-test comparison of the parental allele vs. the control B73 allele. QTL support intervals were calculated by adding a single flanking marker for the QTL at a step of 0.1 cM to the full model and testing the significance at the P = 0.05 level.
Pleiotropy between pairs of traits in the joint linkage analysis was evaluated for QTL with overlapping support intervals in SAS. Correlations between allelic effect estimates were used to detect the significant pleiotropic QTL. Pearson correlation coefficients were considered to be significant at raw P = 0.0083 after FDR correction (P = 0.05).
Data availability
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article and its supplemental tables, or are available as datasets in Liu et al. 2016.
Results
QTL analysis of kernel weight
An in-depth QTL analysis of kernel weight has been described previously (Liu et al. 2016), based on the full dataset of eight populations evaluated in seven replications and an additional two populations evaluated in four replications. However, because we wanted to compare the genetic architecture of kernel weight and kernel shape in the same set of experimental materials, we reanalyzed kernel weights based on a reduced dataset of 10 populations from only the five replications where we also collected additional kernel size and shape data.
Using the reduced dataset, we identified five Wt50k QTL (Table S3), where three of the QTL were also identified exactly as in the analysis of the full dataset (Liu et al. 2016) and the other two QTL shifted chromosomal locations only slightly compared to the full dataset. These differences in QTL detection between the full (Liu et al. 2016) and current reduced datasets are likely due to the number of populations analyzed and the number of replications and environmental effects on the data included in the analysis.
Phenotypic framework of kernel weight, size, and shape
We measured eight kernel-related traits in the ten introgression populations in a subset of locations/replicates (Table 1). Kernel size traits included area, perimeter, length, and width, while kernel shape traits included roundness and length/width ratio (L/W). We also estimated kernel density in a term called FFD by dividing Wt50k by kernel area. Broad-sense heritability for these traits ranged from 0.72 to 0.96, with length, perimeter, and area showing the highest heritability, and FFD had the lowest heritability (Table 1). The heritability of Wt50k varied slightly, from 0.87 (Liu et al. 2016) to 0.89 when analyzing the full and partial datasets, respectively.
Table 1. Descriptive statistics for the traits in this study.
| Traits | Locations (Reps) | No. Samples | Mean | SD | Minimum | Maximum | H2 |
|---|---|---|---|---|---|---|---|
| Wt50k (g) | 2 (5) | 856 | 12.65 | 1.20 | 6.79 | 16.52 | 0.890 |
| Area (mm2) | 2 (5) | 856 | 58.13 | 4.29 | 44.12 | 72.76 | 0.945 |
| Width (mm) | 2 (5) | 856 | 6.51 | 0.29 | 5.61 | 7.57 | 0.876 |
| Length (mm) | 2 (5) | 856 | 10.99 | 0.53 | 8.72 | 12.40 | 0.951 |
| L/W | 2 (5) | 856 | 1.69 | 0.09 | 1.32 | 1.95 | 0.872 |
| Roundness | 2 (5) | 856 | 81.14 | 1.83 | 76.38 | 89.56 | 0.877 |
| Perimeter (mm) | 2 (5) | 856 | 32.10 | 1.37 | 27.00 | 36.34 | 0.956 |
| FFD (mg/mm2) | 2 (5) | 856 | 4.35 | 0.27 | 2.52 | 5.45 | 0.721 |
Reps, replicates; No., number; Wt50k, weight of 50 kernels; L/W, length/width; FFD, factor form density. SD, standard deviation. H2, Broad-sense heritability.
Wt50k was highly positively correlated with all the original kernel size traits except roundness and L/W (Table 2). Roundness and L/W thus describe the kernel shape traits, but not seed weight. We found that roundness and L/W show significant but weak correlations with area, a critical kernel size trait, which indicates that kernel size and kernel shape in maize are independent of each other just as in wheat (Gegas et al. 2010).
Table 2. Pearson correlation coefficients among kernel weight and shape traits.
| FFD | Area | Perimeter | Roundness | Width | Length | L/W | |
|---|---|---|---|---|---|---|---|
| Wt50k | 0.643** | 0.779** | 0.709** | 0.034 | 0.674** | 0.588** | −0.027 |
| FFD | 0.035 | −0.003 | 0.249** | 0.220** | −0.075* | −0.231** | |
| Area | 0.940** | −0.172** | 0.704** | 0.845** | 0.165** | ||
| Perimeter | −0.389** | 0.507** | 0.925** | 0.388** | |||
| Roundness | 0.556** | −0.649** | −0.988** | ||||
| Width | 0.255** | −0.567** | |||||
| Length | 0.649** |
significant at P < 0.05; ** significant at P < 0.001. FFD, factor form density; L/W, length/width; Wt50k, weight of 50 kernels.
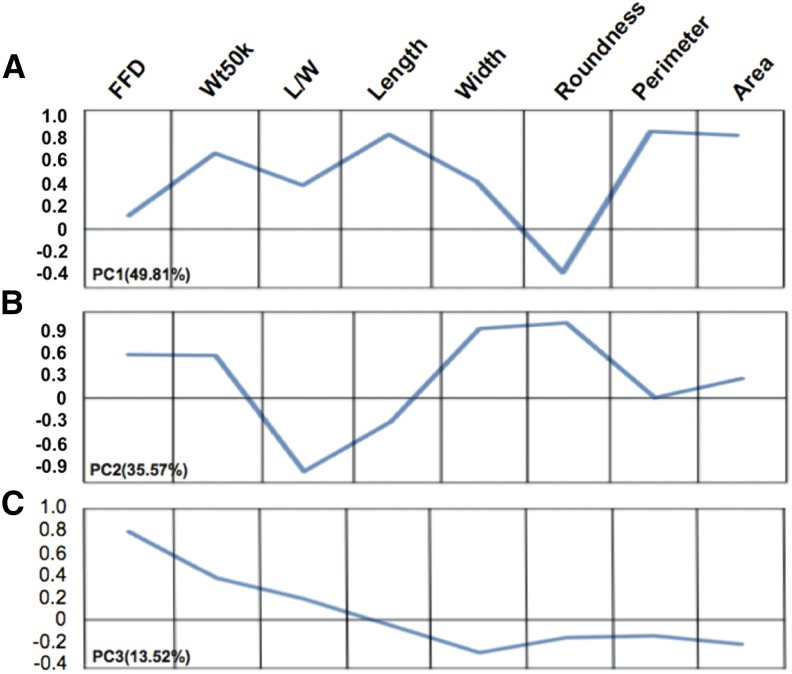
In order to simplify the relationships among kernel traits, PCA was performed on the kernel size and shape traits (Figure S1). Three significant PCs (PC1-3) with eigenvalues greater than 1 were extracted that together explained 98.9% of the variance (Figure S1, A and B). The PCs are linear combinations of the original kernel traits that are independent of each other, and represent different combinations of the traits based on their variable loadings (Figure 1): PC1 primarily represented variance in kernel size (area, perimeter, and length); PC2 mainly captured variance in kernel shape (roundness, L/W) and width; and PC3 was related to variance in kernel density (FFD). The first two PCs have almost equal (∼0.6) loadings for kernel weight, while the loading for PC3 is approximately 0.4. Because each of the PCs describes different combinations of kernel shape traits (e.g., PC1 represents kernel size, PC2 represents roundness, etc.), each PC loading for kernel weight may reflect different components of kernel weight.
Figure 1.
PCA of kernel weight, size, and shape traits. Wt50k variance is captured by all three PCs. (A) Area, perimeter, and length have large effects in PC1. (B) Roundness, width, and L/W have large effects in PC2. (C) PC3 describes variation in FFD. y-axis: component loading. Variance explained is annotated after each PC. FFD, factor form density; L/W, length/width; PC, principal component; PCA, PC analysis; Wt50k, weight of 50 kernels.
Kernel trait QTL identified by joint linkage mapping
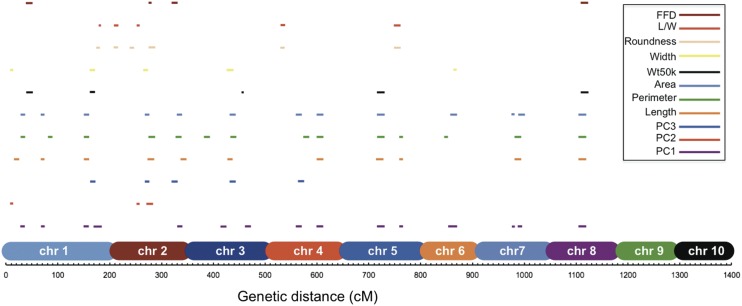
We performed joint linkage QTL analysis on each of the original traits, as well as the PC traits, in order to identify the loci responsible for kernel trait differences between teosinte and maize. We identified 43 QTL for kernel size traits, 11 QTL for kernel shape traits, four QTL for FFD, and five QTL for Wt50k (Figure 2 and Table S3). The 63 QTL were distributed only on chromosomes 1–8, with no QTL on chromosomes 9 and 10. For the newly defined PC traits, PC1, PC2, and PC3, the total number of QTL detected were 15, 3, and 5, respectively (Figure 2 and Table S3). QTL for PCs collectively explained 62.51%, 21.70%, and 31.98% of the total variance, respectively, and were shared among seven to 10 populations (Table S4).
Figure 2.
Distribution of QTL for kernel weight, size, and shape traits on genome. x-axis, the genetic distance (cM) of whole genome in NILs mapping population, and chromosomes 1–10 were labeled with different colors. The length of the QTL lines is proportional to the support interval length. Chr, chromosome; FFD, factor form density; L/W, length/width; NIL, introgression line; PC, principal component; QTL, quantitative trait loci; Wt50k, weight of 50 kernels.
Several QTL were found in common between the derived PCs and kernel size, shape, and weight (Figure 2). For example, QTL for FFD, Wt50k, area, perimeter, length, and PC1 were identified on chromosomes 5 and 8. For the PC QTL, most had overlapping QTL for kernel size. For Wt50k, four of the five QTL had corresponding QTL for other kernel size, with the only exception of QTL for Wt50k on chromosome 3. These findings are consistent with the phenotypic framework analysis, where kernel weight was highly correlated with kernel size. Kernel weight is likely a composite trait controlled by various aspects of kernel shape, size, and density, and that any of these three aspects can be used to increase seed weight separately, as well as in combination. While PCA was able to simplify the relationships among the traits such that the components of kernel weight were split into the various PCs that are independent of each other, our data are not conclusive on the exact relationship between kernel weight and various size and shape traits.
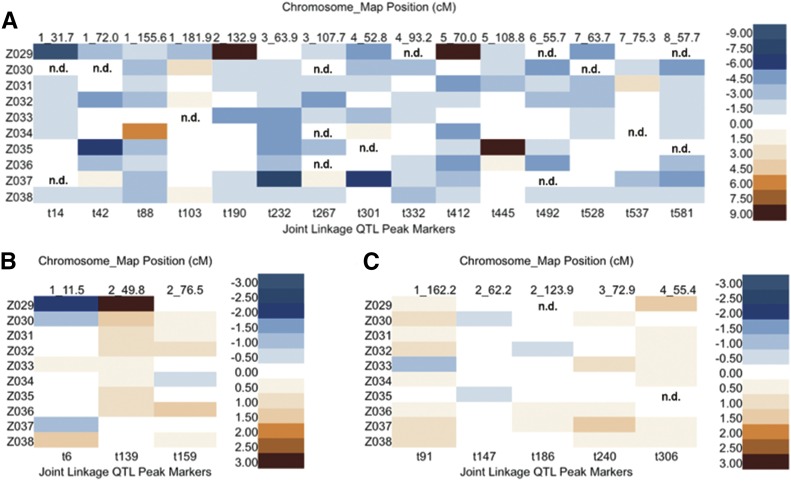
Additive allelic effects were estimated relative to B73 (Figure 3). While the biological meaning of PCs and their QTL effects may be difficult to interpret, their trait loadings can be used to represent a composite of correlated traits in a way that removes the interdependence among traits. Inherent to PCA, the first PC always captures the most variance, with subsequent PCs explaining decreasing amounts of variance. It is then not surprising that when we compared effects between PC1, PC2, and PC3, we found that PC1 effects had a much wider range (−8.08 − 24.82) than PC2 and PC3 (−2.22 − 4.95 and −1.33 − 1.82, respectively (Figure 3 and Table S4). Allelic series, or the detection of both negative and positive additive allele effects relative to the B73 allele, were identified for 60%, 67%, and 40% of the PC1, PC2, and PC3 QTL, respectively (Figure 3).
Figure 3.
Heat map of additive effects for PCs QTL. The top horizontal axis lists the chromosome number and genetic map position for each QTL, while the bottom horizontal axis displays the QTL peak SNPs marker selected by linkage analysis. The vertical axis shows 10 NIL populations in order. Allelic affects are color coded with 2.00 increments for PC1 (A), and 0.50 increments for PC2 (B) and PC3 (C). n.d. indicates that allelic effects could not be determined, as there were no NILs carrying an introgression at the QTL. NIL, introgression line; PC, principal component; QTL, quantitative trait loci; SNP, single nucleotide polymorphism.
Pleiotropic QTL affect kernel traits
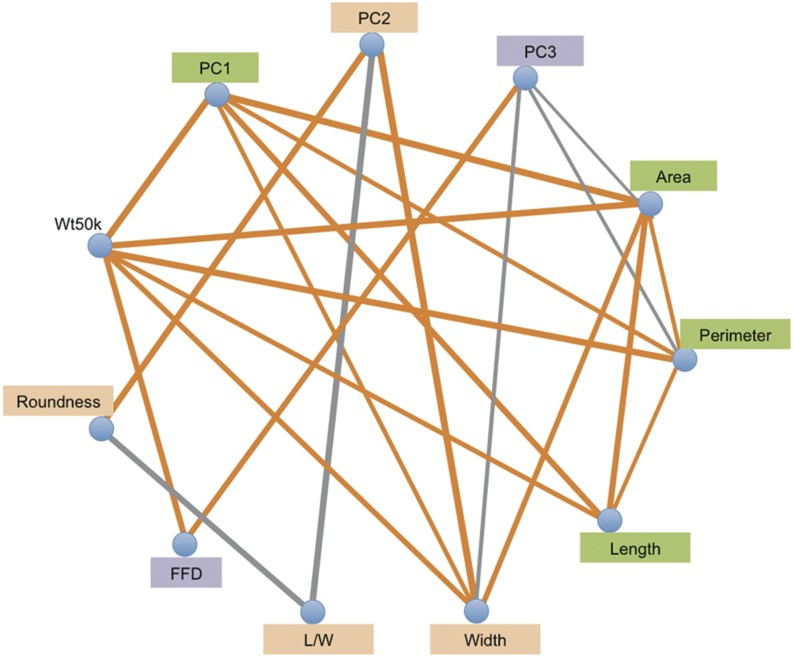
Maize-teosinte introgression populations provide substantial power to detect pleiotropy among overlapping QTL for multiple traits. Pleiotropy was assessed by correlating the allelic effects for overlapping QTL across the ten populations (Figure 4 and Table S5). If a QTL has large positive or negative effects for two traits in many of the same populations, the allelic effects at that locus will be significantly correlated and pleiotropy will be inferred. Positive pleiotropy was observed between kernel weight and kernel size traits (area, perimeter, and length) and was observed among the size traits themselves (Figure 4). Wt50k also had positive pleiotropy with FFD. In contrast to kernel size traits, the kernel shape traits (roundness and L/W) show negative pleiotropy with each other. This was expected as width is in the denominator of this ratio. Weak pleiotropy was observed between the kernel size and shape trait groups, which suggests that they have distinct genetic components. In addition, the PCA traits showed patterns of pleiotropy that were consistent with their observed phenotypic correlations with the kernel traits (Figure 4).
Figure 4.
Pleiotropy for kernel traits in maize-teosinte NILs populations. Gray and orange lines between traits indicate negative and positive correlations between different QTL additive effects, respectively, with line width proportional to the degree of pleiotropy. FDR = 0.05 (raw P-value = 0.0083) was used as the significance threshold for effect correlation. FFD, factor form density; L/W, length/width; NILs carrying an introgression at the QTL. NIL, introgression line; PC, principal component; QTL, quantitative trait loci; Wt50k, weight of 50 kernels.
Discussion
Comparative genetic analysis revealed several candidate genes underlying maize kernel size and shape QTL
Seed size and shape are among the most important domestication syndrome traits for many plants, including rice, wheat, sorghum, and maize. Synteny and colinearity among land plants, especially among the grasses, allows us to analyze the genetic architecture of the same traits across species in a comparative manner. This comparative analysis can also help identify candidate genes underlying the QTL if candidates have been identified, cloned, and verified in other species.
In the current study, joint linkage mapping identified more than 60 QTL, including QTL for kernel area and length with moderate allelic effects, that colocalize with kernel weight QTL (Figure 2). Another strategy to map QTL is genome-wide association mapping (GWAS), which has higher mapping resolution, even to the single-gene level in species and populations with low linkage disequilibrium (Flint-Garcia et al. 2009). Unfortunately, the BC4 backcross population structure of the teosinte NILs is not a suitable platform for GWAS due to the limited recombination. The GWAS approach has been used in other species and maize populations to identify candidate genes for the same or similar traits. Interestingly, GWAS has poor power to identify rare alleles/variants even if they have a large effect. It was reported recently that several rare alleles are associated with grain size and yield in rice (Zhang et al. 2012; Song et al. 2015; Hu et al. 2015), and more are expected to be identified and verified in further studies. Hence, to date, linkage mapping has played a very important role in identifying rare alleles of intermediate to large effect, though GWAS methodologies are being developed to improve the identification of rare variants. In addition, transcriptional data are also helpful in the identification of candidate genes expressed in the appropriate tissues and time points (Sekhon et al. 2014). Here, we combine the findings of numerous studies which use mutant analysis, linkage mapping, GWAS, and transcriptomic analysis to understand and interpret our QTL results.
Using this comparative genetic analysis strategy, several candidate genes were identified for our kernel size and shape QTL, including known genes such as ZmSH1 (Lin et al. 2012), gln5 (Martin et al. 2006), ZmGW2 (Li et al. 2010a), and mn1 (Gupta et al. 2006), and unknown genes that have not been identified in maize but their orthologs were reported to relate to grain size and yield in other crop plants. For example, association analysis in sorghum association identified the gene Sb04g015420 to be strongly associated with sorghum seed size (Zhang et al. 2015). The maize ortholog, GRMZM2G00812, has not been reported to associate with kernel size previously, but is potentially a candidate for our QTL on chromosome 5 (marker t412; Table S3).
FFD describes differences in grain density and has been defined as grain weight / (grain length × grain width) in wheat (Giura and Saulescu 1996). In our study, we modified the FFD trait to mean kernel weight divided by kernel area, based on differences in seed size and shape parameters between maize and wheat. The QTL on chromosome 2 controlling FFD has a strong candidate gene, miniature 1 (mn1) (Gupta et al. 2006), under its peak. The maize gene mn1 is the ortholog of GIF1 in rice (Weng et al. 2008). GIF1 encodes a cell wall invertase required for carbon partitioning during early grain fill. It is known that grain fill is an important trait that contributes greatly to grain weight, but the exact mechanism was unknown. Because this QTL was identified to control only FFD and not any other kernel size traits, we hypothesize that mn1-mediated grain filling might contribute to kernel weight through regulation of kernel density, not size, at least in maize.
Mapping QTL with PCs identified some QTL that were not detected by univariate QTL analysis
To help understand the genetic control of multiple traits, we used PCA as our multivariate analysis method for related kernel traits in the study. PCA is widely used to decompose correlated variables into a smaller set of uncorrelated variables. The eigenvectors of the eigenvalues of the phenotypic covariance matrix, or the PCs, can be considered as new traits for QTL identification (Gilbert and Le Roy 2003; Topp et al. 2013). Mapping QTL with PCs can increase the statistical power to detect QTL by combining information across traits and removing the noise caused by trait correlations, and is used widely in both animal science (Gilbert and Le Roy 2003; Musani et al. 2006) and plant science (Choe and Rocheford 2012; Topp et al. 2013). The first three PCs together explained 98.9% of the variance in the original dataset (Figure S1, A and B), of which PC1 captured almost 50% of the variance (Figure 1A).
While PCA results in abstract PC values that have seemingly little biological meaning, these PCs are composite traits comprised of each of the original traits, as indicated by their different loadings for each trait (Figure 1, y-axis represents loadings), and can be used as phenotypes in QTL analysis (Topp et al. 2013). When comparing the QTL profiles for the individual kernel traits to PC-derived traits, we found that, in most cases, the PC-QTL analysis yielded similar results to QTL mapping with individual traits with patterns predicted by the PC loadings (Figure 1). However, PC-QTL analysis also identified additional chromosomal regions which were not detected by univariate analysis (e.g., the two QTL on chromosome 3 for PC1; Figure 2 and Table S3). This identification of novel QTL is likely due to these QTL being associated with multiple traits.
Genomic regions controlling domestication syndrome were identified
According to previous studies, a handful of genomic regions were believed to have strong effects on domestication traits (Doebley 2004). These regions were located on both arms of chromosome 1, the long arm of chromosome 3, and the short arms of chromosome 2, 4, and 5 (Doebley and Stec 1993; Doebley 2004). Our study not only identified QTL in these five regions, but also in additional regions located on chromosomes 2, 6, 7, and 8 (Figure 2 and Table S3). Many of our kernel phenotypes differed from these early studies, which included plant and ear morphology traits.
The genomic segment on long arm of chromosome 1 straddles the cloned domestication gene teosinte branched 1 (tb1) (Doebley et al. 1995), a member of the TCP family of transcriptional regulators (Cubas et al. 1999). This region affected many kernel traits in our study, including kernel length, perimeter, area, width, and weight, and the new defined traits PC1 and PC3 (Table S3). The strongest of the kernel length QTL (marker t88; Table S3) has an alternate candidate gene, YABBY, under its peak. The YABBY gene is an important transcription factor involved in plant development and is an excellent candidate gene for maize kernel size, since it was reported to control the fruit size in tomato (Cong et al. 2008). In rice, YABBY was positionally cloned and named OsSh1 (Shattering 1) because of its important role in seed shattering (Fukuta and Yagi 1998). Recently, SbSh1 was map-based cloned in sorghum and it was revealed that Sh1 genes were under parallel selection during maize, rice, and sorghum domestication (Lin et al. 2012). The dual role of YABBY in fruit size in tomato and shattering in grasses suggest that the YABBY gene could play a pleiotropic role in controlling seed size and shattering simultaneously in maize as well. While we acknowledge that QTL peaks are quite broad and can encompass hundreds of genes, it is nonetheless interesting to speculate about the possibility of parallel selection across species and multiple traits. Until this QTL is further characterized for each trait (e.g., by map-based cloning), the mechanism of action for this transcription factor remains unknown.
The QTL on chromosomes 5 and 8 are also very important because of their pleiotropic effects. Both have strong effects on kernel weight, area, perimeter, and length (Figure 2), and the QTL on chromosome 5 may also affect KRN (Liu et al. 2016). The most likely reason for the pleiotropic effects of the QTL on chromosome 5 is its location near the centromere, where the low-recombination environment of the pericentromeric region causes clusters of genes to act as a single QTL. One strong candidate gene for the QTL on chromosome 5 is ZmGW2, one of the two maize orthologs of GW2 which controls grain size and weight in rice. A QTL for kernel weight was mapped to the ZmGW2 region, and ZmGW2 was found to associate with kernel weight by altering kernel size in maize (Li et al. 2010a). The GW2 gene, which encodes a RING-type E3 ubiquitin ligase, alters grain width and weight and with very little effect on grain length in rice (Song et al. 2007). Interestingly, it seems that GW2 affects kernel weight differently in maize than in rice, as our QTL affects kernel length but not width as is the case in rice. GS3, a gene that controls grain length and weight in rice (Fan et al. 2006), was also found to operate differently in maize (Li et al. 2010b) and wheat (Gegas et al. 2010).
Pleiotropy analysis revealed the potential to improve yield and kernel composition in maize
One of the greatest challenges in breeding high-quality varieties is the strong phenotypic correlation among kernel quality traits (Simmonds 1995; Ge et al. 2005). For the crop breeding community, it has been a long standing problem that they have been able to improve either yield or quality, but almost never improve both simultaneously. Most improvements in quality are usually accompanied by a reduction in yield because of this close association. Our study showed that this problem also exists for kernel size and shape as these traits are significantly correlated both phenotypically and genetically (Figure 4 and Table 2). Because kernel size and shape were believed to relate to kernel yield and quality, respectively, in rice and wheat. Understanding the genetic basis of kernel size and shape, as well as any possible genetic constraints preventing the maximization of both traits, is especially crucial from the applied perspective. After the initial genetic analysis of kernel size and shape, we conducted pleiotropy analysis for the same kernel size and shape traits, and identified some alleles that alter one trait without affecting the others. For example, no interactions were found between kernel size traits (area, perimeter, and length) and the kernel shape traits of L/W and roundness. This suggests that kernel size and shape are different traits under substantially independent genetic control, could have evolved independently, and could be manipulated separately in breeding programs. This study has shown the close relationship between kernel size and kernel weight in maize. However, it is still not clear whether there is any relationship between kernel shape and kernel composition in maize. Meta-analysis to link kernel size and shape to kernel composition is a potential way to elucidate this relationship in the future. Our analysis of pleiotropy provides insight for breeding and biotechnology strategies to alter maize kernel weight, which may also have applications in other crop plants.
Supplementary Material
Acknowledgments
We wish to thank AgReliant for the production of the doubled haploid lines from the Z031 population, and the McMullen, Flint-Garcia, and Buckler groups for growing the trials, data collection, and providing ear and seed samples. We also thank the anonymous reviewers for their helpful comments on the manuscript. This research was supported by the National Science Foundation (IOS-0820619) and United States Department of Agriculture (USDA)-Agriculture Research Service (ARS). Mention of a trademark, vendor, or proprietary product does not constitute a guarantee or warranty of the product by the USDA and does not imply its approval to the exclusion of other products or vendors that may also be suitable. The USDA-ARS, Midwest Area, is an equal opportunity, affirmative action employer, and all agency services are available without discrimination.
Footnotes
Supplemental material is available online at www.g3journal.org/lookup/suppl/doi:10.1534/g3.116.030155/-/DC1
Communicating editor: K. Dawe
Literature Cited
- Abbo S., Pinhasi van-Oss R., Gopher A., Saranga Y., Ofner I., et al. , 2014. Plant domestication vs. crop evolution: a conceptual framework for cereals and grain legumes. Trends Plant Sci. 19: 351–360. [DOI] [PubMed] [Google Scholar]
- Beadle G., 1939. Teosinte and the origin of maize. J. Hered. 30: 245–247. [Google Scholar]
- Beavis W. D., Smith O. S., Grant D., Fincher R., 1994. Identification of Quantitative Trait Loci Using a Small Sample of Topcrossed and F4 Progeny from Maize. Crop Sci. 34: 882–896. [Google Scholar]
- Buckler E. S., Holland J. B., Bradbury P. J., Acharya C. B., Brown P. J., et al. , 2009. The genetic architecture of maize flowering time. Science 325: 714–718. [DOI] [PubMed] [Google Scholar]
- Choe E., Rocheford T. R., 2012. Genetic and QTL analysis of pericarp thickness and ear architecture traits of Korean waxy corn germplasm. Euphytica 183: 243–260. [Google Scholar]
- Clark D., Dudley J. W., Rocheford T. R., LeDeaux J. R., 2006. Genetic Analysis of Corn Kernel Chemical Composition in the Random Mated 10 Generation of the Cross of Generations 70 of IHO × ILO. Crop Sci. 46: 807–819. [Google Scholar]
- Cong B., Barrero L. S., Tanksley S. D., 2008. Regulatory change in YABBY-like transcription factor led to evolution of extreme fruit size during tomato domestication. Nat. Genet. 40: 800–804. [DOI] [PubMed] [Google Scholar]
- Cook J. P., McMullen M. D., Holland J. B., Tian F., Bradbury P., et al. , 2012. Genetic architecture of maize kernel composition in the nested association mapping and inbred association panels. Plant Physiol. 158: 824–834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cubas P., Lauter N., Doebley J., Coen E., 1999. The TCP domain: a motif found in proteins regulating plant growth and development. Plant J. 18: 215–222. [DOI] [PubMed] [Google Scholar]
- Doebley J., 2004. The genetics of maize evolution. Annu. Rev. Genet. 38: 37–59. [DOI] [PubMed] [Google Scholar]
- Doebley J., Stec A., 1993. Inheritance of the morphological differences between maize and teosinte: comparison of results for two F2 populations. Genetics 134: 559–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doebley J., Stec A., Gustus C., 1995. teosinte branched1 and the origin of maize: evidence for epistasis and the evolution of dominance. Genetics 141: 333–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers A. D., 1995. Grain size and morphology: Implications for quality, pp. 19–24 in Wheat Structure, Elsevier. [Google Scholar]
- Evers A., Cox R., Shaheedullah M., Withey R., 1990. Predicting milling extraction rate by image analysis of wheat grains. Asp. Appl. Biol. 25: 417–426. [Google Scholar]
- Fan C., Xing Y., Mao H., Lu T., Han B., et al. , 2006. GS3, a major QTL for grain length and weight and minor QTL for grain width and thickness in rice, encodes a putative transmembrane protein. Theor. Appl. Genet. 112: 1164–1171. [DOI] [PubMed] [Google Scholar]
- Field A., 2009. Discovering Statistics Using SPSS, SAGE Publishing Ltd., London. [Google Scholar]
- Flint-Garcia S. A., Bodnar A. L., Scott M. P., 2009. Wide variability in kernel composition, seed characteristics, and zein profiles among diverse maize inbreds, landraces, and teosinte. Theor. Appl. Genet. 119: 1129–1142. [DOI] [PubMed] [Google Scholar]
- Frary A., Nesbitt T. C., Grandillo S., Knaap E., Cong B., et al. , 2000. fw2.2: a quantitative trait locus key to the evolution of tomato fruit size. Science 289: 85–88. [DOI] [PubMed] [Google Scholar]
- Fukuta Y., Yagi T., 1998. Mapping of a Shattering Resistance Gene in a Mutant Line SR- 5 Induced from an indica Rice Variety, Nan-jing11. Breed. Sci. 48: 345–348. [Google Scholar]
- Fuller D. Q., 2007. Contrasting patterns in crop domestication and domestication rates: recent archaeobotanical insights from the Old World. Ann. Bot. (Lond.) 100: 903–924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia D., Fitz Gerald J. N., Berger F., 2005. Maternal control of integument cell elongation and zygotic control of endosperm growth are coordinated to determine seed size in Arabidopsis. Plant Cell 17: 52–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge X. J., Xing Y. Z., Xu C. G., He Y. Q., 2005. QTL analysis of cooked rice grain elongation, volume expansion, and water absorption using a recombinant inbred population. Plant Breed. 124: 121–126. [Google Scholar]
- Gegas V. C., Nazari A., Griffiths S., Simmonds J., Fish L., et al. , 2010. A genetic framework for grain size and shape variation in wheat. Plant Cell 22: 1046–1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert H., Le Roy P., 2003. Comparison of three multitrait methods for QTL detection. Genet. Sel. Evol. 35: 281–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giura A., Saulescu N. N., 1996. Chromosomal location of genes controlling grain size in a large grained selection of wheat (Triticum aestivum L.). Euphytica 89: 77–80. [Google Scholar]
- Goldman I. L., Rocheford T. R., Dudley J. W., 1993. Quantitative trait loci influencing protein and starch concentration in the Illinois Long Term Selection maize strains. Theor. Appl. Genet. 87: 217–224. [DOI] [PubMed] [Google Scholar]
- Gross B. L., Olsen K. M., 2010. Genetic perspectives on crop domestication. Trends Plant Sci. 15: 529–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta P. K., Rustgi S., Kumar N., 2006. Genetic and molecular basis of grain size and grain number and its relevance to grain productivity in higher plants. Genome 49: 565–571. [DOI] [PubMed] [Google Scholar]
- Hammer K., 1984. Das domestikationssyndrom. Die Kult. 32: 11–34. [Google Scholar]
- Harlan J. R., de Wet J. M. J., Price E. G., 1973. Comparative evolution of cereals. Evolution (N. Y). 27: 311–325. [DOI] [PubMed] [Google Scholar]
- Holland J. B., Nyquist W. E., Cervantes-Martinez C. T., 2003. Estimating and interpreting heritability for plant breeding. Plant Breed. Rev. 22: 9–112. [Google Scholar]
- Hu J., Wang Y., Fang Y., Zeng L., Xu J., et al. , 2015. A rare allele of GS2 enhances grain size and grain yield in rice. Mol. Plant 8: 1455–1465. [DOI] [PubMed] [Google Scholar]
- Huang R., Jiang L., Zheng J., Wang T., Wang H., et al. , 2013. Genetic bases of rice grain shape: So many genes, so little known. Trends Plant Sci. 18: 218–226. [DOI] [PubMed] [Google Scholar]
- Huang X., Qian Q., Liu Z., Sun H., He S., et al. , 2009. Natural variation at the DEP1 locus enhances grain yield in rice. Nat. Genet. 41: 494–497. [DOI] [PubMed] [Google Scholar]
- Jiang W.-B., Huang H.-Y., Hu Y.-W., Zhu S.-W., Wang Z.-Y., et al. , 2013. Brassinosteroid Regulates Seed Size and Shape in Arabidopsis. Plant Physiol. 162: 1965–1977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovach M. J., Sweeney M. T., McCouch S. R., 2007. New insights into the history of rice domestication. Trends Genet. 23: 578–587. [DOI] [PubMed] [Google Scholar]
- Li Q., Li L., Yang X., Warburton M. L., Bai G., et al. , 2010a Relationship, evolutionary fate and function of two maize co-orthologs of rice GW2 associated with kernel size and weight. BMC Plant Biol. 10: 143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q., Yang X., Bai G., Warburton M. L., Mahuku G., et al. , 2010b Cloning and characterization of a putative GS3 ortholog involved in maize kernel development. Theor. Appl. Genet. 120: 753–763. [DOI] [PubMed] [Google Scholar]
- Lin Z., Li X., Shannon L. M., Yeh C.-T., Wang M. L., et al. , 2012. Parallel domestication of the Shattering1 genes in cereals. Nat. Genet. 44: 720–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Wang L., Sun C., Zhang Z., Zheng Y., et al. , 2014. Genetic analysis and major QTL detection for maize kernel size and weight in multi-environments. Theor. Appl. Genet. 127: 1019–1037. [DOI] [PubMed] [Google Scholar]
- Liu L., Tong H., Xiao Y., Che R., Xu F., et al. , 2015. Activation of Big Grain1 significantly improves grain size by regulating auxin transport in rice. Proc. Natl. Acad. Sci. USA 112: 11102–11107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., Cook J., Melia-Hancock S., Guill K., Bottoms C., et al. , 2016. Expanding maize genetic resources with predomestication alleles: Maize–teosinte introgression populations. Plant Genome 9: 1–11. [DOI] [PubMed] [Google Scholar]
- Luo Y., Zhu Z., Chen N., Duan B., Zhang L., 2004. Grain types and related quality characteristics of rice in China. Chinese J. Rice Sci. 18: 135–139. [Google Scholar]
- Martin A., Lee J., Kichey T., Gerentes D., Zivy M., et al. , 2006. Two cytosolic glutamine synthetase isoforms of maize are specifically involved in the control of grain production. Plant Cell 18: 3252–3274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuoka Y., Vigouroux Y., Goodman M. M., G. J. Sanchez, E. Buckler et al, 2002. A single domestication for maize shown by multilocus microsatellite genotyping. Proc. Natl. Acad. Sci. USA 99: 6080–6084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMullen M. D., Kresovich S., Villeda H. S., Bradbury P., Li H., et al. , 2009. Genetic properties of the maize nested association mapping population. Science 325: 737–740. [DOI] [PubMed] [Google Scholar]
- Messmer R., Fracheboud Y., Bänziger M., Vargas M., Stamp P., et al. , 2009. Drought stress and tropical maize: QTL-by-environment interactions and stability of QTLs across environments for yield components and secondary traits. Theor. Appl. Genet. 119: 913–930. [DOI] [PubMed] [Google Scholar]
- Moles A. T., Ackerly D. D., Webb C. O., Tweddle J. C., Dickie J. B., et al. , 2005. A brief history of seed size. Science 307: 576–580. [DOI] [PubMed] [Google Scholar]
- Musani S. K., Zhang H.-G., Hsu H.-C., Yi N., Gorman B. S., et al. , 2006. Principal component analysis of quantitative trait loci for immune response to adenovirus in mice. Hereditas 143: 189–197. [DOI] [PubMed] [Google Scholar]
- Piperno D. R., Ranere A. J., Holst I., Iriarte J., Dickau R., 2009. Starch grain and phytolith evidence for early ninth millennium B.P. maize from the Central Balsas River Valley, Mexico. Proc. Natl. Acad. Sci. USA 106: 5019–5024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekhon R. S., Hirsch C. N., Childs K. L., Breitzman M. W., Kell P., et al. , 2014. Phenotypic and Transcriptional Analysis of Divergently Selected Maize Populations Reveals the Role of Developmental Timing in Seed Size Determination. Plant Physiol. 165: 658–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shomura A., Izawa T., Ebana K., Ebitani T., Kanegae H., et al. , 2008. Deletion in a gene associated with grain size increased yields during rice domestication. Nat. Genet. 40: 1023–1028. [DOI] [PubMed] [Google Scholar]
- Simmonds N. W., 1995. The relation between yield and protein in cereal grain. J. Sci. Food Agric. 67: 309–315. [Google Scholar]
- Song X.-J., Huang W., Shi M., Zhu M.-Z., Lin H.-X., 2007. A QTL for rice grain width and weight encodes a previously unknown RING-type E3 ubiquitin ligase. Nat. Genet. 39: 623–630. [DOI] [PubMed] [Google Scholar]
- Song X. J., Kuroha T., Ayano M., Furuta T., Nagai K., et al. , 2015. Rare allele of a previously unidentified histone H4 acetyltransferase enhances grain weight, yield, and plant biomass in rice. Proc. Natl. Acad. Sci. USA 112: 76–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian F., Bradbury P. J., Brown P. J., Hung H., Sun Q., et al. , 2011. Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat. Genet. 43: 159–162. [DOI] [PubMed] [Google Scholar]
- Topp C. N., Iyer-Pascuzzi A. S., Anderson J. T., Lee C.-R., Zurek P. R., et al. , 2013. 3D phenotyping and quantitative trait locus mapping identify core regions of the rice genome controlling root architecture. Proc. Natl. Acad. Sci. USA 110: E1695–E1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S., Wu K., Yuan Q., Liu X., Liu Z., et al. , 2012. Control of grain size, shape and quality by OsSPL16 in rice. Nat. Genet. 44: 950–954. [DOI] [PubMed] [Google Scholar]
- Weng J., Gu S., Wan X., Gao H., Guo T., et al. , 2008. Isolation and initial characterization of GW5, a major QTL associated with rice grain width and weight. Cell Res. 18: 1199–1209. [DOI] [PubMed] [Google Scholar]
- Westoby M., Falster D. S., Moles A. T., Vesk P. A., Wright I. J., 2002. Plant Ecological Strategies: Some Leading Dimensions of Variation Between Species. Annu. Rev. Ecol. Syst. 33: 125–159. [Google Scholar]
- Zhang D., Li J., Compton R. O., Robertson J., Goff V. H., et al. , 2015. Comparative Genetics of Seed Size Traits in Divergent Cereal Lineages Represented by Sorghum (Panicoidae) and Rice (Oryzoidae). G3 (Bethesda) 5: 1117–1128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X., Wang J., Huang J., Lan H., Wang C., et al. , 2012. Rare allele of OsPPKL1 associated with grain length causes extra-large grain and a significant yield increase in rice. Proc. Natl. Acad. Sci. USA 109: 21534–21539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y., Zhang X., Kang X., Zhao X., Zhang X., et al. , 2009. SHORT HYPOCOTYL UNDER BLUE1 associates with MINISEED3 and HAIKU2 promoters in vivo to regulate Arabidopsis seed development. Plant Cell 21: 106–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article and its supplemental tables, or are available as datasets in Liu et al. 2016.