Markov Chain evaluation of acute postoperative pain transition states

Abstract

Prior investigations on acute postoperative pain dynamicity have focused on daily pain assessments, and so were unable to examine intra-day variations in acute pain intensity. We analyzed 476,108 postoperative acute pain intensity ratings clinically documented on postoperative days 1 to 7 from 8,346 surgical patients using Markov Chain modeling to describe how patients are likely to transition from one pain state to another in a probabilistic fashion. The Markov Chain was found to be irreducible and positive recurrent, with no absorbing states. Transition probabilities ranged from 0.0031 for the transition from state 10 to state 1, to 0.69 for the transition from state zero to state zero. The greatest density of transitions was noted in the diagonal region of the transition matrix, suggesting that patients were generally most likely to transition to the same pain state as their current state. There were also slightly increased probability densities in transitioning to a state of asleep or zero from the current state. Examination of the number of steps required to traverse from a particular first pain score to a target state suggested that overall, fewer steps were required to reach a state of zero (range 6.1–8.8 steps) or asleep (range 9.1–11) than were required to reach a mild pain intensity state. Our results suggest that Markov Chains are a feasible method for describing probabilistic postoperative pain trajectories, pointing toward the possibility of using Markov decision processes to model sequential interactions between pain intensity ratings and postoperative analgesic interventions.

1. Introduction

Each year, over 50 million inpatient surgeries are performed in the United States, and over 60% of surgical patients will suffer from severe acute postoperative pain [3,10]. Chapman and others have demonstrated that for many surgical patients, postoperative pain will remain steady, or even increase, over the first several days after surgery when pain intensity is measured via daily averages of postoperative pain [2,11]. Further, mounting evidence suggests that sustained levels of severe acute postoperative pain may be an independent predictor of developing chronic postsurgical pain [32,33]. Altogether, these results suggest that the temporal characteristics of acute pain represent an important feature in assessing and treating this prevalent source of postoperative suffering.

Importantly, the above prior investigations used daily pain assessments and so were unable to account for intra-day variations in acute pain intensity. This methodological tradeoff offers opportunities for further consideration at a higher temporal resolution, given that clinical pain assessment and management are implemented over hours rather than days, and many common analgesics function pharmacokinetically on an hourly rather than daily basis [25,40,44,51]. Approaches such as ecological monetary assessment (EMA), which use repeated collection of real-time intra-subject data while that subject functions within the environmental domain of interest, can use random sampling of current-state assessments to minimize biases due to recall or altered environmental settings [22,46,49]. Ecological monetary assessment approaches also offer their own analytical challenges, given the opportunity to examine transitions among said momentary states.

One approach to evaluating changes in acute postoperative pain scores over time is to evaluate the probabilities of transitioning from a given pain state, as measured by the numerical rating scale (NRS), to another (or the same!) pain state during the next pain assessment through the use of Markov Chains (MCs)[21]. This approach to modeling acute postoperative pain is attractive because it considers postoperative pain as a stochastic process, where randomness in the behavior of the system is accepted and modeled probabilistically, rather than as a deterministic process [6,50]. MCs therefore model the course of pain states through which a patient will progress during their postoperative recovery. Of particular interest, patient and clinical factors can be incorporated into the model to create personalized transition matrices that depict differences in the temporal dynamics of pain as a function of patient characteristics and clinical factors.

Here, we use over 400,000 acute postoperative pain intensity ratings measured at an hourly, rather than daily, time frame after surgery to characterize changes in postoperative pain scores as an MC. Our primary aim was to define and characterize MC transition matrices for a mixed surgical cohort, as well as MC transition matrices stratified by age, sex, and type of surgery. Our secondary aim was to examine the sequence of transitions among pain states, in a probabilistic fashion, using MC modeling methods to determine how many transition steps were necessary to reach a target pain state given an initial pain state on the basis of age, sex, and type of surgery.

2. Methods

This study was a retrospective cohort study conducted in accordance with the STROBE guidelines, and was approved by the University of Florida Institutional Review Board [39].

2.1 Description of data

Surgical case data were obtained from the University of Florida’s Integrated Data Repository (IDR), which is a large database of validated fields obtained from electronic medical record systems used for patient tracking, billing, surgery, and hospital documentation purposes [51]. Subjects were those patients aged 21 and over receiving non-ambulatory surgery at UF Health at the University of Florida over a 1-year period beginning in May 2011. Surgical case exclusion criteria included obstetric surgery, as well as those patients who received multiple separate surgeries within the study period in order to avoid contamination of pain scores from the effects of surgeries preceding or following the case of interest.

To account for potential nonlinear effects of age, patient age data were empirically binned into the following age groups: 21 to 39, 40 to 64, 65 to 84, and 85 or greater. The types of surgeries were identified using Current Procedural Terminology codes that were further organized using the Clinical Categorization Software system (CCS) [26]. A sample of common procedures spanning a range of affected tissues were selected based on the CCS method of grouping surgeries; these types of surgery identifiers were used for stratification by type of surgery. Stratifications by age group and sex included subjects from the entire cohort meeting the above inclusion criteria. This hybrid approach to stratification permitted inclusion of the broadest possible cohort while still offering comparison of smaller and more similar subpopulations.

All pain scores were documented by clinical staff using the NRS on an 11-point system ranging from 0 to 10. Pain scores were entered using the EPIC electronic medical record system; the UFHealth implementation offers education on the administration of the NRS query at the point of data entry to improve the veracity of collected data, including a contextualization using the Defense and Veterans Pain Rating System [8]. Pain scores were generally recorded every 4 hours per nursing protocol, with a repeat query within 1 hour following administration of analgesic medications for breakthrough pain; this documentation schedule was modified as needed for different clinical settings such as the intensive care unit and post-anesthesia care unit, where assessments were recorded more often as needed. Structured analgesic frameworks were used for each surgical population. When a patient was identified as sleeping, clinical staff documented this as a separate and non-zero pain rating labeled “asleep,” and so this was included as a 12th state positioned below zero on the NRS. Missing observations, including those where the patient was labeled as “off unit,” were presumed to be missing at random and so were removed from the analysis. All pain scores were labeled with a corresponding date and time stamp, as were the end times of the patient’s surgical procedure, defined as the closure of the wound and readiness for emergence from anesthesia [53]. For each pain score, the time in minutes following the end of surgery was calculated to enable a common reference point. Notably, times of postoperative pain scores were only used to ensure the appropriate range and order of the pain intensity ratings; the actual times themselves were not included in this implementation of the MC.

To consider the quantification of pain scores using categorical scales, the above NRS pain intensity ratings were also grouped into the following states: asleep, zero, mild (1–4), moderate (5–6), and severe (7–10) [24,27,28,31]. While our work considered state transitions among pain intensity ratings, the transition matrix could be expanded to consider other dimensions of pain, such as side effects or pain-related function. Extracting such information from electronic medical record systems at-scale can present numerous challenges, and requires a substantially larger set of observations to account for the expanded matrix. Yet, the potential benefits of offering multi-objective optimizations under sequential, uncertain conditions may prove to yield a substantial improvement in medical decision-making in acute pain medicine.

2.2 Characterization of MCs

We begin with a basic description of the Markov property. Assume that we are interested in taking measurements from a system (or an object) over time. Also assume that the values of these measurements are discrete and we take these measurements at regular intervals. The sequence of observations can then be modeled as a discrete time stochastic process [34]. A discrete time stochastic process is called an MC if its behavior in the future can be predicted using its current state only, independent of the past [5]. That is, according to the Markov assumption, the sequence of events preceding the present state do not necessarily influence the future state, as it is the probability distribution conditioned on the present state that determines the probabilistic outcome of the future state. (Note that this can be partially circumvented by conditioning not only on the current state but also preceding states, thus inducing a “memory” effect.)

In the context of this work, we assume that a patient reports pain scores ranging from asleep, or 0 to 10 (ie, at any given time the patient is in one of these 12 states), and the probability that a patient will report a pain score of, say 1, only depends on its last reported pain score. The history of pain scores prior to this assessment do not factor into this prediction (that is of course, if we were making this prediction before the patient reports his/her pain level). Although intuitively problematic, data by Chapman and others suggest that our current understanding of postoperative pain trajectories does not render this assumption completely invalid [2,11,37]. Typically, when the MC has a finite set of states, these probabilities are summarized in a matrix and the matrix is called the transition matrix (TM) of the process [15,41]. The TM fully defines the behavior of the system over time and in our case, the evolution of pain scores over time. By convention, the rows of the TM define the current state and the columns refer to the next state of the system. For example, in our study, when we want to predict the pain state in the next measurement given that a patient reports a current pain level of 5, we refer to row numbered 5 and read the probabilities in that row. Note that when we refer to prediction, we really mean a probability of being at a particular state at the next assessment rather than an actual prediction of what the next pain score will be.

As with all statistical models, there exists an inevitable collision between reality and the assumptions of a modeling approach. Below, we denote four specific threats to the Markovian assumption within the context of acute postoperative pain, and offer solutions moving forward:

1. The state-space is not properly defined, with differing intervals corresponding to the discrete time epochs (and these intervals being conditional on time). The irregular timing inherent to the clinical assessment of acute postoperative pain offers a number of challenges to a host of analytical approaches. Within the context of Markov chains, this can be addressed through the use of partially-observable Markov processes, such that before modeling the probability of a transition from one pain state to another, we first model the probability of a pain assessment occurring. While offering potential for substantially improved accuracies of modeling effects of sequential decisions, partially observable Markov processes are incredibly complex models which are difficult to implement and carry significant computational requirements. With notable caveats, simpler frameworks that consider reasonable assumptions may thus provide a reasonable, tractable solution in practice.

2. The regime of transition probabilities is conditional on time and not fully exchangeable. While the Markovian assumption requires independence of state-transition probabilities from time itself, the mechanistic realities of wound healing suggest that for a subset of patients there is a general decline in pain intensity with each sequential postoperative day. However, data from Chapman suggest that this is far from guaranteed for a substantial proportion of surgical patients [10]. Additionally, given sufficient data with mixing amongst state-transition probabilities, Markov chains can be reconstructed to maintain a “memory effect” that accounts for prior state transitions. This can be done by expanding the number of rows and columns of the transition matrix to consider state prior to the initial state. For instance, instead of considering the probability of transitioning from state 1 to state 2, we consider the prior state of 1 to be those where the preceding state may have been a state of asleep or zero, such that we expand the number of potential states to asleep:1 to 2, zero:1 to 2, etc. Further work is necessary to determine under which time intervals the transition probabilities are stable (eg over hours, particular postoperative days, or weeks), although this will require substantially increased numbers of observations across the considered time intervals given the large number of possible stratifications.

3. As specified, there are hidden (or mixed) Markov states that dominate the probabilities. For example, sleeping is unlikely to occur in high pain states unless a pain treatment (opioid) is administered. Such an intervention is conditional on the previous pain state. The Markov Chains presented here offer only a first approximation of the elicited pain states emanating from a complex milieu of patient, environmental, and therapeutic factors. Similar to issues inherent with the irregular assessment timing described in point 1, the environmental context underlying the pain assessment may carry a very strong effect, and is difficult to consider across nearly all statistical methodological approaches. This difficulty is made all the more challenging in the case of sequential, conditional environmental changes and actions that are likely to influence the underlying transitional probabilities for pain states. While the Markovian approach offers at least a framework for such sequential and conditional factors, it also unveils the need for incredibly large datasets that account for an exponentially-increasing number of possible combinations of state transitions, environmental, and timing factors. Building on any future increase in available data, further work is also necessary in the form of Markovian Decision Processes which directly account for interceding actions between states.

4. Within-person transition probabilities are aggregated across all individuals (and time) and ignore any individual differences. For instance, the probability that person A transitions from 10 to 5 may not be the same as person B for a given time. This relegates the current approach to a population-level analysis, and less relevant to predicting an individual patient at a particular time. This limitation can be partially addressed through staged stratification as demonstrated below, although each increase in stratification stringency necessitates ever-larger numbers of observations across a given population.

Given the above assumptions, it is necessary to provide the proper context of this analysis. Markovian methods are not determined to offer an absolute approach to modeling postoperative pain trajectories; indeed, more traditional statistical approaches such as Cox regressions and latent growth curve analyses may offer much more information on the apportioning of variance when compared to Markovian methods. Notably, a finite state Markov Chain, {X_t, t = 1,…} with states j = 1, .., m is conceptually equivalent to an autoregressive model of order one, AR(1) (ie Y_t = B’Y_t−1 + u_t, where Y_t are unit vectors of size m with Y_tj = 1 if X_t = j , B is an appropriate square matrix and u_t are iid random vectors with mean 0 and independent of Y_{t − 1 ,} Y_{t − 2,} …). The estimation of a Markov transition matrix is analogous to that of estimating B in the AR(1) model. However, each of these approaches requires compromises in other domains.

Despite these limitations to Markovian methods, this approach offers a unique insight into how postoperative patients transition from one state to another in a probabilistic, rather than deterministic, manner. While large-scale population-level descriptions of pain state data have been offered, we are unaware of large-scale population-level assessments that focus on changes in pain states [45,52]. Indeed, if the purpose of analgesic therapy is to aid patients in transitioning to a more comfortable pain intensity rating, then a probabilistic assessment of the likelihood of transitioning to a lower pain intensity, to an asleep state, or even to a higher pain intensity (perhaps due to the overwhelming effects of physical therapy) can permit conditional considerations of analgesic efficacy. Markovian methods are also not dependent upon continuous data types, carry no presumptions about underlying distributions, and can easily accommodate categorical data across multiple domains. We refer the reader to the maxim of “all statistical models are wrong…some are useful (George Box).”

To this end, it is important to note that Markovian modeling methods, which are an extension of the work reported here, can also permit the simultaneous and sequential consideration of pain states as well as the effects of clinical decisions made upon those states even under uncertain conditions [1,50]. This sequential decision-making under uncertain conditions represents a cornerstone of clinical practice in acute pain medicine. Before such Markovian decision processes can be fully realized, the predicate MCs must first be explored.

2.3 Calculation of MC parameters

Code used for conversion of the flat file into transition matrices is given in Appendix A.

After initializing relevant variables, the series of pain intensity ratings were indexed by time to each patient. For each patient, the algorithm then counted the number of times a patient transitioned from an initial pain score to the subsequent pain score; for instance, a patient who moved from 3 to 5 to 3, to 5, on the NRS scale would have the following counts: 3->5: 2, 5->3: 1. Within each patient, no transition was calculated for the final pain assessment given that there was no information on transition status. Note that here, the term “initial pain state” reflects not necessarily the very first observation for a patient, but rather the pain rating that precedes the next rating on a per-patient basis.

Given a total of 144 (12 × 12) possible transitions, the algorithm then created an empty matrix such that the rows represented the initial pain state, and the columns the next pain state. The TM was created per-row by inserting the number of transitions from the initial pain state to the next pain state into each cell within the row and then dividing each cell in the row by the sum of transition counts for that row. In this way, the sum of the probabilities in each row equaled 1. For example, given an initial pain state of 3, the algorithm counted how often the next pain state was asleep vs. 0 vs. 1 vs. 2…vs 10. If there were a total of 12 instances where the initial pain state were 3, and there was one observation each from a transition from 3 to each of the 12 possible states, then each cell within the row for initial pain state 3 would have a value of 0.083 (which, when multiplied by 12, equals 1).

For each patient, the following stratifications were recorded: age group, sex, and type of surgery. Separate TMs were created for each level within each stratification and were reported for visual inspection and comparison. The number of patients receiving each type of CCS-organized surgical type were rank ordered, and 5 of the top 10 types of surgery were empirically chosen to offer a disparate set of surgical types: total knee replacement, total hip replacement, spinal fusion, hysterectomy, and heart valve replacement.

This code was first run on a series of 4-patient subsamples to manually validate the counts, proportions, and row sums.

2.4 Models of sequential state transitions

As noted above, given an initial pain state i, the probability that the next pain state will be j can be calculated by looking for the jth column corresponding to the ith row of the transition matrix [42]. To determine the probability of the pain score after two transitions, or steps, the TM can be raised to the 2nd power, and the jth column again matched to the ith row. This can be repeated for the 3rd, 4th, 5th, and nth steps by raising the transition matrix to the 3rd, 4th, 5th, and nth power.

For example, let us suppose that we would like to know what our patient’s pain score will likely be following a very large number of steps (perhaps 1,234 steps representing a very long hospitalization). Given an initial pain state of 3, if we would like to examine the probability that the pain score would be 6 following the aforementioned 1,234 steps, we would raise the transition matrix to the 1,234 power, find the row representing pain intensity rating of 3, and then find the column representing a pain intensity rating of 6. The value of this cell would represent the probability that the 1,234 pain score would equal 6 given an initial pain score of 3.

As n becomes very large (eg, 1,234, as used above), the rows of the TM converge on a stationary distribution of probabilities. One way to interpret these probabilities is that they correspond to the fraction of patients that will be in a particular pain state during hospitalization. As an example, suppose we have 4 pain states with steady-state probabilities of 0.2, 0.4, 0.3, and 0.1. Suppose also that we have 100 patients in the hospital (at different stages of recovery); when a doctor walks into the hospital, she expects to see 20 patients at a pain state of 0, 40 at state 1, 30 at state 2, and 10 at state 3. While this offers the same output as a simple calculation of the distribution of pain intensity ratings, the existence of the stationary distribution helps define the MC as ergodic, meaning that one can reach each state from every other state. The stationary distribution is independent of the starting condition; in other words, whether beginning with a 0 or 10 pain intensity rating, the MC will settle into the same distribution [42]. This stationary distribution corresponds to the eigenvector of the TM for an eigenvalue of 1 [15]. We used existing mathematical software packages to compute the aforementioned eigenvector and, equivalently, the steady-state distribution. Separate stationary distributions were calculated for each stratification level for sex, age group, and type of surgery.

Another quantity of interest is first passage times and the associated probability distributions [7,12]. In this context, the first passage time shows how many steps it would take to reach a destination pain intensity rating for a given initial pain intensity rating by using the probabilities encoded in the TM. This being a probabilistic quantity, we can answer the following questions: (1) what is the average number of steps taken to go from one state to another, (2) given an initial state, what is the probability of reaching another state in less than, say, t steps, and perhaps more usefully, (3) given an initial state and a fixed probability “p,” of transitioning amongst states, at most, how many steps does it take to go from the initial state to a target state with probability “p”? For example, after starting in pain state 10, a patient would reach a pain state of zero within 50 transition steps with almost certainty (ie, close to probability 1). The cumulative probabilities of reaching state zero following t transition steps were stratified by age, sex, and type of surgery. Note that while we do not clinically advocate for a pain intensity rating of zero as a universal goal of clinical care, this rating offers a mathematical lower-bound that is convenient for modeling the progression of the Markov Chains.

Stationary distributions were compared across multiple dimensions of stratification as exploratory analyses. To compare multiple distributions, we employed the k-sample Anderson-Darling test [48]. The Anderson-Darling test considers whether a given sample of data comes from a given probability distribution, and assumes that there are no parameters to be estimated in the distribution under consideration. When indicated, specific 2-sample Kolmogorov-Smirnov testing was performed to test for the equality of continuous distributions, with the Holm-Sidak correction for multiple comparisons [29]. These quantified comparisons were performed alongside qualitative representation of distributions using histograms and kernel density estimates, which are shown in Appendix A.

TMs were created using python 2.7.8, numPy, version 1.9, and pandas, version 0.14.1. Statistical comparisons were completed using SciPy 0.14.

3. Results

3.1 Characterization of the Transition Matrix (TM)

Demographic information for the examined cohort is given in Table 1.

Table 1.

Sociodemographics of study cohort

Variable	Levels	Value
Pain state		476108
(No. of obs)	Asleep	66441
	0	142485
	1	8555
	2	24709
	3	28250
	4	30344
	5	40375
	6	32036
	7	33367
	8	34016
	9	14549
	10	20981
Age (mean ± SD)		56.1 ± 16.3
Age groups	21–39	1460
(No. of obs)	40–64	4029
	65–84	2656
	≥85	201
Sex	Male	4193
(No. of obs)	Female	4153
Type of surgery	Types of procedures	146
(No. of obs)	Total hip arthroplasty	299
	Total knee arthroplasty	281
	Spinal fusion	226
	Hysterectomy	200
	Heart valve procedure	227

Figure 1 demonstrates the asymmetrical TM for the entire cohort of surgical patients. Given the absence of zeroes within the TM, we can define it as an irreducible MC given that every state can be reached from every other state. A special case of this is the positive recurrent nature of this matrix because it is possible to return to each initial state; details of this characteristic will be given below. Finally, there were no absorbing states of this matrix.

Fig. 1.

Transition matrix of postoperative pain scores for study cohort. The transition matrix demonstrates the probability of transitioning from a current pain score state, denoted by rows, to the next pain score state, denoted by columns. The probabilities for each row sum to one. The transition matrix is asymmetric and irreducible.

Transition probabilities in this global transition matrix ranged from 0.0031 for transition from state 10 to 1, to 0.69 for transition from state zero to state zero. The greatest density of transitions was noted in the diagonal region of the TM, suggesting that patients were generally most likely to transition to the same pain state. There were also slightly increased probability densities in transitioning to a state of asleep or zero. Overall, the structure of the TM was maintained when using pain intensities binned into categories of asleep, zero, mild, moderate, and severe (Appendix B).

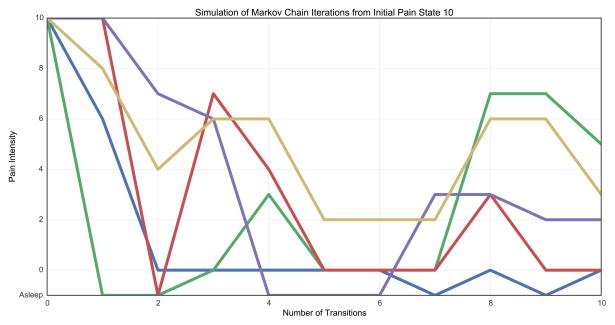
Figure 2 demonstrates a simulation of Markov chain (MC) iterations through 10 sequential transitions from a select, representative sample of initial pain states. These models demonstrate that when analyzed as a MC, postoperative pain scores are very likely to move in a non-monotonic fashion. In other words, unlike many linear models of pain, the MC offers a probabilistic method to demonstrate how pain scores may cycle between high and low in a manner somewhat irrespective of the initial conditions.

Fig. 2.

Simulation of Markov Chain iterations from select initial pain states. Ten sequential transitions are simulated from initial pain states of asleep (A), 0 (B), 5 (C), and 10 (D) using the Markov Chain.

3.2 Characterization of stationary distributions

For the entire cohort, stationary distribution values were as follows: 0.14 (asleep), 0.299 (0), 0.018 (1), 0.053 (2), 0.06 (3), 0.065 (4), 0.086 (5), 0.068 (6), 0.07 (7), 0.07 (8), 0.03 (9), and 0.041 (10). Figure 3 provides an overview of the TMs stratified by sex, age group, and type of surgery. Further details on the kernel density estimates for stationary distributions can be found in Appendix A.

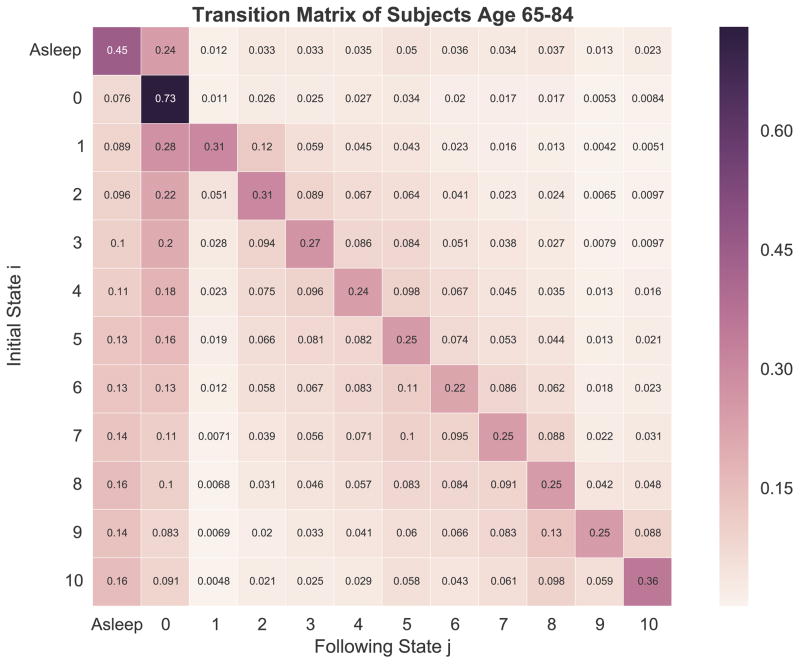
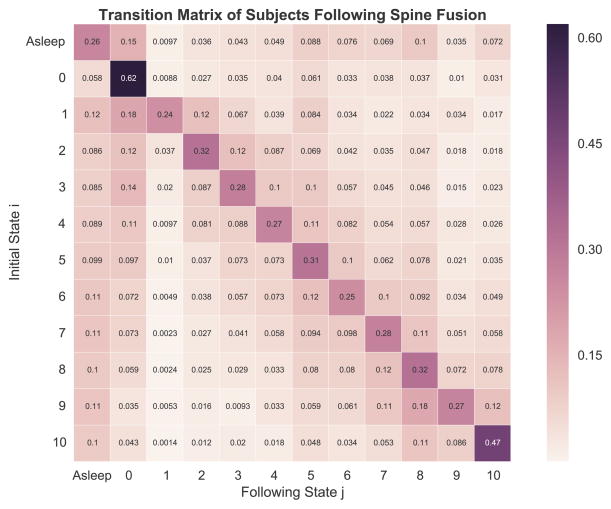
Fig. 3.

Overview of transition matrices stratified by sex, age group, and type of surgery. Separate transition matrices were created for males (A), females (B), age 21–39 (C), age 40–64 (D), age 65–84 (E), age 85 or greater (F), total hip arthroplasty (THA, panel G), total knee arthroplasty (TKA, panel H), spine fusion (I), hysterectomy (J), and heart valve surgery (K).

When stratified by sex, the stationary values for state asleep, 0, 1, 2, and 3 were higher in males than females, and for states 4 through 10 were higher in females compared with males (Fig. 4A). However, omnibus comparison of the stationary distributions using the Anderson-Darling (AD) test suggested no overall difference in the distributions by sex (AD statistic = 0.85, P = .86).

Fig. 4.

Steady-state distributions by sex, age group, and type of surgery. The steady-state distributions were calculated using eigenvector (lambda = 1) method and approximate a univariate distribution of pain scores across the study period for each stratification. Separate distributions were calculated for stratifications by sex (A), age group (B), and type of surgery (C).

When stratified by age group, younger patients had lower steady-state probabilities in the state asleep and 0 to 3, and higher values in states 4 to 10 (Fig. 4B). Omnibus comparison of the stationary distributions using the Anderson-Darling test suggested an overall difference in the distributions across different age groups (AD statistic = 2.46, P = .03). Serial two-sample Kolmogorov-Smirnov testing between each age group pair suggested differences between 21–39 years and ≥85 years (P = .005) and 40–64 years and ≥85 years (P = .02); following correction for multiple comparisons using the method of Holm-Sidak, the corrected P value for 21–39 years vs ≥85 years was .03 and for 40–64 years vs ≥85 years was .1.

When stratified by type of surgery, there was significant heterogeneity in steady-state probabilities, with the greatest differences found in the states asleep and zero (Fig. 4C). Here, patients receiving total hip arthroplasty and heart valve surgeries had notably higher probabilities for zero; for the asleep state, the highest probabilities were found for heart valve surgeries and spine fusion. For states 8 to 10, spine fusion had greater steady-state probabilities compared with other types of surgery. Omnibus comparison testing of the stationary distributions using the Anderson-Darling test suggested no overall differences in the distributions by type of surgery (AD statistic = 0.68, P = .21). Exploratory serial two-sample KS testing between types of surgery suggested possible differences between total hip arthroplasty and heart value surgery (P = .02), total knee arthroplasty and heart valve surgery (P = .02), spinal fusion and heart valve surgery (P = .02), and hysterectomy and heart valve surgery (P = .02); following correction for multiple comparisons using the method of Holm-Sidak, the corrected P values across all comparisons ranged from 0.183-1 with a corrected alpha of 0.005.

3.3 MC traversal to target pain states

To determine the effect of the MC on the series of pain state transitions that patients experienced, we examined the first passage times from multiple perspectives. Here, the first passage time measures how many steps are required for a subject to move from an initial state, such as a pain intensity rating of 10, to a target state, such as a pain intensity rating of zero. We excluded the times required to reenter the existing state, which were denoted as zero in these analyses. Figure 5 highlights the first passage times from each possible initial state to each possible destination state. Notably, fewer steps were required to reach a state of zero (range 6.1–8.8 steps) or asleep (range 9.1–11) than were required to reach a mild pain intensity state of one (range 72–77 steps), two (range 23–27 steps), or three (range 20–22 steps). For these mild pain scores, greater numbers of steps were required not only from pain states reflecting higher initial pain intensity ratings, but also those states of asleep and zero.

Fig. 5.

First passage times from initial to destination pain states. For each possible initial pain state, indicated by columns in this figure, the number of steps required until reaching the examined target destination state were calculated. For instance, for an initial pain state of 1, approximately 11 transition steps were required until reaching a pain state of “asleep.” The number of steps required to reach the same pain state were not calculated and are indicated by 0s across the diagonal. Note that the axes of this figure are switched from those of the transition matrix to better highlight disparities among the first passage times.

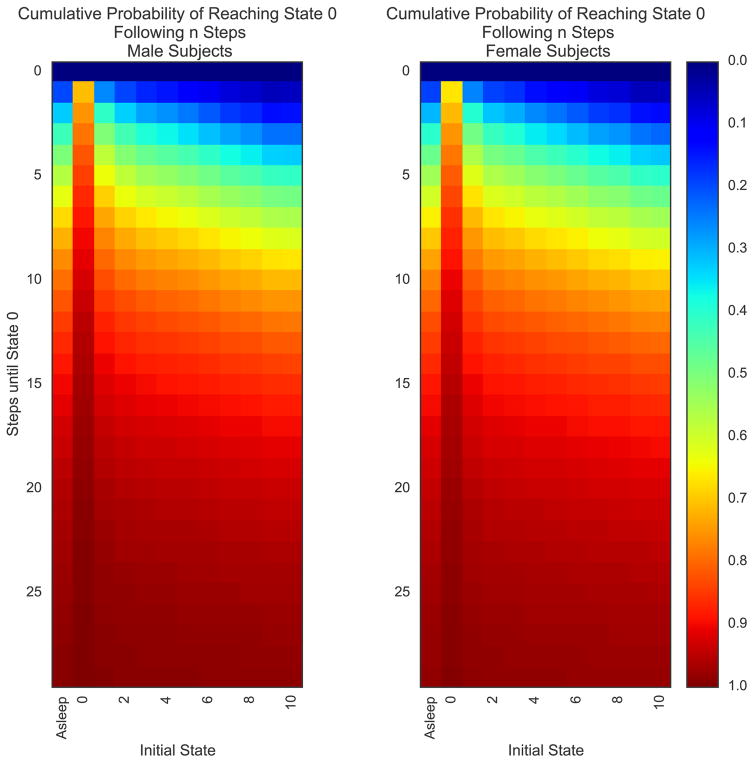
One of the core clinical questions arising from this analysis pertains to the number of steps required for a patient to reach a pain score of zero following his/her surgery. Using the first passage time measures, we examined the cumulative probabilities of reaching a pain intensity rating of zero following n transition steps (Fig. 6, A and B). We then examined the cumulative probability of reaching state zero following n steps when stratified by sex (Fig. 6C), age group (Fig. 6D), and type of surgery (Fig. 6E). Across all stratifications, patients most rapidly arrived at a state of 0 when starting at zero, followed by initial states of one, 2, and asleep. While the initial values of this first-step consideration are the same as the jth column vector for j = 0 of the original transition matrix, this approach better highlights the skewed cumulative probabilities of reaching a state of zero with increasing numbers of steps. For instance, given an initial state of 1, the cumulative probability of reaching zero after 2, 3, and 4 steps increases to 0.4, 0.5, and 0.57. Over the same number of steps, the cumulative probability after 2, 3 and 4 steps increases only to 0.14, 0.23, and 0.32 for an initial pain state of 10.

Fig. 6.

Cumulative probabilities of reaching pain state of 0 following n transition steps. The cumulative probabilities of reaching state 0 following n transition steps are demonstrated as a cumulative distribution function for each of the initial states (A). To improve the clinical interpretability of the CDF, heat maps were created for the entire cohort (B) as well as stratifications by sex (C), age group (D), and type of surgery (E). In each heat map, the x-axis denotes the initial states, and the y-axis the number of steps until reaching state 0. The color of each cell denotes the probability, based upon the Markov Chain, of achieving a pain score of 0 within the number of steps (y-axis) depending upon the initial state (x-axis).

4. Discussion

Our results demonstrate that the population-based stochastic matrix of acute postoperative pain scores carries a defined structure across multiple dimensions of stratification. While the most common transitions occurred within the same state (eg, from 0 to 0), we also found a preponderance of transitions to the states of “asleep” and zero. These two destination states were not necessarily synonymous with transitions to mild pain scores. Rather, even patients beginning in lower pain states had a greater probability of transitioning to a moderate to severe pain rating rather than an intensity rating of one. This finding parallels earlier findings by Chestnut and Dexter in characterizing the overall statistical distribution of NRS pain scores after surgery, findings which pointed to a generally Gaussian distribution with a separate density at 0 [16]. One notable departure from this parallel is the state transitions for patients reporting a pain intensity of 10; such patients most often transitioned to a subsequent score of 10, followed in probabilistic rank by a sleep state or score of 8. The probability of transitioning to a non-asleep or non-8 pain state was commonly 5- to 10-fold lower. This pattern held even in the TM of binned pain intensity ratings, whereby patients were most likely to transition from severe pain to severe pain (0.54), followed by moderate (0.16) or asleep (0.12) before mild (0.11) or zero (0.068).

The inclusion of the “asleep” outcome permitted us to differentiate transitions in the upper left corner of the TM, an area that has received comparably little attention. Here, we find that asleep patients are much more likely to transition to either a state of 0 or one indicating moderate to severe pain rather than a state of mild pain intensity. This is in general agreement with prior findings demonstrating that sleep deprivation and acute pain exacerbation are intricately linked in a feed-forward type of association [13,35]. This finding raises several clinical questions as to the nature of sleep emergence in the acute pain setting. Clinical interpretation of these findings would be greatly aided by additional studies examining the concomitant analgesic interventions, and their pharmacokinetic profiles, surrounding the sleep period given the heterogeneity of data on interruptions in normal sleep patterns associated with opioid analgesics [9,14,20,38,43]. Likewise, our work suggested that a pain score of zero was far from an “absorbing” state, but rather one from which patients may still readily transition back to a high-intensity pain rating. Such findings align with the results of Apfelbaum et al., which demonstrated a high proportion of patients suffering from moderate to severe pain following discharge, despite presumably minimal pain intensity ratings as a condition of discharge from the hospital [3].

When stratified by sex, the stationary distributions suggested that males would eventually spend more time in the asleep, 0, and 1 to 3 pain states, whereas females would, by comparison, spend more time than males in states 4 to 10. Similarly, when stratified by age group, our results showed that younger patients were more likely to eventually spend more time in higher pain states compared with older patients. Each of these findings is in strong agreement with prior literature suggesting that female sex and younger age are associated with higher postoperative pain scores [4,18,19,36,47]. Our model extends these findings to suggest that such differences are not only a reflection of aggregate measures over large blocks of time, but also reflect the convergence point following multiple transition steps.

In the stratification of stationary distributions by type of surgery, the differences between heart valve surgery and spine fusion are of special note. Following heart valve surgery, many patients at our institution will require a period of endotracheal intubation and mechanical ventilation whereby they are sedated with continuous infusions of sedative-hypnotics and potent opioids. Following their extubation, recovery, and discharge, acute pain management is often a lesser issue than for other surgical populations, such as following spine fusion [23].

In agreement with above findings from our analyses of stationary distributions and TM structural features, measures of the first passage time from initial to target pain states were notable for the prolonged number of steps required to achieve a pain state of 1 during iterations of the MC. Indeed, even starting from a mild pain score, the model suggests that patients were more likely to encounter a severe pain state rather than a pain state of 1. Our results suggested only minimal differences in the cumulative probabilities of reaching state 0 through multiple transitions when stratified by sex, although here again males seemed to have a higher likelihood of reaching zero earlier than females, even beyond the 1st transition. When specifically focusing on the cumulative probability of reaching a pain state of 0 within n steps, older patients had higher probabilities after a smaller number of steps compared with younger patients, whereby younger patients not only had relatively longer step requirements to reach an equivalent probability of 0 pain intensity, but also required fewer steps to transition from mild to severe pain intensity ratings. A similar pattern was also seen during stratifications by type of surgery, whereby patients undergoing heart valve repair had greater probabilities of reaching 0 after a small number of steps compared with total knee arthroplasty, total hip arthroplasty, and spine fusion.

These findings offer a way forward in evaluating the progression of analgesia for postoperative patients by offering a methodology to measure how often patients transition from high pain intensity ratings to more favorable intensity ratings between and within separate cohorts of surgical patients. Prior work has demonstrated significant heterogeneity in how postoperative pain scores change over time [2,11,37]. Despite prior clinical belief that pain scores regularly and consistently diminished over the first several days after surgery, these teams independently demonstrated that a substantial proportion of patients suffer from a flat, or even positive in slope, postoperative pain trajectory based upon daily pain assessments. Notably, the above findings have relied upon variants of regression, which offer an excellent approach for exploring the sources of variance contributing to the observed clinical outcome. However, these approaches provide limited guidance on how best to make clinical choices to optimize individual patient outcomes. Such limitations are compounded in the setting of sequential decisionmaking under uncertain conditions.

The MCs characterized here represent an important step in optimizing our clinical decision-making to account for the assessment-to-assessment heterogeneity in pain intensity ratings. The above TMs form a core component of Markovian Decision Processes that have seen widespread application in a number of industries [17,30]. Markov decision processes extend the state-state TMs to state-action matrices such that at each state, one can choose an action that is available for that state [54]. Following the chosen action, the Markov decision process again considers this updated state, the actions available, and then selection among these actions based upon the objective at hand. For example, following hysterectomy, given a pain state of 6, with possible actions that include an opioid, nerve block, or no intervention, the Markov decision process can be used to determine a choice that will minimize the pain score, minimize the risk of nausea, or minimize the risk nephrotoxicity, etc. Thus, such a framework permits modeling of not just pain-related outcomes, but also those interventions most likely to lead to the desired outcomes of interest. The outcome of such actions can then be compared against a standard MC to determine the added value of the recommendation when compared with the expected, prior distribution of outcomes.

In addition to the limitations inherent to using clinical data, the Markovian approach to modeling postoperative pain is limited by a number of assumptions, including the Markov property itself. Nevertheless, it is remarkable that our results, using the most basic of Markovian approaches, still offered very strong agreement with prior findings using more established methods of evaluating temporal trajectories of postoperative pain. Importantly, an MC-based approach to pain assessment does not incorporate several contextual features that could influence pain-state transitions (e.g., activity level, before vs. after physical therapy session, timing of last dose of analgesics, etc.), nor does it consider local series of transitions. Given a sufficiently large dataset, extensions of the MC such as dynamic Bayesian networks could potentially incorporate these factors. However, the increase in the number of observations required would be immense. For instance, to consider the effects across n historical state transitions (e.g., the last n pain scores rather than the current pain score), there would exist 12_n such histories across the population, and consequently 12_n by 12*(12ⁿ⁺¹) parameters to predict.

In conclusion, the application of MCs to postoperative acute pain scores offers a unique opportunity to characterize the probabilistic traversal of patients through sequential pain states. Our work must be validated through repetition across multiple centers and additional types of surgery. Downstream application of MCs to postoperative acute pain offers a unique opportunity to provide data-driven, outcome-oriented clinical decision support in a sequential, adaptable fashion, an approach necessary to suitably address and optimize acute pain management in the postoperative patient.

Supplementary Material

Supplementary Materials_ Appendix 1. Appendix A.

Code used for all calculations in this manuscript are given in the attached Jupyter/iPython notebook. This notebook is presented in HTML format to improve readability. This notebook contains additional details and descriptions of the mathematics contained within the coding of functions related to our use of Markov Chains and related algorithmic approaches.

Supplementary Materials_ Appendix 2. Appendix B.

To address questions regarding cut-points of pain scores, analyses were repeated using pain intensity ratings binned into categories of asleep, zero, mild, moderate, and severe.

Summary.

Markov Chain transition matrices of postoperative pain scores suggest a preponderance of transitions within the same pain state.