Independent Component Analysis Involving Autocorrelated Sources With an Application to Functional Magnetic Resonance Imaging

Abstract

Independent component analysis (ICA) is an effective data-driven method for blind source separation. It has been successfully applied to separate source signals of interest from their mixtures. Most existing ICA procedures are carried out by relying solely on the estimation of the marginal density functions, either parametrically or nonparametrically. In many applications, correlation structures within each source also play an important role besides the marginal distributions. One important example is functional magnetic resonance imaging (fMRI) analysis where the brain-function-related signals are temporally correlated.

In this article, we consider a novel approach to ICA that fully exploits the correlation structures within the source signals. Specifically, we propose to estimate the spectral density functions of the source signals instead of their marginal density functions. This is made possible by virtue of the intrinsic relationship between the (unobserved) sources and the (observed) mixed signals. Our methodology is described and implemented using spectral density functions from frequently used time series models such as autoregressive moving average (ARMA) processes. The time series parameters and the mixing matrix are estimated via maximizing the Whittle likelihood function. We illustrate the performance of the proposed method through extensive simulation studies and a real fMRI application. The numerical results indicate that our approach outperforms several popular methods including the most widely used fastICA algorithm. This article has supplementary material online.

1. INTRODUCTION

Independent component analysis (ICA) is an effective data-driven technique for extracting the source signals from their mixtures (Hyvärinen, Karhunen, and Oja 2001; Stone 2004). It aims to solve the “blind source separation” problem by expressing a set of observed mixed signals as linear combinations of independent latent random variables (or source signals or components). It has many important applications, especially in functional magnetic resonance imaging (fMRI) analysis (McKeown, Hansen, and Sejnowsk 2003; Stone 2004; Huettel, Song, and McCarthy 2008; Calhoun, Liu, and Adali 2009).

The ICA problem can be formally expressed as follows. Suppose there are M mixed signals of length T each, which are stored in the observed signal matrix X. ICA then allows one to decompose X as

$${\mathbf{X}}_{M\times T}={\mathbf{A}}_{M\times M}{\mathbf{S}}_{M\times T},$$ (1)

where A is a nonrandom mixing matrix and S is a matrix of independent source signals. The goal of ICA is to recover the latent source signals (rows of S) as

$$\mathbf{S}=\mathbf{WX}\text{with}\mathbf{W}={\mathbf{A}}^{-1}.$$ (2)

Many ICA procedures have been developed over the last fifteen years. The majority of the methods are based on estimates of the marginal densities of the sources, either parametrically or nonparametrically. Parametric approaches include infomax (Bell and Sejnowski 1995), which estimates the density parameters via minimization of mutual information, and is equivalent to maximum likelihood estimation using high-order cumulants (Comon 1994; Cardoso 1999); or fastICA (Hyvärinen, Karhunen, and Oja 2001) that maximizes non-Gaussianity as measured by the approximated negative entropy. (Note that the sources should not have a Gaussian distribution in order for the mixing matrix to be identifiable.)

Parametric approaches sometimes can be too rigid. More flexible nonparametric methods include estimating the score function using kernel approximation (Vlassis and Motomura 2001), kernel density estimation (Bach and Jordan 2003; Boscolo, Pan, and Roychowdhury 2004; Chen and Bickel 2005; Chen 2006; Shen, Hüper, and Smola 2006), smoothing splines (Hastie and Tibshirani 2003), B-spline approximation (Chen and Bickel 2006), and logsplines (Kawaguchi and Truong 2009). Two other relaxations of the basic ICA model are subspace ICA (Hyvärinen and Hoyer 2000; Sharma and Paliwal 2006) that allows the sources to form mutually independent subgroups and does not require the sources within the same subgroup to be independent; and AMICA (Palmer et al. 2008) that uses mixtures of Gaussian scale mixtures to model the sources, which was extended to include mixtures of linear processes (Palmer, Kreutz-Delgado, and Makeig 2010). Note that when all the sources are mutually independent, subspace ICA reduces to ordinary ICA (Hyvärinen and Hoyer 2000).

All the above methods, however, only make use of the marginal densities (with the exception of the recent extention of AMICA), which do not contain information about the correlation structures within the source signals. For example, in fMRI studies the experiment-stimulus related signals or physiological signals such as heartbeat or breathing are usually periodic, and therefore embedded in the fMRI data are some autocorrelation or colored noise structures within the signals (Bullmore et al. 2001). Such information is not incorporated when using the marginal-density-based ICA methods. In this article we develop ICA approaches that take into account the correlation structures within the sources. Our methods are applicable to analyze other imaging modality data such as EEG and MEG, as well as financial time series. See Hyvärinen, Karhunen, and Oja (2001) for more details.

An fMRI dataset is four-dimensional consisting of a three-dimensional image (or a 3D volume) being observed over time. Each 3D fMRI image consists of a certain number of two-dimensional slices, and each slice is made up of individual cuboid elements called voxels. The data are usually represented as a space-time matrix of dimension V × T, where V is the number of voxels in one image and T is the number of time points in the experiment. Thus each column of the matrix represents an fMRI image with V voxels and each row is the time course observed at one specific voxel.

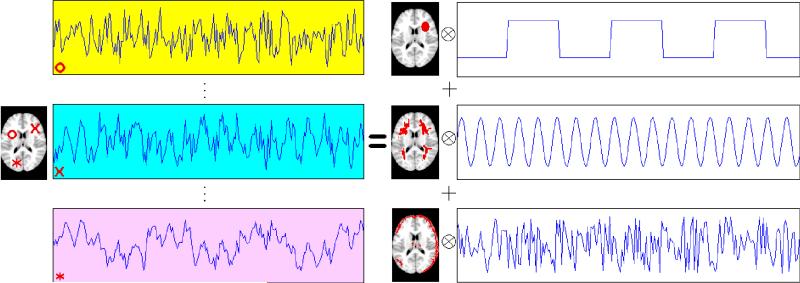
The recorded time series can be viewed as a mixture of source signals that are temporally correlated, corresponding to the experimental stimuli, physiological functions such as heartbeat and respiration, subject movement, etc. This is illustrated graphically in Figure 1. For simplicity, this toy example considers only one slice of the brain. The left side of the figure plots the voxel time series (or the rows of the matrix) from three exemplary voxels in this slice. Note that each voxel is marked using a different symbol that is matched with its corresponding time series plot. The goal of ICA is to recover the (three) independent temporal sources [the rows of S in (1)], which are displayed on the right side of the figure, and represent an experimental stimulus, cardiac, or respiratory effect, and a movement effect, respectively. The columns of the mixing matrix A in (1) are shown as the spatial maps, where the voxels activated by the corresponding temporal signals are colored as red. Note that typical fMRI data have a high-spatial dimension (V ≈ 200,000), which is much larger than the number of extracted independent components (M = 3 in our example). Hence dimension reduction is usually performed prior to ICA of fMRI data.

Figure 1.

Illustration of ICA in fMRI studies. Simulated fMRI data (left) are modeled as the outer product of three spatial maps and their corresponding temporal components (right). The time series plots of three randomly selected voxels are depicted on the left side of the plot.

The applications of ICA to fMRI are classified into two categories based on their goals: spatial ICA (sICA) and temporal ICA (tICA). The sICA looks for independent image components (columns of A). The tICA, however, assumes independence of time courses (rows of S). In both cases, we view a single image component (one column of A) as one spatially distributed set of voxels that is induced by the corresponding time course in one row of S. The current article focuses on temporal ICA.

To the best of our knowledge, Pham and Garat (1997) is the first ICA procedure that takes into account the autocorrelation structures within the sources. The authors imposed certain parametric correlation assumptions on the sources. Specifically, they assumed that the spectral density of each source was known up to some scale parameters, and proposed a quasi-maximum likelihood method to recover the sources. Their formulation is in the spectral domain, and builds upon the asymptotic independence and normality of discrete Fourier transform (DFT). Since the spectral densities are known except the scale parameters, the authors used the corresponding (known) separating filters in the quasi-likelihood, and only needed to maximize the likelihood to get estimates for the scale parameters and the mixing matrix.

Although the spectral domain approach of Pham and Garat (1997) is natural and innovative, their assumption that the spectra of the sources are known can be unrealistic in practice. In this article, we relax that assumption and propose a new spectral domain ICA procedure for sources with autocorrelation, that is, colored sources. In particular, our procedure assumes certain parametric time series models for the source signals, and estimates the model parameters through parametric spectral density estimation. (Note that our method covers the special scenarios when the source signals are white or uncorrelated.) In addition, we use the Newton–Raphson method to improve the optimization efficiency, and incorporate the Lagrange multiplier method for orthogonal constraints.

On a related note, an earlier attempt to examine the source autocorrelation was described by Pearlmutter and Parra (1997). They introduced the contextual ICA by considering

$${\mathbf{X}}_t=\sum _{u=0}^p{\mathbf{A}}_u{\mathbf{S}}_{t-u},$$

a multivariate version of the autoregressive process of order p: AR(p). The autocorrelation is clearly specified by the convolution relationship. In fact, this formulation is also referred to as convolutive ICA. See Dyrholm, Makeig, and Hansen (2007) for a very thorough survey of this topic. Thus the instantaneous ICA of the traditional approach is a special case of convolutive ICA where p = 0. In practice, the AR order p will be ideally small and one way to achieve this is to model each source S_t by a moving-average process of order q: MA(q). The parameters are estimated via the likelihood derived from the standard time-domain method in time series, with logistic distribution as the baseline distribution. Dyrholm, Makeig, and Hansen (2007) suggested to use Bayesian information criterion (BIC) to estimate the parameters p and q.

By contrast, our approach is to embed the autocorrelation into the sources via the instantaneous ICA. For instance, if each source is modeled by an autoregressive model with the same order p, then our model yields the convolutive ICA described above. The choice of p for all sources is convenient for the comparison (with the convolutive ICA). We can in fact allow each source to have a different AR order. Moreover, we can enhance the flexibility by fitting an autoregressive and moving-average process of orders p and q [ARMA(p, q)] to each source. The model parameters p and q can be of course source specific and can be estimated via an information based method such as AIC or BIC. The autocorrelation related parameters or the coefficients of the ARMA process are estimated using the Whittle likelihood, which is a discrete Fourier transform (DFT) based method. Thus this is a distribution-free approach, see Section 2.3 for a more detailed description of our method. Also an authoritative comparison between the two likelihood approaches is documented in Dzhaparidze and Kotz (1986).

Estimating the mixing matrix has an important application in studying brain function using fMRI through activity detection. Many statistical methods have been developed that can be roughly classified into either hypothesis-driven or data-driven approaches. Hypothesis-driven approaches are based on conventional regression models to identify voxels whose time series are significantly correlated with the experimental task(s). Examples include statistical parametric mapping (Friston et al. 2007), a variety of Bayesian techniques implemented in FSL (Woolrich et al. 2009), diagnosis procedures for noise detection (Zhu et al. 2009), and many others described therein. Evidently, this voxelwise approach is very popular, but connecting the activated voxels for region-of-interest (ROI) analysis is something else to be desired (Huettel, Song, and McCarthy 2008). Alternatively, data-driven approaches for ROI analysis via mixing matrix estimation include principal component analysis (PCA) (Viviani, Gron, and Spitzer 2005), dynamic factor models (Park et al. 2009), clustering methods (Venkataraman et al. 2009), and ICA (McKeown, Hansen, and Sejnowsk 2003; Esposito et al. 2005; Calhoun, Liu, and Adali 2009; Sui et al. 2009). Our approach takes these data-driven procedures a step further by exploiting the temporal correlation structures while detecting the brain activation. It is therefore a temporal ICA procedure.

The rest of the article is structured as follows. Section 2 describes our proposed method for handling colored sources. We illustrate its performance and compare it against several existing ICA methods through simulation studies in Section 3. The considered ICA methods are also applied to analyze a real fMRI dataset in Section 4. We finally conclude the article in Section 5.

2. COLORED INDEPENDENT COMPONENT ANALYSIS

This section presents the details of our procedure for handling colored sources. We start with some basic definitions in Section 2.1, followed by a discussion on the Whittle likelihood in Section 2.2. For the purpose of easy understanding and presentation, we first describe the procedure for autoregressive (AR) processes in Section 2.3. This is an important leading case as Worsley et al. (2002) suggested that AR models are the most commonly used time series approaches for the temporal correlation structure in fMRI analysis. We then discuss in Section 2.4 how this procedure can be simplified to the special case of white noise processes, and in Section 2.5 how it can be extended to general autoregressive moving average (ARMA) processes.

2.1 Preliminaries

We start with several definitions in spectral analysis. Consider a vector-valued stationary process X(t) = (X₁(t), . . . , X_M(t))^⊤, t = 0, ±1, ±, . . . , with mean zero and the covariance function c_XX(u) = cov(X(t), X(t + u). If ${\sum }_{u=-\infty }^{\infty }\mid {\mathbf{c}}_{\mathbf{XX}}\left(u\right)\mid <\infty$, we define the M × M spectral density matrix of the series X(t) as

$${\mathbf{f}}_{\mathbf{XX}}\left(r\right)=\frac{1}{2\pi }\sum _{u=-\infty }^{\infty }{\mathbf{c}}_{\mathbf{XX}}\left(u\right)\exp \{-iru\},r\in \mathbb{R},$$

where r is the angular frequency per unit time, or simply the frequency. The jth diagonal element of f_XX, f_XjXj, is the spectral density of the univariate time series X_j(t). For a more detailed discussion of spectral density, see Brillinger (2001).

In practice, we suppose that X(t), t = 0, 1. . . , T – 1, are observed. Consider the Fourier frequencies r_k = (2πk)/T, k = 0, ..., T – 1. Then, we can define the discrete Fourier transform (DFT) of X(t), t = 0, 1, ..., T – 1, as

$$\phi (r_k,\mathbf{X})={(\phi (r_k,X_1),\dots ,\phi (r_k,X_M))}^{\top }=\sum _{t=0}^{T-1}\mathbf{X}\left(t\right)\exp \{-i{r}_{k}t\},$$

and its second-order periodogram as

$$\tilde{\mathbf{f}}(r_k,\mathbf{X})=\frac{1}{2\pi T}\phi (r_k,\mathbf{X}){\phi }^{\ast }(r_k,\mathbf{X}),$$

where φ* is the conjugate transpose of the vector φ.

Considering the source signals S(t) = (S₁(t), . . . , S_M(t))^⊤, t = 0, 1, . . . , T – 1, we can similarly define their spectral density matrix f_SS, DFT, and periodogram. Since the sources are mutually independent, we have that f_SS = diag{f₁₁, . . . , f_MM}, where f_jj is the spectral density of the jth source.

2.2 The Whittle Likelihood

To minimize the bias in estimation associated with the misspecification of the time series distributions, Whittle (1952) formulated a likelihood approach by utilizing the asymptotic distributional properties of DFT (see theorem 4.4.1 of Brillinger 2001). Specifically, suppose that we were able to observe the source signals and compute their periodograms: f̃(r_k, S₁), . . ., f̃(r_k, S_M). In addition, if the sources are stationary with finite moments, then it can be shown that f̃(r_k, S_j) is asymptotically $f_{jj}\left(r_k\right){\chi }_2^2∕2$, independent of the other variates for k = 0, 1, . . . , T – 1 and j = 1, . . . , M (see theorem 5.2.6 of Brillinger 2001). Thus the source log-likelihood is given by

$$L({\mathbf{f}}_{\mathbf{SS}};\mathbf{S})=-\frac{1}{2}\sum _{j=1}^M\sum _{k=0}^{T-1}\left\{\frac{\tilde{f}(r_k,S_j)}{f_{jj}\left(r_k\right)}+\ln f_{jj}\left(r_k\right)\right\},$$ (3)

where f_SS is the diagonal matrix of the power spectra of the sources.

This is known as the Whittle likelihood in the literature and is being introduced to ICA for the first time here. Asymptotic properties of the Whittle likelihood-based procedure can be found in Dzhaparidze and Kotz (1986). Other than the desirable property that the periodograms are independently distributed, one can see it is also advantageous that the source autocorrelation can be examined through their power spectra. This forms the core of our method.

Our next step is to express the above log-likelihood in terms of the periodograms computed from the observed mixed signals. Using the mixing relationship (2) and the linearity of DFT, the log-likelihood (3) can be rewritten as

$$L(\mathbf{W},{\mathbf{f}}_{\mathbf{SS}};\mathbf{X})=-\frac{1}{2}\sum _{j=1}^M\sum _{k=0}^{T-1}\left\{\frac{{\mathbf{e}}_j^{\top }\mathbf{W}\tilde{\mathbf{f}}(r_k,\mathbf{X}){\mathbf{W}}^{\top }{\mathbf{e}}_j}{f_{jj}\left(r_k\right)}+\ln f_{jj}\left(r_k\right)\right\}+T\ln \mid \det \left(\mathbf{W}\right)\mid ,$$ (4)

where e_j = (0, 0, . . . , 0, 1, 0, . . . , 0)^⊤ with the jth entry being 1.

Once (4) is available, we maximize it to obtain the estimates of the unmixing matrix W and the parameters in the power spectra of the sources (see Section 2.3). The maximum Whittle likelihood approach can be interpreted as assigning a different weight of $\left({\mathbf{e}}_j^{\top }\mathbf{W}\right)\cdot \left({\mathbf{W}}^{\top }{\mathbf{e}}_j\right)∕f_{jj}\left(r_k\right)$ to the source periodogram f̃ at the Fourier frequency r_k. This procedure will be referred to as cICA hereafter, where c stands for color sources.

We make two remarks here. First, under this formulation, the novelty is the estimation of the autocorrelations of the sources, which was not considered in Pham and Garat (1997); they assumed the spectral densities f_jj were known a priori. Second, the maximization of the log-likelihood is subject to some identifiability constraints. ICA methods are known to have permutation and scale ambiguity problems. Specifically, for a permutation matrix P and a scalar a, we have X = W⁻¹S = W⁻¹(aP)(aP)⁻¹S. To ensure the identifiability of W and S, we restrict W to be full rank matrix satisfying the following identifiability conditions proposed by Chen and Bickel (2005):

1. max_1≤k≤M W_jk = max_1≤k≤M |W_jk| for 1 ≤ j ≤ M, where W_jk is the (j, k)th entry of W;

2. W₁ ≺ ··· ≺ W_M where W_j is the jth row of W. For $\forall \mathbf{a}$, $\mathbf{b}\in {\mathbb{R}}^M$, we define a ≺ b if there exists a k ∈ {1, ..., M} such that the kth element of a is smaller than the corresponding element of b, while all the elements before the kth entry are equal between a and b (i.e., a_k < b_k and a_j = b_j, 1 ≤ j ≤ k – 1, where a_k is the kth element of a).

2.3 ICA for AR Sources and Its Algorithm

2.3.1 Penalized Whittle Likelihood

We first consider autoregressive (AR) models for the source signals, and assume that the jth source S_j follows a stationary AR(p_j) process given by

$$\begin{array}{cc}{S}_j\left(t\right)-\sum _{k=1}^{p_j}{\varphi }_{j,k}{S}_j(t-k)={ϵ}_j\left(t\right),\hfill & \hfill \\ \hfill & t=0,\dots ,T-1,j=1,\dots ,M,\hfill \end{array}$$

where {ϕ_j,k} are the AR parameters and ${ϵ}_j\left(t\right)\sim \mathrm{WN}(0,{\sigma }_j^2)$. The corresponding power spectrum is given by

$$f_{jj}\left(r\right)=\frac{{\sigma }_j^2}{2\pi {\mid {\Phi }_j\left(\exp \{-ir\}\right)\mid }^2},r\in \mathbb{R},$$

where Φ_j(z) = 1 – ϕ_j,1z – · · · – ϕ_j,pjZ^pj is the corresponding AR polynomial.

Denote ϕ_j = (ϕ_j, 1, ···, ϕ_j,pj)⊤, $\varphi ={({\varphi }_1^{\top },\dots ,{\varphi }_M^{\top })}^{\top }$, and ${\sigma }^2={({\sigma }_1^2,\dots ,{\sigma }_M^2)}^{\top }$.

The Whittle log-likelihood (4) can be rewritten as

$$L(\mathbf{W},\varphi ,{\sigma }^2;\mathbf{X})=-\frac{1}{2}\sum _{j=1}^M\sum _{k=0}^{T-1}\left\{\frac{2\pi {\mathbf{e}}_j^{\top }\mathbf{W}\tilde{\mathbf{f}}(r_k,\mathbf{X}){\mathbf{W}}^{\top }{\mathbf{e}}_j}{{\sigma }_j^2∕{\mid {\Phi }_j\left(\exp \{-i{r}_k\}\right)\mid }^2}+\ln \frac{{\sigma }_j^2∕2\pi }{{\mid {\Phi }_j\left(\exp \{-i{r}_k\}\right)\mid }^2}\right\}+T\ln \mid \det \left(\mathbf{W}\right)\mid .$$ (5)

If the data are prewhitened, the unmixing matrix W is orthogonal (Hyvärinen, Karhunen, and Oja 2001). In this case, the Whittle likelihood can be further simplified by dropping the last term, T ln | det(W)|. To incorporate the orthogonal constraints on the unmixing matrix, we propose to use Lagrange multiplier (Bertsekas 1982). More specifically, we consider minimizing the following penalized negative Whittle log-likelihood,

$$F(\mathbf{W},\varphi ,{\sigma }^2,\lambda )=-L(\mathbf{W},\varphi ,{\sigma }^2;\mathbf{X})+{\lambda }^{\top }\mathbf{C},$$ (6)

where λ = (λ₁, . . . , λ_M(M+1)/2)^⊤ is the Lagrange parameter vector, and C is a M(M + 1)/2-dimensional vector with the {(j – 1)M + k}th element being C_(j–1)M+k = (WW^⊤ – I_M)_jk, j = 1, . . ., M, k = 1, . . ., j. Note that we need only M(M + 1)/2 constraints since the matrix WW^⊤ – I_M is symmetric.

We remark that there are other orthogonal constrained ICA algorithms based on optimization over a set of all orthonormal matrices known as the Stiefel manifold. For instance, see Edelman, Arias, and Smith (1998), Amari (1999), Douglas (2002), Plumbley (2004), Ye, Fan, and Liu (2006).

2.3.2 Iterative Estimation Algorithm

The minimization of the penalized criterion (6) is nontrivial. The computation involves nonlinearly the M(M + 1)/2 elements of the unmixing matrix, as well as the AR model parameters ϕ and σ², for a given set of the AR orders {p_j}. In addition, the true AR orders also need to be estimated using model selection criteria. As such, our estimation algorithm will be carried out in an iterative manner: alternating between updating the ICA unmixing matrix and estimating the AR parameters (along with model selection) for a fixed unmixing matrix, as opposed to joint optimization of the unmixing and the AR parameters.

We start the iteration procedure with a certain set of the AR orders followed by minimization of the criterion (6) in the following manner. First, start with an initial value of W̃, then estimate ϕ and σ² by maximizing the unpenalized Whittle log-likelihood (5). Alternatively, we can first recover the sources via S̃ = W̃X, and then estimate the AR model parameters ϕ using the Yule–Walker procedure (Brockwell and Davis 1991). Our experience through numerical studies suggests that the two methods give similar results, while the Yule–Walker procedure is computationally faster. Hence, in the remainder of the article, we concentrate on the Yule–Walker procedure, and refer to the corresponding cICA procedure as cICA–YW.

Once the AR coefficients ϕ are estimated, we can estimate the variances σ² using

$${\tilde{\sigma }}_j^2(\tilde{\mathbf{W}},\tilde{\varphi })=\frac{2\pi }{T}\sum _{k=0}^{T-1}{\mathbf{e}}_j^{\top }\tilde{\mathbf{W}}\tilde{\mathbf{f}}(r_k,\mathbf{X}){\tilde{\mathbf{W}}}^{\top }{\mathbf{e}}_j{\mid {\tilde{\Phi }}_j\left(\exp \{-i{k}_k\}\right)\mid }^2.$$ (7)

Given the estimates $\tilde{\varphi }$ and ${\tilde{\sigma }}^2$, we propose to obtain the updated estimate of the unmixing matrix W by minimizing the penalized criterion (6). Since (6) is nonlinear with respect to W, we use the Newton–Raphson method with Lagrange multiplier. To begin with, we find the first and second derivatives of (6) with respect to W and λ, denoted as Ḟ(W, λ; ϕ, σ²) and H(W, λ; ϕ, σ²), respectively. Then we obtain the one-step Newton–Raphson update for W and λ as

$${(\widehat{\mathbf{W}},\widehat{\lambda })}^{\top }={(\tilde{\mathbf{W}},\tilde{\lambda })}^{\top }-{\left(\mathbf{H}(\tilde{\mathbf{W}},\tilde{\lambda };\tilde{\varphi },{\tilde{\sigma }}^2)\right)}^{-1}\stackrel{.}{F}(\tilde{\mathbf{W}},\tilde{\lambda };\tilde{\varphi },{\tilde{\sigma }}^2).$$ (8)

Finally, the above two steps are iterated to update (W, λ) and (ϕ, σ²) alternatingly until convergence. To gauge the algorithm convergence, we use Amari error (Amari et al. 1996) as the convergence criterion, which is defined as

$$d_{\mathrm{Amari}}({\mathbf{W}}_1,{\mathbf{W}}_2)=\frac{1}{M}\sum _{i=1}^M\left(\frac{{\sum }_{j=1}^M\mid a_{ij}\mid }{{\max }_j\mid a_{ij}\mid }-1\right)+\frac{1}{M}\sum _{j=1}^M\left(\frac{{\sum }_{i=1}^M\mid a_{ij}\mid }{{\max }_i\mid a_{ij}\mid }-1\right),$$ (9)

where W₁ and W₂ are two M × M matrices, W₂ is invertible and a_ij is the ijth element of ${\mathbf{W}}_1{\mathbf{W}}_2^{-1}$. This criterion has been used in the context of ICA (Bach and Jordan 2003; Chen and Bickel 2005). When the Amari error between $\widehat{\mathbf{W}}$ and $\tilde{\mathbf{W}}$ is less than some threshold, the iteration stops and we claim the algorithm converges. In our numerical studies the algorithm usually converges within 30 iterations.

In practice, the true AR order of each source is not known and needs to be estimated. We embed the order selection within the updating step for the AR model parameters, and dynamically determine the suitable model for each iteration. In particular, we consider the AR order p_j to vary between 0 and some threshold. We then select the “optimal” order using a conventional model selection criterion such as the Akaike Information Criterion (AIC) (Akaike 1974).

The complete iterative algorithm (with order selection) is summarized as follows:

2.4 ICA for White Noise Sources

We now consider the case of white noise sources. Before proceeding, we remark that the Whittle likelihood approach is essentially a second cumulant based method. Thus it will be challenging to apply our method to separate sources with identical power spectra, especially for ICA involving prewhitened data from a mixture of white noise sources. Therefore, we focus on situations in which the dataset is an orthogonal mixture of white noise sources with different variances. Now, since the mixing matrix A is orthogonal, it will not be necessary to invoke the prewhitening step.

Suppose the jth white noise source has variance ${\sigma }_j^2$. Then its spectral density f_jj equals ${\sigma }_j^2∕\left(2\pi \right)$. The Whittle log-likelihood is given by

$$L(\mathbf{W},{\sigma }^2;\mathbf{X})=-\frac{1}{2}\sum _{j=1}^M\sum _{t=0}^{T-1}\left\{\frac{{\mathbf{e}}_j^{\top }\mathbf{W}\tilde{\mathbf{f}}(r_k,\mathbf{X},T){\mathbf{W}}^{\top }{\mathbf{e}}_j}{{\sigma }_j^2∕\left(2\pi \right)}+\ln ({\sigma }_j^2∕\left(2\pi \right))\right\}.$$ (10)

Note that if the sources are white noise, we apply the same weight to all the frequencies when we maximize the Whittle log-likelihood (10). We also use the Lagrange multiplier to ensure the identifiability of the unmixing matrix, and consider minimizing a penalized negative Whittle log-likelihood similar to (6).

The estimation of σ and W can be iterated as in cICA. There is no need to estimate the AR coefficients nor select the AR order. We refer to this method as wICA. In Section 3.2 we show that with white noise sources, the wICA is very competitive with conventional ICA methods; furthermore, the wICA and cICA perform similarly, which suggests that the model selection step of cICA works well.

2.5 Extension to General ARMA Processes

The cICA procedure in Section 2.3 can also be extended to general ARMA processes in a relatively straightforward way.

Suppose the jth source follows some stationary ARMA(p_j, q_j) model so that

$${\Phi }_j\left(B\right)S_j\left(t\right)={\Theta }_j\left(B\right){ϵ}_j\left(t\right),{ϵ}_j\left(t\right)\sim \mathrm{WN}(0,{\sigma }_j^2),$$

where B is the backshift operator, Φ_j(z) = 1 – ϕ_j,1z – · · · – ϕ_j,pjz^p_j, and Θ_j(z) = 1 + θ_j,1z + ··· + θ_j,qjz^q_j. According to Brockwell and Davis (1991), the power spectrum of this source is given by

$$f_{jj}\left(r\right)=\frac{{\sigma }_j^2}{2\pi }\frac{{\mid {\Theta }_j\left(e^{-ir}\right)\mid }^2}{{\mid {\Phi }_j\left(e^{-ir}\right)\mid }^2},r\in \mathbb{R}.$$

We can update the Whittle log-likelihood (5) with the above power spectrum. The iterative cICA algorithm of Section 2.3 can still be used to estimate the parameters, except that special care is needed when estimating the time series model parameters and selecting the AR/MA orders of the model. For the sake of saving space, we omit the details of the technical derivation, and refer the readers to Brockwell and Davis (1991). We consider general ARMA processes in the simulation studies of Section 3.

3. SIMULATION STUDIES

3.1 Simulation Study I: Blind Separation of Colored Sources

According to the ICA model (1), we first generated the source matrix S and the M × M mixing matrix A seperately. We considered M = 5 and simulated five independent stationary ARMA time series under four different sample sizes (T = 128, 256, 512, 1024). The five sources were generated as:

• S₁: AR(2), ϕ₁ = 1, ϕ₂ = −0.21 with white noise from uniform$[-\sqrt{3},\sqrt{3}]$;

• S₂: AR(1), ϕ₁ = 0.3 with white noise from N(0, 1);

• S₃ (1) ϕ₁ = 0.8 with white noise from t(3);

• S₄ MA (1), θ₁ = 0.5 with white noise from Weibull(0.5, 0.5);

• S₅: White noise from double exponential(1).

We generated the 5 × 5 orthogonal mixing matrix A randomly. The data matrix X was obtained as X = AS. The simulation was replicated 100 times. Our method, cICA–YW, was compared with several popular existing ICA methods, including extended Infomax (Lee, Girolami, and Sejnowski 1999), fastICA (Hyvärinen, Karhunen, and Oja 2001), Kernel ICA (KICA) (Bach and Jordan 2003), Prewhitening for Charateristic Function based ICA (PCFICA) (Chen and Bickel 2005), and AMICA (Palmer, Kreutz-Delgado, and Makeig 2010).

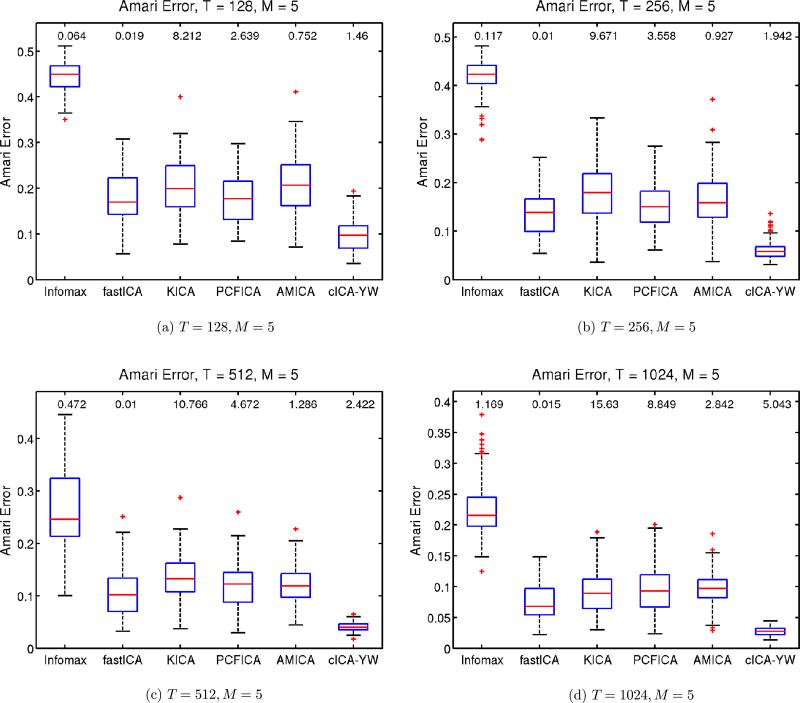
Following the practice of Bach and Jordan (2003) and Chen and Bickel (2005), we use the Amari error between the true unmixing matrix and its estimate as a performance criterion to compare the methods. Figure 2 shows the boxplot of the Amari error for each method under the different sample sizes. The median computation time for each method is also provided at the top of the corresponding boxplot. The cICA–YW procedure outperformed the other ICA methods uniformly, and the advantage increased with sample size. As far as the computing time is concerned, fastICA, Infomax, cICA–YW, and AMICA are the top four fastest methods. In summary, cICA–YW provides very good estimates in a fairly short time. The cICA–YW improved the performance over the other ICA methods by making use of the temporal correlation structures within the sources.

Figure 2.

Simulation Study I: Performance comparison for ARMA sources. Sample sizes T = 128, 256, 512, 1024. Number of sources M = 5. The boxplots show the Amari error between the true unmixing matrix and the estimated unmixing matrix for the various methods. The median computation time is at the top of the corresponding boxplot. The cICA–YW provides more accurate estimates than its competitors in a fairly short time. Infomax stands for the extended Infomax as described in the text.

3.2 Simulation Study II: Blind Separation of White Sources

We also examined the performance of wICA and cICA–YW when the sources are white noises. In this second simulation study, three and five sources (M = 3, 5) were generated under two different sample sizes (T = 1024, 2048). Three of the white noise sources were simulated from uniform(−1, 1), N(0, 1) and double exponential (1) distributions. For the five-source setup, the two additional white noise sources were generated from t(3) and Weibull(1, 1). Again we randomly generated the orthonormal mixing matrix A. For reasons discussed in Section 2.4, the data were not prewhitened. We compared the performance of wICA, cICA–YW, extended Infomax, KICA, PCFICA, and AMICA over 100 simulation runs. Due to the ill performance of the fastICA without prewhitening, the corresponding result is not included.

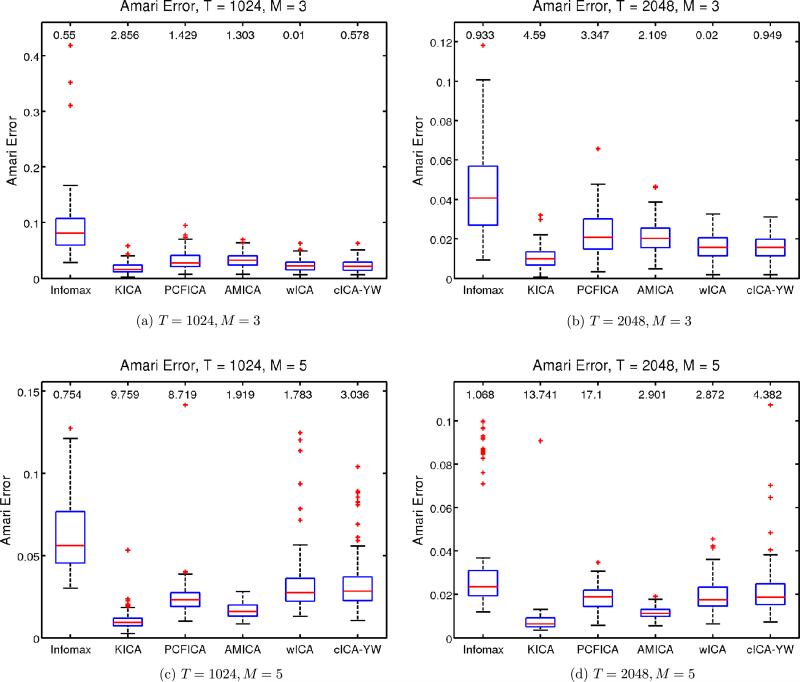
Figure 3 shows the boxplots of the Amari error for each method under the four simulation setups, along with the median computation time in seconds. The AMICA performed best followed by KICA for both sample sizes. The wICA and cICA–YW gave comparable results in terms of the Amari distance when the number of sources is M = 3. For M = 5, wICA and cICA–YW become comparable as the sample size increases. This confirms that the model selection step of cICA–YW still works well for white noise cases. All the methods are comparable in terms of Amari distance.

Figure 3.

Simulation Study II: Performance comparison for white noise sources. Sample sizes T = 1024, 2048. Number of sources M = 3, 5. The boxplots show the Amari error between the true unmixing matrix and the estimated unmixing matrix obtained by various ICA methods. The median computation time of each method is provided on top of the corresponding boxplot. The wICA and cICA–YW provide comparable estimates as the other existing ICA methods. Infomax stands for the extended Infomax as described in the text.

3.3 Simulation Study III: Detection of Activated Brain Regions

3.3.1 Simulation Description

As discussed in Section 1, our research is primarily motivated by the application of fMRI analysis. The current simulation study is designed to compare the performance of the various ICA methods in analyzing a toy fMRI dataset. Below we describe the procedure for generating the pseudo-fMRI data.

In this simulation, we first generated the V × M spatial map matrix A and the M × T time series matrix S, which were then multiplied to give the V × T data matrix. In particular, we consider M = 4 temporal independent components that are of length T = 512; each corresponding spatial map consists of 10 slices and each slice has 20 × 20 voxels, which results in a total of 4000 voxels for each spatial component. The final data matrix is 4000 × 512 in dimension.

The four temporal components are assumed to represent the task function, heart beating, breathing, and noise artifact respectively. For the task function, we considered a simple rest-activation block design with 18 seconds for each rest or activation period (a frequency of 0.0052 Hz); for the heartbeat component, we used a harmonic function with a frequency of 1.71 Hz; and for the breathing component, a harmonic function with a frequency of 0.3 Hz. These frequencies were chosen so that they have meaningful physiological interpretations. The data were sampled every 0.3 seconds.

The four underlying independent temporal components were generated as follows:

• S₁: Task function with noise = Task function + σ₁Z₁;

• S₂: Heartbeat with noise = sin(2π1.17t + 1.61) + σ₂Z₂;

• S₃: Breathing with noise = sin(2π0.3t + 1.45) + σ₃Z₃;

• S₄: S₄(t)= −0.85S₄(t – 1) −0.7S₄(t – 2)+0.2S₄(t – 3) + ϵ₄(t), ϵ₄(t)~ i.i.d. uniform($-\sqrt{3},\sqrt{3}$).

The noises added to the three signal components were generated as follows:

• Z₁(t)=0.8Z₁(t – 1) + ϵ₁(t), ϵ₁(t) ~ i.i.d. uniform($-\sqrt{3},\sqrt{3}$);

• Z₂(t)= −0.6Z₂(t – 1) – 0.5Z₂(t – 2) + ϵ₂(t), ϵ₂(t) ~ i.i.d. uniform($-\sqrt{3},\sqrt{3}$);

• Z₃(t) = 0.1Z₃(t – 1) – 0.8Z₃(t – 2) + ϵ₃(t), ϵ₃(t) ~ i.i.d. uniform($-\sqrt{3},\sqrt{3}$).

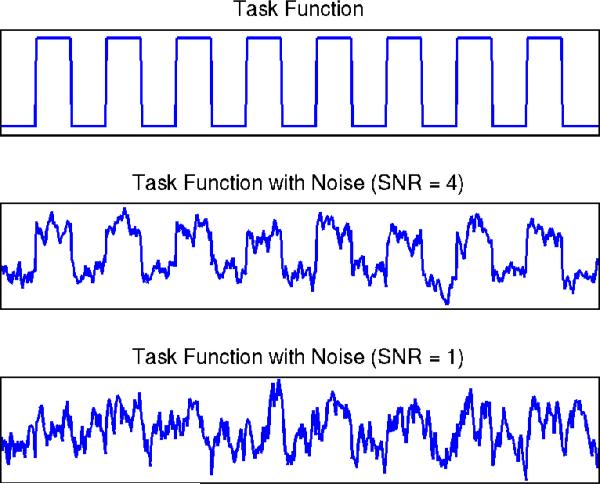
It is worthwhile to consider different signal-to-noise ratios (SNR), since the sources of interest can contain other irrelevant variabilities (Huettel, Song, and McCarthy 2008). Figure 4 displays the task function at different SNR levels. At a higher SNR level, we can easily distinguish the task function, whereas it is harder to observe the task function at a lower SNR level. Hence, in the current study, we considered four different setups: SNR = 0.5, 1, 2, 4, and studied the effects of SNR on the performance of the various ICA methods. In defining SNR, we follow the suggestion of Bloomfield (2000).

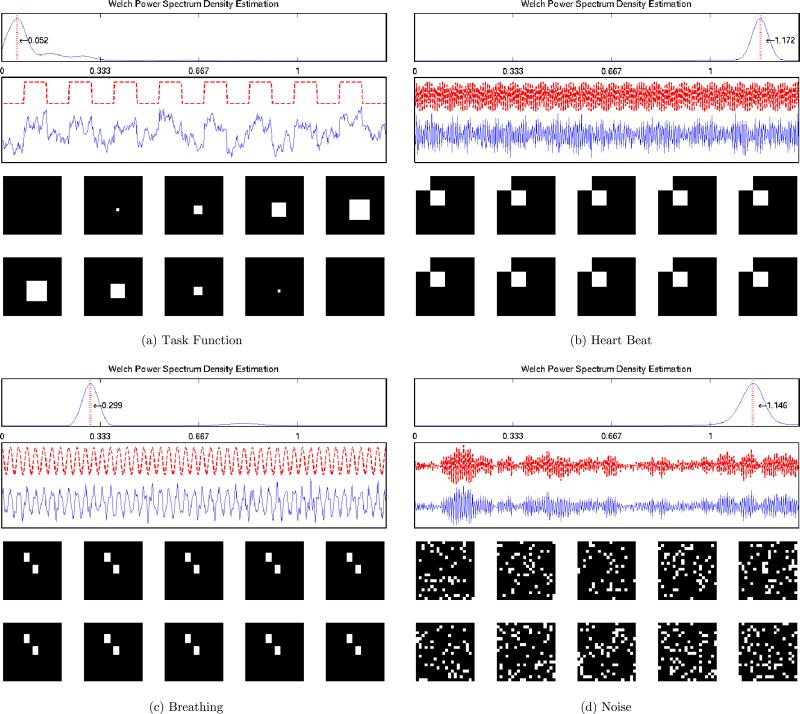
Figure 4.

Simulation Study III: Task function at different SNR levels. The online version of this figure is in color.

Given a SNR level, for each of the first three source signals we calculated the corresponding noise standard deviation as ${\sigma }_j=\sqrt{\left(\text{Variance of the signal}\right)∕(\text{Variance of the noise}\cdot \mathrm{SNR})}$. The true temporal components at SNR = 1 (blue solid line) are illustrated in Figure 5 below the noise-less task functions (red dotted line). The spectral density curve for each component is also displayed at the top of each panel, which is estimated using Welch's power spectrum estimator (Welch 1967). The red vertical line represents the main frequency of each component. Each temporal component is displayed above the corresponding spatial map. We replicated the simulation 100 times for each SNR.

Figure 5.

Simulation Study III: The true independent temporal components, spectral densities and spatial maps. The four temporal signals (task, heartbeat, breathing, and noise) are displayed sequentially from top left to bottom right with the corresponding spatial maps. The activated voxels are colored as white and nonactivated voxels are colored as black.

Each voxel of a spatial map (i.e., a column of A) takes a binary value 1 or 0, where the voxels with value 1 represent the regions that are activated by the corresponding temporal stimulus, and the voxels of 0 indicate no activation. When plotting the spatial maps in Figure 5, the activated voxels are colored white and the nonactivated voxels are colored black. For the spatial map corresponding to the noise temporal component, we randomly selected 15% of the entries and coded them as 1. The voxels that correspond to none of the temporal components will remain zero.

3.3.2 Analysis and Results

We first column centered each simulated data matrix (Hastie and Tibshirani 2003). Due to the high dimension of the data matrix, before applying the ICA methods, we then used singular value decomposition (SVD) for dimension reduction (Petersen et al. 2000). In particular, we extracted the leading M = 4 SVD components which actually explained 99% of the raw data variance in all the simulation runs; we then approximated the raw data matrix X using ŨD̃Ṽ^⊤, where the diagonal entries of the diagonal matrix D̃ are first M singular values, and the columns of Ũ and Ṽ are the forst M left and right singular vectors, respectively.

Finally, the ICA algorithms were applied to X̃ = D̃Ṽ^⊤ to obtain the temporal component matrix Ŝ and the mixing matrix Â. In terms of decomposing the original matrix X, the spatial map matrix were estimated as à = ŨÂ, where each column is the spatial map corresponding to one recovered temporal component in Ŝ.

The independent components extracted by ICA are ordered arbitrarily. To match each recovered component with the original sources, we calculate the correlation between the recovered component and each of the 4 true temporal source signals, and the source that has the largest absolute correlation is identified as the match.

To identify the activated voxels in each spatial map, we followed the suggestion of McKeown et al. (1998): z scores were calculated for each map by subtracting the mean of the map and dividing the standard deviation of the map. The voxels with |z| ≥ 1 then were identified as those that were activated.

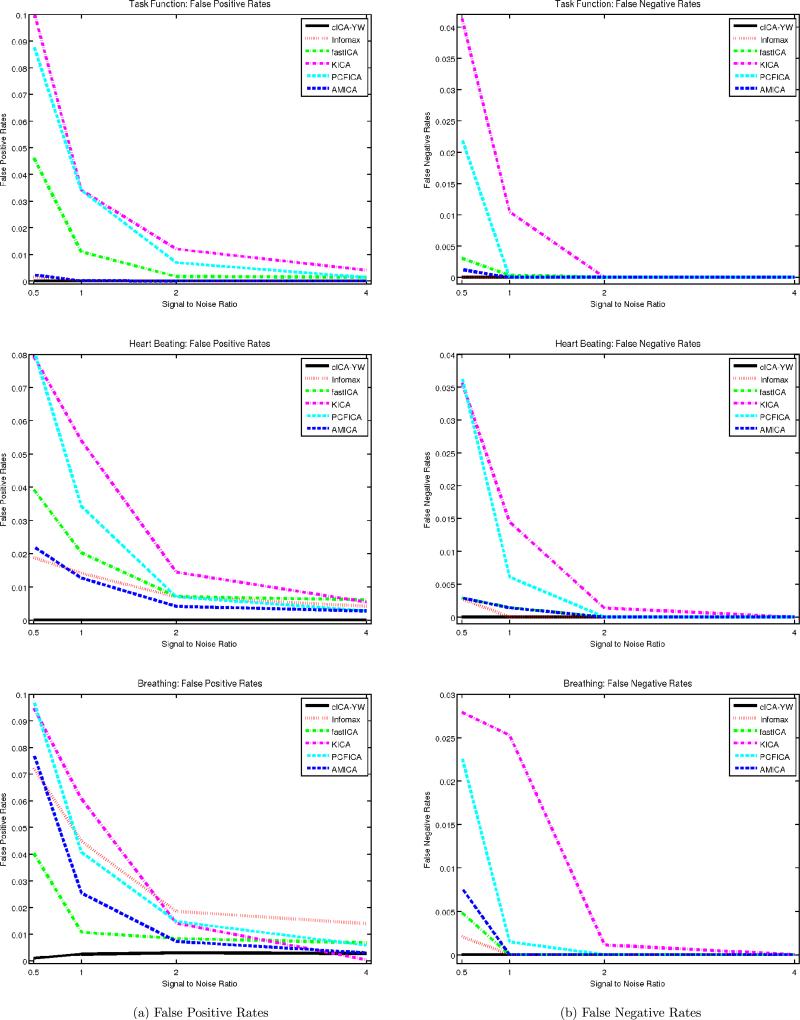
To gauge the performance of the ICA algorithms, we calculated the false positive and false negative rates for each estimated spatial map. Each column of Figure 6 displays the average of the false positive/negative rates over the 100 simulation runs under different SNRs. The rows correspond to the spatial maps for the task function, heartbeat, and breathing, respectively. In each panel, six ICA methods are compared: cICA–YW (black solid line), Infomax (red dotted line), fastICA (green dash–dot line), KICA (margenta dash–dot line), PCFICA (cyan dashed line), and AMICA (blue dashed line). The x-axis represents the four different SNRs (0.5, 1, 2, 4). The cICA–YW performed uniformly better than the other methods, having the smallest false positive and false negative rates. In addition, the false positive and false negative rates generally decreased as the SNR increased (except for Infomax).

Figure 6.

Simulation Study III: Comparisons of false positive and false negative rates. Four different SNRs are considered. False positive and false negative rates are averaged over 100 simulation runs and displayed at left and right columns respectively. The cICA performs uniformly better than the other five methods.

As a visual comparison of the detected spatial activation regions, we averaged the estimated spatial maps across the first five simulations. The average spatial maps are plotted for SNR = 1 in the six rows of Figure 7 for the six ICA methods, respectively. In each row, the average spatial maps for the first three independent components (task function, heartbeat, and breathing) are displayed sequentially. We observe that cICA–YW [panels (a)] detected the spatial activation regions much better than its peers, whose noisier results for all three source signals are clearly shown (when comparing with the true regions depicted in Figure 5).

Figure 7.

Simulation Study III: Spatial maps detected by cICA–YW, Infomax, fastICA, KICA, PCFICA, and AMICA under SNR = 1. The average spatial maps (the relative frequency of each voxel detected as activated out of the first five runs) are colored using white (1) to black (0) with gray scale. The cICA–YW detects the spatial activation much better than the other ICA methods.

We also conducted a similar simulation study for random event-related design. The task function is random event-related contaminated with white noises (instead of correlated), where the time intervals between two consecutive random events follow a Poisson distribution with a mean of 4.5 seconds. (The other three sources follow the same models as in the above block design; hence their noises are correlated.) The study results indicated that the cICA–YW still leads the pack. These results along with the previous results for other values of SNR are available in the supplementary materials.

4. APPLICATION TO REAL FMRI DATA

4.1 Data Description

Experimental finger-tapping data were obtained from our collaborators (Sen et al. 2010; Lewis et al. 2011). The main neurological interest of the experiment was to identify the brain regions responsible for the finger-tapping tasks. Two hundred MR scans were acquired on a modified 3T Siemens MAGNETOM Vision system with a 3 second scan to scan repetition time (TR). Each scan consisted of 49 contiguous slices containing 64 × 64 voxels. Therefore, we have 64 × 64 × 49 voxels at each of the 200 time points. Each voxel is a 3 mm × 3 mm × 3 mm cube.

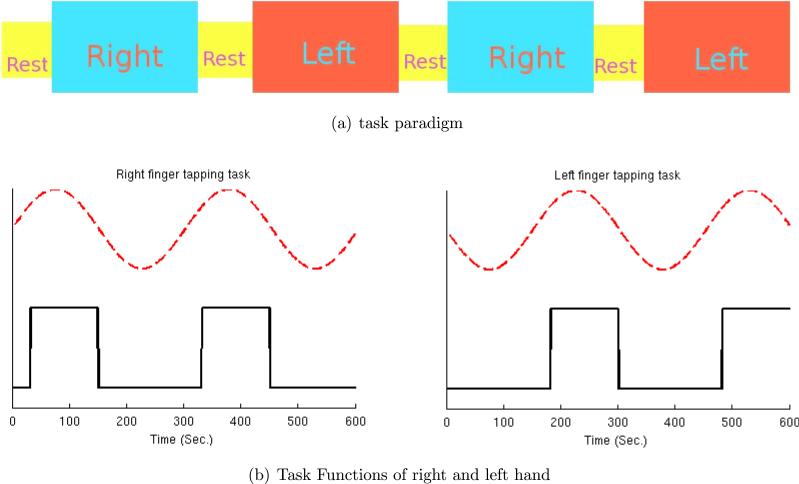
The dataset was obtained by a control subject performing three different tasks alternatively: rest, right-hand finger tapping, and left-hand finger tapping. Figure 8(a) illustrates the experimental paradigm. Each rest period lasted 30 seconds (10 time points) and each finger-tapping task period lasted 120 seconds (40 time points). The block design task functions are displayed as the black solid lines in Figure 8(b). The red dashed lines stand for the sine curves of the main task frequency (0.0033 Hz).

Figure 8.

(a) Experimental paradigm. (b) Task functions for right/left finger-tapping (black solid lines) with task sine curve of main frequency (0.0033 Hz, red dashed lines).

4.2 Analysis

The dataset was first preprocessed using FSL (Smith et al. 2004). The preprocessing included brain image extraction using the Brain Extraction Tool (BET), motion correction using Motion Correction with FSL's Linear Image Registration Tool (MCFLIRT), slice time correction, spatial smoothing using FWHM 6 mm × 6 mm × 6 mm, and highpass temporal filtering using a local linear fit. We removed the background voxels using the mask file obtained during the preprocessing step. The dimension of the final data matrix was 68,963 voxels × 200 time points.

FMRI images usually are of high dimension, especially in terms of the number of voxels. To reduce dimension, we used the supervised singular value decomposition (SSVD) algorithm of Bai et al. (2008), which was shown to work better than SVD when doing ICA for fMRI. (We made the same observation in analyzing this dataset.)

We then employed the entropy matching method (Li, Adali, and Calhoun 2006) implemented in the Group ICA fMRI Toolbox (GIFT) (Calhoun et al. 2001) to select the number of independent components to extract, which was suggested to be 13. Hence we extracted the leading 13 SSVD components, which formed a low-rank approximation of the fMRI data matrix as Ũ_68,963×13D̃_13×13 ${\tilde{\mathbf{V}}}_{13\times 200}^{\top }$, where the columns of Ũ are the first 13 left supervised singular vectors, the columns of Ṽ are the corresponding right supervised singular vectors, and the diagonal matrix D̃ has the 13 supervised singular values on the diagonal. Finally, we applied the six ICA methods (cICA–YW, Informax, fastICA, KICA, PCFICA, and AMICA) to the reduced data matrix, X̃ = D̃Ṽ^⊤, to estimate the temporal independent sources and the mixing matrix Â. The corresponding spatial maps were then estimated as ŨÂ.

4.3 Results

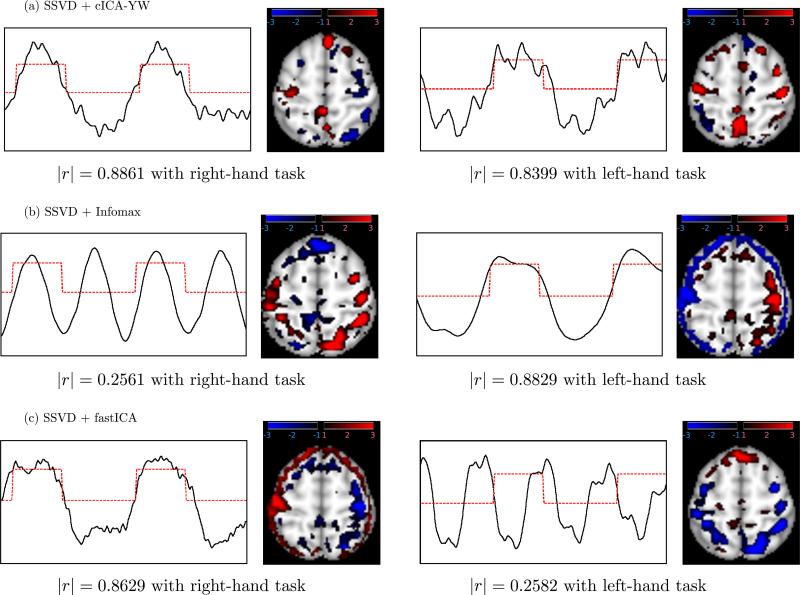
Figures 9 and 10 plot, for each of the six ICA methods, the first two temporal independent components having the highest absolute correlation (|r|) with the right- or left-finger tapping functions, along with the corresponding spatial maps. These results indicate that cICA–YW can recover brain function-related signals of interest more accurately and sensitively than the other ICA methods.

Figure 9.

Real fMRI analysis: Temporal independent components (ICs) and corresponding spatial maps for (a) cICA–YW, (b) Infomax, (c) fastICA. The ICs (black solid lines) of the first two components having the largest absolute correlation (indicated) with finger-tapping tasks (red dash lines) are displayed. Activated areas are colored blue–black or red–black gradient in the spatial maps. The comparison (Figures 9 and 10) suggests that cICA–YW can recover the task-related signals of interest more accurately; in addition, it can detect the regions activated by the tasks more sensitively.

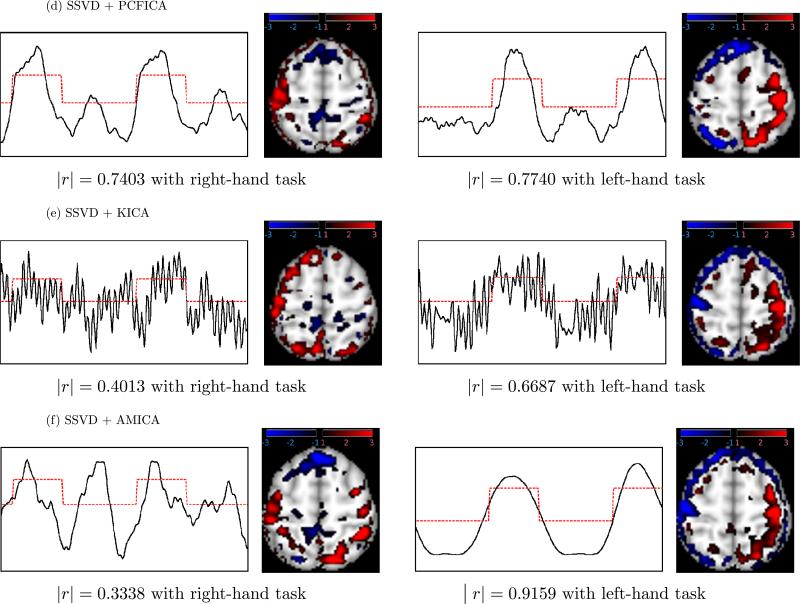
Figure 10.

Real fMRI analysis: Temporal independent components (ICs) and corresponding spatial maps for (d) PCFICA, (e) KICA, and (f) AMICA. The ICs (black solid lines) of the first two components having the largest absolute correlation (indicated) with finger-tapping tasks (red dash lines) are displayed. Activated areas are colored blue–black or red–black gradient in the spatial maps. The comparison (Figures 9 and 10) suggests that cICA–YW can recover the task-related signals of interest more accurately; in addition, it can detect the regions activated by the tasks more sensitively.

Each temporal component is displayed as a black solid line whereas the task function with the highest absolute correlation is depicted by a red dotted line. To display the spatial map, we transformed the subject's anatomical brain structure into a reference image using FMRIB's Linear Image Registration Tool (FLIRT), which is built into FSL. Next, using MRIcron (Rorden 2007), several slices containing brain regions of interest were selected and are shown with the component graphs. Activated voxels having z < −1 were colored according to a blue–black color gradient and those having z > 1 were colored according to a red–black color gradient. A darker color represents less activation and a brighter color represents higher activation. The areas with z < −3 or z > 3 are colored blue and red, respectively.

Due to the sign ambiguity of ICA, we carefully interpreted the results taking into account the signs of the spatial and temporal components. For the cICA–YW method, as shown in the first column of Figure 9(a), the left (contralateral) primary motor cortex (PMC), colored red, was activated when the task was completed with the right hand (|r| = 0.8861 with the right-hand task). The meaning of negative z scores in fMRI data is subject to interpretation, although one explanation may be that they represent decreased activation in a particular region. Using this rationale, during the right hand task, the right PMC (blue) showed less activation. The second column of Figure 9(a) demonstrates that the method can detect activity in bilateral PMC (red) during the left hand task (|r| = 0.8399 with the left-hand task).

The two components obtained by cICA–YW display activity in the corresponding contralateral PMC, the lateral and medial parietal areas, and the anterior prefrontal. The PMC is the final output center for motor tasks and thus activation in this region is consistent with known biology and recent fMRI studies demonstrating increased activity in this region during the performance of a variety of motor tasks (Haslinger et al. 2001; Gowen and Miall 2007; Lewis et al. 2007). In addition, recent imaging studies have shown the lateral and medial parietal areas are involved in the postural configuration of the arm during the planning and execution of movements, spatial attention, and representing the goals and functions of the hands (see Vingerhoets et al. 2010). Although referred to as one of the least understood regions of the brain (Semendeferi et al. 2001), the anterior prefrontal region is implicated in maintaining multiple tasks and their scheduling of operation (Koechlin and Hyafil 2007). The functions underlying both the parietal and frontal regions are integral parts of the motor task employed in the current study and thus activity in these regions is not unexpected. The control subject is strongly right handed and it was interesting to note that in the PMC, activity during the right-hand task revealed only contralateral activity, whereas during the left-hand task the activity was more bilateral activity. These results suggest that use of the nondominant hand may require increased (bilateral) neural activity in the PMC.

Figure 9(b) depicts the components with the strongest correlation with the right-hand task (|r| = 0.2561) and left-hand task (|r| = 0.8829) obtained by Infomax. Both components have weaker correlations with the task functions than those obtained by the cICA–YW method and also appear to include other signals (possibly physiological functions such as heart beat and breathing). In addition, the spatial maps appear to include some artifacts which do not have very clear biological meaning.

Figure 9(c) shows the components obtained by fastICA. The left column displays the component with the strongest correlation with the right-hand task (|r| = 0.8629). Activity is observed in the left contralateral PMC (red) but there also appears to be substantial nonspecific activity (in red) that may represent some artifact or correlation to functions unrelated to the task. Similar to cICA–YW, there was decreased activity in the right PMC (blue) during this task, but there also was increased nonspecific (blue) activity. The right panel of Figure 9(c) shows the best fastICA component to correlate with the left hand task. The correlation obtained (|r| = 0.2582) is significantly smaller than that generated using our cICA–YM and it is unclear what the “decreased” (blue) activity represents biologically. The spatial map also appears to include a potential artifact and does not match to the task function of interest.

The components obtained by PCFICA are displayed in Figure 10(d). The first independent component (IC) (|r| = 0.7403 with right-finger tapping) and the second IC (|r| = 0.7740 with left-finger tapping) have weaker correlations with the task functions of interest compared to our cICA–YW method, although this method does detect activity in appropriate PMC structures.

Figure 10(e) depicts the results obtained by KICA. The first IC (|r| = 0.4013 with right-finger tapping) and the second IC (|r| = 0.6687 with left finger tapping) have much weaker correlations with the task functions compared to the cICA–YW method and also appear to include other signals (possibly physiological functions such as heartbeat and breathing). In addition, the spatial maps appear to include some artifacts possibly caused by head motion.

The two components obtained by AMICA are reported in Figure 10(f). The component displayed in the left column of Figure 10 has weaker correlation with the right-hand task (|r| = 0.3338). Although the correlation with left-hand task function (|r| = 0.9159) is higher than that obtained using our cICA–YM, and the activation is observed in the right contralateral PMC (red), there also appears to be substantial nonspecific activity (in red) that may represent some artifact unrelated to the task.

5. CONCLUSION

In this article we introduced a new ICA method, cICA–YW, and compared its performance against several other established methods, including Infomax and fastICA. The method was developed using the spectral domain approach to model the correlation structures of the latent source signals, and the parameters were estimated via the Whittle likelihood procedure. The advantage of taking into account the temporal correlation over the existing methods was clearly demonstrated. The comparative simulation studies were conducted using a wide variety of time series models for the source signals, including white noise, where our method fared very well. In a real fMRI application involving motor tasks, the new ICA method also detected relevant brain activities more accurately and sensitively.

We conclude this section by mentioning a possible future research direction. We intend to extend our method to take into account both correlation structures within each source and between the sources similar to those considered by subspace ICA and AMICA. Research along this direction could be fruitful.

Algorithm.

The cICA–YW Algorithm

Initialize W̃, $\tilde{\lambda }$.

While the Amari error (9) is greater than the convergence threshold,

1. Estimate the sources by S̃ = W̃X. For j = 1, . . . ,M,

(a) Estimate ${\tilde{\varphi }}_j$ using the Yule–Walker method with the order p̃j selected by AIC.

(b) Compute ${\tilde{\sigma }}_j^2$ according to (7).

2. Update W̃ and $\tilde{\lambda }$ via the Newton–Raphson updating (8), using the estimates $\tilde{\varphi }$ and ${\tilde{\sigma }}^2$.