A SEmi-Adiabatic Matched-phase Spin echo (SEAMS) PINS Pulse-pair for B₁-insensitive Simultaneous Multi-slice Imaging

Abstract

Purpose

Simultaneous multi-slice (SMS) imaging is a powerful technique that can reduce image acquisition time for anatomical, functional, and diffusion weighted magnetic resonance imaging. At higher magnetic fields, such as 7 Tesla, increased radiofrequency (RF) field inhomogeneity, power deposition, and changes in relaxation parameters make SMS spin echo imaging challenging. We designed an adiabatic 180° Power Independent of Number of Slices (PINS) pulse and a matched-phase 90° PINS pulse to generate a SEmi-Adiabatic Matched-phase Spin echo (SEAMS) PINS sequence to address these issues.

Methods

We used the adiabatic Shinnar Le-Roux (SLR) algorithm to generate a 180° pulse. The SLR polynomials for the 180° pulse were then used to create a matched-phase 90° pulse. The pulses were sub-sampled to produce a SEAMS PINS pulse-pair and the performance of this pulse-pair was validated in phantoms and in vivo.

Results

Simulations as well as phantom and in vivo results, demonstrate multi-slice capability and improved B₁-insensitivity of the SEAMS PINS pulse-pair when operating at RF amplitudes of up to 40% above adiabatic threshold.

Conclusion

The SEAMS PINS approach presented here achieves multi-slice spin echo profiles with improved B₁-insensitivity when compared to a conventional spin echo.

Introduction

Magnetic resonance imaging (MRI) at high magnetic fields, such as 7 Tesla (7T), offers increased signal-to-noise ratio (SNR) and enhanced contrast when compared to conventional field strengths (1,2). This increased SNR can be parlayed into unprecedented spatial resolution or faster acquisitions for structural, functional, and spectroscopic imaging sequences (1-4). Spin echo preparations are often used for diffusion-weighted imaging (5-8) and may also be useful for functional MRI (9,10) at high magnetic fields. However, spin echo imaging at 7T faces several challenges that must be overcome in order to capitalize on the potential advantages. Three of these issues are: 1) increased inhomogeneity in the applied radiofrequency (RF) field (B₁ field) leading to non-uniformities in signal and contrast when using conventional RF pulses (11); 2) increased RF power deposition in tissue, as measured by the specific absorption rate (SAR), limiting the strength and number of RF pulses in sequences (11); and 3) changes in characteristic T₁ and T₂ tissue relaxation parameters that affect sequence timing and image contrast (2,12,13).

Simultaneous multi-slice (SMS) imaging using multiband (MB) excitation and parallel imaging is a powerful technique which may be applied to reduce MR image acquisition time (14-18). SMS imaging is achieved by simultaneously exciting several slices in the region of interest (12-15). With the use of multiple receiver coil channels, the sensitivity profiles of the coils are used to disentangle the slices during reconstruction (18,19). One method of creating multi-slice excitations uses RF pulses with slice profiles that are spatially shifted off-center through a sinusoidal modulation of the wave form. The complex summation of these individual component RF pulses, with shifted spatial slice profiles, results in a single composite MB RF pulse. However, the RF power deposition of this type of MB pulse increases with the number of slices (17). Due to the quadratic increase of power deposition with field strength, the number of slices achievable by the conventional SMS technique at 7T is restricted by transmitter B₁ peak power and SAR safety limits. Furthermore, conventional MB composite pulses, particularly 180° MB pulses used in spin echo SMS sequences, are susceptible to slice amplitude and profile attenuation due to the significant B₁ field variation at 7T.

An alternative multi-slice pulse design method, the Power Independent of the Number of Slices (PINS) technique, may be used to produce pulses that excite multiple discrete slices simultaneously without increasing power deposition above that required for a single slice excitation (20). This is accomplished by interleaving the single-slice RF waveform, modulated with a comb function, with a gradient pulse train. The RF pulse used as the basis for the PINS pulse can be designed to provide the desired bandwidth (BW) and duration. Thus, specialized RF pulses, designed to address the technical challenges of ultra-high field MRI, may be transformed into multi-slice pulses through the application of the PINS technique. Previous work has applied the PINS technique to adiabatic VERSE-DANTE pulses to help combat the effect of B₁ inhomogeneity (21). However, adiabatic pulses generate non-linear phase across the selected slice profile and, in a typical spin echo sequence, a linear phase across the slice can only be achieved through the application of a second, identical adiabatic RF pulse. This twice-refocused approach permits the use of adiabatic pulses in a spin echo sequence, but at the cost of increased echo time (TE) and SAR. It has been shown that it is possible to design an excitation pulse to generate a complementary phase profile across the slice that corrects the phase deposited by a quadratic-phase adiabatic 180° pulse (22-24). Combining these two RF pulses results in a semi-adiabatic excitation-refocusing pulse-pair that can be used for spin echo based imaging applications. Conversion to a multi-slice pulse-pair is then possible through application of the PINS technique.

In this work, we designed, implemented, and validated an adiabatic Shinnar Le-Roux (SLR) 180° PINS pulse and a matched-phase 90° PINS pulse to generate a multi-slice spin echo with refocused quadratic phase and improved immunity to B₁-inhomogeneity. The pulse-pair was used as the basis of a SEmi-Adiabatic Matched-phase Spin echo (SEAMS) PINS sequence, which may be applied to accelerate spin echo sequences, especially when imaging at high fields.

Methods

Pulse-pair design and implementation

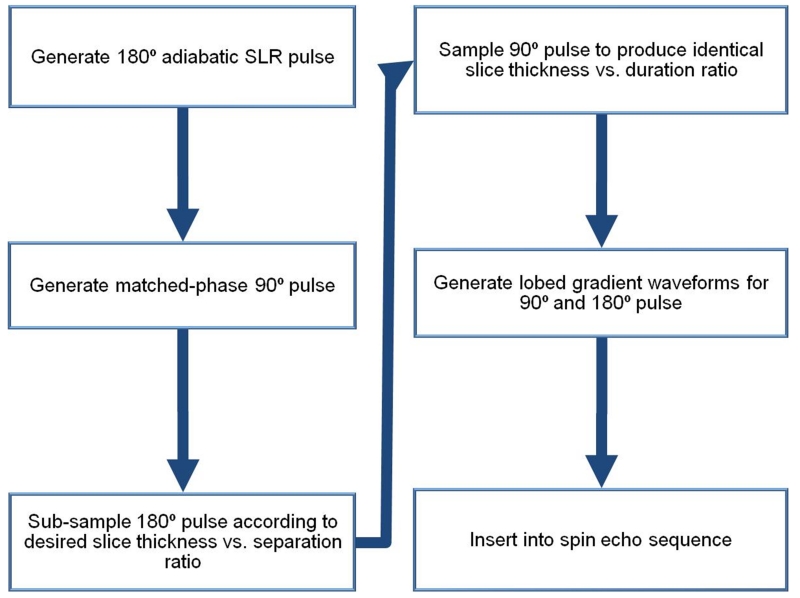
Figure 1 is an overview of the design path used to develop a SEAMS PINS sequence. We used the adiabatic SLR algorithm (25,26) to create a 180° pulse with a bandwidth of 1.11 kHz, a duration of 7 ms and peak RF amplitude of 17 μT. As previously described in (26), the frequency profile of the 180° pulse design was the response of a least-squares linear-phase filter set to have the desired bandwidth. The filter design was done using the “firls” function in MATLAB (The Mathworks Inc., Natick, Massachusetts, USA) f_FIR = firls(N,F,AW) where N is the number of samples, F is a vector of frequency band edges given in the range [0,π] but normalized to [0,1], A is a vector that specifies the desired amplitude of the frequency response of the filter, and W contains the relative ripple amplitudes of the pass and stop bands. For our design N = 355, $F=\frac{1}{\pi }\left[00.005\pi 0.025\pi \pi \right]$, A = [1 1 0 0] (a low pass filter), and W = [0.1/8 $\sqrt{0.01∕2}$]. To introduce adiabatic behavior and distribute RF energy more uniformly, 2500 cycles of quadratic phase was applied across the frequency response for the filter. The B₁₈₀(z) polynomial was then calculated as the Fourier transform of the resultant frequency profile and a minimum-phase A₁₈₀(z) polynomial was calculated from B₁₈₀(z). The A₁₈₀(z) and B₁₈₀(z) polynomials were used as inputs for the inverse SLR transform to produce an RF pulse waveform which was truncated, as described by Balchandani et al (26), to the portion of the result of the inverse SLR transform over which 98% of the RF power is deposited. This produced the desired pulse duration of 7 ms.

Figure 1.

Schematic diagram showing design flow of a SEAMS PINS pulse-pair.

In the second step, we designed the matched-phase 90° pulse as described in previous work (22). Note that this 90° pulse compensates the nonlinear quadratic phase deposited by the 180° pulse, but is inherently not adiabatic. Since high flip-angle RF pulses, such as 180° pulses, are more sensitive to B₁ variation than lower flip-angle excitation pulses, using an adiabatic 180° pulse with a matched non-adiabatic 90° pulse still greatly diminishes the deleterious effects of B₁ inhomogeneity on the spin echo signal (22). To obtain complementary phase in the excitation pulse, the B₉₀(z) polynomial was calculated from the B₁₈₀(z) polynomial using Equation 1.

$$B_{90}=\frac{1}{\sqrt{2}}{B}_{180}^2$$ (1)

The A₉₀(z) polynomial was then calculated from B₉₀(z) and both polynomials were set as inputs to the inverse SLR transform to generate the matched-phase 90° pulse. We set the pulse duration of the 90° pulse to be equivalent to the 180° pulse, as described by Park et al. (23) in condition II for phase-matching. Next, the resulting matched-phased semi-adiabatic pulse-pair was transformed into a PINS pulse-pair.

The adiabatic PINS 180° refocusing pulse was created by sampling the adiabatic SLR 180° pulse with a comb function, creating evenly spaced nulls in the pulse waveform interleaved between RF pulse samples or lobes. The number of lobes in the 180° pulse (n) was calculated using Equation 2 (21) to achieve a ratio between slice thickness (Th) and slice separation (S) of ~1/8, given the refocusing pulse bandwidth (BW) and RF pulse duration (t_rf).

$$n=BW\times t_{rf}\times \left(\frac{\mathrm{S}}{\mathrm{Th}}\right)$$ (2)

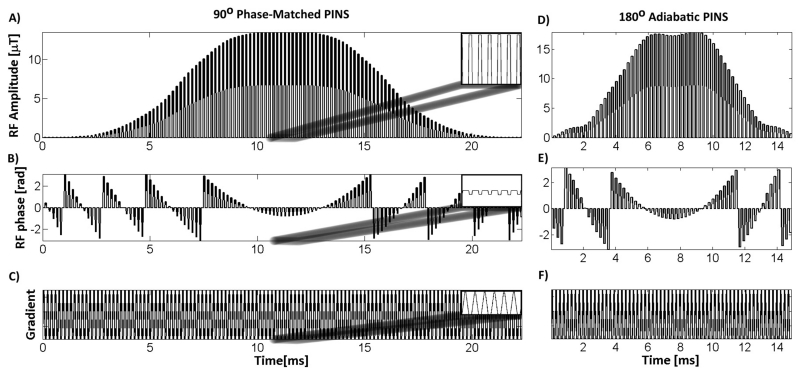
Figure 2 illustrates the resulting magnitude (Figure 2D) and phase (Figure 2E) of a 14 ms (t_rf = 7 ms), 62-lobe, 180° pulse. The excitation pulse was sampled to create the same slice separation and thickness ratio as the refocusing pulse. This resulted in a 90° pulse with 124 equally spaced lobes, magnitude and phase shown in Figures 2A and B. In our particular implementation, the total time (including the gradient lobes) of the excitation pulse was designed to be 50% longer than the total duration of the spin echo refocusing pulse in order to adhere to peripheral nerve stimulation (PNS) system limits. The excitation pulse consists of twice as many lobes as the refocusing pulse, however each RF lobe is 1/2 the duration, resulting in a total of 7 ms of RF sampling for both pulses. The RF nulls are the same duration for both the excitation and the refocusing pulse; thus the gradient lobe amplitude (Figure 2C) played with the excitation pulse were identical to the gradient lobes used during the refocusing pulse (Figure 2F). We could not shorten the gradient lobes any further without exceeding PNS limits on our system. The final excitation pulse design was 21 ms in total duration including 14 ms of null time to play gradients and 7 ms of RF sampling.

Figure 2.

SEAMS PINS pulse-pair. Amplitude of the SEAMS PINS RF waveform for matched-phase A) excitation and D) refocusing. Associated phase for the B) excitation and E) refocusing pulses. C&F) Gradient waveforms timed to coincide with the nulls in the RF pulse. The insets in A, B, and C show the details of a 1 ms section of the waveforms.

The gradient pulse trains, for both the excitation (Figure 2C) and refocusing (Figure 2F) pulses, were designed to interleave within the nulls of the PINS pulse. The time-integral of each gradient lobe (A) is given in Equation 3 where G(t) is the gradient amplitude and τ is the duration of the gradient lobe. In order to maximize A for a fixed small τ and typical maximum gradient slew rate on human scanners, each gradient lobe was designed to be triangular, with a maximum amplitude G_amp.

$$A={\int }_{t_o}^{t_o+\tau }G\left(t\right)\mathit{dt}=\frac{1}{2}{G}_{\mathit{amp}}\tau$$ (3)

Thus, the separation between the slices can be calculated using Equation 4 where γ is the gyromagnetic ratio.

$$S=\frac{1}{\frac{\gamma }{2\pi }A}=\frac{2}{\frac{\gamma }{2\pi }{G}_{\mathit{amp}}\tau }$$ (4)

Final Pulse Sequence and Reconstruction

The completed SEAMS PINS pulse-pair and associated gradient train were inserted into a spin echo pulse sequence, replacing the conventional excitation and refocusing pulses, to create the SEAMS PINS sequence. We validated the performance of the pulse-pair for spin echo imaging in phantoms and in humans.

To reconstruct the aliased images, a set of weighting factors, corresponding to the individual coil sensitivities for each slice position, had to be calculated. In order to calculate this weighting, a low resolution (64×64) data set was acquired over the entire volume. For reconstruction, the raw data from each coil was retrieved and combined with the weighting factors, and a slice-GRAPPA MATLAB (The Mathworks Inc., Natick, Massachusetts, USA) script (19,27) was modified to calculate the weights and un-alias the overlapping signals into individual separated slices.

Simulations

The A_PINS(z) and B_PINS(z) polynomials were used to simulate the final SEAMS PINS pulse-pair spectral profile. When the initial longitudinal magnetization is assumed to be 1, Equations 5-7 are equivalent to the calculations performed by a discrete-time Bloch simulator (25).

$$M_{\mathit{xy}}=2\mathit{conj}\left(A_{\mathit{PINS}90}\right(z\left)\right)\ast B_{\mathit{PINS}90}\left(z\right)$$ (5)

$$M_{\mathit{ref}}=B_{\mathit{PINS}180}\left(z\right)\ast B_{\mathit{PINS}180}\left(z\right)$$ (6)

$$M_{\mathit{fin}}=\mathit{conj}\left(M_{\mathit{xy}}\right)M_{\mathit{ref}}$$ (7)

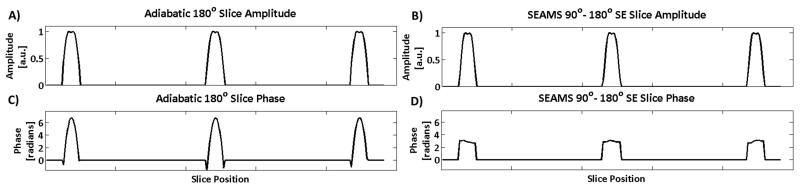
Where M_xy is the transverse magnetization after the initial excitation by the matched-phase 90° PINS pulse and M_ref is the refocusing profile for the adiabatic PINS 180° pulse. The final magnetization (M_fin) at the spin echo can be calculated as the effect of the 180° pulse on the transverse magnetization produced by the 90° pulse (Equation 7) (25). The multi-slice magnitude and phase profiles of the adiabatic PINS refocusing pulse, obtained using Equation 6, are shown in Figures 3A and 3C. The magnitude and phase of the multi-slice spin echo profile obtained using Equation 7 are shown in Figures 3B and 3D. The nearly flat phase obtained across the slices in the final spin echo, after the application of the linear refocusing slice gradient, demonstrates that the quadratic phase is largely refocused in the final spin echo. This phase-matching obviates the need for a second adiabatic refocusing pulse that might otherwise be required to cancel non-linear phase.

Figure 3.

Slice Profiles for 180° adiabatic PINS pulse and final spin echo at three different slice positions. The A) amplitude and C) phase of multi-slice profile produced by the 180° adiabatic PINS pulse and the B) amplitude and D) phase of spin echo generated by the matched-phase adiabatic PINS pulse-pair. C) Quadratic phase deposited across the slices by the 180° adiabatic PINS pulse is largely refocused in D) the spin echo, due to compensation by the matched-phase excitation pulse.

The B₁-insensitivity of the SEAMS PINS pulse-pair was investigated by simulating the spin echo profile (using Equation 7) for RF overdrive factors ranging from 0.5 to 1.5, in increments of 0.1. The RF overdrive factor (ODF), given in Equation 8, is a way of measuring the sequence response to a degree of B₁-inhomogeneity. ODF is equal to the RF amplitude of the applied pulse (P_app) divided by the RF amplitude of the pulse at adiabatic threshold (P_thresh).

$$\mathrm{ODF}=\frac{p_{\mathit{app}}}{p_{\mathit{thresh}}}$$ (8)

Therefore, an ODF of 1.5 would mean a 50% increase of pulse amplitude above the adiabatic threshold. Maximum magnetization for the center slice was compared to a conventional non-adiabatic spin echo pulse-pair for the same range of ODFs. In the case of the conventional spin echo, ODF was calculated as the ratio of the applied RF pulse amplitude to the nominal RF pulse amplitude (i.e. the amplitude at which the pulse was designed to operate to achieve a flip angle of 180°).

Phantom experiments

The performance of the SEAMS PINS pulse-pair was verified in a cylindrical water phantom (water bottle) and a spherical water phantom. All experiments were performed on a 7T actively shielded whole body MRI scanner (Siemens MAGNETOM 7T, Siemens, Erlangen), equipped with a SC72CD gradient coil (G_max = 70 mT/m and max slew rate = 200 T/m/s), using a single channel transmitter and a 32-channel receive head coil (Nova Medical, Wilmington, MA). Pulse sequence parameters for the phantom experiments are summarized in Table 1.

Table 1.

Pulse sequence parameters for the reference scan and SEAMS PINS image acquisition for in vivo and phantom scans.

Sequence	TR [ms]	Nav	TE [ms]	FOV [mm×mm]	Matrix	Gradient [mT/m]	Thickness [mm]	Total Time [min:sec]
Phantom Reference	8.6	1	4	250×250	64×64	N/A	5	0:28
Phantom PINS	300	2	43	250×250	512×512	10.4	5	2:52
Human Reference	8.6	1	4	240×240	64×64	N/A	5	0:27
Human PINS	300	4	43	240×240	256×256	10.4	5	5:20

The slice-selectivity and B₁-insensitivity of the pulse sequence were tested on a cylindrical water phantom (created using a water bottle) by applying the SEAMS PINS sequence with the readout gradient played along the slice-select (axial) direction. This made it possible to obtain a projection through the multi-slice profile. We then applied the SEAMS PINS sequence with the RF pulses powered at ODF = 0.5-1.5 in steps of 0.1, in order to determine whether the measured B₁-insensitivity of the multi-slice profile agreed with simulated behavior.

Phantom experiments on a spherical water phantom were conducted to demonstrate in-plane slice behavior for a range of B₁ values as well as successful separation of overlapping slices. The SEAMS PINS sequence was powered with ODF = 0.5, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, and 2.0. For this experiment, the readout gradient was played out in the conventional way, perpendicular to both the phase-encode and the slice-select gradients. The resulting aliased images were separated using the weightings calculated from a low resolution reference scan of the volume. A 10.4 mT/m gradient was used with a SEAMS PINS sequence designed to obtain a 1/8 slice separation ratio for 5 mm thick slices, resulting in a slice separation of 40 mm. In the spherical phantom with 18 cm diameter, this produced 4 slices across the field of view.

In vivo experiments

The SEAMS PINS sequence was used to scan the brain of a healthy human volunteer. Institutional Review Board approval and informed consent were obtained prior to scanning. The in vivo images were acquired with the same sequence parameters as the phantom images, but with a FOV of 240 mm × 240 mm. A 10.4 mT/m gradient was used with the slice thickness of 5 mm and a slice separation of 40 mm. To measure B₁-insensitivity of SEAMS PINS, images were acquired with ODF = 1.0, 1.1, 1.2, 1.4, and 1.6. The acquisition parameters for these scans are summarized in Table 1. The SNR was measured on the in vivo image as the mean signal acquired from 225 pixels divided by the standard deviation of the noise signal, acquired from 225 pixels in a non-image region.

Results

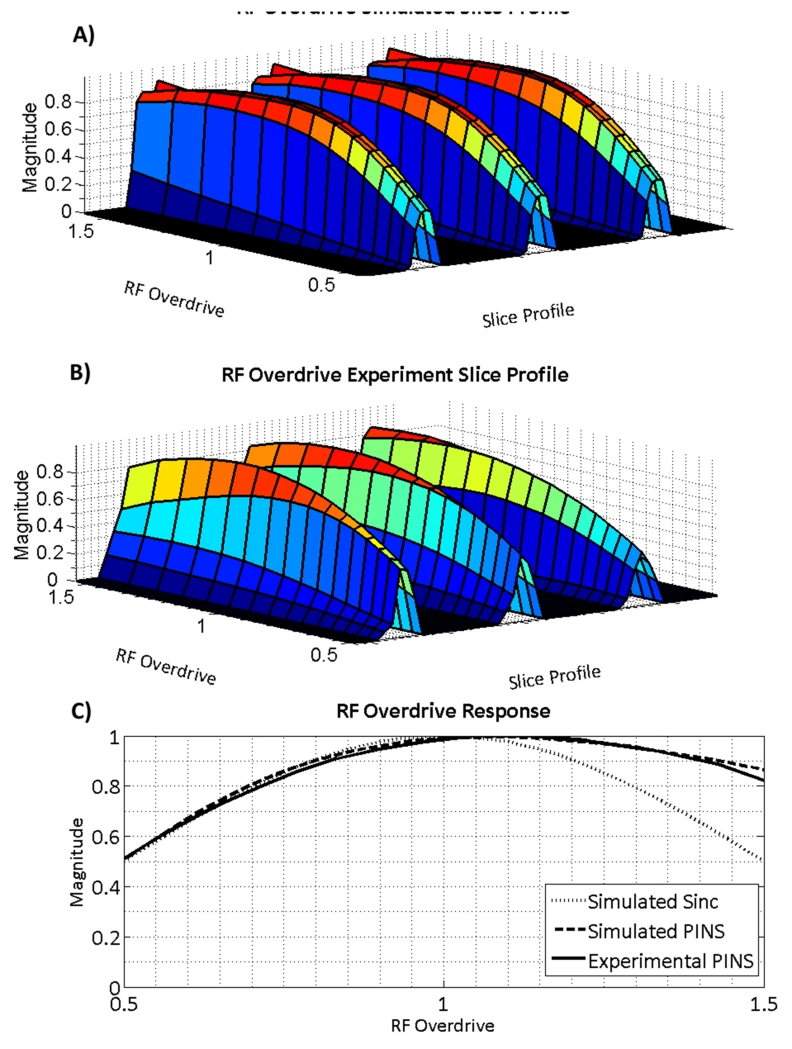
Figure 4 compares the data from the cylindrical water phantom, scanned with increasing RF power, to the simulated magnetization profiles for SEAMS PINS. The magnitude of the projection through the multi-slice profile for a range RF overdrive factors is plotted in Figure 4. Figure 4A shows the simulated slice profile and Figure 4B shows the measured slice profile in the cylindrical phantom experiment. In both figures, the slice parameters and position of the projection through the slices remain fixed. As expected, the amplitude of the selected slices increases as the angle of the excitation pulse approaches 90° and the spin echo refocusing pulse approaches adiabatic threshold (i.e. ODF = 1). Past the adiabatic threshold for the refocusing pulse, magnetization declines at a much slower rate owing to the B₁-insensitive behavior of the 180° pulse. Some loss of amplitude of the magnetization occurs due to the non-adiabatic behavior of the excitation pulse. Figure 4C compares the slice magnitude of a conventional windowed sinc 90°-180° spin echo pulse-pair to the simulated and experimental center slice magnitude in images produced by the SEAMS PINS pulse-pair, for a range of RF overdrive factors. Although there is some loss of slice signal as RF is overdriven above adiabatic threshold (ODF = 1) due to the non-adiabatic behavior of the 90° pulse, the SEAMS PINS pulse-pair still achieves much slower signal decay than the conventional spin echo, due to the B₁-immunity imparted by the adiabatic 180° PINS pulse.

Figure 4.

Behavior of simulated slice profiles and measured slice profiles in a phantom as RF amplitude is varied for SEAMS PINS. A) Simulation of the multi-slice pulse profile and B) central cross-section of the slices measured from imaging a cylindrical water phantom plotted for ODFs ranging from 0.5 to 1.5. C) Simulated and measured phantom slice profile amplitudes obtained using the SEAMS PINS sequence compared with simulated slice profile amplitudes obtained using a conventional non-adiabatic spin echo sequence.

Figure 5 illustrates the slice selection (profile of axial slices) of the SEAMS PINS sequence in a phantom. Figure 5A shows a coronal slice of a cylindrical water phantom. Figure 5B shows the multiple slice profiles obtained by using the SEAMS PINS sequence with the readout gradient in the slice-select direction. The slices shown in Figure 5B were 5 mm thick (full width at half maximum) and the separation between the center of each slice was 40 mm, as expected from the pulse design. The SEAMS PINS slice projection has been overlaid on the coronal water bottle slice image to provide a position reference. When the maximum gradient amplitude is decreased from 10.4 mT/m to 5.2 mT/m, the slice thickness and the slice separation increases to 10 mm and 80 mm, respectively (Figure 5C), although the slice thickness to separation ratio remains constant at 1/8.

Figure 5.

Slice profiles in cylindrical water phantom. The projection of the slice profile obtained by acquiring the readout direction parallel to the slice-select direction is overlaid on A) a conventionally acquired coronal image of the phantom. The slice profiles were acquired using gradient amplitudes of B) 10.4 mT/m - resulting in three 5 mm slices separated by 40 mm; and C) 5.2 mT/m - resulting in two 10 mm slices separated by 80 mm.

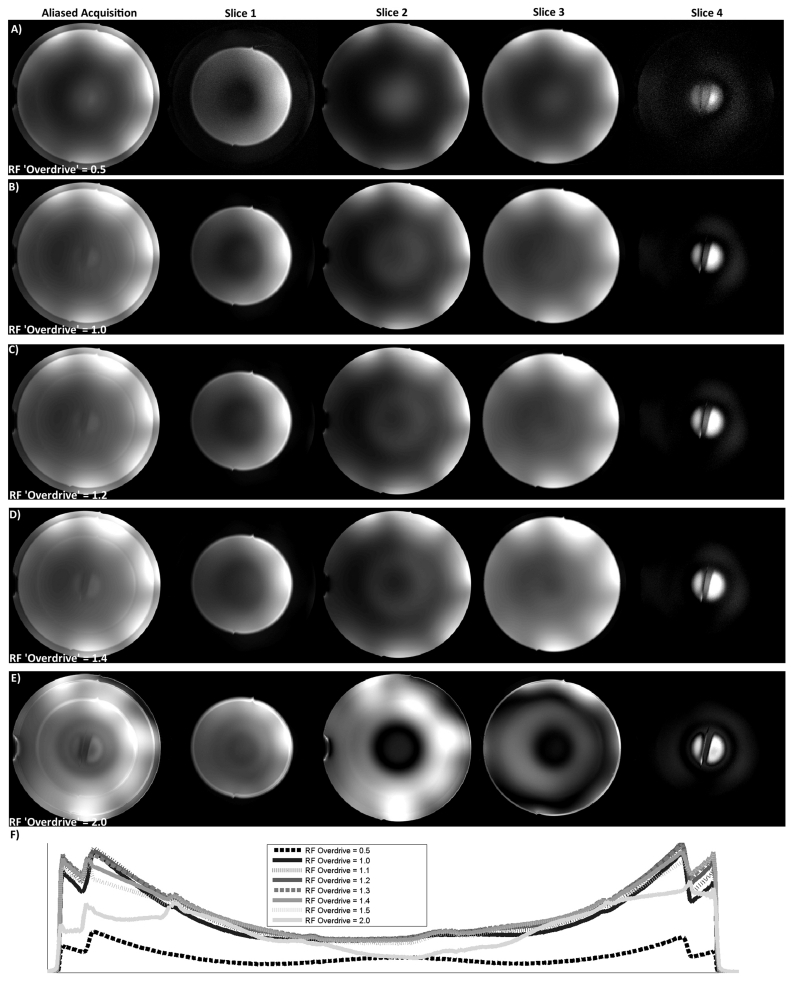
The B₁-insensitivity of the SEAMS PINS sequence was explored through experiments on a spherical water phantom (Figure 6). When the RF excitation and refocusing pulses were underpowered (Figure 6A, ODF = 0.5), the un-aliased image quality is poor, as expected. Figure 6B illustrates an image acquired with the RF amplitude set to achieve adiabatic threshold at the center of the spherical phantom, while Figures 6C and 6D illustrate the images acquired with an increase in RF amplitude of 20% and 40%, respectively (ODF = 1.2 and 1.4). As shown in Figure 6E, significant image degradation occurs with an ODF of 2.0 due to the non-adiabatic behavior of the 90° pulse and deterioration of phase-matching as the pulse-pair is overdriven (22). However, for a range of RF overdrive (up to 40%) images remain largely invariant, especially when compared to the center slice obtained through a conventional spin echo acquisition for the same range of ODFs (Figure 6, right column). This demonstrates the robust behavior of the SEAMS PINS pulse-pair in the presence of the B₁ variation typically observed in vivo at 7T. Figure 6F plots the central line projection through images obtained at the range of tested RF overdrive values. The semi-adiabatic behavior of the SEAMS PINS sequence in the spherical phantom is consistent with simulated and measured values in the cylindrical water phantom.

Figure 6.

Spherical water phantom images at different RF overdrive factors. Multiple overlapping slices obtained using SEAMS PINS (left column), 4 disentangled individual slices obtained from SEAMS PINS image (middle 4 columns), and single central slice obtained using a conventional spin echo sequence (right column) when RF pulse amplitude was set to A) 50% of adiabatic threshold (ODF = 0.5); B) adiabatic threshold at the center of the sphere (ODF = 1); C) 20% above adiabatic threshold (ODF = 1.2); D) 40% above adiabatic threshold (ODF = 1.4); and E) 100% above adiabatic threshold (ODF = 2). F) Central cross sections of slice 2 of the SEAMS PINS phantom images obtained at ODFs ranging from 0.5 to 2. These data show the robust behavior of the pulse-pair in the presence of moderate B₁ variation (typically observed over most of the cortex in vivo at 7T) when compared to a standard SE sequence. However for severe changes in B₁, as shown in F), pulse-pair behavior begins to degrade due to B₁-sensitivity of the non-adiabatic 90° pulse and deterioration of phase-matching.

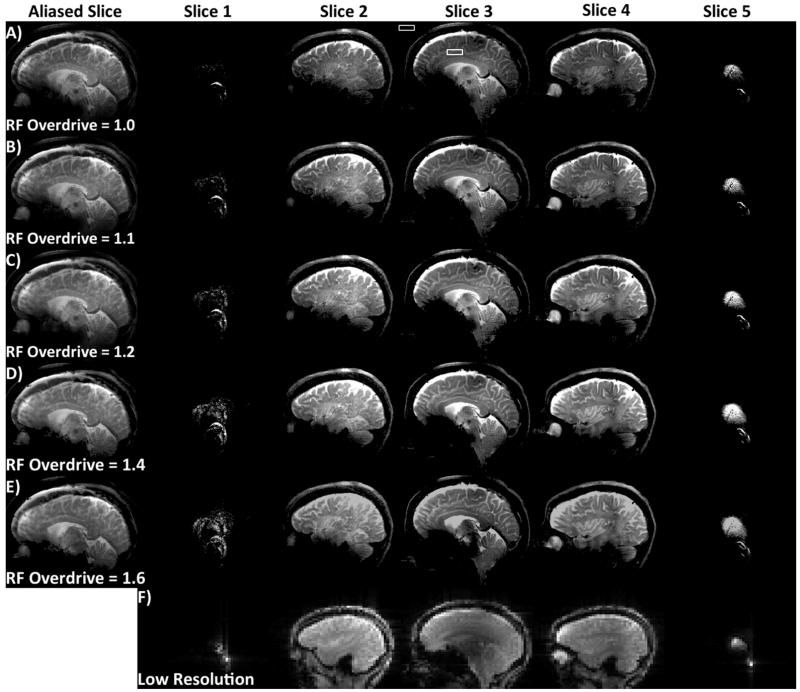
In vivo brain images obtained using the SEAMS PINS sequences are shown in Figure 7. The sum-of-squares images obtained by combining the image data from the 32 receive coils contains 5 overlapping slices (Figure 7A-E, left-most column) are shown for ODFs of 1, 1.1, 1.2, 1.4, and 1.6 in Figures 7A-E. The signal in the brain was measured in the solid white box showed in Figure 7A, and the noise measurement was taken from the region indicated by the dashed white box. The two measured values were used to compute the SNR. The same measurement, repeated in each image in the ODF experiment resulted in an SNR that ranged from a high of 48 (ODF = 1.2), to a low of 34 (ODF = 1.6). The SNR for ODF=1.0, 1.1., and 1.4 were 42, 46, and 43, respectively. The slices were disentangled using the low resolution reference scans (Figure 7F), into 5 separate slices (Figures 7, remaining columns).

Figure 7.

Reconstructed multiple sagittal human brain images acquired using the SEAMS PINS sequence. Aliased slice (left) and individual un-aliased slices (right) for an image obtained at A) adiabatic threshold, B) ODF = 1.1, C) ODF = 1.2, D) ODF = 1.4, and E) ODF = 1.6. Dotted and solid white squares (in A, Slice 3) indicate ROIs used to measure SNR. F) Low-resolution reference images obtained to estimate the coil sensitivity profile.

Discussion

The SEAMS PINS sequence is capable of producing separable multi-slice spin echo profile with improved immunity to B₁ variation when compared to conventional spin echo sequences. Simulations show that for a conventional spin echo, a 20% percent increase in B₁ results in more than 10% signal loss; in the SEAMS sequence, an increase of 41% is required to see the same level of loss. Phantom data and in vivo experiments showed that the SEAMS PINS pulse sequence provides improved B₁-insensitivity when compared to the traditional spin echo and resulted in minimal image quality variations over a 40% increase in transmit B₁, making it a valuable pulse-pair for high-field sequences. Figure 4 illustrates the window of B₁-insensitivity of the SEAMS PINS sequence. In Figures 6 and 7, phantom and in vivo images are shown over a 40% increase in RF amplitude above the adiabatic threshold. Note that B₁ insensitivity of transmission is demonstrated through the stability of the overdriven images in Figures 6 and 7. Image shading resulting from signal attenuation due to inhomogeneous B₁ reception profiles still exists; however this will only alter SNR, not contrast. When the B₁ amplitude is increased past an ODF of 1.4 to twice the adiabatic threshold (Figure 6E), both the non-adiabatic behavior of the 90° pulse and loss of phase-matching create overall signal and contrast variation. In the in vivo experiment (Figure 7), overall image quality was best when the center of the image was overdriven (ODF = 1.2 and 1.4; Figures 7D and 7E) as compared to the case in which the center of the image was at adiabatic threshold (ODF = 1.0, Figure 7A) but the off-center portions of the image were underdriven below adiabatic threshold. However, when ODF = 1.6 (Figure 7E) the center of the image begins to lose signal as the pulse-pair amplitude exceeds the adiabatic range of behavior. Deterioration of phase-matching as RF amplitude increases beyond adiabatic threshold is an inherent disadvantage of the adiabatic matched-phase single-refocused spin echo approach when compared with an adiabatic twice-refocused spin echo (28). However, the use of a second identical refocusing pulse in a twice-refocused spin echo sequence would also significantly increase the minimum achievable TE and RF power deposited by the pulse sequence. Both shortening tissue T₂ values (12) and a quadratic increase in SAR with field strength necessitate the use of single-refocused, shorter TE alternatives for spin echo imaging at 7T. The matched-phase adiabatic pulse-pair provides a low-SAR alternative for achieving a spin echo with greater immunity to B₁ than conventional spin echo pulse-pairs.

Pulse BW and sampling rate, as well as gradient amplitude and duty cycle can be manipulated in order to adjust slice thickness and slice separation achieved by the SEAMS PINS pulse-pair. For the same gradient pulse shape and amplitude, decreasing the pulse BW alters the ratio of slice thickness to slice separation, resulting in thinner slices separated by the same distance. However, a minimum RF pulse BW must be maintained in order to achieve an adiabatic 180° pulse; thus there is a lower bound on how far the ratio can be adjusted using BW. The minimum slice thickness for our in vivo SEAMS PINS acquisition was gradient slew rate limited on our whole body scanner due to PNS safety limits. This is probably also true for head-only gradient systems with higher maximum slew-rates. Nevertheless, this hardware limitation exists for all RF methods employing interleaved gradient blipping and RF sampling (i.e. 2D excitation, spectral-spatial RF pulses, etc). Given a required pulse BW and maximum gradient amplitude, thinner slices can either be obtained by reducing the RF sampling rate, resulting in a reduced slice separation, or by increasing the total duration of the pulse.

The SEAMS PINS sequence presented here uses a phase-matched 90°-180° pulse-pair to achieve a minimum TE of 40 ms, including crushers, and gradient refocusing time. In comparison, an adiabatic PINS double echo with a PINS excitation would require a minimum TE of 53 ms, assuming comparable BW, crushers, gradient limits, and RF amplifier hardware limitations. Calculation of the SEAMS PINS SAR (SAR_SEAMS) and an adiabatic twice- refocused sequence (SAR_adiaatic) results in a relative SAR ratio (SAR_seams/SAR_adiabatic) of 0.56.

The TE could be shortened further by using a shorter 90° pulse which is still designed to unwind the phase of the 180° pulse. However, using this variant of the pulse-pair would result in degradation of the slice profile in the presence of B₀ inhomogeneity. Shortening the 90° pulse can also be accomplished through shorter nulls. A consequence of this strategy is the need to increase the gradient slew rate maximum in order to achieve the same slice thickness, which may be limited by PNS constraints.

Successful separation of the multiple slices was demonstrated using a conventional readout. However, these pulses may be used to excite and separate more closely spaced slices by introducing inter-slice image shifts in the phase encoding direction using the CAIPIRINHA technique (29).

The pulse-pair may be integrated into any sequence that uses a single spin-echo. Diffusion MRI or spin echo functional MRI sequences are good candidates at high field strengths. For shorter TE, B₁-insensitive multi-slice refocusing, a self-refocused adiabatic pulse as described in (22) may also be modulated in the same way to generate a self-refocused adiabatic PINS pulse.

Conclusions

A SEAMS PINS pulse sequence utilizing matched-phase adiabatic SLR pulses to generate a multi-slice spin echo was designed, implemented, and validated in phantoms and in vivo at 7T. Improved B₁-immunity was demonstrated by the SEAMS PINS sequence (10% signal loss over 41% increase in B₁) when compared to a traditional spin echo sequence (10% signal loss over a 20% increase in B₁). Quadratic phase deposited by the adiabatic 180° pulse was successfully refocused by the 90° pulse, obviating the need for a second adiabatic 180° pulse and therefore providing a 44% lower-SAR than a comparable twice-refocused adiabatic solution. Number of slices, slice thickness and separation are fully adjustable through changes in sampling frequency and/or gradient moment.

This technique may be applied in vivo to accelerate any spin echo sequence including those used for structural imaging, diffusion weighted imaging and functional imaging, while providing improved immunity to B₁-inhomogeneity.