3D printed microfluidic circuitry via multijet-based additive manufacturing

Abstract

The miniaturization of integrated fluidic processors affords extensive benefits for chemical and biological fields, yet traditional, monolithic methods of microfabrication present numerous obstacles for the scaling of fluidic operators. Recently, researchers have investigated the use of additive manufacturing or “three-dimensional (3D) printing” technologies – predominantly stereolithography – as a promising alternative for the construction of submillimeter-scale fluidic components. One challenge, however, is that current stereolithography methods lack the ability to simultaneously print sacrificial support materials, which limits the geometric versatility of such approaches. In this work, we investigate the use of multijet modelling (alternatively, polyjet printing) – a layer-by-layer, multi-material inkjetting process – for 3D printing geometrically complex, yet functionally advantageous fluidic components comprised of both static and dynamic physical elements. We examine a fundamental class of 3D printed microfluidic operators, including fluidic capacitors, fluidic diodes, and fluidic transistors. In addition, we evaluate the potential to advance on-chip automation of integrated fluidic systems via geometric modification of component parameters. Theoretical and experimental results for 3D fluidic capacitors demonstrated that transitioning from planar to non-planar diaphragm architectures improved component performance. Flow rectification experiments for 3D printed fluidic diodes revealed a diodicity of 80.6 ± 1.8. Geometry-based gain enhancement for 3D printed fluidic transistors yielded pressure gain of 3.01 ± 0.78. Consistent with additional additive manufacturing methodologies, the use of digitally-transferrable 3D models of fluidic components combined with commercially-available 3D printers could extend the fluidic routing capabilities presented here to researchers in fields beyond the core engineering community.

Introduction

The controlled manipulation of fluids at submillimeter length scales yields significant and wide-ranging advantages for chemical and biological applications, including drug screening, quantitative cell biology, and molecular diagnostics.^1,2 Historically, the scaling of fluidic systems has primarily relied on micromachining technologies that were developed for semiconductor and microelectromechanical systems (MEMS) industries.³ Notably, “soft lithography” techniques for micro-molding and bonding elastomeric materials, such as poly(dimethylsiloxane) (PDMS), have served as the basis for the majority of current microfluidic systems.^4–6 In response to increasing demands for external (i.e., “off-chip”) equipment and regulation to execute “on-chip” fluidic routines,^7–9 investigators have drawn inspiration from integrated electronic circuitry to develop integrated microfluidic circuits (IFCs) capable of autonomous functionalities.¹⁰ In particular, researchers have demonstrated IFCs comprised of two-layer fluidic capacitors,¹¹ three-layer fluidic diodes^11,12 and transistors,¹² and five-layer fluidic transistors that enable pressure-based gain¹³ for biochemical applications, including autotitration, immunodetection, and cellular loading, culture, and screening.^10–15 At present, continued progress remains hindered by a wide range of limitations inherent to conventional IFC fabrication protocols: (i) clean room-based wafer processing can be exceedingly cost, time, and labor-intensive (with added difficulties associated with user access), (ii) manual procedures for aligning and assembling multiple layers can adversely impact device precision and reproducibility, and (iii) the intrinsic restriction of monolithicity renders relatively common features of macroscale fluidic components (e.g., circular channels with varying diameter, non-planar physical architectures, etc.) challenging or impossible to recreate in microscale domains.^16–19 These limitations not only limit the freedom with which one can design microscale structures, but also vastly increase the design cycle time associated with implementing desired device modifications.^20–22 Consequently, the potential for building microfluidic systems by means of additive manufacturing has gained increasing interest in recent years.

Additive manufacturing – widely referred to as “three-dimensional (3D) printing” – encompasses three general approaches for fabricating 3D structures via point-by-point and/or layer-by-layer processes: (i) extrusion-based deposition, (ii) stereolithography (SLA), and (iii) multijet modelling (MJM). Although extrusion or nozzle-based methods represent the predominant technique for generating submillimeter-scale cellular constructs,²³ for microfluidic applications, the innate trade-off between nozzle size and fabrication time has restricted its use to those in which fugitive inks (i.e., sacrificial materials) are deposited, casted, and removed.^24–26 A key characteristic of IFCs is that, with the exception of fluidic resistors, fluidic circuit components require both static (i.e., fixed) and dynamic (i.e., deformable or movable) physical elements. This condition further renders IFC construction via extrusion-based approaches impractical. Conversely, a number of SLA-based microfluidic modules – primarily resistor-like components (e.g.,, fluidic channels, junctions, mixers, and ports) – have been demonstrated for applications including microdroplet generation and cell culture.^27–29 Recently, investigators have extended these methods to enable SLA-fabricated moving valves,^30,31 with Au et al. presenting peristaltic pump and cell perfusion chamber IFCs comprised of three and four integrated fluidic valves, respectively.³¹ Although SLA technologies for microfluidic device fabrication are improving, current resolutions remain on the order of hundreds of microns, and only one material can be 3D printed.^27–31 The latter restriction prevents the use of sacrificial support materials, which are required for constructing highly-complex physical geometries, overhanging features, and free-floating structures. In contrast, MJM approaches enable resolutions on the order of tens of microns as well as numerous materials – including sacrificial support materials – to be 3D printed simultaneously.^32,33 Despite these advantages, MJM has not yet been utilized to construct IFCs comprised of both static and dynamic internal elements.

Here we investigate the use of MJM methodologies for the design and construction of key fluidic circuit components, including 3D printed fluidic capacitors, diodes, and transistors (with gain-customization). Both theoretical and experimental approaches are employed to elucidate the operating characteristics and key tunable parameters of these fluidic components. In addition, we examine the potential for 3D printing multiple fluidic operators simultaneously as fully-integrated fluidic circuits, including full-wave fluidic rectifiers (comprised of four fluidic diodes) as well as single-input-actuated multi-fluid perfusion chambers (comprised of four distinct fluidic transistors). The theoretical and experimental results provide a necessary foundation for future MJM-based IFCs, which offer a promising means to realize large-scale fluidic processors capable of sophisticated functionalities.

Experimental

Fluidic operators via multijet modelling (MJM) concept

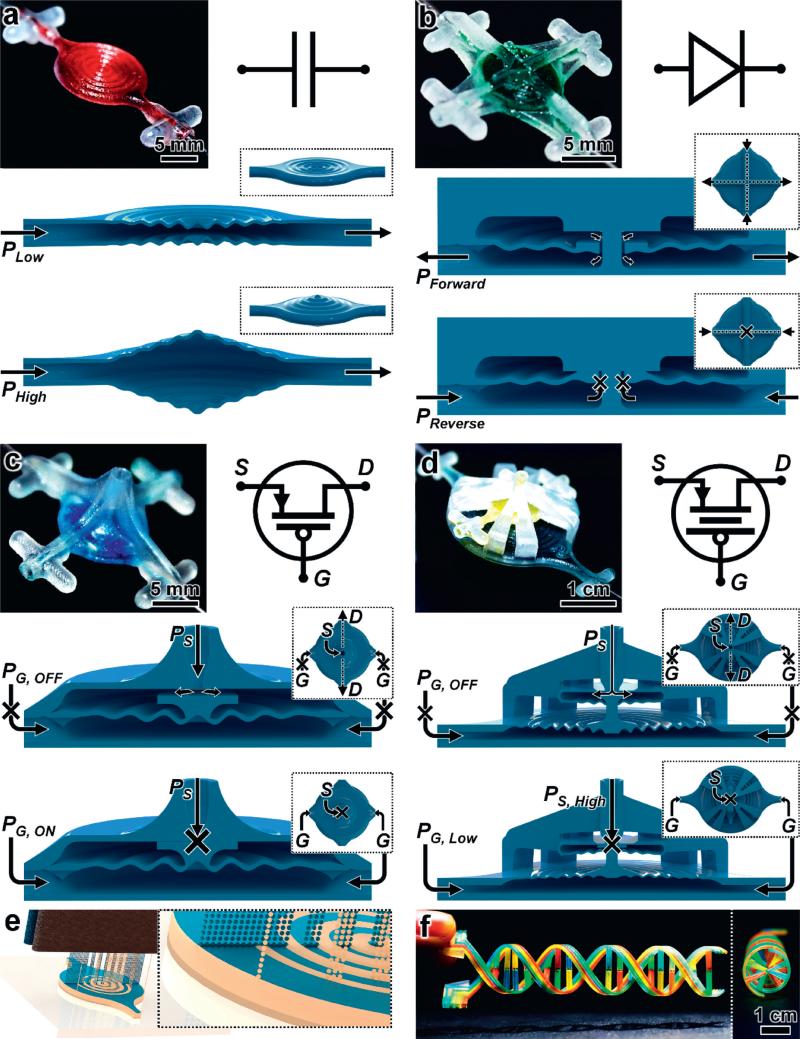
We designed a fundamental class of microfluidic operators – including fluidic capacitors (Fig. 1a), fluidic diodes (Fig. 1b), and fluidic transistors with gain-customization (Fig. 1c and d) – with respect to the MJM 3D printing process (Fig. 1e). MJM entails layer-by-layer, parallel inkjet deposition and photocuring of photoplastic resin and sacrificial support materials simultaneously (Fig. 1e; ESI† Fig. S1; Movie S1†). The inclusion of a support material that can be removed after completion of the MJM process enables fluidic devices with highly-complex physical architectures to be readily constructed (e.g.,, Fig. 1f).

Fig. 1.

3D printed fluidic circuit components via multijet modelling (MJM). (a–d) Fabrication results, analogous electronic circuit symbols, and conceptual operating principles for 3D printed: (a) fluidic capacitors, (b) fluidic diodes, (c) fluidic transistors, and (d) enhanced-gain fluidic transistors. The fluidic components operate based on pressure (P) inputs. The 3D fluidic transistors (c, d) are analogous to p-channel MOSFET transistors, with gate (G) regulation of source (S) to drain (D) fluid flow (Q_SD). (e) Conceptual illustration of the MJM process for simultaneous inkjet deposition of photoplastic (blue) and sacrificial support (beige) materials. (f) A 3D printed DNA-inspired architecture comprised of eight fluidic channels (750 μm in diameter) filled with discrete solutions of dye-coloured fluid.

To explore possible benefits facilitated by such structural complexity, we designed 3D fluidic capacitors with varying diaphragm designs, such as the damped sinusoidal cross-section shown in Fig. 1a as well as an undamped sinusoidal cross-section and a planar (i.e., flat) cross-section. The 3D fluidic capacitors include parallel diaphragms that deform outward in response to increasing input pressure in order to store larger volumes of fluid within the component. As the input pressure is decreased, the diaphragms restore to their initial, undeformed states, thereby displacing the excess (i.e., stored) fluid volume (Fig. 1a).

We also designed a 3D fluidic diode (i.e., passive fluid flow rectifier) in which the diaphragm element is adapted with a circular aperture in the center (Fig. 1b). This opening allows for fluid to flow from the top input ports, through the center orifice, and then out of the component via the bottom output ports. In contrast, reversing the flow polarity induces diaphragm deformation that promotes physical contact with the static top surface, thereby obstructing the flow of fluid through the component (Fig. 1b).

To achieve transistor-like functionalities, we integrated a piston feature into the center of the diaphragm (Fig. 1c and d). Similar to a p-channel MOSFET, the absence of a gate input – i.e., a gate pressure (P_G) – facilitates unobstructed flow from the source input to the drain outputs. The magnitude of this source-to-drain fluid flow (Q_SD) can be actively regulated by modulating P_G with respect to the source pressure (P_S) in order to physically restrict the source channel output with the top surface of the piston element via diaphragm deformation (Fig. 1c). One significant feature of electronic transistors is gain – a property that allows for a small gate input to have a large effect on source-to-drain flow. To enable the fluidic analogue of pressure gain (A_P):¹³

$$A_P=\frac{P_{\mathrm{S}}}{P_{\mathrm{G}}},$$

we designed a 3D fluidic transistor architecture in which the source-to-drain region diaphragm is connected to a gate region diaphragm through an extended piston element (Fig. 1d). Because the force on the blocking piston is roughly proportional to the product of the region pressure times the corresponding diaphragm area, a lower P_G can overcome a higher P_S to actuate the piston and restrict Q_SD.

3D modelling and theoretical simulations

To build the 3D models for all of the 3D fluidic circuit components in this work, we used the computer-aided design (CAD) software, SolidWorks (SolidWorks Corp., Waltham, MA). We also designed female port components (with side protrusions to support manual handling) to enable chip-to-world interconnects with male catheter couplers (#SP20/12, Instech Laboratories, Plymouth Meeting, PA), which can be connected to external tubing or to other 3D printed components via additional integrated ports. We assembled the 3D CAD models of the ports, components, and systems within the Solidworks software, and exported the assemblies to the STL format – a standard file type for 3D printers.^28,29 We rendered all of the conceptual illustrations using the PhotoView 360 extension in SolidWorks.

We imported the 3D CAD models into the commercial finite element analysis (FEA) software, COMSOL Multiphysics version 4.3a (COMSOL, Inc., Palo Alto, CA), and simulated experimental conditions. We performed large deformation fluid–structure interaction (FSI) simulations. To ensure adequate resolution in topologically sensitive regions of large deformations and small gaps, we used a first-order adaptive finite element mesh. In addition, we designed the input conditions to ensure simulation termination upon mesh intersection (e.g.,, the top surface of the transistor piston contacting the source output channel) in order to avoid topological changes.

We employed the arbitrary Lagrangian–Eulerian (ALE) method to couple the fluid flow Eulerian description with a Lagrangian description of linear-elastic solid deformation. The hydrodynamics equations assuming laminar and incompressible flow were solved using pressure inlet and outlet boundary conditions, while all other boundaries were set to have no-slip conditions. The material properties of the 3D printed photocurable plastic material, VisiJet M3 Crystal (3D Systems, Rock Hill, SC; ρ = 1.02 × 10³ kg m⁻³; E = 1.46 GPa), were used to perform all of the theoretical simulations. For the simulations of the 3D fluidic diode and fluidic transistor, we modelled water (ρ = 10³ kg m⁻³; η = 10⁻³ Pa s) as the input fluid. For the 3D fluidic transistor simulations, solid deformation of the 3D printed material was further determined subject to fluid boundary pressures and an applied pressure boundary load emulating the transistor gate pressure. These assumptions allowed for a steady-state solution for each parameterized fluid and gate pressure.

MJM-based fabrication

All of the IFC components and systems in this paper were built via the MJM additive manufacturing process (Fig. 1e) using ProJet 3000HD 3D printers (3D systems) in the Center for Interdisciplinary Biological Inspiration in Education and Research (CiBER) and the Center for Information Technology Research in the Interest of Society (CITRIS) Invention Lab at the University of California, Berkeley. We imported the 3D CAD models of the fluidic circuit components and systems (in STL format) into the ProJet Accelerator software (3D systems) under the “Ultra High Definition” mode, which converts the models into single-layer slices (32 μm in height). The system uses piezo printhead technology to deposit (spray) either photocurable plastic resin or casting wax materials layer-by-layer using two different printheads: one for the photoplastic build material (Fig. 1a – blue) and one for the sacrificial wax support material (Fig. 1a – beige). Each layer is exposed to UV for photocuring, and the surface is milled to hold tolerance. This process is repeated until fabrication completion. For the components presented in this work, the average build time ranged from approximately four to six hours (ESI† Fig. S1a; Movie S1), with structure height (i.e., the total number of discrete layers) being the critical factor affecting the overall print time. Following completion of the 3D printing process, the components typically adhered to the aluminium build plate (ESI† Fig. S1b–d), which was removed from the printer and placed on an ice pack for five minutes. The low temperature allowed for the aluminium build plate to shrink slightly relative to the components, resulting in the 3D printed devices (including the sacrificial wax support material) detaching from the aluminium substrate (ESI† Fig. S1e).

Following the 3D printing process, we developed and employed a protocol to remove the residual wax support material from the exterior and interior of the 3D printed components. Initially, we placed the components in an oven heated to 80 °C for ten minutes to remove (i.e., melt) the bulk of the exterior wax. Next, we immersed the devices in a bath of 100% food grade mineral oil (Bayes 160-2, Lab-Clean, Los Alamitos, CA) at 80 °C for three minutes to liquefy the internal wax. We then inputted hot mineral oil through the components using a syringe to displace the internal residual wax. Lastly, we used pressurized air to evacuate the remaining mineral oil and allowed the components to dry. This process necessitated that each 3D fluidic circuit component and system be designed in consideration of the wax removal process. This was accomplished by ensuring that each component was designed with a symmetrically-placed outlet port to complement each input port, thereby allowing for simplified wax removal processing. For cases in which the added ports were superfluous to component functionality (e.g.,, for the 3D fluidic diode and transistor designs), we sealed such ports using catheter plugs (#SP20/12, Instech) after the sacrificial wax removal process. ESI† Fig. S1f–i show 3D printed fluidic circuit components following the wax removal process and then filled with dye-coloured fluids, corresponding to the: (f) 1 cm-in-diameter (left) and 2 cm-in-diameter (right) fluidic capacitors, (g) fluidic diode, (h) fluidic transistor without gain-enhancement, and (i) fluidic transistor with gain-enhancement. ESI† Fig. S2 shows SEM micrographs of fabrication results.

Experimental setup and analysis

We used the MAESFLO system (Fluigent, Paris, France), which includes both the Microfluidic Flow Control System (MFCS) and the FLOWELL microfluidic flow sensor, and the Sensirion SLI-1000 flow sensor to regulate the input pressures while simultaneously monitoring the flow rates of DI water through the 3D printed devices. We connected all of the fluidic components to the Fluigent system and flow sensors via catheter couplers (Instech) and Tygon microbore tubing (#06420-03, Cole Parmer, Vernon Hills, IL). We conducted all experiments under room temperature environment (20–25 °C). To examine the performance of the 3D printed fluidic capacitor designs, we connected the input port to the Fluigent system and sealed the outlet of the capacitor using a catheter plug (Instech) during testing. Using the Fluigent MAESFLO software, we incrementally increased the pressure within the fluidic capacitor. Once the pressure stabilized at each value, we measured the width at the center of the fluidic capacitor diaphragm using callipers. The corresponding deformations were extrapolated from the quantified values.

For experimental testing of the 3D printed fluidic diodes, we connected one of the top channel ports and one of the bottom channel ports to independently-controlled pressure sources of the Fluigent system. We sealed the remaining two component ports. To monitor the direction and magnitude of fluid flow, we connected the Fluigent and Sensirion flow rate sensors in series with the flow path, with the Sensirion sensor placed adjacent to the bottom channel port of the fluidic diode. For the forward flow case, the pressure corresponding to the top channel input port was greater than that of the bottom channel input port, resulting in fluid flow from the top channel port, through the diode, and out the bottom channel port. In contrast, the reverse flow case entailed a relatively larger pressure input to the bottom channel port compared to the top channel input, resulting in the potential for fluid to flow with the opposite polarity (from the bottom to the top of the fluidic diode). To determine the relationship between the directional pressure input and the resulting flow behavior, we wrote and used a computer-controlled pressure script in the Fluigent software, which linearly varied the two pressure inputs up to 30 kPa, while the resulting fluid flow through the fluidic diodes was electronically recorded by the flow rate sensors. Similarly, for the half-wave rectifier test of the 3D printed fluidic diode, we wrote a pressure script designed to apply repeating sinusoidal pressure sweeps – corresponding to a pressure gradient of approximately 30 kPa – to both the top and bottom channel ports (180° out of phase), while simultaneously recording the flow polarity and magnitude using the flow sensors. Vacuum (i.e., negative pressure) was not used during any of the fluidic diode-based experiments. All values reported with negative polarity for the 3D printed fluidic diode refer to positive pressures or flow rates corresponding to the designated reverse direction. Quantification of the experimental diodicity (Di) was assessed for non-transitional regions (i.e., P > 5 kPa corresponding to both the positive and negative flow directions).

To test the functionality of both of the 3D printed fluidic transistor designs (i.e., with and without gain-enhancement), we connected the source input port and a gate input port to independently-controlled pressure sources of the Fluigent system. We connected one of the drain output ports to the Fluigent and Sensirion flow rate sensors in series and sealed the remaining two component ports. To examine the combinational effects of both P_S and P_G on the magnitude of Q_SD, we wrote and used a computer-controlled pressure script in the Fluigent Scite software. We designed the script to sweep through a linear range of P_S inputs of up to 50 kPa for each distinct input P_G of up to approximately 55 kPa and 25 kPa for the 3D fluidic transistor without and with gain-enhancement, respectively. The resulting Q_SD through the fluidic transistors was electronically recorded during the testing process by the flow sensors.

We experimentally investigated the full-wave fluidic rectification potential of both planar and vertically-stacked IFC architectures through similar procedures to those used for the half-wave rectification tests of the 3D printed fluidic diode. We connected two supply ports to independently-controlled pressure sources of the Fluigent system. We connected the Fluigent and Sensirion flow sensors in series across two output flow ports and sealed the remaining eight ports. We designed and wrote a pressure script to apply repeating sinusoidal input pressures to both of the supply ports (180° out of phase), while simultaneously recording the flow polarity and magnitude across the two output ports using the flow sensors.

For testing of a P_G-actuated multi-fluid perfusion controller, we connected a single pressure source from the Fluigent system to four discrete supplies of dye-coloured DI water, which were each connected to distinct source input ports corresponding to four parallel fluidic transistors. We also connected a separate pressure source from the Fluigent system to the P_G input port and then sealed the remaining five ports. We set P_S = 1 kPa, and then varied P_G from 0 kPa to 50 kPa while optically monitoring the proportion of each fluidic stream within the flow chamber. We used the freely-available software, ImageJ (NIH, Bethesda, MD), to quantify the average fluidic stream proportions for testing of the multi-flow controller.

For each component design, approximately three experiments were performed on three distinct 3D printed devices. Using the Python 2.7 programming language, we designed and wrote code to process, quantify, and plot the experimental results. Quantified experimental results are presented in the text as mean ± standard deviation.

Results and discussion

3D printed fluidic capacitors

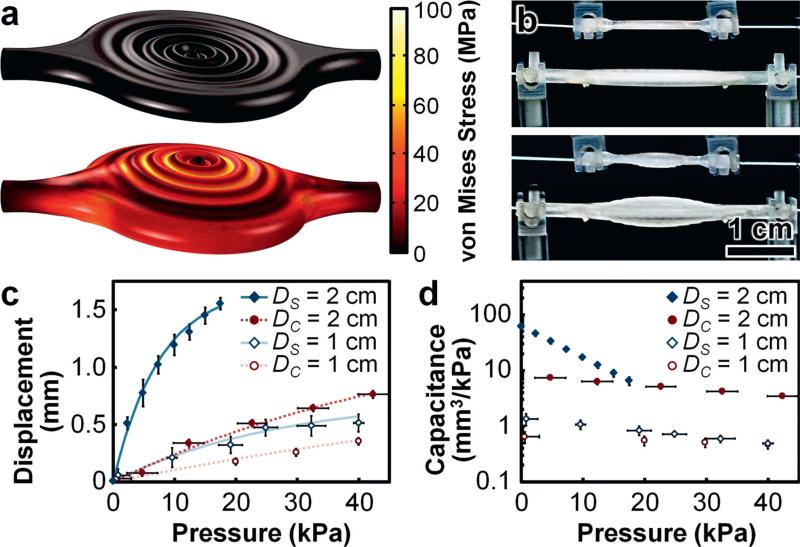
We performed theoretical simulations of 3D fluidic capacitors with different diaphragm designs to elucidate the effects of varying physical characteristics on fluidic component functionalities (Fig. 2a; ESI† Fig. S3; Movie S2). The simulation results revealed three primary trends. Firstly, both of the 3D fluidic capacitors with sinusoidal cross-sectional designs exhibited larger displacements in response to applied pressures compared to the fluidic capacitor with a planar cross-sectional design (Fig. 2a; ESI† Fig. S3a–c). Secondly, these results corresponded to the undamped sinusoidal design yielding the largest volume storage capacities in response to applied pressures, with the damped sinusoidal design exhibiting the next-largest volume changes, and the planar design revealing the smallest volume changes of the 3D fluidic capacitors modelled (ESI† Fig. S3d). Lastly, the simulation results revealed that the undamped sinusoidal design exhibited the largest magnitudes of maximum von Mises stress in response to applied pressures compared to the planar and damped sinusoidal designs, which yielded relatively similar results for maximum von Mises stress (ESI† Fig. S3e). Thus, for cases in which both diaphragm mechanical integrity and fluidic storage capacity are critical requirements, the theoretical simulation results suggest that the damped sinusoidal cross-sectional design is best suited among those examined (Fig. 2a; ESI† Fig. S3; Movie S2).

Fig. 2.

3D fluidic capacitor results. (a) Theoretical simulation results for physical deformation and von Mises stress distributions for the 3D fluidic capacitor (1 cm-in-diameter) under 0 kPa (top) and 400 kPa (bottom) applied pressures (see also ESI† Fig. S3; Movie S2). (b) 1 cm-in-diameter and 2 cm-in-diameter 3D printed fluidic capacitors with input air pressures of 0 kPa (top) and 25 kPa (bottom). (c, d) Experimental results for (c) diaphragm displacement and (d) capacitance versus input air pressure. D_S and D_C denote diameters of 3D printed fluidic capacitor diaphragms with damped sinusoidal and planar (control) cross-sectional designs, respectively. Error bars denote standard deviation.

Experimental testing demonstrated that increasing the diaphragm diameter drastically improved the diaphragm displacement, volume change, and capacitive performance at lower pressures (Fig. 2b–d). In addition, consistent with the theoretical simulations, the experimental results also revealed that the 3D printed fluidic capacitors with damped sinusoidal cross-sections out-performed their planar counterparts with respect to applied pressure and diameter size (Fig. 2c and d). These trends indicate architecturally complex, yet operationally advantageous physical characteristics through which one can enhance the performance of integrated, deformable diaphragms – critical dynamic elements of numerous IFC components. These results also provide a basis for informing the design of additional IFC components comprised of integrated and/or adapted diaphragm elements.

3D printed fluidic diodes and diode-based circuits

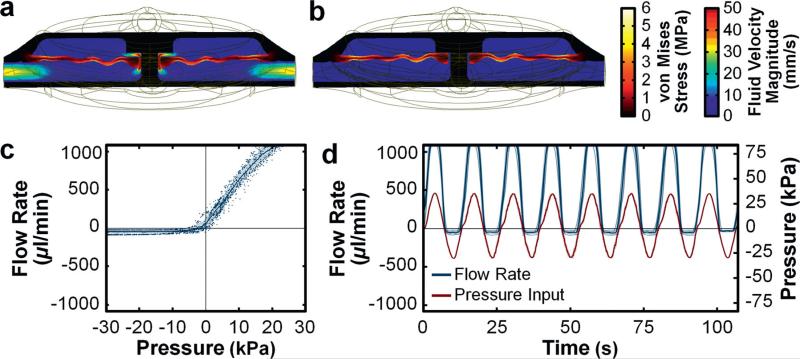
Theoretical simulations of the dual structural and fluidic functionalities of the 3D fluidic diode revealed fundamental polarity-based differences in flow behavior (Fig. 3a and b; ESI† Fig. S4; Movie S3). For the forward flow case, increasing the magnitude of the input pressure in the forward (top-to-bottom) direction (P_Forward) resulted in corresponding increases in fluid flow through the diode component (Fig. 3a; ESI† Fig. S4). For low magnitudes of input pressure in the reverse (bottom-to-top) direction (P_Reverse), the fluid flow rates through the diode were similar to those of the forward flow case (ESI† Fig. S4). As the magnitude of P_Reverse increased, however, the diaphragm element approached the top surface of the fluidic diode, thereby increasing the fluidic resistance through the component and restricting reverse fluid flow (Fig. 3b; ESI† Fig. S4). The simulation results revealed a maximum reverse flow rate of 77.28 μl min⁻¹ for P_Reverse = 6.02 kPa (ESI† Fig. S4; Movie S3). For P_Reverse > 6.02 kPa, the reverse flow rate approached 0 μl min⁻¹ (Fig. 3b; ESI† Fig. S4; Movie S3).

Fig. 3.

3D fluidic diode results. (a, b) Cross-sectional views of theoretical simulation results for fluid velocity field and von Mises stress distributions of the 3D fluidic diode for (a) P_Forward = 15 kPa, and (b) P_Reverse = 15 kPa (see also ESI† Fig. S4; Movie S3). (c) Experimental results for directional fluid flow versus pressure. (d) Experimental results for half-wave fluidic rectification. Error bands denote standard deviation; negative experimental pressures/flow rates denote positive pressure/flow in the reverse direction.

Although simulation results of 3D fluidic diode performance revealed fully-blocked fluid flow at higher reverse pressures (Fig. 3b; ESI† Fig. S4; Movie S3), we did not discern such behavior during experimentation (Fig. 3c). Rather, we observed a degree of residual fluid flow in response to reverse input pressures. For fluidic diodes, a non-dimensional figure of merit to account for such phenomena is quantified as:

$$\mathrm{Di}=\frac{R_{\text{Reverse}}}{R_{\text{Forward}}},$$

where R denotes the hydrodynamic resistance impeding either forward (top-to-bottom) flow or reverse (bottom-to-top) flow. The experimental results for the polarity-based difference in flow behavior (Fig. 3c) yielded a Di of approximately 80.6 ± 1.8. In addition, we investigated an additional metric of fluidic diode functionality: its ability to serve as a half-wave rectifier. In response to an oscillating input pressure, the 3D printed fluidic diode exhibited significant forward bias of the flow polarity (Fig. 3d). After approximately 75 periods of repeated forward and reverse pressure cycling of over 25 kPa, the 3D printed fluidic diodes tested did not exhibit variations in flow performance, which suggests that the 3D printed material has sufficient tolerance for typical microfluidic operations.³⁴

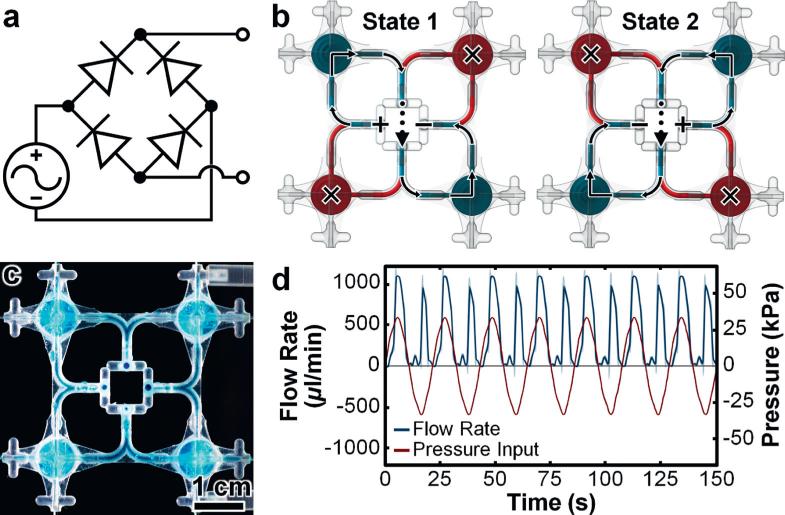
The integration of multiple fluidic components as parts of larger fluidic networks represents an essential condition of IFCs. To assess this capability for MJM-based systems, we designed a full-wave bridge rectifier IFC with four fluidic diodes (Fig. 4a). In contrast to IFC configurations in which fluidic channels are fully-embedded within rectangular blocks (e.g.,, conventional soft lithography-based devices), in this work, we designed IFCs using suspended piping approaches to minimize material requirements (Fig. 4b and c). Through two principal states, the 3D full-wave fluidic rectifier affords a distinguishing operational characteristic: the ability to maintain a consistent output flow polarity regardless of the input polarity (Fig. 4b; ESI† Fig. S5; text). Experiments with the 3D printed full-wave fluidic rectifier (Fig. 4c) revealed such phenomena, with positively-biased output flow polarities for both positive and negative supply input polarities (Fig. 4d). After approximately 45 repeated cycles of oscillating input pressure, the output flow behaviour – results that stem from the simultaneous operations of the four integrated 3D printed fluidic diodes – did not indicate undesired fluctuations (e.g.,, flow disparities due to internal leakage). We also designed a 3D full-wave fluidic rectifier with a vertically-stacked architecture (ESI† Fig. S6) to examine highly non-planar IFC configurations. The vertically-stacked IFC also promoted positively-biased output flow in response to both input polarities; however, the experimental results revealed increased variations in the flow profile compared to the planar configuration (Fig. 4d; ESI† Fig. S6b).

Fig. 4.

3D full-wave fluidic rectifier. (a) Circuit diagram. (b) Conceptual illustrations of the two primary flow states (see also ESI† Fig. S5). Red and teal coloured fluids denote obstructed and unobstructed flow, respectively. (c) Fabrication results. (d) Experimental results for full-wave fluidic rectification. Error bands denote standard deviation; negative pressures/flow rates denote positive pressure/flow in the reverse direction.

3D printed fluidic transistors and transistor-based circuits

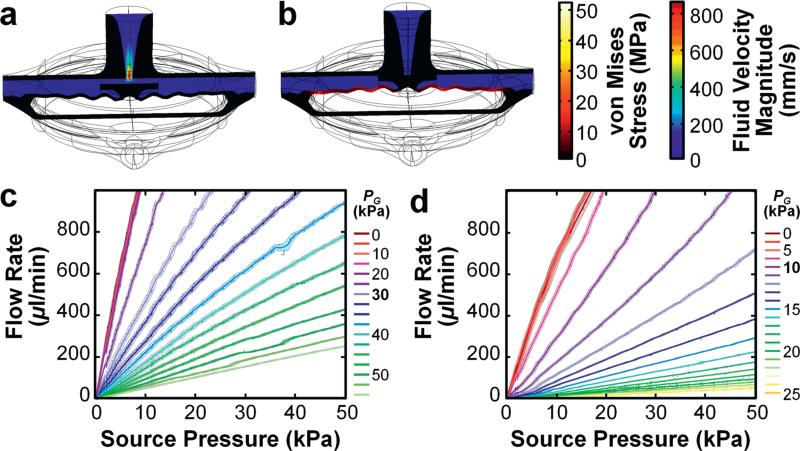
Microfluidic valving represents the most widely-employed operation in IFCs.³ To determine the potential efficacy of MJM-based fluidic transistors to execute such functions as well as provide insight into their structural, fluidic, and pressure-based performance, we simulated two distinct types of input conditions for the 3D fluidic transistor without gain-enhancement: (i) constant P_S input increments with varying P_G inputs (Fig. 5a and b; ESI† Fig. S7a and b; Movie S4), and (ii) constant P_G input increments with varying P_S (ESI† Fig. S7c). The theoretical simulations included the application of vacuum pressure to the gate (i.e., P_G < 0), which revealed that significantly increasing the vacuum pressure did not greatly enhance Q_SD, with a difference in Q_SD of 4.97% from P_G = 0 to P_G = −200 kPa (Fig. 5a; ESI† Fig. S7a and c; Movie S4). In contrast, for P_G > 0, the simulation results revealed that Q_SD decreased dramatically with increasing P_G – a consequence of the piston element's top surface approaching the source output, which physically increases the source-to-drain hydrodynamic resistance to obstruct Q_SD (Fig. 5b; ESI† Fig. S7b and c; Movie S4).

Fig. 5.

3D fluidic transistors results. (a, b) Cross-sectional views of theoretical simulation results for fluid velocity field and von Mises stress distributions of the 3D fluidic transistor for P_S = 30 kPa and (a) P_G = 0 kPa, and (b) P_G = 200 kPa (see also ESI† Fig. S7; Movie S5). (c, d) Experimental results for source-to-drain fluid flow (Q_SD) versus P_S for varying P_G for 3D printed fluidic transistors designed (c) without and (d) with pressure-gain enhancement. All error bars/bands denote standard deviation.

We experimentally tested the 3D printed fluidic transistor and its enhanced-gain counterpart to examine the effects of varying P_S and P_G inputs on Q_SD (Fig. 5c and d). The 3D printed fluidic transistor without and with gain enhancement exhibited activation threshold pressures (P_G,Th) of 15 kPa and 5 kPa, respectively, prior to which Q_SD appeared independent of P_G. For P_G > P_G,Th, increasing P_G decreased Q_SD, with the enhanced-gain design supporting reduced flow rates at comparatively lower P_G inputs. Quantified results revealed A_P of 0.87 ± 0.23 and 3.01 ± 0.78 for the fluidic transistor without and with gain enhancement, respectively (Fig. 5c and d). Although both the simulation (Fig. 5a and b; ESI† Fig. S7; Movie S4) and experimental results (Fig. 5c and d) revealed P_G-regulation of Q_SD, we did not observe fluidic phenomena analogous to saturation behavior of electronic transistors (e.g.,, a constant-flow region at higher P_S inputs). Thus, an important caveat to the transistor analogy is that the 3D printed fluidic transistors exhibit operating characteristics of p-channel MOSFETs biased in the triode region.

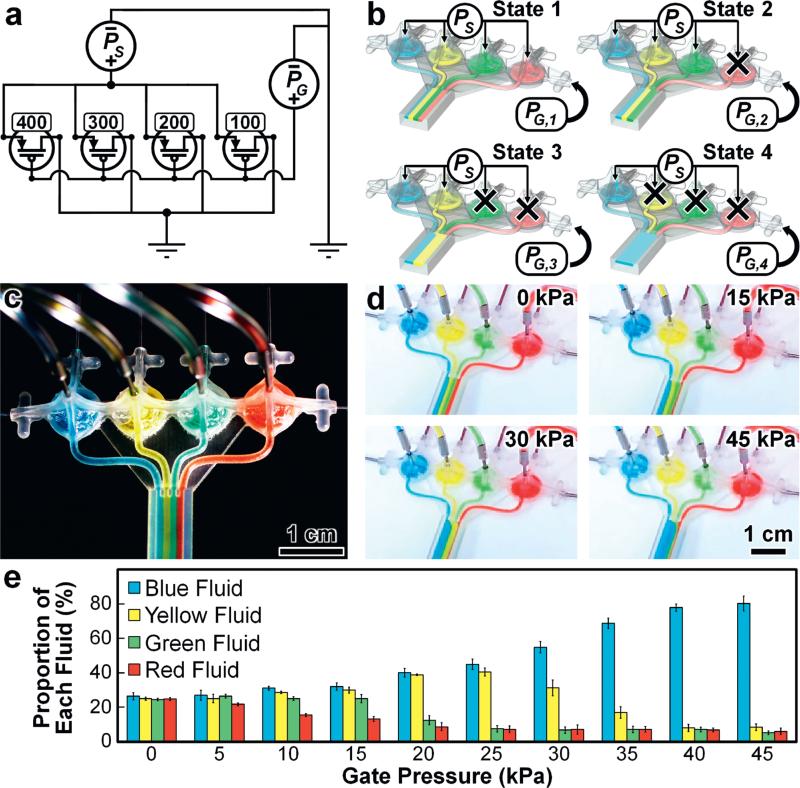
One of the critical barriers to IFC practicality and adoption is the “tyranny of microfluidic interconnects” – a characteristic description that refers to the condition associated with conventional approaches that increasing the number of independently operated fluidic valves demands an increasing number of distinct, off-chip control inputs.¹⁰ To investigate the potential to bypass such limitations (and thereby enhance on-chip automation) via the facile physical tunability afforded by MJM-based IFC components (ESI† Fig. S8), we designed a multi-fluid perfusion controller IFC that utilizes a single P_G input to regulate four distinct fluidic transistors (Fig. 6a). The four 3D fluidic transistor designs include differing relaxed state distances between the piston element's top surface and the source outlet (D_PS; ESI† Fig. S8d), corresponding to D_PS dimensions of approximately 100 μm (red), 200 μm (green), 300 μm (yellow), and 400 μm (blue) (Fig. 6a–c). A uniform and constant P_S is applied to all four discrete fluidic streams while the single P_G input is increased to sequentially restrict Q_SD in specified 3D fluidic transistors based on each D_PS design. Experimental results for the 3D printed multi-flow controller corresponding to the four key fluidic states are presented in Fig. 6d (see also ESI† Movie S5). Quantified results for the proportions of each fluidic stream in response to varying P_G suggest effective regulation of multiple fluidic profiles via a single gate input control; however, the data reveal a degree of leakage flow through ‘closed-state’ components for all values of P_G tested (Fig. 6e; ESI† Movie S5).

Fig. 6.

3D P_G-actuated multi-flow controller. (a) Circuit diagram. Numeric values denote the relaxed state distance between the top surface of the piston element and the source outlet for each fluidic transistor (D_PS; ESI† Fig. S8d). Units are in μm. (b) Conceptual illustrations of the four primary flow states (P_G,1 < P_G,2 < P_G,3 < P_G,4; P_S = constant). Ports without arrows are sealed during device operation. (c) Fabrication results. (d) Experimental results for four distinct fluidic streams under constant P_S = 1 kPa and varying P_G (see also ESI† Movie S6). (e) Quantified fluidic stream proportions for constant P_S = 1 kPa and varying P_G. All error bars/bands denote standard deviation.

Theoretical versus experimental performance

One of the primary differences between the theoretical simulations and experimental results for the MJM-based 3D fluidic components was the blocking efficacy. Specifically, we found that the ability to fully inhibit fluid flow through the 3D printed fluidic diode and transistor components – behaviour predicted by the simulations (Fig. 3a and b; 5a and b; ESI† Fig. S4; S7b and c) – was not evident during experimentation (Fig. 3c and d; 5c and d). Instead, we consistently observed residual fluid flow during experimental testing (Fig. 3c and d; 5c and d; 6d and c; ESI† Movie S5) – a phenomenon that is analogous to leakage current associated with electronic circuit components. This result is likely a by product of the current resolution of the MJM process, which produced components with a degree of surface roughness that was not reflected in the ideal geometries modelled. Specifically, SEM micrographs of fabricated results revealed in and out-of-plane resolutions of approximately 32 μm, with surface roughness of ±95 μm in-plane and ±31 μm out-of-plane (ESI† Fig. S2). Such non-planar microtopography would physically prevent the formation of the complete seals between parallel surfaces observed in the theoretical models. At present, the magnitude by which similar issues also impact fluidic components constructed via alternate additive manufacturing technologies (e.g.,, SLA) has not yet been investigated. Thus, it is unclear whether the observed leakage flow is distinctive to MJM-based components specifically or 3D printed fluidic components in general. To alleviate such issues, post-processing procedures (e.g.,, surface treatments) could be developed and implemented to reduce surface irregularities. This issue could also be mitigated by improvements in MJM resolution – an advancement that would support further scaling of 3D printed IFCs as well.

In addition to the fluidic blocking behaviour, we also observed a second notable difference between the simulation and experimental results. The experimental testing revealed that the fabricated 3D printed fluidic components exhibited far greater mechanical flexibility than that predicted from the theoretical simulations. One benefit of this flexibility was that the diaphragm displacement for the 3D printed fluidic capacitors was approximately three times greater during experimentation compared to the displacements predicted by the simulations, with respect to the input pressures (Fig. 2a and c; ESI† Fig. S3c). This result is also likely due to current MJM resolutions as potential fabrication inaccuracies, such as diaphragm elements constructed thinner in parts than the designed 150 μm thickness (ESI† Fig. S2; S8), could lead to enhanced flexibility compared to the ideal models used for the theoretical simulations.

Conclusions

A number of emerging additive manufacturing technologies afford unprecedented levels of physical versatility at submillimeter length scales. In this work, we examined the use of MJM approaches for the design and construction of fundamental IFC components and systems. The 3D printed fluidic capacitors, diodes, and transistors investigated here exhibited operational characteristics consistent with their electrical analogues, both independently and as part of integrated networks. Nonetheless, future work should study potential methods by which the observed residual flow through ‘closed’ interactions could be reduced or eliminated. In this work, devices were fabricated using the MJM material, Visijet M3 Crystal, as a demonstrative example; however, recent investigations have found this material (as well as numerous SLA materials) to exhibit limited optical characteristics and biocompatibility for applications such as cell culture and analysis.³⁵ Thus, for situations in which such properties are desired, the use of alternative MJM materials (e.g.,, clear, biocompatible MED610 (ref. 36)) and/or post-processing procedures (e.g.,, to provide biocompatible surface coatings) would be better suited. By modifying geometric parameters of the 3D fluidic components (ESI† Fig. S8), one can readily customize core component functionalities. In addition, the 3D component models can be assembled as desired to achieve a diverse array of integrated fluidic processors and networks (e.g.,, ESI† Movie S6). Consistent with the benefits of additive manufacturing technologies is the potential for participation and use across broad academic disciplines and backgrounds. In contrast to traditional methods of IFC construction, which typically necessitate technical training and access to microfabrication facilities, access to a single MJM 3D printer represents the only critical barrier to replicating all of the presented IFC components and systems on-site. Consequently, this inherent accessibility could support IFC adoption by researchers outside of traditional engineering communities, such as those in mainstream chemical and biological fields.