Learning Adaptive Forecasting Models from Irregularly Sampled Multivariate Clinical Data

Abstract

Building accurate predictive models of clinical multivariate time series is crucial for understanding of the patient condition, the dynamics of a disease, and clinical decision making. A challenging aspect of this process is that the model should be flexible and adaptive to reflect well patient-specific temporal behaviors and this also in the case when the available patient-specific data are sparse and short span. To address this problem we propose and develop an adaptive two-stage forecasting approach for modeling multivariate, irregularly sampled clinical time series of varying lengths. The proposed model (1) learns the population trend from a collection of time series for past patients; (2) captures individual-specific short-term multivariate variability; and (3) adapts by automatically adjusting its predictions based on new observations. The proposed forecasting model is evaluated on a real-world clinical time series dataset. The results demonstrate the benefits of our approach on the prediction tasks for multivariate, irregularly sampled clinical time series, and show that it can outperform both the population based and patient-specific time series prediction models in terms of prediction accuracy.

Introduction

With a wide adoption and availability of electronic health records (EHRs), the development of models of clinical multivariate time series (MTS) and tools for their analysis is becoming increasingly important for meaningful applications of EHRs in computer-based patient monitoring, adverse event detection, and improved patient management. (Bellazzi et al. 2000; Clifton et al. 2013; Lasko, Denny, and Levy 2013; Liu and Hauskrecht 2013; Liu, Wu, and Hauskrecht 2013; Schulam, Wigley, and Saria 2015; Ghassemi et al. 2015; Durichen et al. 2015).

In general, a number of models representing various time series data and their behaviors exist (Hamilton 1994). However, modeling of clinical time series data still presents numerous challenges that come from special characteristics of clinical data (Liu and Hauskrecht 2015). Briefly, clinical time series are distinguished from other time series data due to the following characteristics:

• multiple variables: the real-world clinical dynamics are multivariate and they often exhibit interactions and co-movements among different time series.

• irregular samples: sequential observations are collected at different times, and the time elapsed between two consecutive observations may vary.

• length variability: the number of observations in each data sequence is limited and the duration they span may vary a lot from patient to patient.

The objective of this work is to study and develop models that can be used for accurate clinical time series forecasting. More specifically we are interested in developing models and methods that can predict future values of MTS for a patient given a history of past observations. This problem is rather challenging for two reasons (1) the time series of past observations made for a patient of interest may be relatively short so it may be very hard to learn a good time series model just from one patient data; (2) the patient-to-patient variability may be large so it is unclear if the population based model derived from many samples of different patients will be sufficient to support the predictions. The majority of existing approaches in the literature tackle the clinical time series forecasting problem by taking one of the two “extreme” approaches: they either build a population based model or a patient-specific model ignoring what is known about the population. In this work we seek to develop a new approach that aims to benefit from the population trend extracted from past data collection and at the same time adapt to patient-specific data, thus allowing one to make more accurate MTS predictions.

We propose and develop a new two-stage adaptive forecasting model to represent both the population and the patient-specific multivariate interactions of clinical MTS. In the first stage, we learn a population model from clinical MTS sequences from many different patients. In this paper we use and experiment with a linear dynamical system (LDS) (Kalman 1960) whose parameters are learned with the help of the EM algorithm. In the second stage, we first express the time series of past observations for a patient in terms of residuals (or differences in between predictions made by the population model and actually observed values), which reflect the patient-specific deviations from the population model. Then we use and model these deviations with a multi-task Gaussian process (MTGP) (Bonilla, Chai, and Williams 2007). In the forecasting phase, we automatically adjust the predictions from the population model based on the new patient-specific observations.

Overall this paper makes the following contributions:

• It presents a new two-stage model to represent the multivariate, irregularly sampled clinical time series, which not only represents the long-term population trend of the dynamics, but captures the multivariate interactions for each patient-specific dynamics.

• The new model is able to automatically adapt its predictions according to the newly observed data for each individual patient without retraining the population-based model.

• We evaluate our approach and its benefits on a real-world clinical MTS dataset.

The remainder of the paper is organized as follows: Background Section introduces the basics of the LDS, GP and MTGP models for time series modeling. Comparison to relevant research work is discussed. In Methodology Section, we describe the details of our two-stage adaptive forecasting model, which consist of a population model learned from the entire collection of sequences and a model of the multivariate temporal interactions based on MTGP. In Experiment Section, we (1) visualize the predictions made by our forecasting model; (2) show the benefits of our model over alternative approaches on a clinical data derived from the Complete Blood Count panel. We summarize our work and outline possible future extensions in Conclusion Section.

Background

In this section, we review the basics of three models widely used to represent time series data: the linear dynamical system (LDS), Gaussian process (GP) and multi-task Gaussian process (MTGP). After that, we discuss the differences between our model and existing approaches.

Notation

We denote clinical MTS data 𝒟 as a collection of observed value set 𝒴 and the time stamp set 𝒳 which contains observations and time stamps, i.e, 𝒟 = (𝒴, 𝒳). We denote a time series data set with N samples as 𝒟 = {D¹, D², ···, D^N} and correspondingly, we have 𝒴 = {Y¹, Y², ···, Y^N}, 𝒳 = {X¹, X², ···, X^N} and D^l = < Y^l, X^l >, l = 1, 2, ···, N.

Without loss of generality, for each MTS sequence D^l, we assume it has n dependent time series with the same length T_l. Hence, we represent Y^l as an n × T_l matrix. Let ${\mathbf{y}}_i^l$ and ${\mathbf{y}}_t^l$ be the ith row and tth column of Y^l. Let $y_{it}^l$ be the tth observation in the ith time series in Y^l. In this work, we assume time series within each sample D^l are obtained at the same time stamps and X^l can be concisely represented as a T_l × 1 vector x^l. Let $x_t^l$ be the tth time stamp in x^l.

Let 𝔼_z[f(·)] denote the expected value of f(·) with respect to z. For both vectors and matrices, the superscript (·)^⊤ denotes the transpose. Let ⊗ denote the Kronecker product. For the sake of notational brevity, we omit the explicit sample index (l) in the rest of Background section.

Linear Dynamical System

The linear dynamical system (LDS) models real-valued MTS ${\{{\mathbf{y}}_t\in {ℝ}^n\}}_{t=1}^T$ using hidden states ${\{{\mathbf{z}}_t\in {ℝ}^d\}}_{t=1}^T$:

$${\mathbf{z}}_t=A{\mathbf{z}}_{t-1}+{\mathit{\epsilon }}_t;{\mathbf{y}}_t=C{\mathbf{z}}_t+{\mathit{\zeta }}_t$$ (1)

Briefly, {z_t} is generated via the transition matrix A ∈ ℝ^d×d. Observations {y_t} are generated from z_t via the emission matrix C ∈ ℝ^n×d (see eq.(1)). ${\{{\mathit{\epsilon }}_t\}}_{t=1}^T$ and ${\{{\mathit{\zeta }}_t\}}_{t=1}^T$ are i.i.d. multivariate normal distributions with mean 0 and covariance matrices Q and R respectively. The initial state (z₁) distribution is also multivariate normal with mean ξ and covariance matrix Ψ. The complete set of the LDS parameters is Ω = {A, C, Q, R, ξ, Ψ}. The LDS is arguably the most commonly used time series model for real-world engineering and financial applications, such as time series prediction (Rogers, Li, and Russell 2013; Li et al. 2009) and visual tracking (Lee, Kim, and Kweon 1995; Funk 2003).

Gaussian Process

The Gaussian process (GP) is a popular nonparametric nonlinear Bayesian model in statistical machine learning (Rasmussen 2006). In time series modeling, each GP is used to model an individual time series, which is represented by the mean function m(x_t) = 𝔼[f(x_t)] and the covariance function K^G(x_t, x_t′) = 𝔼[(f(x_t) − m(x_t))(f (x_t′) − m(x_t′))], where f(x) is a real-valued process and x_t and x_t′ are two time stamps. The GP can be used to calculate the posterior distribution p(f(x^*)|(x, y_i,:)) of f values for an arbitrary set of time stamps x^*, given a set of observed values y_i,: from time series i at time stamps x.

Due to the ability of exact inference, GP based model are widely used in time series regression and forecasting tasks, where time stamps are modeled as the input of GP and observations are modeled through the predicted mean function of the time series (Stegle et al. 2008; Clifton et al. 2013; Lasko, Denny, and Levy 2013; Liu and Hauskrecht 2014).

Multi-task Gaussian Process

The multi-task Gaussian process (MTGP) is an extension of GP which models multiple tasks (e.g., multivariate time series) simultaneously by utilizing the learned covariance between related tasks. MTGP uses K^C to model the similarities between tasks and uses K^G to capture the temporal dependence with respect to time stamps. The covariance matrix of MTGP is shown as follows:

$$K^M=K^C\otimes K^G+D\otimes I_T$$ (2)

where K^C is a positive semi-definite (PSD) matrix that specifies the inter-task similarities and $K_{ij}^C$ measures the similarity between task i and task j. D is an n × n diagonal matrix in which D_ii is the noise variance ${\delta }_i^2$ for the ith task.

Exact inference of MTGP can be done by using the standard GP formulations and the details can be found in (Bonilla, Chai, and Williams 2007) and its clinical application can be found in (Ghassemi et al. 2015; Durichen et al. 2015).

Related Work

The majority of existing work on clinical time series forecasting models each clinical time series separately (Marlin et al. 2012; Clifton et al. 2013; Lasko, Denny, and Levy 2013; Liu and Hauskrecht 2014; Schulam, Wigley, and Saria 2015) which does not allow one to represent dependences among the different time series. Our model deals with multivariate data and aims to capture interactions among all variables and their dynamics.

The works that try to capture MTS and dependences among its time series include (Ghassemi et al. 2015; Durichen et al. 2015). In (Ghassemi et al. 2015; Durichen et al. 2015) the authors apply MTGP to clinical MTS modeling and forecasting. However, their models that are learned from time series for just one patient are very simple and results in either constant or simple parametric mean functions. This is too restrictive to represent real clinical MTS with large variability. In addition, this approach does not take advantage of time series collected for other patients. Our approach tackles the problem in two stages and with a combination of two models: we first use an LDS to model the population trend, and then take advantage of MTGP to capture the individual-specific short-term variability. (Fox et al. 2011) utilizes the beta process to build the joint model for multiple related time series (not necessarily clinical). It requires intensive MCMC posterior computations, which is often infeasible to do in real clinical settings.

Finally, we would like to note that the majority of methods mentioned above fail to generalize to forecasting models for a collection of clinical MTS of varying lengths. They are not able to adapt their forecasts when new values are observed without retraining the model.

Methodology

In this section, we propose a two-stage model that (1) is learned from a collection of past patient time series data of varying lengths; (2) captures the patient-specific short-term multivariate interactions; (3) automatically adjusts its predictions when new observations for the target patient are obtained without retraining the population model.

Stage 1: Learning A Population Model

In the first stage, we would like to learn a population model from all available data sequences to represent the trend of the entire population. We choose an LDS model to model the population trend, which is a classical and widely used discrete-time model for real-valued sequence analysis. The LDS is Markovian and assumes the dynamic behavior of the system is captured well using a small set of real-valued hidden-state variables and linear state transitions corrupted by a Gaussian noise. It has a mathematically predictable behavior, and both exact inference and predictions for LDS models can be done efficiently.

Direct Value Interpolation

In spite of the advantages of LDS models, they are restricted to discrete time domain where observations are regularly sampled. In order to apply the discrete-time LDS model over our irregularly sampled clinical data, we follow (Adorf 1995; Dezhbakhsh and Levy 1994; Åström 1969; Bellazzi et al. 1995; Kreindler and Lumsden 2006; Rehfeld et al. 2011; Liu and Hauskrecht 2014) and apply the direct value interpolation (DVI) technique to discretize each irregularly sampled clinical sequence and that replaces it with a regularly sampled time series data.

The DVI approach assumes that all observations are collected regularly with a pre-specified sampling frequency r. However, instead of actual readings, the values at these time points are estimated from readings at time points closest to them using various interpolation techniques. The interpolated (regular) time series, i.e., ${\stackrel{\sim }{\mathbf{y}}}_{i,:}^l$, is then used to train a discrete-time LDS model. We put a tilde sign (·̃) over 𝒴, Y^l, ${\mathbf{y}}_{i,:}^l$ and ${\mathbf{y}}_t^l$ to indicate the discretized observations. T̃_l is the length of discretized sequence for patient l. The approach is illustrated in Figure 1.

Figure 1.

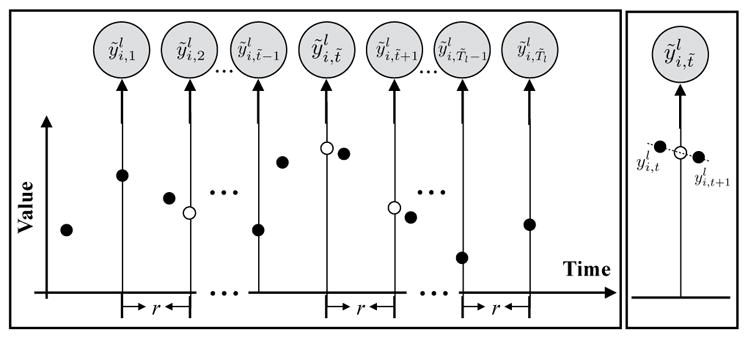
Transformation of an irregularly sampled time series ${\mathbf{y}}_{i,:}^l$ to a discrete time series ${\stackrel{\sim }{\mathbf{y}}}_{i,:}^l$ by DVI. The empty circles denote the interpolated values with no readings. The right panel illustrates the linear interpolation process.

A possible limitation of the DVI data transformation is possible information loss: as we can see from Figure 1, some observations in individual time series are discarded during this discretization process. However, given that LDS is building a coarse level population model over the entire collection of data (many patients), this loss is less important. We also note that patient-specific observations are not discarded in the second stage of our approach that captures fine grained patient-specific multivariate interactions by MTGP.

EM Learning

In order to learn the unified population model over the entire discretized clinical sequences, we build our model upon the probabilistic formulation of the LDS model and follow the EM learning algorithm proposed by (Ghahramani and Hinton 1996). We extend its formulation to multiple sequences setting. The log joint probability distribution of the LDS model over the entire collection of clinical sequences of varying lengths is:

$$log\left(p(\stackrel{\sim }{\mathcal{Y}},\mathcal{Z})\right)=\sum _{l=1}^{N}logp({\mathbf{z}}_1^l)+\sum _{l=1}^N\sum _{t=1}^{{\stackrel{\sim }{T}}_l}logp({\stackrel{\sim }{\mathbf{y}}}_t^l\mid {\mathbf{z}}_t^l)+\sum _{l=1}^N\sum _{t=2}^{{\stackrel{\sim }{T}}_l}logp({\mathbf{z}}_t^l\mid {\mathbf{z}}_{t-1}^l)$$ (3)

where 𝒵 = {Z¹, Z², ···, Z^N} and Z^l is the corresponding hidden state sequence of Ỹ^l.

E-Step

Since the hidden state Markov chain collection 𝒵 defined by the LDS is unobserved, we cannot learn the LDS directly. Instead, we infer the hidden state expectations. The E-step infers a posterior distribution of latent states 𝒵 given the observation sequences 𝒴̃, p(𝒵|𝒴̃).

The E-step requires computing the expected log likelihood of the log joint probability with respect to the hidden state distribution, i.e., 𝒬 = 𝔼_𝒵[log p(𝒵, 𝒴̃)], which depends on three types of sufficient statistics $\mathbb{E}[{\mathbf{z}}_t^l\mid {\stackrel{\sim }{\mathbf{Y}}}^l],\mathbb{E}[{\mathbf{z}}_t^l{({\mathbf{z}}_t^l)}^{\top }\mid {\stackrel{\sim }{\mathbf{Y}}}^l]$ and $\mathbb{E}[{\mathbf{z}}_t^l{({\mathbf{z}}_{t-1}^l)}^{\top }\mid {\stackrel{\sim }{\mathbf{Y}}}^l]$. Here we follow the backward algorithm in (Ghahramani and Hinton 1996) to compute them. The backward algorithm is presented in Section A2 in the supplemental material.

$$\mathcal{Q}=\sum _{l=1}^N{\mathbb{E}}_{{\mathbf{Z}}^l}\left[logp({\mathbf{z}}_{:,1}^l)\right]+\sum _{l=1}^N\sum _{t=1}^{{\stackrel{\sim }{T}}_l}{\mathbb{E}}_{{\mathbf{Z}}^l}\left[logp({\stackrel{\sim }{\mathbf{y}}}_t^l\mid {\mathbf{z}}_t^l)\right]+\sum _{l=1}^N\sum _{t=2}^{{\stackrel{\sim }{T}}_l}{\mathbb{E}}_{{\mathbf{Z}}^l}\left[logp({\mathbf{z}}_t^l\mid {\mathbf{z}}_{t-1}^l)\right]$$ (4)

M-Step

In the M-step, we try to find Ω that maximizes the likelihood lower bound 𝒬 (eq.(4)). As we can see, 𝒬 function is differentiable with respect to (Ω = {A, C, R, Q, ξ, Ψ}). Each of these parameters is estimated similarly to (Ghahramani and Hinton 1996) by taking the corresponding derivative of the eq.(4), setting it to zero, and by solving it analytically. Due the the space limit, update rules for A, C, R, Q, ξ, Ψ are listed in Section A3 in the supplemental material.

Stage 2: Learning Multivariate Interaction Models

A population model built from a collection of clinical data for multiple patients is crucial since each individual sequence is usually very short. The learned model from the entire population is more robust and stable. However, the prediction task is performed patient by patient and the forecasting model should also reflect and take into account the variations specific to the current patient. To address this problem, we model the patient-specific multivariate interactions by using an MTGP. More specifically, instead of simply modeling the clinical time series trends (the mean function of MTGP) by using constants or simple known parametric forms (e.g., linear functions) (Ghassemi et al. 2015; Durichen et al. 2015), we use the population model (learned in Stage 1) to reflect the time series tendency and build an MTGP on a residual signal that reflects the deviations of patients’ true observations and the predictions made by the population LDS model. We define the multivariate residual time series as follows:

Definition 1. (Multivariate Residual Time Series)

For each patient l, given time series Y^l and its corresponding predictions Ŷ^l from model Ω, a multivariate residual time series R^l represents the deviations from Y^l to Ŷ^l, i.e., R^l = Y^l − Ŷ^l.

Notice that each residual time series R^l is computed by using the true observations Y^l (not the discretized sequence Ỹ^l), there is no information loss for each patient under the prediction task and R^l is irregularly sampled.

The multivariate residual time series reflect each patient’s unique variations from the general population and they are distinguished patient by patient. Furthermore, clinical events usually only affect a handful of measurements within a small time window. Hence, for each patient l, we model these transient deviations nonparametrically using an MTGP. The MTGP has mean 0 and a squared exponential covariance function (eq.(2)), which is the most frequently-used example in literature (Rasmussen 2006). In eq.(2), K^G is defined as follows:

$$K^G(x_{i,t},x_{j,t^{\prime }})=\alpha exp\left(-\frac{{(x_{i,t}-x_{j,t^{\prime }})}^2}{2{\beta }^2}\right)$$ (5)

The complete parameter set Λ in the MTGP model is Λ = {α, β, δ_i, K^C} where i = 1, ···, n. In this work, we adopt the Cholesky decomposition and the “free-form” parameterization techniques (K^C = LL^⊤) to learn the parameter set Λ by minimizing the negative log marginal likelihood via gradient descent (Rasmussen 2006; Ghassemi et al. 2015).

Usually the MTGP model has the computation limitation that it has 𝒪(n³T³) compared with n × 𝒪(T³) for standard GP models (T is the length of the time series). However, this limitation is not as relevant in our application setting, given that the number of clinical observations is very limited and clinical time series are usually short span.

Adaptive Prediction

In the real clinical setting, a successful forecasting model needs to be adaptive, that is, when newly observed values are obtained, the model should efficiently adapt to the new change and utilize new values to make better predictions. In this work, we develop a new adaptive prediction algorithm based on the Kalman filtering algorithm (Kalman 1960) that utilizes our two-stage forecasting model.

Let u denote the current patient we consider in our prediction task. Y^u is an n × T_u matrix which denotes the current observed values for patient u. Given an arbitrary future time stamp t* (t* > T_u), the value ${\widehat{\mathbf{y}}}_{t\ast }^u$ is predicted as follows:

• Step 1. Compute the discretized observations Ỹ^u by using DVI on Y^u.

• Step 2. Infer patient-specific hidden dynamics by using population model Ω and Ỹ^u. This step adaptively computes the patient-specific hidden state Z^u using patient’s latest observations. Details are provided in Section A1 in the supplemental material¹.

• Step 3. Make predictions by using the population model Ω and Z^u. Note that we need to predict the value at time points closest to the target time t*, and after that, apply the interpolation approach to estimate the target value. The prediction made by the population model is ${\widehat{\mathbf{y}}}_{t\ast }^u(\mathrm{\Omega })$

• Step 4. Use the population model to predict patient u’s known observations (Y^u) adaptively, denoting as Ŷ^u. Compute the residual time series for patient u, i.e., R^u = Y^u − Ŷ^u.

• Step 5. Learn the MTGP model Λ^u from R^u to capture the patient-specific short-term variability.

• Step 6. Predict patient-specific short-term variability ${\widehat{\mathbf{y}}}_{t\ast }^u({\mathrm{\Lambda }}^u)$ by using Λ^u at the target time t*.

• Step 7. Compute the final prediction ${\widehat{\mathbf{y}}}_{t\ast }^u$ by combining ${\widehat{\mathbf{y}}}_{t\ast }^u(\mathrm{\Omega })$ and ${\widehat{\mathbf{y}}}_{t\ast }^u({\mathrm{\Lambda }}^u)$, i.e., ${\widehat{\mathbf{y}}}_{t\ast }^u={\widehat{\mathbf{y}}}_{t\ast }^u(\mathrm{\Omega })+{\widehat{\mathbf{y}}}_{t\ast }^u({\mathrm{\Lambda }}^u)$.

Summary

Algorithm 1 summarizes our two-stage adaptive forecasting model and its learning and prediction parts.

Algorithm 1.

Learning and Prediction Procedures

INPUT: Train data collection 𝒟 = {< Yl, xl >}, where l = 1, ···, N. DVI sampling frequency r. Number of hidden states in LDS d. Current observations Yu for patient u who is being predicted. An arbitrary future time stamp t* (t* > Tu).

PROCEDURE: // Stage1: Learning the population model. {Ỹl} = DV I({Yl}, {xl}, r). Ω = LearnLDS({Ỹl}). // Stage2: Learning the multivariate interaction model. Compute residual time series Ru. Λu = LearnMT GP (Ru). // Adaptive Prediction: Predicting ${\widehat{\mathbf{y}}}_{t\ast }^u$ by Ω and Λu. Trend prediction: ${\widehat{\mathbf{y}}}_{t\ast }^u(\mathrm{\Omega })=\mathit{PredictLDS}(\mathrm{\Omega },t\ast )$. Variability prediction: ${\widehat{\mathbf{y}}}_{t\ast }^u({\mathrm{\Lambda }}^u)=\mathit{PredictMTGP}({\mathrm{\Lambda }}^u,t\ast )$. ${\widehat{\mathbf{y}}}_{t\ast }^u={\widehat{\mathbf{y}}}_{t\ast }^u(\mathrm{\Omega })+{\widehat{\mathbf{y}}}_{t\ast }^u({\mathrm{\Lambda }}^u)$.

OUTPUT: Prediction at time stamp $t_{\ast }:{\widehat{\mathbf{y}}}_{t\ast }^u$.

Experimental Evaluation

In this section we evaluate our approach on a real-world clinical dataset. We demonstrate the benefits our adaptive approach both (1) qualitatively by visualizing time series predictions made for one of the patients, and (2) quantitatively by comparing the prediction accuracy of our two-stage adaptive forecasting model to alternative approaches. We would also like to note that the hyper parameters (e.g., DVI sampling frequency r, number of hidden states in LDS d) used in our methods are selected (in all experiments) by the internal cross validation approach while optimizing models’ predictive performance.

Clinical Data

We test our two-stage adaptive model on a clinical MTS data obtained from EHRs of post-surgical cardiac patients in PCP database (Hauskrecht et al. 2010; 2013). We take 500 patients from the database who had their Complete Blood Count (CBC) tests ² done during their hospitalization. The MTS data consists of six individual CBC lab time series: mean corpuscular hemoglobin concentration (MCHC), mean corpuscular hemoglobin(MCH), mean corpuscular volume(MCV), mean platelet volume(MPV), red blood cell(RBC) and red cell distribution width(RDW). In the following experiments, we have randomly selected 100 patients out of 500 as a test set and used the remaining 400 patients for training the models.

Baselines

We compare our proposed approach (LDS+reMTGP) to the following methods. Some of these are widely used in both clinical pharmacology and machine learning communities:

• Mean of the entire population (P_Mean).

• Mean of each individual patient (I_Mean).

• Gaussian process regression model (GP) for each individual time series with a squared exponential covariance function (eq.(5)). (Rasmussen 2006)

• Multi-task Gaussian process model (MTGP) for MTS with a squared exponential covariance function (eq.(2)). (Ghassemi et al. 2015; Durichen et al. 2015)

• Standard LDS-based population model with adaptive prediction (LDS).

• The LDS-based population model combined with the Gaussian process regression model for each individual residual time series (LDS+reGP). It is a special (simpler) version of our model.

Evaluation Metrics

We evaluate and compare the performance of the different methods by calculating the average Mean Absolute Percentage Error (Avg-MAPE) of models’ predictions. Avg MAPE measures the prediction deviation proportion in terms of true values:

$$\text{Avg-MAPE}=\frac{{\sum }_{l=1}^N{\sum }_{i=1}^n{\sum }_{t=1}^{T_l}\mid 1-{\widehat{y}}_{it}^l/y_{it}^l\mid }{n{\sum }_{l=1}^N{T}_l}\times 100\%$$

where |·| denotes the absolute value; $y_{it}^l$ and ${\widehat{y}}_{it}^l$ are the tth true and predicted values from time series i for patient l.

Results

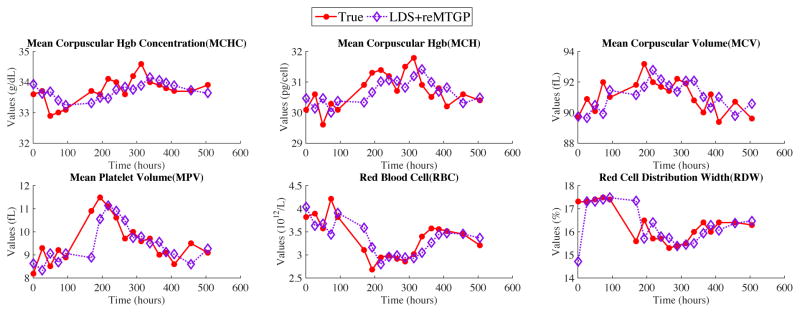
Figure 2 shows the one-step-ahead MTS predictions made by our approach (LDS+reMTGP) for one patient from our test set. The LDS population model is trained on a 400-patient clinical MTS training set. As can be seen from Figure 2, our model is able to capture very well the trend of the true MTS dynamics. More specifically, LDS+reMTGP can quickly adapt to sudden changes in the true signal and its short term variability (ups and downs), as can be observed, for example, in MPV, RBC, RDW subgraphs of Figure 2.

Figure 2.

Clinical MTS predictions for one patient. The population based LDS model is trained on 400 patient sequences.

Figure 3 compares our new method LDS+reMTGP in terms of Avg-MAPE to various state-of-the-art approaches listed in Baselines subsection. Due to the poor performance of the P_Mean and I_Mean methods, we don’t visualize it in Figure 3; however, all numerical results are included and listed in the supplemental material. Since our two-stage approach has to fit the parameters of the GP or MTGP models of the residual time series it may experience some initial period in which it is not stable and may lead to suboptimal predictions. To reflect this, Figure 3 shows the Avg-MAPE performance of all methods when they start to predict with a fixed delay corresponding to the different number of initial observations (initial observation sequence length). For example, when the initial observation sequence length is set to 4 the Avg-MAPE reflects the errors of all one-step-ahead predictions the method makes when starting from four initial observations for the target patient (that is, when all predictions the model can make for sequences of 0, 1, 2, 3 initial observations are ignored). The results show that the population-based LDS model is the best performer when very little is known about the target patient and when patient’s observation sequences are short. However, LDS+reGP and LDS+reMTGP) methods outperform the LDS rather quickly and become superior when more than five initial observations for the target patient become available and are considered. In contrast to the LDS, pure patient-specific models (GP and MTGP) that ignore any population data adapt very slowly and do not reach the performance of LDS or our methods even for the initial observation sequence of length 20. Finally, a simple population-based method (P_Mean) and a simple patient-specific method (I_Mean) lag behind (see supplemental material for the results) and perform much worse than more advanced time series prediction models.

Figure 3.

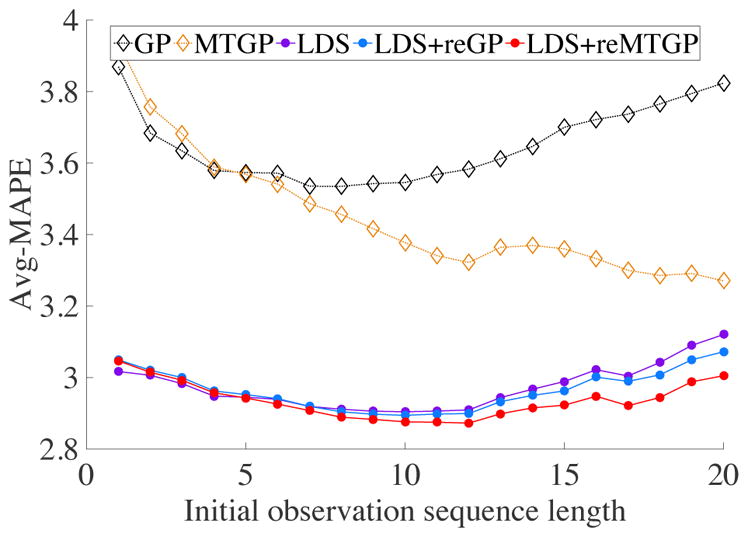
Avg-MAPE results with different initial observation lengths.

Conclusion

In this paper, we presented a new two-stage adaptive forecasting model for irregularly sampled multivariate clinical time series data. In contrast to the traditional time-series forecasting models, our model learns from both the population data (time series for other patients) and the target patient data (time series of past observations for the target patient). Our experimental results demonstrate that our model can outperform after a short adaptation period other prediction models and approaches. In the future, we plan to study the different ways of combining/switching among the different prediction models in order to improve their overall prediction accuracy.