Abstract
Is working memory capacity determined by an immutable limit—e.g. four memory storage slots? The fact that performance is typically unaffected by task instructions has been taken as support for such structural models of memory. Here, we modified a standard working memory task to incentivize participants to remember more items. Participants were asked to remember a set of colors over a short retention interval. In one condition, participants reported a random item’s color using a color wheel. In the modified task, participants responded to all items and their response was only considered correct if all responses were on the correct half of the color wheel. We looked for a trade-off between quantity and quality—participants storing more items, but less precisely, when required to report them all. This trade-off was observed when tasks were blocked, when task-type was cued after encoding, but not when task-type was cued during the response, suggesting that task differences changed how items were actively encoded and maintained. This strategic control over the contents of working memory challenges models that assume inflexible limits on memory storage.
Our subjective experience of the visual world is rich and detailed. However, we can hold very little information in mind from one instant to the next (Noë, Pessoa, & Thompson, 2000; O’Regan, 1992; Simons & Chabris, 1999; Simons & Levin, 1997; Rensink, 2000, 2002). These limits are clearly observed in memory tasks that require participants to remember visual features over short durations. Even when presented with items that vary along a simple feature dimension (e.g color, or orientation) people remember only a few items (Luck & Vogel, 1997; Vogel, Woodman, & Luck, 2001). These stark limits in capacity are not only surprising (Levin, et al., 2000), but working memory limits appear to be an important component of individual differences in cognitive ability (Alloway & Alloway, 2010; Cowan et al., 2005; Engle et al., 1999; Fukuda, Vogel, Mayr & Awh, 2010; Kyllonen & Christal, 1990), and are correlated with important measures such as academic success (Alloway & Alloway, 2010). This suggests that working memory is a core cognitive system and that understanding this system can provide general insights into cognitive function.
Over the last twenty years there has been considerable work trying to understand the source of limits in visual working memory (Alvarez & Cavanagh, 2004; Bays & Husain, 2008; Fougnie, Suchow, & Alvarez, 2012; Irwin 1992; Luck & Vogel, 1997; Rensink, 2002; Sims, Jacobs, Knill, 2012; Todd & Marois, 2004; Swan & Wyble, 2014; Van den Berg, et al., 2012; Vogel & Machizawa, 2004; Vogel et al., 2001; Wilken & Ma, 2004; Woodman & Luck, 2005; Woodman & Luck, 2008; Zhang & Luck, 2008). One influential idea is that memory limits arise because only three to four representations may be stored at once (Luck & Vogel, 1997; Vogel et al., 2001; Zhang & Luck, 2008), and that this limit is immutable by task demands. This suggests that the structure underlying working memory limits can be directly observed by measuring performance in easy to conduct psychophysical experiments.
In support of inflexible structural limits, studies have shown that participants do not store more items in memory when task demands are changed to encourage them to do so (Machizawa, Goh, & Driver, 2012; Murray, Nobre, Astle, & Stokes, 2012; Zhang & Luck, 2011). In these studies, participants were given financial incentives to encourage storage of more items, but these incentives did not appear to lead to strategic shifts in memory capacity—consistent with immutable structural limits. However, these studies may not have provided strong evidence that working memory limits are immutable. The absence of an effect could be explained by participants not understanding the financial incentives or the incentives not being strong enough to alter behavior. This concern is magnified since the cost of storing more items is unknown. Studies have used financial incentives that work under the assumption that the change in quality from storing more items is equivalent to the trade-off seen at earlier set sizes (e.g. Zhang & Luck, 2011). But the cost need not be linear; and a failure to motivate behavior under these assumptions does not mean that behavior cannot be motivated with stronger incentives. Our goal is to provide an intuitive and compelling incentive to store all the items in a display in order to provide the strongest test of the flexibility of our working memory system.
In our standard task, participants were shown five colorful circles. After a short memory interval a single, random location was cued and participants were asked to report the color from that location as precisely as possible (Wilken & Ma, 2004; Zhang & Luck, 2008), with reward proportional to accuracy. We developed a variant of this task, the get-them-all task, which incentivizes participants to remember all items but relaxed the demands on memory quality: Participants had to respond on the correct half of the color wheel for all five responses. This is a strong test of whether working memory is truly immutable or whether people can store more items if properly motivated. Our analyses were restricted to the first response to properly compare performance for the two tasks.
To preview our results, we found evidence of a trade-off between quantity and quality—participants stored more items in the get-them-all task but at reduced quality. This trade-off was observed even when the condition cue was given after stimulus offset (post-encoding), suggesting that observers can strategically control the allocation of memory resources during maintenance. The trade-off was not found if the cue appeared at the retrieval stage, suggesting that the results of Experiments 1–2 reflect strategic allocation of memory resources during encoding and maintenance.
Experiment 1 – Evidence for quantity-quality trade-offs in working memory
Methods
Participants
Power analyses with an estimated effect size of .6 were used to determine that we could achieve a power value of at least 80% by running eighteen participants. We used that sample size for all studies. No data was excluded from any experiment. Eighteen volunteers (10 females) between the ages of 18 and 27 participated for money or course credit. The participants of all studies were drawn from the Harvard community. All studies were performed in accordance with Harvard University regulations and approved by the Committee on the Use of Human Subjects in Research under the Institutional Review Board for the Faculty of Arts and Sciences.
Stimuli
Participants were asked to remember the color of five colorful circles (.5° radius) that were evenly spaces along an imaginary circle (3.5° radius) centered on a fixation dot. Circle colors were drawn randomly from a set of 180 equiluminant colors evenly distributed in the CIE L*a*b* color space (centered at L=54, a=18, b=-8, with a radius of 59). Each participant performed two tasks, the standard task and the get-them-all task1. The tasks were run in separate, back-to-back sessions of 135 trials each (the order of the tasks was randomized across participants). In both tasks, trials began with a 1200ms presentation of the memory stimulus of five colorful circles, followed by a blank 900ms retention interval (Figure 1).
Figure 1.

Trial timeline for Experiment 1. Left: Standard task trial. Right: Get-them-all task trial. The tasks were performed in separate blocks.
Standard task
Participants’ memory was tested by highlighting a random location and asking participants to adjust the color of this item to match the remembered color of the item corresponding to the cued location (Figure 1 left) (Prinzmetal, Amiri, Allen, & Edwards, 1998; Wilken & Ma, 2004; Zhang & Luck, 2008). The cued item was highlighted by presenting a solid white circle at this location (non-probed locations had hollow circles instead). Participants adjusted the color by selecting a value along a circular color wheel (6° radius, centered on fixation). A black selection bar was positioned outside the currently selected color. Its position reflected the angular position of the mouse cursor relative to fixation. Once a participant moved the mouse, the solid circle at the probed location updated to the currently selected color, and this color was continuously updated as the mouse was moved. Participants clicked a mouse button once they were happy with the color selection. Following this report, participants were given feedback on how accurate the response was, and were told the amount of bonus points they received (see bonus point section for details).
Get-them-all task
Participants’ memory was tested by asking them to report the color of all 5 items in a display (Figure 1 right). Items were reported sequentially, in a random order. As in the standard task, a random position was highlighted and participants adjusted the color to match the corresponding memory item. If the participant reported a color within 90° of the correct color, this response was considered correct and the participant was asked about a new item, selected at random from the set of untested positions. Participants were briefly shown the correct color after selecting a response. Specifically, the center core of the circle changed to the correct color while the outer diameter remained the chosen color, providing feedback on the disparity between colors. If all five items were reported correctly the participant earned bonus points and a cash register ‘cha-ching’ sound was presented. If any response was incorrect, a buzzer sounded and the trial immediately ended, awarding zero bonus points. To ensure that the change in task demands was obvious, participants were told that forgetting even one item per trial would cut their expected payoff in half, due to the probability of guessing incorrectly.
Bonus points
Participants were incentivized to perform well by a monetary reward that scaled with the number of bonus points earned (assessed independently for each task and summed). Bonus point rules were different across the two tasks and served to reinforce differences in the tasks. In the standard task, bonus points served to reward participants for minimizing the error of the reported item. Participants were given bonus points equal to the inverse error (180 minus the absolute difference in degrees between the response and the true value). In the ‘get-them-all’ task, 500 bonus points were awarded if the participant got all five items correct. Otherwise zero points were awarded. We derived these two point systems to award roughly similar amounts of points if participants were storing 3 of 5 items at 20° precision, guessing randomly on the remainder (numbers were based on previous empirical estimates, e.g. Zhang & Luck, 2008). Participants earned $1 for every 5000 points earned (max $5 per task; combined average $8.8). Bonus point rules were explained to participants. In between trials, text appeared on screen to inform participants of the number of points earned on the previous trial and the cumulative point total for the current task. This feedback was presented for 1500ms prior to a 1000ms blank intertrial interval.
Data analysis procedure
To estimate how many items people remember and how well they remember them we analyzed the distribution of response errors (using only the first response for the get-them-all task). Our analyses assume that responses to items not in memory will be random and not centered on the correct value. On the other hand, responses to remembered items will be distributed around the correct value with the width of this distribution signifying how well items were remembered. To estimate the quantity of items remembered, we first measured the proportion of responses that were centered on the correct response (i.e. responses that were not random guesses). This measure tells us the probability that any one item was in memory. To estimate quantity remembered we multiplied this measure by the number of items in the display (five in all experiments). To measure quality, we determined how much spread there was around the correct answer when participants were not guessing (response precision). More formally, we modeled the error distributions as a mixture of circular normal and uniform distributions (Zhang & Luck, 2008) with 3 parameters—mixture parameter (how many trials are guess trials), a standard deviation parameter (how wide was the normal distribution), and a mu parameter (where was the normal distribution centered relative to the true value). The mu parameter did not differ across conditions in any study and is not considered further. The mixture and standard deviation parameters correspond to the quantity and quality of memory representations, respectively. Data were fit using the MemToolbox (Suchow, Brady, Fougnie, & Alvarez, 2013).
Parameter estimates were derived using Markov Chain Monte Carlo to find the maximum a posteriori values given the errors on the task. The model was fit separately for each subject and task condition. To determine whether task affected the quality and quantity of memory, parameter estimates were compared using paired t-tests to determine whether guess rate or standard deviation differed between tasks.
In addition to this standard mixture model we have also analyzed the data using slightly modified models that estimated how often participants report a color that was on the display but not in the location tested (Bays, Catalao, & Husain, 2009) or that allow precision to vary across trials (Fougnie, Suchow, & Alvarez, 2012; van Den Berg, et al, 2012). The results converged across different models. Parameter estimates for alternate models are listed in the Supplemental Notes. Finally, because the behavioral model of working memory is still an area of debate (Luck & Vogel, 2013; Ma, Husain, & Bays, 2014) we also include analyses in the Supplemental Notes that are less dependent on the underlying model of memory.
Results and Discussion
Report error distributions for each task are shown in Figure 2A (using only the first response for the get-them-all task). These distributions were modeled as a mixture of a circular normal and a uniform distribution (Zhang & Luck, 2008) to estimate the quantity and quality of memory. Participants guessed more often in the standard task (20.3%) than in the get-them-all task (9.6%), t(17)=4.5, p<.001, Cohen’s d = 1.05 (Figure 2B left), suggesting that participants remembered more items in the get-them-all task. Indeed, we can estimate the number of items in memory (capacity) by multiplying non-guess rate (1-guess rate) by the set size (5) (Cowan, 2001; Zhang & Luck, 2008). Capacity (K) increased from 3.99 items in the standard task to 4.52 items in the get-them-all task. While participants were able to store more items, these items were maintained with reduced quality—standard deviation estimates were larger in the get-them-all task (27.6°) than in the standard task (22.7°), t(17)=3.8, p=.001, Cohen’s d = .90 (Figure 2B right).
Figure 2.

Experiment 1 results (analyzing only the first response for each trial). A: Response error histograms for the standard task (left) and get-them-all task (right). The solid line indicates the best fitting mixture model of each condition. B: Model parameter estimates for guess rate (left) and standard deviation (right) for the standard task (black) and get-them-all task (gray). Note that larger standard deviation values imply worse precision. All error bars are the standard error of the difference in parameter estimates across tasks (between-subject error).
These results revealed a trade-off in quantity and quality across the two tasks, in stark contrast to previous reports (Machizawa, et al., 2012; Murray, et al., 2012; Zhang & Luck, 2011). These previous studies argued against a flexible working memory system. While the failure to observe a trade-off between quantity and quality in previous tasks does suggest limits in the flexibility of memory, it does not imply that our memory system is completely inflexible. Indeed, the get-them-all task is a more powerful test of flexibility. It is intuitive and strongly encourages participants to store all items even if that results in large costs in item quality. Thus, working memory appears to have malleable limits rather than hard limits on capacity.
We encouraged participants to respond to our task manipulations by rewarding good performance with bonus points. These point systems were developed to reward roughly equal points if participants could store 3 items at 20° of precision. In actuality, participants received about twice as many points in the get-them-all task (44,405) than the standard task (20,146), presumably because guess rates were lower than expected and because participants were able to trade off capacity and precision in the get-them-all task. We considered whether performance differences could have arisen from the scoring systems. To test this, we replicated the results on 18 naïve participants but eliminated bonus points (and performance-based monetary incentives). Similar results were found. Guess rates were lower in the get-them-all condition (15.7% (K = 4.2 items) compared to 25.7% (K = 3.7 items), t(17)=3.9, p=.001, Cohen’s d = .91) and quality was still worse (29.6° compared to 26.1°, t(17)= 2.6, p=.02, Cohen’s d = .61), suggesting that differences in point incentives did not play a role in influencing our results.
Given the discrepancy between our findings and the existing literature, we explored whether the trade-offs we observed could be explained by the encoding duration. We conducted a replication on 18 naïve participants using an encoding duration of 200ms. The only other change was that the display radius and memory item radius were increased to 5.0° and 0.6°of visual angle, respectively, to allow for fast encoding of the display items. The presence of a trade-off did not depend on encoding duration, demonstrating that our results are resilient to minor changes in methodology. Guess rates were still lower in the get-them-all condition (22.1% (K=3.9 items) compared to 32.1% (K=3.4 items), t(17)=3.64, p=.002, Cohen’s d = .86) and quality was still worse (30.5° compared to 25.0°, t(17)=3.2, p<.001, Cohen’s d = .75.
Finally, we also consider the possibility that the get-them-all task encouraged verbal/categorical encoding and this led to lower guess rates and greater stimulus uncertainty (worse precision). To address this possibility we first looked for evidence of categorical effects in the error data and compared these effects across tasks. Strong categorical effects should produce a step function when the reported value is plotted against the actual value (Zhang & Luck, 2008). Such plots (Supplementary Figure 1A) do not reveal any difference across tasks. However, this approach has been criticized as not sufficiently sensitive to the presence of less dramatic categorical effects (Bae, Olkkonen, Allred, & Flombaum, 2015). Another method of comparing categorical effects is to compare the deviance in model parameters across differences in the probed item’s color (Bae, et al., 2014, 2015). If the get-them-all task relied to a greater extent on a verbal or categorical label, then we would expect to see greater deviance in the parameter estimates by probe color value. However, we see no evidence of such differences across tasks (see Supplemental Notes). Given the size of the behavioral performance between the two tasks, if a verbal strategy was completely driving the effect, one would expect to see deviances in parameter estimates by probe color. However, a null result is not sufficient to conclude that there is no difference between the tasks in dependency on verbal information. Future work, ideally involving many more trials of each possible probe color, will be necessary to settle this question.
To provide converging evidence against a verbal encoding strategy, we replicated our results while having participants perform an articulatory suppression task to see if the trade-offs would disappear when verbal encoding was made more challenging (n=16). Specifically, we had participants repeat the word ‘the’ at a 3 Hz rate to reduce participants’ ability to verbalize stimuli (Allen, Hitch, & Baddeley, 2009; Logie, Brockmole, & Jaswal, 2011). Importantly, we were still able to observe a trade-off when verbal encoding was discouraged. Guess rates were lower (20.7% (K=4.0 items) compared to 30.2% (K=3.5 items), t(15)=3.5, p=.003, Cohen’s d = .87) and quality was worse (29.0° compared to 23.8°, t(15)=2.2, p=.05, Cohen’s d = .54) in the get-them-all condition.
Experiment 2 – Quantity-quality trade-offs can occur during maintenance
The previous experiment demonstrates that participants can remember more items if properly motivated. In the next two studies we explore the locus of this effect, as working memory has multiple stages (Woodman & Vogel, 2005): To perform accurately, participants must encode items into working memory, store information over a short duration, and then successfully use this information to generate a response. Since participants knew the upcoming trial type, we were not able to determine which stage(s) of processing are affected by task manipulations. In Experiments 2 & 3 the standard and get-them-all tasks were intermixed in blocks, and we did not reveal the task type to participants until some point into the trial. In Experiment 2, participants were informed by a cue following stimulus presentation (post-encoding). In Experiment 3, participants were informed during the response stage (post-storage). To preview our results, we found evidence of a performance trade-off between the task types in Experiment 2, but not Experiment 3, suggesting that changes across tasks reflect differences in how the items were maintained.
Methods
Eighteen volunteers (11 females) between the ages of 18 and 28 participated for monetary compensation or course credit. Participants completed the experiment in two hour-long sessions run on separate days. Sessions consisted of 5 blocks (day 1) or 7 blocks (day 2) of 40 trials each. As before, there were two task types: standard task and get-them-all. In contrast to Experiment 1, the task types were now intermixed in blocks and the two were indistinguishable during the encoding interval (Figure 3). Task type was indicated by a cue (shown for 500ms) presented 300ms after stimulus offset. The cue was a white circle with either the number 1 (standard task) or the number 5 (get-them-all). Since participants may need a full second to adapt to the task cue (Oberauer, 2001) we increased the retention interval to 1500ms to increase the probability of the cue impacting memory maintenance. This experiment was identical to Experiment 1 in all other respects.
Figure 3.
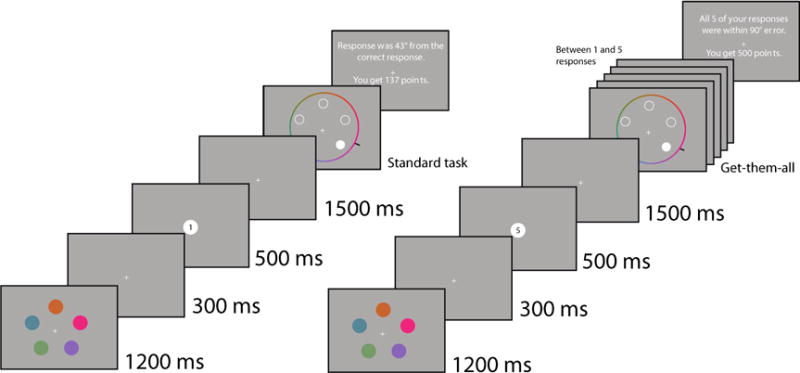
Trial timeline for Experiment 2. Left: Standard task trial. Right: Get-them-all task trial. Task type was indicated after encoding with a cue (“1” = report 1 item; “5” = get-them-all).
Results and Discussion
Report error distributions were modeled as a mixture of a circular normal and a uniform distribution to estimate the capacity and precision of memory for each task. Participants stored fewer items in the standard task than in the get-them-all task. Guess rates were 19.7% (K=4.01 items) in the standard task and 15.6% (K=4.22 items) in the get-them-all task, t(17)=3.9, p=.001, Cohen’s d = .92 (figure 4 left). In addition, memory quality was better (lower standard deviation estimates) in the standard task (24.0°) than in the get-them-all task (27.5°), t(17)=7.8, p<.001, Cohen’s d = .96 (figure 4 right).
Figure 4.

Experiment 2 results. A: Response error histograms for the standard task (left) and get-them-all task (right). The solid line indicates the best fitting mixture model of each condition. B: Model parameter estimates (based on the first response for each trial) for Experiment 2 for guess rate (left) and standard deviation (right) for the standard task (black) and get-them-all task (gray). Note that larger standard deviation values imply worse precision.
We compared the difference in parameter values across tasks for the current study relative to Experiment 1 (independent sample t-tests). There was some evidence for reduced trade-offs in this study. The change in guess rate was larger in Experiment 1 than Experiment 2, t(34) = 2.52, p < .02. However the change in precision did not differ, t(34) = 0.91, p = .37. Thus there is some evidence that trade-off effects are, perhaps unsurprisingly, weaker when the task cue is presented 300ms after stimulus offset.
Working memory is a dynamic process. Performance declines with longer durations between presentation and test (Gold et al., 2005; Magnussen, 2000; Phillips, 1974; Sperling, 1960; Vergauwe, Barrouillet, Camos, 2009; Yang, 1999; Zhang & Luck, 2011). In addition, there is evidence suggesting that information in working memory can be overwritten by a probe stimulus (Wheeler & Treisman, 2002; Sligte, Scholte, Lamme, 2008). The present findings suggest that we have strategic control over how working memory processes play out over time (see also Makovski & Jiang, 2007; Matsukura & Hollingworth, 2011; Williams, Hong, Kang, Carlisle, & Woodman, 2013; Williams & Woodman, 2012) perhaps resulting in a greater prioritization of quantity in the get-them-all task relative to the standard task.
These results replicate the trade-off found in Experiment 1. When the task encouraged participants to store more items we found lower guess rates but increased variation in responses around the target. This trade-off cannot be due entirely to differences in how stimuli were encoded, as we find a trade-off even when there were no differences between conditions during stimulus encoding.
Experiment 3 – No quantity-quality trade-offs during retrieval
The results of Experiments 1 and 2 demonstrate that performance in a simple color working memory task depends on whether the task encourages storing all the items or minimizing the average error of a response. Furthermore, we found that changes in task performance can occur beyond the initial encoding stage, during the storage and/or response stages. In Experiment 3 we determine whether the trade-off would be observed if participants were not informed of the task type until the response stage. Failure to observe a trade-off would support the conclusion that differences in tasks reflect differences in how items are encoded and actively maintained.
Methods
Eighteen volunteers (9 females) between the ages of 18 and 26 participated for money or course credit. This experiment was similar to Experiment 2 except that we moved the cue to appear only during the response stage (Figure 5). Data for one participant was removed because the individual guessed on over half the trials. Note that no other participants in all studies were close to this a priori cutoff (the next highest was 33%) and that this individual was greater than 5 standard deviations away from the global average.
Figure 5.
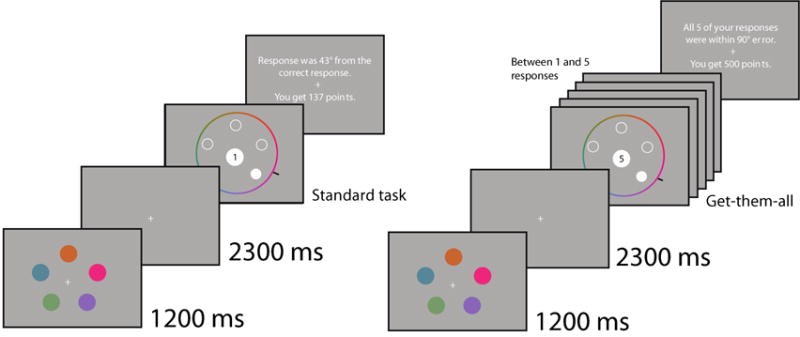
Trial timeline for Experiment 3. Left: Standard task trial. Right: Get-them-all task trial. Task type was indicated during response.
Results and Discussion
Report error distributions were modeled as a mixture of a circular normal and a uniform distribution to estimate the capacity and precision of memory in each task. Participants were just as likely to guess across both tasks (standard task: guess rate 15.4%, K=4.23 items; get-them-all task: guess rate 14.8%, K=4.26 items), t(16)=.48, p=.64, Cohen’s d = .12 (Figure 6 left). Even though there was no evidence of differences in quantity, there was some evidence for differences in quality. Standard deviation was marginally lower in the standard task (25.6°) than in the get-them-all task (27.1°), t(16)=1.80, p=.09, Cohen’s d = .43 (Figure 6 right).
Figure 6.

Experiment 3 results. A: Response error histograms for the standard task (left) and get-them-all task (right). The solid line indicates the best fitting mixture model of each condition. B: Model parameter estimates (based on the first response for each trial) for Experiment 3 for guess rate (left) and standard deviation (right) for the standard task (pink) and get-them-all task (blue). Note that larger standard deviation values imply worse precision.
One potential explanation for differences in quality is that participants were slightly less careful during motor responses in the get-them-all condition because it didn’t matter if they were off by a couple of degrees. Importantly, we find no evidence of a trade-off and the difference in standard deviation is small here compared to the previous studies. Indeed, not only was there no evidence of a trade-off, but the trade-offs that we did observe in Experiment 1 were significantly greater relative to the current study. To compare whether the tasks had a reduced influence for this task relative to Experiment 1 we compared the change in each parameter estimate across experiments (using independent sample t-tests). The present study showed reduced task effects for both guess rate, t(33) = 3.68, p < .001, and precision, t(33) = 2.14, p < .04.
The results suggest that the trade-offs in quality and quantity found in Experiments 1 and 2 cannot be explained by differences in retrieval strategies encouraged by each task. Note that we are not able to rule out the possibility that the trade-off manifests during retrieval, but that it requires preparation during the maintenance interval.
General Discussion
Contrary to the assumption that performance on working memory tasks reflects an immutable structural limit on memory capacity (Murray, et al. 2012; Zhang & Luck, 2011), we found evidence for strategic trade-offs between quantity and quality in working memory. We tested participants’ memory for colorful circles in two tasks. We used a standard task that was similar to continuous color report tasks used in many studies (Bays & Husain, 2008; Bays et al., 2009; Brady et al., 2013; Fougnie et al., 2010, 2012, 2013; Wilken & Ma, 2004; van Den Berg et al., 2012; Zhang & Luck, 2008, 2009, 2011). We contrasted the standard task with a novel variant that lowered demands on precision and strongly encouraged storage of all memory items. We found a trade-off—lower guess rate and worse precision in the get-them-all task—when the tasks were blocked (Experiment 1) and when the task condition was cued after encoding (Experiment 2), but not when the task was cued during response (Experiment 3). Taken together, these findings suggest that the encoding and maintenance operations that support working memory are, at least partially, under voluntary control and that an individual can store more items if properly motivated and if the optimal strategy is clear.
The present findings help constrain theories on working memory limits and to rule out models that suggest inflexibility in performance. According to one class of theories, termed slot models, performance limits arise because only a handful of items may be stored at once (Cowan, 2001, 2006; Luck & Vogel, 1997), and immutability in memory performance is used to infer immutability in storage limits (Machizawa, et al., 2012; Murray, et al., 2012; Zhang & Luck, 2011). Here we show that performance limits cannot purely reflect an immutable bound on storage capacity because participants were able to store more items when properly motivated. We have shown that estimates of the number of items in memory increase by about a half an item in the get-them-all task (the extent of increase may have been limited by ceiling effects). While it remains a matter of debate whether item capacity estimates are appropriate performance metrics (Ma, Husain, & Bays, 2014), this finding suggests caution in interpreting performance in these tasks as estimates of an immutable capacity limit.
The finding that quantity estimates increase under specific task instructions has important implications for slot models. Our results are not necessarily inconsistent with slot models, as there are potential explanations for the performance differences across tasks. For example, the task trade-offs could reflect that participants stored some items in multiple slots to improve precision in the standard condition (Zhang & Luck, 2008). Alternatively, slot models could accommodate these results by proposing that performance on working memory tasks is influenced by multiple memory systems. For example, performance limits on standard working memory tasks may arise from a contribution of memory for individual items and memory of global ensemble properties (Brady, Konkle, & Alvarez, 2011; Brady & Alvarez, 2011). Tasks that stress accurate representations might preferentially involve individual item representations while tasks that allow coarse representations could draw more on memories for ensembles. Importantly, these possibilities raise the issue of how one should estimate the number of memory slots from behavior, and what conclusions one is able to draw from capacity measures in standard tasks.
Another class of theories propose that memory storage is mediated by a flexible resource allocated based on task demands (Alvarez & Cavanagh, 2004; Bays & Husain, 2008; Wilken & Ma, 2004). In this framework, there is a cost for dividing memory resources: as the number of items increases, the precision with which each one is stored decreases. Given that low-resolution items appear more variable in quality (Fougnie, et al., 2012; van Den Berg, et al, 2012), and appear more difficult to retrieve or maintain (Brady et al., 2013), there is a high cost to storing more, lower-resolution items in memory. Thus, unless participants are properly motivated to store more items with less precision, their default strategy might favor storing fewer, more stable item representations. Critically, in this view the typical limit of about 3 items in memory reflects a strategic choice (the number of items that can be maintained with stability), as opposed to an immutable structural limit on the number of items that can be stored.
While the findings are not inconsistent with resource models, they do highlight some practical constraints. Participants were not able to remember all five items in the get-them-all task, suggesting that participants do not have boundless flexibility in allocating resources (Alvarez & Cavanagh, 2004). Indeed, the lack of flexibility in previous studies (e.g. Zhang & Luck, 2009) suggests that while storing items is possible, it may be more taxing or costly than is often assumed by resource models. And it is unclear how this flexibility interacts with memory load. Would we see the same flexibility if participants were asked to remember ten items (an amount far beyond item-limit estimates)? Further explorations on the limits of flexibility may offer a productive way of comparing theoretical models.
We found sizeable changes in the quantity and quality could be induced with a change to a standard continuous report task. We cannot be certain that we have observed the full limit of the flexibility of memory, or whether other task modifications could further induce participants to store more items. These findings raise questions regarding the extent to which the limits observed in any working memory task are the manifestation of a core cognitive limit as opposed to the modal cognitive setting optimized for the demands of particular laboratory tasks.
A final implication from our results is that we have strategic control over more than what gets encoded into working memory, but also in how memories unfold over time. While theoretical models often characterize visual working memory as a static state (but see Zhang & Luck, 2011), there is considerable evidence that the available information depends on temporal delay (Gold et al., 2005; Magnussen, 2000; Phillips, 1974; Sperling, 1960; Vergauwe, et al., 2009; Yang, 1999) and may be disrupted by the onset of new visual information (Sligte, et al., 2008; Wheeler & Treisman, 2002). In Experiment 2 we found that the task altered performance even after the task type was cued long after the stimuli were presented. This suggests that the temporal dynamics of working memory are under strategic control: observers can choose to maintain items that would otherwise be forgotten, at the cost of remembering items less well. This finding is consistent with other studies showing strategic control over the contents of memory over time (Makovski & Jiang, 2007; Matsukura & Hollingworth, 2011; Williams, et al., 2013; Williams & Woodman, 2012). Existing theories should consider the temporal properties of working memory and the degree to which these properties are under conscious control.
Conclusion
An assumption of many models is that performance limitations on working memory tasks arise due to structural limitations on storage capacity—we can only retain information about a few items, regardless of motivation. However, using a task that encouraged participants to remember more items, we found that participants were able to store more, but that items were not remembered as well. This trade-off in quantity versus quality suggests flexibility in the expression of memory limits. The typical limit of about three to four simple items does not reflect an immutable upper bound on storage capacity—if it did, then participants would be unable to adjust their encoding and maintenance strategy to remember more items. Just as we have learned about the nature of our working memory system by studying its limitations, an understanding of its flexibility may provide insights and constrain theory.
Supplementary Material
Acknowledgments
This work was supported by NIH grant 1F32EY020706 to D.F. and NIH grant R03-086743 to G.A.A.
Footnotes
The tasks have distinct names in the paper for clarity. These names were not conveyed to the participants, however there were instructions at the beginning of each block that indicated the differences between tasks.
References
- Allen RJ, Hitch GJ, Baddeley AD. Cross-modal binding and working memory. Visual Cognition. 2009;17(1–2):83–102. [Google Scholar]
- Alloway TP, Alloway RG. Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology. 2010;106(1):20–29. doi: 10.1016/j.jecp.2009.11.003. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Cavanagh P. The capacity of visual short-term memory is set both by visual information load and by number of objects. Psychological science. 2004;15(2):106–111. doi: 10.1111/j.0963-7214.2004.01502006.x. [DOI] [PubMed] [Google Scholar]
- Bae GY, Olkkonen M, Allred SR, Flombaum JI. Why Some Colors Appear More Memorable Than Others: A Model Combining Categories and Particulars in Color Working Memory. Journal of Experimental Psychology: General. 2015;144(4):744–763. doi: 10.1037/xge0000076. [DOI] [PubMed] [Google Scholar]
- Bae GY, Olkkonen M, Allred SR, Wilson C, Flombaum JI. Stimulus-specific variability in color working. Journal of Vision. 2014;14(4):1–23. doi: 10.1167/14.4.7. [DOI] [PubMed] [Google Scholar]
- Bays PM, Catalao RFG, Husain M. The precision of visual working memory is set by allocation of a shared resource. Journal of Vision. 2009;9:1–11. doi: 10.1167/9.10.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bays PM, Gorgoraptis N, Wee N, Marshall L, Husain M. Temporal dynamics of encoding, storage, and reallocation of visual working memory. Journal of Vision. 2011;11(10) doi: 10.1167/11.10.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brady TF, Alvarez GA. Hierarchical Encoding in Visual Working Memory Ensemble Statistics Bias Memory for Individual Items. Psychological Science. 2011;22(3):384–392. doi: 10.1177/0956797610397956. [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle TF, Gill J, Oliva A, Alvarez GA. Visual long-term memory has the same limit on fidelity as visual working memory. Psychological Science. 2013;24(6):981–990. doi: 10.1177/0956797612465439. [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle T, Alvarez GA. A review of visual memory capacity: Beyond individual items and towards structured representations. Journal of Vision. 2011;11:1–34. doi: 10.1167/11.5.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24(1):87–114. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Cowan N. Working memory capacity. Psychology Press; 2005. [Google Scholar]
- Cowan N, Elliott EM, Saults JS, Morey CC, Mattox S, Hismjatullina A, Conway ARA. On the capacity of attention: Its estimation and its role in working memory and cognitive aptitudes. Cognitive Psychology. 2005;51:42–100. doi: 10.1016/j.cogpsych.2004.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, Conway AR. Working memory, short-term memory, and general fluid intelligence: a latent-variable approach. Journal of experimental psychology: General. 1999;128(3):309. doi: 10.1037//0096-3445.128.3.309. [DOI] [PubMed] [Google Scholar]
- Fougnie D, Alvarez GA. Object features fail independently in working memory: Evidence for a probabilistic feature-store model. Journal of Vision. 2011;11:1–12. doi: 10.1167/11.12.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Asplund CL, Marois R. What are the units of storage in visual working memory? Journal of Vision. 2010;10(12):741. doi: 10.1167/10.12.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fougnie D, Cormiea SM, Alvarez GA. Object-based benefits without object-based representations. Journal of Experimental Psychology: General. 2013;142(3):621. doi: 10.1037/a0030300. [DOI] [PubMed] [Google Scholar]
- Fougnie D, Suchow JW, Alvarez GA. Variability in the quality of visual working memory. Nature Communications. 2012;3:1229. doi: 10.1038/ncomms2237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuda K, Vogel E, Mayr U, Awh E. Quantity, not quality: The relationship between fluid intelligence and working memory capacity. Psychonomic Bulletin & Review. 2010;17(5):673–679. doi: 10.3758/17.5.673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JM, Murray RF, Sekuler AB, Bennett PJ, Sekuler R. Visual memory decay is deterministic. Psychological Science. 2005;16(10):769–774. doi: 10.1111/j.1467-9280.2005.01612.x. [DOI] [PubMed] [Google Scholar]
- Huang L. Visual working memory is better characterized as a distributed resource rather than discrete slots. Journal of Vision. 2010;10(14):8. doi: 10.1167/10.14.8. [DOI] [PubMed] [Google Scholar]
- Irwin DE. Memory for position and identity across eye movements. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18(2):307. [Google Scholar]
- Kyllonen PC, Christal RE. Reasoning ability is (little more than) working-memory capacity?! Intelligence. 1990;14(4):389–433. [Google Scholar]
- Levin DT, Momen N, Drivdahl IV SB, Simons DJ. Change blindness blindness: The metacognitive error of overestimating change-detection ability. Visual Cognition. 2000;7(1–3):397–412. [Google Scholar]
- Logie RH, Brockmole JR, Jaswal S. Feature binding in visual short-term memory is unaffected by task-irrelevant changes of location, shape, and color. Memory & Cognition. 2011;39(1):24–36. doi: 10.3758/s13421-010-0001-z. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. The capacity of visual working memory for features and conjunctions. Nature. 1997;390(6657):279–281. doi: 10.1038/36846. [DOI] [PubMed] [Google Scholar]
- Luck SJ, Vogel EK. Visual working memory capacity: from psychophysics and neurobiology to individual differences. Trends in cognitive sciences. 2013;17(8):391–400. doi: 10.1016/j.tics.2013.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma WJ, Husain M, Bays PM. Changing concepts of working memory. Nature neuroscience. 2014;17(3):347–356. doi: 10.1038/nn.3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machizawa MG, Goh CC, Driver J. Human visual short-term memory precision can be varied at will when the number of retained items is low. Psychological science. 2012;23(6):554–559. doi: 10.1177/0956797611431988. [DOI] [PubMed] [Google Scholar]
- Makovski T, Jiang YV. Distributing versus focusing attention in visual short-term memory. Psychonomic bulletin & review. 2007;14(6):1072–1078. doi: 10.3758/bf03193093. [DOI] [PubMed] [Google Scholar]
- Magnussen S. Low-level memory processes in vision. Trends in neurosciences. 2000;23(6):247–251. doi: 10.1016/s0166-2236(00)01569-1. [DOI] [PubMed] [Google Scholar]
- Murray AM, Nobre AC, Astle DE, Stokes MG. Lacking control over the trade-off between quality and quantity in visual short-term memory. PloS one. 2012;7(8):e41223. doi: 10.1371/journal.pone.0041223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noe A, Pessoa L, Thompson E. Beyond the grand illusion: What change blindness really teaches us about vision. Visual Cognition. 2000;7(1–3):93–106. [Google Scholar]
- Oberauer K. Removing irrelevant information from working memory: a cognitive aging study with the modified Sternberg task. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27(4):948. [PubMed] [Google Scholar]
- O’Regan JK. Solving the “real” mysteries of visual perception: The world as an outside memory. Special issue: Object perception and scene analysis. Canadian Journal of Psychology. 1992;46(3):461–488. doi: 10.1037/h0084327. [DOI] [PubMed] [Google Scholar]
- Phillips WA. On the distinction between sensory storage and short-term visual memory. Perception and Psychophysics. 1974;16:283–290. [Google Scholar]
- Prinzmetal W, Amiri H, Allen K, Edwards T. The phenomenology of attention. Part 1: Color, location, orientation, and “clarity.”. Journal of Experimental Psychology: Human Perception and Performance (in press) [Google Scholar]
- Rensink RA. Visual search for change: A probe into the nature of attentional processing. Visual Cognition. 2000;7(1–3):345–376. [Google Scholar]
- Rensink RA. Change detection. Annual Review of Psychology. 2002;53(1):245–277. doi: 10.1146/annurev.psych.53.100901.135125. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Morey RD, Cowan N, Zwilling CE, Morey CC, Pratte MS. An assessment of fixed-capacity models of visual working memory. Proceedings of the National Academy of Sciences. 2008;105(16):5975–5979. doi: 10.1073/pnas.0711295105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons DJ, Chabris CF. Gorillas in our midst: Sustained inattentional blindness for dynamic events. Perception-London. 1999;28(9):1059–1074. doi: 10.1068/p281059. [DOI] [PubMed] [Google Scholar]
- Simons DJ, Levin D. Change blindness. Trends in Cognitive Science. 1997;1:261–267. doi: 10.1016/S1364-6613(97)01080-2. [DOI] [PubMed] [Google Scholar]
- Sims CR, Jacobs RA, Knill DC. An ideal observer analysis of visual working memory. Psychological review. 2012;119(4):807. doi: 10.1037/a0029856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sligte IG, Scholte HS, Lamme VAF. Are There Multiple Visual Short-Term Memory Stores? PLoS ONE. 2008;3(2):e1699. doi: 10.1371/journal.pone.0001699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling G. The information available in brief visual presentations. Psychological Monographs. 1960:74. [Google Scholar]
- Swan G, Wyble B. The binding pool: A model of shared neural resources for distinct items in visual working memory. Attention, Perception, & Psychophysics. 2014:1–22. doi: 10.3758/s13414-014-0633-3. [DOI] [PubMed] [Google Scholar]
- Suchow JW, Brady TF, Fougnie D, Alvarez GA. Modeling visual working memory with the MemToolbox. Journal of vision. 2013;13(10) doi: 10.1167/13.10.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd JJ, Marois R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 2004;428(6984):751–754. doi: 10.1038/nature02466. [DOI] [PubMed] [Google Scholar]
- van den Berg R, Shin H, C WC, George R, Ma WJ. Variability in encoding precision accounts for visual short-term memory limitations. Proceedings of the National Academy of Sciences. 2012;109:8780–8785. doi: 10.1073/pnas.1117465109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergauwe E, Barrouillet P, Camos V. Visual and spatial working memory are not that dissociated after all: a time-based resource-sharing account. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2009;35(4):1012. doi: 10.1037/a0015859. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Machizawa MG. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428(6984):748–751. doi: 10.1038/nature02447. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, Luck SJ. Storage of features, conjunctions, and objects in visual working memory. Journal of Experimental Psychology: Human Perception and Performance. 2001;27(1):92–114. doi: 10.1037//0096-1523.27.1.92. [DOI] [PubMed] [Google Scholar]
- Wheeler ME, Treisman AM. Binding in short-term visual memory. Journal of Experimental Psychology: General. 2002;131(1):48–64. doi: 10.1037//0096-3445.131.1.48. [DOI] [PubMed] [Google Scholar]
- Wilken PA, Ma WJ. A detection theory account of change detection. Journal of Vision. 2004;4:1120–1135. doi: 10.1167/4.12. [DOI] [PubMed] [Google Scholar]
- Williams M, Hong SW, Kang MS, Carlisle NB, Woodman GF. The benefit of forgetting. Psychonomic bulletin & review. 2013;20(2):348–355. doi: 10.3758/s13423-012-0354-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams M, Woodman GF. Directed forgetting and directed remembering in visual working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2012;38(5):1206. doi: 10.1037/a0027389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodman GF, Vogel EK. Fractionating Working Memory Consolidation and Maintenance Are Independent Processes. Psychological Science. 2005;16(2):106–113. doi: 10.1111/j.0956-7976.2005.00790.x. [DOI] [PubMed] [Google Scholar]
- Woodman GF, Vogel EK. Top-down control of visual working memory consolidation. Psychonomic Bulletin & Review. 2005;15:223–229. doi: 10.3758/pbr.15.1.223. [DOI] [PubMed] [Google Scholar]
- Yang W. Lifetime of human visual sensory memory: Properties and neural substrate. 1999. University of Pennsylvania Institute for Research in Cognitive Science Technical Report No. IRCS-99-03. [Google Scholar]
- Zhang W, Luck S. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453(7192):233–23. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. Sudden death and gradual decay in visual working memory. Psychological Science. 2009;20(4):423–428. doi: 10.1111/j.1467-9280.2009.02322.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, Luck SJ. The Number and Quality of Representations in Working Memory. Psychological Science. 2011;22(11):1434–1441. doi: 10.1177/0956797611417006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


