Effect of sampling rate and filter settings on High Frequency Oscillation detections

Abstract

Objective

High Frequency Oscillations (HFOs) are being studied as a biomarker of epilepsy, yet it is unknown how various acquisition parameters at different centers affect detection and analysis of HFOs. This paper specifically quantifies effects of sampling rate (FS) and anti-aliasing filter (AAF) positions on automated HFO detection.

Methods

HFOs were detected on intracranial EEG recordings (17 patients) with 5 kHz FS. HFO detection was repeated on downsampled and/or filtered copies of the EEG data, mimicking sampling rates and low-pass filter settings of various acquisition equipment. For each setting, we compared the HFO detection sensitivity, HFO features, and ability to identify the ictal onset zone.

Results

The relative sensitivity remained above 80% for either FS ≥2 kHz or AAF ≥500 Hz. HFO feature distributions were consistent (AUROC<0.7) down to 1 kHz FS or 200 Hz AAF. HFO rate successfully identified ictal onset zone over most settings. HFO peak frequency was highly variable under most parameters (Spearman correlation <0.5).

Conclusions

We recommend at least FS ≥2 kHz and AAF ≥500 Hz to detect HFOs. Additionally, HFO peak frequency is not robust at any setting: the same HFO event can be variably classified either a ripple (<200 Hz) or fast ripple (> 250 Hz) under different acquisition settings.

Significance

These results inform clinical centers on requirements to analyze HFO rates and features.

1. Introduction

High frequency oscillations (HFOs) are short, rare events with high power in approximately 80–500 Hz and have been suggested as a biomarker of epilepsy (Bragin et al., 2002; Engel et al., 2009; Wu et al., 2010; Blanco et al., 2011; Park et al., 2012; Haegelen et al., 2013; Kerber et al., 2014). Research often focuses on HFOs as a biomarker of ictal onset tissue (Cho et al., 2014; Dumpelmann et al., 2014; Malinowska et al., 2014; Okanishi et al., 2014; Gliske et al., 2016). HFOs have also been considered as a biomarker of a pre-ictal state (Pearce et al., 2013; Malinowska et al., 2014). Most prior HFO studies require offline processing of high temporal resolution EEG. This processing is either done manually (Urrestarazu et al., 2007) or using automated algorithms (Blanco et al., 2011; Pearce et al., 2013; Gliske et al., 2016). However, as HFOs have gained considerable favor as a potential clinical biomarker (Jacobs et al., 2012), the need to implement them in the clinical realm is becoming more pressing. Regardless of the mechanism by which HFOs become available to more clinicians, it is imperative to account for the inevitable differences that exist between different acquisition systems. The most obvious example is that many HFO studies utilized high temporal resolution acquisition systems sampling up to 30,000 Hz, yet now many EEG companies are offering sampling rates of 1,000–16,000 Hz within the clinical hardware—will these newer clinical systems successfully record HFOs? The objective of this paper is to analyze this question by quantifying how sampling rate and anti-aliasing filter (AAF) parameters affect HFO detection and analysis. We then propose guidelines that will assure acquisition equipment has sufficient accuracy to allow comparison with past HFO research.

In order to compare the effect of various sampling rates on the same data set, we analyze “gold standard” 5 kHz intracranial EEG data, then perform similar analyses on the same data after downsampling and/or low-pass filtering to simulate different acquisition parameters. In this manner, we can directly compare each HFO detection in the original 5 kHz data sample with the HFO detections at the other sampling rates and AAF settings. This analysis allows direct comparison of the number of HFOs detected in each paradigm, using each channel as its own internal gold standard. It also provides insight into how acquistion settings affect HFO correlation with patient outcomes and the measured signal properties of the HFOs. This paper utilizes data from 17 patients from two centers, representing 1.5 million interictal HFOs at 5 kHz and over 68 days of interictal recording time.

2. Methods

2.1. Patient population

EEG data from patients who underwent intracranial EEG monitoring were selected from the IEEG Portal (Wagenaar et al., 2015) and from the University of Michigan. All patients had intracranial subdural or depth electrodes manufactured by either PMT (Chanhassen, MN) or Ad-Tech (Racine, WI), with standard electrode size and spacing. From the IEEG Portal, all patient data available in May 2014 were searched for the following inclusion criteria: sampling rate of at least 5,000 Hz, a recording time of over two hours including at least one hour of interictal data, data recorded with traditional, clinical intracranial electrodes, and metadata regarding the resected volume (RV) or clinically determined epileptogenic zone. Patients that had both macro- and microelectrode recordings were included, but the microelectrode data were not analyzed herein. This yielded nine patients, which had all been recorded at the Mayo Clinic using a Neurolynx (Bozeman, MT) acquisition system with sampling rate of 32 kHz and 9 kHz cutoff frequency AAF (Worrell et al., 2008), then later downsampled to 5 kHz when stored to the Portal. Of these nine patients, eight have been analyzed in previous publications (Blanco et al., 2010; Blanco et al., 2011; Pearce et al., 2013; Gliske et al., 2016). Additionally, data from eight patients at the University of Michigan were recorded at 30 kHz (Blackrock, Salt Lake City, AAF 10 kHz) and down-sampled to 5 kHz, resulting in a total patient population of 17. Four of the eight Michigan patients were previously analyzed (Gliske et al., 2016), but with a 3 kHz rather than 5 kHz sampling rate. The downsampling procedure, used for all patients' data, included a lowpass filter at 2 kHz. Of the 17 patients, nine were known to have undergone resection with ILAE Class I surgery outcome. One of these patients had the entire region resected (MC-12), and thus eight Class I patients are usable for assessing the correlation between HFOs and RV. These eight patients are hereafter labeled the “good surgery outcome patients”. For three of the Michigan patients (UM-05, UM-07, UM-08), one 24-hour block of interictal data was also analyzed at 30 kHz, 15 kHz, and 10 kHz sampling rates, to verify that the chosen 5 kHz “gold standard” sampling rate is sufficiently high.

All patients were adults with refractory epilepsy who underwent long-term monitoring in preparation for resective surgery. All data were acquired with approval of local IRB and all patients consented to share their deidentified data. Further details about the patient population and attribution for studies on the IEEG portal are provided in Table 1.

Table 1.

Patient table. Note that patients MC-01 to MC-08 correspond to patients SZ01–SZ08 in Blanco et al. (2011), and subject identifiers match that of Gliske et al (2016). MC patients were recorded with a Neuralynx acquisition system and UM patients were recorded with a Blackrock acquisition system. Age for the MC patients is based on Blanco et al. (2011). Interictal time per patient and number of qHFOs is were limited to high quality data times.

Subject	IEEG.org Identifier	Age	Sex	Num. Elec. (Subd., Dep.)	Interictal Time [hr:min]	Num. of Interictal qHFOs	qHFO Rate [min−1 chan−1]	ILAE Score	Seizure Focus
MC-01	I001_P034_D01	35	F	40, 0	7:20	5,509	0.31	1	FL
MC-03	I001_P012_D01	21	F	28, 8	1:45	334	0.09	5	TL
MC-06	I001_P016_D01	42	M	23, 0	19:39	2,733	0.10	1	PL
MC-10	I001_P001_D01	†	M	55, 7	92:45	98,341	0.29	5	TL
MC-11	I001_P002_D01	†	F	0, 15	114:45	59,566	0.58	†	MTL
MC-12	I001_P005_D01	†	M	28, 8	32:55	5,738	0.08	1	TL
MC-16	I001_P010_D01	†	F	48, 8	39:50	6,679	0.05	†	TL
MC-17	I001_P013_D01	†	F	72, 0	39:48	9,889	0.06	1	PL
MC-18	I001_P019_D01	†	M	16,0	50:24	4,020	0.08	†	TL
UM-01	UMich-001-01	23	M	75, 0	19:56	109,669	1.22	5	FL/PL
UM-02	UMich-002-01	46	M	95, 0	64:22	441,214	1.20	1	OL
UM-03	UMich-003-01	43	M	41, 0	129:12	276,167	0.87	1	LF
UM-04	UMich-004-01	26	F	61, 20	42:25	69,236	0.34	1	TL
UM-05	UMich-005-01	37	F	61, 0	192:57	72,546	0.10	NA	TL
UM-06	UMich-006-01	26	F	0, 20	22:52	42,725	1.56	NA	TL
UM-07	UMich-007-01	38	M	96, 0	220:59	115,472	0.09	1	TL/PL
UM-08	UMich-008-01	25	F	61, 0	159:14	195,814	0.34	1	TL
TOTAL				784, 102	1251:06	1,515,652

^†Unknown. Num. Elec.: number of electrodes. Subd.: subdural, i.e., cortical surface. Dep.: depth. qHFOs: quality high frequency oscillations. FL: frontal lobe. PL: parietal lobe. OL: occipital lobe. TL: temporal lobe. MTL: medial temporal lobe.

For each patient, the RV was determined based on official clinical reports, written by the treating physicians/surgeons. Patients UM-02 and UM-03 had multiple subpial transections in addition to resection, as the clinical ictal onset zone was found to extend to eloquent areas. For the purposes of this paper and identifying the ictal onset zone, these regions are considered part of the RV as they represent surgically modified regions. We also note that, while HFOs are used in a pseudo-prospective fashion to identify the ictal onset zone prior to resection, the verification is performed after surgical resection, in which case it is actually the theoretical “epileptogenic zone” that has been removed, which may be larger than the clinical onset zone (Luders et al., 2008). However, for the remainder of this paper only the term “ictal onset zone” will be used for simplicity.

2.2. HFO detections

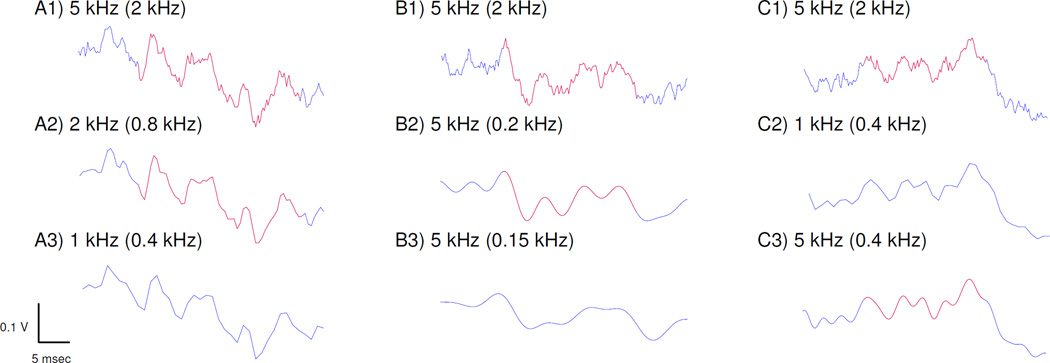
To investigate the effect of sampling rate on HFO detections, the 5 kHz data were downsampled to either 500 Hz, 1 kHz, 2 kHz, 2.5 kHz, or 4 kHz. We chose these values to span the common range of acquisition equipment that might be considered for HFO detections. For sampling rates that are downsampled by an integer factor, the Matlab (Mathworks, Natick, MA) function downsample was used, which applies a Chebyshev lowpass filter at 0.4 times the desired frequency as an AAF and then resamples the data at a given integer factor. For the other two sampling rates (2 kHz and 4 kHz), a custom function was designed using identical filters but including linear interpolation in the resampling step. The qHFO detection method (Gliske et al., 2016) was applied to the 5 kHz data to establish a gold standard for HFOs, artifacts, and data quality. This method was previously manually validated by expert reviewers, using patients from both centers that were included among the patient cohort of this study (Gliske et al., 2016). The qHFO method utilizes a common average reference, calculates baseline HFO detections with a sensitive HFO detector (in this case, the Staba HFO detector (Staba et al., 2002)) then excludes those detections that are coincident with automatically-detected artifacts and low-quality data. Note, the Staba detector identifies HFOs by using a bandpass filter in 80–500 Hz, and identifies times where the rectified signal is over five standard deviations from baseline, rejecting detections with less than 6 peaks. For sampling rates other than 5 kHz, the HFO detection step was performed independently on the data from each sampling rate, but the same set of artifact and data-quality detections from the 5 kHz data are used, rather than recomputing all of these detections at the lower sampling rate. The rationale is that the focus of this work is the effect of sampling rate upon just the HFO detections, and we desired to remove the confounding factor of the sampling rate's effect upon the data quality assessment. Note, the Staba HFO detector utilizes a bandpass filter with an upper threshold of 500 Hz. In cases where 500 Hz was above the Nyquist frequency, 0.4 times the sampling rate was used as the upper edge for the band pass filter to compute Staba detections. To investigate the effect of the AAF, Staba HFO detections were again computed using the 5 kHz data, but in this case an additional lowpass filter was applied before using the Staba HFO detector. A 10th order, bidirectional Butterworth filter was used to apply AAFs at nine positions spanning 100 Hz to 1 kHz. Note that these calculations used the original 5 kHz data without any of the above downsampling. The type and order of filter is representative of filters commonly used in commercial acquisition systems. In all cases, data were processed using Matlab and the General Data Flow Package (Gliske et al., 2016). Example detected HFOs are shown in Fig. 1, focusing on cases where the HFO was not detected over the full range of sampling rates and AAF positions.

Figure 1. Example HFO detections.

Detected HFOs are shown in red. (A) HFO detected in the original data (A1) is still detected when downsampled to 2 kHz (A2) but not at 1 kHz (A3). Note the low pass filter settings in parentheses, which are created by the Chebyshev filter in the downsampling procedure at 0.4 times the sampling rate. (B) Another original HFO (B1) is still detected when sampling rate remains at 5 kHz and a Butterworth antialiasing filter (AAF) is applied at 200 Hz (B2) but is not detected at 150 Hz (B3). (C) The variability in detection is not simply due to filter setting. In this case, the original HFO (C1) is not detected when downsampled to 1 kHz (C2) but is detected when 5 kHz data are filtered to the same level (C3, 0.4 kHz). Note the clear difference in data quality between C2 and C3 due to sampling rate.

HFOs occuring within 30 minutes of seizures were redacted as not interictal (Pearce et al., 2013; Gliske et al., 2016). To limit times of low data quality (which affects the denominator when computing the HFO rate), the mean qHFO rate per channel was computed for each gold standard data file, each file containing 5–120 minutes, with 30 minutes typical for UM patients and 120 minutes typical for MC patients. Files with a rate less than 0.01 qHFOs / min / channel were not analyzed.

2.3 Relative sensitivity of HFO detections

To quantify how many HFO events are detected by using the different settings, we calculate the relative sensitivity of gold standard events that are also detected at the lower sampling rate or AAF position. The relative sensitivity at a given setting is calculated as the fraction of gold standard qHFO detections that overlap (time and channel) with at least one detection at the lower setting, across all channels in a given patient. The relative sensitivity is computed per patient and then averaged over patients.

Additionally, we stratified the relative sensitivity within or outside the clinically-determined ictal onset zone and resected volume, using data from the patients with good surgical outcomes. A χ² test was used to assess whether the difference between inside and outside each region was greater than the inter-patient variability and the Wilcoxon Signed Rank test was used to assess whether the sensitivity was significantly higher for within versus without the given regions.

2.4. HFO features

Eight HFO features were considered for the following studies: duration, amplitude (sum of the squared sample values), mean line length per msec (mean of the absolute value of the difference between consecutive samples times the sampling rate), peak frequency, and power in four frequency bands (80–125 Hz, 125–150 Hz, 150–175 Hz, 145–200 Hz). The peak frequency and power in the frequency bands was computed by first computing the energy spectral density (ESD) via Thomson's Multitaper method (Matlab's pmtm function). The peak frequency was defined as the frequency at which the peak with maximal power occurs in the ESD between 80 Hz and 500 Hz (AAF scan) or (FS scan) the minimum of 500 Hz or 0.4 times the sampling rate (the imposed AAF due to downsampling). The power in the frequency bands was computed by the RMS of the ESD for the given frequency ranges. Note, all features are computed on the raw waveforms (as opposed to computing after applying a 80–500 Hz bandpass filter), using a common average reference.

We assess how the acquisition setting affected the features of detected HFOs at both the population and individual HFO level. There are two primary effects. First, the relative sensitivity can be feature-dependent, which would appear as a selection bias in which only a subset of the HFOs, which specific features, is detected. Second, different sampling rates or AAF positions can distort the signal, in which case the HFO may or may not be detected, and will have a different appearance and features. While both effects are present at the population level, only the latter is present at the individual HFO level.

At the population level, we compare distributions of HFO features using the area under the receiver operator curve (AUROC). This measure demonstrates whether it is possible to classify which acquisition setting (gold standard vs. a given, alternate setting) was used when analyzing a given feature. We cannot foresee all the various scenarios where one might be classifying HFOs based on features. However, if a given feature does not distinguish the acquisition setting used for recording HFOs, then it is likely that the choice of acquisition setting will not be a confounding factor when using the same feature for another classification problem. AUROC values range from 0.5 to 1.0, with 0.5 implying indistinguishable distributions and 1.0 implying completely separable distributions. The optimal value in the context of this paper is 0.5, as we desire the HFO feature distribution at lower settings to be similar to those in the gold standard. An AUROC value less than 0.7 was used as the threshold for acceptable amount of change to the feature distribution.

At the individual HFO level, we use the Spearman correlation coefficient to assess whether the feature of a given HFO computed at one setting is correlated with the same feature of the same HFO computed a different setting. Specifically, to compute the Spearman correlation coefficient for a given acquisition setting, we limit the analysis to “matched” HFOs—HFOs that were detected in both the gold standard data and the given alternate acquisition setting. Each HFO in this set has two sets of features—those computed using a) the detection range and waveform from the gold standard data, and b) the detection range and waveform from the other acquisition setting. We can then compute the correlation between feature set (a) versus (b). Spearman's correlation coefficient was selected as nonlinear monotonic changes to HFO features are likely not to effect classification performance. Spearman's correlation coefficient measures the similarity between two variables, allowing for monotonic changes over the sample, and takes values between −1 (perfect anti-correlation) and 1 (perfect correlation), with values near zero being no correlation. Instead of selecting a fixed threshold value a priori, we base our decision of sufficiently high correlation based on the observed asymptotic values.

2.5. Impact on identifying the ictal onset zone

One of the main clinical uses of HFOs being investigated is the identification of the ictal onset zone. Such identification is traditionally performed by expert reviewers who analyze the standard intracranial EEG to find which electrodes are first activated in seizures, which we refer to herein as the “clinically-identified ictal onset zone.” However that determination is still just an approximation, and is limited by the sparse electrode coverage inherent in intracranial EEG. One of the primary goals of analyzing HFOs is to use them to improve identification of the ictal onset zone, which might be different from the clinical determination. Therefore we also compare the ictal onset zone as predicted by HFO rates alone, without any human interpretation. We applied our previously published automated method (Gliske et al., 2016), without any retuning or adjustment, to all data equally from each good surgery outcome patient for each sampling rate and AAF setting. This method automatically identifies any channels that are anomalously higher in HFO rate than the rest (labeling them as “identified ictal onset zone”), or makes no assignation (i.e. chooses “no electrodes”) if none meet the criteria. The results for each acquisition setting were then compared descriptively.

2.6. Verification of Gold Standard Sampling Rate Selection

In order to assess whether the 5 kHz “gold standard” is a sufficiently high sampling rate, one day of interictal data from each of three patients (UM-05, UM-07, and UM-08) was analyzed at higher sampling rates: 10 kHz, 15 kHz and the original 30 kHz. The 5 kHz data was still used for detecting artifacts, but the relative sensitivity was again computed relative to these higher sampling rates. The results are shown in Table 2. The relative sensitivities for sampling rates less than 5 kHz are within a few percent regardless of the choice of standard reference, and relative sensitivities seem to approach an asymptotic value >90% for sampling rates >3 kHz. Thus, 5 kHz sampling rate is a sufficiently high gold standard.

Table 2.

Relative sensitivities at different sampling rates. For each choice of standard reference (rows), the data were then downsampled to various levels (columns) and the relative sensitivity calculated (i.e. the proportion of HFOs detected at the lower rate). The top row is the 5 kHz gold standard used for the rest of the paper. Values are given as mean with standard error of the mean in parenthesis. Note, the 5 kHz row is identical to Fig. 1A and uses all 17 patients, whereas the higher sampling rate rows (10, 15, 20 kHz) utilize only 24 hours each of three patients (UM-05, UM-07, UM-08).

	500 Hz	1 kHz	2 kHz	3 kHz	4 kHz	5 kHz	10 kHz	15 kHz
5 kHz	0.19 (0.02)	0.60 (0.04)	0.83 (0.02)	0.90 (0.02)	0.94 (0.01)	1
10 kHz	0.17 (0.04)	0.57 (0.05)	0.79 (0.03)	0.87 (0.02)	0.91 (0.02)	0.94 (0.02)	1
15 kHz	0.17 (0.04)	0.57 (0.05)	0.79 (0.02)	0.87 (0.02)	0.91 (0.02)	0.94 (0.01)	0.97 (0.01)	1
20 kHz	0.17 (0.04)	0.57 (0.05)	0.79 (0.02)	0.87 (0.02)	0.90 (0.01)	0.93 (0.01)	0.97 (0.01)	0.98 (0.01)

3. Results

3.1. Effect of acquisition settings on HFO detection

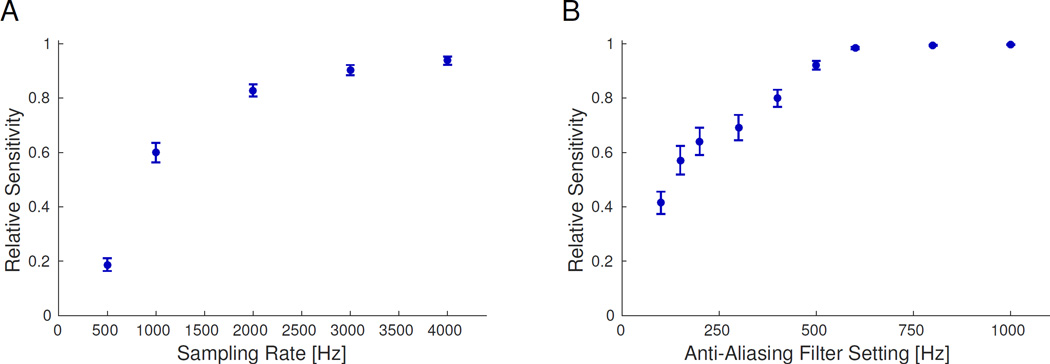
Figure 2 presents the relative sensitivity as a function of sampling rate (Fig. 2A) and AAF position (Fig. 2B). For sampling rate, the relative sensitivity is fairly flat above 3 kHz, though 2 kHz is still quite high (83%). For AAF position, however, the relative sensitivity is near 100% for all positions above 500 Hz (note that the AAF calculations were all done with sampling rate of 5 kHz). These results did not change when stratifying by channels within and without the resected volume (RV) or clinically determined ictal onset zone (not shown), nor did results change qualitatively when stratifying by electrode type (subdural versus depth) or hospital of origin. Although the relative sensitivity was slightly higher within the RV (p < 0.001, Wilcoxon signed rank test), the change was not significant relative to the inter-patient variability (p < 0.7, χ² test). The difference in relative sensitivities within versus without the clinically determined ictal onset zone failed to reach statistical significance for either test. Thus, these results indicate that sampling rates at least 2 kHz and AAF at least 500 Hz are sufficient to identify HFOs, and their effects are similar across all recorded channels.

Figure 2. Effect of acquisition parameters on HFO detection.

Overall relative sensitivity sensitivity for each considered sampling rate (A) and anti-aliasing filter (AAF) position (B). The sensitivity is the proportion of HFOs detected at each setting in relation to the gold standard (5000 Hz sampling and 2000 Hz AAF). Error bars are the standard error on the mean. Note, the sensitivity reaches a nearly asymptotic limit for ≥2 kHz sampling rate and >500 Hz AAF.

3.2 Effect of acquisition settings on HFO Features

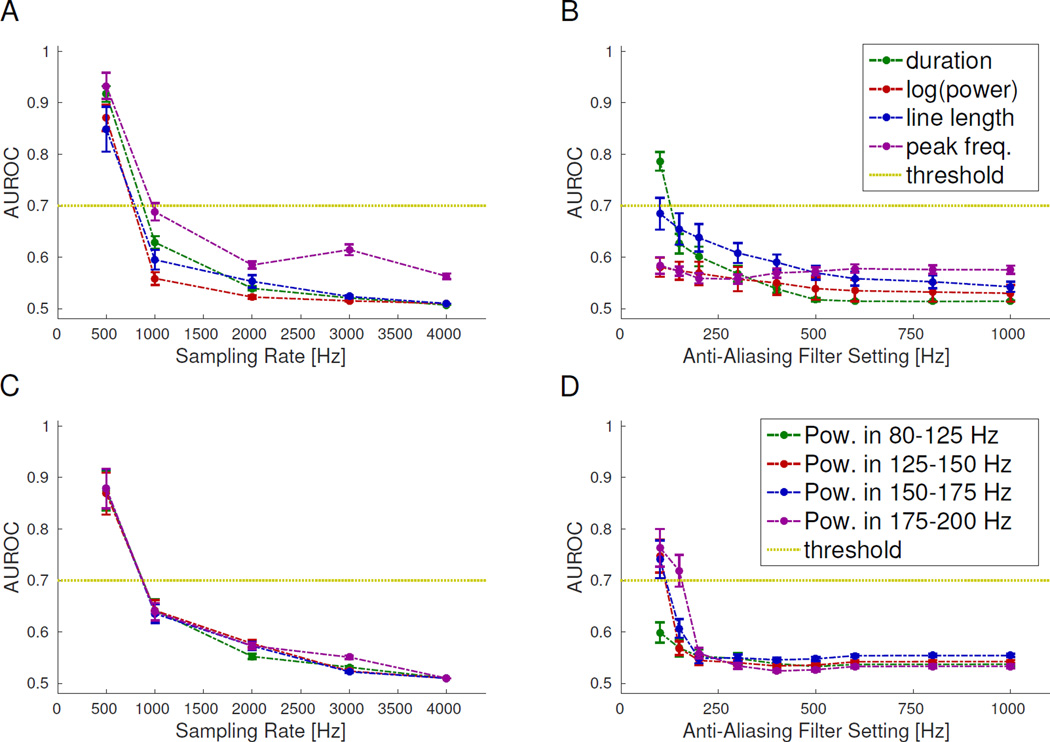
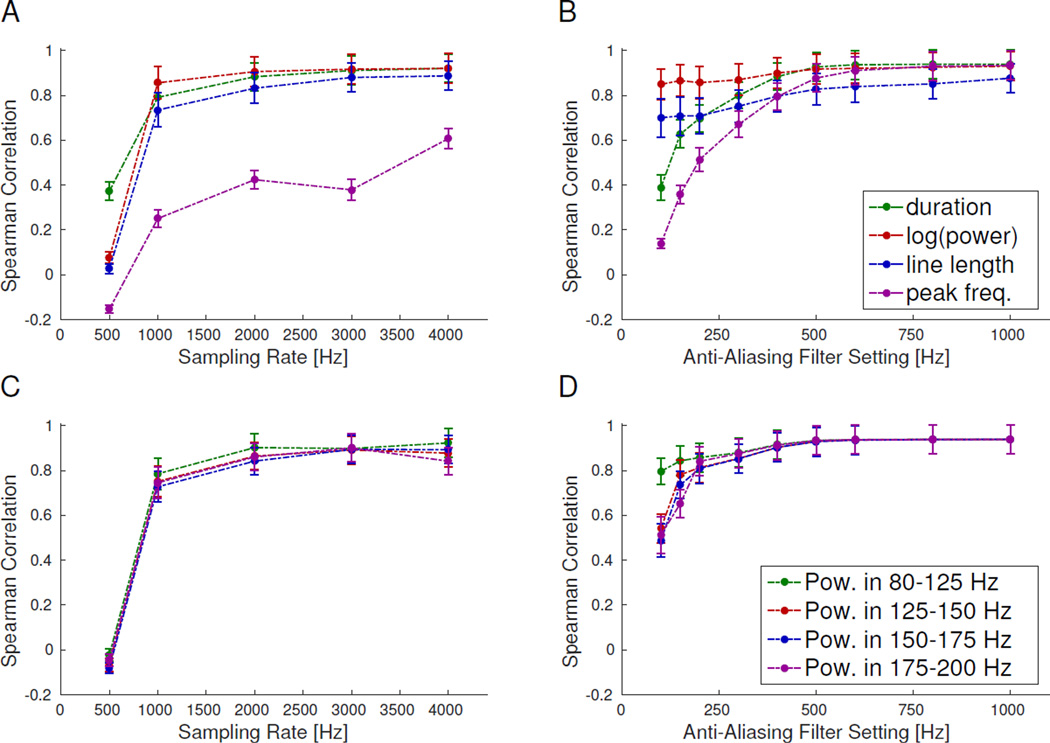
Analysis of HFO features is thought to be the next major step in improving their utility; thus, we assessed the effect of sampling rate and AAF positions on several common HFO features. It is important to point out that for this feature analysis, we did not use the bandpass filter when computing the features. Thus, while the detector identifies the temporal location of each HFO by applying a bandpass filter to the data, we compute the HFO features using the raw data before bandpass filtering. The AUROC quantified the alterations in the HFO feature distributions at the population level (Fig. 3); where values < 0.7 indicate that the lower-resolution data are essentially indistinguishable from the gold standard, which is the desired situation. While there is a gradual change in all features with lower settings, we deem the change acceptable for sampling rates of 1 kHz or greater (Fig. 3A and 3C) and for AAF greater than 200 Hz (Fig. 3B and 3D). As expected, the power in the frequency bands is unaffected by AAF positions outside each given frequency band. On the individual HFO level, the HFO features are fairly stable over a broad range (Fig 4). Note that for the Spearman correlation, higher values indicate the lower resolution data correlate well with the gold standard. For most features, the asymptotic value of the Spearman correlation is >0.7, occurring with sampling rates ≥1 kHz and AAF ≥500 Hz. However, the correlation for peak-frequency is significantly lower than for the other features for all lower sampling rates tested (<0.7 even at 4 kHz, Fig. 4A).

Figure 3. Comparison of HFO feature distributions.

Area under the receiver operator curve (AUROC) between HFO feature distributions for the gold standard versus other sampling rates (A&C) or anti-aliasing filter (AAF) positions (B&D). A low AUROC (<0.7, dashed line) is desirable, meaning the data at lower settings is difficult to distinguish from the gold standard data. All AUROC values are below this threshold for ≥1 kHz sampling rate and ≥200 Hz AAF. Error bars are the standard error on the mean.

Figure 4. Correlation between individual HFO features.

Spearman correlation of HFO features between gold standard and other sampling rates (A&C) or anti-aliasing filter (AAF) positions (B&D) shows how individual HFOs change with different settings. The correlation is between the same feature being computed on the same HFO, but using the waveform with different sampling rates or AAF positions. All features reach a near asymptotic limit for ≥1 kHz sampling rate and >500 Hz AAF, and most features have similar behavior at different settings. However, peak frequency has considerably worse correlation with lower sampling rates. Error bars are the standard error on the mean.

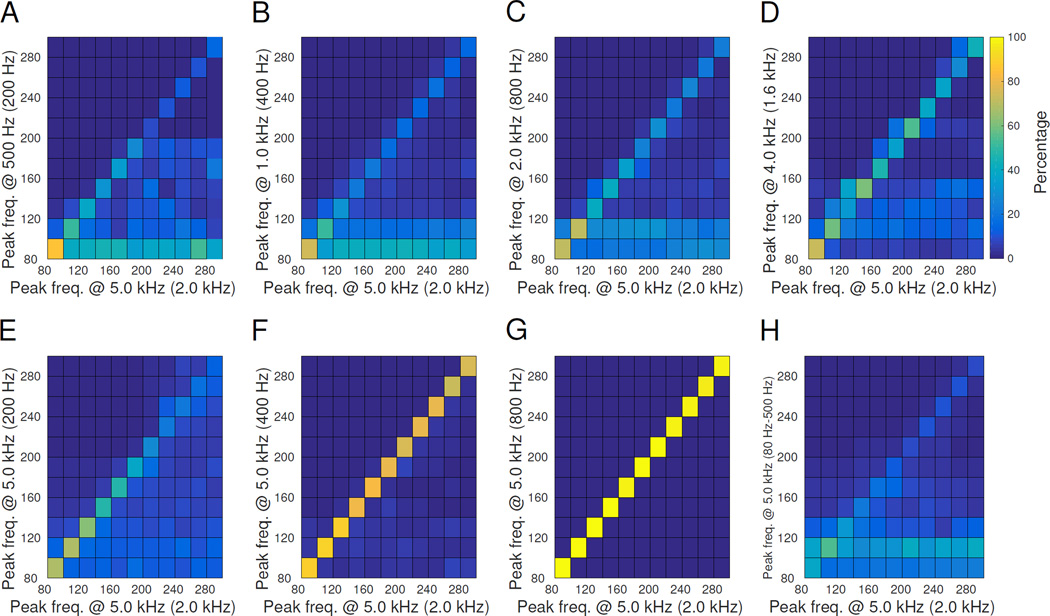
To further investigate the unexpectedly low correlation of peak frequency, we consider the normalized distribution of “detected” peak frequency (computed at various settings) as a function of the “gold standard” peak-frequency computed with the 5 kHz-sampled data. These are shown as 2D histograms in Fig. 5. In this case, a perfect diagonal line, e.g. Fig. 5G, is the optimal result, meaning the detected peak frequency is always the same as the gold standard. For all of the sampling rate scan plots (Fig. 5A–D), at the lower sampling rate many of the detected HFOs have peak frequency <140 Hz, despite the fact that they were originally higher in the gold standard data. Thus many fast ripples (peak frequency >200 Hz) would be detected as ripples (peak frequency < 200 Hz). Altering the AAF (Fig. 5 E–G), however, does not have this effect: this smearing of peak frequency is not present until AAF reaches 200 Hz (Fig. 5E), at which point the results are expected given the filter cutoff frequency.

Figure 5. Smearing matrix comparisons.

These plots show how the calculated peak frequency changes when the same data are acquired at different settings. The gold standard is along the x-axis, while the detected parameters are along the y-axis, i.e. horizontal is the true peak frequency, vertical is the perceived peak frequency. The ideal case is in G, in which HFOs of all frequencies in the gold standard are correctly detected, forming a diagonal line. Conversely, the other plots have a percentage of HFOs of every frequency that are incorrectly interpreted as having lower peak frequency. Lower sampling rate (A-D) disrupted peak frequency, as did adding a bandpass filter (H). Lower AAF (E-G) had minimal effects for AAF ≥400 Hz. AAF position is noted in parenthesis after the sampling rate. In vertical pairs A&E, B&F and C&G the AAF is the same with different sampling rate. The colorbar for all plots is shown next to D; all panels are normalized so that each column sums to 100%.

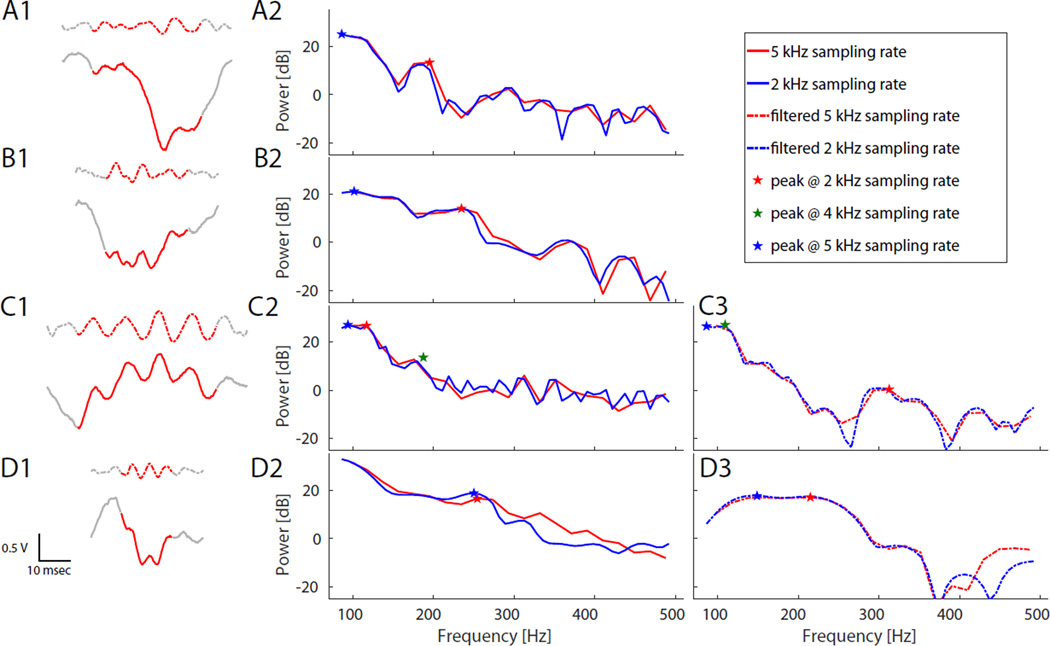
Thus, perceived HFO peak frequency is highly dependent upon the sampling rate. We hypothesize that this is not due to straightforward transformations such as aliasing, as the effect occurs when aliasing should not be present, i.e. when sampling rate is greater than twice the signal frequency. Rather, it appears to be more complex, due to several characteristics of the recorded data that produce HFOs. We analyzed a large number of the HFOs in which the peak frequency changed with different sampling rates to determine the cause, and found a number of potential mechanisms (Fig. 6). First, background EEG signals tend to have a relatively high level of activity in the fast gamma (80–130 Hz) range, creating a “tail” in the power spectrum (the decreasing trend from left to right in Fig. 6). It is often difficult to decide what is the background and what is the oscillation, both for human reviewers and for an algorithm. Second, HFOs often have considerable frequency jitter, and thus in the frequency domain they usually have a broadband appearance, and assigning a single “peak frequency” to such a situation is often ambiguous and the answer can vary at different sampling rates. Third, HFOs are relatively short, which translates into poor resolution in the power spectrum at all considered sampling rates. Fourth, HFOs and EEG background are both quite noisy, which creates large fluctuations in the power spectra that are greatly affected by the resolution. These effects are all very common among detected HFOs, and thus in combination it is often very difficult to assign a discrete “peak” frequency. The confusion is even more pronounced with data acquired at different sampling rates, because each of these effects can vary considerably with different parameters.

Figure 6. Effect of sampling rate on peak frequency.

Example HFOs and their corresponding Energy Spectral Densities (ESD, calculated with ‘pmtm’ function in Matlab) demonstrate how the calculated peak frequency varies with different sampling rates. Left panel (A1,B1,C1,D1) shows four examples of raw (solid) and 80–500 Hz bandpass-filtered (dashed) data. Middle and right panels shows ESD for raw (solid, (A2,B2,C2,D2)) and filtered (dashed, (C3,D3)) data sampled at 5 kHz and 2 kHz. (A) HFO with 200 Hz oscillation that is difficult to distinguish from downward-sloping high gamma baseline. (B) Broadband oscillation does not stand out well from background, and has ambiguous peak. (C) Poor resolution of HFOs often produces noisy ESD background. Location of peak frequency detected with data sampled at 4 kHz is also shown in this panel (green star; ESD data not shown). On panels A, B, and D, the 4 kHz peak was identical to 2 kHz (not shown) (C3&D3) Bandpass-filtering the data does not mitigate the uncertainty, in these cases potentially changing the detected peak frequency from >250 Hz to < 200 Hz, or vice versa. (D) HFOs can appear as wide band events.

Finally, we considered whether restricting the analysis to bandpass-filtered data (80–500 Hz) would mitigate some of these effects. In aggregate, it is clear that the detected peak frequency is also unreliable after bandpass filtering, even with data sampled at 5 kHz (Fig. 5H). We tested individual HFOs at various settings with and without bandpass filtering, and found that peak frequency was still unreliable due to the same effects as above (Fig. 6 C3,D3). Thus we conclude that calculating the peak frequency of HFOs is not robust and highly sensitive to the sampling rate in both raw and bandpass-filtered data.

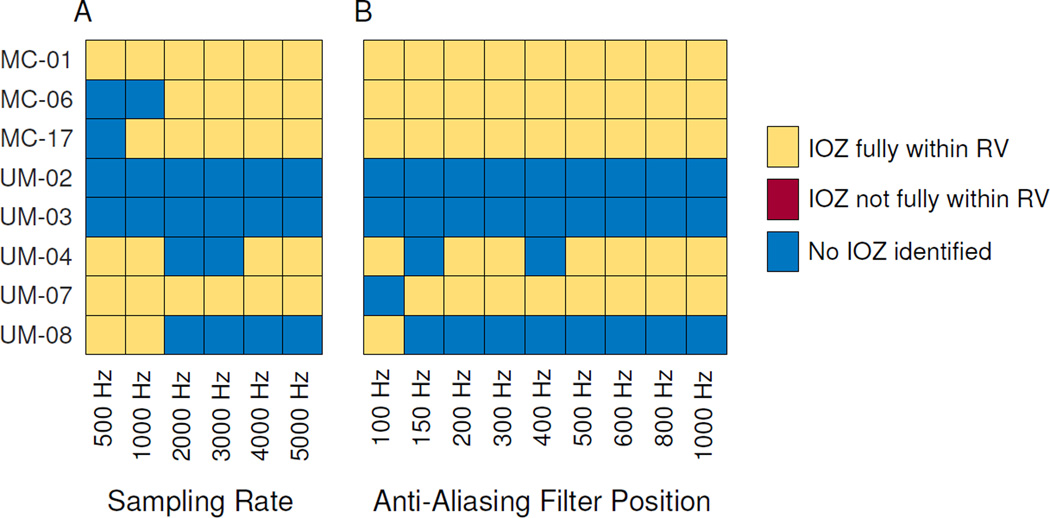
3.3. Automated identification of the ictal onset zone

Although there are differences in both the number and features of HFOs when using lower sampling rates and AAF acquisition settings, a more pertinent clinical question is whether the altered data would have any bearing on the clinical applicability of HFOs. As a practical comparison of the different settings, we used an automated prediction algorithm that determines if any electrodes have anomalously-high interictal HFO rates, which have been shown to be highly correlated with the ictal onset zone (Gliske et al., 2016). The results from the gold standard data (5 kHz) are compared with each acquisition setting (Fig. 7) for patients who became seizure free after surgery. While there are subtle changes in which patient's data allow predictions, the overall ability to identify ictal onset zone appears quite stable over the full range of acquisition parameters: three patients have no changes with any parameter change, and four only change at very low settings. None of the patients had any ‘false positive’ identification of an erroneous ictal onset zone.

Figure 7. Automated identification of ictal onset zone.

Ictal onset zone is predicted by identifying which, if any, electrodes have anomalously-high HFO rates. Results are shown per patient and per sampling rate (A) and anti-aliasing filter position (B). Algorithm-identified ictal onset (IOZ) channels are classified as either being fully within the resected volume (RV), not fully within the RV, or in some cases, no channels were identified. Even though several patients’ answer change with different settings, there were never any predictions outside the RV, which would have corresponded to a false positive prediction in these patients with class I outcome. Note that because the algorithm was performed without any patient-specific tuning, sometimes higher resolution does not improve the ability to predict IOZ due to higher baseline HFO rates (e.g. UM-08).

Two patients appear to perform better at lower rates (UM-04, UM-08), due to a nuance of the algorithm. The algorithm only identifies an ictal onset zone if there are channels with “anomalously high” HFO rates. When overall HFO rates increase, the criteria to be “anomalously high” is more strict. In these patients, the rates of all HFOs increased enough that the threshold was too high to identify any ictal onset zone using this unsupervised algorithm. Adjusting parameters of the algorithm could potentially mitigate this effect. However, we felt it important to use the published algorithm with no modification over the full range of acquisition parameters.

4. Discussion and Conclusions

Combining the above results regarding impacts on detection rate, feature distributions, and clinical utility, we are able to recommend that HFOs should be sampled with at least 2 kHz sampling rate and 500 Hz AAF. Note, these recommendations are lower bounds. A wise upper bound on the AAF is 0.4 times the sampling rate, based on an imperfect filter-cutoff and the Nyquist frequency. High sampling rates may improve HFO feature analysis, and thus for HFO feature analysis we recommend 5 kHz. However, the difference between 2 kHz and 5 kHz was not found to be large. HFOs at 1 kHz are still acceptable, but the HFO detection rate is much lower and some features are biased by the sampling rate, and therefore we do not recommend it. For analyses based solely on HFO rates, such as rate-based determination of the clinical onset zone, the HFOs detected at 500 Hz are still meaningful, although the features are not reliable and the low sensitivity will require much longer acquisition times. In fact, although 500 Hz data only takes half the storage cost as 1 kHz data, only 1/3 as many HFOs are detected. Thus, to have the same statistical power, one would need to record the 500 Hz data for three times as long—taking more total storage space than if the study were done at 1 kHz. Note, these recommendations come with a caveat—this analysis focused on only the effect of sampling rate and anti-aliasing filter positions. Other differences between equipment, especially in regard to noise characteristics, can also significantly affect the HFO detection sensitivity.

The result that the ictal onset zone can be determined well over the full range of parameters may be unexpected. However, we note that the decrease in sensitivity was almost the same within and without the resected volume. The relative number of recorded HFOs is thus still meaningful, despite the decrease in the overall number. As long as the recording is long enough to record a sufficiently high number HFOs, the ictal onset zone is still distinguishable. For example, if the ictal onset zone channels have 10 times as many HFOs as other channels, one could randomly remove half of the HFOs and the ictal onset zone channels would still have 10 times as many HFOs as other channels and thus still be distinguishable. However, the lower sensitivities would require longer recordings in order to obtain the same number of HFOs.

The poor correlation in HFO peak-frequency also merits further discussion. It is important to point out that typical use of automated HFO detectors to label ripples or fast ripples is inherently different than human methods: human methods typically use different filter settings for detecting ripples versus fast ripples (Urrestarazu et al., 2007), whereas automated methods typically use one filter to identify HFOs, and then afterwards separate HFOs into ripples and fast ripples (Blanco et al, 2011). It is unclear whether effects noted with automated HFO detectors would affect human-detector based analyses as well. However, for an algorithm calculating the peak frequency of any given HFO, our findings indicate that the result will vary depending upon the sampling rate of the data. We demonstrate that this effect was due to several noisy characteristics of HFOs and the underlying EEG data.

One of the most important outcomes of our paper is to show that the primary method used by many neuroscientists to classify HFOs, namely the peak frequency, is undependable. It appears that either we as a community lack a robust method of determining peak frequency of HFOs in clinical data, or that our conceptual understanding of human HFOs as narrow-band events with a single defining frequency may need updating. We conclude that peak frequency alone is an insufficient and unreliable feature for analyzing HFOs. Thus classifying individual HFOs as either “ripples” (< 200 Hz) or “fast ripples” (> 200 Hz) should not be a primary aspect of HFO analysis or interpretation.

Highlights.

• –Sampling rate and anti-aliasing filters (AAF) affect High Frequency Oscillation (HFO) detection.
• –Sampling rate ≥2 kHz and AAF ≥500 Hz should be used to analyze HFOs; lower settings are still useful.
• –Calculating peak HFO frequency is unreliable and highly dependent upon the sampling rate.