Abstract
Brain functional connectivity (FC) network, estimated with resting‐state functional magnetic resonance imaging (RS‐fMRI) technique, has emerged as a promising approach for accurate diagnosis of neurodegenerative diseases. However, the conventional FC network is essentially low‐order in the sense that only the correlations among brain regions (in terms of RS‐fMRI time series) are taken into account. The features derived from this type of brain network may fail to serve as an effective disease biomarker. To overcome this drawback, we propose extraction of novel high‐order FC correlations that characterize how the low‐order correlations between different pairs of brain regions interact with each other. Specifically, for each brain region, a sliding window approach is first performed over the entire RS‐fMRI time series to generate multiple short overlapping segments. For each segment, a low‐order FC network is constructed, measuring the short‐term correlation between brain regions. These low‐order networks (obtained from all segments) describe the dynamics of short‐term FC along the time, thus also forming the correlation time series for every pair of brain regions. To overcome the curse of dimensionality, we further group the correlation time series into a small number of different clusters according to their intrinsic common patterns. Then, the correlation between the respective mean correlation time series of different clusters is calculated to represent the high‐order correlation among different pairs of brain regions. Finally, we design a pattern classifier, by combining features of both low‐order and high‐order FC networks. Experimental results verify the effectiveness of the high‐order FC network on disease diagnosis. Hum Brain Mapp 37:3282–3296, 2016. © 2016 Wiley Periodicals, Inc.
Keywords: mild cognitive impairment, functional connectivity, low‐order and high‐order networks, brain disease diagnosis
INTRODUCTION
Alzheimer's disease (AD), a serious brain disorder, is the most prevalent form of dementia in elderly people worldwide, accounting for about 50% to 80% of dementia cases [Association, 2012]. Due to the aging of society, it was predicted that 1 in 85 people will be affected by this disease by 2050 [Brookmeyer et al., 2007]. The predominant clinical symptoms of AD include a decline in some important brain cognitive and intellectual abilities, such as memory, thinking, and reasoning. It becomes even worse over time due to the degeneration of specific nerve cells, presence of neuritic plaques, and neurofibrillary tangles [McKhann et al., 1984]. This disease severely interferes the daily life of (AD) patients, and eventually causes death, without any effective clinical treatment so far. Mild cognitive impairment (MCI), as an intermediate stage of brain cognitive decline between AD and normal aging, shows mild symptoms of cognitive impairment. Individuals with MCI may progress to probable AD with an average conversion rate of 10% to 15% per year, and more than 50% within 5 years [Gauthier et al., 2006; Petersen et al., 2001]. Due to this high conversion rate, the identification of early mild cognitive impairment (eMCI) is important to reduce the risk of developing AD by providing appropriate pharmacological treatments and behavioral interventions. Thus, the accurate diagnosis of eMCI has drawn much attention of researchers during the last decades. However, the diagnosis of eMCI is very challenging and much more difficult due to its mild clinical symptoms. Under such circumstance, extensive research efforts [Bishop, 2006; Hastie et al., 2001] have been dedicated to aid the diagnosis of AD and MCI/eMCI, by analyzing neuroimaging data with different modalities, such as Magnetic Resonance Imaging (MRI) [Cuingnet et al., 2011; Davatzikos et al., 2011] and Positron Emission Tomography (PET) [Foster et al., 2007]. The widely‐used classification algorithms include support vector machine (SVM) [Jie et al., 2014b; Zhang et al., 2011], Bayesian network [Seixas et al., 2014], multi‐task and sparse learning [Huang et al., 2010; Suk et al., 2014a], deep neural networks [Li et al., 2015; Liu et al., 2015; Suk et al., 2013, 2014b], and so forth.
Recently, resting‐state functional Magnetic Resonance Imaging (RS‐fMRI), which uses the blood‐oxygenation‐level‐dependent (BOLD) signal as neurophysiological index, has been successfully applied to early diagnosis of AD/eMCI before the clinical symptoms [Smith et al., 2011; Sporns, 2011; Wee et al., 2013, 2015, 2012a, 2012b]. The BOLD signal is sensitive to spontaneous and intrinsic neural activity within the brain thus can be used as an efficient and noninvasive way for investigating neurological disorders at a whole‐brain level. Functional connectivity (FC), defined as the temporal correlation of BOLD signals in different brain regions, can exhibit how structurally segregated and functionally specialized brain regions interact with each other [Friston et al., 1993; Greicius, 2008]. In the literature [Jie et al., 2014a; Wee et al., 2013, 2015, 2012a], FC is often modeled as a network using graph theoretic techniques. Differences between normal and disrupted FC networks caused by pathological attacks, in terms of both topological structure and connection strength, provide an important biomarker to understand pathological underpinnings of AD/eMCI. Therefore, modeling FC network plays an essential role for accurate diagnosis. So far, several different modeling methods [Jie et al., 2014a, 2014b; Wee et al., 2015, 2012a] have been proposed, where their main differences lie in the definition of network structure and also the correlation computation. Herein, network structure refers to the representation of network vertex and edge while the correlation computation means how to define an appropriate weight for each edge. For network structure in nearly all existing methods, a vertex is always corresponding to a specific brain region, and an edge is used to characterize the FC between brain regions, in terms of correlation of their regional mean RS‐fMRI (BOLD) time series. For correlation computation, different methods have been explored, among which the pairwise Pearson's correlation coefficient [Jie et al., 2014b; Wee et al., 2012a] and the sparse representation [Jie et al., 2014b; Tibshirani et al., 2005; Wee et al., 2015; Wright et al., 2009] are the two popular approaches. The advantage of pairwise Pearson's correlation coefficient is its simplicity in computation. In contrast, although sparse representation requires much more computational time, it may lead to networks with better discriminability.
However, computing the correlation based on the entire time series of RS‐fMRI data simply measures the FC between brain regions with a scalar value, which is fixed across time. This actually implicitly hypothesizes the stationary interaction patterns among brain regions. As a result, this method may overlook the complex and dynamic interaction patterns among brain regions, which are essentially time‐varying. In fact, some recent research studies [Allen et al., 2014; Damaraju et al., 2014; Hutchison et al., 2013; Leonardi et al., 2013] have indicated that the FC contains rich dynamic temporal information. For example, Damaraju et al. [2014] used static FC based on the full time courses and dynamic FC computed based on sliding windows respectively to analysis schizophrenia disease and advocated the use of dynamic analysis to better understand FC. Leonardi et al. [2013] assumed non‐stationary FC can reflect additional and rich information about brain organization. They estimated whole‐brain dynamic FC using sliding windows and then used principal component analysis to reveal hidden patterns of coherent FC dynamics across multiple subjects. Following this line, Wee et al. [2013, 2015] also utilized a sliding window approach to partition the entire time series of RS‐fMRI data into multiple overlapping segments of subseries. Then, a set of temporal FC networks, one for each segment, is constructed for each subject. Note that all vertex for those temporal FC networks are still corresponding to the same brain regions, while the weights for all networks are computed simultaneously based on the inverse covariance estimation [Friedman et al., 2008; Huang et al., 2010] regularized by different kinds of prior penalties [Danaher et al., 2014; Yang et al., 2015], that is, making the adjacent networks have similar topology and connection strength. By taking account of the dynamic property of the FC, this method succeeds in discovering rich discriminative information for eMCI diagnosis. However, for each subject, this approach needs to solve a sparsity regularized inverse covariance estimation problem for obtaining the weights of all networks, which demands a specialized optimization algorithm. More importantly, the weight matrix of each temporal FC network depends on its relative position in the whole time series, when all temporal networks are estimated simultaneously. Thus, if the relative positions of two temporal FC networks are switched, the weight matrices of all temporal FC networks could be changed. Therefore, this approach is inherently sensitive to the chronological order of temporal FC networks, and may cause the phase mismatch among different subjects.
Recently, due to the breakthrough of deep neural networks [Hinton and Salakhutdinov, 2006] in the areas of speech, signal, image, and video recognition [Graves et al., 2013; Krizhevsky et al., 2012], researchers realize that feature learning [Bengio et al., 2013] plays a more and more important role in pattern recognition systems. Specifically, deep neural networks is able to automatically learn the discriminative representations or features from the raw data in a greedy layer‐by‐layer manner, in which high‐level features can be derived from low‐level features to form a hierarchical representation. In such a way, the features generated in high‐level layers usually contain more abstract and semantic information of the raw data, thus greatly improving the classification accuracy. However, deep models, including the popular deep belief network [Hinton et al., 2006] and convolutional neural network [LeCun et al., 1998], usually involve a huge number of parameters. This makes the training process, performed particularly via back propagation [Rumelhart et al., 1986], very computationally expensive, and also requires a large amount of training samples. As a result, the direct application of deep learning for AD and eMCI diagnosis is very challenging due to the limited sample size. However, this feature learning strategy sheds light on the importance of generating high‐level features from low‐level features in pattern recognition.
Inspired by the above methods, we propose in this article the novel notions of high‐order correlation and high‐order FC network, and further develop a simple but effective framework for eMCI classification. As we have described above, the conventional FC network treats brain region or the associated RS‐fMRI time series as a vertex, in either a dynamic [Wee et al., 2013, 2015] or static [Wee et al., 2013, 2015] fashion, and then computes their correlation to represent the interaction between brain regions. In this study, this kind of correlation is called low‐order correlation, and the corresponding network is called low‐order FC network. Remarkably different from the low‐order FC network, each vertex of the high‐order FC network (we propose) corresponds to one pair (or even multiple pairs) of brain regions, with each edge characterizing how pairs of brain regions interact with each other. In this way, the high‐order FC network is able to reveal higher‐level and more complex interaction relationships than the conventional low‐order FC network approaches. Importantly, the high‐order FC network is invariant to the chronological order of temporal low‐order FC networks, thus allowing the consistent and meaningful comparisons across different subjects. Furthermore, following the principle of our proposed method, we can further extend the high‐order correlation in a greedy layer‐by‐layer manner, as in deep neural networks, so that more abstract and complex interaction patterns can be extracted from the raw RS‐fMRI time series. Also, it is worth noting that, different from deep learning models, which usually involve many parameters (weights connecting neurons in different layers) and require massive training data and expensive computational resource to optimize these parameters, our high‐order correlation can model complex interaction relationships among brain regions without introducing too many parameters, thus avoiding over‐fitting to a certain extent in the case of small samples. Moreover, both low‐order and high‐order FC networks can be further integrated to yield the improved performance.
In summary, our method based on both high‐order and low‐order FC networks has the following advantages: (1) it takes into account the time‐varying properties of intrinsic FC; (2) it characterizes higher‐level and more complex interaction patterns among brain regions; (3) it owns preferable invariance to the chronological order of temporal low‐order FC networks; (4) it is simple and easy to implement; and (5) it has high discriminability in discriminating eMCIs and healthy controls.
The rest of the article is organized as follows. In Materials and Method section, we introduce the proposed learning framework for construction of high‐order FC network and also its combination with low‐order FC network for eMCI classification. Then, we describe experiments and report respective results in Experimental results and discussion section. Finally, we discuss and conclude this study in Conclusion section.
MATERIALS AND METHOD
Data Acquisition
In this study, we used the publically available neuroimaging data from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database [Jack et al., 2008]. ANDI was launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and nonprofit organizations. Initially, the goal of ADNI is to define biomarkers for use in clinical trials and to determine the best way to measure the treatment effects of AD therapeutics (adni.loni.ucla.edu). Now, its goal has been extended to detect AD at a pre‐dementia stage using biomarkers. Multiple biomarkers, including MRI, PET, and related neuropsychological assessments are combined together to detect the progression of eMCI and early AD. Determining sensitive and specific biomarkers can facilitate the development of new treatments, reduce the time and cost of clinical trials, and promote our understanding of the biological underpinnings of AD/eMCI.
In this work, we used the same dataset as in [Wee et al., 2013], which is briefly described as follows. Twenty nine eMCI subjects (13F/16M) and 30 normal controls (NCs) (17F/13M) were selected from ADNI 2 dataset. Subjects from both groups were age‐matched (P = 0.6174) with mean age (year) for eMCI and NC groups as 73.6 ± 4.8 and 74.3 ± 5.7. All subjects were scanned with the same scanning protocol at different centers using 3.0T Philips Achieva scanners. The following parameters were used: TR/TE = 3,000/30 mm, flip angle = 80°, imaging matrix = 64 × 64, 48 slices, 140 volumes, and slice thickness = 3.3 mm. The first 10 volumes of each subject were discarded to ensure magnetization equilibrium. The generated RS‐fMRI time series was preprocessed using SPM8 software (https://www.fil.ion.ucl.ac.uk/spm/software/spm8/), with further correction and normalization. RS‐fMRI was regressed to reduce the effects of nuisance signals including ventricle, white matter signals and six head‐motion profiles. Then, automated anatomical labeling template was used to parcellate the regressed RS‐fMRI images into 116 regions‐of‐interest (ROIs), that is, brain regions. The mean RS‐fMRI time series of each brain region, which contains 130 volumes, was calculated and band‐pass filtered (0.01 ≤ f ≤ 0.08Hz). For more detailed data processing procedure, please refer to [Wee et al., 2015].
Proposed Framework
Typical procedures of FC‐based eMCI classification usually include the following components: network construction, feature extraction and selection, and classification. This study mainly focuses on the first step, that is, network construction, and thus simple existing methods are applied to implement other steps.
In Figure 1, we provide the flowchart of the high‐order FC network construction and its application in eMCI identification. Specifically, the proposed framework includes the following eight steps: (1) partition the entire RS‐fMRI time series into multiple overlapping segments of subseries; (2) construct a collection of temporal low‐order FC networks/matrices, one for each segment; (3) stack all temporal low‐order FC networks/matrices of all subjects together [Leonardi et al., 2013] to obtain a correlation time series for each element in the same location of those stacked matrices; (4) group all these correlation time series into different clusters using clustering algorithm; (5) construct a high‐order FC network for each subject, by taking the mean correlation time series for each cluster as a new vertex and the pairwise Pearson's correlation coefficient between each pair of these new vertices as weight; (6) calculate weighted‐graph local clustering coefficients [Rubinov and Sporns, 2010] as a simple feature representation for the high‐order FC networks; (7) select a subset of discriminative features from the high‐order features (local clustering coefficients) with the sparse learning [Tibshirani, 1996]; and (8) construct a SVM model [Cortes and Vapnik, 1995; Vapnik, 1998] on the selected subsets of high‐order features for classification.
Figure 1.
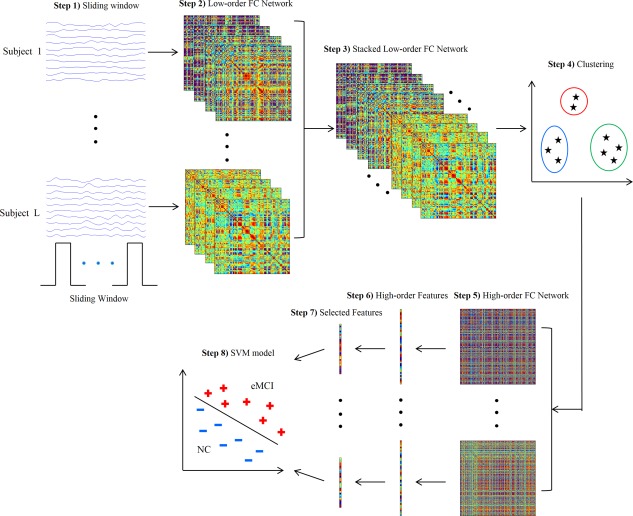
Framework for construction of high‐order FC network. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
In addition to the construction of above high‐order FC network, we also construct a conventional low‐order FC network over the entire RS‐fMRI time series for each subject. Then, following the same Steps (6)–(8), we extract low‐order features (local clustering coefficients) from this low‐order FC network, perform feature selection, and build another SVM model based on these low‐order features. Finally, the classification scores of two SVM models are fused by the weighted averaging to produce the final classification.
In the following subsections, we describe the above steps in detail. Steps (1) and (2) are described in Construction of temporal low‐order FC networks subsection, Steps (3)–(5) are described in Construction of high‐order FC network subsections and Reduction of high‐order FC network by clustering subsection, and Steps (6)−(8) are described in Feature extraction, selection and classification subsection.
Construction of temporal low‐order FC networks
Suppose the regional mean RS‐fMRI time series associated with the ‐th ROI of the ‐th subject is expressed as , where is the total number of temporal image volumes. Let the correlation between the ‐th and the ‐th ROIs of the ‐th subject be:
| (1) |
Then, a FC network can be established using the conventional method by treating as vertices and as the weights of edges, each connecting each pair of vertices. Different from this global method, in [Wee et al., 2015], the entire mean time series is partitioned into multiple segments of overlapping subseries using a sliding window approach. Each segment describes the RS‐fMRI series during a relatively shorter time period.
Specifically, suppose the length of the sliding window is and the step size between two successive windows is . Let denote the ‐th segment of subseries extracted from , which comprises image volumes. The total number of segments generated by this approach is given by , thus we have . For the ‐th subject, the ‐th segment of subseries in all ROIs can be expressed in a matrix form as , where is the total number of ROIs. Then, the entry for the ‐th temporal FC matrix for the ‐th subject is computed as:
| (2) |
which represents the pairwise Pearson's correlation coefficients between the ‐th and the ‐th ROIs of the ‐th subject using the ‐th segment of subseries. For the ‐th subject, the larger the value of , the stronger the associated correlation between the ‐th and the ‐th ROIs in the ‐th window. Taking as vertices and as the weights of edges connecting each pair of vertices, we can establish temporal FC networks for the ‐th subject, which describe the temporal variation of the connection strength for all ROI pairs.
For each ROI pair in the ‐th subject, we can concatenate all for to obtain a correlation time series . Given ROIs, the total number of the correlation time series is for the ‐th subject, considering the symmetry of correlation coefficients. It should be emphasized that the correlation time series is different from the regional mean RS‐fMRI time series . The former characterizes the variation of correlation between ROI pair along the time, whereas the latter just records the variation of mean BOLD signal within the ‐th ROI during an RS‐fMRI scanning period. As a result, the correlation time series is able to reveal more detailed temporal interaction information between different brain regions.
Construction of high‐order FC network
As stated in the Introduction section, the main goal of this article is to reveal the intrinsic relationship between correlation time series , not just the original RS‐fMRI time series as in all existing methods. To achieve this goal, we propose to calculate Pearson's correlation coefficients for the ‐th subject as follows:
| (3) |
for each pair of correlation time series and . Thus, indicates how the correlation between the ‐th and the ‐th ROIs influence the correlation between the ‐th and the ‐th ROIs. As a result, the correlation in Eq. (3) can extract interaction information from up to four different ROIs, whereas the correlation in Eq. (2) involves only two different ROIs. In other words, the correlation coefficient is able to characterize more complex and abstract interaction patterns among brain regions. More importantly, due to the element‐wise computation for Pearson's correlation, is invariant to the order of elements in and , thus owning better robustness against subject differences. Thus, taking as new vertices and as the weights of new edges, each connecting vertices and , we can finally obtain a new high‐order FC network . As is the correlation computed based on each pair of the correlation time series in , we refer as the high‐order correlation and the corresponding network as the high‐order FC network. On the contrary, is termed as the low‐order correlation and the associated network as the temporal low‐order FC network. To give a comprehensive comparison, Figure 2 illustrates the computation procedure from the low‐order correlation to the high‐order correlation. Table 1 displays the concepts of the low‐order and the high‐order FC networks.
Figure 2.
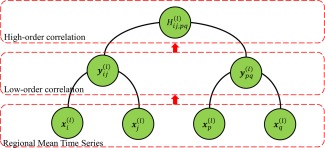
Calculation of the high‐order correlation from the low‐order correlation layer by layer. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Table 1.
Comparison of four types of low‐order and high‐order functional connectivity networks
| Name |
|
|
|
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| Network | Type | Low‐order | Low‐order | High‐order | High‐order | ||||
| Vertex | Entity | Brain region | Brain region | Brain region pair | Multiple brain region pairs | ||||
| Notation |
|
|
|
|
|||||
| Number |
|
|
|
|
|||||
| Meaning | RMTS | Windowed RMTS | CTS | mean CTS | |||||
| Edge/Weight | Notation |
|
|
|
|
||||
| Number |
|
|
|
|
|||||
| Meaning | Correlation between entire RMTS | Correlation between windowed RMTS | Correlation between CTS | Correlation between mean CTS of clusters |
RMTS: Regional mean time series.
CTS: Correlation time series.
Reduction of high‐order FC network by clustering
As discussed above, the total number of the correlation time series for the ‐th subject is proportional to . Then, the total number of the high‐order correlation coefficients in Eq. (3), which are calculated based on paired correlation time series, is proportional to . In our case, , which will lead to a large‐scale high‐order FC network, containing at least thousands of vertices and millions of edges. This is mainly because, given a fixed number of ROIs, the scale of high‐order FC network increases exponentially with the range of interaction. Consequently, it will cause serious computational issues. On one hand, it will result in very high computation complexity in both the network construction and the subsequent feature extraction stage. On the other hand, the generalization performance of the learning system trained by such a large‐scale network can be aggravated by the curse of dimensionality, inter‐subject variability, and noisy features.
To deal with these issues, we propose a network reduction strategy to significantly reduce a large‐scale high‐order FC network into a small‐scale one, thus mitigating the curse of dimensionality to a large extent. The main idea is to group the correlation time series within each subject into different clusters for discovering the intrinsic common interaction patterns. Then, the correlation calculation between the original correlation time series can be converted into that between the respective mean correlation time series in clusters. In such a way, we can directly construct a small‐scale high‐order FC network instead of the original large‐scale one, largely without losing vital interaction information. As a result, this strategy not only cuts down the computation time and the storage requirements but also significantly improves the generalization performance of the high‐order FC network. Essentially, this whole procedure is similar to dimensionality reduction [Chen et al., 2014] for high‐dimensional data, and thus it can be termed as network reduction in this article. An illustration of network reduction is shown in Figure 3.
Figure 3.
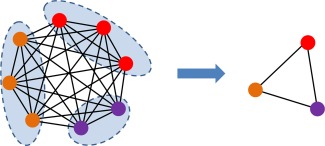
High‐order FC network reduction. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
To be specific, in order to group the correlation time series for the ‐th subject into different clusters, and meanwhile guarantee the consistency of clustering results across different subjects, for all subjects are first stacked together, i.e., . Then, an unsupervised clustering algorithm [Chen et al., 2014; Ward, 1963] is utilized to divide the resulting into different clusters , where consists of the index pair if is included in the ‐th cluster, and is the total number of clusters, . Those assigned to the same cluster will have the similar pattern of variation along the time, while different clusters will show large differences. Then, the mean correlation time series of the ‐th cluster in the ‐th subject can be calculated by averaging of those correlation time series assigned to this cluster, that is,
| (4) |
where denotes the number of elements in . Finally, taking as vertices, we can calculate the pairwise Pearson's correlation coefficient between and as:
| (5) |
In such a way, we can build a much smaller high‐order FC network than the original . Note that the total number of edges in is proportional to , but the reduced contains only edges. A complete comparison of four FC networks as discussed in this article is summarized in Table 1.
Feature extraction, selection, and classification
After FC networks have been established, we use the weighted‐graph local clustering coefficients [Rubinov and Sporns, 2010; Watts and Strogatz, 1998] to extract features from each network. The weighted‐graph local clustering coefficient is computed for each vertex in a network to quantify the probability that the neighbors of this vertex are also connected to each other. It describes the local connectivity or “cliqueness” of a network. For the sake of brevity, suppose we are given a network with vertices. The weight of the edge connecting vertex and vertex is denoted by . Then, the weighted‐graph local clustering coefficient for vertex is defined as:
| (6) |
where denotes the set of vertices directly connected to vertex , and is the number of elements in . As we finally construct two FC networks ( and ) for each subject, two groups of features can be generated using Eq. (6). Here, the feature vector derived from the low‐order FC network is referred to as low‐order feature vector, while that derived from the high‐order FC network is referred to as high‐order feature vector. Specifically, the former consists of 116 clustering coefficients, one for each parcellated ROI. The latter consists of clustering coefficients, one for each cluster generated in network reduction.
The feature vector extracted from FC networks possibly contains some irrelevant or redundant features for eMCI diagnosis. To reduce the effect of those irrelevant or redundant features for improving the generalization performance, we adopt ‐norm regularized least squares regression, known as LASSO (Least Absolute Shrinkage and Selection Operator) [Tibshirani, 1996], to select a small set of crucial features relevant to eMCI disease, due to its simplicity and efficiency. Specifically, the feature vector extracted from the FC networks of each subject is used as a predictor to regress the associated category label for this subject, i.e., +1 for eMCI and −1 for NC. Moreover, ‐norm (instead of the traditional squared ‐norm regularization [Bishop, 2006]) is imposed on linear regression coefficients to shrink many of them toward zero, implying that the associated features do not contain useful discriminative information for classification. In such a way, we can jointly achieve the fitting error minimization as well as sparse variable selection, and a hyperparameter is introduced to control the strength of ‐norm regularization.
After selecting important features with LASSO, we use SVM [Chen et al., 2011; Cortes and Vapnik, 1995; Vapnik, 1998] with a simple linear kernel for disease identification. SVM seeks a maximum margin hyperplane to separate the samples of one class from those of other class. The empirical risk on training data and the complexity of the model can be balanced by the hyperparameter , thus guaranteeing good generalization ability on unseen data. Herein, we construct two SVM models, one for low‐order features and another for high‐order features. Then, the decision scores from the two SVM models are further fused by linear combination, with a weight , to give the final classification results.
Evaluation Methodology
Because of the limited number of samples, in this work, we use leave‐one‐out cross‐validation (LOOCV) to evaluate the generalization performance of our proposed classification approach. As the performance of our approach is dependent on some hyperparameters, such as in clustering, in feature selection, in SVM model, and in decision fusion, it is important to adjust these hyperparameters to proper values. We use a nested LOOCV procedure to determine optimal values for these hyperparameters in the following ranges: , , , and . Specifically, suppose the whole dataset consists of subjects. Then, subjects are used for training, to find the optimal classification model. The rest one is used for testing, to evaluate the classification accuracy of the above model. We repeat the above procedure times, each time leaving out a different subject for testing. In such a way, we can have classification results, one for each subject. Finally, the average accuracy across subjects is computed as performance measurement. To determine the optimal hyper‐parameters, in each repeat of the above procedure, we perform another LOOCV on the training samples. That is, for each combination of values for hyperparameters, we select one subject from training subjects for testing and the rest are used for training. This procedure will repeat times, which can yield the average classification accuracy under a specific combination of hyperparameter values. Then, the hyperparameter values that lead to the highest performance across tests are selected and used to construct the optimal model based on all training subjects. The constructed model will be finally applied to the left‐out testing subject.
EXPERIMENTAL RESULTS AND DISCUSSION
Classification Accuracy
In this work, we compare the proposed eMCI diagnosis framework with three closely related methods, including the partial correlation network (PAC), Pearson's correlation network (PEC), and sparse temporally dynamic network (STDN) [Wee et al., 2015]. PAC and PEC characterize the correlation between brain regions using the entire RS‐fMRI time series. In contrast, STDN and our method both apply sliding windows to partition the time series, thus establishing multiple dynamic (time‐varying) FC networks. All the methods use weighted‐graph local clustering coefficients as features of FC networks and the linear SVM as the classification method. Note that STDN needs to concatenate the features extracted from all low‐order FC networks, thus generating a long feature vector, especially in the case of dense sliding windows. Therefore, t‐test and SVM recursive feature elimination are combined to accurately select features. In contrast, due to the network reduction, the number of features in our case is much less than that in STDN and sparse learning is used for feature selection because of its simplicity and high efficiency. The proposed learning framework was implemented on MATLAB R2012b. The LASSO feature selection algorithm was performed using SLEP toolbox [Liu et al., 2009], and SVM classification was implemented using LIBSVM [Chang and Lin, 2001]. Similar to [Wee et al., 2015], we set and in our sliding window approach, thus generating total 61 windows. To compare different methods, we use the following performance indexes: accuracy (ACC), area under ROC curve (AUC), sensitivity (SEN), specificity (SPE), Youden Index (Youden), F‐score, and balanced accuracy (BAC). The experimental results are reported in Table 2, where HON denotes the high‐order FC network, and FON denotes the combination of the high‐order and low‐order FC networks.
Table 2.
Performance comparison between our proposed learning framework and three other methods in eMCI classification
| Method | ACC | AUC | SEN | SPE | Youden | F‐score | BAC |
|---|---|---|---|---|---|---|---|
| PAC [Wee et al., 2015] | 0.6271 | 0.6598 | 0.6552 | 0.6000 | 0.2552 | 0.6333 | 0.6276 |
| PEC [Wee et al., 2015] | 0.6610 | 0.6138 | 0.5517 | 0.7667 | 0.3184 | 0.6154 | 0.6592 |
| STDN [Wee et al., 2015] | 0.7966 | 0.7920 | 0.7586 | 0.8333 | 0.5920 | 0.7857 | 0.7920 |
| HON | 0.8644 | 0.9000 | 0.8621 | 0.8667 | 0.7287 | 0.8621 | 0.8644 |
| FON | 0.8814 | 0.9299 | 0.8621 | 0.9000 | 0.7621 | 0.8772 | 0.8810 |
The numbers marked bold indicate the best performance.
As we can see from Table 2, the performance of time‐varying networks remarkably outperforms the conventional methods, that is, PAC and PEC. This indicates the temporal patterns contained in FC network are a significant disease biomarker for improving the diagnosis performance between eMCI patients and NCs [Allen et al., 2014; Chang et al., 2013; Smith et al., 2012]. Moreover, our proposed learning framework achieves better results in terms of all performance indexes, in comparison with STDN. For instance, it improves the diagnosis accuracy by at least 6%. The combination of low‐order and high‐order FC networks further improves the performance by 8%. The area under receiver operating characteristic curve (AUC) reaches 0.9299 for the combined low‐order and high‐order FC networks. Besides, by following DeLong's test [DeLong et al., 1988] which allows for the comparison of two AUCs calculated on the same dataset, we have also performed non‐parametric statistical significance test to compare different methods. The results show that our proposed methods can significantly outperform both PEC and PAC under 95% confidence interval. However, our methods are not significantly better than STDN (with P‐value = 0.097 for FON, and 0.128 for HON) although our methods improve the AUC by more than 13%. We speculate that this is mainly caused by the small number of subjects used in our study, thus the correct classification of two or more testing subjects can remarkably increase the accuracy and AUC. In the future, we will continue to evaluate our proposed methods on the larger dataset.
Low‐Order FC Network
Figure 4 illustrates the average low‐order FC network across all eMCI and NC subjects, respectively. As can be seen, the difference between two networks is not remarkable, implying poor performance of the low‐order network in discriminating between eMCI and NC subjects as shown in Table 2. Note that the positive correlation coefficients in Figure 4 reflect synchronized activity between brain regions, while negative correlation coefficients reflect a kind of anti‐correlation or competitive relationship between brain regions. This phoneme has been noticed by many works [Fox et al., 2009; Uddin et al., 2009] and both positive and negative correlations reflect genuine physiological processes [Goelman et al., 2014]. The low‐order FC network of one example subject using pairwise Pearson's correlation coefficients is shown in Figure 5a. This network provides a global view for the interaction relationship between different brain regions. The correlation between a pair of brain regions is simply a positive or negative value, with no any temporal change. To gain more insights about temporal information contained in RS‐fMRI time series, the sliding window approach is applied to produce a collection of temporal low‐order FC networks, some of which are depicted in Figure 5b–g. Comparing Figure 5a,b–g, we can find that the temporal low‐order FC network can characterize temporal variation of the correlation patterns between different brain regions.
Figure 4.
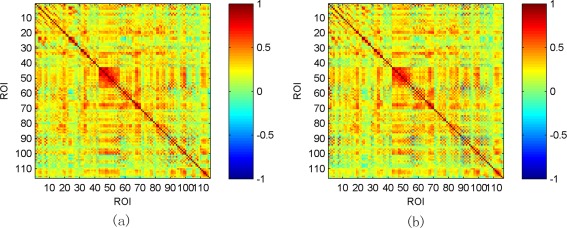
Averaged low‐order FC networks for all eMCI subjects (a) and NC subjects (b), respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 5.
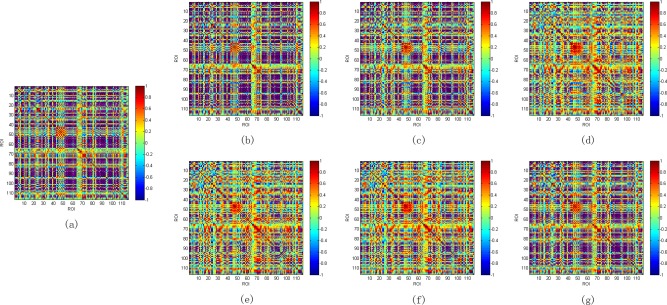
Static and temporal low‐order FC networks for one eMCI subject. (a) static network; (b–g) temporal networks generated by sliding window approach. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Clustering and High‐Order FC Network
In the experiments, we use Ward's linkage clustering [Chen et al., 2014; Ward, 1963], a widely used hierarchical clustering algorithm, to group the correlation time series into different clusters. An important advantage of this clustering method is that it does not involve initialization, reduces the dependence on extra hyperparameters, and meanwhile enhances the robustness of clustering results. In Figure 6a, some ROI pairs are selected and their corresponding correlation time series are depicted. We can see that, for many ROI pairs, their temporal correlations actually undergo large variation over the entire duration of RS‐fMRI scan. For example, both the magnitude and the direction of correlation relationship have significant changes for some ROI pairs. Figure 6b illustrates the corresponding clustering results of these correlation time series when . Note that three clusters with different colors are depicted for the sake of simplicity. Figure 6c further shows the mean correlation time series computed from the clusters. It is obvious that the correlation time series with similar temporal dynamics are classified into the same cluster while those with dissimilar dynamic patterns are partitioned into different clusters. In such a way, we can discover the dominant dynamic pattern underlying all correlation time series. Therefore, we can use the mean correlation time series of each cluster as a vertex in the high‐order FC network, to remarkably reduce the network scale and computation complexity. The resulting high‐order FC networks averaged across all eMCI and NC subjects are shown in Figure 7a,b, respectively.
Figure 6.
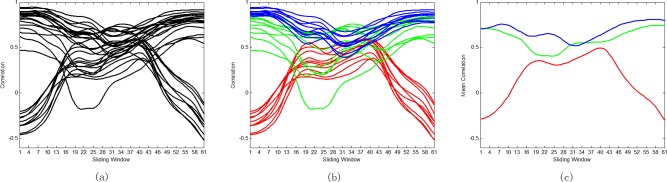
Some selected correlation time series and clustering results for one eMCI subject. (a) Original correlation time series; (b) Three different clusters of correlation time series; (c) the mean correlation time series of each cluster. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 7.
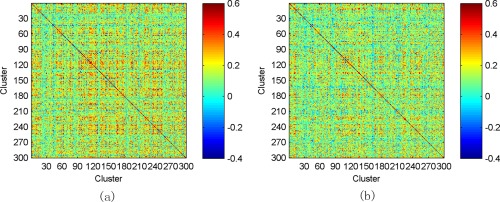
Averaged high‐order FC networks for all eMCI subjects (a) and NC subjects (b), respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Influence of Clustering on Accuracy
The effectiveness of the FC network is essential to the diagnosis accuracy of the proposed learning framework. If the constructed network is poor (in the sense that the biomarkers for distinguishing eMCI from normal aging cannot be identified), the final diagnosis accuracy of eMCI cannot be guaranteed (no matter what feature selection or classification methods are used in the subsequent stages). Hence, we should also investigate how the variation of the constructed network affects the performance of the whole diagnosis system. In this experiment, we mainly focus on the impact of clustering number on the identification accuracy, as this is an important factor distinguishing our high‐order FC network from the existing temporal low‐order FC network STDN [Wee et al., 2015]. Accordingly, we change the value of from 100 to 700 with a Step 100, and report the diagnosis performances of HON and FON in Figure 8. As we can see, the high‐order FC network yields a relatively robust and preferable performance, when varies between 300 and 400. But, when becomes too small or too large, the diagnosis accuracy decreases gradually. This can be understood from two aspects. First, when is too small, numerous correlation time series even with fundamentally different temporal dynamics are probably classified into the same cluster. It can seriously reduce the purity of each cluster, thus make the high‐order correlation (calculated based on the mean of each cluster) unreliable. Second, when is too large, similar correlation time series may be partitioned into different clusters. This will increase the number of features extracted from the high‐order FC network, thus leading to more redundant features and making the feature selection difficult.
Figure 8.
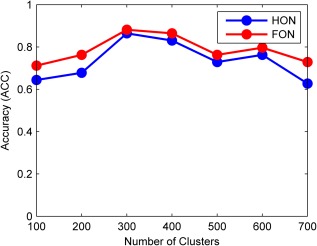
The variation of recognition accuracy against different number of clusters. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Most Discriminative Regions and Clusters
As described in the Evaluation methodology section, the proposed framework is evaluated by nested LOOCV, thus yielding different training set and different hyperparameter values in each leave‐one‐out fold. As a result, different set of features could be selected in each fold, from the low‐order and the high‐order FC networks, and fed into the SVM for classification. Hence, we define the most discriminative brain regions and clusters as the ones with larger normalized weight during the construction of the optimal SVM models corresponding to the low‐order and the high‐order FC networks, respectively. The selected brain regions and clusters, as well as the associated normalized weights from the low‐order and the high‐order FC networks ( ), are shown in Figure 9. Note that, for the high‐order network, we use a clustering technique to reduce its scale, and thus the entire cluster, which may contain multiple ROI pairs, will be selected.
Figure 9.
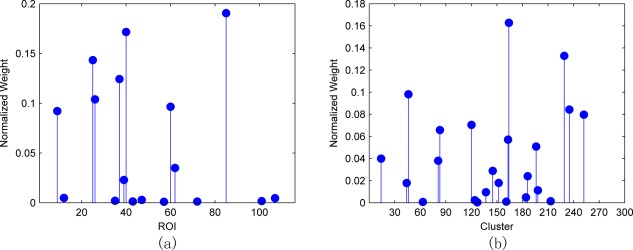
Feature selection results. (a) ROI selection from the low‐order FC networks; (b) cluster selection from the high‐order FC networks. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
In summary, the top 10 most discriminative brain regions selected from the low‐order FC network are listed in Table 3. We also provide some citations showing the importance of corresponding brain regions. We can see that many of these selected brain regions are consistent with the observations reported in the previous literatures [Echávarri et al., 2011; Jacobs et al., 2012; Kosicek and Hecimovic, 2013; Salvatore et al., 2015]. For example, Echávarri et al. [2011] have observed that parahippocampal gyrus and hippocampus are important biomarkers, while the former can discriminate better than the latter in terms of AD diagnosis. Asrami [Asrami, 2012] found that middle temporal gyrus is one of the most important regions for AD/MCI prediction. In addition, we also note that some brain regions are selected on one hemisphere but not the other one. This is also observed in some works [Wee et al., 2012a; Zhu et al., 2014]. It may be because feature selection using sparse regression can filter out some regions which are redundant or highly correlated. As for the high‐order FC network, as each cluster usually comprises of multiple ROI pairs, we use the same color to depict the ROI pairs of the same cluster in Figure 10. It should be emphasized that Figure 10 is not a correlation matrix, but shows the importance of each selected cluster, according to Figure 9b.
Table 3.
ROIs selected from the low‐order FC network
| No. | ROI index | ROI name | Citations |
|---|---|---|---|
| 1 | 85 | Middle temporal gyrus left | [Kosicek and Hecimovic, 2013] |
| 2 | 40 | ParaHippocampal gyrus right | [Echávarri et al., 2011] |
| 3 | 25 | Orbitofrontal cortex (medial) left | [Salvatore et al., 2015] |
| 4 | 37 | Hippocampus left | [Echávarri et al., 2011; Salvatore et al., 2015] |
| 5 | 26 | Orbitofrontal cortex (medial) right | [Salvatore et al., 2015] |
| 6 | 60 | Superior parietal gyrus right | [Jacobs et al., 2012; Kosicek and Hecimovic, 2013] |
| 7 | 9 | Orbitofrontal cortex (middle) left | [Salvatore et al., 2015] |
| 8 | 62 | Inferior parietal lobule right | [Jacobs et al., 2012; Kosicek and Hecimovic, 2013] |
| 9 | 39 | ParaHippocampal gyrus left | [Echávarri et al., 2011] |
| 10 | 12 | Inferior frontal gyrus (opercular) right | [Salvatore et al., 2015] |
Figure 10.
Importance of each cluster (same color), selected from the high‐order FC network, in eMCI classification. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
CONCLUSION
In this article, we propose a high‐order FC network and its combination with the conventional low‐order FC network for eMCI diagnosis. This work is motivated from two aspects. The first is from the fact that the intrinsic interaction patterns between different brain regions are temporally nonstationary, thus evaluating the correlations over the entire period of an RS‐fMRI scanning period could ignore the rich information contained in each local time. The second is from the assumption that different pairs of brain regions could influence each other, and their high‐order correlation could contain important discriminative information for diagnosis of neurodegenerative diseases. But this is consistently overlooked in the existing methods, as all of them just characterize the correlations among brain regions with respect to the raw RS‐fMRI time series, either globally or locally. Following these motivations, we put forward an interesting approach for constructing the high‐order FC network. Specifically, the sliding window approach is utilized first to partition the entire RS‐fMRI time series into multiple overlapping segments of subseries. Then, multiple low‐order FC networks are established for each subject, thus also forming the correlation time series for each pair of brain regions. Then, the correlation between correlation time series can be calculated, from which the discriminative features can be derived. Finally, SVM is used to perform the final classification. In addition, a decision‐level fusion method is also used to combine the scores from the high‐order and the low‐order FC networks to boost the final classification accuracy.
One limitation of this work is the loss of interpretability of high‐order FC networks, because a clustering technique is used to reduce the scale of high‐order FC networks. The clustering coefficients, in such a case, reflect the local connectivity in terms of clusters which consists of multiple brain regions with similar temporal dynamics. In the experiments, we found only a small number of clusters are informative for diagnosis. A possible solution to handle this problem is to select a small number of correlation time series before constructing high‐order FC networks. In such a way, we can retain the interpretability of the resulting networks and at the same time reduce the computation and storage cost. Another method is to perform an addition selection over the correlation time series within each selected clusters. Then, we can gain some insight about which correlation time series are important. In the future work, we will investigate these strategies to further improve high‐order FC networks.
ACKNOWLEDGMENT
The authors declare no conflict of interest.
REFERENCES
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD (2014): Tracking whole‐brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asrami FF (2012): Alzheimer's Disease Classification using K‐OPLS and MRI. Linköping University. [Google Scholar]
- Association AS (2012): 2012 Alzheimer's disease facts and figures. Alzheimer's Dement 8:131–168. [DOI] [PubMed] [Google Scholar]
- Bengio Y, Courville A, Vincent P (2013): Representation learning: A review and new perspectives. IEEE Trans Pattern Anal Mach Intell 35:1798–1828. [DOI] [PubMed] [Google Scholar]
- Bishop, C (2006): Pattern Recognition and Machine Learning. New York: Springer. [Google Scholar]
- Brookmeyer R, Johnson E, Ziegler‐Graham K, Arrighi HM (2007): Forecasting the global burden of Alzheimer's disease. Alzheimer's Dement 3:186–191. [DOI] [PubMed] [Google Scholar]
- Chang C, Lin C (2001): LIBSVM: A Library for Support Vector Machines. Citeseer. [Google Scholar]
- Chang C, Liu Z, Chen MC, Liu X, Duyn JH (2013): EEG correlates of time‐varying BOLD functional connectivity. Neuroimage 72:227–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Yang J, Ye Q, Liang J (2011): Recursive projection twin support vector machine via within‐class variance minimization. Pattern Recognit 44:2643–2655. [Google Scholar]
- Chen X, Xiao Y, Cai Y, Chen L (2014): Structural max‐margin discriminant analysis for feature extraction. Knowl Based Syst 70:154–166. [Google Scholar]
- Cortes C, Vapnik V (1995): Support‐vector networks. Mach Learn 20:273–297. [Google Scholar]
- Cuingnet R, Gerardin E, Tessieras J, Auzias G, Lehéricy S, Habert MO, Chupin M, Benali H, Colliot O; Alzheimer's Disease Neuroimaging Initiative (2011): Automatic classification of patients with Alzheimer's disease from structural MRI: A comparison of ten methods using the ADNI database. Neuroimage 56:766–781. [DOI] [PubMed] [Google Scholar]
- Damaraju E, Allen E, Belger A, Ford J, McEwen S, Mathalon D, Mueller B, Pearlson G, Potkin S, Preda A (2014): Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage 5:298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danaher P, Wang P, Witten DM (2014): The joint graphical lasso for inverse covariance estimation across multiple classes. J R Stat Soc Ser B (Stat Methodol) 76:373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davatzikos C, Bhatt P, Shaw LM, Batmanghelich KN, Trojanowski JQ (2011): Prediction of MCI to AD conversion, via MRI, CSF biomarkers, and pattern classification. Neurobiol Aging 32:2322.e19–2322.e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong ER, DeLong DM, Clarke‐Pearson DL (1988): Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 837–845. [PubMed] [Google Scholar]
- Echávarri C, Aalten P, Uylings H, Jacobs H, Visser P, Gronenschild E, Verhey F, Burgmans S (2011): Atrophy in the parahippocampal gyrus as an early biomarker of Alzheimer's disease. Brain Struct Funct 215:265–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster NL, Heidebrink JL, Clark CM, Jagust WJ, Arnold SE, Barbas NR, DeCarli CS, Turner RS, Koeppe RA, Higdon R (2007): FDG‐PET improves accuracy in distinguishing frontotemporal dementia and Alzheimer's disease. Brain 130:2616–2635. [DOI] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME (2009): The global signal and observed anticorrelated resting state brain networks. J Neurophysiol 101:3270–3283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R (2008): Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9:432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Frith C, Liddle P, Frackowiak R (1993): Functional connectivity: The principal‐component analysis of large (PET) data sets. J Cereb Blood Flow Metab 13:5–14. [DOI] [PubMed] [Google Scholar]
- Gauthier S, Reisberg B, Zaudig M, Petersen RC, Ritchie K, Broich K, Belleville S, Brodaty H, Bennett D, Chertkow H (2006): Mild cognitive impairment. Lancet 367:1262–1270. [DOI] [PubMed] [Google Scholar]
- Goelman G, Gordon N, Bonne O (2014): Maximizing Negative Correlations in Resting‐State Functional Connectivity MRI by Time‐Lag. PLoS One 9:15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graves A, Mohamed AR, Hinton GE (2013): Speech recognition with deep recurrent neural networks IEEE International conference on acoustics, speech and signal processing. IEEE, pp 6645–6649.
- Greicius M (2008): Resting‐state functional connectivity in neuropsychiatric disorders. Curr Opin Neurol 21:424–430. [DOI] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Friedman JJH (2001): The elements of statistical learning. New York: Springer. [Google Scholar]
- Hinton GE, Salakhutdinov RR (2006): Reducing the dimensionality of data with neural networks. Science 313:504–507. [DOI] [PubMed] [Google Scholar]
- Hinton GE, Osindero S, Teh YW (2006): A fast learning algorithm for deep belief nets. Neural Comput 18:1527–1554. [DOI] [PubMed] [Google Scholar]
- Huang S, Li J, Sun L, Ye J, Fleisher A, Wu T, Chen K, Reiman E; Alzheimer's Disease Neuroimaging Initiative (2010): Learning brain connectivity of Alzheimer's disease by sparse inverse covariance estimation. NeuroImage 50:935–949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez‐Castillo J (2013): Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bernstein MA, Fox NC, Thompson P, Alexander G, Harvey D, Borowski B, Britson PJ, L, Whitwell J, Ward C, Dale AM, Felmlee JP, Gunter JL, Hill DL, Killiany R, Schuff N, Fox‐Bosetti S, Lin C, Studholme C, DeCarli CS, Krueger G, Ward HA, Metzger GJ, Scott KT, Mallozzi R, Blezek D, Levy J, Debbins JP, Fleisher AS, Albert M, Green R, Bartzokis G, Glover G, Mugler J, Weiner MW (2008): The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods. J Magn Reson Imaging 27:685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs HI, Van Boxtel MP, Jolles J, Verhey FR, Uylings HB (2012): Parietal cortex matters in Alzheimer's disease: An overview of structural, functional and metabolic findings. Neurosci Biobehav Rev 36:297–309. [DOI] [PubMed] [Google Scholar]
- Jie B, Shen D, Zhang D (2014a) Brain connectivity hyper‐network for MCI classification. In: Medical Image Computing and Computer‐Assisted Intervention–MICCAI 2014. Springer; pp 724–732. [DOI] [PubMed] [Google Scholar]
- Jie B, Zhang D, Gao W, Wang Q, Wee CY, Shen D (2014b): Integration of network topological and connectivity properties for neuroimaging classification. IEEE Trans Biomed Eng 61:576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosicek M, Hecimovic S (2013): Phospholipids and Alzheimer's disease: Alterations, mechanisms and potential biomarkers. Int J Mol Sci 14:1310–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton GE (2012): Imagenet classification with deep convolutional neural networks, Proc. Neural Information and Processing Systems, pp 1097–1105.
- LeCun Y, Bottou L, Bengio Y, Haffner P (1998): Gradient‐based learning applied to document recognition. Proc IEEE 86:2278–2324. [Google Scholar]
- Leonardi N, Richiardi J, Gschwind M, Simioni S, Annoni JM, Schluep M, Vuilleumier P, Van De Ville D (2013): Principal components of functional connectivity: A new approach to study dynamic brain connectivity during rest. NeuroImage 83:937–950. [DOI] [PubMed] [Google Scholar]
- Li F, Tran L, Thung K‐H, Ji S, Shen D, Li J (2015): A robust deep model for improved classification of AD/MCI patients. IEEE J Biomed Health Inform 19:1610–1616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Ji S, Ye J (2009): SLEP: Sparse Learning with Efficient Projections, Vol. 6 Arizona State University; p 491. [Google Scholar]
- Liu S, Liu S, Cai W, Che H, Pujol S, Kikinis R, Feng D, Fulham MJ (2015): Multimodal Neuroimaging Feature Learning for Multiclass Diagnosis of Alzheimer's Disease. IEEE Trans Biomed Eng 62:1132–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM (1984): Clinical diagnosis of Alzheimer's disease Report of the NINCDS‐ADRDA Work Group* under the auspices of Department of Health and Human Services Task Force on Alzheimer's Disease. Neurology 34:939–939. [DOI] [PubMed] [Google Scholar]
- Petersen RC, Doody R, Kurz A, Mohs RC, Morris JC, Rabins PV, Ritchie K, Rossor M, Thal L, Winblad B (2001): Current concepts in mild cognitive impairment. Arch Neurol 58:1985–1992. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, Hinton GE, Williams RJ ( 1986): Learning internal representations by error propagation. Parallel Distrib. Process 1:318–362. [Google Scholar]
- Salvatore C, Cerasa A, Battista P, Gilardi MC, Quattrone A, Castiglioni I; Alzheimer's Disease Neuroimaging Initiative (2015): Magnetic resonance imaging biomarkers for the early diagnosis of Alzheimer's disease: A machine learning approach. Front Neurosci 9:307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seixas FL, Zadrozny B, Laks J, Conci A, Saade DCM (2014): A Bayesian network decision model for supporting the diagnosis of dementia, Alzheimer's disease and mild cognitive impairment. Comput Biol Med 51:140–158. [DOI] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi‐Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW (2011): Network modelling methods for FMRI. Neuroimage 54:875–891. [DOI] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF (2012): Temporally‐independent functional modes of spontaneous brain activity. Proc Natl Acad Sci USA 109:3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O (2011): The human connectome: A complex network. Ann N Y Acad Sci 1224:109–125. [DOI] [PubMed] [Google Scholar]
- Suk HI, Lee SW, Shen D; Alzheimer's Disease Neuroimaging Initiative (2013): Latent feature representation with stacked auto‐encoder for AD/MCI diagnosis. Brain Struct Funct 220:841–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk HI, Lee SW, Shen D, Initiative ADN (2014a): Subclass‐based multi‐task learning for Alzheimer's disease diagnosis. Front Aging Neurosci 6:168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk HI, Lee SW, Shen D; Alzheimer's Disease Neuroimaging Initiative (2014b): Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage 101:569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R (1996): Regression shrinkage and selection via the lasso. J R Stat Soc Ser B (Methodol) 58:267–288. [Google Scholar]
- Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K (2005): Sparsity and smoothness via the fused lasso. J R Stat Soc Ser B (Stat Methodol) 67:91–108. [Google Scholar]
- Uddin LQ, Clare Kelly A, Biswal BB, Xavier Castellanos F, Milham MP (2009): Functional connectivity of default mode network components: Correlation, anticorrelation, and causality. Hum brain Mapp 30:625–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik VN (1998): Statistical Learning Theory, Vol. xxiv New York: Wiley; 736 p. [Google Scholar]
- Ward JH Jr (1963): Hierarchical grouping to optimize an objective function. J Am Stat Assoc 58:236–244. [Google Scholar]
- Watts DJ, Strogatz SH (1998): Collective dynamics of ‘small‐world’ networks. Nature 393:440–442. [DOI] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Denny K, Browndyke JN, Potter GG, Welsh‐Bohmer KA, Wang L, Shen D (2012a): Resting‐state multi‐spectrum functional connectivity networks for identification of MCI patients. PloS One 7:e37828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee C‐Y, Yap P‐T, Zhang D, Wang L, Shen D (2012b): Constrained sparse functional connectivity networks for MCI classification. In: Medical Image Computing and Computer‐Assisted Intervention–MICCAI 2012. Springer. pp 212–219. [DOI] [PMC free article] [PubMed]
- Wee C‐Y, Yang S, Yap P‐T, Shen D (2013): Temporally dynamic resting‐state functional connectivity networks for early MCI identification. In: Machine Learning in Medical Imaging. Springer. pp 139–146. [DOI] [PMC free article] [PubMed]
- Wee CY, Yang S, Yap PT, Shen D, Alzheimer's Disease Neuroimaging Initiative (2015): Sparse temporally dynamic resting‐state functional connectivity networks for early MCI identification. Brain Imaging Behav 1–15, doi: 10.1007/s11682-015-9408-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y (2009): Robust face recognition via sparse representation. IEEE Trans Pattern Anal Mach Intell 31:210–227. [DOI] [PubMed] [Google Scholar]
- Yang S, Lu Z, Shen X, Wonka P, Ye J (2015): Fused multiple graphical lasso. SIAM J Optim 25:916–943. [Google Scholar]
- Zhang D, Wang Y, Zhou L, Yuan H, Shen D, Alzheimer's Disease Neuroimaging Initiative (2011): Multimodal classification of Alzheimer's disease and mild cognitive impairment. Neuroimage 55:856–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Suk HI, Shen D (2014): Matrix‐similarity based loss function and feature selection for Alzheimer's disease diagnosis. In: IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH. pp 3089–3096. [DOI] [PMC free article] [PubMed]


