Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Aug 9;7:12496. doi: 10.1038/ncomms12496

Force sensitivity of multilayer graphene optomechanical devices

P Weber 1, J Güttinger 1, A Noury 1, J Vergara-Cruz 1, A Bachtold 1,a
PMCID: PMC4980493  PMID: 27502017

Abstract

Mechanical resonators based on low-dimensional materials are promising for force and mass sensing experiments. The force sensitivity in these ultra-light resonators is often limited by the imprecision in the measurement of the vibrations, the fluctuations of the mechanical resonant frequency and the heating induced by the measurement. Here, we strongly couple multilayer graphene resonators to superconducting cavities in order to achieve a displacement sensitivity of 1.3 fm Hz−1/2. This coupling also allows us to damp the resonator to an average phonon occupation of 7.2. Our best force sensitivity, 390 zN Hz−1/2 with a bandwidth of 200 Hz, is achieved by balancing measurement imprecision, optomechanical damping, and measurement-induced heating. Our results hold promise for studying the quantum capacitance of graphene, its magnetization, and the electron and nuclear spins of molecules adsorbed on its surface.

Inline graphicGraphene is a promising material for the design of mechanical resonators. Here, the authors fabricate a multilayer graphene resonator coupled to a superconducting cavity, to achieve efficient readout of mechanical vibrations and quantitatively investigate its force sensing performance.

Considerable effort has been devoted to developing mechanical resonators based on low-dimensional materials, such as carbon nanotubes1,2,3,4,5,6,7,8,9,10,11,12, semiconducting nanowires13,14,15,16,17,18,19,20,21,22, graphene23,24,25,26,27,28,29 and monolayer semiconductors30,31,32. The specificity of these resonators is their small size and their ultra-low mass, which enables sensing of force and mass with unprecedented sensitivities7,10. Such high-precision sensing capabilities hold promise for studying physical phenomena in new regimes that have not been explored thus far, for instance, in spin physics33, quantum electron transport34,35, light-matter interaction19 and surface science36,37. However, the transduction of the mechanical vibrations of nanoscale mechanical systems into a measurable electrical or optical output signal is challenging. As a result, force and mass sensing is often limited by the imprecision in the measurement of the vibrations, and cannot reach the fundamental limit imposed by thermo-mechanical noise.

A powerful method to obtain efficient electrical readout of small resonators is to amplify the interaction between mechanical vibrations and the readout field using a superconducting microwave cavity27,28,29. Increasing the field in the cavity improves the readout sensitivity and eventually leads to dynamical back-action on the thermo-mechanical noise. This effect has been studied intensively on comparatively large micro-fabricated resonators, resulting for instance in enhanced optomechanical damping38,39, ground-state cooling of mechanical vibrations40,41 and displacement imprecision below the standard quantum limit42,43. Another phenomenon often observed when detecting and manipulating the motion of mechanical resonators is the induced heating that can occur through Joule dissipation and optical adsorption28,44. Heating is especially prominent in tiny mechanical resonators because of their small heat capacity. An additional difficulty in characterizing mechanical vibrations is related to the fluctuations of the mechanical resonant frequency, also called frequency noise, which are particularly sizable in small resonators endowed with high-quality factors Q10.

Here we study the force sensitivity of multilayer graphene mechanical resonators coupled to superconducting cavities. In particular, we quantify how the force sensitivity is affected by dynamical back-action, Joule heating and frequency noise upon increasing the number of pump photons inside the cavity. We demonstrate a force sensitivity of 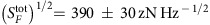Inline graphic, of which ≈50% arises from thermo-mechanical noise and ≈50% from measurement imprecision. The force sensitivity tends to be limited by measurement imprecision and frequency noise at low pump power, and by optomechanical damping and Joule heating at high pump power.

Results

Thermal force noise and imprecision force noise

A fundamental limit of force sensing is set by the thermo-mechanical noise of the eigenmode that is measured. According to the fluctuation-dissipation theorem, the associated thermal force noise is white and is quantified by

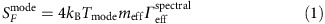graphic file with name ncomms12496-m2.jpg

where Tmode is the temperature of the mechanical eigenmode, and meff is its effective mass8,45. This force noise is transduced into a mechanical resonance with line width 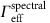Inline graphic and height Inline graphic in the displacement spectrum (Fig. 1). Importantly, equation (1) shows that the low mass of graphene decreases the size of the thermo-mechanical force noise. However, a drawback of tiny resonators with high Q-factors is their tendency to feature sizable frequency noise that broadens the resonance and, therefore, increases the size of the force noise10,46.

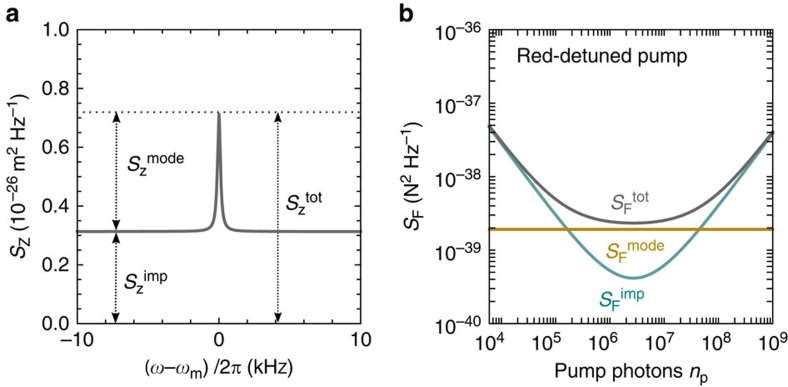
Figure 1. Mechanical displacement and force sensitivity.

Figure 1

Open in a new tab

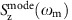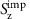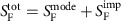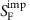(a) Mechanical displacement spectrum Sz close to the mechanical resonance frequency ωm/2π. The total displacement spectral density Inline graphic at ωm is the sum of the displacement noise Inline graphic and the displacement imprecision Inline graphic. (b) Corresponding force sensitivity Inline graphic (dark grey). The individual components are the thermal force noise Inline graphic (dark yellow) and the imprecision force noise Inline graphic (turquoise), given by equations (1) and (2), respectively. The quantum back-action noise is neglected for simplicity. For the plots most of the parameters are those of device B, but we estimate the mass assuming that the graphene flake is a single layer. Further we choose nadd=0.5, Tbath=0.015 K, and np=2·105 in a (see text).

Measuring mechanical vibrations with high accuracy is key to resolving small forces, since the imprecision in the measurement contributes to the force sensitivity. The force sensitivity 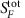Inline graphic is given by the sum of the thermal force noise 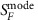Inline graphic and the imprecision force noise Inline graphic, where the latter is the result of the white noise background with strength 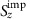Inline graphic in the displacement spectrum (Fig. 1a). The challenge with mechanical resonators based on low-dimensional systems is to reach the limit 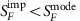Inline graphic. When detecting the motion of graphene resonators with microwave cavities, one typically operates in the resolved sideband limit27,28,29, where the cavity decay rate κ is significantly smaller than the mechanical resonance frequency ωm. This is interesting for force sensing, because pumping on the red sideband allows to enhance the mechanical damping rate by Γopt, and therefore to reduce the harmful effect of frequency noise, as we will discuss below. In addition, this allows to increase the measurement bandwidth, as is often done in magnetic resonance force microscopy experiments33 while keeping 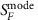Inline graphic constant. The drawback of red sideband pumping compared to pumping at the cavity resonant frequency is an increased imprecision force noise at high pump powers. In the red-detuned pump regime, the measurement imprecision contributes to the force sensitivity by the amount

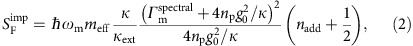graphic file with name ncomms12496-m11.jpg

with κext the external coupling rate of the cavity, nadd the noise added by the amplifier chain at the output of the device, Γmspectral the intrinsic line width of the resonator, np the number of pump photons in the cavity, and g0 the single-photon optomechanical coupling. Figure 1b shows the pump power dependence of the force sensitivity 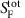Inline graphic expected in the absence of Joule heating and frequency noise. The increase of 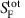Inline graphic at high np is due to the dynamical back-action, which enhances the mechanical line width by Γopt=4npg02/κ.

Device characterization

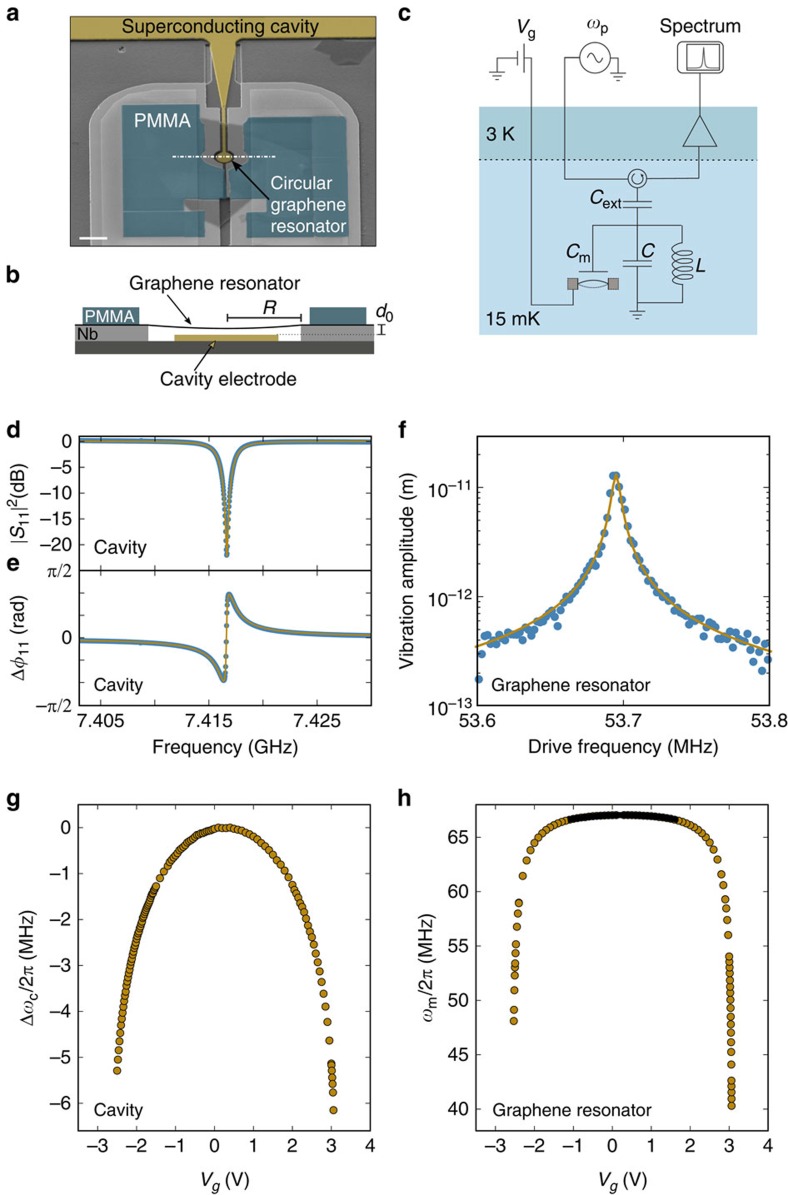
Our devices consist of a suspended graphene mechanical resonator capacitively coupled to a superconducting niobium (Nb) cavity (Fig. 2a–c). The graphene resonators are circular with a radius of R≈1.6 μm. Here we present data of two devices. The graphene resonator of device A has a thickness of approximately 25 layers, and the one of device B 5–6 layers. This corresponds respectively to an effective mass of meff=(4.1±0.8)·10−17 kg and (9.6±0.8)·10−18 kg. The uncertainty results from extracting the mass with different methods including optical contrast measurements, thickness measurements with atomic force microscopy and the measured electrostatic softening of the mechanical resonators (see Supplementary Note 1 and Supplementary Equation 2). The fundamental mode of devices A and B vibrates at ωm/2π=67 MHz and ωm/2π=46 MHz at Vg=0 V, respectively. Here Vg is the constant voltage applied between the graphene flake and the superconducting cavity. In order to improve the attachment of the graphene flake to its support, we clamp it between cross-linked poly(methyl metracylate) and the contact electrodes; the detailed fabrication is described elsewhere29. The separation between the graphene resonator and the cavity counter electrode at Vg=0 V is assumed to be equal to the hole depth, which is typically d0≈85 nm in our devices as measured with atomic force microscopy. Varying Vg allows us to tune the separation between the graphene resonator and the cavity counter electrode24,29,47,48,49, modifying the graphene-cavity capacitance, the cavity frequency ωc and ωm (Fig. 2g,h). The superconducting cavity is a coplanar waveguide resonating at about ωc/2π=7.4 GHz. We choose a single-port, quarter wavelength, reflection geometry, so that the cavity is connected to ground on one end, allowing to apply a well-defined constant voltage between the cavity and the graphene flake. The other end of the cavity is coupled to a transmission line via a capacitor Cext with a coupling rate κext=2π × 850 kHz for device A; the total cavity decay rate is κ=κext+κint=2π × 1.8 MHz (see Methods). Here κint accounts for the internal energy loss.

Figure 2. Device and characterization.

Figure 2

Open in a new tab

(a) False-colour image of the device. The cavity is coloured in dark yellow. The graphene flake is clamped in between niobium support electrodes (grey) and cross-linked poly(methyl metracylate) (turquoise). The scale bar is 5 μm. (b) Schematic cross-section of the graphene resonator along the white dashed dotted line in a. (c) Schematic of the measurement circuit. The graphene mechanical resonator is coupled to the superconducting LC cavity through the capacitance Cm. The separation d between the suspended graphene flake and the cavity counter electrode is controlled by the constant voltage Vg. The cavity is pumped with a pump tone at ωp and the output signal is amplified at 3 K. (d) Reflection coefficient |S11|2 and (e) reflected phase Δφ11 of the superconducting cavity of device A at Vg=3.002 V. The dark yellow lines are fits to the data using κint/2π=950 kHz and κext/2π=850 kHz using equation (7) (see Methods). (f) Driven vibration amplitude of the graphene resonator of device A as a function of drive frequency. The driving voltage is 22 nV and Vg=3.002 V. The dark yellow line is a lorentzian fit to the data. (g) Resonant frequency ωc/2π of the superconducting cavity as a function of Vg. (h) Resonant frequency ωm/2π of the graphene resonator as a function of Vg. The black line is the Vg dependence of ωm expected from electrostatic softening (see Supplementary Note 1).

We detect the vibrations of the graphene resonator with high precision by pumping the cavity with an electromagnetic field, and probing its mechanical sideband. This sideband is generated by the capacitive modulation of the pump field at frequency ωp/2π by the graphene vibrations at ωm/2π. We usually set ωp=ωc−ωm and probe the electromagnetic field that exits the cavity at ωc. We measure the device at the cryostat base temperature of 15 mK if not stated otherwise. The cavity output field is amplified with a high electron-mobility-transistor mounted at the 3 K stage of the cryostat. Mechanical noise spectra are detected with a spectrum analyser at room temperature. For a detailed description of the measurement set-up, see Supplementary Fig. 1 and Supplementary Note 2. In addition, we perform ring-down measurements to determine the mechanical dissipation rate 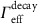Inline graphic of the graphene resonator. Spectral measurements are not suitable for quantifying reliably 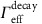Inline graphic because of the potentially substantial frequency noise of graphene resonators.

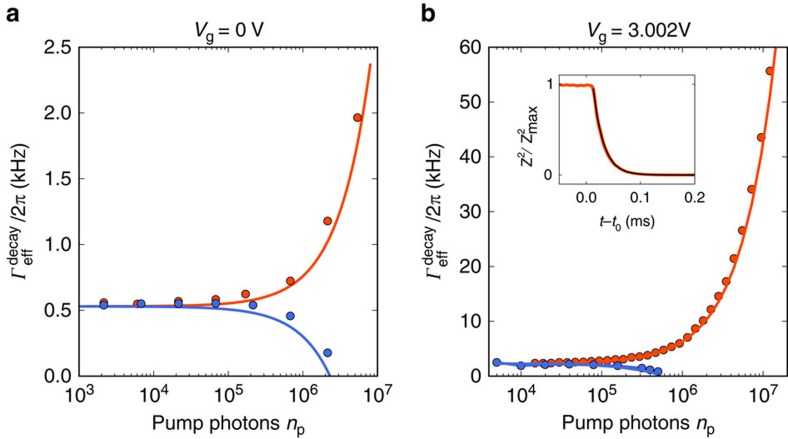
We characterize the single-photon optomechanical coupling and show that the coupling can be significantly enhanced by deflecting the membrane towards the cavity electrode. For this, we quantify the optomechanical scattering rate Γopt using ring-down measurements at Vg=0 V and Vg=3.002 V for device A. Figure 3a,b shows the measured dissipation rate 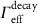Inline graphic as a function of cavity pump photon number np for blue and red detuned pumping. 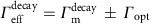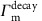The measurements are well described by Inline graphic where Inline graphic corresponds to the intrinsic mechanical dissipation rate, and ± to red and blue detuned pumping at ωp=ωc∓ωm, respectively. By increasing Vg from 0 to 3.002 V we obtain a strong increase of the optomechanical coupling from g0=2π × 9.7 Hz to g0=2π × 42.6 Hz. We estimate that the separation d between the membrane and the cavity counter electrode is reduced from 88 to 33 nm when varying Vg from 0 to 3.002 V. The calibration of both g0 and np is robust, while the quantification of the reduction of d is approximative; see Supplementary Notes 1 and 3, Supplementary Fig. 2 and Supplementary equations (1), (3)–(5).

Figure 3. Effective mechanical energy decay rates extracted from ring-down measurements.

Figure 3

Open in a new tab

Mechanical dissipation rate 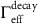Inline graphic measured on device A with the ring-down technique as a function of the number np of pump photons in the cavity at Vg=0 V and Vg=3.002 V, where np is proportional to the microwave power Pin applied at the input of the cryostat (see Supplementary Note 3). Red and blue data points correspond to red and blue detuned pumping, respectively. The measurements are well described by 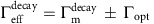Inline graphic (red and blue lines) using g0/2π=9.7 Hz in a and g0/2π=42.6 Hz in b. The inset in b shows a ring-down measurement for np=1.4·106. We plot the normalized vibration amplitude as a function of time t. The resonator is driven with a capacitive driving force for t<t0. At t0 the drive is switched off and the vibration amplitude decays freely (t>t0). We fit the data with an exponential decay (black line) using 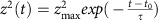Inline graphic with a decay rate Inline graphic. The vibration amplitude in ring-down measurements is larger than that in undriven displacement spectra, so that the motion in ring-down measurements can be resolved with lower np.

Thermal calibration and sideband cooling

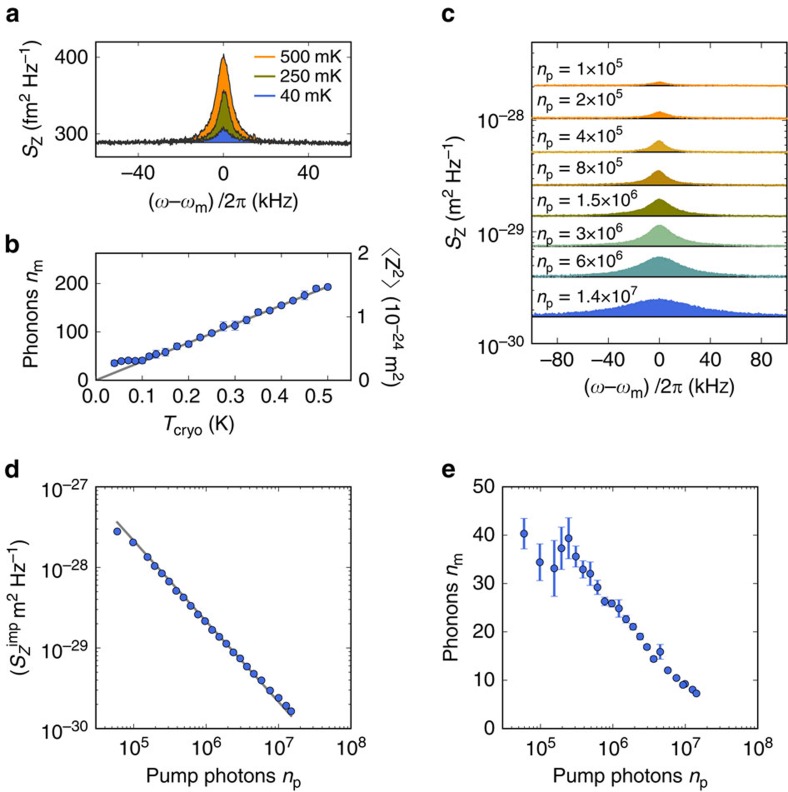
In order to calibrate the mechanical phonon occupation and the mode temperature Tmode, we measure the mechanical thermal motion spectrum while varying the cryostat temperature40. This is done by pumping the cavity with a weak pump tone on the red sideband. The integrated area of the thermal resonance is proportional to the mode temperature according to the equipartition theorem. For temperatures above 100 mK the area is linearly proportional to the cryostat temperature, showing that the mode is in thermal equilibrium with the cryostat (Fig. 4b). This linear dependence serves as a precise calibration to relate the resonance area to the averaged phonon occupation nm and the mode temperature Tmode. Below 100 mK the mechanical mode does not thermalize well with the cryostat. The origin of this poor thermalization at low temperature may be related to the heating induced by the pump field (see below)28, and a non-thermal force noise50 such as the electrostatic force noise related to the voltage noise in the device. As a next characterization step, we investigate the mechanical phonon occupation when increasing the power of the pump tone on the red sideband and keeping the temperature of the cryostat constant at Tcryo=15 mK. The measured resonance gets broader and its area smaller (Fig. 4c), showing that the mechanical mode is damped and cooled38,39. At the largest available pump power, the phonon occupation reaches nm=7.2±0.2 (Fig. 4e). This is the lowest phonon occupation reached in a mechanical resonator based on graphene27,28,51. The error in the estimation of nm is given by the standard error obtained from five successive spectral measurements.

Figure 4. Thermal calibration and sideband cooling of fundamental mechanical mode with red-detuned pumping.

Figure 4

Open in a new tab

(a) Selected thermo-mechanical noise spectra for different temperatures and np=6·104. (b) Plot of the measured mechanical mode temperature of device A, expressed in phonon occupation nm, as a function of cryostat temperature at Vg=3.002 V where ωm/2π=53.7 MHz and np=6·104. On the right y-axis, we display the variance of the vibration amplitude 〈z2〉, which is obtained by integrating the thermal resonance, as is shown in a. The phonon occupation is quantified with 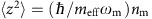Inline graphic (see Supplementary Note 3). The error bars are given by the standard deviation of 5 spectral measurements. (c) Mechanical displacement spectral density Sz measured for different pump photon number. The cryostat temperature is 15 mK. Note that the curves are not offset. (d) Displacement imprecision as a function of cavity pump photon population. The line is a fit of equation (3) with nadd=32. (e) Average phonon number nm as a function of np. The error bars are given by the standard deviation of five spectral measurements.

Displacement sensitivity and force sensitivity

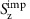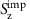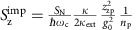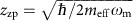The improved coupling allows us to achieve also an excellent displacement sensitivity Inline graphic (Fig. 4d). At the largest pump power, we obtain Inline graphic, which compares favourably to previous works27,51,52. The error in Inline graphic is given by the uncertainty in the estimation of meff. We obtain Inline graphic from the noise floor of the measured power spectral density SN using Inline graphic with Inline graphic the zero-point motion amplitude27. The displacement sensitivity scales as 1/np (Fig. 4d). By comparing the measurement to the expected displacement sensitivity

graphic file with name ncomms12496-m25.jpg

we obtain that the equivalent noise added by the amplifier chain is nadd=32. This is a reasonable value for a high electron-mobility-transistor amplifier mounted at 3 K42,53.

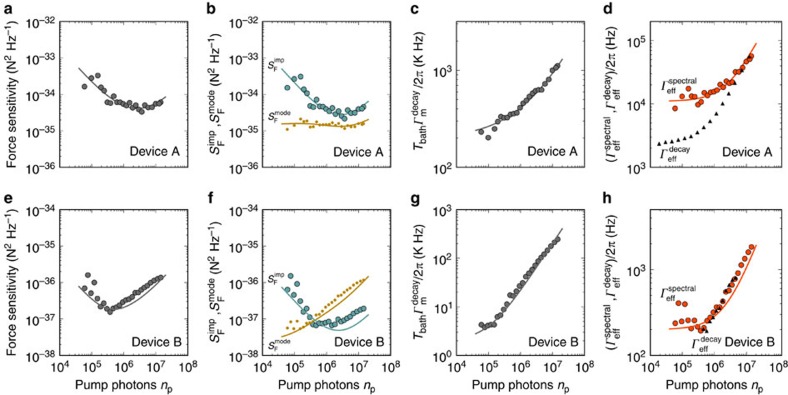
We now quantify the force sensitivity as a function of the microwave pump power (Fig. 5a,e). Since the mechanical resonances in the measured displacement spectra are well described by Lorentzian line shapes, the thermal force noise is quantified using 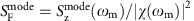Inline graphic with the effective mechanical susceptibility 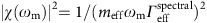Inline graphic. Similarly, we obtain the imprecision force noise with 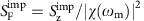Inline graphic. 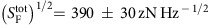The best force sensitivity we achieve for device A is Inline graphic with a mechanical bandwidth of 20 kHz (Fig. 5a,d). In device B we reach a force sensitivity of Inline graphic with a mechanical bandwidth of 0.2 kHz (see Fig. 5e,h). The error in the estimation of the force sensitivity is obtained from both the uncertainty in the mass and the fluctuations in the measurement of Inline graphic, which we evaluate by calculating the standard error of 10 measurements. This force sensitivity compares favourably with the best sensitivities obtained with micro-fabricated resonators (Inline graphic)42,45, albeit it is not as good as that of resonators based on carbon nanotubes8,10. Compared to previous devices, the mechanical bandwidth of graphene resonators is much higher, which enables faster detection of sudden force changes.

Figure 5. Characterization of the force sensitivity.

Figure 5

Open in a new tab

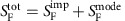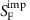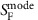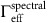(a) Force sensitivity Inline graphic as a function of cavity pump photon population measured when pumping the cavity on the red sideband. (b) Imprecision force noise Inline graphic (turquoise) and thermal force noise Inline graphic (dark yellow) versus np. The data in a,b are fitted to equations (2), (6). (c) Product of the bath temperature Tbath and the intrinsic mechanical decay rate Inline graphic as a function of cavity pump photon occupation. The line is a fit to the data. (d) Effective spectral mechanical line width Inline graphic and energy decay Inline graphic as a function of np. The data are fitted to Inline graphic with δΓnoise/2π=8.7 kHz (red line). (e–h) Equivalent to (a–d) but for device B. The lowest value for the force sensitivity in e is 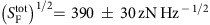Inline graphic. In e and f the data are fitted with nadd=22 and in h we use g0/2π=7.3 Hz, κ/2π=2.5 MHz and δΓnoise/2π=0.145 kHz. All the measurements on device A are performed at Vg=3.002 V and on device B at Vg=0 V. The cryostat temperature is 15 mK.

Discussion

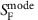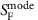We plot both Inline graphic and Inline graphic as a function of cavity pump photon population in Fig. 5b. As expected, the imprecision force noise decreases at low np and increases at high np due to the enhanced damping caused by the optomechanical back-action. The thermal force noise Inline graphic appears roughly constant when varying np as a result of the competing effects of Joule heating and frequency noise. Joule heating is caused by the microwave current in the graphene flake induced by the pump field. This results in the increase of the temperature Tbath of the thermal bath coupled to the mechanical mode as well as the mechanical dissipation rate26,28. We can infer the product 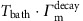Inline graphic from the measurements of nm and 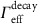Inline graphic in Figs 3b and 4e using

graphic file with name ncomms12496-m38.jpg

When increasing the pump power, Joule heating significantly increases the product Inline graphic (Fig. 5c), and therefore the size of the thermal force noise (equation (1)). We see next that the effect of frequency noise leads to the opposite dependence of the thermal force noise on pump power. Frequency noise enhances the spectral line width by the amount δΓnoise,

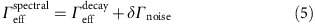graphic file with name ncomms12496-m40.jpg

when the fluctuations of the resonant frequency are described by a white noise8. The measurements of Inline graphic and Inline graphic as a function of pump power can be well described by equation (5) with δΓnoise/2π=8.7 kHz (Fig. 5d). Importantly, Fig. 5d shows that 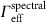Inline graphic is comparable to 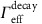Inline graphic at large pump power, showing that the relative contribution of δΓnoise to 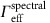Inline graphic gets negligible upon increasing np. As the cooling efficiency described by equation (4) remains unaltered by frequency noise (see chapter 7 in54), the thermal force noise is quantified by

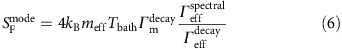graphic file with name ncomms12496-m46.jpg

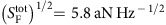Taking into account the measured effects of Joule heating and frequency noise in equation (6), the thermal force noise Inline graphic is expected to remain roughly constant as a function of np (dark yellow line in Fig. 5b), in agreement with the measurements. Overall, the best force sensitivity we achieve in this device is Inline graphic at np≈4·106 (Fig. 5a). While the force sensitivity in this device is primarily limited by the measurement imprecision, the thermal force noise is affected to a large extent by frequency noise at low np and by Joule heating at high np.

In device B, the graphene resonator has a lower mass and a narrower mechanical line width, two assets for high force sensitivity (Fig. 5e–h). The spectral line width corresponds to a mechanical quality factor of Q≈200,000. In this device we reach a force sensitivity of Inline graphic at np≈4·105 (see Fig. 5e). In an attempt to improve the thermal anchoring of device B compared to device A, the graphene contact electrodes contain an additional Au layer between the graphene and the Nb layer28,55. The normal metal layer is expected to increase the thermal conductance between the graphene flake and the contact electrodes through electron diffusion, which allows for better heat dissipation into the contacts. However, device B is still strongly affected by Joule heating, which substantially increases the value of Inline graphic when increasing the pump power (Fig. 5f,g). The heating is so strong that we are not able to reduce the phonon occupation nm with sideband cooling. We attribute the strong heating to the fact that the resonator is significantly thinner than the one of device A and therefore has a smaller heat capacity. The effect of frequency noise on the spectral line width is negligible for pump powers above np≈4·105. We do not know the origin of the frequency noise but it might be related to charged two-level fluctuators in the device. The force sensitivity is here primarily limited by the measurement imprecision at low np, and by the thermo-mechanical force noise and Joule heating at high np.

In the future, the force sensitivity of graphene optomechanical devices can be further improved using a quantum-limited Josephson parametric amplifier53. This readout will improve the measurement imprecision, by lowering nadd in Inline graphic. In addition, it will be possible to resolve the thermal vibrations with lower pump power, which is crucial to reduce Joule heating while working with low-mass graphene resonators. A quantum-limited amplifier with nadd=0.5 may allow to achieve 47 zN Hz−1/2 force sensitivity at 15 mK taking the mass of a single-layer graphene resonator with the diameter and the quality factor of device B (Fig. 1b). With only modest device improvements, it may be possible to probe the fundamental limit of continuous displacement detection imposed by quantum mechanics, since the force noise associated to quantum backaction Inline graphic is approaching Inline graphic measured at np=1.4 × 107 for device A. Force sensing with resonators based on two-dimensional materials hold promise for detecting electron and nuclear spins33 using superconducting cavities compatible with relatively large magnetic fields56, and studying the thermodynamic properties of two-dimensional materials, such as the quantum capacitance and the magnetization35.

Methods

Cavity characterization

In Fig. 2d,e we plot the coefficient |S11|2 and the phase of the reflected signal when sweeping the frequency over the cavity resonance at ωc/2π=7.416 GHz. To extract the external coupling rate κext and the internal loss rate κint we fit the measurement with the line shape expected for a one-port reflection cavity57

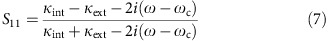graphic file with name ncomms12496-m54.jpg

which yields κint/2π=950 kHz and κext/2π=850 kHz at Vg=3.002 V for device A. The rates of Device B are κint/2π=800 kHz and κext/2π=1700  kHz at Vg=0 V.

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

Additional information

How to cite this article: Weber P. et al. Force sensitivity of multilayer graphene optomechanical devices. Nat. Commun. 7:12496 doi: 10.1038/ncomms12496 (2016).

Supplementary Material

Supplementary Information

Supplementary Figures 1 & 2, Supplementary Notes 1-3, Supplementary References

ncomms12496-s1.pdf (253.7KB, pdf)

Acknowledgments

We thank P. Verlot and M. Dykman for discussions. We acknowledge financial support by the ERC starting grant 279278 (CarbonNEMS), the EE Graphene Flagship (contact no. 604391), from MINECO and the Fondo Europeo de Desarrollo Regional (FEDER) through grant MAT2012-31338 and FIS2015-69831-P, the Fundació Privada Cellex, the Severo Ochoa Excellence Grant, and the Generalitat through AGAUR.

Footnotes

Author contributions P.W. fabricated the devices, the process being developed by P.W. and J.G. P.W., J.G. and A.N. carried out the experiment with support from J.V.C. The data analysis was done by P.W. and J.G. with inputs from A.B. The experimental setup was built by J.G. with support from P.W. P.W. and A.B. wrote the manuscript with comments from J.G. and A.N. A.B. and J.G. conceived the experiment and supervised the work.

References

  1. Sazonova V. et al. A tunable carbon nanotube electromechanical oscillator. Nature 431, 284–287 (2004). [DOI] [PubMed] [Google Scholar]
  2. Jensen K., Kim K. & Zettl A. An atomic-resolution nanomechanical mass sensor. Nat. Nanotech. 3, 533–537 (2008). [DOI] [PubMed] [Google Scholar]
  3. Chiu H. Y., Hung P., Postma H. W. C. & Bockrath M. Atomic-scale mass sensing using carbon nanotube resonators. Nano Lett. 8, 4342–4346 (2008). [DOI] [PubMed] [Google Scholar]
  4. Lassagne B., Tarakanov Y., Kinaret J., Garcia-Sanchez D. & Bachtold A. Coupling mechanics to charge transport in carbon nanotube mechanical resonators. Science 325, 1107–1110 (2009). [DOI] [PubMed] [Google Scholar]
  5. Steele G. A. et al. Strong coupling between single-electron tunneling and nanomechanical motion. Science 325, 1103–1107 (2009). [DOI] [PubMed] [Google Scholar]
  6. Gouttenoire V. et al. Digital and FM demodulation of a doubly clamped single-walled carbon-nanotube oscillator: towards a nanotube cell phone. Small 6, 1060–1065 (2010). [DOI] [PubMed] [Google Scholar]
  7. Chaste J. et al. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotech. 7, 301–304 (2012). [DOI] [PubMed] [Google Scholar]
  8. Moser J. et al. Ultrasensitive force detection with a nanotube mechanical resonator. Nat. Nanotech. 8, 493–496 (2013). [DOI] [PubMed] [Google Scholar]
  9. Ganzhorn M., Klyatskaya S., Ruben M. & Wernsdorfer W. Strong spin-phonon coupling between a single-molecule magnet and a carbon nanotube nanoelectromechanical system. Nat. Nanotech. 8, 165–169 (2013). [DOI] [PubMed] [Google Scholar]
  10. Moser J., Eichler A., Güttinger J., Dykman M. I. & Bachtold A. Nanotube mechanical resonators with quality factors of up to 5 million. Nat. Nanotech. 9, 1007–1011 (2014). [DOI] [PubMed] [Google Scholar]
  11. Benyamini A., Hamo A., Kusminskiy S. V., von Oppen F. & Ilani S. Real-space tailoring of the electron-phonon coupling in ultraclean nanotube mechanical resonators. Nat. Phys. 10, 151–156 (2014). [Google Scholar]
  12. Häkkinen P., Isacsson A., Savin A., Sulkko J. & Hakonen P. Charge sensitivity enhancement via mechanical oscillation in suspended carbon nanotube devices. Nano Lett. 15, 1667–1672 (2015). [DOI] [PubMed] [Google Scholar]
  13. Ayari A. et al. Self-oscillations in field emission nanowire mechanical resonators: a nanometric dc-ac conversion. Nano Lett. 7, 2252–2257 (2007). [DOI] [PubMed] [Google Scholar]
  14. Gil-Santos E. et al. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotech. 5, 641–645 (2010). [DOI] [PubMed] [Google Scholar]
  15. Arcizet O. et al. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 7, 879–883 (2011). [Google Scholar]
  16. Nichol J. M., Hemesath E. R., Lauhon L. J. & Budakian R. Nanomechanical detection of nuclear magnetic resonance using a silicon nanowire oscillator. Phys. Rev. B 85, 054414 (2012). [Google Scholar]
  17. Nichol J. M., Naibert T. R., Hemesath E. R., Lauhon L. J. & Budakian R. Nanoscale Fourier-transform magnetic resonance imaging. Phys. Rev. X 3, 031016 (2013). [Google Scholar]
  18. Sansa M., Fernández-Regúlez M., Llobet L., San Paulo A. & Pérez-Murano F. High-sensitivity linear piezoresistive transduction for nanomechanical beam resonators. Nat. Commun. 5, 4313 (2014). [DOI] [PubMed] [Google Scholar]
  19. Gloppe A. et al. Bidimensional nano-optomechanics and topological backaction in a non-conservative radiation force field. Nat. Nanotech. 9, 920–926 (2014). [DOI] [PubMed] [Google Scholar]
  20. Montinaro M. et al. Quantum dot opto-mechanics in a fully self-assembled nanowire. Nano Lett. 14, 4454–4460 (2014). [DOI] [PubMed] [Google Scholar]
  21. Mathew J. P. et al. Nanoscale electromechanics to measure thermal conductivity, expansion, and interfacial losses. Nano Lett. 15, 7621–7626 (2015). [DOI] [PubMed] [Google Scholar]
  22. Nigues A., Siria A. & Verlot P. Dynamical backaction cooling with free electrons. Nat. Commun. 6, 8104 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Bunch J. S. et al. Electromechanical resonators from graphene sheets. Science 315, 490–493 (2007). [DOI] [PubMed] [Google Scholar]
  24. Chen C. et al. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotech. 4, 861–867 (2009). [DOI] [PubMed] [Google Scholar]
  25. Eichler A. et al. Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene. Nat. Nanotech. 6, 339–342 (2011). [DOI] [PubMed] [Google Scholar]
  26. Miao T., Yeom S., Wang P., Standley B. & Bockrath M. Graphene nanoelectromechanical systems as stochastic-frequency oscillators. Nano Lett. 14, 2982–2987 (2014). [DOI] [PubMed] [Google Scholar]
  27. Singh V. et al. Optomechanical coupling between a multilayer graphene mechanical resonator and a superconducting microwave cavity. Nat. Nanotech. 9, 820–824 (2014). [DOI] [PubMed] [Google Scholar]
  28. Song X., Oksanen M., Li J., Hakonen P. J. & Sillanpää M. A. Graphene optomechanics realized at microwave frequencies. Phys. Rev. Lett. 113, 027404 (2014). [DOI] [PubMed] [Google Scholar]
  29. Weber P., Güttinger J., Tsioutsios I., Chang D. E. & Bachtold A. Coupling graphene mechanical resonators to superconducting microwave cavities. Nano Lett. 14, 2854–2860 (2014). [DOI] [PubMed] [Google Scholar]
  30. Lee J., Wang Z., He K., Shan J. & Feng P. X. L. High frequency MoS2 nanomechanical resonators. ACS Nano 7, 6086–6091 (2013). [DOI] [PubMed] [Google Scholar]
  31. van Leeuwen R., Castellanos-Gomez A., Steele G. A., van der Zant H. S. J. & Venstra W. J. Time-domain response of atomically thin MoS2 nanomechanical resonators. Appl. Phys. Lett. 105, 041911 (2014). [Google Scholar]
  32. Wang Z. & Feng P. X. L. Dynamic range of atomically thin vibrating nanomechanical resonators. Appl. Phys. Lett. 104, 103109 (2014). [Google Scholar]
  33. Rugar D., Budakian R., Mamin H. J. & Chui B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329–332 (2004). [DOI] [PubMed] [Google Scholar]
  34. Bleszynski-Jayich A. C. et al. Persistent currents in normal metal rings. Science 326, 272–275 (2009). [DOI] [PubMed] [Google Scholar]
  35. Chen C. et al. Modulation of mechanical resonance by chemical potential oscillation in graphene. Nat. Phys. 12, 240–244 (2016). [Google Scholar]
  36. Wang Z. et al. Phase transitions of adsorbed atoms on the surface of a carbon nanotube. Science 327, 552–555 (2010). [DOI] [PubMed] [Google Scholar]
  37. Tavernarakis A. et al. Atomic monolayer deposition on the surface of nanotube mechanical resonators. Phys. Rev. Lett. 112, 196103 (2014). [DOI] [PubMed] [Google Scholar]
  38. Arcizet O., Cohadon P. F., Briant T., Pinard M. & Heidmann A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 444, 71–74 (2006). [DOI] [PubMed] [Google Scholar]
  39. Gigan S. et al. Self-cooling of a micromirror by radiation pressure. Nature 444, 67–70 (2006). [DOI] [PubMed] [Google Scholar]
  40. Teufel J. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011). [DOI] [PubMed] [Google Scholar]
  41. Chan J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011). [DOI] [PubMed] [Google Scholar]
  42. Teufel J. D., Donner T., Castellanos-Beltran M. A., Harlow W. J. & Lehnert K. W. Nanomechanical motion measured with an imprecision below that at the standard quantum limit. Nat. Nanotech. 4, 820–823 (2009). [DOI] [PubMed] [Google Scholar]
  43. Anetsberger G. et al. Measuring nanomechanical motion with an imprecision below the standard quantum limit. Phys. Rev. A 82, 061804 (2010). [Google Scholar]
  44. Meenehan S. M. et al. Silicon optomechanical crystal resonator at millikelvin temperatures. Phys. Rev. A 90, 011803 (2014). [Google Scholar]
  45. Mamin H. J. & Rugar D. Sub-attonewton force detection at millikelvin temperatures. Appl. Phys. Lett. 79, 3358 (2001). [Google Scholar]
  46. Zhang Y., Moser J., Güttinger J., Bachtold A. & Dykman M. I. Interplay of driving and frequency noise in the spectra of vibrational systems. Phys. Rev. Lett. 113, 255502 (2014). [DOI] [PubMed] [Google Scholar]
  47. Singh V. et al. Probing thermal expansion of graphene and modal dispersion at low-temperature using graphene nanoelectromechanical systems resonators. Nanotechnology 21, 165204 (2010). [DOI] [PubMed] [Google Scholar]
  48. Bao W. et al. In situ observation of electrostatic and thermal manipulation of suspended graphene membranes. Nano Lett. 12, 5470–5474 (2012). [DOI] [PubMed] [Google Scholar]
  49. Chen C. et al. Graphene mechanical oscillators with tunable frequency. Nat. Nanotech. 8, 923–927 (2013). [DOI] [PubMed] [Google Scholar]
  50. Rocheleau T. et al. Preparation and detection of a mechanical resonator near the ground state of motion. Nature 463, 72–75 (2009). [DOI] [PubMed] [Google Scholar]
  51. Barton R. A. et al. Photothermal self-oscillation and laser cooling of graphene optomechanical systems. Nano Lett. 12, 4681–4686 (2012). [DOI] [PubMed] [Google Scholar]
  52. Cole R. M. et al. Evanescent-field optical readout of graphene mechanical motion at room temperature. Phys. Rev. Appl. 3, 024004 (2015). [Google Scholar]
  53. Castellanos-Beltran M., Irwin K., Hilton G., Vale L. & Lehnert K. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nat. Phys. 4, 929–931 (2008). [Google Scholar]
  54. Dykman M. I. ed. Fluctuating Nonlinear Oscillators Oxford (2012). [Google Scholar]
  55. Fong K. C. et al. Measurement of the electronic thermal conductance channels and heat capacity of graphene at low temperature. Phys. Rev. X 3, 041008 (2013). [Google Scholar]
  56. Samkharadze N. et al. High-kinetic-inductance superconducting nanowire resonators for circuit QED in a magnetic field. Phys. Rev. Appl. 5, 044004 (2016). [Google Scholar]
  57. Aspelmeyer M., Kippenberg T. J. & Marquardt F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391 (2014). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1 & 2, Supplementary Notes 1-3, Supplementary References

ncomms12496-s1.pdf (253.7KB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES