Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Jun 20;12(8):3449–3455. doi: 10.1021/acs.jctc.6b00231

Localization of Millisecond Dynamics: Dihedral Entropy from Accelerated MD

Anna S Kamenik 1, Ursula Kahler 1, Julian E Fuchs 1,*, Klaus R Liedl 1,*
PMCID: PMC4980685  PMID: 27322931

Abstract

graphic file with name ct-2016-00231p_0005.jpg

Here, we demonstrate a method to capture local dynamics on a time scale 3 orders of magnitude beyond state-of-the-art simulation approaches. We apply accelerated molecular dynamics simulations for conformational sampling and extract reweighted backbone dihedral distributions. Local dynamics are characterized by torsional probabilities, resulting in residue-wise dihedral entropies. Our approach is successfully validated for three different protein systems of increasing size: alanine dipeptide, bovine pancreatic trypsin inhibitor (BPTI), and the major birch pollen allergen Bet v 1a. We demonstrate excellent agreement of flexibility profiles with both large-scale computer simulations and NMR experiments. Thus, our method provides efficient access to local protein dynamics on extended time scales of high biological relevance.

1. Introduction

Macromolecules in solution steadily undergo conformational changes at room temperature.1 Various structural studies on diverse model systems have shown that the conformational plasticity of proteins plays a key role in molecular mechanisms such as catalytic activity,2 biomolecular recognition,3−5 and allosteric regulation.6 Thus, characterizing dynamics of biological macromolecules is crucial to understanding their biological activity and function.7,8 Molecular dynamics (MD) simulations have proven to be an efficient tool to capture the flexibility of macromolecules.9 Yet, state-of-the-art MD simulations routinely capture dynamics on the nanosecond to microsecond time scale, while many biologically significant motions appear on the millisecond time scale or slower.10 Inherent limitations in conformational sampling can either be overcome by usage of dedicated simulation hardware11 or by application of enhanced sampling algorithms.12,13 Accelerated MD (aMD) is a promising enhanced sampling technique, which improves the efficiency of conventional MD (cMD) simulation without a priori knowledge of the potential energy surface.14 Introduction of a continuous, non-negative bias potential increases escape rates from local energy basins. Thus, the conformational space is sampled more extensively at negligible computational overhead costs.15,16 Subsequently, the original energy landscape can be reconstructed by Boltzmann reweighting.17−19

The versatile applicability of aMD simulations has repeatedly been proven on manifold macromolecular systems.20−25 Current aMD studies predominantly focus on analyzing the global dynamics of the obtained conformational ensembles.26−28 Yet, for a comprehensive understanding of biomolecular properties, it is crucial to be able to localize flexibility in specific protein domains.29−33

Current approaches estimating local dynamics in aMD simulations are limited to expensive large-scale calculations of amide-order parameters from multiple aMD trajectories on various acceleration levels.34,35 Rather than approximations of NMR observables, a straightforward approach based on the thermodynamics of a system would be desirable. So far, no metric is available to directly quantify local flexibility from aMD trajectories based on the captured thermodynamics of the system. We propose residue-wise dihedral entropy as the first methodology to efficiently characterize local dynamics of macromolecules from aMD simulations.36,37 To confirm the validity and efficiency of our approach, we apply the metric to the model systems alanine dipeptide (Di-Ala) and bovine pancreatic trypsin inhibitor (BPTI). The conformational dynamics of BPTI have been investigated thoroughly in NMR experiments38−41 as well as in large-scale computer simulations.11 It has already been demonstrated in previous studies that metrics for local flexibility in a 1 ms cMD simulation of BPTI track the characteristic motions of BPTI, known from NMR and global flexibility studies.29,38−42 Here, we show that residue-wise dihedral entropies deriving from a 500 ns aMD and a 1 ms cMD simulation of BPTI correlate remarkably. Application of our metric on aMD trajectories provides a possibility to track low-frequency local dynamics on the millisecond time scale.

Additionally, we apply our metric to cMD and aMD simulations of the major birch pollen allergen Bet v 1.0101 (Bet v 1a). Bet v 1a is a highly immunogenic storage protein and most prominent for causing seasonal pollen allergy in the Northern Hemisphere.43,44 Despite a sequence similarity of more than 95%45,46 and minor differences in their 3D structures, the more than 13 reported isoforms of Bet v 1a vary strongly in their immunogenicity.47 Investigations on differences in proteolytic stability and ligand binding of different isoforms and mutants of Bet v 1a suggest a linkage between immunogenic potential and conformational flexibility.47−49

The accuracy of our results is underlined by comparison to NMR data,47 displaying analogous trends in experimentally and computationally estimated flexibility. Our results show that dihedral entropies from aMD simulations are an efficient tool to describe local protein dynamics on the millisecond time scale.

2. Methods

MD simulations were performed with the AMBER14 simulation package.50 All structures were prepared in MOE (Molecular Operating Environment, Chemical Computing Group, version 2014.0901)51 using the protonate3D tool.52 With tleap of the AmberTools1550 package, all three systems were soaked into a truncated octahedral solvent box of TIP3P water molecules.53 For Di-Ala, the minimum wall distance was set to 12 Å and for BPTI and Bet v 1a to 10 Å. Parameters for all three systems derive from the AMBER force field 99SB-ILDN.54 All systems were carefully equilibrated using a multistep equilibration protocol.55 Precedent cMD simulations as well as all aMD simulations were performed in NpT ensemble using pmemd.cuda.56 Bonds involving hydrogen atoms were restrained by applying the SHAKE algorithm,57 allowing a time step of 2.0 fs. Atmospheric pressure of the system was preserved by weak coupling to an external bath using the Berendsen algorithm.58 The Langevin thermostat59 was used to maintain the temperature during simulations at 300 K for Di-Ala and BPTI and 310 K for Bet v 1a (human body temperature).

All aMD simulations were performed using the dual-boost protocol60 implemented in pmemd.cuda.56 Thereby the total potential is accelerated and an extra boosting is applied to the dihedral potential. It has been shown that dual-boost aMD simulations sample the diffusive solvent motions more extensively. Ensemble averages as well as entropy estimates converge faster than in dihedral-boost aMD simulations.26,60 All simulations were analyzed using cpptraj61 in AmberTools15,50 the reweighting protocol provided by Miao et al.,18 and in-house scripts. The free energy profile was reconstructed from the aMD simulations via Boltzmann reweighting using a Maclaurin series expansion (up to the tenth order) as the approximation for the exponential term, as suggested in previous studies.15

The local backbone flexibility profiles were estimated from the resulting reweighted one-dimensional free energy profiles and state populations, respectively, of the backbone dihedrals Φ and Ψ. The entropy is calculated by integration of the reweighted state populations of a given dihedral. A high entropy of a residue backbone dihedral indicates high local backbone flexibility.29,36

In the presented work, we prioritized dihedral entropies SΨ over SΦ in the representation protein dynamics as they captured the backbone dynamics more comprehensively.62,63 Yet, SΨ alone does not reflect the entire backbone dynamics, and dihedral entropies SΦ were calculated as well (SI).

Alanine Dipeptide

For the reference cMD simulation of alanine dipeptide (Di-Ala), a 10 μs trajectory comprising 100,000 frames, previously performed in our group, was reanalyzed.29 Residue-wise dihedral entropies of the reference cMD simulations were calculated from probability density functions reconstructed by nonparametric kernel density estimation.36,37 As proposed by Botev et al.,64 we optimize the bandwidth of the kernel function by cross validation, resulting in a continuous probability density function for each dihedral. We periodically duplicate our data to minimize the overestimated flexibility at the boundaries. The entropy for each dihedral Sx was calculated by integration of kB · p(x) · log(p(x)) on its probability density function p(x) as described in Huber et al.36,37 The standard deviations were calculated by splitting the trajectory into 100 segments.

For the aMD calculations, the solvated and equilibrated Di-Ala system was simulated for 1 μs and stored as 500,000 equal-spaced snapshots (2 ps spacing). The aMD boosting parameters were calculated as suggested in previous studies15 (see SI for further information). To minimize the statistical noise (and capture dynamics corresponding to 10 μs of cMD), the resulting trajectory was divided into 200 segments of 5 ns each (2500 frames) using the segments for averaging (SI, Figure S4). From the reweighted dihedral populations, a Ramachadran plot was created to ensure sufficient and accurate sampling of conformational space (SI, Figure S1).

To compare aMD and cMD free energies, we calculated the free energy of the cMD trajectory using the reweighting protocol by Miao et al.18 We investigated several different bin sizes, and the jaggedness of the cMD profile disappears only using a bin size above 20° (SI, Figure S2). However, as also suggested by Miao et al.,18 we observe a bin size of 6° to be a reasonable compromise between accuracy and statistical noise.

BPTI

D. E. Shaw Research kindly provided us with a long time scale 1.03 ms trajectory comprising 4,140,000 snapshots as a cMD reference.11 We used the same joint neutron/X-ray refined structure of BPTI (PDB: 5PTI)38 as Shaw et al. as the starting structure for our large scale cMD and aMD simulations. A 500 ns aMD simulation was performed, and the trajectory was stored as 250,000 snapshots. The aMD boosting parameters were calculated as suggested by Pierce et al.15 and can be found in the Supporting Information. To localize the observed dynamic hot spots, we calculated dihedral entropies as described earlier for 1 ms and 1 μs of cMD and 500 ns of aMD sampling time.

Bet v 1a

On the basis of the crystal structure of Bet v 1a with PDB ID 4A88,65 we sampled 3 μs of cMD simulations on Bet v 1a. Suitable aMD boosting parameters for Bet v 1a were determined by a systematic search (SI). We performed a 1 μs aMD simulation stored as 100,000 equally spaced snapshots. The trajectory was split in 50 segments of 20 ns each (2000 snapshots) and reweighted as described above. Subsequently, dihedral entropies were calculated and averaged over all 50 segments. NMR order parameters were kindly provided by Grutsch et al.; the experimental setup has been described elsewhere.47

3. Results

Alanine Dipeptide

To establish our approach, we calculated backbone dihedral entropies for Φ and Ψ of alanine dipeptide from 5 ns aMD sampling and used a 10 μs cMD simulation as a reference (Figure 1). We find a significant reproduction of local minima and overall shape of the potential energy surface for the backbone dihedral Φ of Di-Ala. As reported before,18 we also observe a shift in the extrema of backbone dihedral Ψ to smaller Ψ values in aMD simulations. Exemplary, in the cMD simulation, an energy minimum is found at −24°, while the corresponding minimum in the aMD results is recovered at −42°. Still the overall energy landscape of the reweighted aMD trajectory is in reliable agreement with the cMD results.

Figure 1.

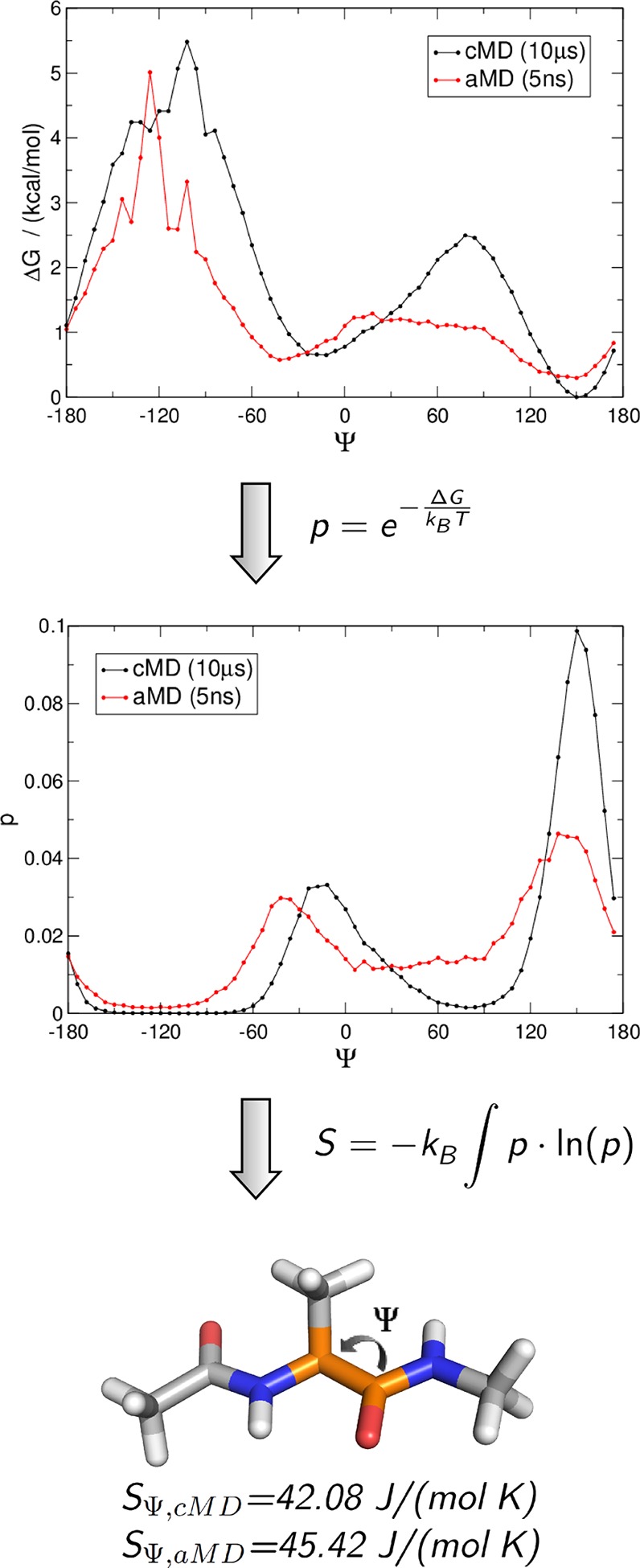
Figure 1

Open in a new tab

From a reweighted aMD trajectory to dihedral entropies of alanine dipeptide: State populations p are calculated from free energy profiles of the backbone dihedral Ψ of a 10 μs cMD (black) and a reweighted 5 ns aMD (red) trajectory. Integration of the resulting state populations leads to the dihedral entropy SΨ,cMD = 42.08 J/(mol K) and SΨ, aMD = 45.42 J/(mol K).

Considering these errors, the resulting dihedral entropies, SΦ,aMD = 41.03 (±2.95) J/(mol K) and SΨ,aMD = 45.42 (±3.25) J/(mol K), agree very well with those of the cMD ensemble, SΦ,cMD = 40.20 (±0.60) J/(mol K) and SΨ,cMD = 42.08 (±0.39) J/(mol K).

BPTI

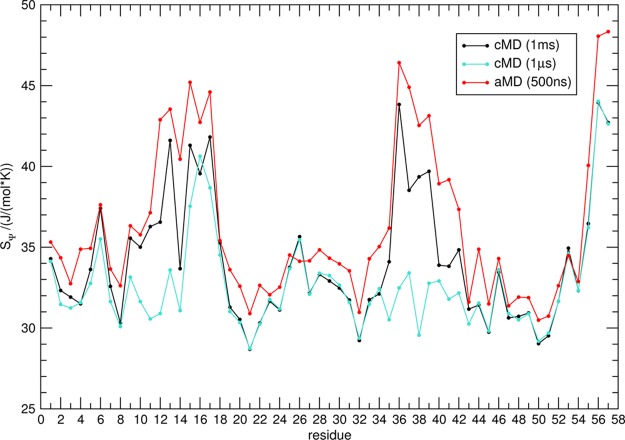
To benchmark our local flexibility metric, we analyzed a 500 ns aMD simulation of BPTI and compared it to a 1 ms cMD simulation provided by D. E. Shaw Research11 (Figure 2). It has been demonstrated previously that 500 ns of BPTI aMD simulation cover a conformational space equivalent to a 1 ms cMD.15 In addition to the findings of Pierce et al., we observe equal assessment of local backbone flexibility for the 500 ns aMD and 1 ms cMD simulation. In the 1 ms reference, cMD maxima of SΨ are found in regions from residues 10–20 and 32–44 and the C-terminal residues from 54–58. Each flexibility hot spot is reproduced in SΨ from 500 ns of aMD sampling. The high similarity of local flexibility in both simulation protocols is reflected in a Spearman rank correlation over the protein length of r = 0.93 for SΨ between cMD and aMD. Comparable agreement between the aMD and reference cMD simulations is also found for SΦ (SI, Figure S5). In contrast, when looking at dihedral entropies from a 1 μs cMD simulation, notable differences are found for SΨ in the regions of residues 10–14 and 32–44. In 1 μs of cMD sampling, no elevation in conformational plasticity is captured in these domains, though this is clearly observed on the millisecond time scale as well as in the aMD-derived ensemble. The deviation of the local dynamics pattern results in a Spearman rank correlation of r = 0.65 for SΨ in 500 ns of aMD and 1 μs cMD sampling.

Figure 2.

Figure 2

Open in a new tab

Comparing local flexibility of BPTI captured in cMD and aMD simulations. Residue-wise dihedral entropies SΨ from a 1 ms cMD simulation (black) and 500 ns aMD simulation of BPTI (red) show remarkable rank correlation (r = 0.93). Local flexibility observed in a 1 μs cMD simulation (turquoise) clearly differs from the aMD results (r = 0.65).

For the dihedral entropies SΨ and SΦ captured in 500 ns of aMD, we find a correlation of r = 0.77. The high correlation of SΨ and SΦ supports the assumption that a similar extent of flexibility is captured in both backbone dihedral angles.

In Figure 3, the flexibility hot spots displayed in Figure 2 are color coded and projected on the BPTI fold. The differences in flexibility captured in 500 ns of aMD (B) and 1 μs cMD (C) are highlighted in (D). Here, SΨ of the 1 μs cMD simulation was subtracted from SΨ resulting in 500 ns aMD. Positive values (blue) indicate domains, which are more flexible in the aMD than in the cMD simulation of 1 μs sampling length. When looking at the structure, the most prominent deviation between 500 ns aMD and 1 μs cMD simulations lies in the local flexibility of the loop regions. Clearly, the dynamic nature of the loop involving residues 32–44 found in the millisecond simulation is not adequately sampled in 1 μs cMD but is accurately represented in aMD sampling of 500 ns length.

Figure 3.

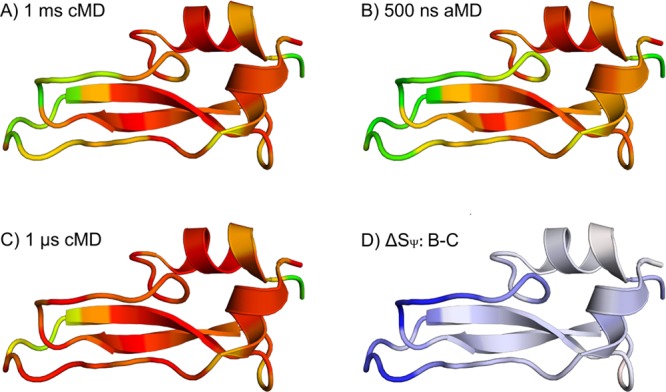
Figure 3

Open in a new tab

Flexibility hot spots of BPTI: Residue-wise dihedral entropies for Ψ (SΨ) from the 1 ms cMD (A), 500 ns aMD simulation (B), and 1 μs cMD (C) are projected on the structure of BPTI (PDB-ID: 5PTI). In panels A, B, and C, the color coding ranges from red (SΨ ≤ 30 J/(mol K)) via yellow to green (SΨ ≥ 45 J/(mol K)). Thus, the most rigid residues are pictured in red, whereas the most flexible ones are colored green. Part D shows the differences in SΨ between 500 ns aMD and 1 μs cMD (ΔSΨ = B – C). The color coding in D ranges from red (ΔSΨ ≤ 15 J/(mol K)) to white to blue (ΔSΨ ≥ 15 J/(mol K)); i.e., blue indicates regions where the aMD simulation captures a higher local flexibility. Thus, the cMD simulation clearly underestimates the conformational dynamics of BPTI in the region of residues 10–14 and 32–44.

Bet v 1a

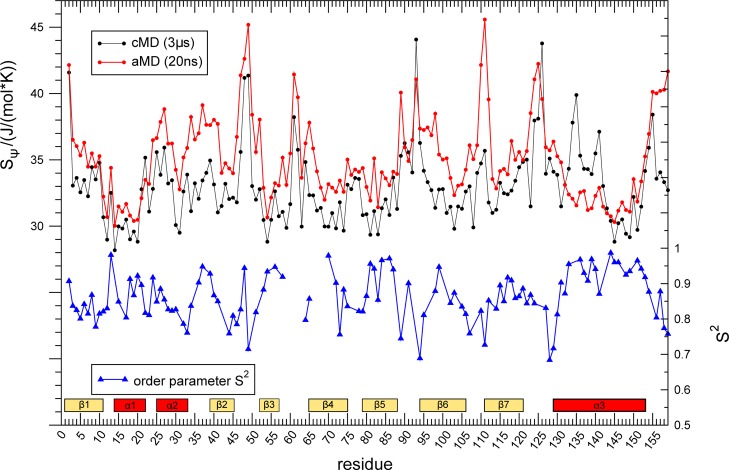
With 159 residues, the major birch pollen allergen Bet v 1a is the largest system in our study. A 1 μs aMD simulation was split into 50 segments, 20 ns each. A 3 μs cMD simulation and order parameters S2 from backbone amide NMR relaxation experiments47 act as references for our metric to quantify local motions in aMD simulations (Figure 4). Order parameters range from zero to one, indicating no or full constriction of internal mobility of backbone amide groups on the ps- to ns-time scale.66 Thus, an anticorrelation is expected since high entropy indicates lower order. As observed for the BPTI system, the aMD-derived ensemble shows higher backbone flexibility for all residues compared to the cMD-derived one. The general flexibility patterns are conserved for most parts of the protein in both simulations. However, especially in the region from α1 to β2 (residues 15–45), enhanced dynamics are visible in aMD, which are not reflected in the cMD simulation. Order parameters S2 show the expected anticorrelation with dihedral entropies of the core domains, i.e., α3-helix and β-sheets 4–7 (residues 70–159). Yet, in contrast to experimental findings, we obtain lowered local dynamics for the α1-helix and the β2-sheet, while for the loop region in between elevated flexibility is observed. These opposing qualitative observations are reflected in a Spearman rank correlation between the Ψ dihedral entropies from aMD simulations and amide order parameters S2 of r = −0.35 for the whole fold. When restricting the correlation analysis to the core helix α3- and β-sheets 5–7 (residues 70–159), the rank correlation is strengthened to r = −0.61.

Figure 4.

Figure 4

Open in a new tab

Local flexibility on different time scales in Bet v 1a: Dihedral entropies SΨ from 20 ns aMD (red) and 3 μs of cMD (black) are compared to experimental ps/ns dynamics66 captured by NMR-derived backbone amide-order parameters S2 (blue)47

4. Discussion

Local flexibility is decisive for biomolecular recognition mechanisms like protein–protein interactions and ligand binding, as well as for protein folding.2−4,6 It has been shown that the flexibility patterns of Bet v 1 are linked to its fold-stability49 and allergenicity.47 Furthermore, studies on the dynamics of proteases found a remarkable correlation between substrate specificity and local flexibility of protease active sites.5 The associated dynamics include motions from the nanosecond to the millisecond time scale.10 Metrics to quantify the amount of global and local motions are indispensable for a holistic understanding of macromolecular interactions.29 Several expedient metrics have been developed to account for global and local flexibility in cMD simulations, such as root-mean-square fluctuation, locally and globally aligned b-factors, or torsional entropies.29,36,67 Dynamics from aMD simulations are currently predominantly described on a global level only.26−28,68 In our study on three model systems of increasing size, we establish an alignment-free internal coordinate-based metric estimating local flexibility in aMD simulations. As expected, enhanced local dynamics are captured using enhanced sampling. As demonstrated for global movements, we are able to describe local protein flexibility on the millisecond time scale after several hundred of nanoseconds of aMD sampling. The residue-wise quantification of motion in a protein backbone is constructed from torsional free energy profiles of reweighted aMD trajectories via calculation of dihedral entropies.36

Investigations on the smallest system in our study, Di-Ala, illustrate the applied work flow. As already outlined in a previous study,18 we also find a shift of minima in the free energy landscape of Ψ in the reweighted aMD trajectory compared to the cMD results. This deviation is most probably generated by the reweighting step when using the Maclaurin series of the tenth order as approximation for the exponential. As shown by Miao et al. for alanine dipeptide, reweighting using cumulant expansion to the second order reconstructs the free energy surface of aMD simulations accurately. Yet, this approach requires the distribution of the boost potential to be exactly Gaussian.69 This may be approximately the case for a small system like Di-Ala, but we observed that it is less successful for larger biomolecular systems such as BPTI (SI, Figure S7). Previous studies on BPTI and other proteins showed accurate results for Maclaurin series expansion of the tenth order.15,27 Thus, we prefer to use Maclaurin series expansion for all systems in our study for consistency.

Overall, a quantitative reproduction of the positions of the local extrema is not essential for our methodology since their exact location has no influence on the resulting entropies. The state probability distribution is generally broader in the aMD ensemble but results in statistically equal dihedral entropies. Thus, the same dynamic tendencies are estimated from the aMD and reference cMD simulation.

BPTI is widely used as a test system for NMR and protein dynamics in general and has been investigated thoroughly over the last decades.41 The group of D. E. Shaw performed large-scale computer simulations and extensive studies on the dynamics of this model system.11 We have demonstrated in previous studies that metrics of local flexibility in a 1 ms cMD simulation of BPTI capture characteristic motions, known from NMR and global flexibility studies.29 These prominent movement motifs comprise the isomerization of a disulfide bridge involving Cys-14 and Cys-38. With our metric, we quantified local flexibility for a 500 ns aMD and a 1 ms cMD simulation of BPTI with a striking Spearman rank correlation of r = 0.93 for SΨ. Thus, we are able to quantify and localize millisecond dynamics with aMD simulations of several hundred nanoseconds length. When compared to a 1 μs cMD simulation, it is evident that these results cannot be obtained with state-of-the-art simulation protocols of the same length (r = 0.65). The differences in captured molecular motions in 500 ns aMD and 1 μs cMD sampling can be traced back to the loop regions (residue 10–14 and 32–44), which comprise the switching disulfide bridge mentioned earlier (SI, Figure S8). The isomerization of this bond, which is described by NMR studies and the calculations of the Shaw group, implies an enhancement of local flexibility in the surrounding region. The characteristic dynamics of the domain are evidently quantified by our metric in 500 ns aMD sampling. These results show that the approach allows access to dynamics of low-frequency motions. Additionally, our metric provides a tool to localize the origin of elevated flexibility thereby identifying domains with prominent dynamics and allowing a residue-wise interpretation.

Bet v 1a is the largest and thereby most challenging system in our study. The boosting parameters for the Di-Ala and BPTI simulations were applied as suggested in previous studies.15,18 For Bet v 1a, we set up six simulations on different levels of acceleration to test the limit of applied acceleration without unfolding the protein (SI). It has been shown that the choice of parameter has a crucial impact on the resulting trajectory and has to be evaluated carefully.16

To estimate the reliability of our findings, we compared a 20 ns aMD trajectory to a conventional 3 μs MD simulation and NMR-derived NH order parameters S2. Flexibility patterns recovered from aMD and cMD simulation are overall in good agreement. Characteristic deviations are observed in the region from helix α1 to the sheet β2 (residues 15–45). These observations are reflected by a Spearman rank correlation of r = 0.51 between the aMD and cMD simulations. We hypothesize that this rather low correlation can primarily be explained by the different time scales captured. Extrapolating from previous studies on BPTI, where 500 ns of aMD sampling covers the dynamics of 1 ms cMD sampling, 20 ns of aMD should correspond to dynamics of around 40 μs. It can be assumed that these flexibilities clearly deviate from motions captured in only 3 μs sampling time.

Comparison of the dihedral entropy profile to order parameters S2 of the backbone amide66 leads to similar findings. NMR order parameters S2 are sensitive to ps- to ns-dynamics, capturing much faster motions than those shown in aMD data. We expect a coupling between slow backbone dynamics, profiled by aMD simulation, and fast motions, captured in NMR data.29 Thus, NMR order parameters S2 represent a method to experimentally probe protein backbone dynamics on residue resolution and an insightful reference to estimate the reliability of our approach. As expected, we observe an anticorrelation between the calculated diheral entropies and the experimental order parameters. Again reasonable agreement is visible for the region reaching from residue 70 to the C-terminus, while for the domain from helix α1 to the sheet β2 (residues 15–45) almost opposing trends are found. These qualitative observations become apparent in a Spearman rank correlation of r = −0.39 between the aMD dihedral entropies and S2 when considering the whole protein. This is only a slight improvement over cMD simulations, where correlations of r = −0.23 for torsional entropies and order parameters are obtained. This might result from dynamics captured by aMD being beyond the scope of the NMR time scale. It has been shown in previous studies that the region from α1 to β2 undergoes a noticeable rigidification upon ligand binding.47 Order parameters and relaxation dispersion profiles of the apo protein confirm the flexible nature of Bet v 1a on a pico- to nanosecond as well as on a micro- to millisecond time scale. Residues from α1 to β2 show elevated dynamics in both experiments. For the remaining parts of the protein (residue 70–159), a correlation of r = −0.61 is found between the aMD dihedral entropies and S2. Here, the correlation of cMD simulations and order parameters is still notably lower with r = −0.35. Additionally, dihedral entropies were calculated from aMD simulations of varying lengths ranging from 10 ns to 1 μs (SI, Figure S10). Again, the resulting entropies show similar flexibility profiles as experimental NMR studies, with exception of the discussed domain reaching from α1 to β2. This emphasizes the presence of complex conformational dynamics on multiple time scales in this area.

With the presented metric, we provide a tool to map low-frequency conformational dynamics of biomolecules at the residue level. With increasing system size, reproduction of the original flexibility profile becomes more challenging. The decorrelation time of aMD and cMD data has been investigated extensively in previous studies.16 It has been shown that the aMD generally reduces the statistical inefficiency of a simulation. An extensive probing of the acceleration parameter is crucial for the reliability of any aMD trajectory. Aggressive boosting enables extensive speedup in conformational exploration, but can lead to a substantial loss of accuracy.16 Particularly the reweighting step is a known but yet not completely solved challenge.19 Some approaches, like boosting of rotatable torsions only (RaMD),70 Gaussian aMD,71 or selectively applied aMD,72 alleviate the impact of the reweighting error.

5. Conclusion

With the present study, we introduce and validate a metric to characterize local protein dynamics on the millisecond time scale. Accelerated MD simulations provide access to time scales 3 orders of magnitude beyond state-of-the-art sampling time. Subsequent calculation of dihedral entropies from aMD trajectories quantifies backbone flexibility of each residue.

The general functionality of our approach is shown on the model system Di-Ala. We calculated dihedral entropies from a 1 ms cMD simulation of BPTI,11 serving as reference to validate and benchmark method and metric. We were able to show that dihedral entropies from only 500 ns of aMD simulation identify the same flexibility hot spots, as observed in the 1 ms cMD trajectory. The results are supported by previous NMR studies,41 which observe local conformational changes in the same regions characterized as most flexible in our study. We applied the procedure on the major birch pollen allergen Bet v 1a. Our study shows good agreement with local dynamics found in a 3 μs cMD simulation as well as with NMR-derived amide-order parameters.47

We encourage the application of dihedral entropies as a local flexibility metric on different aMD protocols. We anticipate our novel metric to facilitate characterizing and thus understanding the influence of molecular dynamics on biomolecular recognition and protein folding.

Acknowledgments

This work was supported by the Austrian Science Fund (FWF) via the grant P26997 “Influence of Protein Folding on Allergenicity and Immunogenicity”. The authors thank Martin Tollinger and Sarina Grutsch for fruitful discussions and for providing experimental data and John Klepeis from D.E. Shaw Research for kindly providing access to the BPTI trajectory. A.S.K. gratefully acknowledges critical feedback and comments by Michael Schauperl and Roland G. Huber.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00231.

  • Figure S1: Ramachandran plot of Di-Ala. Figure S2: Evaluation of different bin sizes. Figure S3: Free energies and state populations of Φ of Di-Ala. Figure S4: Additional statistical evaluation of dihedral entropies for Di-Ala and for Bet v 1a (Figure S9). Figure S5: Sϕ of BPTI. Figures S6 and S7: Different sampling lengths and reweighting protocols compared for BPTI. Figure S8: Isomerization of the disulfide bridge in BPTI. Figure S9: Representative results using different acceleration parameters and sampling times for the aMD simulation of Bet v 1a. (PDF)

Author Present Address

J. E. Fuchs: Medicinal Chemistry/Structural Research, Boehringer Ingelheim RCV GmbH & Co. KG, Vienna, Austria

The authors declare no competing financial interest.

Supplementary Material

ct6b00231_si_001.pdf (12.3MB, pdf)

References

  1. Falke J. J. Science 2002, 295, 1480–1481. 10.1126/science.1069823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Henzler-Wildman K. A.; Thai V.; Lei M.; Ott M.; Wolf-Watz M.; Fenn T.; Pozharski E.; Wilson M. A.; Petsko G. A.; Karplus M.; Huebner C. G.; Kern D. Nature 2007, 450, 838–844. 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
  3. Boehr D. D.; Nussinov R.; Wright P. E. Nat. Chem. Biol. 2009, 5, 954–954. 10.1038/nchembio1209-954d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Fischer M.; Coleman R. G.; Fraser J. S.; Shoichet B. K. Nat. Chem. 2014, 6, 575–583. 10.1038/nchem.1954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Fuchs J. E.; Huber R. G.; Waldner B. J.; Kahler U.; von Grafenstein S.; Kramer C.; Liedl K. R. PLoS One 2015, 10, e0140713. 10.1371/journal.pone.0140713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Schnell J. R.; Dyson H. J.; Wright P. E. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 119–140. 10.1146/annurev.biophys.33.110502.133613. [DOI] [PubMed] [Google Scholar]
  7. Fenwick R. B.; Esteban-Martin S.; Salvatella X. Eur. Biophys. J. 2011, 40, 1339–1355. 10.1007/s00249-011-0754-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hensen U.; Meyer T.; Haas J.; Rex R.; Vriend G.; Grubmuller H. PLoS One 2012, 7, e33931. 10.1371/journal.pone.0033931. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Durrant J. D.; McCammon J. A. BMC Biol. 2011, 9, 1–9. 10.1186/1741-7007-9-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Henzler-Wildman K.; Kern D. Nature 2007, 450, 964–972. 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
  11. Shaw D. E.; Maragakis P.; Lindorff-Larsen K.; Piana S.; Dror R. O.; Eastwood M. P.; Bank J. A.; Jumper J. M.; Salmon J. K.; Shan Y. B.; Wriggers W. Science 2010, 330, 341–346. 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
  12. Bernardi R. C.; Melo M. C. R.; Schulten K. Biochim. Biophys. Acta, Gen. Subj. 2015, 1850, 872–877. 10.1016/j.bbagen.2014.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Wenzel W.; Hamacher K. Phys. Rev. Lett. 1999, 82, 3003–3007. 10.1103/PhysRevLett.82.3003. [DOI] [Google Scholar]
  14. Hamelberg D.; Mongan J.; McCammon J. A. J. Chem. Phys. 2004, 120, 11919–11929. 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
  15. Pierce L. C. T.; Salomon-Ferrer R.; de Oliveira C. A. F.; McCammon J. A.; Walker R. C. J. Chem. Theory Comput. 2012, 8, 2997–3002. 10.1021/ct300284c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. de Oliveira C. A. F.; Hamelberg D.; McCammon J. A. J. Phys. Chem. B 2006, 110, 22695–22701. 10.1021/jp062845o. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Cukier R. I.; Morillo M. J. Chem. Phys. 2005, 123, 234908. 10.1063/1.2137704. [DOI] [PubMed] [Google Scholar]
  18. Miao Y. L.; Sinko W.; Pierce L.; Bucher D.; Walker R. C.; McCammon J. A. J. Chem. Theory Comput. 2014, 10, 2677–2689. 10.1021/ct500090q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Shen T. Y.; Hamelberg D. J. Chem. Phys. 2008, 129, 034103. 10.1063/1.2944250. [DOI] [PubMed] [Google Scholar]
  20. Bucher D.; Grant B. J.; Markwick P. R.; McCammon J. A. PLoS Comput. Biol. 2011, 7, e1002034. 10.1371/journal.pcbi.1002034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Markwick P. R. L.; McCammon J. A. Phys. Chem. Chem. Phys. 2011, 13, 20053–20065. 10.1039/c1cp22100k. [DOI] [PubMed] [Google Scholar]
  22. Wang Y.; Markwick P. R. L.; de Oliveira C. A. F.; McCammon J. A. Biophys. J. 2012, 102, 413A–413A. 10.1016/j.bpj.2011.11.2259. [DOI] [Google Scholar]
  23. Kappel K.; Miao Y.; McCammon J. A. Q. Q. Rev. Biophys. 2015, 48, 479–487. 10.1017/S0033583515000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kalenkiewicz A.; Grant B. J.; Yang C.-Y. Biology 2015, 4, 344–66. 10.3390/biology4020344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mucksch C.; Urbassek H. M. PLoS One 2013, 8, e64883. 10.1371/journal.pone.0064883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Minh D. D. L.; Hamelberg D.; McCammon A. J. Chem. Phys. 2007, 127, 154105. 10.1063/1.2794754. [DOI] [PubMed] [Google Scholar]
  27. Thomas J. R.; Gedeon P. C.; Grant B. J.; Madura J. D. Biophys. J. 2012, 103, L1–L3. 10.1016/j.bpj.2012.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Bai Q.; Zhang Y.; Li X.; Chen W.; Liu H.; Yao X. Phys. Chem. Chem. Phys. 2014, 16, 24332–24338. 10.1039/C4CP03331K. [DOI] [PubMed] [Google Scholar]
  29. Fuchs J. E.; Waldner B. J.; Huber R. G.; von Grafenstein S.; Kramer C.; Liedl K. R. J. Chem. Theory Comput. 2015, 11, 851–860. 10.1021/ct500633u. [DOI] [PubMed] [Google Scholar]
  30. Fuchs J. E.; von Grafenstein S.; Huber R. G.; Wallnoefer H. G.; Liedl K. R. Proteins: Struct., Funct., Genet. 2014, 82, 546–555. 10.1002/prot.24417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Edgeworth M. J.; Phillips J. J.; Lowe D. C.; Kippen A. D.; Higazi D. R.; Scrivens J. H. Angew. Chem., Int. Ed. 2015, 54, 15156–15159. 10.1002/anie.201507223. [DOI] [PubMed] [Google Scholar]
  32. Sinha N.; Smith-Gill S. J. Cell Biochem. Biophys. 2005, 43, 253–273. 10.1385/CBB:43:2:253. [DOI] [PubMed] [Google Scholar]
  33. Sinha N.; Mohan S.; Lipschultz C. A.; Smith-Gill S. J. Biophys. J. 2002, 83, 2946–2968. 10.1016/S0006-3495(02)75302-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Salmon L.; Pierce L.; Grimm A.; Ortega Roldan J.-L.; Mollica L.; Jensen M. R.; van Nuland N.; Markwick P. R. L.; McCammon J. A.; Blackledge M. Angew. Chem., Int. Ed. 2012, 51, 6103–6106. 10.1002/anie.201202026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Markwick P. R. L.; Cervantes C. F.; Abel B. L.; Komives E. A.; Blackledge M.; McCammon J. A. J. Am. Chem. Soc. 2010, 132, 1220–1221. 10.1021/ja9093692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Huber R. G.; Eibl C.; Fuchs J. E. Protein Sci. 2015, 24, 174–181. 10.1002/pro.2601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Huber R. G.; Fuchs J. E.; von Grafenstein S.; Laner M.; Wallnoefer H. G.; Abdelkader N.; Kroemer R. T.; Liedl K. R. J. Phys. Chem. B 2013, 117, 6466–6472. 10.1021/jp311418q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wlodawer A.; Walter J.; Huber R.; Sjolin L. J. Mol. Biol. 1984, 180, 301–329. 10.1016/S0022-2836(84)80006-6. [DOI] [PubMed] [Google Scholar]
  39. Wagner G.; Demarco A.; Wuthrich K. Biophys. Struct. Mech. 1976, 2, 139–158. 10.1007/BF00863706. [DOI] [PubMed] [Google Scholar]
  40. Wagner G.; Bruhwiler D.; Wuthrich K. J. Mol. Biol. 1987, 196, 227–231. 10.1016/0022-2836(87)90524-9. [DOI] [PubMed] [Google Scholar]
  41. Otting G.; Liepinsh E.; Wuthrich K. Biochemistry 1993, 32, 3571–3582. 10.1021/bi00065a008. [DOI] [PubMed] [Google Scholar]
  42. Xue Y.; Ward J. M.; Yuwen T.; Podkorytov I. S.; Skrynnikov N. R. J. Am. Chem. Soc. 2012, 134, 2555–2562. 10.1021/ja206442c. [DOI] [PubMed] [Google Scholar]
  43. Ipsen H.; Lowenstein H. J. Allergy Clin. Immunol. 1983, 72, 150–159. 10.1016/0091-6749(83)90523-7. [DOI] [PubMed] [Google Scholar]
  44. Moverare R.; Westritschnig K.; Svensson M.; Hayek B.; Bende M.; Pauli G.; Sorva R.; Haahtela T.; Valenta R.; Elfman L. Int. Arch. Allergy Immunol. 2002, 128, 325–335. 10.1159/000063855. [DOI] [PubMed] [Google Scholar]
  45. Ferreira F.; Hirtenlehner K.; Jilek A.; GodnikCvar J.; Breiteneder H.; Grimm R.; Hoffmann-Sommergruber K.; Scheiner O.; Kraft D.; Breitenbach M.; Rheinberger H. J.; Ebner C. J. Exp. Med. 1996, 183, 599–609. 10.1084/jem.183.2.599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Swoboda I.; Jilek A.; Ferreira F.; Engel E.; Hoffmannsommergruber K.; Scheiner O.; Kraft D.; Breiteneder H.; Pittenauer E.; Schmid E.; Vicente O.; Heberlebors E.; Ahorn H.; Breitenbach M. J. Biol. Chem. 1995, 270, 2607–2613. 10.1074/jbc.270.6.2607. [DOI] [PubMed] [Google Scholar]
  47. Grutsch S.; Fuchs J. E.; Freier R.; Kofler S.; Bibi M.; Asam C.; Wallner M.; Ferreira F.; Brandstetter H.; Liedl K. R.; Tollinger M. Biophys. J. 2014, 107, 2963–2972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Freier R.; Dall E.; Brandstetter H. Sci. Rep. 2015, 5, 12707. 10.1038/srep12707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Machado Y.; Freier R.; Scheiblhofer S.; Thalhamer T.; Mayr M.; Briza P.; Grutsch S.; Ahammer L.; Fuchs J. E.; Wallnoefer H. G.; Isakovic A.; Kohlbauer V.; Hinterholzer A.; Steiner M.; Danzer M.; Horejs-Hoeck J.; Ferreira F.; Liedl K. R.; Tollinger M.; Lackner P.; Johnson C. M.; Brandstetter H.; Thalhamer J.; Weiss R. J. Allergy Clin. Immunol. 2016, 137, 1525–1534. 10.1016/j.jaci.2015.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Case D.; Berryman J.; Betz R.; Cerutti D.; Cheatham T. III; Darden T.; Duke R.; Giese T.; Gohlke H.; Goetz A.; Homeyer N.; Izadi S.; Janowski P.; Kaus J.; Kovalenko A.; Lee T.; LeGrand S.; Li P.; Luchko T.; Luo R.; Madej B.; Merz K.; Monard G.; Needham P.; Nguyen H.; Nguyen H.; Omelyan I.; Onufriev A.; Roe D.; Roitberg A.; Salomon-Ferrer R.; Simmerling C.; Smith W.; Swails J.; Walker R.; Wang J.; Wolf R.; Wu X.; York D.; Kollman P.. AMBER 2015; University of California: San Francisco, 2015. [Google Scholar]
  51. Molecular Operating Environment (MOE), version 2014.09; Chemical Computing Group Inc.: Montreal, QC, Canada, 2014. [Google Scholar]
  52. Labute P. Proteins: Struct., Funct., Genet. 2009, 75, 187–205. 10.1002/prot.22234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  54. Lindorff-Larsen K.; Piana S.; Palmo K.; Maragakis P.; Klepeis J. L.; Dror R. O.; Shaw D. E. Proteins: Struct., Funct., Genet. 2010, 78, 1950–1958. 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Wallnoefer H. G.; Liedl K. R.; Fox T. J. Comput. Chem. 2011, 32, 1743–1752. 10.1002/jcc.21758. [DOI] [PubMed] [Google Scholar]
  56. Salomon-Ferrer R.; Goetz A. W.; Poole D.; Le Grand S.; Walker R. C. J. Chem. Theory Comput. 2013, 9, 3878–3888. 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
  57. Ciccotti G.; Ryckaert J. P. Comput. Phys. Rep. 1986, 4, 346–392. 10.1016/0167-7977(86)90022-5. [DOI] [Google Scholar]
  58. Berendsen H. J. C.; Postma J. P. M.; Van Gunsteren W. F.; Dinola A.; Haak J. R. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  59. Adelman S. A.; Doll J. D. J. Chem. Phys. 1976, 64, 2375–2388. 10.1063/1.432526. [DOI] [Google Scholar]
  60. Hamelberg D.; de Oliveira C. A. F.; McCammon J. A. J. Chem. Phys. 2007, 127, 155102. 10.1063/1.2789432. [DOI] [PubMed] [Google Scholar]
  61. Roe D. R.; Cheatham I.; Thomas E. J. Chem. Theory Comput. 2013, 9, 3084–3095. 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
  62. Ramachandran G. N.; Ramakrishnan C.; Sasisekharan V. J. Mol. Biol. 1963, 7, 95–99. 10.1016/S0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
  63. Wood M. J.; Hirst J. D. Proteins: Struct., Funct., Genet. 2005, 59, 476–481. 10.1002/prot.20435. [DOI] [PubMed] [Google Scholar]
  64. Botev Z. I.; Grotowski J. F.; Kroese D. P. Ann. Math. Stat. 2010, 38, 2916–2957. 10.1214/10-AOS799. [DOI] [Google Scholar]
  65. Kofler S.; Asam C.; Eckhard U.; Wallner M.; Ferreira F.; Brandstetter H. J. Mol. Biol. 2012, 422, 109–123. 10.1016/j.jmb.2012.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Mittermaier A.; Kay L. E. Science 2006, 312, 224–228. 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
  67. Kidera A.; Go N. J. Mol. Biol. 1992, 225, 457–475. 10.1016/0022-2836(92)90932-A. [DOI] [PubMed] [Google Scholar]
  68. Miao Y.; Nichols S. E.; McCammon J. A. Phys. Chem. Chem. Phys. 2014, 16, 6398–6406. 10.1039/c3cp53962h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Jing Z.; Sun H. J. Chem. Theory Comput. 2015, 11, 2395–2397. 10.1021/acs.jctc.5b00236. [DOI] [PubMed] [Google Scholar]
  70. Doshi U.; Hamelberg D. J. Chem. Theory Comput. 2012, 8, 4004–4012. 10.1021/ct3004194. [DOI] [PubMed] [Google Scholar]
  71. Miao Y.; Feher V. A.; McCammon J. A. J. Chem. Theory Comput. 2015, 11, 3584–3595. 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Wereszczynski J.; McCammon J. A. J. Chem. Theory Comput. 2010, 6, 3285–3292. 10.1021/ct100322t. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct6b00231_si_001.pdf (12.3MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES