Excited-State Dipole and Quadrupole Moments: TD-DFT versus CC2

Abstract

The accuracies of the excited-state dipole and quadrupole moments obtained by TD-DFT are assessed by considering 16 different exchange-correlation functionals and more than 30 medium and large molecules. Except for excited-state presenting a significant charge-transfer character, a relatively limited dependency on the nature of the functional is found. It also turns out that while DFT ground-state dipole moments tend to be too large, the reverse trend is obtained for their excited-state counterparts, at least when hybrid functionals are used. Consequently, the TD-DFT excess dipole moments are often too small, an error that can be fortuitously corrected for charge-transfer transition by selecting a pure or a hybrid functional containing a small share of exact exchange. This error-cancelation phenomena explains the contradictory conclusions obtained in previous investigations. Overall, the largest correlation between CC2 and TD-DFT excess dipoles is obtained with M06-2X, but at the price of a nearly systematic underestimation of this property by ca. 1 D. For the excess quadrupole moments, the average errors are of the order of 0.2–0.6 D·Å for the set of small aromatic systems treated.

1. Introduction

Time-Dependent Density Functional Theory (TD-DFT)^1,2 has been in the limelight of quantum chemistry during the past decade. Indeed, paralleling the success of DFT for the ground-state (GS), TD-DFT has now become the most widely applied method to explore the excited-state (ES) properties of medium and large compounds,³ with applications appearing in many applied fields of chemical science. Besides the choice of a basis set, two approximations are generally made while running TD-DFT calculations: the adiabatic formalism is used,⁴ inducing the loss of memory effects, and a specific exchange-correlation functional (XCF) is selected to describe the nonclassical component of the electron–electron interactions. Though these two approximations are certainly not independent of each other, it remains in practice easier to change the XCF than to go beyond the adiabatic approximation, and the vast majority of the benchmarks of TD-DFT have therefore considered this latter aspect. These benchmarks have been mainly focused on both vertical and 0–0 transition energies, and to a lesser extended ES geometries, and have much less considered the determination of other properties as illustrated by ref (5) reviewing TD-DFT benchmarks. In this framework, the present investigation is devoted to the ES dipole (μ) and traceless quadrupole (Q) moments with a focus on medium and large π-conjugated molecules.

To the best of our knowledge, there are no previous work devoted to the benchmarking of TD-DFT for ES quadrupole calculations, while the previous investigations devoted to the assessment of XCFs in the framework of calculations of the excited-state dipole moments (μ^ES) and/or the excess dipole moment (Δμ, the difference between ES and GS dipoles) have mainly considered small compounds. The first comparisons probably appeared in 2002 when Furche and Ahlrichs used experimental values to assess the performances of three generalized gradient approximations (GGAs) and two global hybrids for seven tiny molecules.⁶ For this set, they found that the errors obtained with the GGA (ca. 0.12 D) were smaller than with the hybrid XCF (ca. 0.17 D). The same year, Amos, Handy, and co-workers compared TD-DFT and EOM-CCSD dipole moments for numerous excited-states in furan and pyrrole,^7,8 in studies devoted to the assessment of the HCTH and B97-1 XCFs. They noted that, contrary to the transition energies, excited-state dipoles are strongly functional dependent, and that this sensitivity is exacerbated for Rydberg states.⁸ These conclusions were refined by King in 2008, using more accurate reference values.⁹ He found that B97-1 provides μ^ES with average deviations of ca. 0.5 D (1.1 D) for a large number of ESs in furan (pyrrole). In what is probably the largest study of μ^ES to date, Thiel and co-workers considered their famous set of 20 compact molecules¹⁰ to assess the quality of the dipole moments obtained with BP86, B3LYP, and BHHLYP using their own CAS-PT2/TZVP values as references.¹¹ They concluded that (i) the DFT dipole moments tend to be too small; (ii) the errors are smaller for the GS than the ES; (iii) the average deviations are similar for n → π* and π → π* transitions; (iv) the average TD-DFT errors are in the 0.6–0.8 D range and only marginally depend on the functional, though these average deviations are slightly smaller with BHHLYP and B3LYP than with BP86. Guido and co-workers reported the Δμ determined on five small molecules using six hybrid XCFs and also obtained excess dipole values quite independent of the selected functional, with cases for which Δμ increased and decreased when increasing the amount of exact exchange included in the XCF.¹² For small charge-transfer (CT) molecules, Tapavicza et al. found that the CC2 and PBE0 μ^ES were nicely matching experiment values, whereas PBE led to too small values.¹³ More recently, Eriksen et al. compared the CAM-B3LYP and EOM-CCSD dipoles of p-nitro-aniline in both gas and condensed phases and found that this range-separated hybrid (RSH) XCF considerably undershoots the magnitude of μ^ES.¹⁴ A few specific investigations also appeared for larger molecules. In 2009, Wong et al. obtained the μ^ES of the two lowest-lying ESs in 12 oligothiophenes and found that the Δμ are significantly larger with B3LYP than with a RSH, but no benchmark values were provided to pinpoint the most accurate functional.¹⁵ In 2010, the Δμ of a set of donor–acceptor benzothiazolium derivatives were determined with B3LYP, CAM-B3LYP, and CC2.¹⁶ For the 20 dyes for which direct comparisons are possible, mean absolute deviations of 5.1 and 1.7 D can be determined for B3LYP and CAM-B3LYP, respectively, indicating that the latter functional is much more accurate for these CT molecules. In 2013, Zaleśny and co-workers compared the def2-QZVP GS and ES dipole moments computed with CC2 and seven XCFs for five photochromic molecules (four spiro derivatives and one push–pull azobenzene).¹⁷ They found that none of the tested XCFs could deliver accurate Δμ in all cases, and, in contrast with the previous studies, that B3LYP and PBE0 were more accurate than RSH for the CT molecule.¹⁷ The same year Peluso’s group investigated the electro-optical properties of a large azobenzene dye and concluded that while BMK could yield a transition wavelength in very good agreement with CC2, the Δμ of the two approaches differed by more than 4 D with the SV(P) atomic basis set.¹⁸ As can be seen from this literature survey, more is needed to obtain a general analysis of the accuracy of the TD-DFT Δμ. Indeed, previous works were typically limited to a small number of XCFs, rather compact or specific compounds, and, more importantly, obtained contradictory conclusions, notably regarding both the accuracy of RSH for evaluating the Δμ of CT ES and the amplitude of the dependency to the selected XCF. This has motivated the present investigation that treats a larger series of “real-life” dyes and compares a large set of XCFs to CC2 reference results.

2. Computational Details

All DFT and TD-DFT calculations have been performed with the Gaussian09.D01 code,¹⁹ using optimal GS geometries determined at the M06-2X/6-31+G(d) level of theory. The Cartesian coordinates of these structures can be found in the SI of ref (20). DFT and TD-DFT calculations were performed using tightened DFT integration grids and the aug-cc-pVTZ atomic basis set. The XCFs benchmarked here are SVWN5,^21,22 BLYP,^23,24 BP86,^23,25 OLYP,^24,26 M06-L,²⁷ M11-L,²⁸ B3LYP,^29,30 PBE0,^31,32 M06,³³ BMK,³⁴ SOGGA11-X,³⁵ M06-2X,³³ M06-HF,³⁶ CAM-B3LYP,³⁷ M11,²⁸ and ωB97X-D,³⁸ the six first being “pure” XCFs (free of exact exchange), the seven next being global hybrid XCFs including a growing fraction of exact exchange, whereas the three last are RSH. Note that the ES dipole moments reported here correspond to the total ES density and do not rely on the so-called 1-particle CI density.

The CC2 calculations have been performed on the same geometries with the Turbomole program,³⁹ systematically using the RI scheme,^40,41 and default convergence parameters that were found to be sufficient for our purposes. Note that we report the relaxed CC2 properties in the following and use them as reference values. As for the TD-DFT calculations, we selected the aug-cc-pVTZ atomic basis set and did not apply the frozen-core approximation, both parameters being chosen to obtain accurate reference values. Of course, CC2 dipole moments are not error free. Nevertheless, by comparing the CC2/TZVP⁴² and CAS-PT2/TZVP¹⁰ μ^GS reported by Thiel, Sauer, and co-workers for their molecular set, a mean absolute error (MAE) as small as 0.11 D is obtained.⁴³ For the μ^ES, the deviations between CC2 and CAS-PT2 values are larger due to the presence of several high-lying ES suffering from strong state-mixing. Nevertheless, by considering the lowest ES of each irreducible representation for the same set of molecules, a MAE of 0.43 D is obtained.⁴⁴ In subsequent works, Thiel, Sauer, and co-workers found that if a quite large atomic basis set has to be selected to reach converged CC2 dipole moments,⁴² the CAS-PT2 and CC2 dipole moments undergo similar variations when increasing the basis set size.⁴⁵ In short, this indicates that, despite their inherent limitations, CC2/aug-cc-pVTZ dipole moments can be safely used to benchmark TD-DFT results.

In the following the GS and ES dipole moments are given as their total values; e.g., for the GS,

1

whereas the Δμ were computed as

2

Obviously, as the total dipoles, this quantity is positive irrespective of the relative amplitudes of ES and GS dipoles. In the Tables below, to give insights into these relative magnitudes, we indicate Δμ in italics when μ^ES < μ^GS. For the calculations of the quadrupoles, we selected only molecules with zero dipole moments and zero off-diagonal quadrupoles. We report below the traceless quadrupole, Q, and more precisely, two of its independent components, Q_yy and Q_zz; Q_xx being trivially obtained.

In Table S-1 in the Supporting Information, we report GS and ES dipole moments obtained for three molecules using three different GS geometries, namely the optimal BLYP/6-31+G(d), B3LYP/6-31+G(d), and M06-2X/6-31+G(d) geometries. It turns our that the μ^GS are only slightly affected by the selected geometry (variations in the 0.05–0.25 D range) and that the GS dipoles given by the different methods undergo similar changes when modifying the structures. For instance, the BLYP, B3LYP, M06-2X, and CC2 μ^GS of 1 (see Scheme 1), respectively increases by +0.23, +0.24, +0.24 and +0.22 D when going from the M06-2X to the BLYP geometry. The μ^ES, especially those obtained at the GGA level, are more sensitive to the structure. For example, the BLYP ES dipole of 3 decreases from 9.83 to 8.87 D when going from the M06-2X to the BLYP geometry. In contrast, both the CC2 and M06-2X μ^ES are less affected by the selected geometry. In short, the conclusions obtained in this work are rather independent of the selected ground-state geometry, but possibly for the ES dipole determined with pure XCF or, to a smaller extent, with global hybrid XCFs presenting a rather limited exact exchange ratio. Therefore, we stick to M06-2X/6-31+G(d) geometries only in the following.

Scheme 1. Representation of the Molecules Considered in Section 3.1.

3. Results and Discussion

All molecules treated herein are experimentally known and their optical spectra have been measured (see ref (20) for references). Likewise, the transition energies determined at various levels of theory can be found elsewhere,²⁰ and are therefore not to be discussed in the present work.

3.1. Dipole Moments: First Set

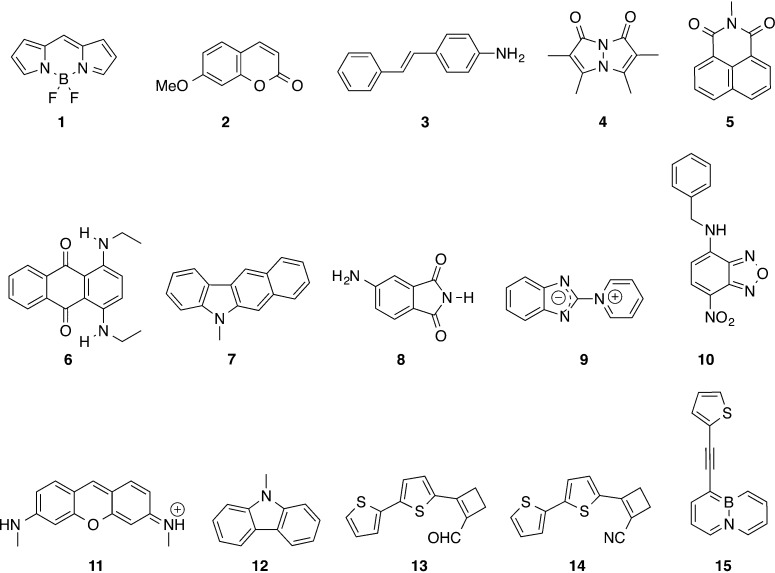
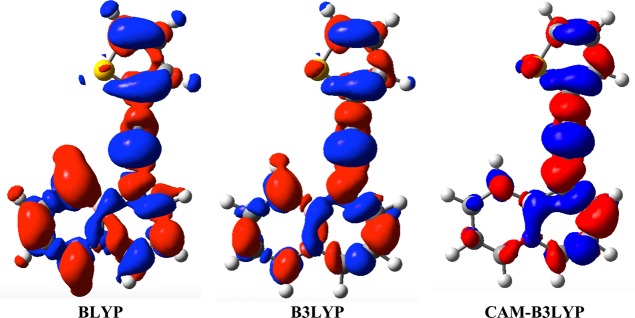
The 15 medium-sized molecules included in the first part of our benchmark are displayed in Scheme 1. They were chosen to be representative of compounds of interest for optical applications with both n → π* and π → π* transitions, local (e.g., 7 and 8) and charge-transfer excitations (e.g., 3 and 14) as well as members of the cyanine (1 and 11) and zwitterionic (9) classes of dyes that are both known to be challenging for TD-DFT.⁴⁶ For the 20 ESs determined from this group, the Δμ values are listed in Table 1, whereas the GS and ES total dipole moments values can be respectively found in Tables S-2 and S-3 in the Supporting Information (SI). First, we notice that the excess dipole is often rather independent of the selected XCF, except for several excited states presenting a significant CT character, that is, A′ in 2, A in 3, A in 13, A in 14, and A′ in 15. This explains why the XCF dependency was found small with the set of Thiel,¹⁰ that contains ESs presenting a limited CT character, but large for other sets of compounds (see Introduction). For 9 that presents a zwitterionic nature it is clear that no XCF delivers a valuable picture for the change of dipole moments, and this is probably related to the very specific electronic structure of this betaine derivative. For CT states, a strong increase of dipole moment upon excitation is, as expected, obtained and the magnitude of this increase is often predicted to be much larger with pure XCFs than with both global and range-separated hybrid XCFs. This trend is related to the well-known short-sightedness of pure DFT functionals that allow an excessive separation between the electron and the hole.^47,48 However, in contrast with the transition energies, RSH do not systematically outperform global hybrids for the Δμ of CT states, for example, they severely underrate the excess dipole for 3, whereas PBE0 is close to the spot. Similarly in 14, M06-L provides a more accurate Δμ than CAM-B3LYP, while for the push–pull 10, all XCFs undershoot the CC2 Δμ by more than 1 D. 15 is another interesting case, as both CC2 and RSH predict a decrease of the amplitude of the dipole moment upon excitation, whereas pure XCFs foresee a large increase. The density difference plots corresponding to the first electronic transition of 15 as given by three XCFs are displayed in Figure 1. As can be seen BLYP gives a strong CT between the thiophene ring and the boron-containing moiety, the magnitude of this CT being attenuated with B3LYP, whereas CAM-B3LYP predicts a more localized π → π* valence excited-state centered around the ethynyl linker and the vicinal rings. Accordingly, the CT distances, as measured by Le Bahers’ metric,⁴⁹ are 2.94, 2.14, and 0.94 Å with BLYP, B3LYP, and CAM-B3LYP, respectively, paralleling the magnitude of the Δμ for these three XCFs. From these different examples, it appears that the most accurate XCF to evaluate the Δμ of CT excited-states is strongly dependent on the investigated molecule, which is in line with the previous contradictory conclusions reported in the literature (see the Introduction). We rationalize this outcome in section 3.3.

Table 1. Excess Dipole Moments Determined through eq 2 and Listed in Debye for the Compounds of Scheme 1^a.

	state	CC2	SVWN5	BLYP	BP86	OLYP	M06-L	M11-L	B3LYP	PBE0	M06	BMK	SOGGA11-X	M06-2X	M06-HF	CAM-B3LYP	M11	ωB97X-D
1	B2 (π → π*)	0.15	0.15	0.14	0.15	0.14	0.14	0.18	0.20	0.22	0.26	0.28	0.30	0.32	0.42	0.34	0.42	0.35
2	A′(π → π*)	3.24	3.80	3.60	3.59	3.59	3.43	3.12	2.98	2.88	2.80	2.75	2.70	2.72	2.56	2.59	2.44	2.46
	A″ (n → π*)	4.26	5.26	5.25	5.25	5.23	5.23	5.27	4.59	4.45	4.47	4.07	4.21	3.83	3.99	4.02	3.81	4.05
3	A (π → π*)	4.34	7.60	7.30	7.55	6.96	7.42	2.56b	4.84	4.64	7.14c	3.81	3.42	3.34	2.22	2.98	2.38	2.79
4	A (π → π*)	0.43	0.54	0.47	0.48	0.40	0.42	3.23b	0.44	0.42	0.37	0.47	0.35	0.47	0.47	0.42	0.43	0.40
	A (n → π*)	2.46	2.81	2.86	2.85	2.87	2.87	13.62b	2.67	2.63	2.73	2.44	2.58	2.33	2.47	2.45	2.33	2.47
5	A (n → π*)	4.84	5.65	5.63	5.65	5.64	5.74	5.89	5.12	4.98	4.99	4.27	4.50	3.80	2.88	4.20	3.54	4.21
	A (π → π*)	1.19c	1.18	1.17	1.14	1.15	1.16	0.78	1.16	1.15	1.06	1.22	1.08	1.26	1.21	1.15	1.19	1.13
6	A (π → π*)	2.79	1.58	1.73	1.71	1.79	2.04	2.23	2.17	2.26	2.36	2.45	2.59	2.69	3.06	2.36	2.48	2.27
7	A (π → π*)	1.78	2.12	2.02	2.10	2.03	2.13	1.68	1.79	1.79	1.57	1.47	1.59	1.62	1.42	1.61	1.63	1.62
8	A(π → π*)	3.88	5.02	5.04	4.97	4.97	5.09	4.50	4.69	4.58	4.29	4.31	4.12	3.86	3.18	3.94	3.52	3.87
9	A1 (π → π*)	12.59	9.45	9.37	9.39	9.33	9.19	9.96	10.60	10.57	10.72	9.74	10.10	9.32	11.23	9.32	10.52	9.48
	B1 (π → π*)	13.80	6.39	6.64	6.60	6.49	6.78	5.98	6.17	6.29	5.55	6.20	5.85	7.59	6.56	6.27	6.34	6.66
10	A (π → π*)	4.20	3.10	3.07	3.04	2.99	2.98	2.70	2.73	2.69	2.53	2.67	2.56	2.76	2.98	2.66	2.77	2.67
11d	B2 (π → π*)	1.31	1.26	1.24	1.26	1.25	1.33	1.42	1.30	1.31	1.29	1.32	1.32	1.30	1.31	1.30	1.36	1.32
12	A′ (π → π*)	1.01	1.24	1.19	1.21	1.20	1.20	1.27	1.17	1.17	0.95	1.10	1.09	1.02	0.89	1.05	0.96	1.05
13	A (n → π*)	4.15	7.91	7.90	7.94	8.01	7.80	7.73	5.38	3.40e	5.16	3.72	4.62	4.04	4.03	4.23	3.89	4.18
	A (π → π*)	5.00	5.90	5.78	5.78	5.83	7.73	4.44	3.83	1.89e	3.28	2.57	2.99	3.05	2.41	2.69	2.35	2.45
14	A (π → π*)	4.72	5.46	5.19	5.25	5.16	4.89	3.63	3.43	3.25	2.73	2.87	2.62	2.74	2.31	2.37	2.12	2.22
15	A′ (π → π*)	2.68	9.27	9.16	8.98	9.03	8.15	8.00	4.62	4.01	3.17	2.69	2.48	2.24	1.25	1.81	1.36	1.61

^aValues in italics indicate that the norm of the total ES dipole is smaller than its GS counterpart.

^bM11-L yields excited-states that have a different nature for those two molecules explaining the large discrepancies.

^cAverage value obtained from two nearly degenerated excited-states (see Table S-3 in the SI for details).

^dDipole moments determined from the center of mass for this charged compound.

^eWith PBE0, there is a strong mixing between the n → π* and π → π* like states that are nearly degenerate.

Figure 1.

Density difference plots for the lowest dipole-allowed state of 15 as determined with three XCFs. The blue (red) regions indicate decrease (increase) of electron density upon transition. A contour threshold of 8 × 10^–4 au has been applied.

In Table 2 we provide a statistical analysis for the data of Table 1: mean signed error (MSE), mean absolute error (MAE), maximal positive and negative deviations as well as the linear determination coefficient (R²) between CC2 and TD-DFT values. The corresponding statistical data for both μ^GS and μ^ES can be found in Table S-4 in the SI. For the GS dipole moments, DFT gives accurate estimates with a MSE in the 0.15–0.35 D range (but always positive indicating an overestimation by DFT), a MAE in the 0.30–0.50 D range (M06-HF being the only XCF to deliver an average absolute error exceeding 0.50 D), and a large determination coefficient (R² > 0.95). The value of the latter tends to increase with the amount of exact exchange included in the XCF. We also note that the two tested meta-GGAs, namely M06-L and M11-L, yield more accurate μ^GS than other pure XCFs. For the considered medium-sized molecules, M06 emerges as the most accurate functional for μ^GS as it delivers the smallest MAE (0.33 D) together with a large R² (0.99), though several other XCFs, e.g., PBE0 and M06-2X, appear to be adequate as well. For the ES dipole moments (see r.h.s. of Table S-4 in the SI), the obtained results are both less accurate and more dependent on the selected functional, and this exacerbated XCF dependence of TD-DFT compared to DFT can be ascribed to the presence of CT ES in the set. The MSE is positive for all pure XCF and negative for all hybrid XCF, indicating that the former overestimate μ^ES (to a larger extent than μ^GS), while the former underestimate μ^ES, in line of conclusions obtained for small molecules.¹⁰ The μ^ES MAEs are significantly larger with the pure XCFs (>1 D, M06-L and M11-L being again the most accurate of the group) than with hybrids (<1 D). The correlation obtained with pure XCF is unsatisfying for the ES dipole (R² < 0.7) indicating that their estimates are rather inconsistent, a problem that is partially solved when a hybrid XCF is applied (R² > 0.8), though the correlation remains worse than that for the GS property. The smallest MAE (0.71 D) is again reached with M06 that also delivers the largest R² (0.93) of the series. In a second group, one finds B3LYP, PBE0, and SOGGA11-X that are slightly less satisfying than M06. The three RSHs deliver larger deviations with respect to the CC2 reference values. For the excess dipole (Table 2), we notice a small MSE for M11-L, due to the partial error compensation between the overestimation of both μ^GS and μ^ES. In contrast, hybrid XCFs that overshoot μ^GS but undershoot μ^ES, logically provide a significantly too small Δμ with the MSE going from −0.45 D for B3LYP to −1.15 D for ωB97X-D. Again, the smallest MAEs (ca. 1.0 D) are reached with the global hybrid XCFs, range-separated hybrids giving slightly larger deviations (ca. 1.1 D). The best correlation between theory and experiment is obtained with M06-2X (R² = 0.96), and all XCFs including large shares of exact exchange provide large R² values, only slightly smaller than the M06-2X value.

Table 2. Statistical Analysis for the Data of Table 1^a.

	MSE	MAE	Max(+)	Max(−)	R2
SVWN5	0.344	1.635	6.596	–7.404	0.634
BLYP	0.296	1.562	6.481	–7.160	0.641
BP86	0.304	1.577	6.309	–7.201	0.644
OLYP	0.263	1.552	6.350	–7.303	0.640
M06-L	0.345	1.588	5.477	–7.015	0.672
M11-Lb	–0.165	1.574	5.320	–7.819	0.489
B3LYP	–0.447	1.000	1.948	–7.630	0.788
PBE0b	–0.577	0.918	1.336	–7.511	0.803
M06	–0.746	1.027	1.007	–8.245	0.847
BMK	–0.920	0.994	0.436	–7.598	0.920
SOGGA11-X	–0.888	0.994	0.469	–7.945	0.903
M06-2X	–0.925	0.953	0.166	–6.203	0.961
M06-HF	–1.099	1.159	0.269	–7.242	0.913
CAM-B3LYP	–1.051	1.089	0.190	–7.525	0.926
M11	–1.149	1.181	0.267	–7.456	0.921
ωB97X-D	–1.076	1.105	0.200	–7.136	0.932

^aMSE, MAE, max(+) and max(−) are the mean signed error, mean absolute error, maximal positive and negative deviations, respectively, whereas R² is the linear determination coefficient. The TD-DFT errors are given with respect to CC2, and are in D (except for R²).

^bFor both M11-L and PBE0, the problematic data have been removed for the statistics (see footnotes in Table 1).

For the rest of this work, we have therefore continued with hybrid functionals only and excluded the pure XCFs that obviously deliver less consistent values.

3.2. Dipole Moments: Second Set

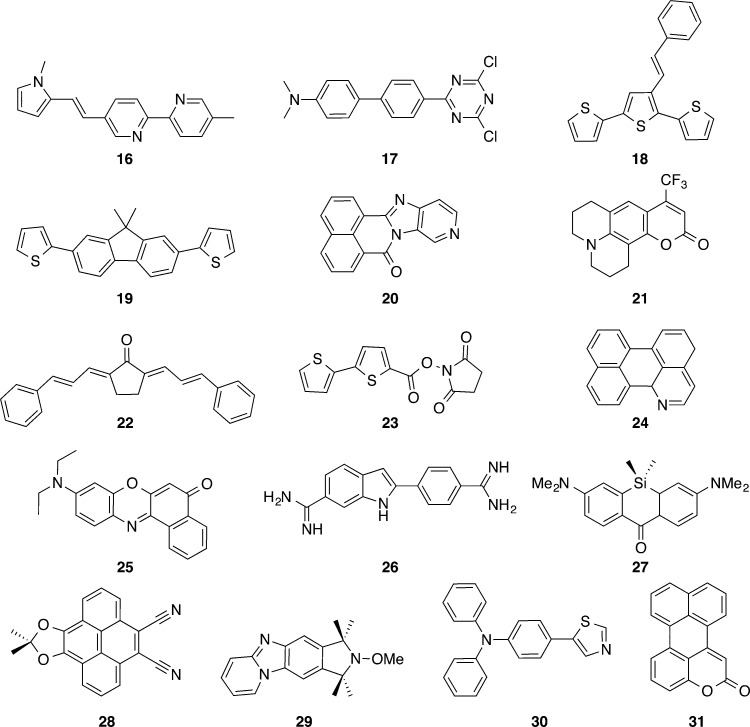
The set of larger molecules represented in Scheme 2 was next considered. In this set, several states with strong CT character, for example, 17, 21, 25, 28, and 30 are included. The Δμ values are listed in Table 3 together with the statistical data, whereas the corresponding μ^GS and μ^ES values are given in the SI. For 17 that presents a huge Δμ at the CC2 level (21.8 D), both B3LYP (19.9 D) and PBE0 (19.9 D) provide more accurate estimates than CAM-B3LYP (16.1 D) and ωB97X-D (14.1 D). In contrast, for 30, the B3LYP (10.6 D) and PBE0 (9.7 D) Δμ values significantly exceed the CC2 reference (7.2 D) that is reasonably reproduced by CAM-B3LYP (6.3 D). This apparent lack of consistency between the CT nature and the adequacy of RSH, already noted above, is discussed in the following section.

Scheme 2. Representation of the Molecules Considered in Section 3.2.

Table 3. Excess Dipole Moment, Determined through eq 2 and Listed in Debye for the Compounds of Scheme 2^a.

	State	CC2	B3LYP	PBE0	M06	BMK	SOGGA11-X	M06-2X	M06-HF	CAM-B3LYP	M11	ωB97X-D
16	A (π → π*)	8.25	8.35	7.91	6.88	6.61	6.32	5.81	4.16	5.25	4.21	4.77
17	A (π → π*)	21.81	19.94	19.93	19.35	18.93	18.22	17.28	11.39	16.07	12.56	14.11
18	A (π → π*)	0.64	3.35	3.25	2.24	0.83	2.01	0.77	0.68	1.81	0.71	0.66
19	A″ (π → π*)	0.24	0.14	0.14	0.10	0.14	0.12	0.15	0.15	0.12	0.16	0.13
20	A′ (π → π*)	3.09	5.21	4.8	4.29	3.22	3.47	2.49	1.03	2.36	1.44	2.12
21	A (π → π*)	7.82	5.95	5.94	5.32	5.77	5.51	5.38	4.77	5.22	4.66	5.05
22	A (n → π*)	1.68	1.98	1.89	1.93	1.65	1.72	1.51	1.50	1.58	1.42	1.56
	B (π → π*)	1.42	3.52	3.62	3.61	3.95	3.74	3.88	3.96	3.83	3.89	3.78
23	A (π → π*)	5.50	4.62	4.41	3.96	4.02	3.70	3.80	3.04	3.43	3.05	3.21
24	A′ (π → π*)	0.74	0.06	0.05	0.11	0.10	0.07	0.17	0.37	0.12	0.24	0.16
25	A (π → π*)	8.48	4.74	4.83	4.62	4.99	4.92	5.10	5.32	4.88	4.80	4.65
26	A (π → π*)	5.20	9.45	8.41	7.56	5.82	5.85	4.82	2.51	4.23	2.83	3.48
27	A″ (π → π*)	2.25	1.38	0.63b	0.43b	1.63	1.34	1.73	1.77	1.59	1.49	1.52
28	A″ (π → π*)	9.46	9.33	9.18	8.83	8.44	8.32	7.82	5.65	7.80	6.82	7.48
29	A (π → π*)	3.13	3.55	3.35	3.25	2.87	2.92	2.69	1.95	2.70	2.30	2.58
30	A (π → π*)	7.17	10.59	9.74	9.03	7.81	7.68	6.55	4.44	6.25	5.11	5.59
31	A′ (π → π*)	2.16	1.94	1.81	1.62	1.42	1.40	1.34	1.17	1.26	1.08	1.22
	MSE		0.298	0.155	–0.256	–0.637	–0.690	–1.044	–2.070	–1.208	–1.898	–1.586
	MAE		1.515	1.437	1.452	1.122	1.310	1.350	2.374	1.629	2.196	1.867
	max(+)		4.250	3.206	2.356	2.533	2.322	2.465	2.538	2.412	2.466	2.362
	max(−)		–3.741	–3.652	–3.853	–3.484	–3.596	–4.530	–10.420	–5.746	–9.249	–7.699
	R2		0.847	0.878	0.892	0.940	0.929	0.951	0.913	0.939	0.923	0.938

^aValues in italics indicate that the norm of the total ES dipole is smaller than its GS counterpart. At the bottom of the Table, satistical data are given.

^bStrong state-mixing for both PBE0 and M06. These states were removed from the statistics.

As can be seen in Table S-7 in the SI, for μ^GS, the MSEs are positive for all XCFs except for M06-HF in this set of larger compounds. The μ^GS MAEs, in the 0.15–0.30 D range, are obviously small for all XCFs. Very large R² are also obtained irrespective of the selected functional, the poorest value being 0.98 with M06-HF. For the μ^ES, all XCFs underestimate the CC2 reference values with an error that roughly increases with the amount of exact exchange included in the functional, for example, the MSE attains −0.25 D with PBE0 but −1.13 D with M06-2X. The MAEs are ca. 1.0–1.5 D with most XCFs, although significantly larger deviations (>2 D) are reached with both M06-HF and M11. The μ^ESR² values are satisfying, though less impressive than for μ^GS (see Table S-7). In short, the most important trend obtained in section 3.1, that is, the overestimation of μ^GS by DFT and the underestimation of μ^ES by TD-DFT is confirmed for the compounds of Scheme 2. Nevertheless, compared to those in section 3.1, the average deviations tend to be smaller for μ^GS but larger for μ^ES. These changes are reflected in the statistical analysis of the Δμ given at the bottom of Table 3: the MSE is positive for B3LYP and PBE0 but negative with all other XCFs. Obviously, the MAEs are rather large, the most accurate functional being BMK (MAE = 1.12 D), the least satisfying being M06-HF (MAE = 2.37 D).

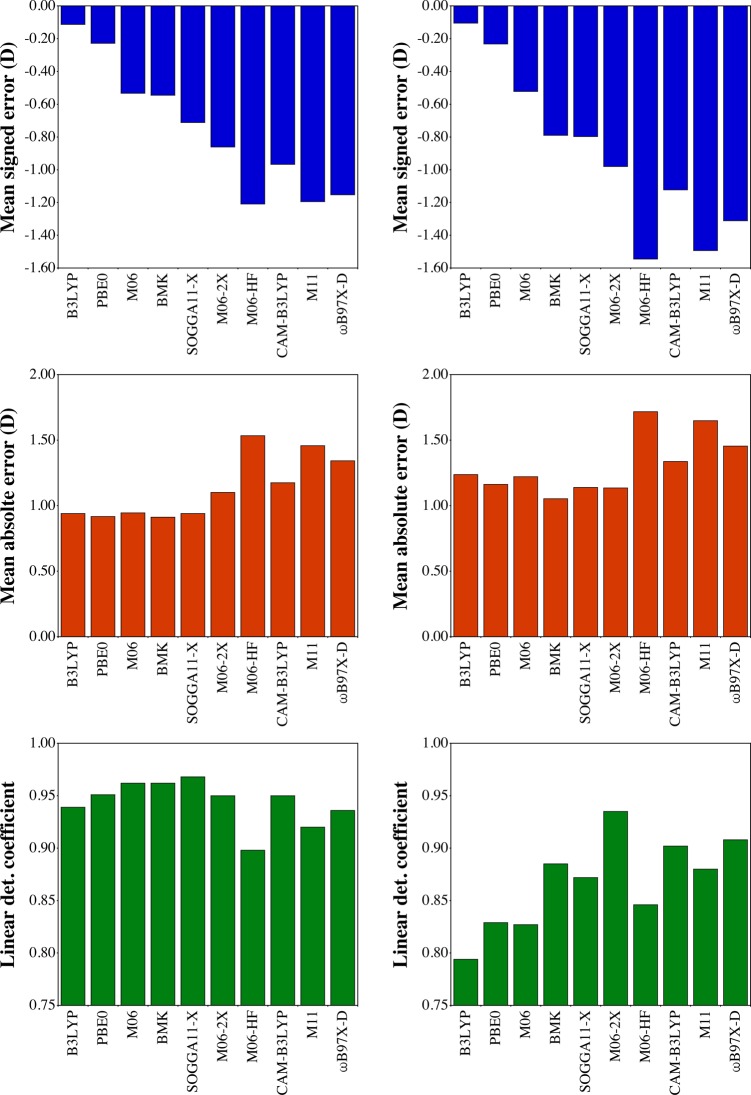
In Figure 2 we provide the MSE, MAE, and R² for both μ^ES and Δμ, considering all 37 cases reported in this work (sections 3.1 and 3.2), the corresponding representations for μ^GS are given in Figure S-1. First, we note that one should expect, on average, an underestimation of μ^ES and Δμ when hybrid XCFs are used, the signed errors being quite large with the three RSHs and M06-HF. For both μ^ES and Δμ, the absolute deviations are of the order of 1 D with B3LYP, PBE0, M06, BMK, SOGGA11-X, and M06-2X, but are again larger with the RSHs and M06-HF. The R² values are in the 0.90–0.95 D range for μ^ES and are more dependent on the selected XCFs for Δμ. Indeed, if B3LYP provides the smallest MSE (top of Figure 2), it delivers the poorest R² for Δμ (<0.8). In contrast M06-2X provides accurate trends with the largest R² for Δμ and large R² for both μ^GS and μ^ES. This success of M06-2X comes at the cost of significantly too small excited-state dipole moments. This behavior of M06-2X for dipole moments—good consistency with a significant but systematic deviation—actually parallels its behavior for 0–0 energies.⁵⁰

Figure 2.

MSE (top), MAE (center), and R² (bottom) obtained for the 37 ES dipole moments (left) and excess dipole moments (right) considered here. See Figure S-1 in the SI for the corresponding graphs for the GS dipole moments.

3.3. Dipole Moments: Charge-Transfer Chains

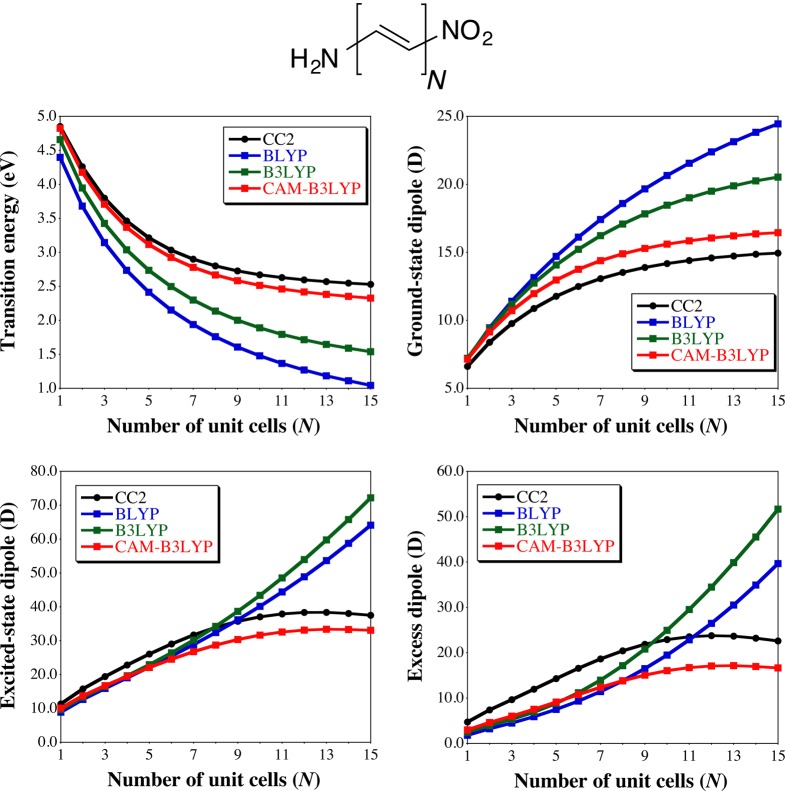
To further investigate the relationship between Δμ and the nature of the XCF in CT compounds, we have considered increasingly long α,ω-NH₂,NO₂-polyene chains (Figure 3). The structures have been optimized at the M06-2X/6-31+G(d) level enforcing the C_s geometry, whereas the electronic properties have been determined with BLYP, B3LYP, and CAM-B3LYP using the aug-cc-pVDZ atomic basis set. Test calculations with the corresponding triple-ζ basis set have given very similar trends. The main results are represented in Figure 3, whereas the Cartesian coordinates and the corresponding transition energies and dipole moments can be found in the SI. When the chain length increases, the transition energy to the lowest (dipole-allowed) excited-state decreases. As expected for such model CT systems,^47,48,51,52 both BLYP and B3LYP deliver too small transition energies, whereas the CAM-B3LYP results nicely match the CC2 values. Indeed, irrespective of the chain length, CAM-B3LYP transition energies are the closest to the CC2 values. We further notice that, consistently with results obtained in the previous sections, all three XCF overestimate μ^GS, with an error that is increasing with chain length for both BLYP and B3LYP but that is remaining rather constant with CAM-B3LYP. As above, the three XCFs underestimate the CC2 μ^ES for rather short chains. However, while the CAM-B3LYP curve nicely follows the CC2 one with a maximal μ^ES reached before 15 unit cells, both BLYP and B3LYP show exploding μ^ES values that attain twice the reference value for the longest compound investigated. These evolutions explain the contradictory conclusions obtained in the literature (see Introduction) regarding the accuracy of RSH for determining the Δμ of CT compounds. On the one hand, as CAM-B3LYP provides too large (too small) μ^GS (μ^ES), the final Δμ values are indeed significantly too small for all chain lengths. On the other hand, one notices on the bottom right panel of Figure 3 that, depending on the chain length, the most accurate XCFs can be B3LYP (N = 9), BLYP (N = 11), or CAM-B3LYP (N = 15), so that even XCFs providing inaccurate CT transition energies can in some cases deliver rather accurate Δμ due to an error compensation phenomenon. However, it remains very clear that the best trends are obtained with the RSH that provides the most physically sound evolution of the excess dipole with chain length.

Figure 3.

Evolution of the transition energy (top left), GS total dipole moment (top right), ES total dipole moment (bottom left), and excess dipole moment (bottom right) for increasingly long push–pull chains. All results are determined with the aug-cc-pVDZ basis set on the planar M06-2X/6-31+G(d) geometries.

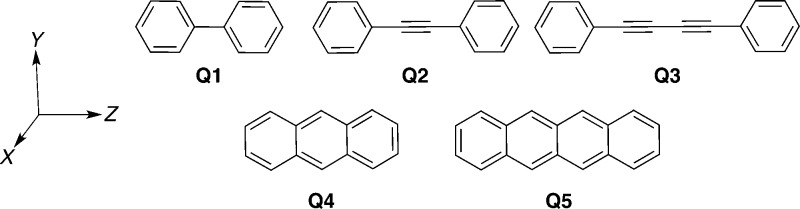
3.4. Quadrupole Moments

For this first investigation of ES quadrupole moments, we have selected the five symmetric aromatic derivatives displayed in Scheme 3 and considered the lowest dipole-allowed π → π* transitions. As for the dipole moments, the GS and ES values are listed in the SI, whereas the excess values, ΔQ, can be found in Table 4. Overall, the CC2 and TD-DFT Q^GS are in good agreement with each other, both in terms of sign and magnitude of the Q_yy and Q_zz components. For the considered set of compounds, we notice a rather limited impact of the amount of exact exchange included in the XCF, though both M06-HF (significantly) and M11 (to a lesser extent), two XCFs with very large amounts of exact echange, tend to give exaggerated contrasts between the Q_yy and Q_zz components compared to CC2. The conclusions are similar for Q^ES. The obtained MAE are of the order of 0.3–0.4 D·Å for Q^GS and 0.2–0.6 D·Å for Q^ES, though M06-HF (and M11 for the GS property) deliver significantly poorer estimates. The obtained R² values between TD-DFT and CC2 are astonishingly large (>0.99 for all XCFs) for Q^GS and remain rather satisfying though less impressive for Q^ES. In other words, as for the dipole moments, TD-DFT provides less accurate excited-state quadrupole moments than DFT does for their ground-state counterparts. All these trends are reflected in the ΔQ listed in Table 4. The errors that can be expected from TD-DFT for this property are therefore ca. 0.4 D·Å, though the most accurate XCF of the series for the excess quadrupoles, namely CAM-B3LYP, delivers tiny MSE, MAE, and maximal deviations together with a very large R². Several other XCFs, such as PBE0 and SOGGA11-X, also yield accurate data. Interestingly, the M06-2X R² is comparatively small, mostly due to the presence of an outlier, Q3.

Scheme 3. Representation of the Molecules Used in the Benchmarks of the Quadrupole Moments, Together with Their Orientation in the Cartesian Axes.

Table 4. Excess Traceless Quadrupole Moments Listed in D·Å for the Compounds of Scheme 3. At the Bottom of the Table, The Results of a Statistical Analysis Are Provided Using the CC2 Values as Reference.

	State		CC2	B3LYP	PBE0	M06	BMK	SOGGA11-X	M06-2X	M06-HF	CAM-B3LYP	M11	ωB97X-D
Q1	B1	Qyy	–0.73	–0.63	–0.60	–1.35	–0.54	–0.67	–0.69	–0.78	–0.62	–1.03	–0.57
		Qzz	1.09	0.78	0.68	3.30	0.57	0.92	0.96	1.27	0.79	2.26	0.63
Q2	B3u	Qyy	0.78	0.94	0.91	0.88	0.91	0.93	0.88	0.84	0.88	0.77	0.87
		Qzz	–2.35	–2.78	–2.72	–2.56	–2.72	–2.68	–2.58	–2.35	–2.60	–2.33	–2.58
Q3	B1	Qyy	1.39	1.87	1.82	1.65	1.79	1.75	3.47	1.82	1.62	2.74	1.57
		Qzz	–3.33	–4.48	–4.33	–3.90	–4.21	–4.09	–6.71	–4.29	–3.80	–5.40	–3.70
Q4	B2u	Qyy	1.48	1.31	1.31	1.43	1.36	1.46	1.46	1.69	1.36	1.42	1.26
		Qzz	–1.72	–1.66	–1.63	–1.75	–1.60	–1.75	–1.68	–1.78	–1.62	–1.60	–1.45
Q5	B2u	Qyy	1.38	1.26	1.26	1.36	1.31	1.40	1.38	1.52	1.32	1.35	1.21
		Qzz	–1.60	–1.58	–1.54	–1.65	–1.52	–1.66	–1.57	–1.51	–1.55	–1.51	–1.37
		MSE		–0.14	–0.12	0.10	–0.10	–0.08	–0.15	0.01	–0.06	0.03	–0.05
		MAE		0.30	0.29	0.41	0.29	0.20	0.61	0.22	0.18	0.52	0.24
		max(+)		0.48	0.43	2.21	0.40	0.36	2.08	0.43	0.23	1.36	0.27
		max(−)		–1.14	–1.00	–0.62	–0.88	–0.76	–3.38	–0.96	–0.47	–2.07	–0.45
		R2		0.97	0.97	0.91	0.97	0.99	0.88	0.99	0.99	0.92	0.98

4. Conclusions

We have investigated 31 ground-state dipole moments and 37 excited-state dipole moments with TD-DFT using the large aug-cc-pVTZ atomic basis set and considering 16 different exchange-correlation functionals. The results have been compared to reference CC2 (relaxed) values obtained on the same structures with the same basis set. Overall, a rather small impact of the selected functional on both μ^GS and μ^ES was found, at the notable exception of states presenting a charge-transfer character. On average, DFT provides too large μ^GS, whereas TD-DFT delivers too small μ^ES, with a magnitude for the error that is larger for the latter property. Consequently, the TD-DFT excess dipole moments tend to be too small, by ca. 1.0–1.5 D. GGA and meta-GGA do not necessarily yield larger deviations than hybrid XCF, but the trends obtained as measured by the correlation with the CC2 values are poorer. This conclusion also holds, to some extent, for hybrid functionals with a small share of exact exchange, e.g., B3LYP. It was known that global hybrid functionals tend to overestimate the electron–hole separation in the charge-transfer state leading to too small transition energies. As this exaggerated separation can compensate the generally too small μ^ES given by TD-DFT, B3LYP or PBE0 can deliver excess dipole moments matching the CC2 data even for strong CT cases, for which the transition energies obtained with these functionals are obviously far from the reference values. A study of increasingly long push–pull systems indicated however that the trends in Δμ are much better reproduced by range-separated hybrids. Overall, the XCF providing the largest correlation with CC2 for excess dipoles is M06-2X, though this functional provides μ^ES too small by ca. 1 D on average. CAM-B3LYP is another successful XCF, also giving a large R² and a relatively small MAE. Eventually, for the five aromatic hydrocarbon derivatives investigated, a generally nice agreement between the excess quadrupole moments given by TD-DFT and CC2 is obtained, with average deviations of the order of 0.4 D.Å.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.6b00498.

• Comparisons between GS and ES dipoles obtained on different geometries for three compounds; raw values for both GS and ES dipoles and corresponding statistical analysis; figures with the key statistical values for the μ^GS of sections 3.1 and 3.2. Structures, transition energies, and dipoles of the increasingly long-push–pull oligomers used in section 3.3. Additional data for the quadrupole moments (PDF)

The author acknowledges the European Research Council (ERC) and the Région des Pays de la Loire for financial support in the framework of a Starting Grant (Marches -278845) and the LumoMat project, respectively. This research used resources of (i) the GENCI-CINES/IDRIS; (ii) CCIPL (Centre de Calcul Intensif des Pays de Loire); (iii) a local Troy cluster; and (iv) HPC resources from ArronaxPlus (Grant ANR-11-EQPX-0004 funded by the French National Agency for Research).

The author declares no competing financial interest.