Genomic Prediction for Quantitative Traits Is Improved by Mapping Variants to Gene Ontology Categories in Drosophila melanogaster

Abstract

Predicting individual quantitative trait phenotypes from high-resolution genomic polymorphism data is important for personalized medicine in humans, plant and animal breeding, and adaptive evolution. However, this is difficult for populations of unrelated individuals when the number of causal variants is low relative to the total number of polymorphisms and causal variants individually have small effects on the traits. We hypothesized that mapping molecular polymorphisms to genomic features such as genes and their gene ontology categories could increase the accuracy of genomic prediction models. We developed a genomic feature best linear unbiased prediction (GFBLUP) model that implements this strategy and applied it to three quantitative traits (startle response, starvation resistance, and chill coma recovery) in the unrelated, sequenced inbred lines of the Drosophila melanogaster Genetic Reference Panel. Our results indicate that subsetting markers based on genomic features increases the predictive ability relative to the standard genomic best linear unbiased prediction (GBLUP) model. Both models use all markers, but GFBLUP allows differential weighting of the individual genetic marker relationships, whereas GBLUP weighs the genetic marker relationships equally. Simulation studies show that it is possible to further increase the accuracy of genomic prediction for complex traits using this model, provided the genomic features are enriched for causal variants. Our GFBLUP model using prior information on genomic features enriched for causal variants can increase the accuracy of genomic predictions in populations of unrelated individuals and provides a formal statistical framework for leveraging and evaluating information across multiple experimental studies to provide novel insights into the genetic architecture of complex traits.

VARIATION for complex traits is due to many interacting loci with small individual effects on each trait as well as environmental influences (Falconer and Mackay 1996). Knowledge of the underlying causal polymorphisms and their effects is thus critical for predicting disease susceptibility in humans, improving production traits in plants and animals, and predicting adaptive evolution. Genetic mapping approaches to dissect the genotype–phenotype map one locus at a time in outbred populations are successful in identifying quantitative trait loci (QTL) with the largest effects, but together these loci typically account for only a small fraction of the total genetic variance (Visscher 2008, 2012; Manolio et al. 2009; Vinkhuyzen et al. 2013; Caballero et al. 2015).

The realization that the effects of the majority of loci affecting complex traits are too small to be individually detected unless sample sizes are huge motivated the development of statistical methods to predict complex trait phenotypes, using all molecular markers simultaneously (Meuwissen et al. 2001). These genomic prediction methods are very successful in predicting phenotypes from marker genotypes in populations with a large amount of linkage disequilibrium (LD), such as selectively bred animals and plants (de Roos et al. 2009; Hayes et al. 2009, 2010; Crossa et al. 2010; Daetwyler et al. 2013). However, genomic prediction does not work well when LD is low, such as across breeds or strains or in outbred populations of largely unrelated individuals (Habier et al. 2007; Makowsky et al. 2011; de los Campos et al. 2013), because many causal polymorphisms will not be in LD with the genotyped markers.

Genomic predictions currently utilize high-density single-nucleotide polymorphism (SNP) genotyping arrays. Given the rapid advances in sequencing technologies, genomic prediction soon will be based on whole-genome sequence data. This will greatly exacerbate the true genomic signal to noncausal marker noise problem. Therefore, the key to better prediction models may be to “guess” which markers could be causal by utilizing prior biological findings, as it appears that the markers associated with trait variation are not uniformly distributed throughout the genome, but enriched in genes that are connected in biological pathways (Lango Allen et al. 2010; O’Roak et al. 2012; Lage et al. 2012; Maurano et al. 2012; Peñagaricano et al. 2013). Here, we extend the commonly used genomic best linear unbiased prediction (GBLUP) model (Meuwissen et al. 2001) by incorporating prior information on gene ontologies (Gene Ontology Consortium et al. 2000). Our model, which we call genomic feature BLUP (GFBLUP), includes an additional genomic effect that quantifies the collective action of a set of markers located in a genomic feature defined by genes, biological pathways, sequence annotation, or other external evidence. We previously used this approach to partition the genomic variance of pathways in health and milk production traits in Danish Holstein dairy cattle (Edwards et al. 2015). Here, we apply it to three quantitative traits (starvation resistance, startle response, and chill coma recovery time) in the largely unrelated inbred, sequenced lines of the Drosophila melanogaster Genetic Reference Panel (DGRP) (Mackay et al. 2012; Huang et al. 2014). Prediction accuracies from previous GBLUP analyses of these traits in the DGRP ranged from zero to very low (Ober et al. 2012, 2015).

The premise of the GFBLUP model is that genomic features are enriched for causal variants affecting the traits. However, in reality, the number, location, and effect sizes of the true causal variants in the genomic feature are unknown. Therefore, we also used simulation to investigate feature- and trait-specific factors that may influence predictive ability, using the GFBLUP model. Genomic feature factors include the proportion of the total genomic variance that can be explained by the genomic feature, the number of noncausal variants that is included, and the distribution of the causal variants in the genome (either distributed randomly or clustered in smaller genome regions). The trait-specific factors include the total genomic heritability of the trait and the number of phenotypic records available for analysis.

Our GFBLUP models applied to the DGRP provide better model fits and have a higher predictive ability than the standard GBLUP model. The GFBLUP models provide novel insight into the genetic architecture of starvation resistance, startle response, and chill coma recovery by identifying genomic features that explain large proportions of genomic variance. Finally, our simulated data generated from DGRP genotypes illustrate factors affecting estimation of genomic parameters, model fit, and predictive ability.

Materials and Methods

DGRP data

Drosophila lines:

The phenotypic and genotypic data originate from the DGRP (Mackay et al. 2012; Huang et al. 2014). All data can be accessed via the Web site http://dgrp2.gnets.ncsu.edu. The DGRP consists of 205 inbred lines obtained by 20 generations of full-sib mating from the offspring of single wild-caught females collected from the Raleigh, North Carolina population, which have full genome sequences (Mackay et al. 2012; Huang et al. 2014). All flies were reared under standard culture conditions (cornmeal–molasses–agar medium, 25°, 60–75% relative humidity, 12-hr light–dark cycle). The DGRP is polymorphic for common inversions and Wolbachia pipientis infection status (Huang et al. 2014). These factors were included in the models described below as fixed effects.

Quantitative trait phenotypes:

Starvation resistance for 197 DGRP lines was assessed by placing 10 same-sex, 2-day-old flies in culture vials containing nonnutritive medium (1.5% agar and 5 ml water) and scoring survival every 8 hr until all flies were dead (Harbison et al. 2004). There were five replicate vials per sex per line (total N = 19,361; female N = 9672; male N = 9689). Chill coma recovery for 159 DGRP lines was measured by transferring 3- to 7-day-old flies without anesthesia to empty vials and placing them on ice for 3 hr. Flies were transferred to room temperature, and the time it took for each individual to right itself and stand on its legs was recorded (Morgan and Mackay 2006). There were two replicates of 50 flies per sex per line (total N = 32,231; female N = 16,170; male N = 16,061). Startle response for 166 DGRP lines was measured by placing single 3- to 7-day-old adult flies, collected under CO₂ exposure, into vials containing 5 ml culture medium and leaving them overnight to acclimate to their new environment. On the next day, between 8 am and 12 pm (2–6 hr after lights on), each fly was subjected to a mechanical disturbance with a gentle tap, and the total amount of time the fly was active in the 45 sec immediately following the disturbance was recorded (Mackay 2001). There were two replicates of 20 flies per sex per line (total N = 13,276; female N = 6674; male N = 6602).

Genotypes:

Genotypes were obtained from whole-genome sequences, using an integrative genotyping procedure (Huang et al. 2014). All analyses were based on segregating biallelic SNPs with minor allele frequencies ≥0.05 and for which the Phred scaled variant quality was >500 and the genotype call rate was ≥0.8, for a total of 1,725,755 SNPs distributed on five chromosome arms (2L, 2R, 3L, 3R, and X).

Genomic features:

Genes grouped according to a specific Gene Ontology (GO) term were considered a genomic feature. Genes were linked to the “biological processes” (BP), “molecular function” (MF), and “cellular component” (CC) GO terms (Gene Ontology Consortium et al. 2000), using the BioConductor package “org.Dm.eg.db” v. 2.14 (Carlson 2013). Only GO terms with at least 10 directly evidenced genes were used in the analyses. SNPs were mapped to FlyBase genes using the v5.49 annotations of the D. melanogaster reference genome (Tweedie et al. 2009; Mackay et al. 2012; Huang et al. 2014). Only the 963,235 SNPs located within genes (i.e., within open reading frames) were used for the genomic feature. In total markers were associated with 10,517 genes and 1145 GO terms. A total of 1,725,755 markers were used in all analyses, and the number of markers linked to a single GO term ranged from 23 to 163,938.

Statistical analyses using linear mixed models

Analyses were performed using two different linear mixed models: a standard GBLUP model and a GFBLUP model using prior information on genomic features. In the following we present details of the models and statistical procedures used to compare the models.

Genomic models:

For each genomic feature (i.e., GO term) a separate analysis was conducted. In each of the GFBLUP analyses we evaluated a single genomic feature based on a linear mixed model including two random genomic effects,

$$\tilde{\mathit{y}}=\mathit{\mu }+\mathit{Z}f+\mathit{Z}r+{\mathit{Z}}_l\mathit{l}+\mathit{e}\left(M_{\text{GFBLUP}}\right),$$

where $\tilde{\mathit{y}}$ is the vector of adjusted phenotypic observations (or simulated phenotypes), $\mathit{\mu }$ is the vector of an overall mean, $\mathit{Z}$ is the design matrix linking observations to genomic values (f and r), ${\mathit{Z}}_l$ is a design matrix for the replicate within-line effects (l), $\mathit{f}$ is the vector of line-specific genomic values captured by genetic markers linked to the genomic feature of interest, $\mathit{r}$ is the vector of line-specific genomic values not captured by genetic markers linked to the genomic feature, and $\mathit{e}$ is the vector of residuals. The random genomic effects and the residuals were assumed to be independent normally distributed values described as follows: $\mathit{f}\sim N\left(0,{\mathit{G}}_{\mathit{f}}{\sigma }_f^2\right),\hspace{0.5em}\mathit{r}\sim N\left(0,\mathit{G}{\sigma }_r^2\right),$ $\mathit{l}\sim N\left(0,{\mathit{I}}_{\mathit{l}}{\sigma }_l^2\right),$ and $\mathit{e}\sim N\left(0,\mathit{I}{\sigma }_e^2\right).$

GBLUP was based on a linear mixed model including only one random genomic effect,

$$\tilde{\mathit{y}}=\mathit{\mu }+\mathit{Z}g+{\mathit{Z}}_l\mathit{l}+\mathit{e}\left(M_{\text{GBLUP}}\right)$$

with the same notation as above except that $\mathit{g}$ is the vector of genomic values captured by all genetic markers. The random genomic values and the residuals were assumed to be independent normally distributed values described as follows: $\mathit{g}\sim N\left(\mathbf{0},\mathit{G}{\sigma }_g^2\right)$ and $\mathit{e}\sim N\left(\mathbf{0},\mathit{I}{\sigma }_e^2\right).$

In the analyses of the simulated data the term for the replicate within-line effects was excluded in both the genomic model analyses.

The additive genomic relationship matrix $\mathit{G}$ (VanRaden 2008) was constructed using all genetic markers as follows: $\mathit{G}=\mathit{W}{W}^{\prime }/m,$ where $\mathit{W}$ is the centered and scaled genotype matrix, and $m$ is the total number of markers. Each column vector of W was calculated as follows: ${\mathit{w}}_{\mathit{i}}=\left({\mathit{m}}_{\mathit{i}}-2p_i\right)/\sqrt{2p_i\left(1-p_i\right)},$ where $p_i$ is the minor allele frequency of the ith genetic marker and ${\mathit{m}}_{\mathit{i}}$ is the ith column vector of the allele count matrix, M, which contains the genotypes coded as 0 or 2 depending on the number of minor alleles. The additive genomic relationship matrix for the genomic feature ${\mathit{G}}_{\mathit{f}}$ was constructed in a similar way, using only the genetic marker set defined by the genomic feature.

Adjusted phenotypes used in genomic model analyses:

The phenotypes used in the GBLUP and GFBLUP model analyses were derived from phenotypic records of the quantitative traits adjusted for relevant factors, using the linear mixed model

$$\mathit{y}=\mathit{X}b+\mathit{Z}g+{\mathit{Z}}_l\mathit{l}+\mathit{e},$$

where $\mathit{y}$ is the vector of phenotypic observations, $\mathit{X}$ is the design matrix, $\mathit{b}$ is the vector of fixed effects of inversion karyotypes and Wolbachia infection status, $\mathit{Z}$ is the design matrix linking observations to genomic values, ${\mathit{Z}}_l$ is a design matrix for the replicate within-line effects, $\mathit{g}$ is the vector of genomic values captured by all genetic markers, $\mathit{l}$ is the vector of replicate within-line effects, and $\mathit{e}$ is the vector of residuals. The random effects ($\mathit{g}$ and $\mathit{l}$) and the residuals were assumed to be independent normally distributed values described as follows: $\mathit{l}\sim N\left(0,{\mathit{I}}_{\mathit{l}}{\sigma }_l^2\right),$ $\mathit{g}\sim N\left(0,\mathit{G}{\sigma }_g^2\right),$ and $\mathit{e}\sim N\left(0,\mathit{I}{\sigma }_e^2\right).$ The adjusted phenotypes used as response variables for genomic model analysis described below were calculated as $\tilde{\mathit{y}}=\mathit{Z}\widehat{\mathit{g}}+{\mathit{Z}}_l\widehat{\mathit{l}}+\widehat{\mathit{e}}.$

Estimation of variance components:

Estimates of the variance components (${\widehat{\sigma }}_f^2,{\widehat{\sigma }}_r^2,{\widehat{\sigma }}_g^2,{\widehat{\sigma }}_l^2\text{, and}\hspace{0.5em}{\widehat{\sigma }}_e^2$) defined in the models described above were obtained using an average information restricted maximum-likelihood (REML) procedure (Madsen et al. 1994; Johnson and Thompson 1995) as implemented in the software DMU (Madsen et al. 1994). In this procedure, we used a generalized inverse of the genomic relationship matrices. This was necessary because these matrices were not full rank due to centering, as well as in cases where the number of genetic markers was smaller than the number of lines.

Model comparisons:

The models were evaluated and compared based on model fit, model predictive ability, and precision of estimated genomic parameters.

Genomic parameters:

Genomic parameters were derived from the estimates of the variance components. Inferences on genomic heritability were based on the following ratios: ${\widehat{h}}_{\mathrm{GBLUP}}^2={\widehat{\sigma }}_g^2/\left({\widehat{\sigma }}_g^2+{\widehat{\sigma }}_e^2\right)$ for GBLUP and ${\widehat{h}}_{\mathrm{GFBLUP}}^2=\left({\widehat{\sigma }}_f^2+{\widehat{\sigma }}_r^2\right)/\left({\widehat{\sigma }}_f^2+{\widehat{\sigma }}_r^2+{\widehat{\sigma }}_e^2\right)$ for GFBLUP. Inference on partitioning of genomic variance in GFBLUP was based on the following ratios: ${\widehat{h}}_f^2={\widehat{\sigma }}_f^2/\left({\widehat{\sigma }}_f^2+{\widehat{\sigma }}_r^2\right)$ and ${\widehat{h}}_r^2={\widehat{\sigma }}_r^2/\left({\widehat{\sigma }}_f^2+{\widehat{\sigma }}_r^2\right).$ These ratios quantify the proportion of total genomic variance captured $\left({\widehat{h}}_f^2\right)$ and not captured $\left({\widehat{h}}_r^2\right)$ by the genetic markers in the genomic feature.

Model fit:

The model fit was assessed using a likelihood ratio (LR) here defined as $2\log l{h}_{M_{\mathrm{G}}}-2\log l{h}_{M_{\mathrm{GF}}},$ where $lh$ is the likelihood of the fitted model. Standard theory shows that the LR test statistic is asymptotically distributed as ${\chi }_{\kappa }^2,$ where $\kappa ,$ the degrees of freedom, is the difference in the number of parameters between the two models. The P-values calculated for assessing the significance of the likelihood-ratio test were based on a ${\chi }^2$-distribution with 1 d.f. However, it has previously been shown that if the null hypothesis value is on the boundary of the parameter space (e.g., ${\sigma }_f^2=0$), the asymptotic distribution of LR test statistics may be approximated by a 50:50 mixture of ${\chi }^2$-distributions with 0 and 1 d.f. (Self and Liang 1987). Alternatively it is possible to derive an empirical distribution of the LR test statistic as we have shown previously (Edwards et al. 2015).

Model predictive ability:

The ability of the models to predict total genomic value was assessed using a cross-validation procedure. In the GFBLUP model the total genomic value is ${\widehat{\mathit{g}}}_{\text{total}}$ = $\widehat{\mathit{f}}$ + $\widehat{\mathit{r}}$ and in GBLUP it is ${\widehat{\mathit{g}}}_{\text{total}}$ = $\widehat{\mathit{g}}.$ In the cross-validation procedure, we estimated genomic parameters using the phenotypes from the lines in the training data (90% of the lines) and predicted the total genomic value of lines in the validation data (10% of the lines). BLUP is used to predict total genomic values in both the GFBLUP and GBLUP models as described below. We then calculated a correlation between the total genomic values predicted with or without the observed phenotypes set to missing. For the simulated data and for the observed DGRP data we defined 50 cross training (validation) data subsets and applied these to each genomic feature. For each genomic feature, the predictive ability was defined as the average correlation of the 50 cross validations. A similar procedure was applied to the GBLUP model serving as a reference. For each genomic feature Welch’s t-test (i.e., unequal variance t-test) was used to test the difference in mean predictive ability of the two models (Welch 1947). For each trait 1145 GO terms were tested. Therefore P-values from Welch’s t-test were adjusted for multiple testing by controlling the false discovery rate as implemented in R (Benjamini and Hochberg 1995; R Core Team 2015).

Prediction of total genomic value using BLUP:

The total genomic value of lines in the validation data was predicted conditional on the observed phenotypes for the lines in the training data. In the GFBLUP model the conditional expectation of the total genomic values for the lines in the validation data $\left({\widehat{\mathit{g}}}_1={\widehat{\mathit{f}}}_1+{\widehat{\mathit{r}}}_1\right)$ given the observed phenotypes for the lines in the training data (${\mathit{y}}_2$) can be written as

$${\widehat{\mathit{g}}}_1=E({\mathit{g}}_1|{\mathit{y}}_2)=\left({\mathit{G}}_{f_{12}}{\widehat{\sigma }}_f^2+{\mathit{G}}_{r_{12}}{\widehat{\sigma }}_r^2\right){\left[{\mathit{G}}_{f_{22}}{\widehat{\sigma }}_f^2+{\mathit{G}}_{r_{22}}{\widehat{\sigma }}_r^2+{\mathit{I}}_{22}{\widehat{\sigma }}_e^2\right]}^{-1}\left({\mathit{y}}_2-{\mathit{X}}_2{\widehat{b}}_2\right),$$

where the genomic relationship matrix for the genomic feature ${\mathit{G}}_f=\left(\begin{array}{ll}{\mathit{G}}_{f_{11}}\hfill & {\mathit{G}}_{f_{12}}\hfill \\ {\mathit{G}}_{f_{21}}\hfill & {\mathit{G}}_{f_{22}}\hfill \end{array}\right)$ is partitioned according to relationships between the lines in the training data (${\mathit{G}}_{f_{11}}$), between the lines in the validation data (${\mathit{G}}_{f_{22}}$), and between the lines in the training and validation data (${\mathit{G}}_{f_{12}}$). A similar partitioning is applied to G_r and I in the GFBLUP model. For the sake of simplicity we have ignored the design matrix Z and the replicate within-line effects in the expression for the conditional expectation. Thus the total genomic value is predicted using the estimated variance components (${\widehat{\sigma }}_f^2,$ ${\widehat{\sigma }}_r^2,$ and ${\widehat{\sigma }}_e^2$) in the training data. The rightmost term, $\left({\mathit{y}}_2-{\mathit{X}}_2{\widehat{\mathit{b}}}_2\right),$ constitutes the phenotypes corrected for fixed effects for the lines in the training data. The inverse term $\left[{\mathit{G}}_{f_{22}}{\widehat{\sigma }}_f^2+{\mathit{G}}_{r_{22}}{\widehat{\sigma }}_r^2+{\mathit{I}}_{22}{\widehat{\sigma }}_e^2\right]$ is essentially the variance–covariance structure for the corrected phenotypes. These two terms together are the standardized and corrected phenotypes for the individuals in the training data, which are projected onto the total genetic covariance structure between the training and the validation data, $\left({\mathit{G}}_{f_{12}}{\widehat{\sigma }}_f^2+{\mathit{G}}_{r_{12}}{\widehat{\sigma }}_r^2\right).$

In the GBLUP model a similar expression for the conditional expectation of the total genomic value for the lines in the validation data given the observed phenotypes for the lines in the training data can be written as

$${\widehat{\mathit{g}}}_1=E\left({\mathit{g}}_1|{\mathit{y}}_2\right)=\left({\mathit{G}}_{12}{\widehat{\sigma }}_g^2\right){\left[{\mathit{G}}_{22}{\widehat{\sigma }}_g^2+{\mathit{I}}_{22}{\widehat{\sigma }}_e^2\right]}^{-1}\left({\mathit{y}}_2-{\mathit{X}}_2{\widehat{b}}_2\right).$$

Implementation:

The GFBLUP and GBLUP modeling approaches are implemented in the R package qgg, which is available at http://psoerensen.github.io/qgg/. This includes fitting a series of linear mixed models, estimating variance components using REML, prediction using BLUP, and cross-validation procedures. Example scripts and data sets are provided for illustrating the GFBLUP and GBLUP modeling approaches. For a specific experimental design with replicated phenotypes within line such as DGRP it is more efficient to use the average information REML procedure (Madsen et al. 1994; Johnson and Thompson 1995) implemented in DMU (Madsen et al. 1994). The aireml function in the qgg package provides an R interface to the DMU that can be downloaded from http://dmu.agrsci.dk/DMU/.

Simulated data

We established a series of simulation studies to investigate factors influencing the power to detect genomic features affecting the trait phenotype, estimation of genomic parameters, and prediction ability of the two tested linear mixed models. The factors varied in the simulations included genomic heritability ($h^2$), proportion of genomic variance explained by causal SNPs in the genomic feature ($h_f^2$), proportion of noncausal SNPs in the genetic marker set defined by the genomic feature (dilution), genome distribution of causal SNPs (causal model) (i.e., how the causal SNPs were physically distributed on the genome: random or clustered), and the number of replicates (i.e., the number of phenotypic records for each line) within lines (N_rep).

Genotypes:

The simulations were based on the real genotype DGRP data set of 205 lines and 1,725,755 SNPs. In all scenarios, there were 1000 causal SNPs. Causal sets were divided into two subsets. The first subset $C_1$ included 100 SNPs and was used as the causal SNP set in the genomic feature that explains 10%, 20%, 30%, or 50% of the total genomic variance. The second subset $C_2$ included 900 SNPs and explained the remaining genomic variance. To mimic relevant genetic scenarios, the genome distribution of the causal SNPs in the genomic feature was simulated using two different causal models: a random and a cluster model. The cluster model simulates the situation in which multiple causal SNPs occur in a limited number of genes, whereas in the random model single causal SNPs occur in a larger number of genes. The main difference is that the genomic variance is associated with a smaller genome region in the cluster model compared to the random model. For the clustered causal model, the 100 causal SNPs in $C_1$ were chosen from 20 randomly selected genome regions spanning 50 SNPs each, and the remaining 900 SNPs in $C_2$ were randomly selected from the complete SNP set (excluding the SNPs in $C_1$). For the random causal model, the SNPs in $C_1$ and $C_2$ were randomly selected from the complete SNP set. To investigate the effects of noncausal SNPs within the causal sets, we added an increasing number of noncausal SNPs (200, 400, 800, … , 2000) to the causal sets, in a process referred to as dilution. The noncausal SNPs were picked either at random in the genome or by sampling SNPs located directly up- and downstream of the causal SNP (referred to as local SNPs).

Phenotypes:

Phenotypes were simulated using the following linear model: y = g₁ + g₂ + e, where g₁ ∼ N(0,G₁*${\sigma }_{g1}^2$), g₂ ∼ N(0,G₂*${\sigma }_{g2}^2$), and e ∼ N(0,I*${\sigma }_e^2$). G₁ and G₂ are the genomic relationship matrices for causal SNPs in C₁ and C₂, respectively. The total phenotypic variance ${\sigma }_{\text{P}}^2={\sigma }_{g1}^2+{\sigma }_{g2}^2+{\sigma }_e^2$ was 100 in all scenarios. We simulated data under additive genomic heritabilities $\left(h^2=\left({\sigma }_{g1}^2+{\sigma }_{g2}^2\right)/\left({\sigma }_{g1}^2+{\sigma }_{g2}^2+{\sigma }_e^2\right)\right)$ of 0.1, 0.3, and 0.5, to analyze scenarios with low to intermediate heritabilities, reflecting those observed in the real data. To analyze scenarios with nonuniform SNP effects, the proportion of additive genomic variance explained by the causal SNPs in $C_1$ $\left(h_f^2={\sigma }_{g1}^2/\left({\sigma }_{g1}^2+{\sigma }_{g2}^2\right)\right)$ was varied across scenarios: 0.1, 0.2, 0.3, and 0.5. These parameters were investigated for N_rep of 5, 10, and 50. Increasing the number of replicates per line decreases the variance of the phenotypic value for each line.

Combining these factors yielded a total of 1440 individual simulated data sets [3 (N_rep) × 3 (h²) × 4 ($h_f^2$) × 2 (causal model) × 20 (dilution)], which were each replicated 50 times. For each data set and replicate we estimated variance components for the GBLUP and GFBLUP models, using REML. Model fit was assessed using the likelihood-ratio test and model predictive ability using the cross-validation procedure described above. The statistics ${\widehat{h}}_f^2,$ ${\widehat{h}}_r^2,{\widehat{h}}_{\mathrm{GFBLUP}}^2,$ ${\widehat{h}}_{\mathrm{GBLUP}}^2,$ LR, power, and predictive ability were calculated and are summarized in Results.

Detection power:

Power was calculated for each of the simulated scenarios defined in detail above. The P-values used for determining the power of the likelihood-ratio test were calculated based on the theoretical ${\chi }^2$-distribution with 1 d.f. For each of the simulated scenarios, power was calculated as the fraction (of 50 replicates) of the analyses that led to a significantly better model fit using the GFBLUP model compared to using the GBLUP model (i.e., the observed P-value was <0.05).

Data availability

The DGRP data can be accessed via the website at http://dgrp2.gnets.ncsu.edu.

Results

The DGRP genotypes include ∼1.7 million common (minor allele frequencies ≥0.05) SNPs derived from genomic sequences of 205 largely unrelated inbred lines (Mackay et al. 2012; Huang et al. 2014). We evaluated and compared GFBLUP and GBLUP models based on model fit, model predictive ability, and precision of estimated genomic parameters, using both observed genotypes and phenotypes for three quantitative traits in the DGRP (chill coma recovery time, starvation resistance, and startle response) (Mackay et al. 2012; Ober et al. 2012, 2015; Huang et al. 2014) and simulated genotypic and phenotypic data.

GBLUP and GFBLUP analyses in the DGRP

We performed GBLUP and GFBLUP prediction analyses for each of the three traits, using 10-fold cross-validation; i.e., the training data consisted of 90% of the lines and the total genomic value was validated in 10% of the lines. Males and females were analyzed separately.

Predictive ability:

The predictive ability of the GBLUP models was low. The predictive ability of GBLUP for females (males) was 0.055$\pm$0.029 (0.00$\pm$0.032) for chill coma recovery, 0.25$\pm$0.029 (0.27$\pm$0.027) for starvation resistance, and 0.25$\pm$0.033 (0.28$\pm$0.029) for startle response. The low values are not statistically different from those previously reported using fivefold cross-validation GBLUP models, which were 0.24 for starvation resistance and 0.23 for startle response in both sexes (Ober et al. 2012) and 0.1 for female and zero for male chill coma recovery time (Ober et al. 2015). Furthermore, predictive ability for starvation resistance and startle response was not improved using either a Bayesian mixture model that allowed for differential shrinkage estimation of SNP effects or a preselection of markers with the highest absolute additive genetic effect or genetic variance explained (Ober et al. 2012).

Compared to the GBLUP model, several GO terms led to significantly greater predictive abilities of the GFBLUP model (P-value adjusted for multiple tests <0.05), and these terms give novel insights regarding the biology of the traits (Table 1, Table 2, and Supplemental Material, Table S1). Further, the GO term with the highest predictive ability within each trait and sex was significantly higher than the predictive ability obtained from the GBLUP model. For chill coma recovery time, 32 GO terms in females and 16 in males had predictive values that were significantly higher; 7 GO terms were the same for males and females. The top GO term in females was “Rho protein signal transduction,” with a predictive ability of 0.37$\pm$0.022; the top GO term in males was “cell projection assembly,” with a predictive ability of 0.32$\pm$0.023 (Table 1, Table 2, and Table S1). For startle response, 11 GO terms in females and 4 in males had predictive values that were significantly higher; 2 GO terms were the same for males and females. The top GO term in females was “retrograde vesicle-mediated transport, Golgi to ER,” with a predictive ability of 0.52$\pm$0.026; the top GO term in males was “spermatogenesis,” with a predictive ability of 0.47$\pm$0.025 (Table 1, Table 2, and Table S1). For starvation resistance, the top GO term in females was “alpha-glucosidase activity,” with a predictive ability of 0.37$\pm$0.027, but this was not significant after adjusting for multiple tests (Table S1). The top GO term for male starvation resistance, “foregut morphogenesis,” was the only significant GO term for this trait following the multiple-testing correction and had a predictive ability of 0.43$\pm$0.022 (Table S1).

Table 1. Ten most significant predictions for chill coma recovery with the GFBLUP model.

Sex	GO IDa	PAb ± SEMc	Padjd	LRe	Hff	Nsetsg	Gene Ontology term
Female	GO:0007266	0.370 ± 0.022	1.8 × 10−10	11.39	0.31	3,139	Rho protein signal transduction
	GO:0005100	0.365 ± 0.023	4.0 × 10−10	12.67	0.37	3,886	Rho GTPase activator activity
	GO:0007173	0.343 ± 0.026	1.9 × 10−8	15.96	0.92	9,674	Epidermal growth factor receptor signaling pathway
	GO:0030031	0.318 ± 0.027	6.7 × 10−7	11.49	0.74	2,700	Cell projection assembly
	GO:0035160	0.309 ± 0.027	1.5 × 10−6	9.65	0.39	5,011	Maintenance of epithelial integrity; open tracheal system
	GO:0016323	0.299 ± 0.026	2.7 × 10−6	9.13	0.47	7,761	Basolateral plasma membrane
	GO:0035277	0.280 ± 0.027	2.3 × 10−5	11.12	0.56	7,582	Spiracle morphogenesis; open tracheal system
	GO:0007494	0.263 ± 0.025	5.8 × 10−5	8.86	0.58	9,614	Midgut development
	GO:0006406	0.288 ± 0.033	8.3 × 10−5	12.53	0.52	1,530	mRNA export from nucleus
	GO:0005089	0.253 ± 0.026	2.2 × 10−4	9.54	0.67	11,922	Rho guanyl-nucleotide exchange factor activity
Male	GO:0030031	0.316 ± 0.023	6.5 × 10−9	9.26	0.62	2,700	Cell projection assembly
	GO:0035160	0.225 ± 0.030	7.0 × 10−4	6.55	0.29	5,011	Maintenance of epithelial integrity; open tracheal system
	GO:0009612	0.220 ± 0.028	7.0 × 10−4	8.50	0.49	3,140	Response to mechanical stimulus
	GO:0032039	0.191 ± 0.022	1.5 × 10−3	5.61	0.25	561	Integrator complex
	GO:0005100	0.197 ± 0.030	4.6 × 10−3	6.24	0.22	3,886	Rho GTPase activator activity
	GO:0007494	0.176 ± 0.026	1.1 × 10−2	7.09	0.46	9,614	Midgut development
	GO:0007266	0.183 ± 0.031	1.2 × 10−2	5.46	0.18	3,139	Rho protein signal transduction
	GO:0016887	0.175 ± 0.027	1.2 × 10−2	3.73	0.33	3,173	ATPase activity
	GO:0001673	0.181 ± 0.032	1.4 × 10−2	6.22	0.25	334	Male germ cell nucleus
	GO:0003015	0.180 ± 0.031	1.4 × 10−2	4.83	0.43	3,394	Heart process

^aGene Ontology ID.

^bPredictive ability.

^cStandard error of the mean.

^dFalse discovery rate adjusted P-values.

^eLikelihood-ratio statistics.

^fProportion of genomic variance explained by feature.

^gNumber of SNPs within feature.

Table 2. Ten most significant predictions for startle response with the GFBLUP model.

Sex	GO IDa	PAb ± SEMc	Padjd	LRe	Hff	Nsetsg	Gene Ontology term
Female	GO:0006890	0.520 ± 0.026	9.1 × 10−6	7.42	0.39	232	Retrograde vesicle-mediated transport; Golgi to ER
	GO:0007436	0.509 ± 0.026	1.9 × 10−5	8.81	0.70	2,740	Larval salivary gland morphogenesis
	GO:0042826	0.431 ± 0.023	1.2 × 10−2	5.47	0.23	404	Histone deacetylase binding
	GO:0051537	0.433 ± 0.026	1.5 × 10−2	5.56	0.28	683	2 iron; 2 sulfur cluster binding
	GO:0072499	0.432 ± 0.027	1.5 × 10−2	6.44	0.48	4,329	Photoreceptor cell axon guidance
	GO:0008237	0.418 ± 0.022	1.5 × 10−2	4.79	0.48	3,873	Metallopeptidase activity
	GO:0019898	0.426 ± 0.027	1.8 × 10−2	4.70	0.34	1,635	Extrinsic component of membrane
	GO:0051015	0.417 ± 0.025	2.5 × 10−2	4.43	0.49	1,682	Actin filament binding
	GO:0043195	0.412 ± 0.024	2.5 × 10−2	4.08	0.45	5,476	Terminal bouton
Male	GO:0007283	0.473 ± 0.025	7.4 × 10−4	7.21	0.73	6,514	Spermatogenesis
	GO:0007436	0.473 ± 0.025	7.4 × 10−4	6.73	0.50	2,740	Larval salivary gland morphogenesis
	GO:0042331	0.458 ± 0.029	7.2 × 10−3	6.23	0.42	1,574	Phototaxis
	GO:0051537	0.432 ± 0.023	1.3 × 10−2	5.41	0.30	683	2 iron; 2 sulfur cluster binding
	GO:0072499	0.411 ± 0.029	2.3 × 10−2	5.35	0.38	4,329	Photoreceptor cell axon guidance
	GO:0046854	0.401 ± 0.028	3.7 × 10−2	4.92	0.39	842	Phosphatidylinositol phosphorylation
	GO:0035075	0.392 ± 0.025	3.7 × 10−2	3.52	0.26	3,637	Response to ecdysone
	GO:0008152	0.387 ± 0.025	4.2 × 10−2	2.86	0.61	10,912	Metabolic process
	GO:0051015	0.383 ± 0.022	4.2 × 10−2	3.19	0.51	1,682	Actin filament binding
	GO:0045167	0.398 ± 0.031	4.6 × 10−2	4.45	0.35	2,409	Asymmetric protein localization involved in cell fate determination

^aGene Ontology ID.

^bPredictive ability.

^cStandard error of the mean.

^dFalse discovery rate adjusted P-values.

^eLikelihood-ratio statistics.

^fProportion of genomic variance explained by feature.

^gNumber of SNPs within feature.

Genomic parameters:

The range of genomic variance explained by significant feature (${\widehat{h}}_f^2$) was between 31% and 92% for chill coma recovery and between 23% and 70% for startle response in females. Males showed a similar range of ${\widehat{h}}_f^2$ for the latter traits and 45% for starvation resistance (Table 1, Table 2, and Table S1). Notably this range of total genomic variance in females and males was explained by only 0.09–0.7% of the total SNPs for chill coma recovery, 0.01–0.6% for startle response, and 0.2% for starvation resistance. These results suggest that the genomic variance is not evenly distributed throughout the genome (as would be the case if the genetic architecture of the three traits approximated an infinitesimal model), but instead appears to be associated with a subset of the genome annotated with different GO terms for each trait. The genomic parameters estimated using the GFBLUP model allow us to put different weights on the individual genetic marker relationships used in the prediction equations, in contrast to the GBLUP model, which weights each element of the genetic marker relationship equally. However, the genomic heritabilities estimated using GBLUP or GFBLUP are very similar. The estimated genomic heritabilities using GBLUP were moderate and similar for males and females for each trait: 0.41 and 0.45 for chill coma recovery, 0.49 and 0.47 for startle response, and 0.55 and 0.57 for starvation resistance for females and males, respectively. In the GFBLUP model analyses, the overall genomic heritability (${\widehat{h}}_{\mathrm{GFBLUP}}^2$), within trait and sex, was similar across all the GO terms used for partitioning the genomic variance.

GBLUP and GFBLUP analyses of simulated data based on DGRP genotypes

The GBLUP and GFBLUP models were compared using simulated data in terms of model fit, model predictive ability, and accuracy of the estimated genomic parameters. The power to detect the genomic feature affecting trait phenotypes was determined based on a likelihood-ratio test (i.e., testing whether the GFBLUP model provides a better fit than the GBLUP model). The simulated data sets were based on the observed DGRP genotypes. We varied several feature- and trait-specific factors that are likely to influence the accuracy of parameter estimates and predictive ability.

Estimation of genomic parameters:

Estimates of genomic heritability (${\widehat{h}}_{\mathrm{G}}^2$and ${\widehat{h}}_{\mathrm{GF}}^2$) were unbiased in all simulation scenarios for both the GBLUP and GFBLUP models (Figure 1). Estimates for GBLUP were centered on the true values of genomic heritability with a similar level of accuracy to that of GFBLUP (results not shown). Increasing the proportion of noncausal SNPs in the genetic marker set defined by the genomic feature (dilution) led to decreased accuracy (larger variance) and bias of the estimated genomic parameters ${\widehat{h}}_f^2$ and ${\widehat{h}}_r^2$ (Figure 1). This pattern was observed in all simulation scenarios. To illustrate, for the case where the genomic heritability was 50% and the genomic feature explained 30% of the genomic variance (i.e., $h^2$ = 0.5 and $h_f^2$ = 0.3) the estimated value ${\widehat{h}}_f^2$ was centered on the true value at a lower level of dilution. However, the standard deviation increased from 0.092 to 0.15 and we observed a downward bias following dilution (with 2000 noncausal SNPs). A similar pattern was observed for ${\widehat{h}}_r^2$ (i.e., the proportion of genomic variance captured by genetic markers not included in the genomic feature) except that the estimates tended to be biased upward.

Figure 1.

Boxplots showing estimates from the GFBLUP model analyses of genomic parameters as a function of the proportion of noncausal SNPs in the genomic feature (dilution). Estimates are proportion of genomic variance captured by the genetic markers in the genomic feature ($h_f^2$ = 0.1, 0.3, or 0.5), proportion of genomic variance captured by genetic markers not included in the genomic feature ($h_r^2$ = 0.9, 0.7, or 0.5), and genomic heritability ($h^2$ = 0.5). Results are for the scenarios where the causal SNPs in the genomic feature are clustered in certain genome regions, adding noncausal SNPs located directly up- and downstream of the causal SNPs, and the number of replicates within lines = 50. The light line with light shading corresponds to the true genomic parameter.

Predictive ability:

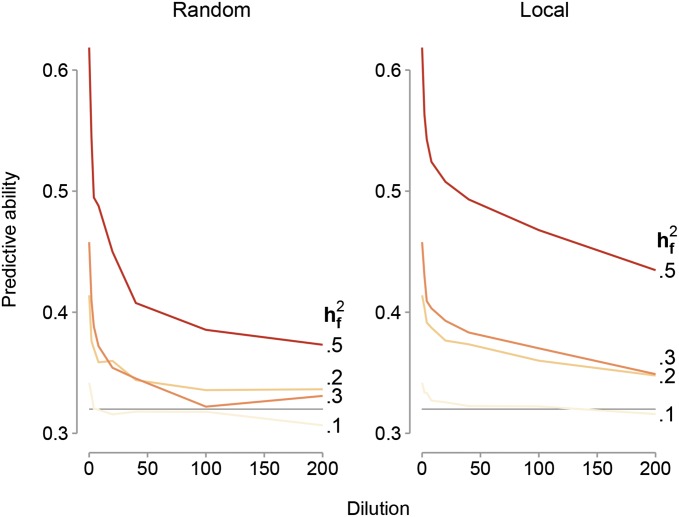
GFBLUP had higher predictive ability (up to 0.62) than GBLUP (0.32 in all scenarios), provided the proportion of the genomic variance explained by the genomic feature was high, with few noncausal SNPs included (Figure 2). The predictive ability of the GFBLUP model is positively correlated with the proportion of genomic variance explained by the genomic feature and negatively correlated with increased dilution (Figure 2). Our results for a genomic heritability of 50% illustrate the general patterns observed across the different simulation scenarios. When the feature explains 10% of the genomic variance, the predictive ability is 0.34 if there is no dilution. Increasing $h_f^2$ from 0.2 to 0.3 to 0.5 increases the predictive ability from 0.42 to 0.46 until a maximum of 0.62 (twice the value obtained using GBLUP). The first dilution, adding 100 noncausal SNPs, has the most prominent effect on predictive ability for all the tested levels of $h_f^2.$ Thereafter predictive ability of the GFBLUP model rapidly declines toward the predictive ability obtained using the GBLUP model. The predictive ability was slightly higher if causal SNPs in the genomic feature were clustered in smaller genome regions rather than distributed randomly across the genome. For both models, predictive abilities were generally independent of the level of genomic heritability ($h^2$ = 0.1, 0.3, or 0.5) and the number of replicates within line (N_rep = 5, 10, or 50).

Figure 2.

Plots showing predictive ability of the GFBLUP model as a function of the proportion of noncausal SNPs in the genomic feature (dilution). Results are for four different levels of the proportion of genomic variance captured by the genetic markers in the genomic feature ($h_f^2$ = 0.1, 0.2, 0.3, or 0.5) for the scenarios where the causal SNPs in the genomic feature are clustered in smaller genome regions, adding noncausal SNPs picked at random in the genome (left) or located directly up- and downstream of the causal SNPs (right), and the number of replicates within lines = 50. The light gray line corresponds to the predictive ability of the GBLUP model.

Detection power:

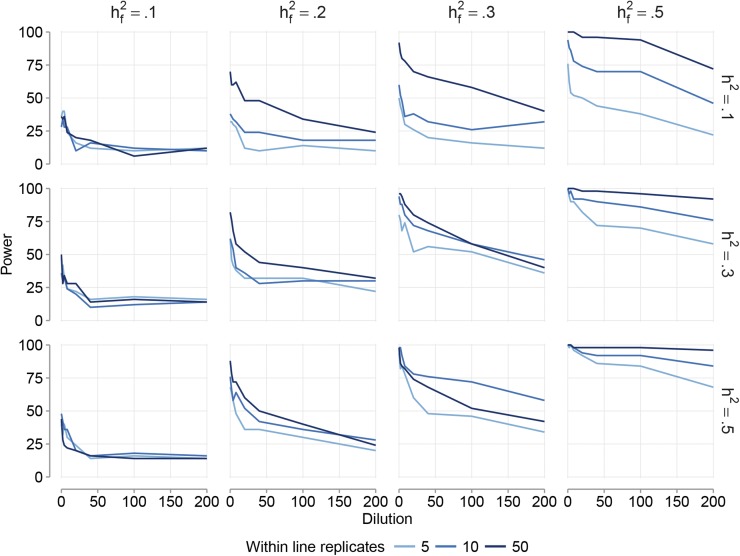
The power to detect genomic features affecting the trait phenotypes was influenced both by trait-specific and by genomic feature-specific factors. The proportion of the genomic variance explained by the genomic feature ($h_f^2$) greatly affected detection power (Figure 3) and robustness to dilution. At low values ($h_f^2$ = 0.1), the power to detect the genomic features was low if the overall trait heritability was low (h² = 0.1), even without dilution. At the highest values ($h_f^2$ = 0.5) the impact of dilution was less severe. This increased robustness to dilution resulted in power >72% in all cluster model scenarios with N_rep = 50 replicates within line and a genomic heritability of 50%. The level of genomic heritability (h²) was positively correlated with power (Figure 3). However, at high $h_f^2$ and in the absence of dilution, all genomic features were detected regardless of overall genomic heritability. Furthermore, if $h_f^2$ was high, high heritability traits were less affected by dilution than low heritability traits (Figure 3). Dilution decreased power in all simulation scenarios (Figure 3). Furthermore, detection power increases with increasing numbers of replicates within line (N_rep = 5, 10, or 50).

Figure 3.

Plots showing detection power of the GFBLUP model as a function of the proportion of noncausal SNPs in the genomic feature (e.g., dilution by adding noncausal SNPs located directly up- and downstream of the causal SNPs). Results are for the scenarios where the causal SNPs in the genomic feature are clustered in certain genome regions for three different levels of genomic heritability ($h^2$= 0.1, 0.3, or 0.5), four different levels of the proportion of genomic variance captured by the genetic markers in the genomic feature ($h_f^2$ = 0.1, 0.2, 0.3, or 0.5), and three different levels of the number of replicates within lines (N_rep = 5, 10, or 50).

Genomic relationships:

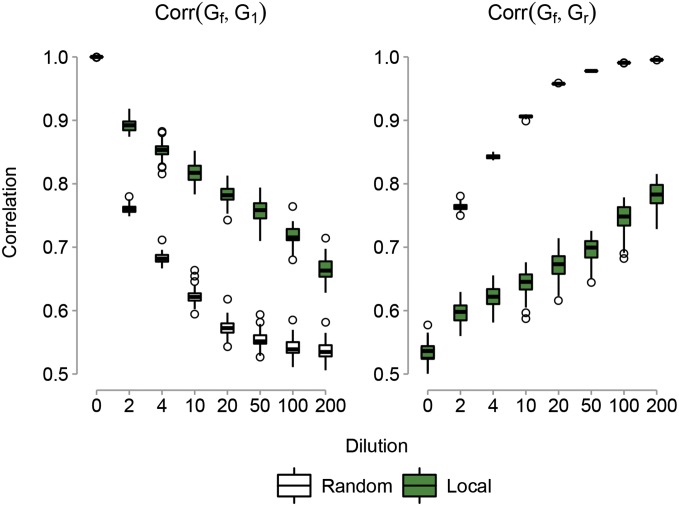
Estimation of genomic parameters, detection power, and predictive ability using the GFBLUP model analyses were based on two genomic relationship matrices: G_f for the genetic marker set defined by the genomic feature and G_r for the remaining set of markers. These “fitted” genomic relationships differ from the true causal relationships that in practice are unknown. Dilution of the true causal relationship by increasing the proportion of noncausal SNPs in the genomic feature decreases the correlation between G_f (the genomic relationships calculated using all genetic markers defined by the genomic feature including causal and noncausal SNPs) and G₁ (the true causal genomic relationships calculated using only the true causal SNPs in the genomic feature). If the true causal SNPs are clustered in a smaller number of genome regions, then the effect of dilution is more “extreme” (Figure 4). The correlation between G_f and G₁ for the clustered causal model quickly decreases as dilution with local (or random) noncausal SNPs increases, leveling off at a value of 0.71 (0.56). In contrast, dilution leads to an increasing correlation between G_f and G_r (the genomic relationships for the set of markers not included in the feature) (Figure 4). For G_f comprising only true causal SNPs, the correlation between G_f and G_r is 0.53 for the cluster causal model. Following dilution of G_f with local (or random) noncausal SNPs, the correlation rapidly increases toward a value of 0.75 (0.99).

Figure 4.

Boxplots showing correlations between different genomic relationship matrices used in the GFBLUP model analyses as a function of the proportion of noncausal SNPs in the genomic feature (dilution). Correlations are between G_f (the genomic relationships calculated using all genetic markers defined by the genomic feature including causal and noncausal SNPs) and G₁ (the true causal genomic relationships calculated using only the true causal SNPs in the genomic feature) or between G_f and G_r (the genomic relationships for the set of markers not included in the feature). Correlations are for the scenarios where the causal SNPs in the genomic feature are clustered in smaller genome regions and adding noncausal SNPs picked at random in the genome (Random) or located directly up- and downstream of the causal SNPs (Local).

Discussion

We applied and evaluated a GFBLUP model, using prior information on genomic features. Genomic features are regions of the genome that are linked to external information. This modeling approach is predicated on the assumption that these regions are enriched for causal variants affecting the trait. Several genomic feature classes can be formed based on different sources of prior information, for example, genes, chromosomes, biological pathways, gene ontologies, sequence annotation, prior QTL regions, or other types of external evidence. We demonstrated that the GFBLUP model using prior information on Gene Ontology categories can increase the predictive ability of the genomic value for three quantitative traits (starvation resistance, startle response, and chill coma recovery) in D. melanogaster. These results were supported by using simulated data generated from DGRP genotypes, further illustrating the impact of trait-specific and genomic feature-specific factors on predictive ability.

The GFBLUP model improves predictive ability in the DGRP

The increase in predictive ability using the GFBLUP model compared to the commonly used GBLUP model was substantial for all traits and both sexes. For females (males) the increase was 0.12 (0.16) for starvation resistance, 0.27 (0.19) for startle response, and 0.33 (0.32) for chill coma recovery time. These differences between the two models correspond to a 48–89% relative increase in predictive ability of genomic values for startle response and starvation resistance and even higher for chill coma recovery time. Our predictive ability using GBLUP was similar to estimates from previous studies (Ober et al. 2012, 2015). Predictive ability using GBLUP decreased when smaller numbers of markers were used; for example, the predictive ability for starvation resistance and startle response dropped to 0.1 when 4863 randomly selected markers were used (Ober et al. 2012). In contrast, the highest-ranked GO term for chill coma recovery in females was associated with a predictive ability of 0.37, using only 3129 markers. We hypothesize that the difference in predictive ability between the two models is that the assumption of the GBLUP model, that the genomic variance is evenly distributed throughout the genome (i.e., the underlying genetic architecture of the trait approaches an infinitesimal model), is not met. Rather, the genomic variance for the three traits assessed seems to be associated with subsets of the genome annotated with specific biological processes that differ among the traits. The markers located in these genome regions have greater weights than the remaining markers in the GFBLUP model analyses, leading to increased predictive ability. Note that the genetic marker relationship matrix used for the GBLUP model is the same for all traits, because of the underlying infinitesimal model assumption of genetic architecture. However, the GFBLUP model permits a different genetic architecture for each of these (genetically uncorrelated) traits, which is more biologically plausible.

Our empirical results were further supported by simulation studies investigating the influence of genomic feature- and trait-specific factors on the predictive ability of GFBLUP. The simulations revealed that it is possible, even under an additive genetic model, to further increase the predictive ability of genomic value for quantitative traits in the DGRP, using the GFBLUP model. This requires that prior information on genomic features highly enriched for causal variants is used. Such information is rapidly becoming available and being refined, given advances in functional and genetic studies of complex traits that continue to increase our understanding of how the putative causal variants are distributed over the genome. Furthermore, improvement in predictive ability for genomic value of complex trait phenotypes may be achieved by accounting for other types of genetic variation due to different types of variants (rare and structural) and nonadditive gene action (dominance and epistasis).

Genomic features predictive of organismal quantitative trait phenotypes:

Several of the high-ranking GO terms in our study have previously been associated with correlated transcriptional modules associated with chill coma recovery time and starvation resistance (Ayroles et al. 2009). These modules are plausibly enriched for causal variants affecting the phenotype (Cookson et al. 2009) that could affect expression of the genes in the module, such as mutations in promoter motifs, transcription enhancers, or silencers in introns or regulatory microRNAs. In addition, if the gene products of the differentially expressed genes are associated with the phenotype, variants that change the structure of the expressed RNA and the transcribed protein could also affect the phenotype.

The GO terms Rho protein signal transduction (GO:0007266) and Rho GTPase activator activity (GO:0005100) had the highest prediction accuracies for male and female chill coma recovery time. There are several ways in which Rho genes may functionally affect the time to recover from a chill-induced coma. Rho proteins function as molecular switches, conducting cues from the external environment to intracellular signal transduction pathways (Tcherkezian and Lamarche-Vane 2007). In addition, members of the Rho family of GTPases are among the important modulators of actin dynamics and neuronal as well as behavioral plasticity. By playing a role in the regulation of actin, these proteins are important in mediating the circadian rhythm and other behaviors in Drosophila (Rao 2013); and circadian rhythm in turn has been associated with chill coma recovery time (Pegoraro et al. 2014). Rho activity also plays a role in the maintenance of ion homeostasis. Chill coma is the result of an inability to maintain ion homeostasis (MacMillan and Sinclair 2011), particularly extracellular [K⁺], and an additional effect of low temperature (Findsen et al. 2014). A RHO activator has been linked to the regulation of [K⁺] channel cell surface expression and thus activity in human cell cultures (Stirling et al. 2009). Finally, analyses of whole-genome sequences of DNA pools from Drosophila populations collected along the North American East Coast reveal patterns of selection in genes involved in major functional pathways such as circadian rhythm and the epidermal growth factor pathway (Fabian et al. 2012), genes in both of which harbor variants that are predictive of chill coma recovery in our study. These examples highlight a possible direct functional link between Rho protein activity and chill coma recovery that can be tested in the future. Similar hypotheses can be developed for the other GO terms that are predictive of the traits investigated.

Genomic feature classes helping biological interpretation:

Applying the GFBLUP model using prior information on genomic features may help open the black box that is the genetic architecture of complex traits. This approach provides novel insight into the biological mechanisms causing trait variation and simultaneously improves predictive ability relative to a commonly used prediction model. Several genomic feature classes can be formed based on different sources of prior information (e.g., genes, chromosomes, biological pathways, gene ontologies, sequence annotation, prior QTL regions, or other types of external evidence). The gain in knowledge depends highly on the quality and complexity of the genomic feature classification scheme upon which the genetic marker sets are based. Genomic features based on physical genome regions, such as chromosomes or single genes, might not increase the information level; however, as additional layers of complexity such as pathways are added, the biological interpretation might become more informative. On the other hand, biological interpretation might be hampered by the definition (or misspecification) of the genomic feature and a potential large overlap in the genetic marker sets between the different genomic feature classes. In the latter case, biological interpretation may be improved by using methods that take the overlap into account (Skarman et al. 2012).

Factors influencing GFBLUP model performance

The simulation study clarified the conditions needed to make genomic partitioning “work” (i.e., harvest the benefits from prior information in terms of model fit and predictive ability). The simulations showed that a GFBLUP model can increase predictive ability compared to a standard GBLUP model, highlighted the importance of maximizing the proportion of causal variants in G_f (and G_r), and indicated some limitations of the GFBLUP modeling approach.

Predictive ability of the GFBLUP model is influenced both by the proportion of genomic variance explained by the genomic feature and by the addition of noncausal SNPs in the feature (dilution). Predictive ability (and detection power) was positively correlated with the proportion of genomic variance explained by the genomic feature and negatively correlated with dilution. Estimates of the proportion of genomic variance explained by the genomic feature (${\widehat{h}}_f^2$) were generally unbiased. However, increased dilution led to decreased accuracy (a larger variance) of the estimated genomic parameters ${\widehat{h}}_f^2$ and ${\widehat{h}}_r^2.$ It is important to note that models were compared based on their ability to predict the genomic values (and not phenotypes). Therefore, the predictive abilities reported in this study were generally independent of the level of genomic heritability and the number of replicates within lines. If we were to predict the trait phenotypes, we would expect an influence of these trait-specific factors on predictive ability, as was the case for detection power.

The GFBLUP model is mos beneficial when the genomic feature is highly enriched for true causal variants. To better understand this phenomenon, it is useful to examine the details of the GFBLUP model. The estimation of genomic parameters in the GFBLUP model was based on two genomic relationship matrices, G_f for the genetic marker set defined by the genomic feature and G_r for the remaining set of markers. The decrease in accuracy of genomic parameter estimates following dilution is caused by the increased correlation between these two genomic relationship matrices. The high correlation between the elements in these matrices makes it difficult for the REML method to estimate and thereby reliably partition the corresponding genomic variances (${\widehat{\sigma }}_f^2\hspace{0.5em}\text{and}\hspace{0.5em}{\widehat{\sigma }}_r^2$). It is also clear from the BLUP equations used in the GFBLUP model (described in Materials and Methods) that inaccurate estimates of genomic variances would affect predictive ability. The estimates of ${\widehat{\sigma }}_f^2\hspace{0.5em}\text{and}\hspace{0.5em}{\widehat{\sigma }}_r^2$ determine the relative contribution of the two genomic relationship matrices in the prediction of the total genomic value. If these estimates deviate from the true value of the parameters, it will lead to less accurate predictions, because there is too much weight on the “wrong” genomic relationships in the prediction equations. Obviously this will also occur if the two genomic relationships differ from the true causal relationships.

In this study we used a GFBLUP model with two genomic effects (f and r in model M_GFBLUP), but in principle it is possible to include multiple genomic feature effects (Speed and Balding 2014; Sørensen et al. 2015). However, as our simulations with only two genomic effects indicate, the complex correlation patterns that are likely to exist between different parts of the genome may lead to inaccurate estimates of the genomic variances and consequently decreased predictive ability. It would also explain why GFBLUP sometimes led to a decrease in predictive ability. GBLUP depends only on the total genomic variance parameter that is reliably estimated and therefore more robust. The linear mixed model used by Gusev et al. (2014) is very similar to our approach. In their analyses they fitted multiple random genomic effects defined by sequence ontologies. They found little improvement in polygenic risk prediction using their model and argue this is because of pervasive LD across categories (e.g., feature classes). This is exactly what we observe in our simulations—when the correlation between the two (or more) genomic relationship matrices is high, we cannot reliably estimate the variance components and therefore there is no improvement in predictive ability.

Predictive ability and genetic relatedness in the study population:

The extent to which utilizing prior biological information will increase the predictive ability of the statistical model depends on the degree of genetic relatedness among the individuals in the mapping population (de los Campos et al. 2013). In a population of highly related individuals the general genomic relationship will be a good approximation for the genomic relationship at the true causal variants. Our results indicate that using an informed choice of subsets of markers with the GBLUP model increases the predictive ability in a population of largely unrelated individuals. In such situations it is important to model the genomic relationship due to the causal variants differently from the overall genomic relationship. Thus the GFBLUP model may also be useful in improving predictive ability in other situations where individuals are largely unrelated, such as human populations and across animal breeds and plant strains. Further work is required to better understand the impact of varying degrees of genetic relatedness on the performance of the GFBLUP model.

GFBLUP model and alternatives

GFBLUP is based on a linear mixed-modeling framework that allows us to adjust for other known genetic and nongenetic factors. In this study we implemented the GFBLUP model, using a REML method (Gusev et al. 2014; Sørensen et al. 2014; Speed and Balding 2014). Bayesian mixture models ignoring prior genomic feature information such as BayesB or BayesR (Meuwissen et al. 2009; Erbe et al. 2012) are relevant alternative methods. Both of these methods allow the contribution from each marker to come from different distributions. However, these models are not necessarily computationally less demanding; they require the same considerations with regard to formulating the models and do not necessarily perform better (Ober et al. 2012). This study adds evidence that an externally informed subset of markers is necessary for a successful partitioning of the genomic variance, as the data themselves may not necessarily indicate which markers should have greater weights. Whereas Bayesian mixture models attempt to assign and estimate marker effects from different distributions, we use prior knowledge to assign a marker set (defined by the genomic feature) to a distribution [i.e., $\mathit{f}\sim N\left(0,{\mathit{G}}_{\mathit{f}}{\sigma }_f^2\right)$ and $\mathit{r}\sim N\left(0,\mathit{G}{\sigma }_r^2\right)$]. We then estimate the parameters for these distributions (${\sigma }_f^2$ and ${\sigma }_r^2$) conditional on the observed data and evaluate whether this is a sensible assignment, using standard model comparison techniques such as cross-validations or likelihood-ratio tests. We therefore conclude that the GFBLUP approach described here provides a general framework for estimating and evaluating the association of genomic features with complex trait phenotypes.

The GFBLUP model can be implemented using a Bayesian mixed model (e.g., Sørensen et al. 2015) or Bayesian mixture models such as BayesRC (MacLeod et al. 2014). BayesRC is the same as BayesR except that, a priori, each SNP is identified as belonging to a specific genomic feature and it allows for differential shrinkage within each genomic feature. The advantage of the BayesRC approach is in cases where enough information is available in the data to reliably allocate the SNPs in the different variance classes defined in the Bayesian mixture model. If this is not the case, we do not expect a major difference in performance in terms of predictive ability.

A key element of the GFBLUP and Bayesian GF mixture models is the use of prior information to reliably partition the genomic variance. These approaches are computationally intensive. However, there are computationally simple approaches to obtain approximate measures of genomic variance (heritability), using only genome-wide association (GWA) summary statistics (Finucane et al. 2015). In this approach, genomic variance is partitioned using single-marker effects obtained from GWA and LD information from a population similar to the one used for obtaining the single-marker effects. In contrast, partitioning of genomic variance using the GFBLUP model requires both the phenotypes and genotypes of the study population. The approximate measures of genomic variance obtained for each genomic feature in the Finucane et al. (2015) study can in principle also be used in the GFBLUP prediction equations or as prior scale parameters in Bayesian models, but was not pursued in their study.

Conclusion

Our GFBLUP modeling approach using prior information on genomic features enriched for causal variants can increase the accuracy of genomic predictions for complex traits in a population of largely unrelated individuals. The simulations revealed that it is possible to further increase the accuracy of genomic prediction for complex traits with a quasi-infinitesimal genetic architecture with many causal polymorphisms each with a small effect, using the GFBLUP model, provided that prior information on genomic features is highly enriched for causal variants. These models provide a formal statistical modeling framework for borrowing and evaluating information across a wide range of experimental studies that may help provide novel insights into genetic and biological mechanisms underlying complex traits.