Simple Penalties on Maximum-Likelihood Estimates of Genetic Parameters to Reduce Sampling Variation

Abstract

Multivariate estimates of genetic parameters are subject to substantial sampling variation, especially for smaller data sets and more than a few traits. A simple modification of standard, maximum-likelihood procedures for multivariate analyses to estimate genetic covariances is described, which can improve estimates by substantially reducing their sampling variances. This is achieved by maximizing the likelihood subject to a penalty. Borrowing from Bayesian principles, we propose a mild, default penalty—derived assuming a Beta distribution of scale-free functions of the covariance components to be estimated—rather than laboriously attempting to determine the stringency of penalization from the data. An extensive simulation study is presented, demonstrating that such penalties can yield very worthwhile reductions in loss, i.e., the difference from population values, for a wide range of scenarios and without distorting estimates of phenotypic covariances. Moreover, mild default penalties tend not to increase loss in difficult cases and, on average, achieve reductions in loss of similar magnitude to computationally demanding schemes to optimize the degree of penalization. Pertinent details required for the adaptation of standard algorithms to locate the maximum of the likelihood function are outlined.

ESTIMATION of genetic parameters, i.e., partitioning of phenotypic variation into its causal components, is one of the fundamental tasks in quantitative genetics. For multiple characteristics of interest, this involves estimation of covariance matrices due to genetic, residual, and possibly other random effects. It is well known that such estimates can be subject to substantial sampling variation. This holds especially for analyses comprising more than a few traits, as the number of parameters to be estimated increases quadratically with the number of traits considered, unless the covariance matrices of interest have a special structure and can be modeled more parsimoniously. Indeed, a sobering but realistic view is that “Few datasets, whether from livestock, laboratory or natural populations, are of sufficient size to obtain useful estimates of many genetic parameters” (Hill 2010, p. 75). This not only emphasizes the importance of appropriate data, but also implies that a judicious choice of methodology for estimation—which makes the most of limited and precious records available—is paramount.

A measure of the quality of an estimator is its “loss,” i.e., the deviation of the estimate from the true value. This is an aggregate of bias and sampling variation. We speak of improving an estimator if we can modify it so that the expected loss is lessened. In most cases, this involves reducing sampling variance at the expense of some bias—if the additional bias is small and the reduction in variance sufficiently large, the loss is reduced. In statistical parlance “regularization” refers to the use of some kind of additional information in an analysis. This is often used to solve ill-posed problems or to prevent overfitting through some form of penalty for model complexity; see Bickel and Li (2006) for a review. There has been longstanding interest, dating back to Stein (1975) and earlier (James and Stein 1961), in regularized estimation of covariance matrices to reduce their loss. Recently, as estimation of higher-dimensional matrices is becoming more ubiquitous, there has been a resurgence in interest (e.g., Bickel and Levina 2008; Warton 2008; Witten and Tibshirani 2009; Ye and Wang 2009; Rothman et al. 2010; Fisher and Sun 2011; Ledoit and Wolf 2012; Deng and Tsui 2013; Won et al. 2013). In particular, estimation encouraging sparsity is an active field of research for estimation of covariance matrices (e.g., Pourahmadi 2013) and in related areas, such as graphical models and structural equations.

Improving Estimates of Genetic Parameters

As emphasized above, quantitative genetic analyses require at least two covariance matrices to be estimated, namely due to additive genetic and residual effects. The partitioning of the total variation into its components creates substantial sampling correlations between them and tends to exacerbate the effects of sampling variation inherent in estimation of covariance matrices. However, most studies on regularization of multivariate analyses considered a single covariance matrix only and the literature on regularized estimates of more than one covariance matrix is sparse. In a classic article, Hayes and Hill (1981) proposed to modify estimates of the genetic covariance matrix $\left({\mathbf{\Sigma }}_{\mathrm{G}}\right)$ by shrinking the canonical eigenvalues of ${\mathbf{\Sigma }}_{\mathrm{G}}$ and the phenotypic covariance matrix $\left({\mathbf{\Sigma }}_{\mathrm{P}}\right)$ toward their mean, a procedure described as “bending” the estimate of ${\mathbf{\Sigma }}_{\mathrm{G}}$ toward that of ${\mathbf{\Sigma }}_{\mathrm{P}}.$ The underlying rationale was that ${\mathbf{\Sigma }}_{\mathrm{P}},$ the sum of all the causal components, is typically estimated much more accurately than any of its components, so that bending would “borrow strength” from the estimate of ${\mathbf{\Sigma }}_{\mathrm{P}},$ while shrinking estimated eigenvalues toward their mean would counteract their known, systematic overdispersion. The authors demonstrated by simulation that use of “bent” estimates in constructing selection indexes could increase the achieved response to selection markedly, as these were closer to the population values than unmodified estimates and thus provided more appropriate estimates of index weights. However, no clear guidelines to determine the optimal amount of shrinkage to use were available and bending was thus primarily used only to modify nonpositive definite estimates of covariance matrices and all but forgotten when methods that allowed estimates to be constrained to the parameter space became common procedures.

Modern analyses to estimate genetic parameters are generally carried out fitting a linear mixed model and using restricted maximum-likelihood (REML) or Bayesian methodology. The Bayesian framework directly offers the opportunity for regularization through the choice of appropriate priors. Yet, this is rarely exploited for this purpose and “flat” or minimally informative priors are often used instead (Thompson et al. 2005). In a maximum-likelihood context, estimates can be regularized by imposing a penalty on the likelihood function aimed at reducing their sampling variance. This provides a direct link to Bayesian estimation: For a given prior distribution of the parameters of interest or functions thereof, an appropriate penalty can be obtained as a multiple of minus the logarithmic value of the probability density function. For instance, shrinkage of eigenvalues toward their mean through a quadratic penalty on the likelihood is equivalent to assuming a normal distribution of the eigenvalues while the assumption of a double exponential prior distribution results in a LASSO-type penalty (Huang et al. 2006).

Meyer and Kirkpatrick (2010) demonstrated that a REML analog to bending is obtained by imposing a penalty proportional to the variance of the canonical eigenvalues on the likelihood and showed that this can yield substantial reductions in loss for estimates of both ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}},$ the residual covariance matrix. Subsequent simulations (Meyer et al. 2011; Meyer 2011) examined the scope for penalties based on different functions of the parameters to be estimated and prior distributions for them and found them to be similarly effective, depending on the population values for the covariance matrices to be estimated.

A central component of the success of regularized estimation is the choice of how much to penalize. A common practice is to scale the penalty by a so-called “tuning factor” to regulate stringency of penalization. Various studies (again for a single covariance matrix, see above) demonstrated that this can be estimated reasonably well from the data at hand, using cross-validation techniques. Adopting these suggestions for genetic analyses and using k-fold cross-validation, Meyer (2011) estimated the appropriate tuning factor as that which maximized the average, unpenalized likelihood in the validation sets. However, this procedure was laborious and afflicted by problems in locating the maximum of a fairly flat likelihood surface for analyses involving many traits and not so large data sets. These technical difficulties all but prevented practical applications so far. Moreover, it was generally less successful than reported for studies considering a single covariance matrix. This led to the suggestion of imposing a mild penalty, determining the tuning factor as the largest value that did not cause a decrease in the (unpenalized) likelihood equivalent to a significant change in a single parameter. This pragmatic approach yielded reductions in loss that were generally of comparable magnitude to those achieved using cross-validation (Meyer 2011). However, it still required multiple analyses and thus considerably increased computational demands compared to standard, unpenalized estimation.

Simple Penalties

In the Bayesian framework, the influence of the prior and thus the amount of regularization is generally specified through the so-called hyperparameters of the prior distribution, which determine its shape, scale, or location. This suggests that an alternative, tuning factor-free formulation for a penalty on the likelihood can be obtained by expressing it in terms of the distribution-specific (hyper)parameters. For instance, when assuming a normal prior for canonical eigenvalues, the regulating parameter is the variance of the normal distribution, with more shrinkage induced the lower its value. This may lend itself to applications employing default values for these parameters. Furthermore, such formulation may facilitate direct estimation of the regulating parameter, denoted henceforth as ν, simultaneously with the covariance components to be estimated (G. de los Campos, personal communication). In contrast, in a setting involving a tuning factor the penalized likelihood is, by definition, highest for a factor of zero (i.e., no penalty) and thus does not provide this opportunity.

Aims

This article examines the scope for REML estimation imposing penalties regulated by choosing the parameters of the selected prior distribution. Our aim is to obtain a formulation that allows uncomplicated use on a routine basis, free from laborious and complicated additional calculations, to determine the appropriate strength of penalization. It differs from previous work such that we do not strive to obtain maximum benefits, but are content with lesser—but still highly worthwhile—improvements in estimates that can be achieved through mild penalties, at little risk of detrimental effects for unusual cases where the population parameters do not match our assumptions for their prior distributions well. The focus is on penalties involving scale-free functions of covariance components that fall into defined intervals and are thus better suited to a choice of default-regulating parameters than functions that do not.

We begin with the description of suitable penalties together with a brief review of pertinent literature and outline the adaptation of standard REML algorithms. This is followed by a large-scale simulation study showing that the penalties proposed can yield substantial reductions in loss of estimates for a wide range of population parameters. In addition, the impact of penalized estimation is demonstrated for a practical data set, and the implementation of the methods proposed in our REML package wombat is described. We conclude with a discussion and recommendations on selection of default parameters for routine use in multivariate analyses.

Penalized Maximum-Likelihood Estimation

Consider a simple mixed, linear model for q traits with covariance matrices ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}}$ due to additive genetic and residual effects, respectively, to be estimated. Let $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ denote the log-likelihood in a standard, unpenalized maximum-likelihood (or REML) analysis and $\mathit{\theta }$ denote the vector of parameters, composed of the distinct elements of ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}}$ or the equivalent. The penalized likelihood is then (Green 1987)

$$\log {\mathrm{ℒ}}_P\left(\mathit{\theta }\right)=\log \mathrm{ℒ}\left(\mathit{\theta }\right)-\frac{1}{2}\psi \mathcal{P}\left(\mathit{\theta }\right)$$ (1)

with the penalty $\mathcal{P}\left(\mathit{\theta }\right)$ a nonnegative function of the parameters to be estimated and ϕ the so-called tuning factor that modulates the strength of penalization (the factor of 1/2 is used for algebraic consistency and could be omitted).

The penalty can be derived by assuming a suitable prior distribution for the parameters $\mathit{\theta }$ (or functions thereof) as minus the logarithmic value of the pertaining probability density. As in Bayesian estimation, the choice of the prior is often somewhat ad hoc or driven by aspects of convenience (such as conjugacy of the priors) and computational feasibility. In the following, we assume $\psi =1$ throughout and regulate the amount of penalization instead via the parameters of the distribution from which the penalty is derived.

Functions to be penalized

We consider two types of scale-free functions of the covariance matrices to be estimated as the basis for regularization.

Canonical eigenvalues:

Following Hayes and Hill (1981), the first type comprises the canonical eigenvalues of ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{P}}={\mathbf{\Sigma }}_{\mathrm{G}}+{\mathbf{\Sigma }}_{\mathrm{E}}.$

Multivariate theory shows that for two symmetric, positive definite matrices of the same size there is a transformation that yields $\mathit{T}{\mathit{T}}^{\prime }={\mathbf{\Sigma }}_{\mathrm{P}}$ and $\mathit{T}\mathbf{\Lambda }{\mathit{T}}^{\prime }={\mathbf{\Sigma }}_{\mathrm{G}},$ with $\mathbf{\Lambda }$ the diagonal matrix of canonical eigenvalues with elements ${\lambda }_i$ (Anderson 1984). This can be thought of as transforming the traits considered to new variables that are uncorrelated and have phenotypic variance of unity; i.e., the canonical eigenvalues are equal to heritabilities on the new scale and fall in the interval $\left[0,1\right]$ (Hayes and Hill 1980). It is well known that estimates of eigenvalues of covariance matrices are systematically overdispersed—the largest values are overestimated and the smallest are underestimated—while their mean is expected to be estimated correctly (Lawley 1956). Moreover, a major proportion of the sampling variation of covariance matrices can be attributed to this overdispersion of eigenvalues (Ledoit and Wolf 2004). Hence there have been various suggestions to modify the eigenvalues of sample covariance matrices in some way to reduce the loss in estimates; see Meyer and Kirkpatrick (2010) for a more detailed review.

Correlations:

The second type of functions comprises correlations between traits, in particular genetic correlations. A number of Bayesian approaches to the estimation of covariance matrices decompose the problem into variances (or standard deviations) and correlations with separate priors, thus alleviating the inflexibility of the widely used conjugate prior given by an inverse Wishart distribution (Barnard et al. 2000; Daniels and Kass 2001; Zhang et al. 2006; Daniels and Pourahmadi 2009; Hsu et al. 2012; Bouriga and Féron 2013; Gaskins et al. 2014). However, overall few suitable families of prior density functions for correlation matrices have been considered and practical applications have been limited. In particular, estimation using Monte Carlo sampling schemes has been hampered by difficulties in sampling correlation matrices conforming to the constraints of positive definiteness and unit diagonals.

Most statistical literature concerned with Bayesian or penalized estimation of correlation matrices considered shrinkage toward an identity matrix, i.e., shrinkage of individual correlations toward zero, although other, simple correlation structures have been proposed (Schäfer and Strimmer 2005). As outlined above, the motivation for bending (Hayes and Hill 1981) included the desire to borrow strength from the estimate of the phenotypic covariance matrix. Similar arguments may support shrinkage of the genetic toward the phenotypic correlation matrix. This dovetails with what has become known as “Cheverud’s conjecture”: Reviewing a large body of literature, Cheverud (1988) found that estimates of genetic correlations were generally close to their phenotypic counterparts and thus proposed that phenotypic values should be substituted when genetic correlations could not be estimated. Subsequent studies reported similar findings for a range of traits in laboratory species, plants, and animals (e.g., Koots et al. 1994; Roff 1995; Waitt and Levin 1998).

Partial correlations

Often a reparameterization can transform a constrained matrix problem to an unconstrained one. For instance, it is common practice in REML estimation of covariance matrices to estimate the elements of their Cholesky factors, coupled with a logarithmic transformation of the diagonal elements, to remove constraints on the parameter space (Meyer and Smith 1996). Pinheiro and Bates (1996) examined various transformations for covariance matrices and their impact on convergence behavior of maximum-likelihood analyses, and corresponding forms for correlation matrices have been described (Rapisarda et al. 2007).

To alleviate the problems encountered in sampling valid correlation matrices, Joe (2006) proposed a reparameterization of correlations to partial correlations, which vary independently over the interval $\left[-1,1\right].$ This involves a one-to-one transformation between partial and standard correlations, i.e., is readily reversible. Hence, using the reparameterization, we can readily sample a random correlation matrix that is positive definite by sampling individual, partial correlations. Moreover, it allows for flexible specification of priors in a Bayesian context by choosing individual and independent distributions for each one. Daniels and Pourahmadi (2009) referred to these quantities as partial autocorrelations (PACs), interpreting them as correlations between traits i and j conditional on the intervening traits, $i+1$ to $j-1.$

Details:

Consider a correlation matrix R of size $q\times q$ with elements ${\rho }_{ij}$ (for $i\ne j$) and ${\rho }_{ii}=1.$ As R is symmetric, let $i<j.$ For $j=i+1,$ the PACs are equal to the standard correlations, ${\pi }_{i,i+1}={\rho }_{i,i+1},$ as there are no intervening variables. For $j>i+1,$ partition the submatrix of R composed of rows and columns i to j as

$$\left(\begin{array}{ccc}1& {{\mathit{r}}^{\prime }}_1& {\rho }_{ij}\\ {\mathit{r}}_1& {\mathit{R}}_2& {\mathit{r}}_3\\ {\rho }_{ij}& {{\mathit{r}}^{\prime }}_3& 1\end{array}\right)$$ (2)

with ${\mathit{r}}_1$ and ${\mathit{r}}_3$ vectors of length $j-i-1,$ with elements ${\rho }_{ik}$ and ${\rho }_{jk},$ respectively, and ${\mathit{R}}_2$ the corresponding matrix with elements ${\rho }_{kl}$ for $k,l=i+1,\dots ,j-1.$ This gives PAC

$${\pi }_{ij}=\frac{{\rho }_{ij}-{{\mathit{r}}^{\prime }}_1{\mathit{R}}_2^{-1}{\mathit{r}}_3}{\sqrt{\left(1-{r^{\prime }}_1{\mathit{R}}_2^{-1}{\mathit{r}}_1\right)\left(1-{r^{\prime }}_3{\mathit{R}}_2^{-1}{\mathit{r}}_3\right)}}$$ (3)

and the reverse transformation is

$${\rho }_{ij}={r^{\prime }}_1{\mathit{R}}_2^{-1}{\mathit{r}}_3+{\pi }_{ij}\sqrt{\left(1-{r^{\prime }}_1{\mathit{R}}_2^{-1}{\mathit{r}}_1\right)\left(1-{r^{\prime }}_3{\mathit{R}}_2^{-1}{\mathit{r}}_3\right)}$$ (4)

(Joe 2006).

Penalties

We derive penalties on canonical eigenvalues and correlations or partial autocorrelations, choosing independent Beta distributions as priors. This choice is motivated by the flexibility of this class of distributions and the property that its hyperparameters—which determine the strength of penalization—can be “set” by specifying a single value.

Beta distribution:

The Beta distribution is a continuous probability function that is widely used in Bayesian analyses and encompasses functions with many different shapes, determined by two parameters, α and β. While the standard Beta distribution is defined for the interval $\left[0,1\right],$ it is readily extended to a different interval. The probability density function for a variable $x\in \left[a,b\right]$ following a Beta distribution is of the form

$$p\left(x\right)=B{\left(\alpha ,\beta \right)}^{-1}{\left(b-a\right)}^{-\left(\alpha +\beta -1\right)}{\left(x-a\right)}^{\alpha -1}{\left(b-x\right)}^{\beta -1}$$ (5)

(Johnson et al. 1995, Chap. 25) with $B\left(\alpha ,\beta \right)=\mathrm{\Gamma }\left(\alpha \right)\mathrm{\Gamma }\left(\beta \right)/\mathrm{\Gamma }\left(\alpha +\beta \right)$ and $B(\cdot )$ and $\mathrm{\Gamma }-4\times (\cdot )$ denoting the Beta and Gamma functions, respectively.

When employing a Beta prior in Bayesian estimation, the sum of the shape parameters, $\nu =\alpha +\beta ,$ is commonly interpreted as the effective sample size of the prior (PSS) (Morita et al. 2008). It follows that we can specify the parameters of a Beta distribution with mode m as a function of the PSS ($\nu \ge 2$) as

$$\alpha =1+\frac{m-a}{b-a}\left(\nu -2\right)\hspace{1em}\text{and}\hspace{1em}\beta =1+\frac{b-m}{b-a}\left(\nu -2\right).$$ (6)

For $\nu >2,$ this yields a unimodal distribution, and for $m=\left(b-a\right)/2$ the distribution is symmetric, with $\alpha =\beta .$ For given m, this provides a mechanism to regulate the strength of penalization through a single, intuitive parameter, the PSS ν.

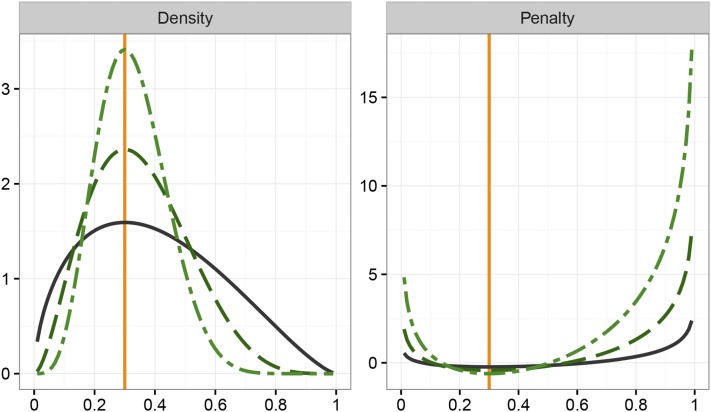
Figure 1 shows the probability density of a variable with a standard Beta distribution on the interval $\left[0,1\right]$ with mode of 0.3 together with the resulting penalty (i.e., minus the logarithmic value of the density), for three values of PSS. For $\nu =2,$ the density function would be a uniform distribution, depicted by a horizontal line at height of 1, resulting in no penalty. With increasing values of ν, the distribution becomes more and more peaked and the penalty on values close to the extremes of the range becomes more and more severe. Conversely, in spite of substantial differences in point mass around the mode, penalty values in proximity of the mode differ relatively little for different values of ν. While $\mathcal{P}\left(\mathit{\theta }\right)$ in (1) was considered nonnegative, penalty values close to the mode can be negative—this does not affect suitability of the penalty and can be overcome by adding a suitable constant.

Figure 1.

Probability densities (left) and corresponding penalties (including a factor of 1/2; right) for a variable with Beta distribution on $\left[0,1\right]$ with mode of $m=0.3$ for effective prior sample sizes of $\nu =4$ (―), $\nu =8$ (– –), and $\nu =16$ (– - –).

Penalty on canonical eigenvalues:

Canonical eigenvalues fall in the interval $\left[0,1\right].$ For q traits, there are likely to be q different values ${\lambda }_i$ and attempts to determine the mode of their distribution may be futile. Hence we propose to substitute the mean canonical eigenvalue, $\overline{\lambda }.$ Taking minus logarithmic values of (5) and assuming the same mode and PSS for all q eigenvalues then gives penalty

$${\mathcal{P}}_{\lambda }=C-\left(\nu -2\right)\left[\overline{\lambda }{\displaystyle \sum _{i=1}^q\log \left({\lambda }_i\right)}+\left(1-\overline{\lambda }\right){\displaystyle \sum _{i=1}^q\log \left(1-{\lambda }_i\right)}\right]$$ (7)

with $C=q\log \left[B\left(1+\overline{\lambda }\left(\nu -2\right),1+\left(1-\overline{\lambda }\right)\left(\nu -2\right)\right)\right].$. This formulation results in shrinkage of all eigenvalues toward $\overline{\lambda },$ with the highest and lowest values shrunk the most.

Penalty on correlations:

Following Joe (2006) and Daniels and Pourahmadi (2009), we assume independent shifted Beta distributions on $\left[-1,1\right]$ for PAC.

Daniels and Pourahmadi (2009) considered several Bayesian priors for correlation matrices formulated via PAC, suggesting uniform distributions for individual ${\pi }_{ij};$ i.e., ${\pi }_{ij}\sim \text{Beta}\left(1,1\right).$ In addition, they showed that the equivalent to the joint uniform prior for R proposed by Barnard et al. (2000), $p\left(\mathit{R}\right)\propto 1,$ is obtained by assuming Beta priors for PAC with shape parameters depending on the number of intervening variables; i.e., ${\alpha }_{i,i+k}={\beta }_{i,i+k}=1+\left(q-1-k\right)/2.$ Similarly, priors proportional to higher powers of the determinant of R, $p\left(\mathit{R}\right)\propto {\left|\mathit{R}\right|}^{t-1},$ are obtained for ${\alpha }_{i,i+k}=t+\left(q-1-k\right)/2$ (Daniels and Pourahmadi 2009). Gaskins et al. (2014) extended this framework to PAC-based priors with more aggressive shrinkage toward zero for higher lags, suitable to encourage sparsity in estimated correlation matrices for longitudinal data.

Both Joe (2006) and Daniels and Pourahmadi (2009) considered Beta priors for PAC with $\alpha =\beta ,$ i.e., shrinkage of all ${\pi }_{ij}$ toward zero. We generalize this by allowing for different shrinkage targets ${\tau }_{ij}$—and thus different shape parameters ${\alpha }_{ij}$ and ${\beta }_{ij}$—for individual values ${\pi }_{ij}.$ This gives penalty

$$\begin{array}{c}{\mathcal{P}}_{\pi }=\frac{q\left(q-1\right)}{2}\left(\nu -1\right)\log \left(2\right)+{\displaystyle \sum _{i=1}^q{\displaystyle \sum _{j=i+1}^q{C}_{ij}}}\\ -\frac{\nu -2}{2}\left[\left({\tau }_{ij}+1\right)\log \left({\pi }_{ij}+1\right)+\left(1-{\tau }_{ij}\right)\log \left(1-{\pi }_{ij}\right)\right]\end{array}$$ (8)

with $C_{ij}=\log \left[B\left(1+\left({\tau }_{ij}+1\right)\left(\nu -2\right)/2,1+\left(1-{\tau }_{ij}\right)\left(\nu -2\right)/2\right)\right].$ Again, this assumes equal PSS for all values, but could of course readily be expanded to allow for different values ${\nu }_{ij}$ for different PACs. For all ${\tau }_{ij}=0,$ (8) reduces to

$$\begin{array}{c}{\mathcal{P}}_{\pi }\left(0\right)=\frac{q\left(q-1\right)}{2}\left[\left(\nu -1\right)\log \left(2\right)+C_0\right]\\ -\frac{\nu -2}{2}{\displaystyle \sum _{i=1}^q{\displaystyle \sum _{j=i+1}^q\log \left(1-{\pi }_{ij}^2\right)}}\end{array}$$ (9)

with $C_0=\log \left[B\left(1+\left(\nu -2\right)/2,1+\left(\nu -2\right)/2\right)\right].$

Maximizing the penalized likelihood

REML estimation in quantitative genetics usually relies on algorithms exploiting derivatives of the log-likelihood function to locate its maximum. In particular, the so-called average information algorithm (Gilmour et al. 1995) is widely used due to its relative computational ease, good convergence properties, and implementation in several REML software packages. It can be described as a Newton(–Raphson)-type algorithm where the Hessian matrix is approximated by the average of observed and expected information. To adapt the standard, unpenalized algorithm for penalized estimation we need to adjust first and second derivatives of $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ for derivatives of the penalties with respect to the parameters, ${\theta }_k,$ to be estimated. These differ if we choose fixed values to determine the modes of the assumed Beta priors (e.g., ${\tau }_{ij}=0$ or the mean ${\lambda }_i$ from a preliminary, unpenalized analysis) or employ penalties that derive these from the parameter estimates.

Canonical eigenvalues:

If $\overline{\lambda }$ in (7) is estimated from the data, its derivatives are nonzero. This gives

$$\begin{array}{c}\frac{\partial {\mathcal{P}}_{\lambda }}{\partial {\theta }_k}=\frac{\partial C}{\partial {\theta }_k}+\left(\nu -2\right)\{\frac{\partial \overline{\lambda }}{\partial {\theta }_k}{\displaystyle \sum _{i=1}^q\log \left(\frac{1-{\lambda }_i}{{\lambda }_i}\right)}\\ +{\displaystyle \sum _{i=1}^q\frac{\partial {\lambda }_i}{\partial {\theta }_k}\left(\frac{1-\overline{\lambda }}{1-{\lambda }_i}-\frac{\overline{\lambda }}{{\lambda }_i}\right)}\}\end{array}$$ (10)

and

$$\begin{array}{c}\frac{{\partial }^2{\mathcal{P}}_{\lambda }}{\partial {\theta }_k\partial {\theta }_m}=\frac{{\partial }^{2}C}{\partial {\theta }_k\partial {\theta }_m}+\left(\nu -2\right){\displaystyle \sum _{i=1}^q\frac{{\partial }^2\overline{\lambda }}{\partial {\theta }_k\partial {\theta }_m}\log \left(\frac{1-{\lambda }_i}{{\lambda }_i}\right)}\\ -\left(\frac{\partial \overline{\lambda }}{\partial {\theta }_k}\frac{\partial {\lambda }_i}{\partial {\theta }_m}+\frac{\partial {\lambda }_i}{\partial {\theta }_k}\frac{\partial \overline{\lambda }}{\partial {\theta }_m}\right)\left(\frac{1}{{\lambda }_i}+\frac{1}{1-{\lambda }_i}\right)\\ +\frac{{\partial }^2{\lambda }_i}{\partial {\theta }_k\partial {\theta }_m}\left(\frac{1-\overline{\lambda }}{1-{\lambda }_i}-\frac{\overline{\lambda }}{{\lambda }_i}\right)\\ +\frac{\partial {\lambda }_i}{\partial {\theta }_k}\frac{\partial {\lambda }_i}{\partial {\theta }_m}\left(\frac{\overline{\lambda }}{{\lambda }_i^2}+\frac{1-\overline{\lambda }}{{\left(1-{\lambda }_i\right)}^2}\right).\end{array}$$ (11)

Derivatives of C involve the digamma and trigamma functions, e.g.,

$$\frac{\partial C}{\partial {\theta }_k}=q\left(\nu -2\right)\frac{\partial \overline{\lambda }}{\partial {\theta }_k}\left[\psi \left(1+\left(\nu -2\right)\overline{\lambda }\right)-\psi \left(1+\left(\nu -2\right)\left(1-\overline{\lambda }\right)\right)\right]$$

with ψ the digamma function. Derivatives of ${\lambda }_i$ required in (10) and (11) are easiest to evaluate if the analysis is parameterized to the canonical eigenvalues and the elements of the corresponding transformation matrix T (see Meyer and Kirkpatrick 2010), so that $\partial {\lambda }_i/{\lambda }_i=1$ and $\partial \overline{\lambda }/{\lambda }_i=1/q$ and all other derivatives of $\overline{\lambda }$ and ${\lambda }_i$ are zero. A possible approximation is to ignore contributions of derivatives of $\overline{\lambda },$ arguing that the mean eigenvalue is expected to be unaffected by sampling overdispersion and thus should change little.

Partial correlations:

Analogous arguments hold for penalties involving correlations. This gives

$$\begin{array}{c}\frac{\partial {\mathcal{P}}_{\pi }}{\partial {\theta }_k}={\displaystyle \sum _{i=1}^q{\displaystyle \sum _{j=i+1}^q\frac{\partial C_{ij}}{\partial {\theta }_k}}}\\ +\frac{\nu -2}{2}\left[\log \left(\frac{1-{\pi }_{ij}}{1+{\pi }_{ij}}\right)\frac{\partial {\tau }_{ij}}{\partial {\theta }_k}+2\left(\frac{{\pi }_{ij}-{\tau }_{ij}}{1-{\pi }_{ij}^2}\right)\frac{\partial {\pi }_{ij}}{\partial {\theta }_k}\right]\end{array}$$ (12)

and

$$\begin{array}{c}\frac{{\partial }^2{\mathcal{P}}_{\pi }}{\partial {\theta }_k\partial {\theta }_m}={\displaystyle \sum }_{i=1}^q{\displaystyle \sum }_{j=i+1}^q\frac{{\partial }^2{C}_{ij}}{\partial {\theta }_k\partial {\theta }_m}+\frac{\nu -2}{2}[\log \left(\frac{1-{\pi }_{ij}}{1+{\pi }_{ij}}\right)\frac{{\partial }^2{\tau }_{ij}}{\partial {\theta }_k\partial {\theta }_m}\\ -\frac{2}{1-{\pi }_{ij}^2}\left(\frac{\partial {\tau }_{ij}}{\partial {\theta }_k}\frac{\partial {\pi }_{ij}}{\partial {\theta }_m}+\frac{\partial {\tau }_{ij}}{\partial {\theta }_m}\frac{\partial {\pi }_{ij}}{\partial {\theta }_k}\right)+2\left(\frac{{\pi }_{ij}-{\tau }_{ij}}{1-{\pi }_{ij}^2}\right)\frac{{\partial }^2{\pi }_{ij}}{\partial {\theta }_k\partial {\theta }_m}\\ -2\left(\frac{1-{\tau }_{ij}^2+{\left({\pi }_{ij}-{\tau }_{ij}\right)}^2}{{\left(1-{\pi }_{ij}^2\right)}^2}\right)\frac{\partial {\pi }_{ij}}{\partial {\theta }_k}\frac{\partial {\pi }_{ij}}{\partial {\theta }_m}]\end{array}$$ (13)

with obvious simplifications if shrinkage targets are fixed or treated as such, so that derivatives of ${\tau }_{ij}$ are zero. As shown in the Appendix, derivatives of correlations and PACs are readily calculated from the derivatives of covariance components for any of the parameterizations commonly utilized in (unpenalized) REML algorithms for variance component estimation.

Simulation Study

A large-scale simulation study, considering a wide range of population parameters, was carried out to examine the efficacy of the penalties proposed above.

Setup

Data were sampled from multivariate normal distributions for $q=9$ traits, assuming a balanced paternal half-sib design composed of s unrelated sire families with 10 progeny each. Sample sizes considered were $s=100,$ 400, and 1000, with records for all traits for each of the progeny but no records for sires.

Population values for genetic and residual variance components were generated by combining 13 sets of heritabilities with six different types of correlation structures to generate 78 cases. Details are summarized in the Appendix and population canonical eigenvalues for all sets are shown in Supplemental Material, File S1. To assess the potential for detrimental effects of penalized estimation, values were chosen deliberately to generate both cases that approximately matched the priors assumed in deriving the penalties and cases where this was clearly not the case. The latter included scenarios where population canonical eigenvalues were widely spread and in multiple clusters and cases where genetic and phenotypic correlations were highly dissimilar. A total of 500 samples per case and sample size were obtained and analyzed.

Analyses

REML estimates of ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}}$ for each sample were obtained without penalization and imposing a penalty on canonical eigenvalues ${\mathcal{P}}_{\lambda },$ as given in (7), and penalties on partial autocorrelations shrinking all values toward zero [${\mathcal{P}}_{\pi }\left(0\right),$ see (9)] and with shrinkage targets for each value equal to the corresponding phenotypic counterpart [${\mathcal{P}}_{\pi }\left(P\right),$ see (8)]. For the latter, penalties on genetic PAC only and both genetic and residual values were examined.

Analyses were carried out considering fixed values for the effective sample size, ranging from $\nu =2.5$ to 24. For penalties on both genetic and residual PAC, either the same value was used for both or the PSS for residual PAC was fixed at $\nu =8.$ In addition, direct estimation of a suitable PSS for each replicate was attempted. As shown in (1), penalties were subtracted from the standard log-likelihood, incorporating a factor of $1/2.$

The model of analysis was a simple animal model, fitting means for each trait as the only fixed effects. A method-of-scoring algorithm together with simple derivative-free search steps was used to locate the maximum of the (penalized) likelihood function. To facilitate easy computation of derivatives of ${\mathcal{P}}_{\lambda },$ this was done using a parameterization to the elements of the canonical decomposition (see Meyer and Kirkpatrick 2010), restraining estimates of ${\lambda }_i$ to the interval of $\left[0.0001,0.9999\right].$

Direct estimation of ν was performed by evaluating points on the profile likelihood for ν [i.e., maximizing $\log {\mathrm{ℒ}}_P\left(\mathit{\theta }\right)$ with respect to the covariance components to be estimated for selected, fixed values of ν], combined with quadratic approximation steps of the profile to locate its maximum, using Powell’s (2006) Fortran subroutine NEWUOA. To avoid numerical problems, estimates of ν were constrained to the interval $\left[2.01,50\right].$ All calculations were carried out using custom Fortran programs (available on request).

Summary statistics

For each sample and analysis, the quality of estimates was evaluated through their entropy loss (James and Stein 1961)

$$L_1\left({\mathbf{\Sigma }}_X,{\widehat{\mathbf{\Sigma }}}_X\right)=\mathrm{tr}\left({\mathbf{\Sigma }}_X^{-1}{\widehat{\mathbf{\Sigma }}}_X\right)-\log \left|{\mathbf{\Sigma }}_X^{-1}{\widehat{\mathbf{\Sigma }}}_X\right|-q$$ (14)

for $X=G,$ E, and P, with ${\mathbf{\sum }}_X$ denoting the matrix of population values for genetic, residual, and phenotypic covariances and ${\widehat{\mathbf{\sum }}}_X$ the corresponding estimate. As suggested by Lin and Perlman (1985), the percentage reduction in average loss (PRIAL) was used as the criterion to summarize the effects of penalization

$$100\left[1-{\overline{L}}_1\left({\mathbf{\Sigma }}_X,{\widehat{\mathbf{\Sigma }}}_X^{\nu }\right)/{\overline{L}}_1\left({\mathbf{\Sigma }}_X,{\stackrel{⌢}{\mathbf{\Sigma }}}_X^0\right)\right],$$ (15)

where ${\overline{L}}_1(\cdot )$ denotes the entropy loss averaged over replicates, and ${\widehat{\mathbf{\Sigma }}}_X^{\nu }$ and ${\widehat{\mathbf{\Sigma }}}_X^0$ represent the penalized and corresponding unpenalized REML estimates of ${\mathbf{\Sigma }}_X,$ respectively.

In addition, the average reduction in $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ due to penalization, $\mathrm{\Delta }\mathrm{ℒ},$ was calculated as the mean difference across replicates between the unpenalized likelihood for estimates ${\widehat{\mathbf{\Sigma }}}_X^{\nu }$ and the corresponding value for estimates ${\widehat{\mathbf{\Sigma }}}_X^0.$

Data availability

The author states that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

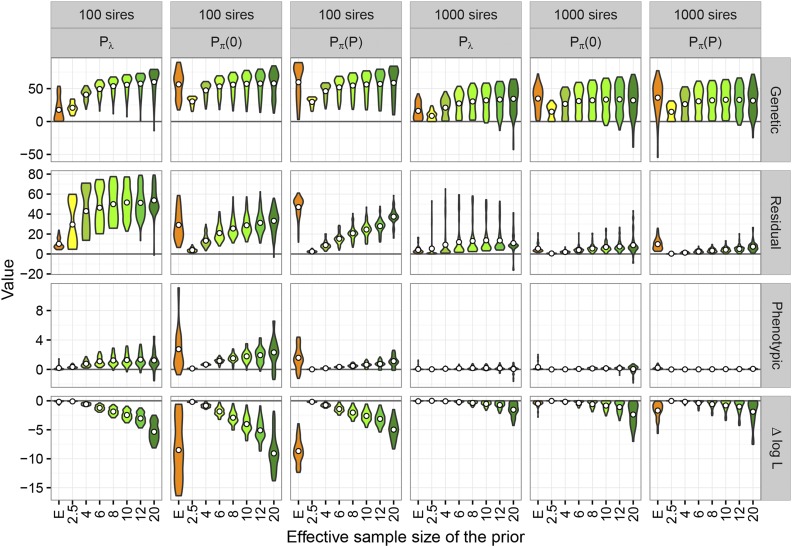
Distributions of PRIAL across the 78 sets of population values together with the corresponding change in likelihood are shown in Figure 2 for two sample sizes, with penalties ${\mathcal{P}}_{\pi }\left(0\right)$ and ${\mathcal{P}}_{\pi }\left(P\right)$ applied to genetic PAC only. Distributions shown are trimmed; i.e., their range reflects minimum and maximum values observed. Selected mean and minimum values are also reported in Table 1. More detailed results for individual cases are reported in File S1.

Figure 2.

Distribution of percentage reduction in average loss for estimates of genetic, residual, and phenotypic covariance matrices, together with corresponding change in log-likelihood ($\Delta \mathrm{ℒ}$) for penalties on canonical eigenvalues (${\mathcal{P}}_{\lambda }$) and genetic, partial autocorrelations, shrinking toward zero [${\mathcal{P}}_{\pi }\left(0\right)$] or phenotypic values [${\mathcal{P}}_{\pi }\left(P\right)$]. Centered circles give mean values. Numerical values on the x-axis are fixed, prior effective sample sizes while “E” denotes the use of a value estimated from the data for each replicate.

Table 1. Selected mean and minimum values for percentage reduction in average loss for estimates of genetic (${\mathbf{\Sigma }}_{\mathrm{G}}$), residual (${\mathbf{\Sigma }}_{\mathrm{E}}$), and phenotypic (${\mathbf{\Sigma }}_{\mathrm{P}}$) covariance matrices together with mean change in unpenalized log-likelihood from the maximum ($\Delta \mathrm{ℒ}$) for penalties on canonical eigenvalues (${\mathcal{P}}_{\lambda }$) and genetic correlations, shrinking partial autocorrelations toward zero [${\mathcal{P}}_{\pi }\left(0\right)$] or phenotypic values [${\mathcal{P}}_{\pi }\left(P\right)$].

		100 sires				400 sires				1000 sires
Penalty	νa	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$
Mean values
${\mathcal{P}}_{\lambda }$	4	41	43	1	−0.6	31	19	0	−0.2	21	9	0	−0.1
	6	49	46	1	−1.2	38	22	0	−0.5	27	12	0	−0.2
	8	54	50	1	−1.9	42	24	0	−0.7	30	13	0	−0.4
	12	58	51	1	−3.0	45	25	0	−1.4	33	13	0	−0.7
	E	18	10	0	−0.2	22	7	0	−0.1	16	4	0	−0.1
${\mathcal{P}}_{\pi }\left(0\right)$	4	47	13	1	−0.9	37	5	0	−0.3	27	2	0	−0.2
	6	53	21	1	−1.8	43	9	0	−0.7	31	4	0	−0.4
	8	56	26	2	−2.9	44	12	0	−1.1	32	6	0	−0.6
	12	58	31	2	−5.1	45	16	1	−2.1	34	8	0	−1.1
	E	56	29	3	−8.5	46	12	1	−1.9	35	5	0	−0.5
${\mathcal{P}}_{\pi }\left(P\right)$	4	46	9	0	−0.7	37	3	0	−0.3	26	1	0	−0.2
	6	52	15	0	−1.4	42	6	0	−0.7	31	2	0	−0.4
	8	55	21	0	−2.0	44	8	0	−1.0	32	3	0	−0.6
	12	57	28	1	−3.1	45	11	0	−1.6	33	5	0	−1.0
	E	60	47	2	−8.7	50	22	1	−3.5	36	10	0	−1.7
Minimum values
${\mathcal{P}}_{\lambda }$	8	12	26	0	−2.9	5	7	0	−1.7	2	2	0	−1.1
	12	1	13	0	−4.7	−11	11	−1	−3.0	−14	4	−1	−2.2
	E	0	4	0	−0.7	1	1	0	−0.6	1	0	0	−0.4
${\mathcal{P}}_{\pi }\left(0\right)$	8	16	11	0	−5.0	2	2	0	−3.0	1	0	0	−1.9
	12	14	11	0	−8.7	−7	2	−1	−5.4	−13	0	−1	−3.4
	E	18	7	−1	−16.4	1	3	−1	−11.6	1	1	0	−2.8
${\mathcal{P}}_{\pi }\left(P\right)$	8	18	7	0	−3.5	4	1	0	−2.9	1	0	0	−2.6
	12	16	12	0	−5.4	−1	2	0	−4.7	−5	0	0	−4.3
	E	3	12	−1	−12.4	−34	7	0	−8.8	−54	3	0	−5.6

^aEffective sample size of the Beta prior. Numerical values are “fixed” values used while E denotes values estimated from the data for each replicate, with means of 3.1, 5.9, and 8.5 (for 100, 400, and 1000 sires, respectively) for ${\mathcal{P}}_{\lambda };$ 31.2, 16.0, and 13.9 for ${\mathcal{P}}_{\pi }\left(0\right);$ 45.4, 36.4, and 34.8 for ${\mathcal{P}}_{\pi }\left(P\right);$ and 34.0, 33.6, and 32.2 for ${\mathcal{P}}_{\rho }\left(P\right).$

Genetic covariances

Overall, for fixed PSS there were surprisingly few differences between penalties in mean PRIAL values achieved, especially for estimates of the genetic covariance matrix. Correlations between PRIAL for ${\widehat{\mathbf{\Sigma }}}_{\mathrm{G}}$ from 0.9 to unity suggested similar modes of action.

For comparison, additional analyses considered penalties on standard correlations, obtained by substituting ${\rho }_{ij}$ for ${\pi }_{ij}$ in (8), (9), (12), and (13). Corresponding PRIAL values (not shown) for these were consistently lower and, more importantly, a considerable number of minimum values were negative, even for small values of the PSS. Clearly this reflected a discrepancy between priors assumed and the distribution of correlations. Transformation to partial autocorrelation yielded a better match and thus yielded penalties markedly less likely to have detrimental effects. While easier to interpret than PAC, penalties on standard correlations based on independent Beta priors are thus not recommended.

Even for small values of ν there were worthwhile reductions in loss for estimates of ${\mathbf{\sum }}_{\mathrm{G}},$ in particular for the smallest sample ($s=100$). Means increased with increasing stringency of penalization along with an increasing spread in results for individual cases, especially for the largest sample size. This pattern was due to the range of population values for genetic parameters used.

Moreover, for small samples or low PSS, it did not appear to be all that important whether the priors on which the penalties were based approximately matched population values or not: “Any” penalty proved beneficial, i.e., resulted in positive PRIAL for ${\widehat{\mathbf{\Sigma }}}_{\mathrm{G}}.$ For more stringent penalization, however, there was little improvement (or even adverse effects) for the cases where there was a clear mismatch. For instance, for ${\mathcal{P}}_{\lambda }$ for $\nu =24$ and $s=100$ sires, there were two cases with negative PRIAL for ${\widehat{\mathbf{\Sigma }}}_{\mathrm{G}}.$ Both of these had a cluster of high and low population values for ${\lambda }_i$ so that the assumption of a unimodal distribution invoked in deriving ${\mathcal{P}}_{\lambda }$ was inappropriate and led to sufficient overshrinkage to be detrimental. On the whole, however, unfavorable effects of penalization were few and restricted to the most extreme cases considered.

Paradoxically, PRIAL values for ${\widehat{\mathbf{\sum }}}_{\mathrm{G}}$ were also relatively low for cases where heritabilities were approximately the same and genetic and phenotypic correlations were similar, so that canonical eigenvalues differed little from their mean (see File S1). This could be attributed to the shape of the penalty function, as illustrated in Figure 1, resulting in little penalization for values close to the mode. In other words, these were cases were the prior also did not quite match the population values: While the assumption of a common mean for canonical eigenvalues clearly held, that of a distribution on the interval $\left[0,1\right]$ did not. This can be rectified by specifying a more appropriate interval. As the unpenalized estimates of ${\lambda }_i$ are expected to be overdispersed, their extremes may provide a suitable range to be used. Additional simulations (not shown) for ${\mathcal{P}}_{\lambda }$ replaced values of $a=0$ and $b=1$ used to derive ${\mathcal{P}}_{\lambda }$ in (7) with $a=\max \left(0,{\widehat{\lambda }}_9-0.05\right)$ and $b=\min \left(1,{\widehat{\lambda }}_1+0.05\right)$ for each replicate, where ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_9$ represented the largest and smallest canonical eigenvalue estimate from a preliminary, unpenalized analysis, respectively. This increased PRIAL for both ${\widehat{\mathbf{\sum }}}_{\mathrm{G}}$ and ${\widehat{\mathbf{\sum }}}_{\mathrm{E}}$ substantially for these cases. However, as the proportion of such cases was low (see File S1), overall results were little affected.

Residual covariances

Differences between penalties were apparent for ${\mathbf{\Sigma }}_{\mathrm{E}}.$ ${\mathcal{P}}_{\lambda }$ involved terms $\log \left(1-{\lambda }_i\right)$ [see (7)], i.e., the canonical eigenvalues of ${\mathbf{\Sigma }}_{\mathrm{E}}$ and ${\mathbf{\Sigma }}_{\mathrm{P}}.$ Hence, ${\mathcal{P}}_{\lambda }$ yielded substantial PRIAL for estimates of both ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}},$ especially for the smaller samples where sampling variances and losses were high. Conversely, applying penalties on genetic PAC resulted in some, but lower improvements in ${\mathbf{\Sigma }}_{\mathrm{E}}$ (except for large ν), but only as a by-product due to negative sampling correlations between ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}}.$ As shown in Table 2, imposing a corresponding penalty on residual PACs in addition could increase the PRIAL in estimates of ${\mathbf{\Sigma }}_{\mathrm{E}}$ markedly without reduction in the PRIAL for ${\mathbf{\Sigma }}_{\mathrm{G}},$ provided the PSS chosen corresponded to a relatively mild degree of penalization. Shrinking toward phenotypic PAC yielded somewhat less spread in PRIAL for ${\mathbf{\Sigma }}_{\mathrm{E}}$ than shrinking toward zero, accompanied by smaller changes in $\log \mathrm{ℒ}\left(\mathit{\theta }\right).$

Table 2. Selected mean and minimum values for percentage reduction in average loss for estimates of genetic (${\mathbf{\Sigma }}_{\mathrm{G}}$), residual (${\mathbf{\Sigma }}_{\mathrm{E}}$), and phenotypic (${\mathbf{\Sigma }}_{\mathrm{P}}$) covariance matrices together with mean change in unpenalized log-likelihood from the maximum ($\text{Δ}\mathrm{ℒ}$) for penalties on both genetic and residual partial autocorrelations, shrinking toward zero [${\mathcal{P}}_{\pi }\left(0\right)$] or phenotypic values [${\mathcal{P}}_{\pi }\left(P\right)$].

	νa		100 sires				400 sires				1000 sires
Penalty	${\nu }_{\mathrm{G}}$	${\nu }_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$	${\mathbf{\Sigma }}_{\mathrm{G}}$	${\mathbf{\Sigma }}_{\mathrm{E}}$	${\mathbf{\Sigma }}_{\mathrm{P}}$	$\mathrm{\Delta }\mathrm{ℒ}$
Mean values
${\mathcal{P}}_{\pi }\left(0\right)$	4	4	48	38	1	−0.9	37	16	0	−0.4	27	7	0	−0.2
	8	4	56	43	2	−2.9	45	20	0	−1.1	33	10	0	−0.6
	8	8	57	48	2	−2.8	45	23	1	−1.1	33	12	0	−0.6
	E	4	57	46	3	−6.6	48	21	1	−1.3	35	10	0	−0.5
	E	${\nu }_{\mathrm{G}}$	61	55	3	−5.3	50	27	1	−1.8	37	14	0	−0.8
	E	E	53	43	3	−9.1	47	24	1	−1.9	35	13	0	−0.5
${\mathcal{P}}_{\pi }\left(P\right)$	4	4	47	37	0	−0.8	37	15	0	−0.4	27	7	0	−0.2
	8	4	55	43	1	−2.2	44	19	0	−1.0	32	9	0	−0.6
	8	8	56	47	1	−2.3	44	22	0	−1.1	32	11	0	−0.6
	E	4	60	57	1	−8.2	51	31	1	−3.5	36	14	0	−1.6
	E	${\nu }_{\mathrm{G}}$	61	60	2	−10.8	46	31	1	−6.5	33	18	0	−3.0
	E	E	61	60	2	−10.7	51	33	1	−4.9	36	15	0	−2.3
Minimum values
${\mathcal{P}}_{\pi }\left(0\right)$	4	4	17	11	0	−1.5	2	1	0	−0.9	0	0	0	−0.6
	8	4	17	17	1	−4.8	3	3	0	−2.9	1	1	0	−1.9
	8	8	16	21	0	−4.6	3	4	0	−2.9	1	1	0	−2.0
	E	4	16	11	0	−12.8	5	4	0	−5.9	1	2	0	−2.9
	E	${\nu }_{\mathrm{G}}$	17	21	−1	−10.6	3	6	0	−6.2	2	2	0	−3.0
	E	E	−70	−139	−5	−17.7	6	−69	−2	−12.3	2	−5	0	−2.9
${\mathcal{P}}_{\pi }\left(P\right)$	4	4	20	10	0	−1.3	2	1	0	−1.0	0	0	0	−0.8
	8	4	21	20	0	−3.7	4	3	0	−3.0	1	1	0	−2.7
	8	8	20	23	0	−3.8	5	5	0	−3.1	1	1	0	−2.7
	E	4	5	24	−1	−10.8	−28	9	0	−7.9	−48	3	0	−4.9
	E	${\nu }_{\mathrm{G}}$	−3	10	−1	−17.0	−32	−28	−3	−16.0	−65	1	−1	−8.5
	E	E	−1	10	−2	−17.4	−30	−6	−2	−9.4	−64	−18	−2	−6.7

^aEffective sample size of the Beta prior for genetic (${\nu }_{\mathrm{G}}$) and residual (${\nu }_{\mathrm{E}}$) correlations. Numbers given are fixed values used while E denotes values estimated from the data for each replicate.

Phenotypic covariances

We argued above that imposing penalties based on the estimate of ${\mathbf{\Sigma }}_{\mathrm{P}}$ would allow us to borrow strength from it because typically ${\mathbf{\Sigma }}_{\mathrm{P}}$ is estimated more precisely than any of its components. Doing so, we would hope to have little—and certainly no detrimental—effect on the estimates of ${\mathbf{\Sigma }}_{\mathrm{P}}.$ Loosely speaking, we would expect penalized estimation to redress, to some extent at least, any distortion in partitioning of ${\mathbf{\Sigma }}_{\mathrm{P}}$ due to sampling correlations. As demonstrated in Figure 2, this was generally the case for fixed values of the PSS less than $\sim \nu =10$ or 12. Conversely, negative PRIAL for estimates of ${\mathbf{\Sigma }}_{\mathrm{P}}$ for higher values of ν flagged overpenalization for cases where population values for genetic parameters did not sufficiently match the assumptions on which the penalties were based.

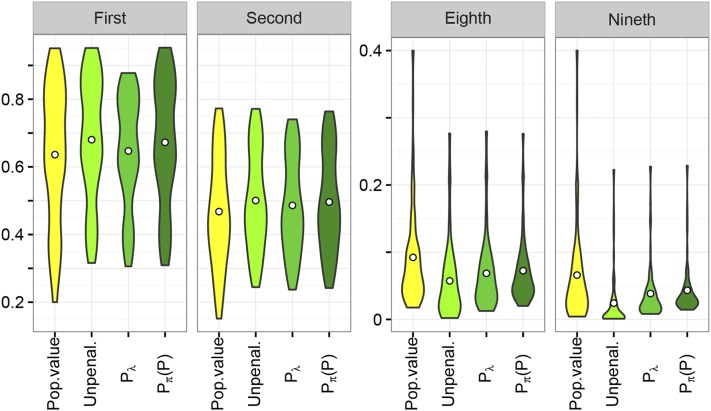
Canonical eigenvalues

Figure 3 shows the distribution of the largest and smallest canonical eigenvalues, contrasting population values with mean estimates from unpenalized and penalized analyses for a medium sample size and a fixed PSS of $\nu =8.$ Results clearly illustrate the upward bias in estimates of the largest and downward bias in estimates of the smallest eigenvalues. As expected, imposing penalty ${\mathcal{P}}_{\lambda }$ reduced the mean of the largest and increased the mean of the smallest eigenvalues, with some overshrinkage, especially of the largest eigenvalue, evident. In contrast, for the small value of $\nu =8$ chosen, the distribution of the largest values from penalized and unpenalized analyses differed little for penalty ${\mathcal{P}}_{\pi }\left(P\right);$ i.e., penalizing genetic PAC did not affect the leading canonical eigenvalues markedly, acting predominately on the smaller values. For more stringent penalties, however, some shrinkage of the leading eigenvalues due to penalties $\mathcal{P}{}_{\pi }{}^{}(P)$ and ${\mathcal{P}}_{\pi }\left(0\right)$ was evident; detailed results for selected cases are given in File S1.

Figure 3.

Distribution of mean estimates of selected canonical eigenvalues comparing results from unpenalized analyses and analyses imposing penalties on canonical eigenvalues (${\mathcal{P}}_{\lambda }$) and genetic, partial autocorrelations, shrinking toward phenotypic values [${\mathcal{P}}_{\pi }\left(P\right)$], with population values in the simulation. Both penalties employ a fixed, prior effective sample size of $\nu =8;$ results shown are for samples with 400 sire families. Centered circles give mean values across the 78 cases considered.

Estimating PSS

On the whole, attempts to estimate the appropriate value of ν from the data were not all that successful. For ${\mathcal{P}}_{\lambda },$ numerous cases yielded an estimate of ν close to the lower end of the range allowed, i.e., virtually no penalty. Conversely, for ${\mathcal{P}}_{\pi }\left(0\right)$ and ${\mathcal{P}}_{\pi }\left(P\right)$ a substantial number of cases resulted in estimates of ν close to the upper bound allowed. This increased PRIAL (compared to fixed values for ν) for cases that approximately matched the priors but caused reduced or negative PRIAL and substantial changes in $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ otherwise. A possible explanation was that the penalized likelihood and thus the estimate of ν might be dominated by ${\mathbf{\sum }}_{\mathrm{E}}.$ However, as shown in Table 2, neither estimating a value for ${\mathbf{\Sigma }}_{\mathrm{G}}$ (${\nu }_{\mathrm{G}}$) while fixing the PSS for ${\mathbf{\Sigma }}_{\mathrm{E}}$ (${\nu }_{\mathrm{E}}$) nor estimating a value for both (either separately or jointly, ${\nu }_{\mathrm{G}}={\nu }_{\mathrm{E}}$) improved results greatly. Moreover, it yielded more cases for which penalization resulted in substantial, negative PRIAL, especially for ${\mathcal{P}}_{\pi }\left(P\right).$ Repeating selected analyses using a sequential grid search to determine optimal values of ν gave essentially the same results; i.e., results could not be attributed to inadequacies in the quadratic approximation procedure. Given the additional computational requirements and the fact that suitable values could not be estimated reliably, joint estimation of PSS together with the covariance components cannot be recommended.

Discussion

Sampling variation is the bane of multivariate analyses in quantitative genetics. While nothing can replace large numbers of observations with informative data and appropriate relationship structure, we often need to obtain reasonably trustworthy estimates of genetic parameters from relatively small data sets. This holds especially for data from natural populations but is also relevant for new or expensive to measure traits in livestock improvement or plant breeding schemes. We have shown that regularized estimation in a maximum-likelihood framework through penalization of the likelihood function can provide “better” estimates of covariance components, i.e., estimates that are closer to the population values than those from standard, unpenalized analyses. This is achieved through penalties targeted at reducing sampling variation.

Simplicity

The aim of this study was to obtain a procedure to improve REML estimates of covariance components and thus genetic parameters that is easy to use without considerable increase in computational requirements and suitable for routine aplication. We have demonstrated that it is feasible to choose default values for the strength of penalization that yield worthwhile reductions in loss for a wide range of scenarios and are robust, i.e., are unlikely to result in penalties with detrimental effects, and are technically simple. While such a tuning-free approach may not yield a maximum reduction in loss, it appears to achieve a substantial proportion thereof in most cases with modest changes in the likelihood compared to the maximum of $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ (without penalization). In contrast to earlier attempts to estimate a tuning factor (Meyer and Kirkpatrick 2010; Meyer 2011), it does not require multiple additional analyses to be carried out, and effects of penalization on computational requirements are thus mostly unimportant.

In addition, we can again make the link to Bayesian estimation, where the idea of mildly or weakly informative priors has been gaining popularity. Discussing priors for variance components in hierarchical models, Gelman (2006) advocated a half-t or half-Cauchy prior with large-scale parameters. Huang and Wand (2013) extended this to prior distributions for covariance matrices that resulted in half-t priors for standard deviations and marginal densities of correlations ρ proportional to a power of $\left(1-{\rho }^2\right).$ Chung et al. (2015) proposed a prior for covariance matrices proportional to a Wishart distribution with a diagonal scale matrix and low degrees of belief to obtain a penalty on the likelihood function that ensured nondegenerate estimates of variance components.

Choice of penalty

We have presented two types of suitable penalties that fit well within the standard framework of REML estimation. Both achieved overall comparable reductions in loss but acted slightly differently, with penalties on correlations mainly affecting the smallest eigenvalues of the covariance matrices while penalties on canonical eigenvalues acted on both the smallest and largest values. Clearly it is the effect on the smallest eigenvalues (which have the largest sampling variances) that contributes most to the overall reduction in loss for a covariance matrix. An advantage of the penalty on correlations is that it is readily implemented for the parameterizations commonly employed in REML estimation, and it is straightforward to extend it to models with additional random effects and covariance matrices to be estimated or cases where traits are recorded on distinct subsets of individuals so that some residual covariances are zero. It also lends itself to scenarios where we may be less interested in a reduction in sampling variance but may want to shrink correlations toward selected target values.

Strength of penalization

Results suggest that penalties on canonical eigenvalues or PAC assuming a Beta prior with a conservative choice of PSS of $\nu =4$–10 will not only result in substantial improvements in estimates of genetic covariance components for many cases, but also result in little chance of detrimental effects for cases where the assumed prior does not quite match the underlying population values. Reanalyzing a collection of published heritability estimates from Mousseau and Roff (1987), M. Kirkpatrick (personal communication) suggested that their empirical distribution could be modeled as $\text{Beta}\left(1.14,1.32\right),$ corresponding to $v=2.46$ and mode of 0.3.

Additional bias

The price for a reduction in sampling variances from penalized analyses is an increase in bias. It is often forgotten that REML estimates of covariance components are biased even if no penalty is applied, as estimates are constrained to the parameter space; i.e., the smallest eigenvalues are truncated at zero or, in practice, at a small positive value to ensure estimated matrices are positive definite. As shown in Figure 3, penalization tended to increase the lower limits for the smallest canonical eigenvalues and thus also for the corresponding values of the genetic covariance matrix, thus adding to the inherent bias. Previous work examined the bias due to penalization on specific genetic parameters in more detail (Meyer and Kirkpatrick 2010; Meyer 2011), showing that changes from unpenalized estimates were usually well within the range of standard errors. Employing a mild penalty with fixed PSS, changes in $\log \mathrm{ℒ}\left(\mathit{\theta }\right)$ from the maximum value in an unpenalized analysis were generally small and well below significance levels. This suggests that additional bias in REML estimates due to a mild penalty on the likelihood is of minor concern and far outweighed by the benefits of a reduction in sampling variance.

Alternatives

Obviously, there are many other choices. As in Bayesian estimation, results of penalized estimation are governed by the prior distribution selected, the more so the smaller the data set available. Mean reductions in loss obtained in a previous study, attempting to estimate tuning factors and using penalties derived assuming a normal distribution of canonical eigenvalues or inverse Wishart distributions of covariance or correlation matrices, again were by and large of similar magnitude (Meyer 2011). Other opportunities to reduce sampling variation arise through more parsimonious modeling, e.g., by estimating ${\mathbf{\Sigma }}_{\mathrm{G}}$ at reduced rank or assuming a factor-analytic structure. Future work should examine the scope for penalization in this context and consider the effects on model selection.

Application

Practical application of REML estimation using the simple penalties proposed is illustrated using the data set considered by Meyer and Kirkpatrick (2010) (available as supplemental material in their article). In brief, this was composed of six traits measured on beef cattle, with 912–1796 records per trait. Including pedigree information on parents, grandparents, etc., without records yielded a total of 4901 animals in the analysis. The model of analysis fitted animals’ additive genetic effects as random and so-called contemporary group effects, with up to 282 levels per trait, as fixed. The latter was a subclass representing a combination of systematic environmental factors to ensure only animals subject to similar conditions were directly compared.

Estimates of ${\mathbf{\Sigma }}_{\mathrm{G}}$ and ${\mathbf{\Sigma }}_{\mathrm{E}}$ were obtained by REML using WOMBAT (Meyer 2007), applying penalties on canonical eigenvalues and partial correlations (shrinking toward zero) using PSS of 4 and 8, and contrasted to unpenalized results. Lower bound sampling errors for estimates of canonical eigenvalues were approximated empirically (Meyer and Houle 2013).

Results are summarized in Table 3. For all penalties and both levels of PSS, deviations in the unpenalized likelihood from the maximum (for the “standard” unpenalized analysis) were small and well below the significance threshold of –1.92 for a likelihood-ratio test involving a single parameter (at an error probability of 5%), emphasizing the mildness of penalization even for the larger PSS. Similarly, changes in estimates of canonical eigenvalues were well within their 95% confidence limits, except for ${\lambda }_1$ for ${\mathcal{P}}_{\lambda }$ with $\nu =8,$ which was just outside the lower limit. As expected from simulation results above (cf. Figure 3), the penalty on canonical eigenvalues affected estimates of the largest values more than penalties on partial correlations. Conversely, the latter yielded somewhat larger changes in the lowest eigenvalues. Estimates for ${\mathcal{P}}_{\lambda }$ with $\nu =8$ agreed well with results from Meyer and Kirkpatrick (2010) (of 0.69, 0.50, 0.38, 0.27, 0.17, and 0.05 for ${\lambda }_1$–${\lambda }_6,$ respectively), which were obtained by applying a quadratic penalty on the canonical eigenvalues and using cross-validation to determine the stringency of penalization.

Table 3. Reduction in unpenalized likelihood ($\text{Δ}\mathrm{ℒ}$) for applied example together with estimates of canonical eigenvalues.

			Canonical eigenvalues
Penaltya	νb	$\text{Δ}\mathrm{ℒ}$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$	${\lambda }_4$	${\lambda }_5$	${\lambda }_6$
Nonec		0	0.887	0.543	0.383	0.239	0.138	0.031
			0.097	0.072	0.066	0.058	0.046	0.029
${\mathcal{P}}_{\lambda }$	4	−0.195	0.815	0.530	0.378	0.242	0.145	0.046
	8	−1.395	0.696	0.478	0.348	0.220	0.138	0.055
${\mathcal{P}}_{\pi }\left(0\right)$	4	−0.117	0.880	0.534	0.377	0.246	0.141	0.049
	8	−0.628	0.867	0.522	0.370	0.259	0.146	0.069
	4,4	−0.172	0.836	0.531	0.376	0.244	0.140	0.048
	8,8	−0.797	0.789	0.520	0.372	0.263	0.148	0.070

^a${\mathcal{P}}_{\lambda },$ penalty on canonical eigenvalues; ${\mathcal{P}}_{\pi }\left(0\right),$ penalty on partial correlations, shrinking toward zero with a single value denoting a penalty on genetic correlations only and two values denoting a penalty on both genetic and residual correlations.

^bEffective sample size of the Beta prior.

^cSecond line gives approximate sampling errors of estimates of canonical eigenvalues.

Corresponding changes in individual parameters were small throughout and again well within the range of ∼95% confidence intervals (sampling errors derived from the inverse of the average information matrix) for the unpenalized analysis. The largest changes in correlations occurred for the pairs of traits with the smallest numbers of records and the higher PSS. For instance, for ${\mathcal{P}}_{\lambda }$ the residual correlation between traits 1 and 4 changed from 0.82 (with standard error of 0.17) to 0.65, while ${\mathcal{P}}_{\pi }\left(0\right)$ on both genetic and residual PAC reduced the estimate of the genetic correlation from 0.48 (standard error of 0.25) to 0.37. Plots with detailed results for individual parameters are given in File S1.

In summary, none of the penalties applied changed estimates significantly and none of the changes in estimates of individual parameters due to penalization were questionable. Indeed, the larger changes described yielded values more in line with literature results for the traits concerned, suggesting that penalization stabilized somewhat erratic estimates based on small numbers of observations.

Implementation

Penalized estimation for the penalties proposed for fixed values of ν has been implemented in our mixed-model package wombat (available at http://didgeridoo.une.edu.au/km/wombat.php) (meyer 2007). For ${\mathcal{P}}_{\lambda }$ a parameterization to the elements of the canonical decomposition is used for ease of implementation, while penalties on correlations use the standard parameterization to elements of the Cholesky factors of the covariance matrices to be estimated. Maximization of the likelihood is carried out using the average information algorithm, combined with derivative-free search steps where necessary to ensure convergence. Example runs for a simulated data set are shown in File S1.

Experience with applications so far has identified small to moderate effects of penalization on computational requirements compared with an unpenalized analysis, with the bulk of extra computations arising from derivative-free search steps used to check for convergence. The parameterization to the elements of the canonical decomposition, however, tended to increase the number of iterations required even without penalization. Detrimental effects on convergence behavior when parameterizing to eigenvalues of covariance matrices have been reported previously (Pinheiro and Bates 1996).

Convergence rates of iterative maximum-likelihood analyses are dictated by the shape of the likelihood function. Newton–Raphson-type algorithms, including the average information algorithm, involve a quadratic approximation of the likelihood. When this is not the appropriate shape, the algorithm may become “stuck” and fail to locate the maximum. This happens quite frequently for standard (unpenalized) multivariate analyses comprising more than a few traits when estimated covariance matrices have eigenvalues close to zero. For such cases, additional maximization steps using alternative schemes, such as expectation maximization-type algorithms or a derivative-free search, are usually beneficial. For small data sets, we expect the likelihood surface around the maximum to be relatively flat. Adding additional “information” through the assumed prior distribution (a.k.a. the penalty) can improve convergence by adding curvature to the surface and creating a more distinct maximum. Conversely, too stringent a penalty may alter the shape of the surface sufficiently so that a quadratic approximation may not be successful. Careful checking of convergence should be an integral part of any multivariate analysis, penalized or not.

Conclusion

We propose a simple but effective modification of standard multivariate maximum-likelihood analyses to “improve” estimates of genetic parameters: Imposing a penalty on the likelihood designed to reduce sampling variation will yield estimates that are on average closer to the population values than unpenalized values. There are numerous choices for such penalties. We demonstrate that those derived under the assumption of a Beta distribution for scale-free function of the covariance components to be estimated, namely generalized heritabilities (a.k.a. canonical eigenvalues) and genetic correlations, are well suited and tend not to distort estimates of the total, phenotypic variance. In addition, invoking a Beta distribution allows the stringency of penalization to be regulated by a single, intuitive parameter, known as effective sample size of the prior in a Bayesian context. Aiming at moderate rather than optimal improvements in estimates, suitable default values for this parameter can be identified that yield a mild penalty. This allows us to abandon the laborious quest to identify tuning factors suited to particular analyses. Choosing the penalty to be sufficiently mild can all but eliminate the risk of detrimental effects and results in only minor changes in the likelihood, compared to unpenalized analyses. Mildly penalized estimation is recommended for multivariate analyses in quantitative genetics considering more than a few traits to alleviate the inherent effects of sampling variation.

Appendix

Population Values

Population values for the 13 sets of heritabilities used are summarized in Table A1. The six constellations of genetic ($r_{\mathrm{G}{}_{ij}}$) and residual ($r_{\mathrm{E}{}_{ij}}$) correlations between traits i and j ($i\ne j$) were obtained as

1. $r_{\mathrm{G}{}_{ij}}=r_{{\mathrm{E}}_{ij}}=0,$

2. $r_{\mathrm{G}{}_{ij}}=0.5$ and $r_{{\mathrm{E}}_{ij}}=0.3,$

3. $r_{{\mathrm{G}}_{ij}}={0.7}^{|i-j|}$ and $r_{\mathrm{E}{}_{ij}}=0.5+0.05i{\left(-1\right)}^j,$

4. $r_{\mathrm{G}{}_{ij}}=-{0.7}^{|i-j|}+0.02i$ and $r_{\mathrm{E}{}_{ij}}=0.5+{\left(-0.2\right)}^{|i-j|},$

5. $r_{\mathrm{G}{}_{ij}}=r_{{\mathrm{E}}_{ij}}=0.7$ for $i,j\in \left[3,7\right]$ and $r_{{\mathrm{G}}_{ij}}=r_{\mathrm{E}{}_{ij}}=0.3$ otherwise, and

6. $r_{\mathrm{G}{}_{ij}}=r_{\mathrm{E}{}_{ij}}=0.6$ for $\left|i-j\right|=1,$ and $r_{\mathrm{G}{}_{ij}}=r_{{\mathrm{E}}_{ij}}$ computed from (4) with ${\pi }_{ij}=0.4$ otherwise.

Phenotypic variances were equal to 1 throughout for correlation I and set to 2, 1, 3, 2, 1, 2, 3, 1, and 2 for traits 1–9 otherwise.

Derivatives of Partial Autocorrelations

Partial autocorrelations [see (3)] can be written as

$${\pi }_{ij}=c_{ij}/\sqrt{v_1{v}_3}$$

with

$$c_{ij}=r_{ij}-{r^{\prime }}_1{\mathit{R}}_2^{-1}{\mathit{r}}_3$$

$$v_x=1-{r^{\prime }}_x{\mathit{R}}_2^{-1}{\mathit{r}}_x\hspace{1em}\text{for}\hspace{1em}x=1,3.$$

This gives partial derivatives of ${\pi }_{ij}$ with respect to parameters ${\theta }_k$ and ${\theta }_m:$

$$\frac{\partial {\pi }_{ij}}{\partial {\theta }_k}=\frac{\partial c_{ij}}{\partial {\theta }_k}\frac{{\pi }_{ij}}{c_{ij}}-\frac{{\pi }_{ij}}{2}\left(\frac{1}{v_1}\frac{\partial v_1}{\partial {\theta }_k}+\frac{1}{v_3}\frac{\partial v_3}{\partial {\theta }_k}\right)$$

$$\begin{array}{c}\frac{{\partial }^2{\pi }_{ij}}{\partial {\theta }_k\partial {\theta }_m}=\frac{1}{\sqrt{v_1{v}_3}}\left[\frac{{\partial }^2{c}_{ij}}{\partial {\theta }_k\partial {\theta }_m}-\frac{1}{2}\frac{\partial c_{ij}}{\partial {\theta }_k}\left(\frac{1}{v_1}\frac{\partial v_1}{\partial {\theta }_m}+\frac{1}{v_3}\frac{\partial v_3}{\partial {\theta }_m}\right)\right]\\ +\frac{{\pi }_{ij}}{2}(\frac{1}{v_1{}^2}\frac{\partial v_1}{\partial {\theta }_k}\frac{\partial v_1}{\partial {\theta }_m}-\frac{1}{v_1}\frac{{\partial }^2{v}_1}{\partial {\theta }_k\partial {\theta }_m}+\frac{1}{v_3{}^2}\frac{\partial v_3}{\partial {\theta }_k}\frac{\partial v_3}{\partial {\theta }_m}\\ -\frac{1}{v_3}\frac{{\partial }^2{v}_3}{\partial {\theta }_k\partial {\theta }_m})\\ -\frac{1}{2}\frac{\partial {\pi }_{ij}}{\partial {\theta }_m}\left(\frac{1}{v_1}\frac{\partial v_1}{\partial {\theta }_k}+\frac{1}{v_3}\frac{\partial v_3}{\partial {\theta }_k}\right).\end{array}$$

Derivatives of the components are

$$\frac{\partial c_{ij}}{\partial {\theta }_k}=\frac{\partial r_{ij}}{\partial {\theta }_k}+{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_3-{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_3}{\partial {\theta }_k}-\frac{\partial {r^{\prime }}_1}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_3$$

$$\begin{array}{c}\frac{{\partial }^2{c}_{ij}}{\partial {\theta }_k\partial {\theta }_m}=\frac{{\partial }^2{r}_{ij}}{\partial {\theta }_k\partial {\theta }_m}-\frac{{\partial }^2{r^{\prime }}_1}{\partial {\theta }_k\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_3\\ -{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{{\partial }^2{\mathit{r}}_3}{\partial {\theta }_k\partial {\theta }_m}+{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{{\partial }^2{\mathit{R}}_2}{\partial {\theta }_k\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_3\\ -\frac{\partial {r^{\prime }}_1}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_3}{\partial {\theta }_m}-\frac{\partial {r^{\prime }}_1}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_3}{\partial {\theta }_k}\\ +\frac{\partial {r^{\prime }}_1}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_3+{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_3}{\partial {\theta }_k}\\ +\frac{\partial {r^{\prime }}_1}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_3+{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_3}{\partial {\theta }_m}\\ -{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_3-{r^{\prime }}_1{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_3\end{array}$$

and

$$\frac{\partial v_x}{\partial {\theta }_k}={r^{\prime }}_x{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_x-2{r^{\prime }}_x{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_x}{\partial {\theta }_k}$$

$$\begin{array}{c}\frac{{\partial }^2{v}_x}{\partial {\theta }_k\partial {\theta }_m}={r^{\prime }}_x{\mathit{R}}_2^{-1}\frac{{\partial }^2{\mathit{R}}_2}{\partial {\theta }_k\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_x-2\frac{{\partial }^2{r^{\prime }}_x}{\partial {\theta }_k\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_x\\ +2\frac{\partial {r^{\prime }}_x}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_x-2{r^{\prime }}_x{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_k}{\mathit{R}}_2^{-1}{\mathit{r}}_x\\ -2\frac{\partial {r^{\prime }}_x}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{r}}_x}{\partial {\theta }_m}+2\frac{\partial {r^{\prime }}_x}{\partial {\theta }_k}{\mathit{R}}_2^{-1}\frac{\partial {\mathit{R}}_2}{\partial {\theta }_m}{\mathit{R}}_2^{-1}{\mathit{r}}_x.\end{array}$$

Decompose the correlation matrix as $\mathit{R}={\mathit{S}}^{-1}\mathit{\Sigma }{\mathit{S}}^{-1}$ with $\mathit{S}=\mathrm{Diag}\left\{s_i\right\}$ the diagonal matrix of standard deviations for covariance matrix $\mathit{\Sigma }.$ This gives the required derivatives of the correlation matrix:

$$\frac{\partial \mathit{R}}{\partial {\theta }_k}={\mathit{S}}^{-1}\frac{\partial \mathit{\Sigma }}{\partial {\theta }_k}{\mathit{S}}^{-1}-{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_k}\mathit{R}-\mathit{R}\frac{\partial \mathit{S}}{\partial {\theta }_k}{\mathit{S}}^{-1}$$

$$\begin{array}{c}\frac{{\partial }^2\mathit{R}}{\partial {\theta }_k\partial {\theta }_m}={\mathit{S}}^{-1}\frac{{\partial }^2\mathit{\Sigma }}{\partial {\theta }_k\partial {\theta }_m}{\mathit{S}}^{-1}-{\mathit{S}}^{-1}\frac{{\partial }^2\mathit{S}}{\partial {\theta }_k\partial {\theta }_m}\mathit{R}-\mathit{R}\frac{{\partial }^2\mathit{S}}{\partial {\theta }_k\partial {\theta }_m}{\mathit{S}}^{-1}\\ -{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_m}{\mathit{S}}^{-1}\frac{\partial \mathit{\Sigma }}{\partial {\theta }_k}{\mathit{S}}^{-1}-{\mathit{S}}^{-1}\frac{\partial \mathit{\Sigma }}{\partial {\theta }_k}{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_m}{\mathit{S}}^{-1}\\ +\mathit{R}\frac{\partial \mathit{S}}{\partial {\theta }_k}{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_m}{\mathit{S}}^{-1}+{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_m}{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_k}\mathit{R}\\ -{\mathit{S}}^{-1}\frac{\partial \mathit{S}}{\partial {\theta }_k}\frac{\partial \mathit{R}}{\partial {\theta }_m}-\frac{\partial \mathit{R}}{\partial {\theta }_m}\frac{\partial \mathit{S}}{\partial {\theta }_k}{\mathit{S}}^{-1}.\end{array}$$

Finally, assuming derivatives of variances ${\sigma }_{ii}$ are available, the required derivatives of standard deviations $s_i=\sqrt{{\sigma }_{ii}}$ are

$$\frac{\partial s_i}{\partial {\theta }_k}=\frac{1}{2s_i}\frac{\partial {\sigma }_{ii}}{\partial {\theta }_k}$$

$$\frac{{\partial }^2{s}_i}{\partial {\theta }_k\partial {\theta }_m}=\frac{1}{2s_i}\left(\frac{{\partial }^2{\sigma }_{ii}}{\partial {\theta }_k\partial {\theta }_m}-\frac{1}{2s_i^2}\frac{\partial {\sigma }_{ii}}{\partial {\theta }_k}\frac{\partial {\sigma }_{ii}}{\partial {\theta }_m}\right).$$

When estimating elements of $\mathit{\Sigma }$ directly, only $\partial {\sigma }_{ii}/\partial {\sigma }_{ii}=1$ are nonzero. Derivatives of covariance matrices when employing a parameterization to the elements of their Cholesky factors are given by Meyer and Smith (1996).

Table A1. Population values ($\times 100$) for sets of heritabilities.

	Trait no.
Set	1	2	3	4	5	6	7	8	9
A	40	40	40	40	40	40	40	40	40
B	60	55	50	45	40	35	30	25	20
C	90	60	50	50	30	30	20	20	10
D	75	70	60	50	40	30	20	10	5
E	70	70	70	40	40	40	10	10	10
F	20	20	20	20	20	20	20	20	20
G	35	30	25	20	20	20	15	10	5
H	60	50	10	10	10	10	10	10	10
I	50	50	20	15	15	10	10	5	5
J	80	40	10	10	10	10	10	5	5
K	30	30	25	25	20	15	15	10	10
L	35	30	30	20	20	15	15	15	10
M	10	10	10	30	30	30	50	50	50