Abstract
Conventional DIC microscope shows the two-dimensional distribution of optical path length gradient encountered along the shear direction between two interfering beams. It is therefore necessary to rotate unknown objects in order to examine them at several orientations. We built new DIC beam shearing assembly, which allows the bias to be modulated and shear directions to be switched rapidly without any mechanically rotating the specimen or the prisms. The assembly consists of two standard DIC prisms with liquid crystal cell in between. Another liquid crystal cell is employed for modulating a bias. All components do not require a special design and are available on the market. We describe techniques for measuring parameters of DIC prisms and calibrating liquid crystal cells. One beam-shearing assembly is added to the illumination path and another one to the imaging path of standard microscope. Two sets of raw DIC images at the orthogonal shear directions and two or three different biases are captured and processed within a second. Then the quantitative image of optical path gradient distribution within a thin optical section is displayed on a computer screen. The obtained data are also used to compute the quantitative distribution of optical phase, which represents refractive index gradient or height distribution. It is possible to generate back the enhanced regular DIC images with any desired shear direction. New DIC microscope can be combined with other techniques, such as fluorescence and polarization microscopy.
Keywords: Differential interference contrast (DIC) microscopy, quantitative phase imaging, optical path gradient, dry mass, liquid crystal devices, live cell imaging
1. INTRODUCTION
Differential interference contrast (DIC) light microscope is a polarizing beam-shearing interference system in which the interfering beams are sheared by a small amount, generally by somewhat less than the radius of an Airy disk. The DIC technique produces a monochromatic shadow-cast image that displays the optical paths gradient projection on the shear direction. Those regions of the specimen where the optical paths increase along a reference direction appear brighter (or darker), while regions where the path differences decrease appear in reverse contrast. As the gradient of optical path grows steeper, image contrast is significantly increased. With conventional DIC the two-dimensional distribution of optical path gradients along the shear direction generates image contrast that is not symmetrical and varies proportionally with the cosine of the angle made by the azimuth of the object and the direction of wavefront shear.
The DIC microscopy demonstrates remarkable optical sectioning capability because its contrast is produced by the optical path difference in a s mall in-focus volume where two interfering beams are spatially separated. Here the beams travel through the different areas of the specimen under investigation. The out-of-focus object introduces practically the same phase disturbance in the both beams because the beams go through almost same area of the specimen. Therefore, the out-of-focus disturbance is suppressed by optical subtraction. The optical section depth becomes thinner if the shear amount is smaller, and the objective and condenser numerical apertures are larger. The narrow optical sectioning DIC phenomenon is similar to removing an out-of-focus haze in the structured illumination microscopy (SIM)1. The SIM employs a single-spatial-frequency grid pattern, which is projected onto the object under investigation. Raw images are taken at three spatial positions of the grid. The out-of-focus picture of the object does not depend on the pattern position. As a result, the out-of-focus haze in SIM is subtracted computationally.
Application of computation subtraction in the DIC should also improve its sectioning capability even further. The computation subtraction of images with different biases is employed in various techniques, such as polarization modulation DIC (PM-DIC)2,3, differential detection DIC (D-DIC) with polarizing beamsplitter4, phase-shifting DIC (PS-DIC)5-7, retardation modulation DIC (RM-DIC)8-10, and orientation-independent DIC (OI-DIC)12,13. In particularly, the PM-DIC removes a background contribution that is insensitive to defocus3. It is shown theoretically and confirmed experimentally that a RM-DIC microscope has stronger optical sectioning than a conventional DIC microscope, and the optical section depth is thinner if a Nomarski prism with smaller shear amount is used10. Our experiments with the OI-DIC microscope using 100x/1.3NA oil immersion objective lens demonstrated the optical section depth about 0.1 μm. The corresponding field depth of a bright-field microscope would be 0.5 μm.
The regular DIC microscope, however, has shortcomings: it requires the proper orientation of a specimen in relation to the optical system in order to achieve best pictures, and its images are not quantitative. In order to obtain quantitative data it is necessary to capture DIC images with orthogonal shear directions. The previous approaches5, 14-18 used mechanical rotation either of the specimen or DIC prism. This takes considerable time and the obtained images can be misaligned. Therefore the previous methods in the DIC microscopy were not suitable for imaging live cells.
To overcome these limitations we have designed and successfully built a new DIC microscope, which allows the bias and shear directions to be switched rapidly without mechanically rotating the specimen or the prisms12,13. In this system we incorporate algorithms that we have developed. The new OI-DIC technique provides quantitative orientation-independent images of phase (dry mass) and phase gradient with highest fidelity and resolution, which cannot be obtained with any other optical microscope.
2. OPTICAL SCHEMATICS OF ORIENTATION-INDEPENDENT DIFFERENTIAL INTERFERENCE CONTRAST (OI-DIC) MICROSCOPE
Principal optical schematic of OI-DIC microscope for the transmitted light is shown in Fig. 1. It contains light source with bandpath filter, crossed linear polarizer and analyzer, two beam-shearing assemblies, phase shifter, objective and condenser lenses, image sensor. The schematic could also include a displacement compensator. Orientation of the polarizers and birefringent components are shown in the picture.
Figure 1.
Principal optical schematics of OI-DIC microscope for the transmitted light.
The beam shearing assemblies can employ regular DIC prisms from the microscope. The first prism in assembly is placed in the designed original position and the second DIC prism is displaced along the microscope optical axis by some distance. The large prism displacement causes a strong non-uniformity of intensity distribution across the view filed and reduces the image contrast significantly. One solution of the displacement problem is the using a custom made second DIC prism, which is designed for the specific position. But this way would require knowledge of the DIC prism design and such prism could be very expensive. The second solution is to extract the bare DIC prisms from their original mounts and put them in new holder at close distance. Thickness of each DIC prism is about 1 mm, and thickness of a liquid crystal cell is about 2 mm. A small displacement of the each DIC prism by 2~3 mm from the designed axial position would not deteriorate the image quality substantially. The third solution is to use the second DIC prism in its original mount and a special displacement compensator. The compensator corrects misalignment in the interfering beams caused by displacement of the prism.
A regular research grade microscope equipped with DIC optics can be modified for obtaining OI-DIC images. In particular, our first experimental setup, which is shown in Fig. 2, was implemented on an upright microscope Olympus BX-61 (Olympus America, Center Valley, PA, http://www.olympus.com). We employed two pairs of regular DIC prisms in their original mounts and 2.2 mm-thick liquid crystal 90° polarization rotators in custom made 7 mm-thick holders. The axial displacement of the outside prism DIC4 in the imaging path was 32 mm up, and the axial displacement of the outside prism DIC1 in the illumination path was 16 mm down. The internal prisms DIC2 and DIC3 were placed in the originally designed positions. We made single displacement compensator, which corrects misalignment in the interfering beams caused by displacements of the both outside prisms. Detail description of the compensator design is quite cumbersome and it will be done in a future publication.
Figure 2.
OI-DIC microscope setup with two switchable beam-shearing DIC assemblies. The first assembly consists of DIC prisms DIC1 and DIC2, and two liquid crystal variable retarders LC1 and LC2. The second beam shearing uses prisms DIC3 and DIC4, and liquid crystal variable retarders LC3.
An example of beam-shearing assembly along with phase shifter is shown in Fig. 3 (center). Here we assume that DIC prisms are made of the positive birefringent crystal such as quartz. The diagrams to the left and right in Fig. 3 depict polarization transformations inside the assembly and the corresponding change of shear directions of the output beams. The left column illustrates a case when the beam polarizations between two prisms are preserved and the shear direction is 45° after the second DIC pris m. The right column describes a rotation of the output shear direction by 90° caused by switching the beam polarizations after the first DIC prism.
Figure 3.
Design of beam-shearing assembly with liquid crystal variable retarders.
The schematic consists of linear polarizer P, phase shifter, pair of DIC prisms (Nomarski or Wollaston) DIC1 and DIC2 with orthogonal shear directions, and 90° polarization rotator. Shear direction of the first prism DIC1 is chosen as the initial X-direction to describe the orientation of the above mentioned optical elements. Azimuth of the transmission axis of the polarizer P is 45° in order to create equal intensities of polarization components that become spatially divided by the first prism.
The phase shifter introduces bias Γ between the X- and Y- polarization components. Principal axis of the phase shifter is parallel to the shear direction. Dependence of the phase retardation on the applied voltage has to be smooth enough in order to achieve the required bias change accurately and quickly. The initial bias can be adjusted by sliding of the wedge component of one of the DIC prisms. In principle, the phase shifter can be installed with the same orientation in any place in the assembly. A standard untwisted nematic liquid crystal cell, Freedericksz cell, which works in the Electrically Controlled Birefringence (ECB) mode19-22, can be employed as phase shifter. The Freedericksz cell configuration is different from the twisted nematic configuration typically used in liquid crystal displays. Conventional Freedericksz ECB cell consists of homogeneously parallel aligned liquid crystal directors. The ECB mode uses the applied voltage to change the tilt of the liquid crystal molecules, as a result, the birefringence is changed as a function of the tilt angle. When no voltage is applied, the liquid crystal molecule's directors are aligned parallel to the cell substrates and the retardance it at a maximum. When a voltage is applied, an electric field is introduced which supplies a torque to the liquid crystal molecules; the retardance is decreased. The molecules near the substrates are not able to fully rotate, and so the retardance does not quite get to zero. Conventional ECB cell has retardance range from 0.1 to two wave (2λ) at 700nm20,21.
It is also possible to use an ECB cell with vertical alignment (VA ECB) as phase shifter19,23. The liquid crystal molecule's directors are aligned perpendicular (vertical) to the cell substrates if no voltage is applied, and the retardance is at a minimum (zero). Applied voltage turns the liquid crystal directors, and so the retardance is increased. The vertically aligned LC cell exhibits the highest contrast value among all LC cells. Another its merit is fast response speed due to thin cell gap. It does not require a compensation film in order to get zero retardance. The VA ECB has some shortcomings, such as lower retardance range from 0 to half wave (λ/2) at 700nm, and reduced contrast for off axis rays.
In opposite to the phase shifter, which changes birefringence smoothly in order to obtain the required bias value, the polarization rotator has two states only. In state of OFF the beam passes through the rotator without modifying the X- and Y- polarization components. In state of ON the polarization rotator switches the X- and Y- components. The rotator can utilize conventional ECB or VA ECB liquid crystal cell, which is similar to one used by the phase shifter. In this case the principal axis of the LC cell has to be orientated at 45°. The LC cell switches polarization by 90° (state ON) when the plate retardation is half wave (λ/2), and preserves beam polarization (state OFF) if the plate retardance is 0 or full wave (λ).
It is convenient to utilize a 90° twisted nematic (TN) cell as the rotator22,23. Currently the TN cells are commonly used in liquid crystal displays and shutters. They are not expensive and less sensitive to the wavelength variation then ECB cells. In the TN cells the LC anchoring (or rubbing) direction at the input surface is perpendicular to that of the output surface. In the inactivated state (voltage is below threshold), the local LC director undergoes a continuous twist of 90° in the region between the plates. Linearly polarized input light propagates through and, under ideal circumstances, follows the director helix as it propagates through the LC structure. Lets us assume that LC anchoring direction at the input surface is oriented along the X-axis and anchoring direction at the output surface is oriented along the Y-axis. In this case, light with initial X-polarization emerges from the LC cell with Y-polarization, and light with initial Y-polarization comes out with X-polarization. In order to reduce interaction between X- and Y- polarization components during the propagation, the cell's rubbing direction should be oriented at 0° or 90°. The phase shifter could compensate a possible phase shift between two polarization components introduced by the rotator. When an electric field is applied across the LC layer, the directors become predominantly parallel to the electric field. The twisted structure is thus distorted, and, with voltage above threshold, begins to vanish. The polarization direction of the light is no longer rotated as light passes through the cell.
One of advantages of using the TN cell is that we do not need to know precise dependence of parameters of the cell on the applied voltage. In the transmitted light with use two rotators and can apply the same voltage to the both cell simultaneously using the same generator output. Typically the Freedericksz voltage threshold occurs at 2-3Vrms. In this case, the voltage ~0.5 Vrms will set both rotators in the state ON, and voltage 5 Vrms will put them in the state OFF.
It is promising to employ ferroelectric liquid crystal (FLC) cell in 90° polarization rotator. They are known for their fast switching speed and bistability. The switching speed is very fast, which is usually a few microseconds. The two states are bistable, which means the electric field is not required once the tilting is finished21,22.
Let us examine in more detail how the beam-shearing assembly works. For example, the initial ray A0 falling on the first prism DIC1 has coordinates (0, 0). Here the first number means a coordinate along the X-axis, and the second one is the coordinate along the Y-axis. The shear plane of the first DIC pris m is parallel to the X-axis. The prism deflects a ray with Y-polarization in the negative direction by 1 unit and shifts a ray with X-polarization in the positive direction by the same amount. It creates a shear distance of two units between the components along the X-axis. Thus, the first output ray A1 has X-polarization and coordinates (1, 0). The Y-polarized second ray B1 has coordinates (−1, 0).
The 90° polarization rotator preserves the linear polarizations of the beams A1 and B1 (state OFF) or turns them by 90° without altering the ray positions (state ON). In the first case (left column) the output rays A2 and B2 are polarized along the X-axis and Y-axis, respectively. In the second case (right column) the rays A’2 and B’2 are polarized along the Y-axis and X-axis, correspondently.
The second DIC prism is oriented orthogonal to the direction of the first prism. So, the shear direction of the second prism lies along the Y-axis. The prism moves position of a ray with Y-polarization by 1 unit in the positive direction and deflects a ray with X-polarization in the negative direction by the same number.
First we consider a case, which is shown on the left side of Fig. 3, where the rotator state is OFF, and therefore the ray polarizations are not changed. Then ray A2 with X-polarization and coordinates (1, 0) passes the second prism with negative displacement by 1 unit in the Y-direction, and the output ray A3 has coordinates (1, −1). In the meanwhile, the coordinates of ray B2 are changed by 1 unit in the positive direction along Y-axis, and the coordinates for output ray B3 are (−1, 1). As a result, in the first case the dual beam that falls on the specimen has shear direction −45°. The first case can be described by the following flow-chart: 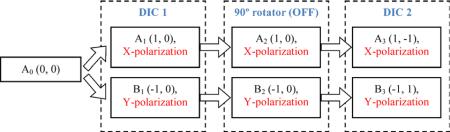
For the second case, after the rotator switches the polarizations by 90°, the ray A’2 is linearly polarized along the Y-axis. Therefore the second DIC prism changes Y-coordinate of the ray by +1, and the output ray A’3 has coordinates (1, 1). Also the second DIC prism deflects the X-polarized ray B’2 by −1, so that the second output ray B’3 has coordinates (1, −1). Hence, the output beam has a shear direction +45°. This case can be illustrated by the next flowchart:  In the both cases (Fig. 4) the shears have the same amount, which equals to the shear introduced by a single DIC prism multiplied by . However, the shear directions are mutually orthogonal. The median axis of two beams passes through point (0, 0) in the both cases. Therefore there is no misalignment between the images.
In the both cases (Fig. 4) the shears have the same amount, which equals to the shear introduced by a single DIC prism multiplied by . However, the shear directions are mutually orthogonal. The median axis of two beams passes through point (0, 0) in the both cases. Therefore there is no misalignment between the images.
Figure 4.

Change of orientation of shear between beam axes caused by switching their polarization states.
3. CALIBRATION OF OI-DIC COMPONENTS
3.1 Measuring shear distance
Shear amount (distance) is the critical parameter of a DIC microscope that determines its contrast, sensitivity, resolution and optical section depth. Another issues with DIC microscopy is that, to derive quantitative information, one must know the amount of image shear. Generally, however, microscope manufacturers do not make that information available. As a result, one must measure this parameter. Munster et al.14 determined the lateral shift by measuring the distance between the center of the bright spot and the center of the dark spot in image of a submicroscopic transparent latex sphere with bias set at π/2. Mehta and Sheppard24 measured shear by studying intensity distribution in the back focal plane of the microscope objective lens. Müller et al.25 used a combination of fluorescence correlation spectroscopy and dynamic light scattering to determine shear. Duncan et al.26 described a measurement setup with using a standard optical wedge.
The described below technique for determining shear distance is faster and more accurate than mentioned. At first we measure a shear angle. Then the shear distance is computed by multiplying the shear angle and standardized reference focal length of the tube lens, as it is explained in the end of this section.
In order to find the shear angle of DIC prism we do not need to know how the passing beam is transformed inside the prism. DIC prism splits an incident monochromatic plane wave into two orthogonally polarized plane wave with slightly different direction of their wavefronts. Fig. 5 illustrates splitting the incident linearly polarized beam into two separate output beams with shear angle ε. Here the shear plane is parallel to the X-axis. As one can see from the picture, the shear angle ε (in radians) equals to derivative of the optical path difference (bias) Λ with respect to the coordinate x:
| (1) |
Figure 5.
Angular splitting the incident beam with two orthogonal polarization components Ex and Ey by DIC prism into two output beams with shear angle ε.
The optical path difference Λ is connected with retardance δ, written in degrees, and wavelength λ in the simple way:
| (2) |
Thus, the shear angle could be found by measuring a derivative of the retardance with respect to the coordinate along the shear direction:
| (3) |
Retardance can be determined with a number of various techniques. In particularly, one could employ the return-path compensation method, which we proposed in 198627-29. This simple technique is similar to the Senarmont compensator30. Because of superposition of the probe and reverse beams the return-path arrangement has the following advantages: (i) owing to a double pass of a beam through a specimen under investigation, the sensitivity threshold is decreased by factor of two; (ii) the same optical elements are utilized twice, in the direct and the reverse beams. It makes the measurement set-up less expensive considerably, which is very important, because one high quality optical polarization element could cost several thousands dollars.
Schematic of the return-path setup is shown in Fig. 6. The device operates as follows. A laser radiates the collimated narrow beam, which is unpolarized or circularly polarized. The beam passes sequentially through a small hole in a screen, Glan-Thompson polarization beam splitter, quarter-wave plate QWP, and DIC prism. The DIC prism under investigation is placed on a linear stage with Vernier micrometer. The stage allows to move the prism in the horizontal direction. The beam passes through the quarter-wave plate and DIC prism two times being reflected from a mirror. The beam splitter deflects the orthogonal polarization component toward a screen. The minimum intensity of the deflected laser beam was visually determined by observing the laser spot brightness on the screen. It is also possible to use a photodiode PD to measure the beam intensity. The intensity of the radiation flux of the deflected orthogonal component I’ is described by the following formula31:
| (4) |
where I is the probing beam intensity, δ is retardance of the DIC prism, ψ is angular orientation of its shear plane, χ is orientation of the principal plane of the polarization beam splitter, ζ is orientation of the fast axis of quarter-wave plate.
Figure 6.
Setup for measuring shear angle of DIC prism with employing the return-path birefringence compensator.
The measuring procedure of retardance derivative consists of the following steps. Before placing the DIC prism under investigation in the setup we look this prism between the crossed polarizers. The shear plane would be perpendicular to the observed color fringes or/and the black fringe. Lets note the shear plane orientation.
Next we take out the quarter-wave plate from the setup, and put the DIC prism into the optical path. In this case, beam intensity on the screen is determined by the next expression:
| (5) |
By rotating the polarization beam splitter from 0° to 180° we achieve two extinctions of the laser spot on the screen. These extinctions differ by 90°. One of the extinction occurs when the beam splitter transmission axis is parallel to the shear plane of the DIC prism, which we noted. In this case the beam splitter angular scale χ points precisely the shear plane orientation ψ.
After that we place the quarter-wave plate QWP into the optical path. The fast axis of the quarter-wave plate has to makes an angle 45° with the shear plane orientation, i.e. ζ = ψ+45°. The beam splitter has to be also rotated by 45°. In this case χ0 = ψ + 45°. Thus, the quarter-wave plate's fast axis is parallel to the beam splitter transmission axis. Laser spot on the screen becomes bright. Using formula (4) we could derive the following equation, which describes the spot's intensity:
| (6) |
Rotating the beam splitter allows to extinguish the spot on the screen. The DIC pris m retardance δ in a point of the laser beam incidence is determined by the simple formula:
| (7) |
where χ is orientation angle of the beam splitter.
Using a linear stage we move the DIC prism in the horizontal direction and measure retardances δ1 and δ2 in two points x1 and x2. The retardance derivative along to the shear direction X could be found by the following formula:
| (8) |
Then we compute the shear angle (in radians):
| (9) |
Instead of finding retardance values in two points only, we can measure dependence of the analyzer angle χ on the laser beam position x and use its derivative in formula above:
| (10) |
Then we compute shear distance d in the object plane and ratio of the shear distance to the Airy disk radius d/rAiry. For the calculation we use standardized reference focal lengths of the tube lenses Lt for infinity-focused objective lens, which are adopted by several microscope manufacturers.
| (11) |
where M is objective lens magnification. In particularly, the reference focal length Lt is 180 mm for Olympus, 164.5 mm for Zeiss, and 200 mm for Nikon and Leica microscopes1.
Radius of Airy disk is rAiry determined by the following equation1:
| (12) |
where NA is objective lens numerical aperture.
In the described setup we utilized a generic green laser pointer with wavelength 532 nm, beam splitting Glan-Thompson polarizer MSBTS-10-45 (Karl Lambrecht, Chicago, IL, http://www.klccgo.com), and precision achromatic quarter-wave plate AQ-100-0545 (Meadowlark, Frederick, CO, http://www.meadowlark.com). Because beam of our laser pointer has significant linearly polarized component we placed a generic circular polarizer for SLR camera between the pointer and the screen. In particularly we employed Tiffen circular polarizer 52HTCP (www.tiffen.com).
The measurement procedure could be simplified with using a custom built assembly with rotatable polarization beam splitter and quarter-wave plate28. This approach would not require taking out and putting in the quarter-wave plate.
Table 1 summaries some results of the shear angle measurements of various DIC prisms currently manufactured by Olympus (Tokyo, Japan, http://www.olympus.com). High-resolution DIC prism U-DICTHR has the smallest shear angle. The prism enables observations with high resolution but less glare even for thick specimen used in developmental and genetic research, such as finely structured diatoms, embryos, zebrafish and C. elegans. All-round prism U-DICT with the intermediate shear angle is suitable for observing a wide range of general specimens, such as tissue. High-contrast DIC prism U-DICTHC has the largest shear angle. Using this prism the high contrast can be obtained even in high magnification observations of thin specimens, such as culture cells.
Table 1.
Measured shear angles, and computed shear distances and ratios of shear distance to Airy disk radius for various combinations of Olympus DIC prisms and objective lenses at wavelength 532nm
| DIC prism type | Shear angle, ε |
Shear distance, d (top); and ratio d/rAiry (bottom) | ||||||
|---|---|---|---|---|---|---|---|---|
| UplanFl 10×/0.30 |
UplanFl 20×/0.50 |
UplanSApo 30×/1.05 Sil |
UplanFl 40×/0.75 |
UplanSApo 60×/1.20 W |
UplanSApo 60×/1.30 Sil |
UplanFl 100×/1.30 Oil |
||
| U-DICTHR | 39 μrad | 0.70μm; 0.65 | 0.35μm; 0.54 | 0.23μm; 0.76 | 0.18μm; 0.40 | 0.12μm; 0.43 | 0.12μm; 0.47 | 0.07μm; 0.28 |
| U-DICT | 75 μrad | 1.35μm; 1.25 | 0.67μm; 1.04 | 0.45μm; 1.46 | 0.34μm; 0.78 | 0.22μm; 0.83 | 0.22μm; 0.90 | 0.14μm; 0.54 |
| U-DICTHC | 149 μrad | 2.68μm; 2.48 | 1.34μm; 2.07 | 0.89μm; 2.89 | 0.67μm; 1.55 | 0.45μm; 1.65 | 0.45μm; 1.79 | 0.27μm; 1.07 |
3.2 Calibration of LC variable retarder for bias modulation
Another parameter, which has to be quantified, is a bias amount introduced by the phase shifter. Any method for measuring retardance could be used to find a dependence of bias on the applied voltage. For example, one could employ the return-path compensation method, which we described in the previous section 3.1. However all calibration methods would require taking the phase shifter out of a microscope and placing it into a separate measuring setup. But on the other hand a phase shift of LC variable retarder depends on the temperature, wavelength, set of incidence angles of the passing rays, etc. Therefore it would be convenient to calibrate the LC variable retarder directly in the OI-DIC microscope (Fig. 1) in order to avoid mismatch between the calibration and actual data.
For measuring dependence of the bias on the applied voltage we could use preliminary calibrated DIC prims. In a transmitted DIC microscope the total optical path difference (bias) between two interfering beams is created by a pair of DIC prisms. One of them is located in the imaging part, and another in the illumination part. Each of the prisms introduces own bias, which is not uniform and has a gradient. However, the prisms are placed and oriented in that way that they mutually compensate the bias gradient. Thus, the total bias distribution becomes even across the objective back focal plane. The bias can be changed by a lateral shifting of one of the DIC prisms along the bias gradient direction. As it was shown in the previous section 3.1 (formula (1)), the unitless bias gradient equals to shear angle (in radians). We can write linear equation for the current bias Λ(x):
| (13) |
where x and x0 are the current and initial positions of the prism, is initial bias. The shear angle ε can be found in Table 1 or it can be measured, as it described the previous section 3.1.
Usually DIC pris m is shifted by a translation screw. Then the bias variation could be determined using the pitch of a screw thread p and revolution number R in the following way:
| (14) |
For example, Olympus high-resolution DIC prism U-DICTHR has translation screw with pitch 2.5 mm. The screw allows maximum 5 rotations. According to the Table 1 the prism shear angle is 40 µrad. Using equation (14) we receive the bias variation Λ = 100 nm per screw 360°-turn and the total range of the bias change Λtot = 500 nm. General Olympus DIC prism U-DICT has 3 mm screw pitch and maximum 5 rotations. Consequently its bias variation Λ is 225 nm per screw turn and the total bias range Λtot is 1125 nm.
Let's consider OI-DIC microscope for the transmitted light (Fig.1). Before calibration the phase shifter and polarization rotators are removed from the microscope. An empty area of the specimen under investigation is placed in the center of view field. The DIC prisms are adjusted for the maximal image darkness. That means the prisms introduce zero total bias. Then the phase shifter is put into the place. Because the polarizer and analyzer are crossed and their transmissial axes are oriented at 45° to the principal axes of the orthogonal DIC prisms the beam intensity in the image central area I(Vrms) could be described by the following equation:
| (15) |
where is beam intensity after the polarizer, Λ1, Λ2, Λ3, and Λ4 are biases contributed by prisms DIC1, DIC2, DIC3, and DIC4, respectively, is combined bias introduced by all prisms, Γ(Vrms) is bias created by the phase shifter, Vrms is effective (rms) value of the applied voltage, and Ic corresponds to a constant offset of the intensity signal.
If the setup is adjusted for the maximal extinction then biases Λ1, Λ2, Λ3, and Λ4 compensate each other and . Thus, in the initial state of the OI-DIC setup, a dependence of beam intensity I0(Vrms) on the applied voltage is determined by the formula:
| (16) |
Next we move laterally one of the DIC prisms by the same distance by rotating the translation screw in the clockwise and counterclockwise directions. According to the linear equation (14) in these cases the prism bias will change by amount . The correspondent dependences of the beam intensity I-1(Vrms) and I1(Vrms) are determined by the following equations:
| (17) |
| (18) |
Using the measured beam intensities I0(Vrms), I-1(Vrms) and I1(Vrms) we could obtain the phase shifter bias Γ(Vrms):
| (19) |
The bias computation formula (19) yields values within [0, λ] interval. In other words, without further analysis, the bias measurement cannot distinguish a certain bias value, say Γ0, Γ0+λ. It is said that the measurement yields wrapped bias information. However, using prior knowledge regarding the continuity of the bias variation, the obtained result can be numerically corrected to cover greater intervals, outside [0, λ], by mathematical operation called phase unwrapping. Mathematically, the unwrapping operation essentially searches for 2π jumps in the signal and corrects them by adding the 2π values back to the signal. For example, Matlab™ has very efficient and fast standard command called “unwrap”.
In order to build the correct bias dependence it is also necessary to take into account a type of LC cell, which is employed in the phase shifter. In particular, retardance of conventional Freedericksz ECB cell decreases with applied voltage. The retardance is minimal and equals about 0.1λ at the highest voltage. In a case of VA ECB cell the retardance is minimal and equals zero when no voltage is applied.
4. COMPUTATION AND EXAMPLE OF OI-DIC IMAGES
A DIC image can be modeled as the superposition of one image over an identical copy that is displaced by a small amount d and phase shifted by bias Γ. For simplicity, consider a phase non-birefringent specimen, which is described in a Cartesian coordinates XOY in the object plane. The specimen is illuminated by monochromatic light with wavelength λ. The intensity distribution I(x,y)in the images depends on specimen orientation and varies proportionally with the cosine of the angle made by the gradients azimuth θ and the direction of wavefront shear11, 32:
| (20) |
where is the initial beam intensity, γ(x,y) and θ(x,y) are the gradient magnitude and azimuth, note i = 1, 2 corresponds to the 1st or 2nd state of shear direction, −45°or +45°, and Ic(x, y) corresponds to a constant offset of the intensity signal. Here we took into account that distance of the shear created by the crossed DIC prisms is .
In order to find two-dimensional distribution of magnitude and azimuth γ and θ we capture two sets of raw DIC images at shear directions −45° and +45° with negative, zero and biases: −Γ, 0, and +Γ 11,32. The following group of equations represents these six DIC images:
| (21) |
where j = −1, 0, 1.
Initially two terms are computed (i = 1, 2):
| (22) |
Using equations (21) we can show that
| (23) |
Using the obtained terms we can calculate the quantitative two-dimension distributions of the gradient magnitude and azimuth of optical paths in the specimen as:
| (24) |
We would like to mention that gradient magnitude represents increment of the optical path difference, which is in nanometers, along lateral coordinate, which is also in nanometers. Thus, the gradient magnitude is unitless. The shear amount d can be measured as it is described in Section 3.1 or found in Table 1.
Notice that the algorithm considered above employs ratios between intensities of light that has interacted with the specimen. Therefore it suppresses contributions of absorption by the specimen, nonuniformity of illumination, etc., which can otherwise deteriorate a DIC image.
Also, after computing the optical path gradient distribution, enhanced regular DIC images Ienh(x,y) can be restored with any shear direction σ, different bias Γ and another shear amount d using the next formula:
| (25) |
The enhanced image provides a calculated image for any desired shear direction and bias without the requirement to directly collect an image for that shear direction and bias. Moreover, the enhanced image will have less noise than a regular DIC image, and it suppresses deterioration of the image due to specimen absorption and illumination nonuniformity.
Optical path difference shows the dry mass distribution of a specimen and can be obtained by computing a line integral11,33. Also other techniques for phase computation can be used, for instance, noniterative Fourier phase integration6, or nonlinear optimization with hierarchical representation34, etc. D.Biggs has developed an iterative deconvolution approach for computation of phase images, based on the same principles as deconvolution techniques normally used to remove out-of-focus haze32,35,36.
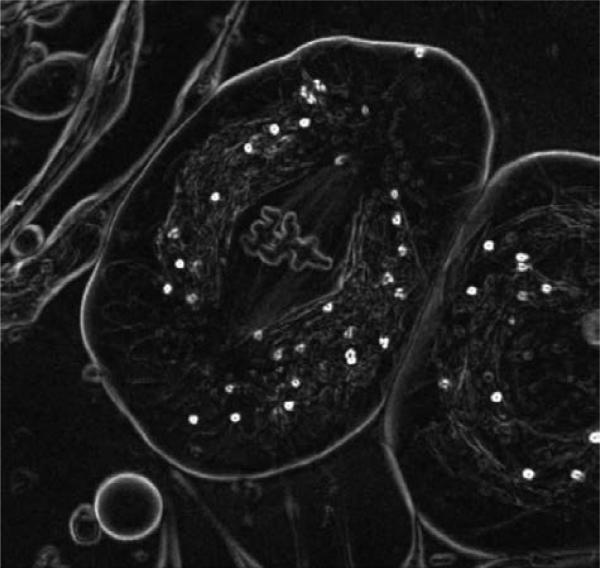
Fig. 7 and 8 show example of the gradient and phase OI-DIC images of a live crane fly spermatocyte during metaphase of meiosis I taken with a Olympus UPlanFl 100x/1.30 oil immersion objective lens and 546/30nm interference filter. Image size is 68 μm × 68 μm. The image acquisition and processing took about 1 second each. The three autosomal bivalent chromosomes are in sharp focus at the spindle equator, along with one of the X-Y sex univalents, which is located on the right. The tubular distribution of mitochondria surrounding the spindle is clearly evident. Both polar flagella in the lower centrosome are in focus, appearing as a letter “L” lying on its side. The experiment was done together with Prof. James LaFountain (State University of New York at Buffalo, Buffalo, NY). The phase image was computed by Dr. David Biggs (KB Imaging Solutions, Waterford, NY) with employing iterative deconvolution approach mentioned above.
Figure 7.
Crane fly spermatocyte (full metaphase of meiosis-I). OI-DIC computed gradient image; brightness is linearly proportional to magnitude of refractive index gradient.
Figure 8.
Crane fly spermatocyte (full metaphase of meiosis-I). OI-DIC computed phase image; brightness is linearly proportional to refractive index.
ACKNOWLEDGEMENTS
This publication was made possible by Grant Number R01-GM101701 from the National Institute of General Medical Sciences, National Institutes of Health. Its contents are solely the responsibility of the author and do not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
REFERENCES
- 1.Oldenbourg R, Shribak M. [Handbook of Optics, Third Edition, Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instruments] McGraw-Hill; New York: 2010. Microscopes; pp. 28.1–28.62. [Google Scholar]
- 2.Holzwarth GM, Webb SC, Kubinski DJ, Allen NS. Improving DIC microcopy with polarization modulation. J. Microscopy. 1997;188(Pt 3):249–254. [Google Scholar]
- 3.Holzwarth GM, Hill DB, McLaughlin EB. Polarization-modulated differential-interference contrast microscopy with a variable retarder. Applied Optics. 2000;39:6288–6294. doi: 10.1364/ao.39.006288. [DOI] [PubMed] [Google Scholar]
- 4.Ooki H, Iwasaki Y, Iwasaki J. Differential interference contrast microscope with differential detection for optimizing image contrast. Applied Optics. 1996;35:2230–2234. doi: 10.1364/AO.35.002230. [DOI] [PubMed] [Google Scholar]
- 5.Hariharan P, Roy M. Achromatic phase-shifting for two-wavelength phase-stepping interferometry. Optics Communication. 1996;126:220–222. [Google Scholar]
- 6.Arnison MR, Larkin KG, Sheppard CJR, Smith NI, Cogswell CJ. Linear phase imaging using differential interference contrast microscopy. J. Microscopy. 2004;214(Pt 1):7–12. doi: 10.1111/j.0022-2720.2004.01293.x. [DOI] [PubMed] [Google Scholar]
- 7.King SV, Libertun AR, Preza C, Cogswell CJ. Calibration of a phase-shifting DIC microscope for quantitative phase imaging. Proc. SPIE. 2007;6443:64430M. [Google Scholar]
- 8.Ishiwata H, Itoh M, Yatagai T. A new method of three-dimensional measurement by differential interference contrast microscope. Optics Communications. 2006;260:117–126. [Google Scholar]
- 9.Ishiwata H, Itoh M, Yatagai T. A new analysis for extending the measurement range of the retardation-modulated differential interference contrast (RM-DIC) microscope. Optics Communications. 2008;281:1412–1423. [Google Scholar]
- 10.Noguchi A, Ishiwata H, Itoh M, Yatagai T. Optical sectioning in differential interference contrast microscopy. Optics Communications. 2009;282:3223–3230. [Google Scholar]
- 11.Shribak M, Inoué S. Orientation-independent differential interference contrast microscopy. Applied Optics. 2006;45:460–469. doi: 10.1364/ao.45.000460. [DOI] [PubMed] [Google Scholar]
- 12.Shribak M. Orientation-independent differential interference contrast microscopy technique and device. 2003 Dec 17; US Patent 7,564,618.
- 13.Shribak M. Orientation-independent differential interference contrast microscopy technique and device. 2003 Dec 17; US Patent 7,233,434.
- 14.Van Munster E, Van Vliet L, Aten J. Reconstruction of optical pathlength distributions from images obtained by a wide-field differential interference contrast microscope. J. Microscopy. 1997;188(Pt2):149–157. doi: 10.1046/j.1365-2818.1997.2570815.x. [DOI] [PubMed] [Google Scholar]
- 15.Preza C, Snyder DL, Conchello JA. Theoretical development and experimental evaluation of imaging models for differential-interference-contrast-microscopy. J. Opt. Soc. Am. A. 1999;16:2185–2199. doi: 10.1364/josaa.16.002185. [DOI] [PubMed] [Google Scholar]
- 16.Hogan H. Getting the small picture. Photonics Spectra. 2003;37(4):58–64. [Google Scholar]
- 17.Danz R, Gretscher P. C-DIC: a new microscopy method for rational study of phase structures in incident light arrangement. Thin Solid Films. 2004;462-463:257–62. [Google Scholar]
- 18.Fabre L, Inoue Y, Aoki T, et al. Differential interference contrast microscope using photonic crystals for phase imaging and three dimensional shape reconstruction. Applied Optics. 2009;48:1347–1357. doi: 10.1364/ao.48.001347. [DOI] [PubMed] [Google Scholar]
- 19.Robinson M, Chen J, Sharp G. [Polarization Engineering for LCD Projection] John Wiley & Sons; West Sussex, England: 2005. [Google Scholar]
- 20.Chipman RA. [Handbook of Optics, Third Edition, Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instruments] McGraw-Hill; New York: 2010. Polarimetry; pp. 15.1–15.46. [Google Scholar]
- 21.Scharf T. [Polarized Light in Liquid Crystals and Polymers] John Wiley & Sons; West Sussex, England: 2007. [Google Scholar]
- 22.Lueder E. [Liquid Crystal Displays : Addressing Schemes and Electro-Optical Effects] John Wiley & Sons; West Sussex, England: 2010. [Google Scholar]
- 23.Gauza S, Wu S-T. [Handbook of Optics, Third Edition, Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instruments] McGraw-Hill; New York: 2010. Liquid Crystals; pp. 8.1–8.40. [Google Scholar]
- 24.Mehta SB, Sheppard CJR. Sample-less calibration of the differential interference contrast microscope. Applied Optics. 2010;49:2954–2968. doi: 10.1364/AO.49.002954. [DOI] [PubMed] [Google Scholar]
- 25.Müller CB, Weiß K, Richtering W, Loman A, Enderlein J. Calibrating differential interference contrast microscopy with dual-focus fluorescence correlation spectroscopy. Optics Express. 2008;16:4322–4329. doi: 10.1364/oe.16.004322. [DOI] [PubMed] [Google Scholar]
- 26.Duncan DD, Fischer DG, Dayton A, Prahl SA. Quantitative Carré differential interference contrast microscopy to assess phase and amplitude. J. Opt. Soc. Am. A. 2011;28:1297–1306. doi: 10.1364/JOSAA.28.001297. [DOI] [PubMed] [Google Scholar]
- 27.Shribak MI. Device for measuring birefringence of reflecting optical data carrier. 1986 Mar 17; USSR Patent 1,414,097.
- 28.Shribak MI. A compensation method for measuring birefringence. Sov. J. Opt. Technol. 1993;60:546–549. [Google Scholar]
- 29.Shribak MI. Autocollimating detectors of birefringence. Proc.SPIE. 1996;2782:805–813. [Google Scholar]
- 30.Hartshorne NH, Stuart A. Crystals and the Polarizing Microscope. 4th ed Edward Arnold; London, United Kingdom: 1970. [Google Scholar]
- 31.Shribak MI. Polarization separation of the forward and reverse beams in the reading of reflective carriers of information. Sov. J. Opt. Technol. 1986;53:389–391. [Google Scholar]
- 32.Shribak M, LaFountain J, Biggs D, et al. Orientation-independent differential interference contrast (DIC) microscopy and its combination with orientation-independent polarization system. J. Biomedical Optics. 2008;13(1):014011. doi: 10.1117/1.2837406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Heise B, Sonnleitner A, Klement EP. DIC image reconstruction on large cell scans. Microscopy Research and Technique. 2005;66:312–320. doi: 10.1002/jemt.20172. [DOI] [PubMed] [Google Scholar]
- 34.Kagalwala F, Kanade T. Reconstructing specimens using DIC microscope images. IEEE Transactions on Systems. Man and Cybernetics – Part B: Cybernetics. 2003;33:728–737. doi: 10.1109/TSMCB.2003.816924. [DOI] [PubMed] [Google Scholar]
- 35.Holmes TJ, et al. [Handbook of Biological Confocal Microscopy] Plenum Press; New York: 1995. Light microscopic images reconstructed by maximum likelihood deconvolution; pp. 389–402. [Google Scholar]
- 36.Biggs D, Andrews M. Acceleration of iterative image restoration algorithms. Applied Optics. 1997;36:1766–1775. doi: 10.1364/ao.36.001766. [DOI] [PubMed] [Google Scholar]