Abstract
Background
Measurement of vascular density has significant value in characterizing healthy and diseased tissue, particularly in brain where vascular density varies among regions. Further, an understanding of brain vessel size helps distinguish between capillaries and larger vessels like arterioles and venules. Unfortunately, few cutting edge methodologies are available to laboratories to rapidly quantify vessel density.
New Method
We developed a rapid microscopic method, which quantifies the numbers and diameters of blood vessels in brain. Utilizing this method we characterized vascular density of five brain regions in both mice and rats, in two tumor models, using three tracers.
Results
We observed the number of sections/mm2 in various brain regions: genu of corpus callosum 161 ± 7, hippocampus 266 ± 18, superior colliculus 300 ± 24, frontal cortex 391 ± 55, and inferior colliculus 692 ± 18 (n=5 animals). Regional brain data were not significantly different between species (p>0.05) or when using different tracers (70kDa and 2000kDa Texas Red; p>0.05). Vascular density decreased (62–79%) in preclinical brain metastases but increased (62%) a rat glioma model.
Comparison with Existing Methods
Our values were similar (p>0.05) to published literature. We applied this method to brain-tumors and observed brain metastases of breast cancer to have a ~2.5-fold reduction (p>0.05) in vessels/mm2 compared to normal cortical regions. In contrast, vascular density in a glioma model was significantly higher (sections/mm2 736 ± 84; p<0.05).
Conclusions
In summary, we present a vascular density counting method that is rapid, sensitive, and uses fluorescence microscopy without antibodies.
Keywords: Vessel Density, Fluorescent Microscopy, Metastases, Immunohistochemistry, TX Red, Indocyanine Green
Graphical Abstract
Vascular density varies significantly between brain regions and between healthy and diseased tissue. However, current methods are arduous and time consuming. Herein we present a rapid simple method to quantify vascular density in brain. Normal brain vasculature is seen with indocyanine green fluorescence within the image.
1. Introduction
Vascular density varies from organ to organ, with some tissues such as lung containing 6-fold higher values than heart (Targan et al., 2003). The brain is a highly vascularized organ, although vessel density varies among regions i.e., thalamus contains 460 vessels/mm2 which is double the number of blood vessels per unit of tissue compared to the superior colliculus (Klein et al., 1986; Wu et al., 2004). Alterations in vessel density are noted in pathological conditions like ischemia, aging, and cancer (Aronen et al., 1994; Eberhard et al., 2000; Farkas and Luiten, 2001; Mann et al., 1986). Clinically, low vascular density is used as a measure of a lack of developmental progress and as an indicator of cerebral palsy or mental retardation in infants (Miyawaki et al., 1998). Similarly a higher density of brain vasculature in stroke patients has been correlated with improved progress and survival due to the increased blood flow to the damaged area (Krupinski et al., 1993). In contrast, higher vessel densities have been associated with lower patient outcome in several types of cancer (Bevilacqua et al., 1995; Nico et al., 2008; Uzzan et al., 2004; Weidner et al., 1993).
Currently, several methods are used to calculate vessel density including the Chalkley method, the Weidner approach, and capillary perfusion of fluorescein isothiocyanate (FITC)-labeled globulin or dextran. Each of these techniques involves manual counting of vessels, which has the limitations of being highly time consuming and difficult to reproduce (Chalkley, 1943; Gobel et al., 1991; Weidner et al., 1991). Human error can be a significant confounding variable in the identification of individual vessels. For example, when the thickness of the tissue sample is so thin that only a small portion of a vessel might be visible, variable human judgement can lead to errors in counting (Nico et al., 2008; Simpson et al., 1996). A review of 43 studies which evaluated vascular density and patient prognosis in breast cancer revealed that only three studies utlized a completely automated methodology to assess vessel density. Of the remaining 40 studies, four used a combined manual and automated system (Uzzan et al., 2004).
To address the limitations of time and human error, we have developed a semiautomated rapid methodology to quickly and accurately assess vascular density of brain tissue. Briefly, the method consists of injecting a large molecular weight fluorescent marker into the peripheral vasculature, allowing the dye to circulate in the blood for approximately 60–120 seconds followed by immediate sacrifice, removal of the brain from the skull within 45 seconds, and immediate freezing in isopentane. Similar to previously published work, in our initial studies, we used the large vascular-impermeant fluorescent dextrans, Texas Red 2000kDa and Texas Red 70kDa, to count the normal brain vascular density of both mice and rats. In subsequent studies we used indocyanine green (ICG), which upon entry to circulation becomes bound to albumin. Albumin is rapidly trapped in the vasculature, and has been used previously as a vascular marker (Habazettl et al., 2010). In studies using Texas Red, we observed that vascular density values in rat and mouse brain showed no significant difference from previously published results using manual counting methods. To expand the application of this method to pathological conditions, we incorporated an experimental brain metastases of breast cancer and an implanted glioma model. Comparison of the metastatic and glioma models showed striking differences in vascular density. Brain metastases generally had a significantly lower number of capillaries per unit of tissue, compared to normal brain, whereas the highly aggressive RG-2 glioma model was 5–6 fold higher in density. In summary, we demonstrate that this methodology has the ability to efficiently and accurately calculate vascular density in normal and pathological brain tissue. Further, this method is easily transferable to numerous labs, which may increase vascular density counting as a variable in neurological studies.
2. Methods
2.1. Chemicals
Lysine fixable dextrans Texas Red 2000kDa MW and Texas Red 70kDa MW were purchased from Molecular Probes (Invitrogen, Eugene, OR). Indocyanine green (ICG) and all other analytical grade chemicals were purchased from Sigma-Aldrich (St. Louis, MO).
2.2. Cell Culture
Human metastatic breast cancer cells transfected with enhanced green fluorescent protein (eGFP) over-expressing Her2 (MDA-MB-231-BR-Her2) and rat glioma (RG-2) cells were cultured in DMEM supplemented with 10% FBS (MDA required Zeocin 300 μg per 500 mL media, Invitrogen). All cells were used in passages 1–10 and maintained at 37°C with 5% CO2. For preparation of cells for injection, cells were grown to 70% confluency, trypsinized, and rinsed twice in 4°C PBS to remove all traces of serum. Cells were resuspended in serum free 4°C DMEM and placed on ice. All cell lines were kindly provided by the laboratory of Dr. Patricia Steeg at the National Cancer Institute.
2.3. Animals
Male F344 rats (220–330 g; n=12), male CD-1 mice (25–30 g, n=12), and female NuNu mice (~25 g; n=12) were obtained from Charles River Laboratories (Kingston, NY); 287Sato/J (Tie-2 GFP; n=3) transgenic female mice were purchased from Jackson Laboratories (Bar Harbor, ME). All studies were approved by the Animal Care and Use Committee at Texas Tech University Health Sciences Center, and conducted in accordance with the 1996 NIH Guide for the Care and Use of Laboratory Animals.
2.4. In Vivo Tumor Models
For development of metastases, female NuNu mice were anesthetized with isoflurane and inoculated with the breast cancer cell line MDA-MB-231-BR-Her2 (1.75×105 cells) in the left cardiac ventricle with the use of a stereotaxic device (Stoelting, Wood Dale, IL) and sterile 28 gauge tuberculin syringes, as previously described (Lockman et al., 2010). Tumor cells seeded the brain and were allowed to grow for 4–6 weeks. Intracranial implantation in F344 rats of RG-2 cells (1.0×105 cells) in 5 μL was accomplished using a stereotaxic frame to inoculate into the caudate-putamen complex at coordinates of 4.5mm lateral to bregma and 4.5mm deep (Ningaraj et al., 2003) after anaesthetizing with ketamine (75–100 mg/kg) and xylazine (6–8 mg/kg). Animals recovered from tumor cell inoculation within 15 minutes. All animals were monitored for signs of lethargy, weight loss, paralysis, and hunched posture. Median survival was 18 days for F344 rats and 32 days for NuNu mice.
2.5. Injection of Vascular Markers
One of the two fluorescent markers (Texas Red MW 2000kDa or Texas Red MW 70kDa) was injected intravenously into F344 rats or CD-1 mice (1.5 mg/animal body weight) via femoral vein using a 31-gauge tuberculin syringe and allowed to circulate for 2 minutes. In tumor studies, on day 30 ± 2 (MDA-MB-231-BR-Her2) and day 7 (RG-2), ICG (1.5 mg/animal), was injected intravenously and allowed to circulate 1 minute. Animals were then euthanized via decapitation under anesthesia (ketamine/xylazine), the brain tissue was rapidly removed (< 45 seconds) and flash frozen in isopentane (−65°C). Care was taken to remove brain rapidly since slower removal may cause changes in the spatial distribution of tracers (Jay et al., 1988; Williams et al., 1991). Sagittal brains sections were sliced at 6μm thickness using a cryostat (Shandon Cryotome®) at −30 ºC. Slices were mounted on glass slides and air-dried with no mounting media or coverslip. Fluorescence images were then obtained from specific brain regions (genu of corpus callosum, hippocampus, superior and inferior colliculus, frontal cortex, caudate putamen) aided by an anatomical atlas (Paxinos and Franklin, 1997; Paxinos and Watson, 1998). The vessel density analysis utilizing the different molecular weight markers and ICG was accomplished by analyzing a subset of tissue sections from each of the brain regions.
2.6. Fluorescence imaging
Fluorescence was observed with an Olympus IX81 stereo microscope (Olympus America Inc., Center Valley, PA) using a 40× objective (NA= 0.6). A 100 Watt short arc mercury lamp was used as the fluorescence light source. Texas Red dextran fluorescence was measured via a DsRed Sputter filter (Chroma Technology: cat # U-M49004XL: excitation 560 nm, emission 645 nm). Likewise, ICG fluorescence was recorded using a Cy7 filter (Chroma Technology: cat # 41009XL: excitation 740 nm, emission 780 nm). A dichromatic mirror prevented emitted light with a wavelength shorter than 565 nm (Texas Red fluorescence) or 770 nm (ICG) to reach the microscope’s camera. Images were acquired with a monochromatic 12-bit cooled CCD camera (Retiga 4000R; QImaging, Surrey, British Columbia) connected to a computer running Slidebook™ 5.0 analysis software (Intelligent Imaging Innovations “3I”, Denver).
2.7. Vessel Density and Size Determination
Slices were analyzed using a binary masking methodology based upon fluorescence to define the vessel locations (Slidebook™ 5.0). Regions of interest were delineated with the help of an anatomical atlas (Paxinos and Franklin, 1997; Paxinos and Watson, 1998) and tissue autofluorescence. Binary masks were created by identifying areas of fluorescent intensity (for both Texas Red and ICG) exceeding a 3-fold threshold above background fluorescence in each channel. Objects exceeding this threshold that were smaller than 1 micron squared (μm2) were excluded from quantitation. Background intensities for each channel were defined by identifying the background peak on the intensity distribution histogram of each image; background intensities were equivalent among each slice evaluated in this study. Briefly, binary masking consisted of defining the vessel based on Texas Red and ICG fluorescence on a voxel by voxel basis. If Texas Red or ICG fluorescence was present (> 3-fold above background) the voxel was considered to belong to a vessel. Vessel densities were calculated per area (mm2). Vessel diameters were determined utilizing the same software and masking system to identify the minor axis length of each object.
2.8. Statistical Analysis
One-way ANOVA analysis followed by Bonferroni’s multiple comparison test was used for vessel density data analysis in control brains during development of the method. For all data, errors are reported as standard error of the mean unless otherwise indicated. For analysis of tumor vessel density, ANOVA analysis with Dunnett’s post-test was used to compare values within each brain region. This test was also used to determine significant differences in tumor vessel diameter. Differences were considered statistically significant at the p< 0.05 level (GraphPad Prism 5.0).
3. Results
3.1. Fluorescence Microscopy Observations of Vessel Density
To develop an efficient technique to identify and calculate brain vessel density, we first perfused transgenic mice expressing Tie-2 driven GFP in brain vasculature to determine whether fluorescent tracers would mark structures other than the vasculature. Intracardially perfused TX Red 70kDa dextran remained within the vasculature and did not stain compartments or structures other than vessels within the brain (Fig 1). We then utilized both rat and mouse injected with Texas Red dextran MW 2000kDa or Texas Red MW 70kDa (circulation time of 2 minutes), or ICG (circulation time of 1 minute) for tumor studies. Objects of interest were based on fluorescence sum intensity (> 3-fold above background) and subsequently counted for each brain region. Representative images are shown of vessel density (F344 and CD-1, 40× magnification) in various brain regions of high vascular density (ie: inferior colliculus with a greater number of vessels) and low vascular density (ie: genu of corpus callosum with fewer vessels) (Fig. 2A). Fig. 2B is a representative image of frontal cortex brain vasculature as identified with red fluorescence (Texas Red 70kDa, 12× magnification); and Fig. 2C shows the overlay of the binary masking technique employed by the software to identify vessels. Smaller red objects are attributed to a minute part of the vessel appearing in the tissue slice.
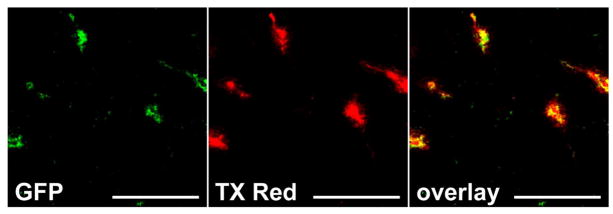
Figure 1. Perfusion of fluorescent tracers label and remain restricted to vessels in brain.
A representative image of Tie-2 driven GFP expression (A) in brain vasculature perfused with TX Red 70kD dextran (B). The overlay (C) of each channel indicates good colocalization and no tracer associated with structures other than brain vasculature. Scale bar = 100μm.
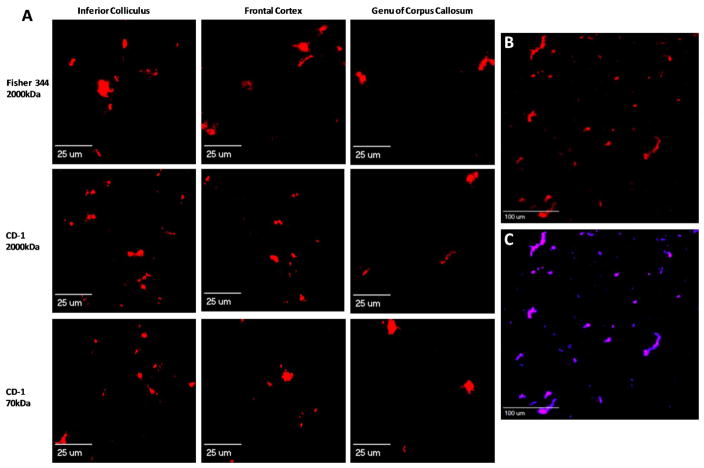
Figure 2. Fluorescence images showing perfused capillaries labeled with TX Red dextrans in different brain regions.
Panel A representative images of capillaries after 2 min in vivo circulation of TX Red 2000 kDa or TX Red 70 kDa (1.5 mg/kg) in F344 rat and CD-1 mouse models (rows). Regional vascular variability is evident by the greater number of red fluorescing objects within the inferior colliculus compared to the genu of corpus callosum. Panels B and C: Images illustrating binary masking in CD-1 mouse frontal cortex region. Panel B illustrates TX Red 70 kDa marked vessels in a 6 μm section. Panel C is the binary mask overlay on images of panel B, identifying capillary sections based on fluorescent intensity.
3.2. Vessel Density Calculations
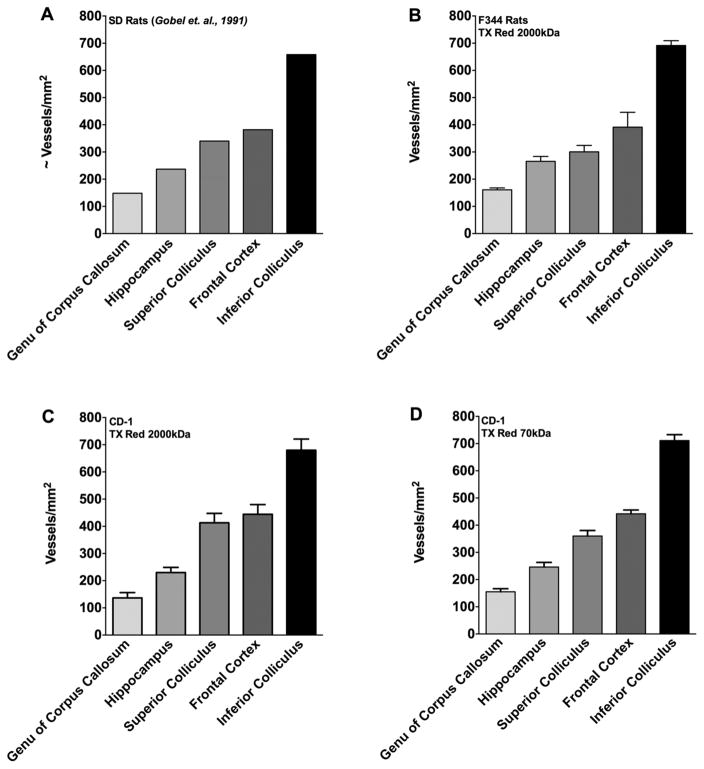
To calculate the density of fluorescently-labeled blood vessels, comprehensive digital microscopy software (Slidebook™ 5.0) was used to select fluorescent objects voxel by voxel and calculate the total number of blood vessels per area (vessels/mm2). Fig. 3A shows the local densities of perfused capillaries as calculated by Gobel et al (1991), who determined vascular densities using two different markers: FITC-globulin and FITC-dextran (both injected in the femoral vein), and FITC-globulin injection into the tail vein. Observed densities varied from ~148 vessels/mm2 in the genu of corpus callosum to ~658 vessels/mm2 in the inferior colliculus. To determine if the current method using fluorescence microscopy would achieve similar values, Texas Red MW 2000kDa was injected into the femoral vein (circulation of 2 minutes). Vessels/mm2 calculated in F344 rats were: genu of corpus callosum 161 ± 7, hippocampus 266 ± 18, superior colliculus 300 ± 24, frontal cortex 391 ± 55, and inferior colliculus 692 ± 18 (n= 5 animals) (Fig. 3B). Vascular densities in previous reports (Gobel et. al, 1991) using identical section thicknesses (6μm) fell within one standard deviation of values obtained in the current study using the Texas Red 2000kDa marker in F344 rats.
Figure 3. Vascular density of various brain regions.
The quantified vascular density of various brain regions are shown . Panel A represents vascular density in male SD rats (data reproduced with permission from (Gobel et al., 1991). Panel B shows vascular density in F344 rats using (2000kDa TxRed), Panel C CD-1 mice (2000kDa TxRed), and Panel D CD-1 mice (70kDa TxRed). No significant differences (p>0.05) in vessel density was observed between previously published work and species. Data were analyzed using one-way ANOVA followed by Bonferroni’s multiple comparison test. All values represent mean ± SEM (n=3–6).
In our second set of experiments, we translated this method to calculate vascular density in the mouse brain, which is a species often used for cancer models but for which there are limited data on brain vascular density. In addition, we compared results observed with Texas Red 2000kDa to those obtained using a smaller molecular weight marker (Texas Red 70kDa) that is known to be vascular impermeant in the 120 second circulation time frame. Values obtained with Texas Red 2000kDa in the mouse (CD-1) brain were: genu of corpus callosum 137 ± 19, hippocampus 230 ± 19, superior colliculus 413 ± 35, frontal cortex 444 ± 36, and inferior colliculus 680 ± 41 (vessels/mm2) (Fig. 3C). Injection of Texas Red 70kDa in CD-1 mice resulted in similar values (One way ANOVA followed by Bonferroni’s multiple comparison’s test; p> 0.05) as Texas Red 2000kDa, ranging from 155 ± 11 in the genu of corpus callosum to 711 ± 22 in the inferior colliculus (Fig. 3D). While the values within the mouse were similar (p> 0.05) using either tracer, a small increase in vascular density was seen in the superior colliculus and frontal cortex regions in the mouse brain compared to the F344 rat, though it was not signficantly different (One way ANOVA followed by Bonferroni’s multiple comparison test; p> 0.05).
3.3. Vessel Size Distribution in Brain
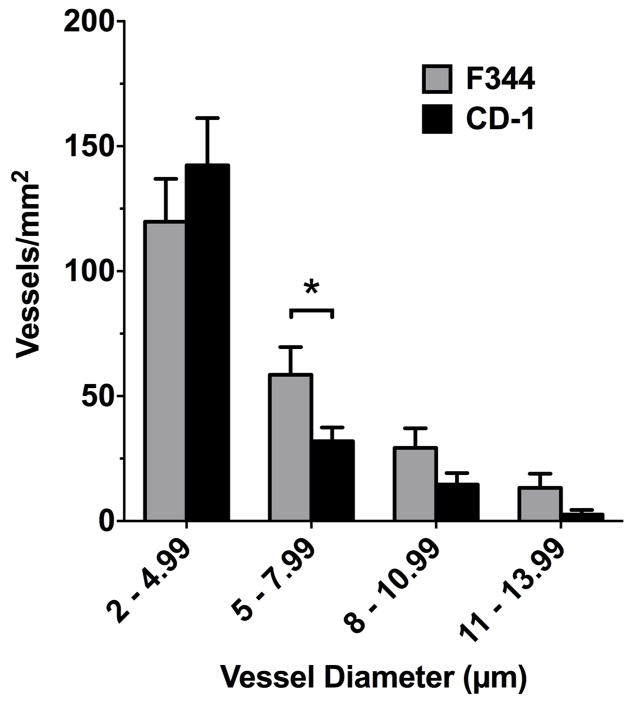
For size analysis of fluorescently labeled vessels, we separated objects of interest (vessels filled with Texas Red 2000kDa) into categories based on minor axis length (diameter). Within both rat and mouse brains, the majority of vessels were in the vessel size range of <10 μm (~81% and ~94%, respectively) (Fig. 4). The size range with the greatest number of vessels was 2–4.99 μm (rat had 168 vessels and mouse had 90). The vessel size range (~10–14 μm) contained ~12% and ~4.8% of vessels counted in the rat and mouse brains, respectively. The rat model produced a greater number of vessels with diameter in the size range of 5–7.99 μm compared with the mouse (p= 0.037) and is consistent with previous reports (Howell et al., 1974). All other vessel sizes were not different between mouse and rat in this study. While previous studies (Heinsen and Heinsen, 1983) agree with these observation, differences in methodology and technology have been known to introduce variability in these measurements of vascular density (Burns et al., 1981; Hunziker et al., 1979).
Figure 4. Size distribution of vascular diameter in control regions of rat and mouse brain.
Data shows comparison between F344 (grey bar) and CD-1 (black bar) vessel diameters. The F344 rat model showed a greater number of vessels in the size range 5–7.99 μm compared to the CD-1 mouse model (* p= 0.037); however, no significant differences (p>0.05) were observed in the distribution of other size ranges. All data include an n=3–5 mice/rats per group and an n>3 brain slices analyzed per rodent. All data represent the number of vessels per mm2 (mean ± SEM).
3.4 Vascular Density Values are Decreased in Preclinical Brain Metastases and Elevated in Implanted Gliomas Regardless of Location
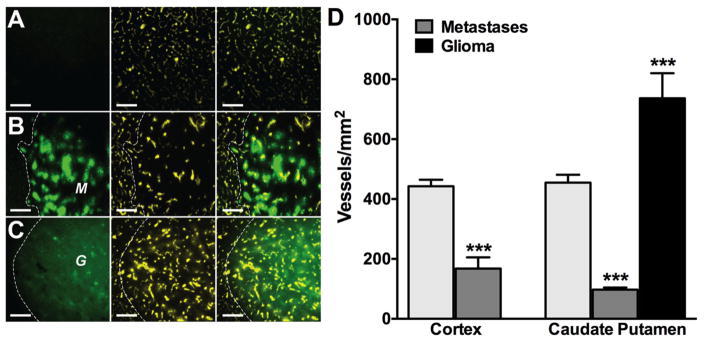
After validation of the current counting technique in normal brain in both rat and mouse, we applied it to two pathological models of brain cancer: experimental brain metastases of breast cancer (MDA-MB-231-BR-Her2) and an intracranially implanted rat glioma model (RG-2). For the brain metastases model, 175,000 MDA-MB-231-BR-Her2 breast cancer cells were injected into the left cardiac ventricle of anesthetized NuNu female mice and allowed to metastasize to brain. To initiate the glioma model, 1.0×105 stably eGFP-transfected rat glioma (RG-2) cells were intracranially implanted in the caudate putamen of anesthetized F344 rats using a stereotaxic apparatus (Stoelting Co.; Wood Dale, IL). Lesions were allowed to develop (~30 days for MDA-MB-231-BR-Her2 and ~7 days for the RG-2 model) and indocyanine green (ICG) was injected intravenously as a near-infrared tracer (Habazettl et al., 2010). Representative images of ICG labeled vasculature are shown here, obtained from normal brain parenchyma (Fig. 5A), a MDA-MB-231-BR-Her2 metastatic lesion (Fig. 5B) and an experimental glioma (Fig. 5C). Qualitatively, a decrease in vessel density is observed in experimental brain metastases (Fig. 5B) compared to the higher densities seen in normal corresponding brain regions (Fig. 5A) and the experimental glioma model (Fig. 5C). As shown in Fig. 5D there is a quantitatively significant (p< 0.001) ~2.5-fold reduction in vessels/mm2 in metastatic lesions (MDA-MB-231-BR-Her2: 168 ± 37) compared with normal brain parenchyma (443 ± 21) in cortical regions. Similarly, vascular density values of experimental lesions in the caudate putamen region of the brain, were also signifcantly (p< 0.001) decreased (MDA-MB-231-BR-Her2: 97 ± 7) compared to the corresponding normal brain region (455 ± 26). In addition, the time frame for development of lesions corresponded to the vessel density and agressiveness of the lesion ie., ~32 days for metastases compared to ~7 days RG-2 gliomas; and vascular density values of the experimental metastases (~138 vessels/mm2 average) were substantially less than (p< 0.001) that observed in the glioma model (736 ± 84).
Figure 5. Vascular density is decreased in metastatic lesions compared to normal brain parenchyma regardless of location.
Representative fluorescence images of GFP (left panel), ICG (center panel), and overlay (right panel) in normal brain (row A), metastatic tumor (row B), and RG2 glioma regions (row C). GFP labelled metastases (M) or glioma (G) are shown with adjacent tissue separated by white dashed lines. Scale bars = 200μm. (D) Vascular density of cortex and metastases (1st and 2nd column) in corresponding cortex region. The 3rd–5th columns show vascular density of cuadate-putamen, metastastes, and glioblastoma in corresponding brain region (caudate-putamen). Statistical significance in cortical samples was determined using Student’s t-test; ***p < 0.001, n=3–5. Significance in caudate putamen region was determined using ANOVA with Bonferroni’s multiple comparison’s test; *** p < 0.0001, n=3–5.
4. Discussion
There are several limitations in current methodologies used to evaluate vascular density. The Chalkley method involves hand counting nuclei within randomly achieved hot spots, but is used to achieve ratios of volumes rather than actual cell numbers (Chalkley, 1943). A second method is immunohistochemical staining of tissue for vessel density analysis. Limitations of this method include differing protocols from one lab to the next such as fixation techniques, antibody dilutions, and long storage periods, all of which can result in protein loss and contribute to human error (Bertheau et al., 1998; Jacobs et al., 1996; Walker, 2006). Lastly, vascular density has been manually calculated using perfused FITC labeled fibronectin or FITC conjugated dextran. While all three methods yield similar results, they all involve time consuming manual calculations (Gobel et al., 1991; Klein et al., 1986). In contrast with the previous methodologies, the current technique put forth in this report utilizes comprehensive digital microscopy software to evaluate microvessel density, yields immediate results thereby reducing counting time, and substantially reduces variability introduced by human observation.
Fluorescent dye based determination of vascular density has become widely employed for quantification. However, a major problem associated with fluorescent markers is photobleaching (the photochemical destruction of the fluorophore due to prolonged periods of exposure to a light source) (Giloh and Sedat, 1982). Common fluorescence dyes such as FITC are prone to rapid bleaching when exposed to excitation light sources, such as the 100 Watt short arc mercury lamp used in this study, and are sensitive to pH and moisture during sample storage (Benchaib et al., 1996); newer generation fluorescence probes exhibit improved photostability and are less susceptible to photobleaching (Lefevre et al., 1996; Titus et al., 1982). To prevent photobleaching in this study, we limited the period of exposure of the fluorophores to 800 milliseconds with a green fluorescent filter and kept the slides in the dark at all times. Focusing of the images was performed in the dark utilizing a small amount of visible light to ensure no exposure to the excitation light until the moment of image capture. Using this technique, the observed total fluorescence intensity emanating from the vasculature did not change more than 7% during imaging (data not shown).
To address the limitation of the potential vascular extravasation of the marker, we selected fluorescent markers either bound to large dextrans (Texas Red 2000kDa and Texas Red 70kDa) or to albumin. Vascular extravasation must be addressed since it would potentially increase vessel density counts and could affect the morphological size analysis of vessels in brain. It has been previously shown that large molecular weight markers are trapped within the vasculature of the brain (Pardridge, 2005). For this study, we chose a dextran conjugated Texas Red tracer which, because of its size and hydrophilic nature, exhibits poor extravasation into brain across an intact BBB. Unlike many classical fluorescent dyes such as fluorescein sodium and FITC, more than 95% of indocyanin green binds protein in plasma (Haglund et al., 1994) which restricts it to the vasculature in brain and making ICG an optimal vascular marker. In our study, we used a circulation time of two minutes, to balance an adequate perfusion of the brain vasculature with minimal to no leakage of the marker into the brain parencyhma (Reese and Karnovsky, 1967). Microscopic evaluation of our data revealed that all vascular sections had sharp fluorescence “edges” indicating the dyes were limited to the vascular space. This method may be applied easily into other laboratories as fluorescent dextrans of varying sizes are often used as vascular markers (Hoffmann et al., 2011), given their price and relative ease of administration. Brain tissue autofluorescence reduces the signal-to-noise ratio and degrades sharp contrasting structure when imaging fluorescent probes emitting in the 340–525nm wavelength ranges (Billinton and Knight, 2001; Duong and Han, 2013). Unlike many classical fluorescence probes such as FITC, Texas Red dextran and ICG are well suited for quantification of vascular density since their emission peak wavelengths occur outside and further red-shifted than most of the spectra of brain autofluorescence (Molitoris et al., 2002). The use of these red-shifted fluorescent probes enhances the signal-to-noise and structural contrast in brain tissue samples.
Early studies in counting brain vascular density presented conflicting numbers, with some groups presenting much lower data than others. While it was recognized that there was potential human error in counting, others groups postulated that not all capillary beds in brain were open during all times. One hypothesis was discussed which suggested that brain capillaries opened and closed over time creating “reserve” capillaries, that could be opened to deliver oxygen and glucose during increased metabolic demand (Klein et al., 1986). A second hypothesis suggested that the opening and closing of capillaries occurred fairly quickly in response to a “stop and go” movement of blood (Ozanne, 1975). However, as vacular density studies progressed, values calculated using a method of capillary perfusion of FITC labeled globulin were compared to values identified with immunofluorescence labeling, and no significant difference in various brain regions were noted (Gobel et al., 1991). Other studies reported similar results using gamma globulin coupled fluorophores and various circulation times, and eventually, it was accepted that brain capillaries appear to be constantly perfused under normal physiological conditions (Klein et al., 1986). Our data are similar to the mentioned studies other than that our calculations are performed with semi-automated software.
This study reports accurate vascular density numbers for CD-1 mice and immune compromised mice (cortical and caudate-putamen regions), which up to now has been signficantly lacking in the literature. Most studies that calculate vascular densities for pathological purposes employ a ratio method, reporting the vessel surface area divided by the brain parenchyma area. For this study, we did not follow the classical design-based stereological approach (Dockery and Fraher, 2007; Muhlfeld, 2014; Walchli et al., 2015). However, our method differed from stereological approaches only by the method in which the tissue sections were cut so that we could identify specific brain regions in which measurements were acquired. All tissue slices were sectioned at equivalent slice thickness and equidistant from another to adhere as close to a stereological approach as possible. In an effort provide comparable data to literature (Gobel et al., 1991), we chose not to transform the vessel densities to a number per unit volume. Of note, it has been determined that microvessels in the cortex of rodents are oriented isotropically (Eins and Bar, 1978) and, therefore, reduces methodological bias in this study. The vascular densities categorized by vessel diameter between mouse and rat had minor variations that were not significantly different except for vessel sizes of 5–7.99 μm in diameter; these results are similar to previous studies (Heinsen and Heinsen, 1983). The small variations observed can likely be attributed to structural differences between rat and mouse nervous tissue as a result of strain-related differences in vascular architecture (Beckmann et al., 1999; Burns et al., 1981; Hunziker et al., 1979; Kitagawa et al., 1998).
To apply a semi-automated technique in a pathological model, we performed vascular density counts in mice with experimental brain metastases and an RG-2 rat glioma implantation model. Vessel density counts in MDA-MB-231-BR-Her2 metastatic lesions within the cortical region were reduced 62% compared to normal brain parenchyma. Vessel densities in metastases in the caudate-putamen complex were decreased to densities 21% of control brain values and 13% of RG-2 gliomas. Implanted gliomas were highly vascular with densities ~1.5 fold greater than normal brain parenchyma. Gliomas are considered highly angiogenic and aggressive with increased vascular density; and metastases have been shown to have vessel densities at only fractions of corresponding normal tissue (Ribatti, 2008; Yano et al., 2000).
In conclusion, the data presented herein confirm the validity of a semi-automated rapid methodology utilizing fluorescence microscopy and comprehensive software to efficiently evaluate brain vessel density. This study puts forth data showing congruence of this semi-automated technique to previously published manual counts. Application of the current technique to a pathological model demonstrated decreased vessel density within metastatic lesions and increased density in cranially implanted gliomas. Since analysis of vessel density plays a critical role in several disease states, this new technique will aid in more efficient data acquisition in both the clinical and laboratory settings.
Highlights.
We describe the development and evaluation of a semi-automated methodology utilizing fluorescence microscopy and comprehensive digital microscopy software to rapidly calculate vascular density within brain and cancerous lesions in brain.
This novel methodology produces data comparable to previously hand counting pathology methods.
Vascular density is decreased in experimental brain metastases of breast cancer compared to corresponding brain regions in a highly angiogenic preclinical glioma model as well as healthy control mice.
Acknowledgments
This research was supported by grants from the National Cancer Institute (R01CA166067-01A1) and Department of Defense Breast Cancer Research Program (W81XWH-062-0033) awarded to P. Lockman. Additional support for this research was provided by WVCTSI through the National Institute of General Medical Sciences of the National Institutes of Health (WVCTSI Award: U54GM104942, and the CoBRE P30 GM103488).
Abbreviations
- BBB
Blood Brain Barrier
- SD
Sprague-Dawley rats
- CD-1
Charles River CD-1 Swiss mice
- F344
Fisher 344 rats
- VD
Vessel/Vascular Density
- kDa
kilodalton
- ICG
Indocyanine Green
- eGFP
Enhanced Green Fluorescent Protein
- MW
molecular weight
- TX Red
Texas Red
- FITC
fluorescein isothiocyanate
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aronen HJ, Gazit IE, Louis DN, Buchbinder BR, Pardo FS, Weisskoff RM, Harsh GR, Cosgrove GR, Halpern EF, Hochberg FH, et al. Cerebral blood volume maps of gliomas: comparison with tumor grade and histologic findings. Radiology. 1994;191:41–51. doi: 10.1148/radiology.191.1.8134596. [DOI] [PubMed] [Google Scholar]
- Beckmann N, Stirnimann R, Bochelen D. High-resolution magnetic resonance angiography of the mouse brain: application to murine focal cerebral ischemia models. J Magn Reson. 1999;140:442–50. doi: 10.1006/jmre.1999.1864. [DOI] [PubMed] [Google Scholar]
- Benchaib M, Delorme R, Pluvinage M, Bryon PA, Souchier C. Evaluation of five green fluorescence-emitting streptavidin-conjugated fluorochromes for use in immunofluorescence microscopy. Histochemistry and cell biology. 1996;106:253–6. doi: 10.1007/BF02484409. [DOI] [PubMed] [Google Scholar]
- Bertheau P, Cazals-Hatem D, Meignin V, de Roquancourt A, Verola O, Lesourd A, Sene C, Brocheriou C, Janin A. Variability of immunohistochemical reactivity on stored paraffin slides. J Clin Pathol. 1998;51:370–4. doi: 10.1136/jcp.51.5.370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevilacqua P, Barbareschi M, Verderio P, Boracchi P, Caffo O, Dalla Palma P, Meli S, Weidner N, Gasparini G. Prognostic value of intratumoral microvessel density, a measure of tumor angiogenesis, in node-negative breast carcinoma--results of a multiparametric study. Breast Cancer Res Treat. 1995;36:205–17. doi: 10.1007/BF00666041. [DOI] [PubMed] [Google Scholar]
- Billinton N, Knight AW. Seeing the wood through the trees: a review of techniques for distinguishing green fluorescent protein from endogenous autofluorescence. Anal Biochem. 2001;291:175–97. doi: 10.1006/abio.2000.5006. [DOI] [PubMed] [Google Scholar]
- Burns EM, Kruckeberg TW, Gaetano PK. Changes with age in cerebral capillary morphology. Neurobiology of aging. 1981;2:283–91. doi: 10.1016/0197-4580(81)90037-3. [DOI] [PubMed] [Google Scholar]
- Chalkley HW. Method for the Quantitative Morphologic Analysis of Tissues. Journal of the National Cancer Institute. 1943;4:47–53. [Google Scholar]
- Dockery P, Fraher J. The quantification of vascular beds: a stereological approach. Experimental and molecular pathology. 2007;82:110–20. doi: 10.1016/j.yexmp.2006.12.011. [DOI] [PubMed] [Google Scholar]
- Duong H, Han M. A multispectral LED array for the reduction of background autofluorescence in brain tissue. Journal of neuroscience methods. 2013;220:46–54. doi: 10.1016/j.jneumeth.2013.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberhard A, Kahlert S, Goede V, Hemmerlein B, Plate KH, Augustin HG. Heterogeneity of angiogenesis and blood vessel maturation in human tumors: implications for antiangiogenic tumor therapies. Cancer Res. 2000;60:1388–93. [PubMed] [Google Scholar]
- Eins S, Bar T. Orientation distribution of blood vessels in central nervous tissue. Sonderb Prakt Metallogr. 1978;8:381–8. [Google Scholar]
- Farkas E, Luiten PG. Cerebral microvascular pathology in aging and Alzheimer’s disease. Prog Neurobiol. 2001;64:575–611. doi: 10.1016/s0301-0082(00)00068-x. [DOI] [PubMed] [Google Scholar]
- Giloh H, Sedat JW. Fluorescence microscopy: reduced photobleaching of rhodamine and fluorescein protein conjugates by n-propyl gallate. Science. 1982;217:1252–5. doi: 10.1126/science.7112126. [DOI] [PubMed] [Google Scholar]
- Gobel U, Theilen H, Schrock H, Kuschinsky W. Dynamics of capillary perfusion in the brain. Blood Vessels. 1991;28:190–6. doi: 10.1159/000158861. [DOI] [PubMed] [Google Scholar]
- Habazettl H, Athanasopoulos D, Kuebler WM, Wagner H, Roussos C, Wagner PD, Ungruhe J, Zakynthinos S, Vogiatzis I. Near-infrared spectroscopy and indocyanine green derived blood flow index for noninvasive measurement of muscle perfusion during exercise. J Appl Physiol. 2010;108:962–7. doi: 10.1152/japplphysiol.01269.2009. [DOI] [PubMed] [Google Scholar]
- Haglund MM, Hochman DW, Spence AM, Berger MS. Enhanced optical imaging of rat gliomas and tumor margins. Neurosurgery. 1994;35:930–40. doi: 10.1227/00006123-199411000-00019. discussion 40–1. [DOI] [PubMed] [Google Scholar]
- Heinsen H, Heinsen YL. Cerebellar capillaries. Qualitative and quantitative observations in young and senile rats. Anat Embryol (Berl) 1983;168:101–16. doi: 10.1007/BF00305402. [DOI] [PubMed] [Google Scholar]
- Hoffmann A, Bredno J, Wendland M, Derugin N, Ohara P, Wintermark M. High and Low Molecular Weight Fluorescein Isothiocyanate (FITC)-Dextrans to Assess Blood-Brain Barrier Disruption: Technical Considerations. Transl Stroke Res. 2011;2:106–11. doi: 10.1007/s12975-010-0049-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell WH, Fulton JF, Ruch TC, Patton HD. Physiology and biophysics: Circulation, respiration and fluid balance. Saunders; 1974. [Google Scholar]
- Hunziker O, Abdel’Al S, Schulz U. The aging human cerebral cortex: a stereological characterization of changes in the capillary net. J Gerontol. 1979;34:345–50. doi: 10.1093/geronj/34.3.345. [DOI] [PubMed] [Google Scholar]
- Jacobs TW, Prioleau JE, Stillman IE, Schnitt SJ. Loss of tumor marker-immunostaining intensity on stored paraffin slides of breast cancer. J Natl Cancer Inst. 1996;88:1054–9. doi: 10.1093/jnci/88.15.1054. [DOI] [PubMed] [Google Scholar]
- Jay TM, Lucignani G, Crane AM, Jehle J, Sokoloff L. Measurement of local cerebral blood flow with [14C]iodoantipyrine in the mouse. J Cereb Blood Flow Metab. 1988;8:121–9. doi: 10.1038/jcbfm.1988.16. [DOI] [PubMed] [Google Scholar]
- Kitagawa K, Matsumoto M, Yang G, Mabuchi T, Yagita Y, Hori M, Yanagihara T. Cerebral ischemia after bilateral carotid artery occlusion and intraluminal suture occlusion in mice: evaluation of the patency of the posterior communicating artery. J Cereb Blood Flow Metab. 1998;18:570–9. doi: 10.1097/00004647-199805000-00012. [DOI] [PubMed] [Google Scholar]
- Klein B, Kuschinsky W, Schrock H, Vetterlein F. Interdependency of local capillary density, blood flow, and metabolism in rat brains. Am J Physiol. 1986;251:H1333–40. doi: 10.1152/ajpheart.1986.251.6.H1333. [DOI] [PubMed] [Google Scholar]
- Krupinski J, Kaluza J, Kumar P, Wang M, Kumar S. Prognostic value of blood vessel density in ischaemic stroke. Lancet. 1993;342:742. doi: 10.1016/0140-6736(93)91734-4. [DOI] [PubMed] [Google Scholar]
- Lefevre C, Kang HC, Haugland RP, Malekzadeh N, Arttamangkul S, Haugland RP. Texas Res-X and rhodamine Red-X, new derivatives of sulforhodamine 101 and lissamine rhodamine B with improved labeling and fluorescence properties. Bioconjug Chem. 1996;7:482–9. doi: 10.1021/bc960034p. [DOI] [PubMed] [Google Scholar]
- Lockman PR, Mittapalli RK, Taskar KS, Rudraraju V, Gril B, Bohn KA, Adkins CE, Roberts A, Thorsheim HR, Gaasch JA, Huang S, Palmieri D, Steeg PS, Smith QR. Heterogeneous blood-tumor barrier permeability determines drug efficacy in experimental brain metastases of breast cancer. Clinical cancer research : an official journal of the American Association for Cancer Research. 2010;16:5664–78. doi: 10.1158/1078-0432.CCR-10-1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann DM, Eaves NR, Marcyniuk B, Yates PO. Quantitative changes in cerebral cortical microvasculature in ageing and dementia. Neurobiol Aging. 1986;7:321–30. doi: 10.1016/0197-4580(86)90158-2. [DOI] [PubMed] [Google Scholar]
- Miyawaki T, Matsui K, Takashima S. Developmental characteristics of vessel density in the human fetal and infant brains. Early Hum Dev. 1998;53:65–72. doi: 10.1016/s0378-3782(98)00043-7. [DOI] [PubMed] [Google Scholar]
- Molitoris BA, Sandoval R, Sutton TA. Endothelial injury and dysfunction in ischemic acute renal failure. Crit Care Med. 2002;30:S235–40. doi: 10.1097/00003246-200205001-00011. [DOI] [PubMed] [Google Scholar]
- Muhlfeld C. Quantitative morphology of the vascularisation of organs: A stereological approach illustrated using the cardiac circulation. Ann Anat. 2014;196:12–9. doi: 10.1016/j.aanat.2012.10.010. [DOI] [PubMed] [Google Scholar]
- Nico B, Benagiano V, Mangieri D, Maruotti N, Vacca A, Ribatti D. Evaluation of microvascular density in tumors: pro and contra. Histol Histopathol. 2008;23:601–7. doi: 10.14670/HH-23.601. [DOI] [PubMed] [Google Scholar]
- Ningaraj NS, Rao MK, Black KL. Adenosine 5′-triphosphate-sensitive potassium channel-mediated blood-brain tumor barrier permeability increase in a rat brain tumor model. Cancer research. 2003;63:8899–911. [PubMed] [Google Scholar]
- Ozanne G, Vilnis V, Severinghaus J. In: Harper AM, editor. Implications of oxygen waves and synchrony for regulation of cerebral microcirculation; Blood flow and metabolism in the brain: proceedings of the 7th International Symposium on Cerebral Blood Flow and Metabolism; Aviemore, Scotland. June 17th–20th, 1975; Aviemore, Scotland: Churchill Livingstone; 1975. [Google Scholar]
- Pardridge WM. The blood-brain barrier: bottleneck in brain drug development. NeuroRx. 2005;2:3–14. doi: 10.1602/neurorx.2.1.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paxinos G, Franklin KB. The mouse brain in stereotaxic coordinates. 2. Academic Press; 1997. [Google Scholar]
- Paxinos G, Watson C. The rat brain in stereotaxic coordinates. 4. Academic Press; San Diego: 1998. [Google Scholar]
- Reese TS, Karnovsky MJ. Fine structural localization of a blood-brain barrier to exogenous peroxidase. The Journal of cell biology. 1967;34:207–17. doi: 10.1083/jcb.34.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribatti DaV A. Overview of Angiogenesis During Tumor Growth. In: Folkman WDFaJ., editor. Angiogenesis: An Integrative Approach from Science to Medicine. Springer Science+Business Media, LLC; New York, NY: 2008. pp. 161–8. [Google Scholar]
- Simpson JF, Ahn C, Battifora H, Esteban JM. Endothelial area as a prognostic indicator for invasive breast carcinoma. Cancer. 1996;77:2077–85. doi: 10.1002/(SICI)1097-0142(19960515)77:10<2077::AID-CNCR17>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Targan SR, Shanahan F, Karp LC. Inflammatory bowel disease : from bench to bedside. 2. Kluwer Academic Pub; Dordrecht ; Boston: 2003. [Google Scholar]
- Titus JA, Haugland R, Sharrow SO, Segal DM. Texas Red, a hydrophilic, red-emitting fluorophore for use with fluorescein in dual parameter flow microfluorometric and fluorescence microscopic studies. Journal of immunological methods. 1982;50:193–204. doi: 10.1016/0022-1759(82)90225-3. [DOI] [PubMed] [Google Scholar]
- Uzzan B, Nicolas P, Cucherat M, Perret GY. Microvessel density as a prognostic factor in women with breast cancer: a systematic review of the literature and meta-analysis. Cancer research. 2004;64:2941–55. doi: 10.1158/0008-5472.can-03-1957. [DOI] [PubMed] [Google Scholar]
- Walchli T, Mateos JM, Weinman O, Babic D, Regli L, Hoerstrup SP, Gerhardt H, Schwab ME, Vogel J. Quantitative assessment of angiogenesis, perfused blood vessels and endothelial tip cells in the postnatal mouse brain. Nature protocols. 2015;10:53–74. doi: 10.1038/nprot.2015.002. [DOI] [PubMed] [Google Scholar]
- Walker RA. Quantification of immunohistochemistry--issues concerning methods, utility and semiquantitative assessment I. Histopathology. 2006;49:406–10. doi: 10.1111/j.1365-2559.2006.02514.x. [DOI] [PubMed] [Google Scholar]
- Weidner N, Carroll PR, Flax J, Blumenfeld W, Folkman J. Tumor angiogenesis correlates with metastasis in invasive prostate carcinoma. Am J Pathol. 1993;143:401–9. [PMC free article] [PubMed] [Google Scholar]
- Weidner N, Semple JP, Welch WR, Folkman J. Tumor angiogenesis and metastasis--correlation in invasive breast carcinoma. N Engl J Med. 1991;324:1–8. doi: 10.1056/NEJM199101033240101. [DOI] [PubMed] [Google Scholar]
- Williams JL, Shea M, Furlan AJ, Little JR, Jones SC. Importance of freezing time when iodoantipyrine is used for measurement of cerebral blood flow. Am J Physiol. 1991;261:H252–6. doi: 10.1152/ajpheart.1991.261.1.H252. [DOI] [PubMed] [Google Scholar]
- Wu EX, Tang H, Jensen JH. High-resolution MR imaging of mouse brain microvasculature using the relaxation rate shift index Q. NMR Biomed. 2004;17:507–12. doi: 10.1002/nbm.921. [DOI] [PubMed] [Google Scholar]
- Yano S, Shinohara H, Herbst RS, Kuniyasu H, Bucana CD, Ellis LM, Davis DW, McConkey DJ, Fidler IJ. Expression of vascular endothelial growth factor is necessary but not sufficient for production and growth of brain metastasis. Cancer Res. 2000;60:4959–67. [PubMed] [Google Scholar]