Fluid motion and shear forces in platelet storage bags with different modes of agitation

Abstract

This study describes a new method for comparison of fluid motion and associated shear forces with various modes of platelet agitation. Fluid motion generated by flatbed, tumbler-type, and circular platelet agitators was investigated. Trajectory tracings of polyethylene beads suspended inside platelet storage bags were used to calculate motion parameters. Mean particle speeds generated by flatbed agitation were approximately 25-fold greater than those generated by 3-RPM tumbler-type agitation, corresponding to a wall shear stress increase of approximately 7-fold for flatbed agitation. As such, flatbed agitation is more likely to contribute to shear-associated changes in platelets than other modes of agitation.

INTRODUCTION

Platelet (PLT) agitation during storage is important for maintaining PLT morphology and pH by enhancing carbon dioxide (CO₂) exchange and helping to regulate rates of oxygen (O₂) consumption [1, 2]. However, deleterious changes in PLTs still occur during storage, a phenomenon known as the PLT storage lesion (PSL) [3]. While minor improvements in storage have been obtained with additive solutions [4], no modification has yet succeeded in preventing the PSL.

Previous studies have examined the contribution of agitation to the PSL. Investigations have shown that agitation can impact the release of granule and cytosolic contents from PLTs during storage, as well as diminish in vivo PLT recovery [5–10]. In these studies, PLT mixing in a “back-and-forth” motion (flatbed) and rotational agitation with the plane of the bag either parallel (tumbler) or perpendicular (circular) to the rotational axis generally have given the best overall performance [2, 6–10]. In contrast, orienting the bag plane at an angle other than 90° to the rotational axis (elliptical), results in higher release of lactate dehydrogenase and β-thromboglobulin, indicative of more PLT damage/activation.

These past observations suggest that the mode of agitation contributes to PLT activation, and by extension, to the PSL. However, the reason why some forms of agitation result in less PLT activation than others is incompletely understood. A hypothesis is that some forms of agitation create larger shear forces inside the PLT bag, a known activator of PLTs in vivo [11]. To investigate this further, we sought to: 1) devise a method to quantify shear forces associated with fluid motion in PLT agitators, and 2) compare shear forces generated by different modes of agitation.

MATERIALS AND METHODS

Particle tracking in PLT storage bags with video imaging

Fluid motion was measured by tracking the movement of 1mm diameter polyethylene plastic beads (Cospheric, Santa Barbara, CA) suspended in 50 mL water and placed inside CLX PLT bags (Pall Corporation, East Hills, NY). Bead and water density were matched (1 g/mL), allowing bead movement to represent fluid movement. The use of water ensured fluid clarity for bead visualization and eliminated inter-experimental variability in fluid density and viscosity. Testing was performed using agitators described in the Figure 1 legend. A video camera (iPhone 3GS, Apple Inc., Cupertino, CA) was attached to each agitator so that the PLT bag remained fixed and in-frame relative to the camera. Thirty second segments were recorded in triplicate at 30 frames per second.

Figure 1.

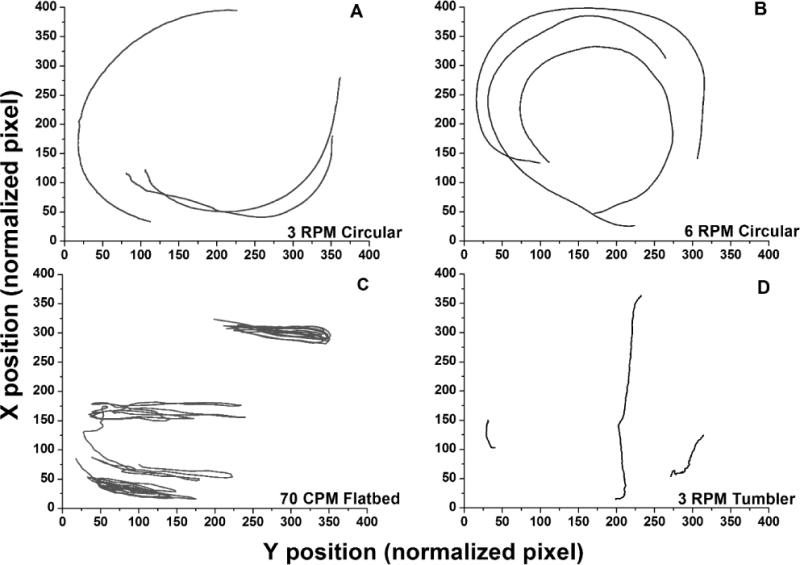
Particle trajectories representative of fluid motion within platelet storage bags obtained with various forms of agitation (n=3 timed collections): A) 3-RPM circular rotator (Model 348, Fisher Scientific, Pittsburgh, PA), B) 6-RPM circular rotator (MedDev Corp., Los Altos, CA), C) 72-CPM flatbed agitator (PF15h, Helmer Inc., Noblesville, IN) and D) 3-RPM tumbler-type rotator. Note that tumbler-type rotation was achieved by affixing the PLT bag to the exterior frame of the 3-RPM circular rotator. The corners of the PLT storage bags were secured to the frame to prevent folding. Tracks represent three particles in each bag followed for 200 image frames corresponding to 6.7 seconds. Longer tracks reflect faster fluid flow. RPM = rotations per minute; CPM = cycles per minute.

Image analysis

Videos were contrast enhanced and analyzed for particle tracking using ImageJ plugins [12,13] with results plotted in Excel (Microsoft Corp., Redmond, WA). Approximately 2500 frames were analyzed for each mode of agitation. Pixel size was calculated based on bag reference distances converted to millimeters. Histogram distributions and curve-fitting were done using Origin (OriginLab, Northampton, MA).

Shear definitions and calculations

Estimations of maximum shear stress and shear rate were made using the sustained maximum measured fluid velocities, vmax. At vmax for the various geometries, laminar flow is expected (Reynolds number < 2000), resulting in a parabolic fluid shape profile between bag walls. The vmax in this profile occurs at the midpoint of fluid height. The velocity profile (and vmax) changes with time, making it difficult to measure the velocity profile directly. However, the velocity profile producing the highest shear stress is determined by the maximum vmax. The determination of the appropriate cutoff of velocity for an estimation of the maximum vmax is based on the observation that velocities with a frequency of < 1% have low precision (see Results), corresponding to unreliable events that occur infrequently.

Wall shear stress was calculated from the following equation: T = −μ(dv/dr) [14], where T is the shear stress, μ is the viscosity, v is fluid velocity, and r is the distance from the bag surface. For laminar flow, shear rate = 2*vmax/R, where R = midpoint of thickness. The maximum reliably observed speed was used as vmax and the midpoint fluid thickness of a full PLT bag was estimated at 1.5 mm. Shear stress (dv/dr) was determined by multiplying by viscosity (μ_water at 22°C = 0.955 cP) [15]. Note that since only the magnitude component of the velocity is relevant in this analysis, data are presented as ‘speed’.

Statistical Analysis

Mean particle speeds were compared using the Kruskall-Wallis and Mann-Whitney U tests. P-values less than 0.05 were considered significant.

RESULTS AND DISCUSSION

Particle paths obtained with agitation, representing fluid motion, are presented in Figure 1. The particle paths shown represent fluid motion relative the surface of the bags, which is the determinant of shear forces experienced by components in the fluid. Increasing the speed of circular agitation from 3 to 6 RPM resulted in 72% larger mean particle path lengths (124.6 mm vs 214.4 mm/6.7 sec). Significant differences were also noted in the distribution of particle speeds (Figure 2). Mean particle speeds generated by flatbed agitation (89.0 mm/s) were significantly higher than those obtained with other forms of agitation (P≪0.0001). The greatest difference observed was between flatbed and 3-RPM tumbler-type agitation, with 24.7-fold greater speeds for flatbed agitation (P<0.0001). Shear rate was substantially higher with flatbed as compared with the other modes of agitation (Figure 2). The rank order for shear rate was the same as noted for particle speeds. The shear rate values calculated for flatbed agitation (378 s⁻¹) were 7.3-fold higher than tumbler agitation (24 s⁻¹). The calculated wall shear stress corresponds to 0.23 dyn/cm² for tumbler-type agitation versus 3.61 dyn/cm² for flatbed agitation (Figure 2).

Figure 2.

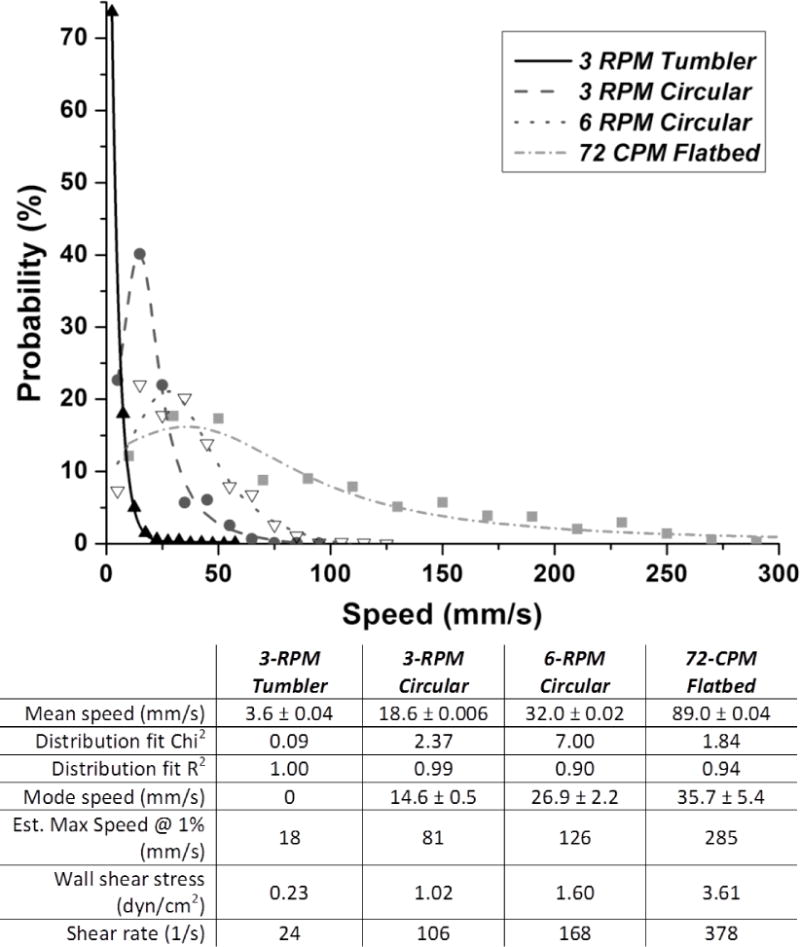
Normalized probability distribution of velocities for particles obtained with various forms of agitation showing higher velocities with flatbed agitation versus circular or tumbler-type agitation. Curves were fit to cumulative data from the triplicate video recordings. Distribution was best described by simple exponential distribution for tumbler data and by Lorentzian distribution for other modes. Table values are derived from curve fits and show +/− SE for mean and mode. Note exponential decay has mode 0 by definition. Abbreviations: RPM = rotations per minute; CPM = cycles per minute.

Based on our analysis, 3-RPM tumbler-type agitation created the lowest particle speeds, shear stress, and rate, while flatbed 72-CPM agitation generated the highest. The sustained shear rate calculated for flatbed agitation was higher than that experienced by PLTs in normal veins, estimated at 20–200 s^-1 [11]. Whether this contributes to PLT activation or damage during storage, however, remains to be examined. The use of water rather than PLT concentrates allowed better standardization of experimental conditions; our intent was to isolate the effect of agitation mode from other variables. We predict that PLT-PLT interactions inside actual PLT concentrates may increase shear stresses, although the relative effect should remain the same. In conclusion, our findings suggests that flatbed agitation is more likely than other modes to contribute to shear-associated PLT degradation or activation, particularly with containers used for whole blood-derived PLTs. The applicability to apheresis-unit containers is not known, and remains to be determined.

Although our findings appear to conflict with older agitation studies [1–10], previous investigations were performed using PLT containers with limited oxygen permeability. As such, adequate gas exchange may have required aggressive agitation. Given the improved permeability of modern PLT bags, findings presented herein suggest that a re-consideration of the optimal mode of PLT storage is in order.